
Local Regression based Colorization Coding
Paul Oh
1
, Suk Ho Lee
2
and Moon Gi Kang
1
1
Institute of BioMed-IT,Energy-IT and Smart-IT Technology(BEST), Yonsei University,
134 Shinchon, Seodaemun-Ku, Seoul, South Korea
2
Dept. of Software Engineering, Dongseo University, 47 Jurye-ro, Sasang-Ku, Busan, South Korea
Keywords: Colorization, Linear Regression, Colorization Matrix, Color Image Compression.
Abstract: A new image coding technique for color image based on colorization method is proposed. In colorization
based image coding, the encoder selects the colorization coefficients according to the basis made from the
luminance channel. Then, in the decoder, the chrominance channels are reconstructed by utilizing the
luminance channel and the colorization coefficients sent from the encoder. The main issue in colorization
based coding is to extract colorization coefficients well such that the compression rate and the quality of the
reconstructed color becomes good enough. In this paper, we use a local regression method to extract the
correlated feature between the luminance channel and the chrominance channels. The local regions are
obtained by performing an image segmentation on the luminance channel both in the encoder and the
decoder. Then, in the decoder, the chrominance values in each local region are reconstructed via a local
regression method. The use of the correlated features helps to colorize the image with more details. The
experimental results show that the proposed algorithm performs better than JPEG and JPEG2000 in terms of
the compression rate and the PSNR value.
1 INTRODUCTION
Colorization refers to the method of colorizing the
monochrome image using only a few number of
color components. In this method, the chrominance
components can be reconstructed with a few number
of colorization coefficients combined together with
the luminance channel. In contrast, colorization
based coding makes use of the fact that the numbers
required to colorize the luminance channel is small,
and tries to select the colorization coefficients in the
encoder which give the best colorization result in the
decoder.
(Cheng and Vishwanathan, 2007) utilizes a
segmentation method and selects the pixels that
represent the colors of the segmented regions
iteratively. But there is no way to reduce the
redundancy of the initially selected representative
pixels. (Ono at al., 2010) reduces the redundancy of
the representative pixel set and extracts further
required pixels for colorization. However, the final
result relies on the randomness of the initially
chosen representative pixels. Furthermore, the
Levin’s colorization process has to be carried out for
each iteration step.
(Lee, at al., 2013) constructs a colorization
matrix which consists of colorization basis by using
a multi-scale meanshift segmentation method. Then,
by solving the L
0
minimization problem, the
optimum colorization coefficients for colorization
are selected. The quality of the output color image is
dependent on how well the colorization matrix is
designed.
In this paper, we propose a novel approach that
designs the colorization matrix based on the use of
linear regression. The proposed method is based on
the fact that the distribution of the chrominance
components in a local region are somewhat
correlated with that of the luminance components.
Therefore, the chrominance components can be
estimated from the luminance components using a
linear mean square error (LMSE) estimator. The
parameters minimizing the LMSE are obtained from
the L
0
minimization problem with respect to the
proposed regression based colorization matrix. As
can be seen from the experimental results, the
compression rate and the quality of the reconstructed
color image becomes good and outperforms those
from the JPEG and the JPEG2000 standard schemes.
153
Oh P., Lee S. and Kang M..
Local Regression based Colorization Coding.
DOI: 10.5220/0004728401530159
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 153-159
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORKS
2.1 Levin’s Colorization
(Levin et al., 2004) proposes an algorithm that
reconstructs the color image from the monochrome
luminance image with a few representative pixels
containing chrominance information. It is based on
the assumption that neighbouring pixels in the
chrominance channel have similar values if they
have similar values in the luminance channel. Let y
denote the luminance vector, u denote the
chrominance vector to be reconstructed, and x is a
sparse vector which has chrominance value only at
the positions of the representative pixels. Then, the
cost function of (Levin et al., 2004) is defined as
2
)( Auxu J
,
(1)
where
WIA
,
I
is a n by n identity matrix, n is
the size of
u
, and
W
is an n by n matrix composed
of weighting components
rs
ω
defined as
otherwise
Ωif0
rs
rs
ω
r
ω
,
(2)
22
2/))()((
r
σsr
rs
eω
yy
.
(3)
Ω
is the set of the representative pixels,
rs
ω is the
weight between
)(ry
and
)(sy
which are the
luminance pixels at
r and s position, and
r
σ
is a
variance of luminance in the 8-neighbourhood pixels
of position
r. To minimize the cost function defined
in Eq. (1),
u
can be solved directly as
xAu
1
(4)
which is due to the fact that
A
is invertible, a fact
proved in previous works.
The matrix
A
is constructed from the luminance
y
and the representative pixels, and
varies for different
sets of representative pixels.
2.2 Colorization Coding using
Optimization
As mentioned in the previous section the selection of
the representative pixels affects the reconstruction of
the color image. Colorization coding tries to choose
a set of representative pixels in the encoder, which
size is small and which gives a good colorization
result in the decoder.
In (Lee, at al., 2013), the colorization process is
generalized using the colorization matrix
C
,
as
following:
Cxu
.
(5)
The Levin’s colorization algorithm can be
expressed by letting
C
equal to
1
A
. Furthermore,
in (Lee, at al., 2013), the matrix
C
is not
necessarily square. The extraction of the colorization
coefficients is formulated as an
L
0
minimization
problem
Cxux
x
s.t.,minarg
0
.
(6)
To satisfy the restricted isometry property (RIP)
condition (Candés et al, 2005) which guarantees that
the solution from the
L
1
minimization is equivalent
to that from the L
0
minimization, a Gaussian random
matrix
G
R
is multiplied to both sides of equation in
Eq. (6) as following:
CxRuRx
x
GG
s.t.,minarg
0
.
(7)
Then, Eq. (7) can be changed into an L
1
minimization problem:
CxRuRx
x
GG
s.t.,minarg
1
.
(8)
The problem in Eq. (8) can be solved by Basis
Pursuit (Chen at al., 1998) or Orthogonal Matching
Pursuit (Tropp and Gilbert, 2007). Actually, (Lee, at
al., 2013) solves the minimization problem
L
0
2
s.t.,minarg xCxu
x
(9)
to set a limit on the number of colorization
coefficients, where
L is a positive number
controlling the desired compression rate.
The colorization matrix is constructed directly
using the multi-scale meanshift segmentation
(Comaniciu and Meer, 2002) on the luminance
channel. The luminance channel is segmented with
kernels of different bandwidths and photometric and
geometric distance weights.
Thus, the colorization matrix can be expressed as
k
CCCC ,,,
21
,
(10)
where
l
C
is a sub matrix constructed from a
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
154
meanshift segmentation of scale l. Here, the entries
of the colorization matrix are either 1 or 0 depending
on whether the corresponding pixel belongs to the
segmented region or not.
3 PROPOSED METHOD
In this paper, we change the entries of the
colorization matrix such that the correlation in the
distribution of the values in the luminance channel is
taken into account. We also show that this is equal
to perform a total regression on the local sub regions.
Similar to the method in (Lee, at al., 2013), the
meanshift segmentation algorithm is performed on
the luminance channel in the encoder to produce
regions from which the colorization vectors are
generated. The meanshift segmentation is performed
using kernels of different bandwidths, where the
different bandwidths are generated using different
photometric and geometric weights.
The colorization matrix C is composed of k sub
matrices, where each sub-matrix corresponds to a
certain scale. Each sub-matrix
l
C
is made up by
using the segmentation result of the scale-l
meanshift segmentation. Denoting the number of
segmented regions corresponding to the scale l by
l
n
, the sub matrix
l
C
can be expressed as
l
nllll 2,2,1,
,,, cccC
.
(11)
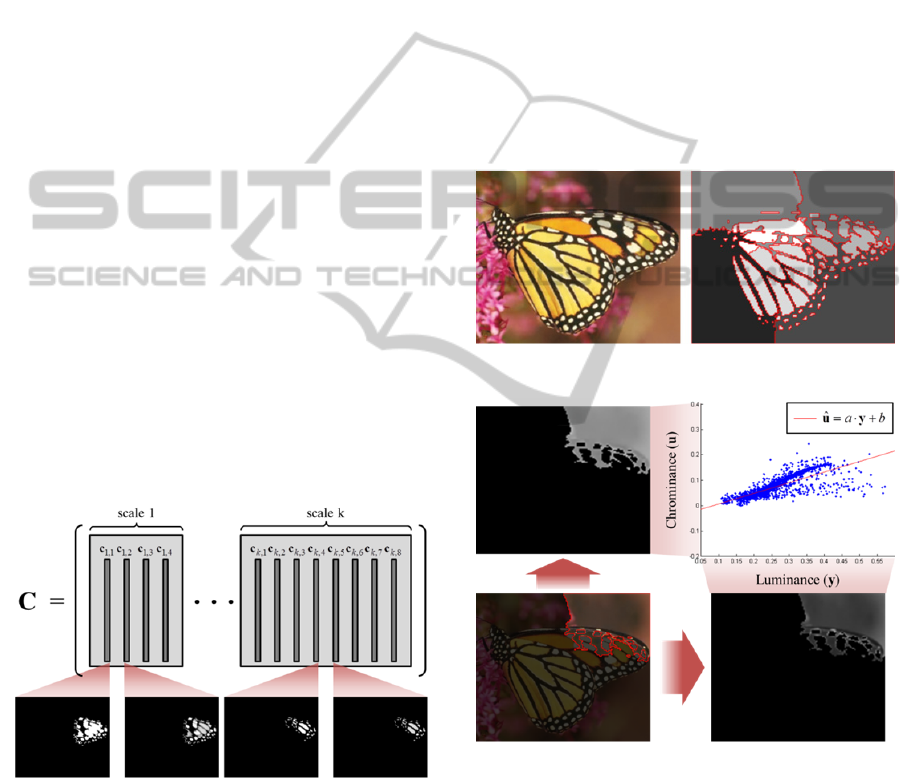
Figure 1: Construction of colorization matrix.
The main difference between the proposed
method and the method in (Lee, at al., 2013) is that
we construct two types of colorization vectors for
each segmented region. The first type consists of the
value 1 and 0, where the value 1 is assigned to the
segmented regions and 0 for the others. The second
type replaces the value 1 with the luminance value at
the same position in the luminance channel and 0 for
the others. The type 1 vectors are placed at the odd
positions in the sub-matrix
l
C
and type 2 vectors are
placed at the even places:
otherwise0
Ωif1
)(
12,
l
i
il
j
jc
,
(12)
and
otherwise0
Ωif)(
)(
2,
l
i
il
jj
j
y
c
.
(13)
The rationale for adding colorization vectors of
type 2, i.e., the vectors expressed in Eq. (13), is
based on the assumption that the chrominance
components have a similar distribution as the
luminance components in the same local region.
Figure 2: single scale meanshift segmentation.
Figure 3: Linear regression of the chrominance function
versus the luminance function in a local region segmented
from Figure 2.
We demonstrate this fact using an exemplary
result. Figure 2 shows the segmentation result using
meanshift segmentation with a certain scale. Figure
3 illustrates the distribution of the chrominance
values versus the distribution of the luminance
values for the right-top segmented region in Figure 3.
It can be observed that the chrominance values
are correlated with the luminance values.
LocalRegressionbasedColorizationCoding
155

Furthermore, it can be observed that the correlation
is nearly linear.
Therefore, the correlation can be expressed by a
line estimated by the linear mean square error
(LMSE) estimator. Then, the chrominance
components can be estimated from the luminance
components by the following linear equation:
1yu
ˆ
ba
,
(14)
where
yu
y
yu
μaμba ,
)var(
),cov(
,
(15)
and
1
denotes the vector having the same size as
y
and with all the entries having the value 1.
Here,
u
μ
is the mean of the chrominance
components, and
y
μ
is the mean of the luminance
components. The object function to be minimized
for each segmented region is
2
mlmlml
e
,,.
u
ˆ
u
,
(16)
where the subscript
ml,
denotes the region
corresponding to the
m
th basis vector of the scale -l
sub matrix. The local approximated chrominance
function based on the linear model in Eq. (14) can be
expressed as
mlmlmlmlml
ba
,,,.,
1yu
ˆ
.
(17)
Now we can observe the fact that the vector
ml ,
y
corresponds to the vector
il 2,
c
in Eq. (13) and
the vector
ml ,
1
to the vector
12, il
c
in Eq. (12).
Therefore, by solving the problem in Eq. (9) with the
matrix containing the colorization vectors in Eq. (12)
and Eq. (13), we are actually computing the linear
coefficients
mlml
ba
,.
,
of the local linear regression
model. However, since the minimization problem of
Eq. (9) produces the coefficients that minimize the
total error in the chrominance differences between
the original and the reconstructed color image, the
linear coefficients are computed to minimize the
following total error in the linear regression model:
lm
ml
eE
.
.
(18)
We also use an initial color reconstruction
method to further reduce the compressed file size.
For the sub-matrix corresponding to scale 1, all the
coefficients corresponding to all the basis vectors in
the sub-matrix are extracted in the encoder and sent
to the decoder. Then, in the decoder, an initial
reconstruction of the color components is done using
these coefficients. This initial reconstruction of the
color components covers the whole domain of the
reconstructed color image, and thus prevents that
some regions become uncoloured. Furthermore,
since all the coefficients are sent for the sub-matrix
of scale-1, the coefficients can be sent in a pre-
defined order, and therefore, there is no need to send
the position information of the coefficients. This
reduces the size of data to be sent and thus gives a
higher compression rate.
Then, for the residual image, i.e., the image
obtained from the subtraction of the original color
image and the initially reconstructed color image,
the coefficients are extracted by the
L
0
minimization.
The whole system flow of the proposed
algorithm is described in Figure 5. In the encoder,
the original color image is divided into the
luminance channel and the chrominance channels.
The chrominance channels are sub-sampled
according to the 4:2:0 format, since the resolution of
chrominance channels are lower than that of
luminance channel. The luminance channel is
encoded with conventional methods such as JPEG or
JPEG2000. The encoded bit stream is sent to the
decoder, and the decompressed luminance channel is
also sub-sampled to the size of the chrominance
channel. The decompressed and sub-sampled
luminance channel is segmented with the multi-
meanshift algorithm. Then, the type 1 and type 2
colorization basis vectors are constructed for each
segmented region. After that, the initial
reconstruction of the chrominance channels is
performed using the sub matrix of scale-1. Then,
further colorization coefficients are extracted from
the residual image.
The bit stream of the luminance channel and the
colorization coefficients are sent to the decoder. The
bit stream of the luminance channel is decoded and
sub-sampled. Using the decompressed luminance
channel, the colorization matrix is constructed in the
same manner as in the encoder. The colorization
process is performed by multiplying the colorization
matrix and the colorization coefficients sent from the
encoder. Then, the colorized chrominance channels
are up-sampled to the size of the luminance channel.
An inverse YUV conversion of the decompressed
luminance channel and the reconstructed
chrominance channels reconstructs the color image.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
156

Figure 4: Overall system of proposed method.
4 EXPERIMENTAL RESULTS
We compared the results of the proposed algorithm
with those of the JPEG and JPEG 2000 standards.
The relative spatial distance weights to the
photometric distance are set to 1, 2, 4, and 8. For
better performance, extra wavelet basis vectors are
cascaded to the colorization matrix to compensate
for the artifact due to the uncorrelated chrominance
components and the compression error in the
luminance channel.
Three different sized color images are used in the
experiment. The first one is called House (256 by
256 pixel size), the second one is called Cap (256 by
256 pixel size), and the last one is called Butterfly
(294 by 250 pixel size).
We used a total of 200 colorization coefficients
in the encoder. A number of 8, 20, and 14
colorization coefficients were extracted in advance
for the initial color reconstruction for the House,
Cap, and Butterfly image respectively. For pre-
extracted coefficients from initial reconstruction, 16
bits are used for each pixel, i.e., 8 bits per
chrominance value. For the other coefficients,
additional 6 bits are used to index the corresponding
colorization vectors. Thus, 0.570, 0.527, and 0.522,
[kB] are required for encoding chrominance
channels of House, Cap, and Butterfly respectively.
The luminance channels are encoded by JPEG2000
in the experiment. The file sizes of luminance
channel of House, Cap, and Butterfly are 6.05, 3.68,
and 4.08 [kB] respectively.
Table 1: Comparison of file sizes and PSNR values.
Image Method Size(KB) PSNR(dB)
House
JPEG 6.86 25.2405
JPEG2000 6.64 26.7628
Proposed 6.62 26.8898
Cap
JPEG 4.27 30.0350
JPEG2000 4.20 31.1059
Proposed 4.20 31.5197
Butterfly
JPEG 4.80 23.8253
JPEG2000 4.63 25.7853
Proposed 4.60 25.9530
For evaluating the performance of each method,
the PSNR measure is used. Table 1 demonstrates
that the objective quality of the reconstructed color
image using the proposed method is superior to that
using the JPEG or JPEG 2000 standards. Figure 5 to
Fig. 10 show that the visual quality is better than
those using JPEG or JPEG2000 standards.
LocalRegressionbasedColorizationCoding
157

Figure 5: Experimental results with 256256 “House”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
Figure 6: Zooming results of “House”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
Figure 7: Experimental results with 256256 “Cap”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
Figure 8: Zooming results of “Cap”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
158

Figure 9: Experimental results with 250294 “Butterfly”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
Figure 10: Zooming results of “Butterfly”.
(a) Original. (b) JPEG. (c) JPEG2000. (d) Proposed.
5 CONCLUSIONS
In this paper, we proposed a colorization coding
method based on the analysis of the local correlation
of the luminance and chrominance components as a
linear regression model. We designed two types of
colorization vectors for each segmented region, and
composed the colorization matrix using these
vectors. The proposed algorithm outperforms the
JPEG and JPEG2000 standards in terms of the
compression rate and the PSNR value. If a lossless
coding such as the run-length coding is applied to
the proposed algorithm, the compression rate can be
enhanced.
For future work, extra colorization vectors which
can depict the uncorrelated region between the
luminance and the chrominance components should
be investigated.
ACKNOWLEDGEMENTS
This work was supported by the National Research
Foundation of Korea (NRF) grant funded by the
Korea government (MSIP)
(No. 2012R1A2A4A01003732).
REFERENCES
Cheng, L., and Vishwanathan, S. V. N., (2007). Learning
to compress images and videos. In Proc. Int. Conf.
Mach. Learn., vol. 227., pp. 161-168.
Ono, S., Miyata, T., and Sakai, Y., (2010). Colorization-
based coding by focusing on characteristics of
colorization bases. In Proc. Picture Coding Symp., pp.
230–233
Lee, S., Park, S.W., Oh, P., Kang, M. G., (2013).
Colorization-based compression using optimization.
IEEE Trans. Image Processing, vol. 22. No. 7, pp.
2627-2636
Levin, A., Lischinski, D., and Weiss, Y., (2004).
Colorization using optimization. ACM Trans. Graph.,
vol. 23, no. 3, pp. 689–694.
Chen, S. S., Donoho, D. L., and Saunders, M. A., (1998).
Atomic decomposition by basis pursuit. SIAM J. Sci.
Comput., vol. 20, no. 1, pp. 33–61.
Tropp, J. A., and Gilbert, A. C., (2007). Signal recovery
from random measurements via orthogonal matching
pursuit. IEEE Trans. Inf. Theory, vol. 53, no. 12, pp.
4655–4666.
Candés, E., and Tao, T., (2005). Decoding by linear
programing. IEEE Trans. Inf. Theory, vol. 51, no. 12,
pp. 4203–4215..
Candés, E., and Tao, T., (2006). Near optimal signal
recovery from random projections: Universal encoding
strategies. IEEE Trans. Inf. Theory, vol. 52, no. 12, pp.
5406–5425..
Donoho, D., (2006). Compressed sensing. IEEE Trans. Inf.
Theory, vol. 52, no. 4, pp. 1289–1306.
Comaniciu, D., and Meer, P., (2002). Mean shift: A robust
approach toward feature space analysis. IEEE Trans.
Pattern Anal. Mach. Intell., vol. 24, no. 5, pp. 603–
619.
LocalRegressionbasedColorizationCoding
159
