Quantitative Analysis of Pulmonary Emphysema using Isotropic

Gaussian Markov Random Fields

Chathurika Dharmagunawardhana

, Sasan Mahmoodi

, Michael Bennett

and Mahesan Niranjan

School of Electronics and Computer Science, University of Southampton, Southampton, SO17 1BJ, U.K.

National Institute for Health Research, Southampton Respiratory Biomedical Research Unit, University Hospital

Southampton NHS Foundation Trust, Tremona Road, Southampton, U.K.

Keywords:

Emphysema, Spatially Varying Parameters, Gaussian Markov Random Fields, Tissue Classiﬁcation.

Abstract:

A novel texture feature based on isotropic Gaussian Markov random ﬁelds is proposed for diagnosis and quan-

tiﬁcation of emphysema and its subtypes. Spatially varying parameters of isotropic Gaussian Markov random

ﬁelds are estimated and their local distributions constructed using normalized histograms are used as effec-

tive texture features. These features integrate the essence of both statistical and structural properties of the

texture. Isotropic Gaussian Markov Random Field parameter estimation is computationally efﬁcient than the

methods using other MRF models and is suitable for classiﬁcation of emphysema and its subtypes. Results

show that the novel texture features can perform well in discriminating different lung tissues, giving compar-

ative results with the current state of the art texture based emphysema quantiﬁcation. Furthermore supervised

lung parenchyma tissue segmentation is carried out and the effective pathology extents and successful tissue

quantiﬁcation are achieved.

1 INTRODUCTION

Emphysema is a critical lung disease causing exten-

sive lung tissue destruction and is currently emerg-

ing as a worldwide health problem. The main causes

of emphysema are smoking or inhaling toxic air and

a genetic disorder known as alpa-1-antitrypsin de-

ﬁciency. The pulmonary function test (PFT) also

known as spirometry and computed tomography (CT)

analysis are the two common approaches used to di-

agnose emphysema. PFT is a clinical test associated

with measuring breath volumes. High resolution CT

(HRCT) image analysis is more informative than PFT

and useful for analyzing pathology distribution, as-

sessing severity and identifying a wide variety of sub

type patterns of pulmonary lung diseases.

The amount of information present in CT imag-

ing have largely increased with the recent technical

developments of medical equipment. Therefore com-

puter aided diagnosis (CAD) of CT scans is widely

preferred (Litmanovich et al., 2009). Partially or

fully automated CAD methods are fast, precise and

highly reproducible compared to subjective visual as-

sessment in medical image processing (Madani et al.,

2001). CAD of emphysema mainly depends on tex-

ture features and intensity information.

In this paper we propose a new texture feature for

emphysema quantiﬁcation based on isotropic Gaus-

sian Markov random ﬁelds (IGMRF). In Markov ran-

dom ﬁeld (MRF) feature extraction, the parameters of

MRF model are used as texture features. The applica-

tion of model based statistical features to emphysema

quantiﬁcation is not commonly used because of the

relatively high computational cost. Also the model

parameters are spatially constant, therefore, subtle

pattern variations which are crucial in tissue discrim-

ination are smoothen out.

However, the parameter estimation of IGMRFs is

simple and fast compared to other MRFs and ide-

ally suited for isotropic texture representation. In ad-

dition, we formulate the novel texture feature based

on IGMRF characterized by spatially varying param-

eters addressing above issues in model based fea-

ture extraction. Spatially varying parameter estima-

tion is closely related to the structural feature extrac-

tion. Therefore, the method itself is a semi parametric

method and integrates the best of both statistical and

structural features.

In this study, distributions of spatially varying pa-

rameters of IGMRFs constructed by normalized his-

tograms are used as a discriminative texture feature.

The approach is used to classify between healthy

Dharmagunawardhana C., Mahmoodi S., Bennett M. and Niranjan M..

Quantitative Analysis of Pulmonary Emphysema using Isotropic Gaussian Markov Random Fields.

DOI: 10.5220/0004728900440053

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 44-53

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

lung tissue (NT) and two sub types of emphysema,

namely centrilobular emphysema (CLE) and parasep-

tal emphysema (PSE). The experimental results show

that normal lung and emphysema, including its sub-

types, can be efﬁciently discriminated using IGMRF

features. The results are also compared against the

state of the art LBP based emphysema quantiﬁcation

(Sørensen et al., 2010) and comparable performances

are achieved.

We also perform supervised lung tissue segmen-

tation on a CT slice dataset (Sørensen et al., 2013)

and achieve satisfactory lung parenchyma pathology

distributions and quantiﬁcation of emphysema and its

subtypes. The quantitative results correlates with the

available labellings of visual inspection by experi-

enced radiologists and emphysema index (EI). The

novel texture features successfully discriminate the

healthy lung tissue from emphysema and can be used

in sub type diagnosis.

The remainder of this paper is organized as fol-

lows. In section 2 currently used methods of emphy-

sema quantiﬁcation are discussed. IGMRF model is

introduced in section 3 and texture feature formula-

tion is explained in section 4. Experimental results

and discussions are elaborated in section 5 and ﬁnally,

conclusions are given in section 6.

2 BACKGROUND

CAD approaches based on lung CT scans for em-

physema quantiﬁcation can be categorized into inten-

sity (CT density) based methods and texture based

techniques. Under intensity based techniques, many

studies have been carried out to ﬁnd an absolute

threshold value below which emphysema is consid-

ered to be present. (Muller et al., 1988) introduced

a method known as ‘emphysema index’ or ‘density

mask’ which measures the relative amount of lung

parenchymal pixels that have attenuation values be-

low -910 HU. Further studies have obtained the op-

timal threshold value for emphysema quantiﬁcation

as -950HU (Litmanovich et al., 2009). An adaptive

thresholding method that also incorporates the infor-

mation of pixel locations on the lung has been intro-

duced by (Hara et al., 2004). Another approach has

been proposed based on mean lung density and voxel

dimensions (Coxson et al., 1999).

Intensity based CAD techniques usually suf-

fer from problems caused by monotonic intensity

changes. This may occur due to several reasons, for

example, the inﬂuence of contrast materials and de-

gree of inspiration of the lung while scanning (Muller

et al., 1988). Secondly there is a degree of corruption

in the CT image due to noise, arising from strict limi-

tations on radiation power that can be applied on a pa-

tient (Sprawls, 1995). Techniques solely based on in-

tensity are highly sensitive to the noise. (H

ame et al.,

2013) proposed a hidden Markov measure ﬁeld model

to obtain more promising emphysema index measures

than standard densitometric approaches showing ro-

bustness to noise resulting from reconstruction ker-

nels. However, intensity and texture based integrated

approaches are the better choice for pulmonary lung

disease analysis using CT (Sørensen et al., 2010).

Texture based CAD techniques are a successful

methodology to use in assessing the presence and dis-

tribution of emphysema and its subtype patterns. The

texture features can be categorized as statistical, spec-

tral and structural features (Litmanovich et al., 2009).

(Uppaluri et al., 1999) used a method known as adap-

tive multiple feature method (AMFM) which assessed

22 independent statistical features in order to classify

different lung tissue patterns. This approach is further

improved by extending it from 2D to 3D by (Xu et al.,

2006), to classify emphysema and early smoking-

related pathologies. (Mishima et al., 1999) attempt to

detect early emphysema on the basis of fractal analy-

sis. Spatial gray level dependence method (SGLDM),

Gray level run length method (GLRLM) and Gray

level Difference Method (GLDM) have also been

used as statistical feature extraction methods for em-

physema diagnosis (Vasconcelos et al., 2010). (De-

peursinge et al., 2010) have used the density his-

togram and quincunx wavelet frame coefﬁcients with

number of pixels below -1000 HU as the feature set to

evaluate emphysema classiﬁcation performance with

different classiﬁers. In (Kim et al., 2009) statistical

texture features as well as shape features are also em-

ployed in lung disease classiﬁcation.

(Sluimer et al., 2003) have used Gaussian, Lapla-

cian of Gaussian and ﬁrst and second order deriva-

tives of Gaussian ﬁlters in different scales and have

obtained the histogram of responses as spectral tex-

ture features. (Depeursinge et al., 2007) have used

discrete wavelet frame (DWF) to classify lung tissue

types including emphysema. However, ﬁlter based

methods require selection of an optimal ﬁlter set and

employing reasonable sizes for ﬁlter kernels.

Structural features encapsulate information on

structures of the texture such as arrangements of tex-

ture primitives. A texton based method has been in-

troduced in (Gangeh et al., 2010). (Sørensen et al.,

2010) applied rotational invariant local binary pat-

terns (LBP) for successful emphysema quantiﬁcation.

This method acquires very compelling results and can

be considered as the current state of the art texture

based emphysema quantiﬁcation method.

QuantitativeAnalysisofPulmonaryEmphysemausingIsotropicGaussianMarkovRandomFields

In the present study we integrate the essence of

statistical and structural properties of texture by for-

mulating a hybrid feature extraction scheme. There-

fore, these features can encapsulate the information

about variations in the texture primitive and its ar-

rangement patterns and also information about sta-

tistical dependencies and pixel interactions. IGMRF

model is used to capture neighbor dependencies and

spatially varying parameter estimation is used to cap-

ture structural information.

3 IGMRF MODEL

Gaussian Markov Random Field (GMRF) is an im-

portant subclass of MRFs and gives simpliﬁed ways

of parameter estimation with less computational bur-

den compared to that of MRFs (Rue and Held, 2005;

Manjunath and Chellappa, 1991; Mahmoodi and

Gunn, 2011). A local conditional probability distri-

bution of GMRF model encapsulates spatial depen-

dencies between a pixel and its neighbors, associat-

ing them in a Gaussian functional form (Petrou and

Sevilla, 2006). Let Ω = {(i, j)|1 ≤i ≤H,1 ≤ j ≤W}

represent the set of grid points on a H ×W regular

lattice corresponding to the pixels in an image region.

The image region on Ω is preprocessed to have zero

mean. The intensity value of the pixel at s = (i, j)

position is given by y

. The local conditional model

of GMRF describing probability of y

given its neigh-

bors y

s+r

, r being relative neighbor position on the

neighborhood

is given by,

p(y

s+r

,α

,σ, j ∈

) =

√

2πσ

exp







−

2σ

−

∑

r∈

¯y

s+r







(1)

where α

is the interaction coefﬁcient which mea-

sures the inﬂuence by a neighbor intensity value at the

neighbor position r. The neighbor pixels in symmet-

ric positions about the considered pixel are assumed

to have identical parameters, i.e. α

= α

−r

(Petrou

and Sevilla, 2006), therefore ¯y

s+r

= (y

s+r

+ y

s−r

), the

sum of two neighbor values situated in symmetric

neighbor positions with respect to the pixel. Then

is the asymmetric neighborhood such that if r ∈

then −r /∈

(Zhao et al., 2007).

IGMRF is a special case of GMRF also known

as circular symmetric GMRF and further simplify

the GMRF model (Kashyap and Khotanzad, 1986).

IGMRFs model non directional isotropic textures in

a simpliﬁed rotational invariant framework with only

two model parameters. Parameter estimation is sim-

ple and fast compared to other MRF models because

Figure 1: Multiresolution circular neighborhood system

corresponding to (R,P) = {(1, 8),(2,16),(3, 24)}.

Figure 2: The ﬁve nearest neighborhood samples N

(k ∈

Ω

) corresponding to (R,P) = (1,8) at pixel s which is used

for spatially varying parameter estimation.

solutions for parameters can be found analytically

and without requiring any matrix inversion. IGMRF

model is given by,

p(y

s+r

,α, σ,r ∈N

) =

√

2πσ

exp







−

2σ

−α

∑

r∈N

s+r







(2)

α and σ are the model parameters to be esti-

mated. y

s+r

are the neighbors in the circular symmet-

ric neighborhood of y

and N

= {r|r ∈

}∪{r|−r ∈

}. Circular neighborhoods used in this study is

shown in ﬁgure 1. R is the radius and P is the number

of neighbors in a circle of radius R. This representa-

tion is similar to the neighbor selection in multireso-

lution LBP (Ojala et al., 2002). Therefore we name

this neighborhood system as multiresolution circular

neighborhood system and represent by (R,P) variable

setting. In each resolution (R,P), the model parame-

ters are separately estimated. The α parameter rep-

resents the strength of interaction on center pixel by

neighbors in a certain resolution and the σ parameter

corresponds to the roughness of the texture. Bilinear

interpolation is used to estimate the neighbor values

at off grid positions similar to (Ojala et al., 2002).

For the problem of emphysema and lung tissue

discrimination this model is more appropriate because

the texture patterns involving the problem have less

directional qualities and more isotropic qualities (see

(Sørensen et al., 2013)). Therefore with a minimal

computational cost, the beneﬁts of statistical model

based feature extraction can be applied on to the prob-

lem of emphysema discrimination.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

Figure 3: Parameter histogram texture feature formulation.

3.1 Parameter Estimation

The choice of using least squares estimation (LSE)

for parameter estimation for GMRF is suggested by

(Manjunath and Chellappa, 1991). LSE is used here

for estimating parameters of the model. The main as-

sumption behind the LSE method is that because (2)

is Gaussian, the estimated value of y

is more proba-

ble to be the mean value of the function (Petrou and

Sevilla, 2006). Therefore from the linear least square

sense the residual will be,

= y

−α

∑

r∈N

s+r

(3)

For least square ﬁtting, given a stationary texture,

sample neighborhoods of the texture are extracted by

linear scanning of the region. Overlapping neighbor-

hoods are also allowed (Li, 2009). When N samples

(≤ H ∗W ) of neighborhoods representing the texture

is given the least square solution is,

α = arg min

∑

s∈Ω

= arg min

∑

s∈Ω

−α

∑

r∈N

s+r

(4)

By setting the ﬁrst derivative to zero the parameter

value can be obtained as,

α =

∑

s∈Ω



∑

r∈N

s+r



∑

s∈Ω



∑

r∈N

s+r



(5)

The variance parameter of the model is then cal-

culated by,

∑

s∈Ω

−α

∑

r∈N

s+r

(6)

The simple forms of solutions obtained for model

parameters given by (5) and (6) can be easily imple-

mented and efﬁciently computed.

4 FEATURE FORMULATION

Spatially varying parameter estimation is performed

here to capture the structural and texel level local in-

homogeneity of the texture. Spatially varying param-

eter estimation is sensitive to the subtle changes in

the texture. (Dharmagunawardhana et al., 2012) have

shown the signiﬁcance in employing spatially vary-

ing parameters in model based statistical texture fea-

ture extraction and shown remarkable results on gen-

eral texture segmentation. The local distributions of

spatially varying parameters are better choice for dis-

criminative texture features than using spatially con-

stant GMRF parameters.

Localized small model estimation is performed

here to estimate spatially varying parameters of

the texture image or patch (Dharmagunawardhana

et al., 2012). Small model estimation considers

using local nearest neighborhood samples in the

region Ω

(⊂ Ω), for the estimation process. Here we

use nearest ﬁve neighborhood samples, i.e N

, k ∈

s + (0,0),s + (1,0), s + (−1,0),s + (0, 1),s + (0,−1)

or k ∈ Ω

and ||k − s||

= 1 (Figure 2). At each

pixel, a localized estimation procedure is carried out

similar to estimation method discussed in section 3.1,

using these ﬁve nearest samples (N = 5). Then the

estimated parameter values at pixel s is,

∑

k∈Ω

∑

r∈N

k+r

∑

k∈Ω

∑

r∈N

k+r

(7)

The variance parameter of the model is given by,

∑

k∈Ω

−α

∑

r∈N

k+r

(8)

Estimating the parameter vectors [α

,σ

]

, for all

the pixels in Ω results in two parameter images corre-

sponding to the two model parameters. The normal-

ized histogram of each parameter image is then con-

catenated into one long vector which is used as the

feature vector of the texture image. The number of

bins and the bin range is manually ﬁxed. Hereafter

we refer to these features as parameter histogram fea-

tures and their construction is graphically illustrated

in ﬁgure 3.

This approach can be seen as the inclusion of

structural information into a statistical model based

technique. (Dharmagunawardhana et al., 2012) have

clearly demonstrated that this technique signiﬁcantly

QuantitativeAnalysisofPulmonaryEmphysemausingIsotropicGaussianMarkovRandomFields

Table 1: Confusion matrices for three class classiﬁcation problem involving the classes NT, CLE and PSE. LBP result is

obtained from (Sørensen et al., 2010).

noInt joint LBP

NT CLE PSE

NT 37 19 3

CLE 10 40 0

PSE 4 2 53

NT CLE PSE

NT 57 2 0

CLE 2 48 0

PSE 1 2 56

NT CLE PSE

NT 55 0 4

CLE 1 49 0

PSE 2 1 56

enhances the discriminative power of model based

features, speciﬁcally for texture classiﬁcation and

segmentation purposes.

5 RESULTS AND DISCUSSION

To evaluate the novel texture feature performance

on emphysema diagnosis and quantiﬁcation we use

the online emphysema dataset from (Sørensen et al.,

2013) which has been also used in performance evalu-

ation of LBP and ﬁlter based features (Sørensen et al.,

2010). The database comprises 115 HRCT slices

of size 512 ×512 and 168 of square patches of size

61 ×61 obtained from a subset of slices. The HRCT

slices belong to a study group of 39 subjects includ-

ing non smokers, smokers and smokers with chronic

obstructive pulmonary disease.

Each slice is labeled according to the leading pat-

tern of interest and severity by an experienced chest

radiologist and a pulmonologist. The leading pat-

terns are normal tissue (NT), centrilobular emphy-

sema (CLE), paraseptal emphysema (PSE) and pan-

lobular emphysema (PLE). The severity of each slice

is classiﬁed as no emphysema (0), minimal (1), mild

(2), moderate (3), severe (4) and very severe (5).

Leading pattern of each patch is also available and

there are 59 NT patches, 50 CLE patches and 59 PSE

patches. In this study, only NT, CLE and PSE classes

are used. However, clinical test results on PFT tests

are currently unavailable for the dataset. Therefore,

correlations of the results with emphysema index and

diagnosis from visual inspection by experience radi-

ologists are considered.

5.1 Emphysema Classiﬁcation

First, the patch dataset is used in a classiﬁcation

framework to identify the discriminative ability of the

texture features. (Sørensen et al., 2010) reported sat-

isfactory classiﬁcation performance for this dataset

with joint LBP using the parameter setting (R,P) =

{(1,8), (2,16)} and a region of interest (ROI) of

size 31 ×31. Following (Sørensen et al., 2010), the

present study also employs 31 ×31 ROIs extracted

from each 61 ×61 patches. For histogram calculation

Figure 4: Leave one subject out classiﬁcation accuracy for

three class problem, NT,CLE and PSE.

bins = {10,20,30,40,50}are evaluated and bins = 40

is selected in the following experiments. The α pa-

rameter bin range is set from −1 to +1. The σ pa-

rameter bin range is set from 0 to 100. The leave

one subject out classiﬁcation technique discussed in

(Sørensen et al., 2010) with nearest neighbor classiﬁer

is used. In each leave one subject out trial, assigned

labels are stored and in the end of all trials assigned

labels are matched against the true labels to calculate

the accuracy (Sørensen et al., 2010). The absolute

sum of difference between histograms is taken as the

distance metric.

The performance of parameter histograms with

and without integrating intensity information is ex-

amined. The technique in which parameter his-

tograms are constructed without integrating inten-

sity information is referred to as ‘noInt’ and the

joint intensity-parameter histograms are represented

by ‘joint’ in this paper. Figure 4 shows the clas-

siﬁcation accuracies obtained for three class prob-

lem, NT, CLE and PSE for noInt and joint features

with various neighborhood systems (R,P). The ac-

curacy gradually decreases with increasing resolution

of the neighborhood system suggesting features from

lower resolutions are more signiﬁcant. The case ‘sub-

set’ represents the integrated features from multires-

olution levels of the neighborhood system (R,P) =

{(1,8), (2,16),(3,24)}. Based only on texture infor-

mation, an accuracy of 77.4% can be obtained for the

case ‘subset’. However, integrating intensity vastly

improves the accuracy to 95.8%. This is comparable

with the accuracies reported for LBP features which is

79.2% with only texture information and 95.2% with

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

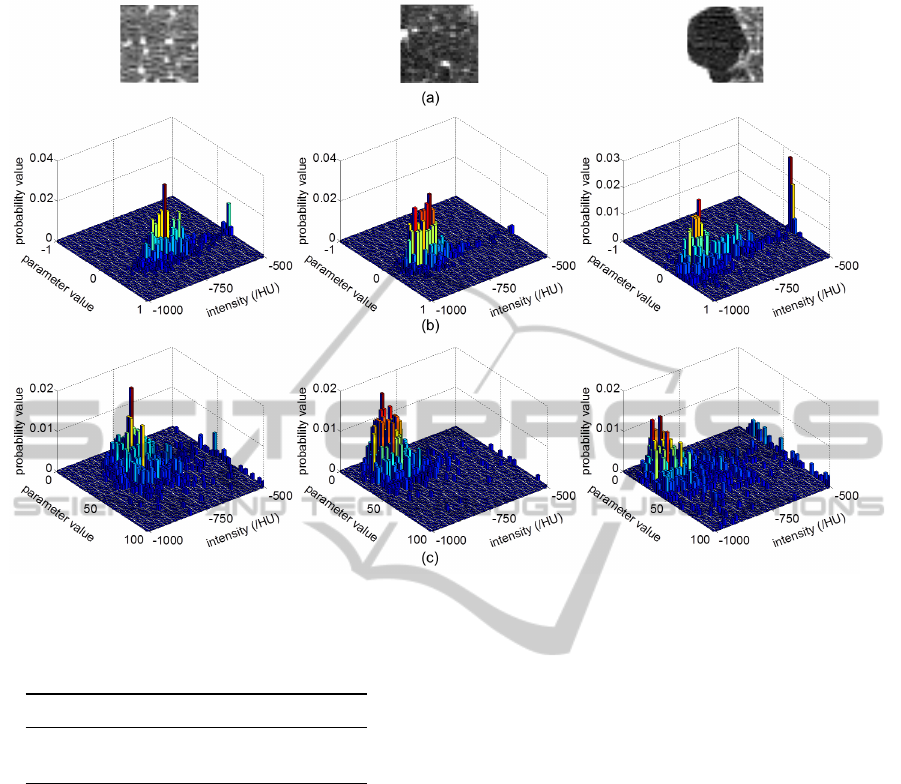
Figure 5: IGMRF parameter histograms. (a) original patches from the three classes NT, CLE, PSE respectively (31 ×31), (b)

α and intensity joint histograms , (c) σ and intensity joint histograms. (R,P) = (1,8) and bins = 40 in each axis are used.

Table 2: Comparison with other GMRF model based texture

feature extraction methods.

joint PL TGMRF

accuracy (%) 94.6 94.0 62.5

time (s) 16.1 50.2 3.09

joint intensity-LBP features (Sørensen et al., 2010).

The confusion matrices obtained for the three

class problem by the proposed features and LBP

method are shown in table 1. The LBP results are

taken from the joint intensity-LBP histogram perfor-

mance reported in (Sørensen et al., 2010). The confu-

sion matrix of noInt features clearly indicate that NT

and CLE classes have higher number of mis-classiﬁed

ROIs as a consequence of disregarding intensity infor-

mation. The joint parameter histogram features and

joint LBP-intensity features perform comparatively

well in discriminating different lung tissues.

Next the performance with other GMRF based

texture features is evaluated for comparison. Table

2 shows the classiﬁcation accuracies for joint param-

eter histogram features proposed here with (R,P) =

(1,8) and bins = 20, parameter local histogram fea-

tures (PL) obtained from the technique in (Dharma-

gunawardhana et al., 2012) with second order neigh-

borhood system and bins = 20 and spatially con-

stant GMRF features (TGMRF) based on (Manju-

nath and Chellappa, 1991) with second order neigh-

borhood system. The joint parameter histogram, PL

features and TGMRF features have a dimensional-

ity of R

2∗bins

, R

5∗bins

and R

respectively. The to-

tal time elapsed for feature extraction of complete

patch dataset in Matlab R2013a environment running

on a 2.67 GHz CPU is also provided. Here, PL and

TGMRF features are integrated with intensity similar

to the joint parameter features.

It can be clearly seen that spatially varying param-

eters are more discriminative compared to spatially

constant features obtained from TGMRF. However

PL is comparatively slower because, ﬁrstly the model

associates many parameters to estimate and secondly

the subsequent histogram construction stage require

more memory and computations. Compared to PL,

the joint parameter histogram features provides faster

feature formulation. The accuracies for joint parame-

ter histogram features and PL are almost similar im-

plying that for this speciﬁc problem IGMRF is sufﬁ-

cient and additional directional information in GMRF

based PL features have not been of much use.

Therefore, based on classiﬁcation performances,

joint feature of IGMRF parameter histograms are a

preferable efﬁcient choice for emphysema and its sub-

QuantitativeAnalysisofPulmonaryEmphysemausingIsotropicGaussianMarkovRandomFields

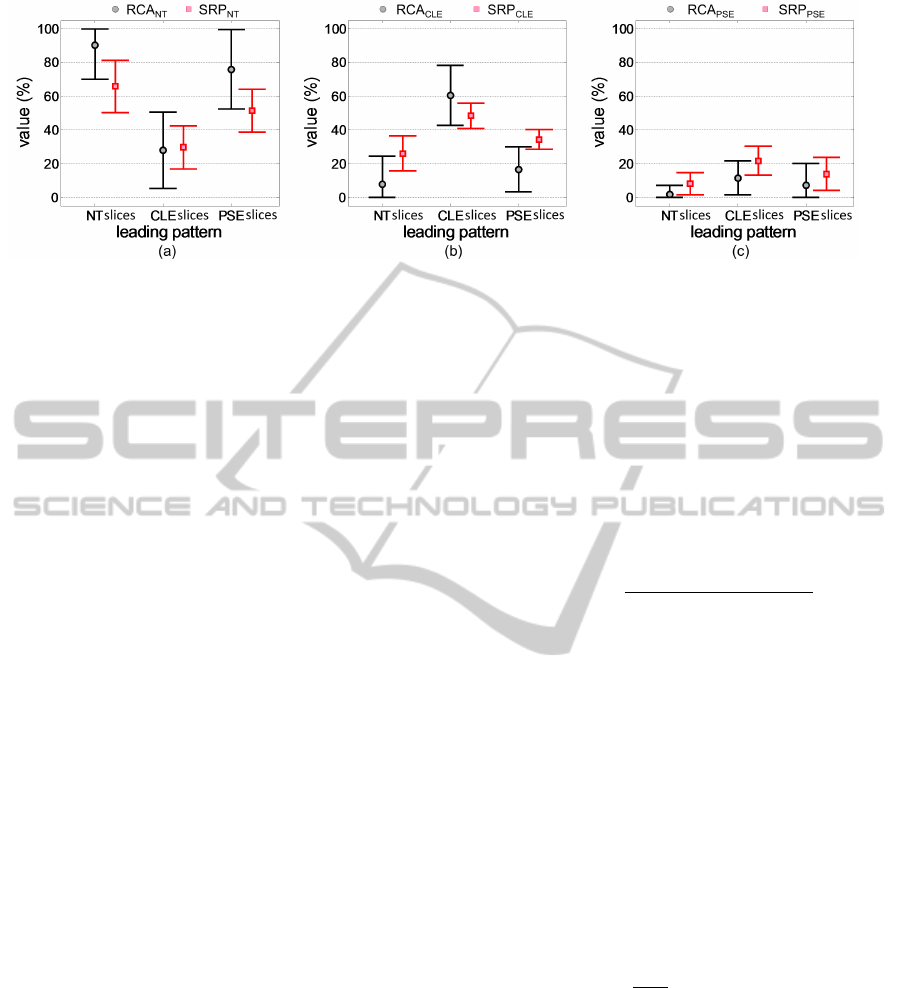
Figure 6: Tissue quantiﬁcation with RCA

and SRP

for each category of slices (NT, CLE and PSE) grouped according to

leading patterns labeled by visual inspection judgments. (a) NT tissue quantiﬁcation, (b) CLE tissue quantiﬁcation, (c) PSE

tissue quantiﬁcation. Note that the error bars are truncated near 0% and 100%.

type diagnosis. Figure 5 shows the joint features of α

and σ parameters of IGMRF. Results could be further

improved by feature selection.

5.2 Emphysema Quantiﬁcation

In this section, we perform lung parenchyma pixel

classiﬁcation of 115 CT slices for emphysema quan-

tiﬁcation. The features extracted from 31×31 labeled

ROIs in section 5.1 are employed as the training mod-

els. The training models obtained from a subset of

PSE ROIs are used. This subset represent moderate

to severe PSE and clearly represent reasonably large

regions of PSE tissue pattern with minimum confu-

sion with NT or CLE class tissue. These PSE ROIs

contains approximately 15% or less near boundary

non parenchymal pixels. This setting of ROIs of PSE

class can employ the prior information that PSE has

high probability of occurrence near the boundary of

the lung parenchyma (Sørensen et al., 2010). During

the slice pixel classiﬁcation all the training patches

belong to the subject of corresponding slice are left

out from training set.

The (R,P) = (1,8) is used with bins = 40 to con-

struct joint parameter histogram features. The 6 slices

out of 115 slices which belongs to class PLE are not

considered because the patch data is unavailable. The

remaining 109 slices with leading patterns NT, CLE

and PSE are employed for tissue quantiﬁcation. Note

that the leading pattern of each slice is available prior

to the quantiﬁcation based on the visual inspection of

experienced radiologists.

First of all, the spatially varying parameters of the

lung parenchyma pixels are estimated. Then a win-

dow of size 31 ×31 is column-wise scanned on the

parameter images and the normalized parameter his-

tograms for each pixel is constructed.

The pixels outside the lung parenchyma is directly

labeled as the background class by thresholding. The

thresholding is based on the knowledge that the CT

density values of lung parenchyma pixels are usually

between −1000HU to −500HU.

Hard and soft classiﬁcation are performed here.

The hard classiﬁcation assigns each pixel a class label

depending on the nearest training model to its feature

vector. The soft classiﬁcation ﬁnds the probability a

pixel belongs to a certain class. We deﬁne the follow-

ing expression to calculate the class probabilities.

p(ω

) =

exp{−D(h

)

}

∑

c=1

exp{−D(h

)

}

(9)

where ω

represent the class and C is the number

of classes. h

is the feature vector of the considered

parenchyma pixel and M

is the nearest feature vec-

tor in the training set to h

from class ω

. D(.) is the

sum of absolute difference distance metric.

The tissue quantiﬁcation is then carried out on

each slice. Two measures are obtained for each slice

by fusing the results of all the lung parenchyma pixels

on it. The relative hard classiﬁcation accuracy RCA

(Sørensen et al., 2010) gives the percentage of lung

tissue belonging to the class ω

. Based on soft classi-

ﬁcation probabilities we deﬁne the soft relative prob-

ability SRP

for a class ω

according to,

SRP

|Ω

∑

s∈Ω

p(ω

) (10)

where Ω

is the lung parenchyma area and |Ω

| is

the number of pixels in the lung parenchyma.

RCA

is a measure about the spatial extent of the

tissue from class ω

. The SRP

measure introduced

here is sensitive to the severe tissue damages localized

in a smaller area which can not be quantiﬁed properly

as a higher degree of tissue damage by RCA

The CT slices are categorized into groups accord-

ing to the leading pattern labellings given by the ra-

diologists. Then the averages and standard deviations

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

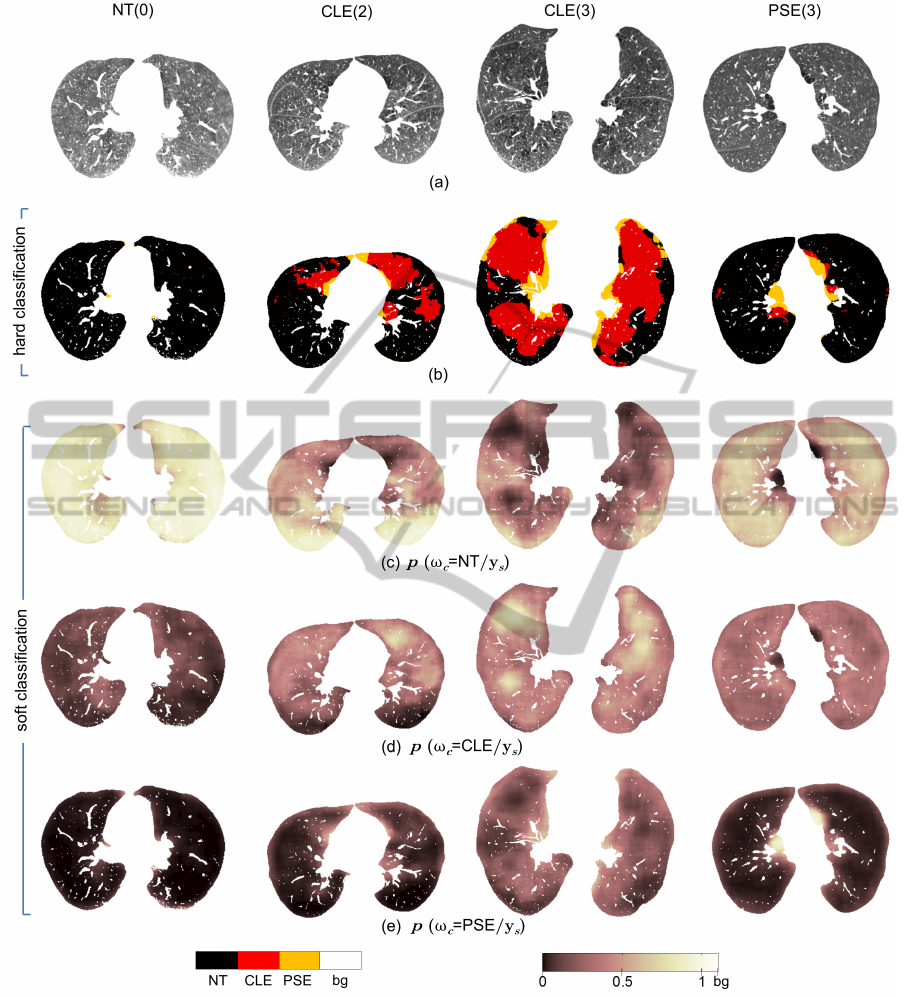
Figure 7: Lung parenchyma pixel classiﬁcation for example slices representing NT, CLE and PSE slice groups. Severity is

indicated in parenthesis. (a) original slices, (b) hard classiﬁcation results, (c) p(ω

= NT /y

) (d) p(ω

= CLE/y

) and (e)

p(ω

= PSE/y

) from soft classiﬁcation. bg - background (pixels outside the lung parenchyma).

of RCA

and SRP

measurements of each catego ry

is calculated separately. Results are shown in ﬁgure

6. The RCA

ωc

and SRP

counts in ﬁgure 6 are con-

sistent with the leading pattern labellings by visual in-

spections. For example, slices having leading pattern

label as NT have a higher RCA

and SRP

counts

and lower RCA

CLE

, RCA

PSE

and SRP

CLE

, SRP

PSE

counts. Most of the slices of PSE group in the consid-

ered slice dataset have minimal or mild PSE except

for one severe PSE slice. Therefore RCA

count

is comparatively high indicating less tissue damage

extent from PSE. However, it is relatively less than

RCA

for NT group.

Furthermore, ﬁgure 6c indicates that slices belong

QuantitativeAnalysisofPulmonaryEmphysemausingIsotropicGaussianMarkovRandomFields

Figure 8: Tissue quantiﬁcation with increasing severity.

to CLE group also have a tendency to contain higher

value of PSE tissue. In real world situation, the CLE

patients have a higher chance of co-existence of CLE

and PSE. The slices belonging to PSE class have a rel-

atively higher mis-classiﬁcations with CLE tissue giv-

ing higher RCA

CLE

and SRP

CLE

compared to RCA

PSE

and SRP

PSE

(ﬁgure 6b and c). RCA

has compara-

tively larger standard deviations (ﬁgure 6). This ex-

plains the relatively low sensitivity of RCA

com-

pared to SRP

for pathology quantiﬁcation.

Figure 7 demonstrates some example lung

parenchyma labeled by using the proposed approach.

The pathology distribution is effectively expressed.

Texture is a regional property, therefore, hard clas-

siﬁcation achieves relatively larger areas of emphy-

sematous tissue than from an intensity based thresh-

olding technique like emphysema index (EI) (Muller

et al., 1988). However, the correlation between to-

tal emphysema tissue count (RCA

CLE

+RCA

PSE

) from

proposed method and EI with −910HU threshold is

large, giving a correlation coefﬁcient of 0.84 (p <

−4

). Moreover, pixels belonging to PSE tissue

are often classiﬁed near the boundary of the lung

parenchyma agreeing to the PSE location dependency

near boundary (Figure 7b). The tendency that the

CLE subjects also have PSE is also clearly reﬂected.

Finally, the severity of the slices and their corre-

sponding tissue percentages are evaluated. The NT

tissue counts RCA

and SRP

are shown in ﬁgure

8. The severity level 5 only has 2 CT slices and is not

considered here. The RCA

and SRP

measures

in ﬁgure 8 gradually reduce with increasing severity.

Therefore the results in ﬁgure 8 have a good correla-

tion with the severity labellings of the slices obtained

by visual inspection.

6 CONCLUSIONS

We have performed emphysema quantiﬁcation using

a novel texture feature which integrates the essence of

model based statistical and structural texture features.

The online available emphysema dataset (Sørensen

et al., 2013) is used here. The proposed texture fea-

ture is used in emphysema classiﬁcation involving the

classes NT, CLE and PSE. These results are compa-

rable with the state of the art texture based LBP em-

physema classiﬁcation. We have also performed su-

pervised lung paremchyma pixel classiﬁcation for tis-

sue quantiﬁcation. The results illustrate convincing

pathology distributions and successful quantiﬁcation

of lung tissues, well correlating with the class and

severity labellings by visual inspection. SRP

mea-

sure obtained from soft classiﬁcation has a higher sen-

sitivity to emphysema pathology quantiﬁcation than

RCA

. Evaluations on other emphysema datasets

and clinical test data are considered in future. Also

feature selection can be greatly helpful to reduce the

higher dimensionality of the features. Nevertheless

proposed feature perform efﬁcient and effective lung

tissue classiﬁcation.

ACKNOWLEDGEMENTS

Authors gratefully acknowledge Dr. Lauge Sørensen

for his kind support and all other researchers who

contributed to making available the online computed

tomography emphysema database. We are also im-

mensely thankful to anonymous reviewers for their

helpful comments.

REFERENCES

Coxson, H. O., Rogers, R. M., Whittall, K. P., Yachkova,

Y. D., Par, P. D., Sciurba, F. C., and Hogg, J. C. (1999).

A quantiﬁcation of the lung surface area in emphy-

sema using computed tomography. 159 (3):851–6.

Depeursinge, A., Iavindrasana, J., Hidki, A., Cohen, G.,

Geissbuhler, A., Platon, A., Poletti, P., and M

uller, H.

(2010). Comparative performance analysis of state-of-

the-art classiﬁcation algorithms applied to lung tissue

categorization. Journal of digital imaging, 23(1):18–

30.

Depeursinge, A., Sage, D., Hidki, A., Platon, A., Poletti,

P. A., Unser, M., and Muller, H. (2007). Lung tis-

sue classiﬁcation using wavelet frames. In Proc. IEEE

Int’l conf. of the Engineering in Medicine and Biology

Society, pages 6259–6262. IEEE.

Dharmagunawardhana, C., Mahmoodi, S., Bennett, M., and

Mahesan, N. (2012). Unsupervised texture segmen-

tation using active contours and local distributions

of Gaussian Markov random ﬁeld parameters. In

Proc. British Machine Vision Conference, pages 88.1–

88.11.

Gangeh, M. J., Sørensen, L., Shaker, S. B., Kamel, M. S.,

Bruijne, M., and Loog, M. (2010). A texton-based

approach for the classiﬁcation of lung parenchyma in

CT images. 13:595–602.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

ame, Y., Angelini, E. D., Hoffman, E. A., Barr, R. G.,

and Laine, A. F. (2013). Robust quantiﬁcation of pul-

monary emphysema with a hidden Markov measure

ﬁeld model. In Proc. 10th IEEE Int’l Symposium on

Biomedical Imaging, pages 382–385. IEEE.

Hara, T., Yamamoto, A., Zhou, X., Iwano, S., Itoh, S., Fu-

jita, H., and Ishigaki, T. (2004). Automated detection

system for pulmonary emphysema on 3D chest CT

images. In Proc. of SPIE, pages 915–919.

Kashyap, R. L. and Khotanzad, A. (1986). A model-based

method for rotation invariant texture classiﬁcation.

IEEE Trans. on Pattern Analysis and Machine Intel-

ligence, (4):472–481.

Kim, N., Seo, J. B., Lee, Y., Lee, J. G., Kim, S. S., ,

and Kang, S. (2009). Development of an automatic

classiﬁcation system for differentiation of obstructive

lung disease using hrct. Journal of digital imaging,

22(2):136–148.

Li, S. Z. (2009). Markov Random Field Modeling in Im-

age Analysis. Springer-Verlag London Ltd, 3rd edn

edition.

Litmanovich, D., Boiselle, P. M., and Bankier, A. (2009).

CT of pulmonary emphysema - current status, chal-

lenges, and future directions. 19:537–51.

Madani, A., Keyzer, C., and AGevenois, P. (2001). Quanti-

tative computed tomography assessment of lung struc-

ture and function in pulmonary emphysema. 18

(4):720–30.

Mahmoodi, S. and Gunn, S. (2011). Snake based unsuper-

vised texture segmentation using Gaussian Markov

random ﬁeld models. In Proc. 18th IEEE Int’l Conf.

Image Processing, pages 1–4.

Manjunath, B. S. and Chellappa, R. (1991). Unsuper-

vised texture segmentation using Markov random

ﬁeld models. IEEE Trans. on pattern analysis and

machine intelligence, 13(5):478–482.

Mishima, M., T. Hirai, H. I., Nakano, Y., Sakai, H., Muro,

S., Nishimura, K., Oku, Y., Chin, K., Ohi, M., Naka-

mura, T., Bates, J. H. T., Alencar, A. M., and Suki,

B. L. (1999). Complexity of terminal airspace ge-

ometry assessed by lung computed tomography in

normal subjects and patients with chronic obstructive

pulmonary disease. In Proceedings of the National

Academy of Sciences, volume 96, pages 8829–8834.

Muller, N., Staples, C., and R. Miller, R. A. (1988). Density

mask, an objective method to quantitate emphysema

using computed tomography. 94:782–787.

Ojala, T., Pietikainen, M., and Maenpaa, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. IEEE Trans.

on pattern analysis and machine intelligence, 24:971–

987.

Petrou, M. and Sevilla, P. G. (2006). Image Processing,

Dealing with Texture. John Wiley & Sons Ltd.

Rue, H. and Held, L. (2005). Gaussian Markov Ran-

dom Fields; Theory and Applications. Chapman &

Hall/CRC.

Sluimer, I. C., Waes, P. F., Viergever, M., and Ginneken, B.

(2003). Computer-aided diagnosis in high resolution

CT of the lungs. 30:3081.

Sørensen, L., Shaker, S. B., and de Bruijne, M. (2010).

Quantitative analysis of pulmonary emphysema using

local binary patterns. IEEE Transactions on Medical

Imaging, 29(2):559–569.

Sørensen, L., Shaker, S. B., and de Bruijne, M. (2013).

Computed Tomography Emphysema Database.

http://image.diku.dk/emphysema database/.

Sprawls, P. (1995). The Physical Principles of Medical

Imaging. Medical Physics Publishing, USA, 2nd edi-

tion.

Uppaluri, R., Hoffman, E., M.Sonka, Hartley, P. G.,

W.Hunninghake, G., and McLennan, G. (1999). Com-

puter recognition of regional lung disease patterns.

160 (2):648–54.

Vasconcelos, V., Silva, J. S., Marques, L., and Barroso,

J. (2010). Statistical textural features for classiﬁca-

tion of lung emphysema in CT images: A compara-

tive study. In Information Systems and Technologies

(CISTI), pages 1–5. IEEE.

Xu, Y., Sonka, M., McLennan, G., Guo, J., and Hoffman,

E. A. (2006). MDCT-based 3-D texture classiﬁca-

tion of emphysema and early smoking related lung

pathologies. 156 (1):25.

Zhao, Y., Zhang, L., Li, P., and Huang, B. (2007). Classi-

ﬁcation of high spatial resolution imagery using im-

proved Gaussian Markov random-ﬁeld-based texture

features. IEEE Trans. on Geoscience and Remote

Sensing, 45(5):1458–1468.

QuantitativeAnalysisofPulmonaryEmphysemausingIsotropicGaussianMarkovRandomFields