Modelling Fluorescent Materials with a Spectral Overlap between

Excitation and Emission Spectrum

Sven Leyre

1,2,3

, Martijn Withouck

1,2

, Guy Durinck

1,2,3

, Geert Deconinck

and Peter Hanselaer

1,2,3

Light & Lighting Laboratory, KU Leuven, Gebroeders Desmetstraat 1, Leuven, Belgium

ESAT/ELECTA, KU Leuven, Kasteelpark Arenberg 10, bus 2445, Leuven, Belgium

SIM (Flemish Strategic Initiative on Materials), SOPPOM program, Technologiepark 935, Zwijnaarde, Belgium

Keywords: Modelling, Fluorescence, Adding-doubling.

Abstract: The adding-doubling method can be used to determine the reflection and transmission characteristics of

fluorescent materials. In this work, the method was adapted to allow the implementation of fluorescent

particles with a significant overlap between excitation and emission spectrum. The proposed method was

validated by comparing its results to the simulation results of traditional Monte Carlo ray tracing. The

average difference over the visible wavelength range between the two methods was found to be smaller than

0.5%. The proposed adding-doubling method was adapted for the simulation of a blue light-emitting diode

with a remote phosphor converter containing YAG:Ce phosphor. It was shown that it is important to take

the spectral overlap between excitation and emission spectrum into account to determine the colour

characteristics with sufficient accuracy.

1 INTRODUCTION

The adding-doubling (AD) method is a commonly

used evaluation method to quickly determine the

reflection and transmission characteristics of a stack

of homogeneous plane parallel layers (Wiscombe,

1969; Hansens, 1969; Prahl et al, 1993). The layers

may contain both surface and bulk scattering.

Recently, the method was extended for fluorescent

layers (Leyre et al, 2012). The method however does

not allow a spectral overlap between excitation and

emission spectrum of the fluorescent material. This

can be a problem for e.g. the prediction of colour

characteristics in lighting.

In white light-emitting diodes (LED) light

sources, blue LEDs are usually combined with a

yellow phosphor to obtain white light (Liu et al,

2010; Lee & Lee, 2006). The most commonly used

phosphor for LED applications is the Yttrium

Aluminium Garnet doped with Cerium (YAG:Ce).

This phosphor has a significant spectral overlap

between excitation and emission spectrum. At high

concentrations of the phosphor, this will cause a red

shift of the emitted spectrum, due to re-absorption

effects in the phosphor (Dhami et al, 1995). It is thus

important to take the spectral overlap between

excitation and emission spectrum into account when

predicting the colour properties of an LED light

source.

In this paper, an improved version of the adding-

doubling method for fluorescent layers is presented,

which allows the implementation of fluorescent

layers with a spectral overlap between excitation and

emission spectrum. First, the theoretical background

for the improved adding-doubling method is

presented, next the method is validated by

comparing the results with traditional Monte Carlo

ray tracing simulations. Finally, the significance of

the spectral overlap is shown by comparing the

predicted colour properties with and without the

overlap taken into account of a blue LED incident on

a remote phosphor converter containing YAG:Ce.

2 THEORETICAL

BACKGROUND

The AD method was first developed by Stokes

(Stokes, 1862) and allows the calculation of

reflection and transmission of a stack of layers. The

method has been adapted to allow the calculation of

reflection and transmission of a homogeneous plane

Leyre S., Withouck M., Durinck G., Deconinck G. and Hanselaer P..

Modelling Fluorescent Materials with a Spectral Overlap between Excitation and Emission Spectrum.

DOI: 10.5220/0004729700330038

In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 33-38

ISBN: 978-989-758-008-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

parallel slab containing bulk scattering (Wiscombe,

1969) and has found its way to the astronomy

(Hansen, 1969) and bio-medical field (Saeys et al,

1993). Recently, the method was adapted to allow

calculation of reflection and transmission of a

fluorescent layer (Leyre et al, 2012). The main

advantage of the AD method over e.g. Monte Carlo

ray tracing simulations is that the AD method is

much quicker. The Monte Carlo approach has the

advantage that it is not limited to plane parallel

geometries.

The AD method departs from the radiative

transfer equation (RTE), representing the light

propagation through a fluorescent layer, given by

Equation 1.

. ( , , ) ( ). ( , , ) . ( , '). ( , ', ). '

( ). ( ). ( ). ( , ', ). ' .

ii i i

M as M s M

MM eX X X X

L L pL d

w QE L d

λ µµ λ µ λ

λ µλ λ λ λ

∇ =−+ + Ω







+ Ω∆











∫

∑

∫

s rs rs ss rs

(1)

In words, this equation represents the change in

spectral radiance L(r,s,λ

) at position r in direction

s. The first term on the right hand side represents the

spectral radiance lost due to absorption and

scattering, the second term is the contribution in the

selected direction s from all other directions s’

integrated over solid angle dΩ’, and the third term is

the contribution at wavelength λ

from all excitation

wavelengths, where the excitation wavelength

region is divided into N wavelength intervals with

central wavelength λ

In Equation 1, µ

and µ

are the absorption and

scattering coefficient and define the average distance

travelled by a photon before being absorbed and

scattered respectively. The phase function p(s,s’)

gives the probability a photon will be scattered in a

certain direction. If the scattering occurs

isotropically, p(s,s’) is a constant. A commonly used

phase function is the Henyey-Greenstein phase

function, which has one free parameter: the

anisotropy factor g, which is identical to the average

of the cosine of the scatter angle (Henyey &

Greenstein, 1941).

The factor w

(λ

) is the weight of the selected

wavelength within the emission spectrum, QE is the

quantum efficiency of the fluorescent material,

(λ

) is the excitation coefficient. If the selected

wavelength λ

is not included in the spectral

emission band of the material, the third term on the

right hand side of Equation 1 disappears (w

(λ

) is

zero) and the RTE for non-fluorescent materials is

obtained (Leyre et al, 2012).

In the AD method, the incident radiance on a

material is divided into cones or channels, which can

be mathematically represented as a vector, where

each element in the vector represents the radiance

within a channel. The reflection and transmission

characteristics are represented in matrices, allowing

the radiance to be distributed over the different

channels.

Equation 2 gives the mathematical representation

of the transmission of the spectral radiance through a

slab (Wiscombe, 1969).

11 0111 011 01

1 01 1 01 0

() (, ) (, ) ()

() (,) (, ) ()

n n nn n

LT T L

θ θθ θθ θ

    

    

    



  



(2)

With L

being the incident spectral radiance and

the transmitted spectral radiance. The radiance is

divided into n channels (represented by the

corresponding polar angle θ). The matrix elements

(θ

,θ

) represent the light propagation from

spectral radiance at position x, channel a to spectral

radiance at position y, channel b. Equation 2 can also

be written as L

, with L

and L

being the

spectral radiance vectors and T

the transmission

matrix.

When dealing with fluorescent layers, the

radiance is not only redistributed angularly, but also

spectrally. The spectral radiance at wavelengths

included in the spectral emission band, has

contributions from all spectral radiances included in

the spectral excitation band. Leyre et al (2012) used

‘conversion matrices’ to handle the spectral

redistribution of the spectral radiance

(mathematically represented in Equation 3).

1 01 0 0

( ) .( ) ( , ).( )

M M XM X

λ λ λλ λ

= +

∑

L TL T L

(3)

In Equation 3, L

(λ

) and L

(λ

) are the

incident and transmitted spectral radiance at

emission wavelength λ

respectively, L

(λ

) is the

incident spectral radiance at excitation wavelength

and T

(λ

, λ

)

is the conversion matrix,

representing the fluorescent contribution at

wavelength λ

from wavelength λ

in the forward

direction. Each wavelength within the excitation

wavelength region will contribute to the emission at

wavelength λ

, this is represented by the summation

in Equation 3, where the excitation wavelength

region is divided into N wavelength intervals with

central wavelength λ

To calculate the reflection and transmission

through a layer which contains bulk scattering or

fluorescence, the AD method starts from a thin

‘single scatter’ layer. The thickness of the layer is

chosen in such a way that a photon will only interact

a single time with the material. The reflection and

transmission characteristics of this ‘single scatter’

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

layer are determined with the RTE, given in

Equation 1. Next, the layer is doubled in size, by

adding two identical layers together and calculating

the reflection and transmission. This step is repeated

until the desired thickness is reached. A more

elaborate explanation of the AD method can be

found in (Leyre et al, 2012).

The AD method starts from Equations 4 and 5,

representing the relationship between the upward

and downward spectral radiance at each side of a

single layer.

1 10 1 01 0

10 1 01 0

() .() .()

( , ). ( ) ( , ). ( )

i ii i

M MM

XM X XM X

λ λλ

λλ λ λλ λ

+ −+

−+

= +

∑

L R L TL

R LT L

)

0 01 0 10 1

01 0 10 1

() .() .()

( , ). ( ) ( , ). ( )

i ii i

M MM

XM X XM X

λ λλ

λλ λ λλ λ

− +−

+−

= +

∑

L R L TL

R LT L

(5)

Herein, the superscripts ‘+’ and ‘-’ represent the

spectral radiance going down- and upwards

respectively. The subscript ‘0’ and ‘1’ for the

radiances represent the spectral radiance on top and

at the bottom of the layer respectively. For the

reflection and transmission matrices, the first

number of the subscripts denotes the incoming

direction of the redistributed radiance (e.g. R

represents the reflection matrices for light incident

on the top of the layer). If the wavelength does not

fall within the emission wavelength region, the third

and fourth term on the right hand side of Equations 4

and 5 will disappear, since the conversion matrices

are null matrices.

The AD method combines Equations 4 and 5 to

obtain the reflection and transmission characteristics

of the doubled layer. It inherently assumes that all

radiances at wavelengths λ

are not included in the

emission wavelength region, i.e. the conversion

matrices in Equations 4 and 5 are null matrices for

all λ

(Leyre et al, 2012). The result of this

approach is that fluorescent materials with an

overlap between excitation and emission wavelength

region, where re-absorption (and re-emission) of

converted photons can occur, cannot be adequately

treated.

To solve this problem, we propose to write the

spectral radiance in vector form for the full spectrum

instead of one vector for each wavelength. As a

result, the reflection and transmission matrices will

allow the conversion of wavelength (both up- and

down-conversion) without the need for special

conversion matrices. Equation 6 now replaces the

equations for each individual wavelength given by

Equation 3.

Equation 6 allows both angular and spectral

redistribution of light with a single matrix. Using the

new vector-matrix notation, the third and fourth term

on the right hand side of Equations 4 and 5 become

obsolete (since the conversion matrices are no longer

required). It is now much easier to obtain the

reflection and transmission characteristics of a

double layer, by combining Equations 4 and 5. The

condition that the excitation wavelengths cannot be

emission wavelengths as well, is no longer relevant.

This allows to obtain the reflection and transmission

characteristics of two combined layers which have a

spectral overlap between excitation and emission

wavelength region. Equations 4 and 5 (without the

third and fourth term on the right hand side) can be

written for two separate second layers. Combining

the equations for the two layers leads to the

reflection and transmission matrices for the

combined layer, given by Equations 7 and 8.

20 21 12 10 12 10 21

()

−

=+−R R T E RR RT

(7)

02 12 10 12 01

()

−

= −T T E RR T

(8)

Herein, E is the unity matrix. To obtain the

transmittance and reflectance of a layer, the incident

radiance vector (L

) in Eq. 6 must be given the

value ‘1’ for the correct angles and wavelengths.

The transmitted radiance vector (L

) can be

calculated using Eq. 6. The transmittance at each

wavelength can be calculated by integration over the

different angles of the radiance represented in the

transmitted radiance vector. In a similar way the

reflectance can be obtained.

3 COMPARISON BETWEEN THE

AD METHOD AND MONTE

CARLO SIMULATIONS

To validate the method described in section 2, the

results of the AD method are compared with

traditional Monte Carlo ray tracing simulations. For

ModellingFluorescentMaterialswithaSpectralOverlapbetweenExcitationandEmissionSpectrum

111 011111 011 1 1 011 11 011 1

11 01111 0111 01 1 011

(, ) (, ,, ) (, , , ) (, ,, ) (, , , )

(,) (,,,) (,,,) (,,, ) (,, , )

(, )

n N nN

n n nn n N nnN

LT T T T

θλ θλθλ θλθλ θλθλ θλθ λ

θλ θλθλ θλθλ θλθλ θλθλ

θλ







 

   

 





011

01 1 1 1 01 1 1 01 1 1 01 1 0 1

01 1 1 01 1 01 1 01 0

(, )

(,)

(, ,, ) (, , , ) (, ,, ) (, , , ) (, )

(, ,,) (, ,,) (, ,, ) (, , , ) (,

N Nn N N NnN N

nN nNn nN N nNnN n

T T T TL

θλ

θλ θλ θλ θ λ θλ θλ θλ θλ θλ

θλθλ θλθλ θλθλ θλθλ θ









  

 

   

  )







(6)

the calculations and simulations, a plastic remote

phosphor converter is modelled. The converter has

optical flat surfaces (only Fresnel reflections at the

air-converter interfaces), has refractive index of 1.5,

thickness of 1 mm, and contains YAG:Ce phosphor

particles. The phosphor particles cause scattering

and fluorescence, the optical properties are taken

from (Liu et al, 2010).

At a concentration of 0.2 g/cm³, the average

scattering coefficient µ

over the visible wavelength

range is 25.71 mm

-1

, and the average anisotropy

factor g is 0.863. For the modelling the Henyey-

Greenstein phase function is selected, since this

allows for easy implementation in the AD method

(Joseph & Wiscombe, 1976). The absorption and

emission spectrum of the phosphor are shown in

Figure 1. An obvious spectral overlap between

excitation and emission spectrum can be noticed,

which makes this phosphor an excellent candidate to

validate the proposed AD method.

The peak absorption at 470 nm at concentration

0.2 g/cm³ is 1.79 mm-1. The QE of the phosphor is

0.87. The phosphor converter is illuminated with a

blue LED, with peak wavelength 460 nm. The

spectral radiant flux of the LED is represented in

Figure 1.

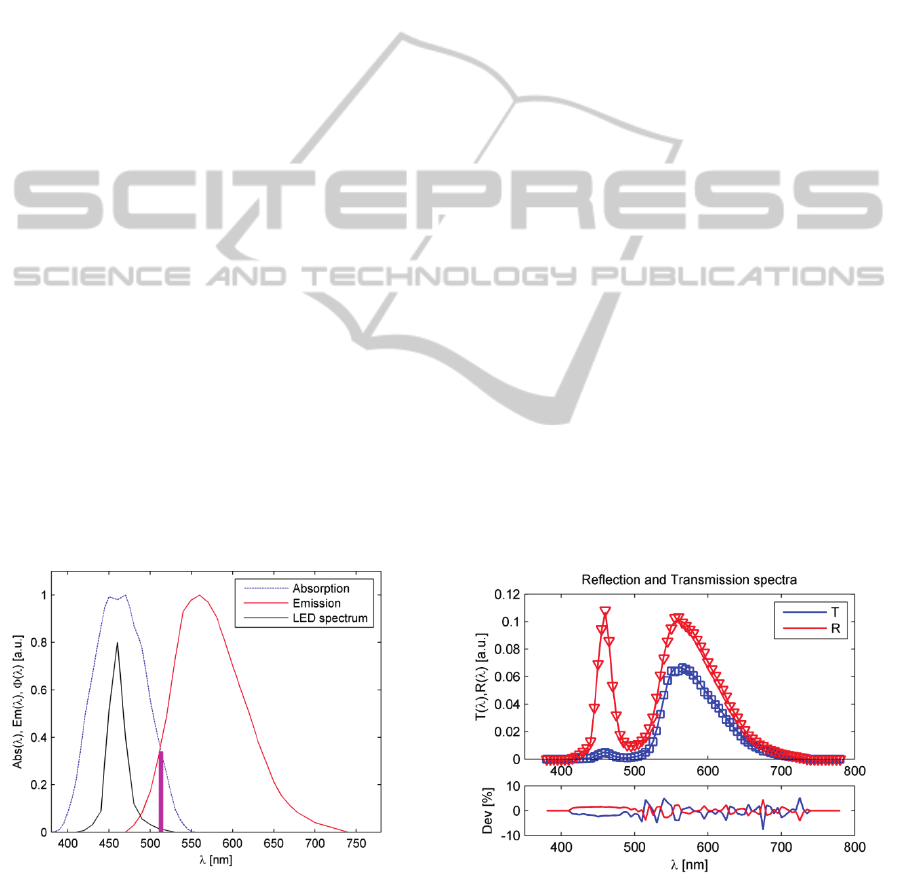
Figure 1: Absorption (blue dashed line) and emission

spectrum (full red line) of the YAG:Ce phosphor, together

with the spectral radiant flux of the blue LED (full black

line). The thick vertical line represents the cut-off for

excitation and emission spectrum if the spectral overlap is

not taken into account.

The Monte Carlo simulations are performed with

the software package TracePro. In this software,

Fresnel reflections are handled by attributing a

probability to each ray to be reflected or transmitted

at an interface according to the Fresnel reflection

and transmission coefficients. The volume scattering

is handled by use of the scattering coefficient and

the anisotropy factor, which can be introduced in the

program for each wavelength. The fluorescence is

handled by tracing the source from short to long

wavelengths. The rays absorbed in the fluorescent

material are stored to the hard disk. When an

emission wavelength is reached, the absorbed rays

are converted to the emission wavelength and given

the appropriate radiant flux. This approach differs

from the standard ray tracing procedure for

fluorescence in the TracePro software and allows for

the simulation of fluorescent materials with a

spectral overlap.

The simulations and calculations are performed

between 380 and 780 nm and in steps of 5 nm, the

concentration of phosphor in the converter is

0.2 g/cm³. The Monte Carlo simulation is performed

with 100 000 rays per wavelength. In Figure 2, the

result of the Monte Carlo simulation and the AD

calculations is shown, together with the relative

deviation between the two methods.

Figure 2: Comparison between the AD method (lines) and

Monte Carlo simulations (marks) for the transmitted

spectrum T (triangles) and the reflected spectrum R

(squares), together with the relative deviation (dev)

between the two methods.

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

From Figure 2, it can be seen that there is only a

very small deviation between the AD calculations

and the Monte Carlo simulations. The average

relative deviation is smaller than 0.5%. Moreover,

given the random variation of the deviation over the

wavelengths, it can be attributed to noise in the

Monte Carlo simulations. It can be concluded that

the AD method can indeed be used to calculate

reflection and transmission of a fluorescent

component with a spectral overlap between

excitation and emission spectrum. The AD method

takes approximately 90 seconds for the full

calculations, the Monte Carlo simulations takes

approximately 15 hours. The AD method thus

decreases the computation time with a factor 600

(for Monte Carlo simulations with 100.000 rays per

wavelength).

4 SIMULATION OF A REMOTE

PHOSPHOR APPLICATION

In the previous section, it was shown that the AD

method can be used for the quick calculation of the

transmitted spectrum through a remote phosphor

converter. Now, the influence of the spectral overlap

of the excitation and emission spectrum on the

colour characteristics of the remote phosphor device

will be investigated by comparing the CIE 1931 x,y

chromaticity coordinates of the transmitted spectrum

with and without the spectral overlap taken into

account. When the spectral overlap is not taken into

account, the excitation and emission spectrum are

cut off at 510 nm (shown in Figure 1). The

concentration of phosphor in the remote phosphor

converter is varied, to show the influence of the

concentration on the difference with and without

spectral overlap taken into account. In Figure 3, the

chromaticity coordinates are represented in the CIE

1931 x,y chromaticity diagram, for a concentration

of 0.01, 0.02, 0.035, 0.05, 0.065, 0.08, 0.1, 0.15,

0.4 g/cm³ YAG:Ce in the remote phosphor

converter.

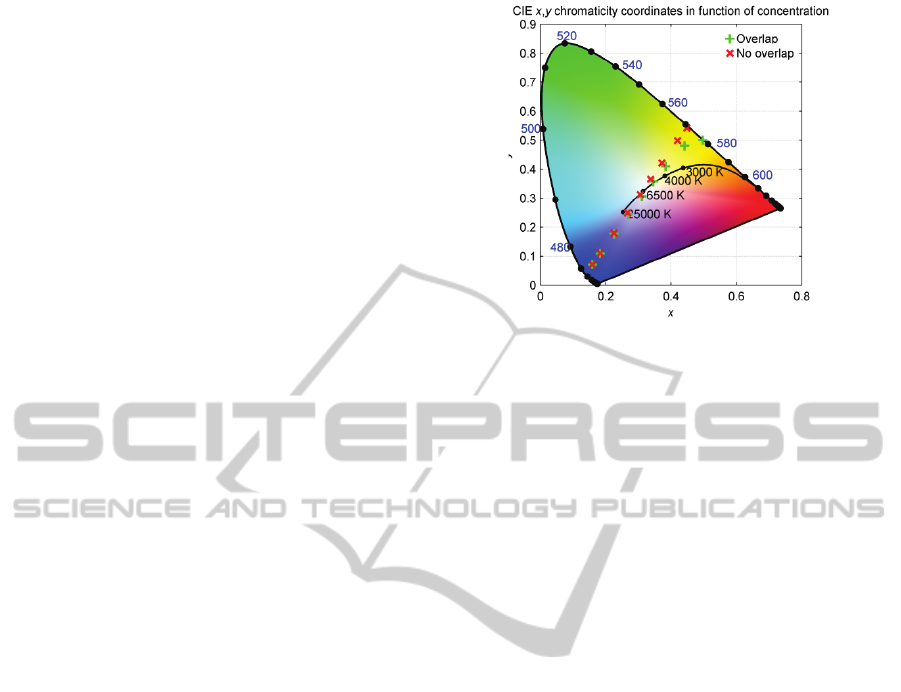
Figure 3: CIE 1931 x,y chromaticity coordinates of the

simulated transmitted spectrum for different

concentrations of YAG:Ce in the remote phosphor

converter, with (+) and without (x) the spectral overlap

between excitation and emission spectrum taken into

account.

From Figure 3, an obvious deviation in

chromaticity coordinates is noticeable, especially at

high concentrations of the phosphor. When the

spectral overlap is not taken into account, the

chromaticity coordinates for various concentrations

of phosphor are on a straight line. In this case, the

‘blue’ (from the LED) and ‘yellow’ (from the

phosphor) part of the spectrum have a fixed spectral

distribution, only the ratio of the ‘blue’ and ‘yellow’

part changes. When the spectral overlap is taken into

account, the ‘yellow’ part of the spectrum is not

constant, since re-absorption effects will red-shift

the ‘yellow’ part. At low concentrations, the red-

shift effect is less pronounced, since the probability

of re-absorption events to occur is much lower at

lower concentrations.

At a concentration of 0.08 g/cm³, the

chromaticity coordinates for the simulated spectrum

with the spectral overlap taken into account are

closest to the Planckian locus. The Correlated

Colour Temperature (CCT) is 5007 K. For the same

concentration, the simulated spectrum without the

spectral overlap taken into account results in a CCT

of 5313 K. The distance between the two simulated

colours is larger than a nine-step Mac Adam ellipse

(MacAdam, 1942). According to the recent

regulations of the European Commission regarding

LED lamps, the colour consistency of light sources

should be within a six-step Mac Adam ellipse

(European Commission, 2012). The correct

simulation of the spectral overlap between excitation

and emission spectrum of the phosphors used in

LED lamps is thus important to determine the colour

ModellingFluorescentMaterialswithaSpectralOverlapbetweenExcitationandEmissionSpectrum

characteristics of the light source with sufficient

accuracy.

The difference in luminous flux of the simulated

source with and without spectral overlap taken into

account is smaller than 3%, the effect on the colour

characteristics is thus the dominant problem when

ignoring the spectral overlap.

5 CONCLUSIONS

In the paper, the adding-doubling (AD) method was

adapted to allow the calculation of reflection and

transmission characteristics of plane parallel

fluorescent layers with a spectral overlap between

excitation and emission spectrum. The proposed

method was validated with traditional Monte Carlo

ray tracing simulations, the deviation between the

two methods was smaller than 0.5%. The

computation time with the AD method was

approximately 90 seconds, while the Monte Carlo

simulations took 15 hours.

The AD method was used to calculate the

transmitted spectrum through a remote phosphor

converter containing YAG:Ce illuminated with a

blue LED. It was shown that it is important to take

the spectral overlap between excitation and emission

spectrum into account to predict the colour

characteristics of the remote phosphor application.

In the future, experiments on a plane parallel

remote phosphor converter will be performed to

verify the conclusions in this work. The presented

method will also be adapted to perform colour

calculations under different illumination geometries

(e.g. an LED with a lambertian intensity

distribution).

ACKNOWLEDGEMENTS

The authors would like to thank the SIM (Flemish

Strategic Initiative for Materials) and IWT (Flemish

agency for Innovation by Science and Technology)

for their financial support through the SoPPoM

project within the SIBO program.

REFERENCES

Dhami, S., de Mello, A. J., Rumbles, G., Bishop, S. M.,

Phillips, D., Beeby, A. (1995). Phthalocyanine

fluorescence at high concentration: dimers or

reabsorption effect? Photochem. Photobiol. 61 (4),

341-346.

European Commission (2012). Commission Regulation

(EU) No 1194/2012 of 12 December 2012

implementing Directive 2009/125/EC of the European

Parliament and of the Council with regard to

ecodesign requirements for directional lamps, light

emitting diode lamps and related equipment. Brussels,

Official Journal of the European Union.

Hansen, J. E. (1969). Radiative transfer by doubling very

thin layers. Astrophys. J. 155, 563-573.

Henyey, L. G., Greenstein, J. L. (1941). Diffuse radiation

in the galaxy. Astrophys. J. 93, 70-83.

Joseph, J. H., Wiscombe, W. J. (1976). The Delta-

Eddington Approximation for Radiative Flux Transfer.

J. Atmos. Sci. 33, 2452-2459.

Lee K. H., Lee, S. W. R. (2006). Process development for

yellow phosphor coating on blue light-emitting diodes

(LEDs) for white light illumination. 8

Electronics

Packaging Technology Conference, Singapore, 6-8

December.

Leyre, S., Durinck, G., Van Giel, B., Saeys, W., Hofkens,

J., Deconinck, G., Hanselaer, P. (2012). Extended

adding-doubling method for fluorescent applications.

Opt. Express 20 (16), 17856-17872.

Liu, Z., Liu, S., Wang, K., Luo, X. (2010). Measurement

and numerical studies of optical properties of YAG:Ce

phosphor for white light-emitting diode packaging.

Appl. Opt. 49 (2), 247-257.

MacAdam, D. L. (1942). Visual Sensitivities to Color

Differences in Daylight. J. Opt. Soc. Am. A 32 (5),

247-274.

Prahl, S. A., van Gemert, M. J. C., Welch, A. J. (1993).

Determining the optical properties of turbid media by

using the adding-doubling method. Appl. Opt. 32 (4),

559–568.

Saeys, W., Velazco-Roa, M. A., Thennadil, S. N., Ramon,

H., Nicolaï, B. M. (2008). Optical properties of apple

skin and flesh in the wavelength range from 350 to

2200 nm. Appl. Opt. 47 (7), 908-919.

Stokes, G. G. (1862). On the intensity of the light reflected

from or transmitted through a pile of plates. Proc. Roy.

Soc. London 11, 545–556.

Wiscombe, W. J. (1976). On initialization, error and flux

conservation in the doubling method. J. Quant.

Spectrosc. Radiat. Transfer 16, 637–658.

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology