
Structural and Functional Changes Occuring During Growth of the
Respiratory System Can Be Quantified and Classified
Clara M. Ionescu
1
, Dana Copot
1
, Hannes Maes
2
, Gerd Vandersteen
2
, Am
´
elie Chevalier
1
and Robin De Keyser
1
1
Ghent University, Department of Electrical Energy, Systems and Automation,
Technologiepark 913, B9052 Zwijnaarde, Belgium
2
Vrije Universiteit Brussel, Department ELEC, Pleinlaan 2, 1050 Brussels, Belgium
Keywords:
Respiratory Impedance, Frequency Response, Nonlinear System, Detection Lines, Spectral Analysis, Forced
Ocillation Technique.
Abstract:
This paper describes the nonlinear effects in the respiratory signals captured by means of the forced oscillation
technique (FOT) non-invasive lung function tests. The measurements are performed using a prototype device
developed such that it overcomes the limitations present in commercial FOT devices and allows the generation
of multisine signals below 4 Hz. The principle of sending detection lines in the frequency domain for char-
acterizing odd and even nonlinear contributions from a nonlinear system are introduced briefly to the reader.
Two detection methods are presented: a robust method based on multiple measurements and a fast method
based on a single measurement. The ingenious combination of the device and the method allow to detect the
nonlinear contributions in the respiratory signals: pressure and flow. The intrinsicly pesent nonlinear effects
are quantified by means of a novel index and analyzed in two groups of healthy volunteers, aged 14 years and
aged 17 years, respectively. The results we obtain suggest that the proposed device, method and index are a
successful combination of lung function testing, signal processing and classification items.
1 INTRODUCTION
The generic evolution of chronic respiratory dis-
ease can be captured in the flowchart from figure 1.
Asthma and COPD (chronic obstructive pulmonary
disease) originate from the interaction of susceptibil-
ity genes and environmental factors that underly the
pathogenesis of the diseases. Inflammation, in the
broadest sense, is the initiator to the structural and
functional changes. These changes have an impact
on each other (arrows) and are responsible for the
excessive airway narrowing that is the fundamental
abnormality leading to symptoms (Northrop, 2010;
Ionescu, 2013; De Melo et al., 2000).
Airway remodeling is the process of modification
and sustained disruption of structural cells and tis-
sues leading to a new airway-wall structure and func-
tions. The underlying principle of asthma and COPD
is caused by concepts in immunology and inflamma-
tion. Acute inflammation is the response of vascu-
larized tissue to injury. The reaction is initiated to
protect the host and to restore its function and tis-
Figure 1: Flowchart of lung inflammation.
sue to normal. However, in COPD and asthma oc-
curs a direct switch from episodic, acute to chronic in-
flammation which results in structural airway remod-
eling and functional changes. The accelerated decline
in lung function is characterized by an alternation in
size, mass or number of structural components. Rea-
sons for the persistence of the chronic inflammation
are not fully clear. But one generally accepts that dif-
110
M. Ionescu C., Copot D., Maes H., Vandersteen G., Chevalier A. and De Keyser R..
Structural and Functional Changes Occuring During Growth of the Respiratory System Can Be Quantified and Classified.
DOI: 10.5220/0004729901100115
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 110-115
ISBN: 978-989-758-011-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ferent causes exist. A defect in the repair process,
infection, genetically influenced abnormal inflamma-
tory response or repeated inhalation/exposure of aller-
gen/noxious agents are all possible causes (Northrop,
2010; Lutchen, 1988; Suki and Lutchen, 1992).
The exact relationship between airway remodel-
ing and functional changes is not clear yet but func-
tional changes plays also an important role in the
progression of chronic lung diseases. This includes
the mechanical airway remodeling due to structural
changes on macroscopic level and is described in the
next chapter. Functional changes will also determine
the lung tissue property. Although airway remodel-
ing is supposed to be a consequence of long-term air-
ways diseases, studies (Ionescu, 2013) suggest that
the remodeling may be a part of the primary pathol-
ogy rather than simply a result of chronic inflamma-
tion. The remodeling of the airways changes individ-
ually and the natural history is not still perfectly un-
derstood. known.
In this paper we report the results of a method
which enables the quantification of these nonlinear
contributions in an objective manner, by introduc-
ing a novel index. This index will be evaluated on
two groups of healthy children, of two different age
groups (i.e. 17 and 19 years old), in order to check
that the proposed index is able to capture differences
in structure and function between the groups. The pa-
per is organize as follows: the next section presents
the method of lung function testing, the method of
frequency response evaluation and the novel index.
The third section presents the groups of children eval-
uated in this study and the results obtained. A con-
clusion section summarizes the outcome of this work
and speculates further use of the method.
2 METHODS
2.1 Signal Processing
The fundamental difference between a linear time in-
variant system and a nonlinear system is that the non-
linear system transfers energy from one frequency in
the input signal to other frequencies in the output sig-
nal.
The influence of nonlinear distortions on the
frequency response function (FRF) measurements
are determined by using a random phase multisine
(Schoukens and Pintelon, 2001; Schoukens et al.,
2005):
U(t) =
N
∑
k=1
A
k
cos(kω
0
t + φ
k
) (1)
as an input signal, with A
k
the non-zero amplitude for
odd k values, ω
0
= 2π f
0
and f
0
= 0.1 Hz, φ
k
the phase
uniformly and independently distributed in the [0;2π]
interval and N the number of sinusoids.
The best linear approximation (BLA) of a nonlin-
ear system can be viewed as a minimization of the
mean squared error between the true output of the
nonlinear system and the output of a linear model.
The estimated BLA
ˆ
G
BLA
( jω
k
) of a wide class of non-
linear systems, obtained using a random phase multi-
sine, can be written as:
ˆ
G
BLA
( jω
k
) = G
BLA
( jω
k
) + G
S
( jω
k
) + N
G
( jω
k
) (2)
with G
BLA
( jω
k
) the true best linear approxima-
tion (BLA) of the nonlinear system, G
S
( jω
k
) the
zero mean stochastic nonlinear contributions and
N
G
( jω
k
) the measurement noise (Schoukens and Pin-
telon, 2001). The stochastic nonlinear contributions
G
S
( jω
k
) can be extracted by averaging from a mani-
fold of experiments M containing different phase re-
alizations in the excitation signal from (1). The mea-
surement noise N
G
( jω
k
) can be minimized by mea-
suring longer, thus by increasing N.
The basic principles for detecting nonlinearities
are shown in figure 2. The output of a linear system,
which is excited with a multi-frequency input signal,
is given on the first row. Only amplitude variations
on the excited (odd) frequencies are observed (red).
However, when this input signal is applied on a non-
linear system (e.g. the respiratory tissue), nonlinear
dynamics become visible and can be measured as ad-
ditional detection lines (second and third row in blue
and green). These distortions are in fact superimposed
to the linear output signal and contribute to the signal
measured at the output (last row). The resulting out-
put signal contains extra information via phase differ-
ences. The nonlinear contributions can be determined
via the identification of the even and odd harmonics
(blue and green).
Figure 3 depicts a schematic of the input and out-
put measurements corrupted by noise and the corre-
sponding BLA. In (Schoukens et al., 2005; Zivanovic
and Schoukens, 2009), a variance analysis procedure
Figure 2: A schematic representation of the input-output
contributions.
StructuralandFunctionalChangesOccuringDuringGrowthoftheRespiratorySystemCanBeQuantifiedandClassified
111
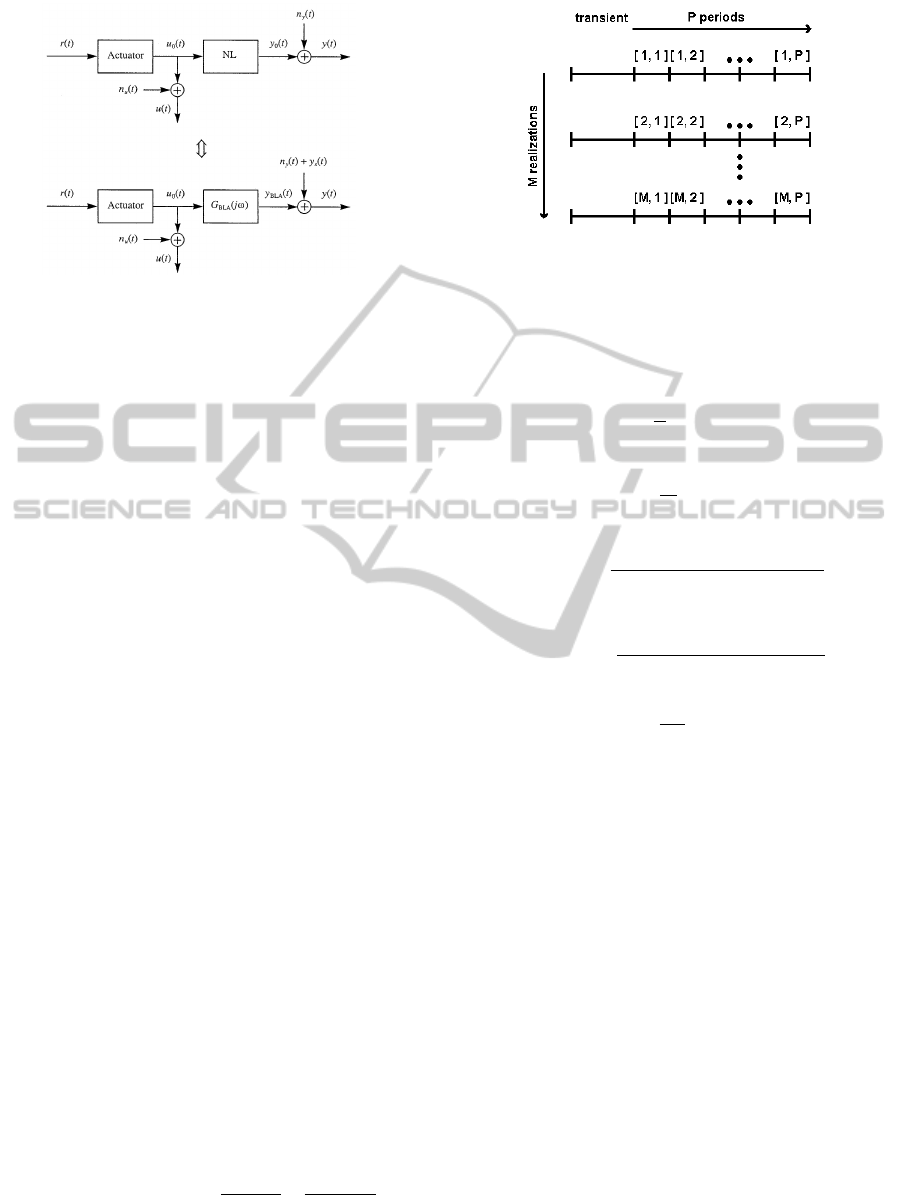
Figure 3: Input u(t) and output y(t) measurements with
noise from a nonlinear system driven by an actuator with
input signal r(t) (top), and its corresponding best linear ap-
proximation (under).
has been proposed that allows to detect and quantify
the stochastic nonlinear distortions G
S
( jω
k
) and the
disturbing noise N
G
( jω
k
). Two measurement meth-
ods can be applied:
• a robust method, which uses different random
phase realizations of an odd multisine excitation
to get information about the stochastic nonlinear
distortions;
• a fast method, which uses only one realization of
an odd random phase multisine with random har-
monic grid.
The information about the stochastic nonlinear
distortions is obtained via the detection lines (non-
excited harmonics) in the output DFT spectrum. To
compensate for spectral impurity of the input, a first
order correction is applied to the output DFT spec-
trum. The use of an odd random phase multisine with
a random harmonic grid provides also a classification
of the nonlinear distortions in even and odd contribu-
tions in the corrected output DFT spectrum.
Figure 4 shows the principle of measuring the
BLA using the robust method, i.e. by averaging be-
tween M realizations with P periods. If the input sig-
nal is known and uncorrupted with noise, one can
obtain the non-parametric estimation of the BLA as
G
BLA
( jω
k
), the variance of the stochastic nonlinear
distortions var(G
S
( jω
k
)) and the variance of the noise
σ
2
GBLA,n
. Given that n
y
(t) is a stochastic signal and
y
s
(t) a periodic signal depending on the phase realiza-
tion of the input (reference) signal r(t), the frequency
response function of the m
th
realization and p period,
G
[m, p]
( jω
k
) can be written as:
G
[m, p]
( jω
k
) = G
BLA
( jω
k
)+
Y
[m]
S
(k)
U
[m]
0
(k)
+
N
[m, p]
Y
(k)
U
[m]
0
(k)
(3)
Next, the BLA, variance of the nonlinear distortions
Figure 4: Measurement procedure for the robust method:
P periods of length N measured from the steady state re-
sponse with an odd multisine input. The experiment is then
repeated M times, each time with a different odd random
phase multisine realization.
and noise variance can be estimated as:
ˆ
G
[m]
( jω
k
) =
1
P
P
∑
p=1
G
[m, p]
( jω
k
) (4)
ˆ
G
BLA
( jω
k
) =
1
M
M
∑
m=1
ˆ
G
[m]
( jω
k
) (5)
ˆ
σ
2
ˆ
G
[m]
(k) =
P
∑
p=1
|G
[m, p]
( jω
k
) −
ˆ
G
[m]
( jω
k
)|
2
P(P − 1)
(6)
ˆ
σ
2
ˆ
G
BLA
(k) =
M
∑
m=1
|G
[m]
( jω
k
) −
ˆ
G
BLA
( jω
k
)|
2
M(M − 1)
(7)
ˆ
σ
2
ˆ
G
BLA,n
(k) =
1
M
2
M
∑
m=1
ˆ
σ
2
ˆ
G
[m]
(k) (8)
var(G
S
( jω
k
)) ≈ M(
ˆ
σ
2
ˆ
G
BLA
(k) −
ˆ
σ
2
ˆ
G
BLA,n
(k)) (9)
Nomenclature:
• U
[m]
0
(k) - input of DFT spectra of m
th
FRF mea-
surements;
• Y
[m, p]
(k) - output of DFT spectra of m
th
FRF mea-
surements;
• G
BLA
( jω
k
) - asymptotic best linear approxima-
tion;
•
ˆ
G
[m]
( jω
k
) - estimated spectrum of m
th
realiza-
tions;
• G
[m, p]
( jω
k
) - frequency response function;
• P - number of periods;
•
ˆ
G
2
BLA
(k) - estimation of best linear approximation;
•
ˆ
σ
2
ˆ
G
BLA
(k) - estimation of the total variance aver-
aged over M experiments;
•
ˆ
σ
2
ˆ
G
BLA,n
(k) - the variance of noise averaged over M
experiments;
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
112

• var(G
S
( jω
k
)) - variance of the stochastic non-
linear distortions with respect to one multisine re-
alization.
The total variance and noise variance averaged over
the M experiments give an indication upon the relia-
bility of the measured frequency response functions.
The variance of the stochastic nonlinear distortion for
each realization gives an indication of how much dis-
tortion is present in the system with each experiment.
The fast method can be considered as a special
case of the robust method, with M = 1. As such,
the variance is expected to have higher values and
less reliability for the fast method than in the robust
method. For all the results presented in this paper,
the robust method was employed with M = 5. Fast
method needs odd detection lines and approximation
in order to predict the odd distortion levels at the ex-
ited bins.
2.2 Signal Measurement
The standard (commercialized) forced oscillation
technique (FOT) is a non-invasive technique which
applies small air pressure oscillations to the respi-
ratory system of a subject who is breathing sponta-
neously (Oostveen et al., 2003; Smith et al., 2005).
The pressure oscillations are generated by means of
a loudspeaker or a fan connected to a chamber. The
loudspeaker, or the fan, is driven by a power ampli-
fier fed with the oscillating signal u(t) generated by
a computer, which generates a pressure oscillation in-
side the chamber. This air pressure oscillation is ap-
plied to the respiratory system by means of a tube con-
necting the chamber and an anti-bacterial filter. There
is always fresh air in the system through the design of
the device. Pressure p(t) and flow q(t) are measured
at the mouthpiece with the combination of two pres-
sure sensors and a pneumotachograph. The excitation
pressure signal is kept within a range of a peak-to-
peak size of 0.1 − 0.3 kPa, typically for patient safety,
comfort and to ensure linearity.
Based on earlier developments (Ionescu et al., ),
an improved, novel (prototype) device was designed
for a lower frequency range than the standard FOT de-
vice (Maes et al., 2013). Lower frequencies hold valu-
able information from medical point of view, since
they are closer to the breathing signal and thus give
valuable information about the respiratory mechanics
in the frequency range of the breathing (0.1 − 0.3 Hz).
The details of the prototype device and the design of
the excitation signal have been given in (Maes et al.,
2013).
2.3 Novel Index for Nonlinear
Contributions
In order to quantify these nonlinear contributions,
the following index has been introduced in (Ionescu,
2013):
T =
P
even
+ P
odd
P
exc
·
U
exc
U
even
+U
odd
(10)
where P represent the pressure and U is the input sig-
nal.
Each variable is the sum of the absolute values of
all the contributions in pressure signal and input flow
signal respectively, at the even non-excited frequen-
cies, the odd non-excited frequencies and the excited
odd frequencies. Only the corrected output pressure
has been taken into account when calculating (10), i.e.
the linear contribution has been estimated and sub-
tracted.
This index expresses a relative ratio of the con-
tributions at the non-excited frequency points, with
respect to the contributions at the excited frequency
points. Furthermore, it gives a relative measure of
the gain between contributions in the input and in the
output of the system. Since this is a nonlinear system
whose output depends on the input, the choice for this
relative measure is technically sound.
2.4 Healthy Volunteers
The measurement campaign was performed at Ghent
University, Campus Ardoyen, during the event of the
’Science Week’ organized in our department. The
children have been performing measurements after
apriori signing a written informed consent, further
supported by a responsible adult (i.e. the teacher who
was responsible for their visit). Also each patient has
fill in a form regarding their health status. The bio-
metric data for the healthy groups are given in table 1,
with values given as mean with standard deviations.
Their respiratory values have been successfully val-
idated as healthy, with reference values for respira-
tory impedance measured by FOT using the predic-
tion models from (Northrop, 2010; Ionescu, 2013).
Hence, the information gathered in this report will
discuss differences based solely on structural changes
between the two age groups as a result of growth.
3 RESULTS AND DISCUSSION
The results of the two groups evaluated by means of
the index from (10) are given in figure 5 as boxplots.
The choice for boxplots is motivated by the fact that
StructuralandFunctionalChangesOccuringDuringGrowthoftheRespiratorySystemCanBeQuantifiedandClassified
113

Table 1: Biometric parameters of the investigated healthy
subjects.
14-years (20) 17-years (158)
Male/Female 1/19 96/61
Age (yrs) 14±0.3 17±0.6
Height (m) 1.63 ± 0.05 1.74 ± 0.08
Weight (kg) 48±8 62±9
BMI 18±2 20±2
it is a straightforward statistical measure providing
outlier percentage score and mean value within each
group. Statistically meaningful differences between
groups are present if the p value is lower than 0.05
(i.e. 95% confidence intervals). For the data mea-
sured and examined in this study, we obtained a p
value of 0.0158, which indicates that the proposed in-
dex is able to capture differences originated by the
variations in the structure of the respiratory system
with growth.
Figure 5: Boxplot of the nonlinear contributions in the two
groups.
Changes in structure and in the respiratory air-
ways and tissue with growth lead to changes in over-
all dynamics and mechanical properties. The dynam-
ics change because of the novel path that air has to
pass during inspiration-expiration process of breath-
ing. Since there are structural changes, the air will
have various aerodynamic properties. The changes
in the material properties of the airway and tissue
will also have an effect on these aerodynamic prop-
erties, e.g. resistance or elasticity of the airways will
produce various response to air pressure oscillations.
By measuring with FOT the air pressure and air flow
involved during unforced breathing, one is able to
characterize the transfer function (i.e. impedance) of
the dynamic respiration (Daroczi and Hantos, 1982;
Ionescu and De Keyser, 2003). By using the special
detection line algorithm presented in section 2.1, it is
possible to separated nicely the linear from the non-
linear contributions in this dynamic process. The re-
sult from figure 5 supports this theory and shows dis-
tinctly the added value of the novel index. It should
be noted that to date, there is no other clinical mea-
sure of nonlinear distortion amount in the respiratory
system.
One may speculate that the nonlinear distortions
tend to be significantly increased in patients diag-
nosed with respiratory disease than in healthy sub-
jects. From clinical insight, this is indeed a valid
conclusion (recall here structural changes discussed
in the introduction of the paper). For instance, the
respiratory system affected by cystic fibrosis is filled
with viscous secretions which will change the hetero-
geneous appearance of the tissues and introduce non-
linear effects originated by turbulent flow, viscoelas-
ticity, excessive inflammation and clogged airways.
The respiratory system affected by asthma is sub-
ject to airway hyper-responsiveness leading to airway
chronic inflammation. This affects the airway remod-
eling, changing airflow dynamics and hence introduc-
ing nonlinear effects from turbulent flow, airway ob-
struction, airway muscle fibrosis etc. In both cases,
changes in structure and morphology will change the
nonlinear behavior of the respiratory system, hence
the values of the proposed index are expected to
change as well.
This preliminary evaluation was performed on a
reasonably large number of healthy volunteers, and it
suggests that measuring nonlinear contributions may
be beneficial to gather insight into the evolution of
respiratory diseases. The fact that respiratory me-
chanics at low frequencies have inherent information
on the viscoelastic properties of airways and tissue is
motivating the development of signal processing al-
gorithms which can cancel the interference with the
breathing of the patient. The challenge is that the
amplitude and frequency of the breathing signal may
vary within the measurement and from one measure-
ment to another, making the detection lines prone to
biased values. The results obtained in these initial
steps are a proof of concept which motivates further
development of the FOT device and the detection al-
gorithm.
4 CONCLUSIONS
This paper presented an integrated approach for de-
tection of nonlinear distortions present in the breath-
ing dynamics as a result of structural and mate-
rial properties. As a preliminary study, the infor-
mation gathered here is crucial for the further de-
velopment and implementation of measuring devices
and algorithms to measure low-frequency respira-
tory impedance in a non-invasive and simple man-
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
114

ner, without requiring breathing maneuvers or com-
plex respiratory tests. The results obtained in these
initial steps are a proof of concept for the added value
of FOT within the clinical onset and motivates fur-
ther development of the detection algorithm. Future
work will include large scale measurements in patient
groups with a wide range of age and a gender balance.
This experiments will help quantify whether a patient
has asthma or COPD based on respiratory measure-
ments using the less-invasive FOT device.
ACKNOWLEDGEMENTS
The authors are grateful for to Mr Stig DOOMS for
performing the measurements, and to Miss Amelie
CHEVALIER for organizing the measurement cam-
paign. This work is sponsored by Ghent University,
Vrije Universiteit Brussel and the Foundation for Sci-
entific Research (FWO- Vlaanderen), Belgium.
REFERENCES
Daroczi, B. and Hantos, Z. (1982). An improved forced os-
cillatory estimation of respiratory impedance. Inter-
national Journal of Bio-Medical Computing, 13:221–
235.
De Melo, P., Werneck, M., and Giannella-Neto, A.
(2000). Effect of generator nonlinearities on respira-
toy impedance. Medical and Biological Engineering
and Computing, 38:102–108.
Ionescu, C. (2013). The human respiratory system: an
analysis of the interplay between anatomy, structure,
breathing and fractal dynamics. Springer, Series in
Bio-Engineering.
Ionescu, C. and De Keyser, R. (2003). A novel parametric
model for the human respiratory system. Proceedings
of the IASTED International Conference on Modeling
and Simulation., pages 246–251.
Ionescu, C., Vandersteen, G., Schoukens, J., Desager, K.,
and De Keyser, R. Measuring nonlinear effects in res-
piratory mechanics: a proof of concept for prototype
device and method. IEEE Transaction on Measure-
ment and Instrumentation.
Lutchen, K. (1988). Optimal selection of frequencies for es-
timating parameters from respiratory impedance data.
IEEE Transaction on Biomedical Engineering, 35(8).
Maes, H., Vandersteen, G., Muehlebach, M., and Ionescu,
C. (2013). A ventilator-based, low-frequent, forced
oscillation technique apparatus. IEEE Transactions
on Measurement and Instrumentation.
Northrop, R. (2010). Non-invasive measurements and de-
vices for diagnosis. CRC Press.
Oostveen, E., MacLeod, D., Lorino, H., Farre, R., Han-
tos, Z., Desager, K., and Marchal, F. (2003). The
forced forced oscillation technique in clinical practice:
methodology, recommendations and further develop-
ments. European Respiratory journal, 22:1026–1041.
Schoukens, J. and Pintelon, R. (2001). System identifica-
tion. A frequency domain approach. IEEE Press.
Schoukens, J., Pintelon, R., Dobrowiecki, T., and Rolain, Y.
(2005). Identification of linear systems with nonlinear
distorsions. Automatica, 41:491–504.
Smith, H., Reinhold, P., and Goldman, M. (2005). Forced
oscillation technique and impulse oscillometry. Euro-
pean Respiratory Monograph, 31(72):105.
Suki, B. and Lutchen, K. (1992). Pseudorandom signals
to estimate apparent transfer and coherence functions
of nonlinear systems - applications to respiratory me-
chanics. IEEE Transactions Biomedical Engineering,
39(11).
Zivanovic, M. and Schoukens, J. (2009). Time-variant har-
monic signal modeling by using polynomial approx-
imation and fully automated spectral analysis. Pro-
ceedings of the 17th European Signal Processing Con-
ference.
StructuralandFunctionalChangesOccuringDuringGrowthoftheRespiratorySystemCanBeQuantifiedandClassified
115
