The Battle of the Giants

A Case Study of GPU vs FPGA Optimisation for Real-time Image Processing

Lars Struyf

, Stijn De Beugher

, Dong Hoon Van Uytsel

, Frans Kanters

and Toon Goedem

EAVISE, ESAT-PSI-VISICS, KU Leuven, Leuven, Belgium

eSATURNUS, Leuven, Belgium

InViso, Eindhoven, The Netherlands

Keywords:

Computer Vision, Real-time, GPU, FPGA.

Abstract:

This paper focuses on a thorough comparison of the two main hardware targets for real-time optimization of

a computer vision algorithm: GPU and FPGA. Based on a complex case study algorithm for threaded isle

detection, implementation on both hardware targets is compared in terms of resulting time performance, code

translation effort, hardware cost, power efﬁciency and integrateability. A real-life case study as described in

this paper is a very useful addition to discussions on a more theoretical level, going beyond artiﬁcial experi-

ments. In our experiments, we show the speed-up gained by porting our algorithm to FPGA using manually

written VHDL and to a heterogeneous GPU/CPU architecture with the OpenCL language. Also, issues and

problems occurring during the code porting are detailed.

1 INTRODUCTION

Many applications have high inherent parallelism

which can be exploited for substantial execution time

speed-ups. Especially for many image processing al-

gorithms, this is the case because of the straightfor-

ward data parallelism possibilities on pixel basis. At

the same time, execution speed is the heel of Achilles

of many vision applications, without real-time perfor-

mance they can not be practically applied in real life.

An example is the endoscopic image enhancement al-

gorithm we describe in this paper, which have to be

implemented with minimal latency in order not to im-

pede the surgeon’s hand-eye coordination during an

operation. Therefore, much effort is put in real-time

optimization of image processing algorithms.

The ﬁrst step is always to perform machine-

independent optimisations on the algorithm. A good

example is the development of the SURF feature de-

tection method (Bay et al., 2008), as a faster alter-

native to SIFT (Lowe, 2004), by approximating the

ﬁlters used by block ﬁlters and exploiting tricks like

integral image pre-calculation.

If on a standard CPU-based platform the required

speed is not reached yet, a next obvious step is imple-

menting the algorithm on speciﬁc hardware, at which

the inherent parallelism can be exploited. This paper

focuses on two frequently used types of parallel hard-

ware, FPGAs and GPUs. FPGAs have shown very

high performance in spite of their low operational fre-

quency by fully extracting the parallelism. On the

other hand, recent GPUs support a large number of

cores, and have a potential for high performance in

many applications. However, the cores are grouped,

and data transfer between the groups is very limited.

Programming tools for FPGA and GPU have been de-

veloped, but the prevailing idea is that it is still difﬁ-

cult to achieve high performance on these platforms

with limited effort.

Both platforms have very distinct properties.

While GPUs excel in raw processing speed in terms

of operations per second, FPGAs are the summit of

ﬂexibility. In this paper we port one complex image

processing algorithm to both platforms to be able to

compare the resulting time performance. Another im-

portant evaluation criterium will be the effort that is

needed for the code translation.

Relevant related work, also comparing GPU and

FPGA for image processing algorithms, include the

work of Cope et al. (Cope et al., 2005) and Asano

et al. (Asano et al., 2009), which were unfortunatly

limited to rather simple image processing tasks (color

correction and two-dimensional convolution ﬁlters),

and rather outdated. More recent work is that of da

Silva et al. (da Silva et al., 2013), which is targeted at

combining the power of GPUs with the ﬂexibility of

112

Struyf L., De Beugher S., Van Uytsel D., Kanters F. and Goedemé T..

The Battle of the Giants - A Case Study of GPU vs FPGA Optimisation for Real-time Image Processing.

DOI: 10.5220/0004730301120119

In Proceedings of the 4th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2014), pages

112-119

ISBN: 978-989-758-000-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

FPGAs in a hybrid FPGA/GPU platform. Their con-

clusions are that the usefullness of the combination is

limited, because of the conﬁned data bandwith avail-

able between GPU and FPGA. However, in their pa-

per they also report on a comparison where the GPU

and the FPGA are used separately. Their results show

that the HLS FPGA compiler outperforms handwrit-

ten code and offers a performance comparable to the

GPU for the application studied.

The remainder of this paper is organised as fol-

lows. In section 2, the threaded isle detection al-

gorithm we start from is detailed. After that, our

code porting efforts towards both GPU (section 3) and

FPGA (section 4) are reported upon. Our results are

presented in section 5. We end with an evaluation in

section 6 and a conclusion in section 7.

2 ALGORITHM

2.1 Algorithm Overview

The goal of the algorithm studied in this paper is to vi-

sually highlight linear structures during videoscopic

inspections. An example result is included as Fig-

ure 1. The algorithm is a chain of four basic build-

ing blocks: preprocessing, feature detection, ﬁltering,

and visualization.

2.1.1 Preprocessing

The image is reduced to a grayscale picture which

discrimates better between linear structures and the

surrounding areas. This step is highly application-

speciﬁc, but can be methodically optimized with su-

pervised training techniques, using a set of expert-

annotated images. In many cases a linear transforma-

tion of the RGB or HSV colorspace or a lookup table

will yield good results.

2.1.2 Feature Detection

The structures to be highlighted are linear. Hence,

any edge or ridge detector can be used to extract these

from the preprocessed image. The algorithm uses

oriented phase congruency energy features (Kovesi,

1999) which are able to detect both strong and weak

edges. This method is based on a convolution of the

image with a ﬁlter bank of 24 log-Gabor-ﬁlters, over

4 scales and 6 orientations. Other edge detecting fea-

tures such as canny gradient strength were found less

appropriate for our intended applications. Of course,

different features can be combined for other applica-

tions.

Figure 1: Vascularization highlighting algorithm illustra-

tion: (left) input image, (right) output image.

2.1.3 Filtering

The goal of the ﬁltering step is to suppress the de-

tected lines that do not bear visual information with

respect to the application at hand. For instance, for the

vascularization highlighting application as described

in section 2.2, a region where a lot of short vessels go

in random directions is probably not pathologic and

therefore not interesting for the detection of tumors.

2.1.4 Visualization

In the last step the ﬁltered mask is combined with the

original image. This step is probably the least inter-

esting from an image processing point of view, but

very important for the optimal transfer of the com-

puted visual information to the human end-user of the

application. For the vascularization highlighting ap-

plication, the saturation of the original image is glob-

ally reduced, while the ﬁltered feature map obtained

in the previous step non-linearly modulates the satu-

ration locally.

2.2 Applications

Such a general linear structure detection algorithm is

useful in a broad range of applications. We detail a

few of them below.

The application that spurred the initial develop-

ment of the line detection algorithm discussed in this

paper is real-time vascularization highlighting dur-

ing endoscopic procedures. Preliminary experiments

have shown that this highlighting is very likely to en-

hance the human detection rate of pathologic tissue,

such as endometriosis and tumors. Most malignant

tumors are linked with increased vascularization and

unregular vessel patterns (Tyrrell et al., 2005), pre-

sumably because of a higher demand caused by ac-

celerated growth. The increased vascularization be-

comes visible around superﬁcial tumors as a star-

shaped structure. While the tumor itself may be very

small and invisible, the vascularization pattern sur-

rounding it is a valuable visual guide towards it. The

TheBattleoftheGiants-ACaseStudyofGPUvsFPGAOptimisationforReal-timeImageProcessing

113

Figure 2: Images of cracks in polished marble acquired by

confocal laser microscopic photography.

same holds for endometriosis, which is also charac-

terized with increased angiogenesis, often to be rec-

ognized as parallel vessels.

Also in other disciplines like colonoscopy, bron-

choscopy, hysteroscopy, vascularizaton patterns are

important for the detection of intestinal, lung, and

uterine tumors.

The software implementation of a vasculariza-

tion highlighting application was already developed

by eSaturnus for early tests with a few key users.

This prototype can process 3 standard deﬁnition video

frames per second and per core of an Intel Xeon E3-

1200 CPU. The work on hardware-accelerated line

detection, as described in this paper, allowed this ap-

plication to deliver smooth, low-latency ﬁltered video

on the same space and power footprint as the original

software-only implementation.

Besides medical applications also various indus-

trial applications beneﬁt from real-time line detection.

One example is automatic crack detection in various

materials, such as natural stone (ﬁg. 2), composites,

plastics, metals, glass and concrete. During produc-

tion or processing of these materials tiny cracks can

cause parts to break with high additional costs. Au-

tomatic detection of cracks in incoming raw materials

using a machine vision system before production can

be used to reduce these costs. Another application for

fast line detection is automatic alignment or placing

objects using robots.

2.3 Code Proﬁling

As a start, the more complex and time consuming

parts of the source code had to be identiﬁed. This

was done by proﬁling the code and analysing the re-

sult to detect the most time consuming parts. Since

the application uses images from a video stream as

input, some parts will be run for every frame, while

other parts are run only once. The proﬁling resulted

in one function comprising six time-consuming loops

through which were computed over every frame: the

six passes of different log-Gabor ﬁlters over the im-

age.

A second time-consuming part of the algorithm is

the preparation of the log-Gabor ﬁlter itself by com-

puting the coefﬁcients. But because these ﬁlters are

kept ﬁxed during the processing of a video stream

they can be precomputed and are not interesting to

spend optimisation effort on.

3 GPU OPTIMISATION

As explained above, we will implement this algorithm

on two different hardware platforms. This section will

detail our GPU implementation, while the next sec-

tion is about the FPGA implementation.

For the GPU implementation of this algorithm, we

chose for the OpenCL language, because of its ability

to target heterogeneous hardware platforms and its ex-

cellent code portability across different GPU vendors.

In the subsections below, we ﬁrst give an overview of

OpenCL and its coding philosophy. After that, the

speciﬁcs of the code porting OpenCL we did are de-

tailed along with the best practices we learned from

this case. Timing results will be given in chapter 5.

3.1 OpenCL

Modern computer platforms include one or more

CPUs and GPUs (and even DSPs amongst others). All

these hardware types are designed and optimized for

a speciﬁc type of calculations. OpenCL, Open Com-

puting Language (Khronos, 2011), is a quite novel

open standard for heterogeneous computing. It is a

framework for writing programs that can use these

platforms in an heterogeneous way. This is in great

contrast to CUDA, developed by Nvidia, which can

exclusively used for Nvidea GPU hardware. OpenCL

allows to write an efﬁcient and portable implementa-

tion of an algorithm which exploits the possibilities

for parallellizing parts of the algorithm on the most

suitable devices (multi-core CPU, GPU, celltype ar-

chitectures or other parallel processors). Since it is

heterogeneous, it is not nessecary to know in advance

which hardware will be used to execute the algorithm.

The used platform can easily be changed by changing

an initialisation variable of the program. Since differ-

ent devices have different instruction sets, the compi-

lation of the OpenCL kernels happens online (during

the execution of the program).

The code is written in the form of kernels. A ker-

nel is a block of code, written in a language based

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

114

Figure 3: The execution of the kernels is divided in work-

groups, which can be subdivided in work items. Each work

item executes an instance of the kernel.

on C99, that can be executed in parallel. For exam-

ple, when each value of a matrix has to be multiplied

by a certain value, each kernel contains the code for

one multiplication and this kernel will be executed

for all elements of the matrix. The execution of the

NDRange (all kernels that have to be executed) is

subdivided into workgroups. A workgroup is subdi-

vided into work-items, which will execute the kernels

in parallel (ﬁgure 3). To distinguish between differ-

ent executing threads, each thread has a unique global

id, and within a workgroup each thread has a unique

local id. Both are assigned for each dimension.

Figure 4: Memory model of a GPU, from slow to fast:

Global memory, Local memory, Private memory.

Figure 4 shows the memory model of a GPU de-

vice. The memory access times are ranging from the

slowest at the bottom (starting with the memory of the

host computer) to the fastest at the top (private mem-

ory). The global memory of the GPU (and CPU) is

shared over all executing work items, the local mem-

ory is shared over the work items in the same compute

unit (workgroup) and the private memory is only ac-

cessible by the running work item.

3.2 Code Porting to OpenCL

OpenCL has the advantage that it is a middleware

built upon C/C++. Hence, porting an algorithm that is

already written in C/C++ to OpenCL is not that com-

plex.

The general approach was to identify the code that

had to be run for every image frame and search for

the loops within that code. Since OpenCL on GPUs is

highly parallel, embarrassingly enough, parallel loops

that iterate over every image pixel are the most efﬁ-

cient to port to OpenCL for the biggest performance

gain.

Porting code to OpenCL can be divided in three

parts. First, the different loops must be ported to

OpenCL kernels, so they can be run on the GPU.

Since the code made use of the highly optimized Intel

Integrated Performance Primitives library, step 2 was

to ﬁnd alternatives for these functions and also port

those to OpenCL. Included in this step is the merging

of several smaller loops into bigger ones. This way,

loops 2, 3 and 4 were merged into one, and the Intel

IPP functions were included in the loops most adja-

cent to them. Step 3 is the elimination of data trafﬁc

between the host and the GPU, as this is very time

consuming over the slow PCI-Express bus.

We encountered some problems during this, al-

though most of them were quickly solved:

• The use of the Intel Integrated Performance Prim-

itives library took some time to get similar func-

tionality that could be ported to the GPU. Since

the IPP library makes excellent use of SSE in-

structions and multiple cores, it was sometimes

difﬁcult to beat the performance of these func-

tions. Optimizing the OpenCL code was neces-

sary to getting higher performance on the GPU.

• Different DFT/iDFT libraries yield different re-

sults. Since the IPP library isn’t very well docu-

mented as to how the different functions are im-

plemented, switching to another library caused

some problems with the results. AMD has it’s

own OpenCL Math library, called APPML, which

can be used as an alternative for Intel’s IPP DFT

functions. But they too don’t share it’s implemen-

tation details with the user.

• Windows/Linux compatibility issues. These is-

sues can mostly be traced back to the different

implementation of the size_t type. In Windows,

this is always four bytes, as in OpenCL. In Linux,

on the other hand, it can be eight bytes for a 64-

TheBattleoftheGiants-ACaseStudyofGPUvsFPGAOptimisationforReal-timeImageProcessing

115

bit OS, the OpenCL size is still only four bytes

though.

The main lesson learned is that the simple tech-

nique of GPU-optimizing only the code parts that are

identiﬁed as the most computationally intensive by

the proﬁler is not a good idea. In many cases, little

is gained (or the result is even slower), because of the

increased need of CPU-GPU data trafﬁc. Data local-

ity, i.e. keeping data as long as possible on the GPU,

is much more important.

3.3 Ease-of-use Evaluation of OpenCL

In this section we will discuss our experiences with

the use of OpenCL as a way to optimize an algorithm

by running it on GPU. We will comment on the learn-

ing curve and give tips and tricks for development.

Learning Curve. Since it is a quite novel standard,

the available literature is still growing. The spec-

iﬁcations released by the Khronos group (Khronos,

2011) are very valuable as a reference for function

calls while developing. It does not only explain how

to use the functions, but also gives possible errors and

shows how to prevent them. Although it is a great

help, it does not contain enough information to ex-

ploit the possibilities of OpenCL to produce the best

implementation. It is necessary to know how OpenCL

works, to fully exploit these opportunities. When we

started using OpenCL, the learning was mostly based

on examples and a trial and error-approach, which re-

sults in a longer learning curve. Now, the available

literature (Tsuchiyama et al., 2009; Benedict et al.,

2011) offers a more complete range of books which

reduces the learning curve drastically and can also

teach the reader a correct way of programming for a

high performance gain.

Development. OpenCL focuses on heterogeneity.

This comes at the cost of a lot of function calls to

set up your execution environment (creating a plat-

form, creating devices, creating a program, creating

command queues, ...). This can be seen as a disad-

vantage, but once these functions are written, they

can easily be reused in later projects without losing

the ﬂexibility it offers. This ﬂexibility allows an easy

change of execution device without modifying your

kernel code. To make optimal use of the possibili-

ties of OpenCL, it is necessary to understand every

detail of the algorithm to implement. Just copy-and-

pasting existing source code to kernel code can give a

speed up, but this will be small compared to an imple-

mentation which exploits the availability of fast mem-

ory, the highest parallellization possible and sequen-

tial memory access. The upcoming amount of (pub-

lic) available libraries of optimized implementations

of commonly used functions (matrix multiplication,

image ﬁltering, convolution, ...) can limit the devel-

oping time, since the developer only needs to focus

on the rest of the algorithm.

4 FPGA OPTIMISATION

4.1 Algorithm Adaptation

Since the architecture of an FPGA is completely dif-

ferent than the architecture of a GPU, not all algo-

rithms that can be ported successfully to a GPU can

also be successfully ported to an FPGA. If an algo-

rithm can be rewritten such that it can handle stream-

ing data without large memory blocks an FPGA im-

plementation is often possible. Examples of such al-

gorithms include simple image ﬁltering operations,

where only a small neighborhood of pixels is neces-

sary at a certain moment. The ﬁrst step in porting im-

age analysis algorithms into FPGAs is to rewrite the

algorithm into a streaming algorithm. In our research

ﬁrst an attempt was made to convert the oriented

phase congruency energy features (Kovesi, 1999)

used by eSaturnus into a streaming algorithm that

ﬁts the proposed FPGA (a Xilinx Spartan6 LX150).

The original algorithm uses 24 oriented log-Gabor

ﬁlters (4 scales, 6 orientations) which are not sepa-

rable in the spatial domain. Calculation in the fre-

quency domain however introduces the need for 24

parallel inverse Fourier transforms which do not ﬁt

on the FPGA. An approximation in the spatial domain

using 3 separable Gaussian derivative kernels can be

made with good results (illustrated in ﬁg. 5). This is

inspired by the DoG approximation of the Laplacian

(Mexican Hat function) in e.g. (Lowe, 2004). How-

ever, since 3 of these kernels are necessary for each

approximation for both the even and odd parts this

results in storing 144 separable ﬁlter results. With

relatively large spatial kernels (e.g. 21×21 pixels)

the internal memory of the FPGA for storage of the

line buffers is not sufﬁcient on the targeted Spartan 6

FPGA. Not even the largest Virtex 7 FPGAs have the

required 2.880 BRAM blocks suitable for such imple-

mentations. Moreover, using external memory would

cost too much data transfer overhead. Therefore, we

switched to an alternative line enhancement algorithm

that yields similar results (in terms of PSNR) for the

FPGA implementation.

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

116

Figure 5: A log-Gabor ﬁlter (kernel shown on the left) is ap-

proximated by a combination of 3 Gaussian derivative ker-

nels (right).

4.2 Orientation Score Algorithm

The orientation score framework (Kalitzin et al.,

1999; Duits and Franken, 2010a; Duits and Franken,

2010b) has been proven very useful for line detec-

tion and enhancement. It is also based on a set of

oriented ﬁlters, similar to the log-Gabor ﬁlters used

in the phase congruency algorithm. However, instead

of calculating phase features in each pixel to enhance

lines a simple group convolution (a convolution not

only over the spatial domain, but also over the orien-

tation domain) is performed that is very suitable for

FPGA implementations. In our experiments 24 ﬁlters

are used (3 scales, 8 orientations) to have a compa-

rable complexity as the phase congruency algorithm.

The ﬁlters are not separable in the spatial domain and

are similar to the log-Gabor ﬁlters. The group convo-

lution is comparable in the number of multiplications

and additions to the phase congruency algorithm, but

can be better optimized for FPGA implementations.

4.3 FPGA Implementation

The orientation score algorithm is implemented di-

rectly in VHDL using simple arithmic operators, reg-

isters, multiplexers and FIFO (First In First Out)

buffers. The data is streamlined through a number

of registers and FIFO buffers in such a way that at a

certain clock cycle all necessary pixels for the N × N

neighborhood are present in registers. Then in parallel

the ﬁlter operations are performed resulting in all 24

ﬁlter results at a certain pixel position in each clock

cycle. These results are again streamlined through

a number of registers and FIFO buffers to obtain an

M × M × 24 neighborhood of all ﬁlter results to per-

form the group convolution, again resulting in one

value per pixel clock. This way, in each clock cycle

one pixel is loaded and one pixel result is presented.

The maximum clock frequency thus determines the

maximum amount of pixels per second that can be

processed. All calculations are ﬁxed-point calcula-

tions with a ﬂexible position of the point. This is pos-

sible without losing accuracy due to the carefully cho-

sen ﬁlter values.

5 RESULTS

In this section, we will ﬁrst examine the timing re-

sults of the GPU implementation (5.1) and the FPGA

implementation (5.2) respectively.

5.1 GPU Results

First we will present the timing results of our

OpenCL-based GPU optimization. In table 1 the dif-

ferent steps of our GPU porting process, as described

in part 3.2, and their respective speed gains can be

found. Results are generated on an Intel Core i7 950,

6GB RAM, AMD Radeon HD6870 with Windows

7 Professional. The software used is Visual Studio

2010, with the AMD Accelerated Parallel Program-

ming (APP) SDK and AMD APPML (APP Math Li-

brary).

Table 1: GPU optimization: processing time/image (in ms)

for 720×576 resolution at different steps of the porting pro-

cess.

Loop 1 Loop 2,3,4 Loop 5 Loop 6 Total w/trafﬁc

Ref. 122.0 214.78 7.14 52.28 396.21 408.40

Step 1 106.75 126.38 8.74 4.51 246.39 303.88

Step 2 67.45 5.24 0.071 5.66 78.54 166.18

Step 3 6.81 0.015 0.0026 0.0019 6.83 40.93

In the reference implementation and step 1 of the

port, loops 2, 3 and 4 were still separated from each

other in loops or different kernels. It is only in step

2 that these kernels were taken together to construct

one big OpenCL kernel. Doing this eliminated a lot

of data trafﬁc from host to GPU and otherwise, which

accounts for the large gain in speed performance. In

step 3, the AMD library with FFT implementation in

OpenCL was used and all dependecies to the IPP li-

brary removed, what resulted in another tremendous

speed-up to 41 ms for a 720×576 image frame. Tak-

ing also the preprocessing and processing times in ac-

count, this boils dow to 65 ms, or more than 15 fps.

The resulting processing speed for different image

resolutions is given the graph of ﬁgure 6. We can see

that for smaller images of e.g. 360×288, the resulting

speed is even more impressive: about 14 ms or about

30 fps.

When reducing the number of scales or orienta-

tions ﬁltered at, the framerate increases also. At 3

scales (instead of 4), SD video is processed at 18 fps.

When the number of orientations is reduced to 4 in-

stead of 6, the framerate is 24 fps.

TheBattleoftheGiants-ACaseStudyofGPUvsFPGAOptimisationforReal-timeImageProcessing

117

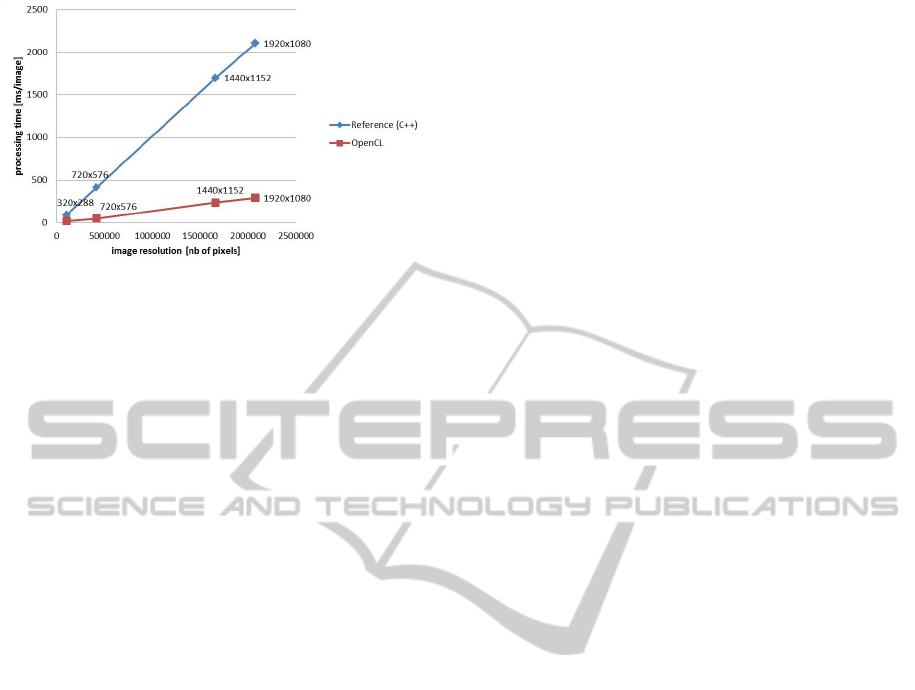
Figure 6: Processing speed results of the GPU implementa-

tion as compared to the reference C++ code started from.

5.2 FPGA Results

The VHDL code is synthesized using the Xilinx ISE

for a Spartan 6 LX150 FPGA. Using a gigabit Ether-

net connection the image data is loaded into the FPGA

and the results are sent back to the PC again. The Gi-

gabit Ethernet PHY (Physical layer) runs at 125MHz

with 8 bits in parallel. Since we use 8 bits per pixel

this results in a pixel clock of 125 Mega Pixel (MP)

per second. The VHDL design runs at 125MHz and

is thus also capable of processing the image at 125

MP per second. Before the output is valid however,

the FIFO buffers need to be ﬁlled. The delay between

ﬁrst pixel in and ﬁrst pixel out is in total a bit over

12000 clock cycles which results of a delay of 96 mi-

croseconds. In practice the demonstration unit is lim-

ited to the bandwidth of the gigabit Ethernet interface

which is below 125 MP per second due to overhead

of the packets. A Full HD video stream at 30 frames

per second is successfully tested.

6 EVALUATION

As explained above, we evaluated different criteria of

the two implementations: speed performance, code

translation effort, hardware cost, power efﬁciency, in-

tegrateability and physical space.

6.1 Speed Performance

On GPU, we achieved real-time performance on stan-

dard deﬁnition (SD) video (15 fps at 720×576 pix-

els). This is already quite impressive, compared to

our initial CPU implementation which only ran at 2

fps at that resolution. But the FPGA implementation

surpasses this greatly by showing timing results of 30

fps at HD resolution (1920×1080 pixels).

6.2 Code Translation Effort

While code porting to GPU via OpenCL was straight-

forward, an implementation on FPGA was much

more of a hassle. The only actual issue for

the OpenCL implementation was ﬁnding OpenCL-

versions of proprietary CPU-optimized software li-

braries. For the FPGA implementation, we were not

able to directly port the available algorithm. After

spending quite some time searching for approximated

ﬁlter kernels, this approach proved unfeasible. There-

fore, we had to make use of a totally different line

detection algorithm for the FPGA version. Moreover,

next to the tedious VHDL coding of the FPGA im-

plementation itself, we spent lots of effort to get the

CPU-FPGA interface working. Happily enough, both

FPGA and GPU developments took about 2-3 man

months because of the experiencedness of our FPGA

developer at InViso.

6.3 Hardware Cost

The actual hardware cost of the two platforms is com-

parable. The mainstream AMD GPU board that we

used in our demonstrator can be bought for around

e 160, while the Spartan 6 board is around e 200.

Note that the compared prices are for evaluation

boards only. The naked component cost for self-

assembly is also not signiﬁcantly different.

6.4 Power Efﬁciency

When measuring the power usage of both platforms

(in full function) with a Watt meter, we observed that

the GPU consumed 65W extra on top of the 135W of

the PC itself, while the FPGA took less than 10W.

6.5 Integrateability

Although the impressive speed gain results of our

FPGA implementation, the integration of such a

hardware platform in an existing PC-based comput-

ing platform showed not obvious. We encoutered

quite some issues during interfacing between PC

and FPGA, which in the end was solved as a UPD

Ethernet connection. Moreover, we see that the

overall processing speed of the FPGA platform was

severely constrained by that interface. For GPU

hardware, these problems were non-existent because

of the seamless hardware integration and the fact

that OpenCL is developed for hybrid CPU/GPU plat-

forms.

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

118

6.6 Physical Space

We see that the FPGA solution ended up very efﬁ-

cient in terms of board space: the unit measures only

5cm×4cm. The computational density of the GPU

solutions is an order of magnitude worse, because the

AMD7850 is a PCB of about 26cm×12cm (with two

huge fans), which even does not ﬁt in a standard desk-

top case.

7 CONCLUSIONS

In this paper, we have compared the optimal imple-

mentation of a complex image processing algorithm

on GPU and FPGA. On both target platforms, we

achieved an impressive speed-up factor, albeit with

quite different amounts of effort.

In general, we can conclude that both FPGA and

GPU platforms have important — but different — ad-

vantages. While the ultimate ﬂexibility of a FPGA-

based system can lead to a speed performance that is

an order of magnitude better than the GPU-based plat-

form, the effort spent in developing a FPGA imple-

mentation of a certain algorithm boils down to quite

more effort as compared to the C/C++ to OpenCL-

translation needed for a GPU implementation. More-

over, we saw that the original algorithm was unsuited

to be implemented in a FPGA, even after an approx-

imated simpliﬁcation, which forced us to rethink the

algorithm and move to a totally different approach. In

terms of physical space and power consumption, the

FPGA is certainly the winner.

Nevertheless, because of the ease to integrate the

GPU implementation in an existing server installa-

tion, eSaturnus chose the latter. At this moment, our

GPU code is running in a real hospital in Berlin as a

clinical try-out.

ACKNOWLEDGEMENTS

This work is partially supported by the European

Commision in the CrossRoads project of the Interreg

IVA program Border Region Flanders-Netherlands.

REFERENCES

Asano, S., Maruyama, T., and Yamaguchi, Y. (2009). Per-

formance comparison of fpga, gpu and cpu in image

processing. In International Conference on Field Pro-

grammable Logic and Applications (FPL), pages 126–

131.

Bay, H., Ess, A., Tuytelaars, T., and Gool, L. V. (2008).

Speeded-up robust features (surf). Computer Vision

and Image Understanding, 110.

Benedict, G. R., David, K., Perhaad, M., and Dana, S.

(2011). Heterogeneous Computing with OpenCL.

Morgan Kaupmann.

Cope, B., Cheung, P., Luk, W., and Witt, S. (2005). Have

gpus made fpgas redundant in the ﬁeld of video pro-

cessing? In Proceedings of IEEE International Con-

ference on Field-Programmable Technology, pages

111–118.

da Silva, B., Braeken, A., D’Hollander, E., Touhaﬁ, A.,

Cornelis, J., and Lemeire, J. (2013). Performance

and toolchain of a combined gpu/fpga desktop. In In

Proceedings of the ACM/SIGDA international sympo-

sium on Field programmable gate arrays (FPGA ’13),

pages 274–274, New York, NY, USA. ACM.

Duits, R. and Franken, E. M. (2010a). Left invariant

parabolic evolution equations on SE(2) and contour

enhancement via invertible orientation scores, part I:

Linear left-invariant diffusion equations on SE(2).

Quarterly of Applied mathematics, AMS, 68:255–292.

Duits, R. and Franken, E. M. (2010b). Left invariant

parabolic evolution equations on SE(2) and contour

enhancement via invertible orientation scores, part I:

Nonlinear left-invariant diffusion equations on invert-

ible orientation scores. Quarterly of Applied mathe-

matics, AMS, 68:293–331.

Kalitzin, S. N., Romeny, B. M. H., and Viergever, M. A.

(1999). Invertible apertured orientation ﬁlters in im-

age analysis. IJCV, 31:145–158.

Khronos (2011). OpenCL - the open standard for paral-

lel programming of heterogeneous systems. Khronos

Group.

Kovesi, P. (1999). Image features from phase congruency.

Videre: A Journal of Computer Vision Research, 1.

Lowe, D. (2004). Distinctive image features from scale in-

variant keypoints. International Journal on Computer

Vision, 60:91–110.

Tsuchiyama, R., Nakamura, T., Lizuka, T., Asahara, A.,

and Miki, S. (2009). The OpenCL Programming book.

Fixstars.

Tyrrell, J., Mahadevan, V., Tong, R., Brown, E., R.K., R. J.,

and Roysam, B. (2005). 2-d/3-d model-based method

to quantify the complexity of microvasculature im-

aged by in vivo multiphoton microscopy. Microvas-

cular Research, 70:165–178.

TheBattleoftheGiants-ACaseStudyofGPUvsFPGAOptimisationforReal-timeImageProcessing

119