A Qualitative Framework for Analysing Homeostasis in Gene Networks

Sohei Ito

, Shigeki Hagihara

and Naoki Yonezaki

Department of Fisheries Distribution and Management, National Fisheries University,

2-7-1 Nagata-Honcho, Shimonoseki, Yamaguchi, Japan

Department of Computer Science, Tokyo Institute of Technology, 2-12-1 Ookayama, Meguro-ku, Tokyo, Japan

Keywords:

Gene Regulatory Network, Homeostasis, Temporal Logic, Realisability.

Abstract:

Toward the system level understanding of the mechanisms contributing homeostasis in organisms, a computa-

tional framework to model a system and analyse its properties is indispensable. The purpose of this work is to

provide a framework which enables testing and validating homeostatic properties on gene regulatory networks

in silico. Based on a qualitative analysis framework for gene networks using temporal logic, we proposed

a novel formulation of homeostasis by the notion of realisability. This formulation of homeostasis yields a

qualitative method to analyse homeostasis of gene networks. In this formulation, homeostasis is captured by

a response not for just an instantaneous stimulation such as dose-response relationships but for any input sce-

nario e.g. oscillating or continuous inputs, which is difﬁcult to be captured by quantitative models. Moreover,

we can consider any number of inputs from an environment without difﬁculty. Such ﬂexibility is a notable

advantage of our framework. We demonstrate the usefulness of our framework in analysing a number of small

but tricky networks.

1 INTRODUCTION

Qualitative methods in modelling and simulation of

gene networks (de Jong et al., 2003; Fages et al.,

2004; Bernot et al., 2004; Batt et al., 2005) are

useful in that we do not need quantitative informa-

tion since such information on kinetic parameters or

molecular concentrations are usually absent, as we

can see from current databases e.g. Reactome (Croft

et al., 2011), GeneCards (Safran et al., 2010), Meta-

cyc (Karp et al., 2002), Ingenuity



Knowledge Base

and KEGG (Kanehisa et al., 2011). Ito et al. (Ito et al.,

2010) proposeda method for analysing gene networks

using linear temporal logic (LTL) (Emerson, 1990), in

which, a gene network is modelled as an LTL formula

which speciﬁes its possible behaviours.

Their method for analysing gene networks is

closely related with veriﬁcation of reactive system

speciﬁcations (Barringer et al., 1984; Pnueli and Ros-

ner, 1989; Abadi et al., 1989; Wong-Toi and Dill,

1991; Mori and Yonezaki, 1993; Vanitha et al., 2000;

Hagihara and Yonezaki, 2006). A reactive system is a

system that responds to requests from an environment

at an appropriate timing. Systems controlling an el-

evator or a vending machine are typical examples of

reactive systems. Biological systems with external in-

puts or signals can be naturally considered as reactive

systems.

Realisability (Pnueli and Rosner, 1989; Abadi

et al., 1989) is a desirable property of reactive sys-

tem speciﬁcations which requires systems to behave

according to a speciﬁcation in reaction to any input

from an environment. In terms of biological systems,

this property means that a system behaves with satis-

fying a certain property (e.g. keeping a concentration

within some range) in reaction to any input from an

environment (e.g. for any stress or stimulation). That

is to say, the system is homeostatic with respect to the

property.

Using this correspondence, we formulate the no-

tion of homeostasis by realisability of reactive sys-

tems. Our formulation captures homeostasis of not

only logical structure of gene networks but also prop-

erties of any dynamic behaviours of networks. For

example, we can analyse in our framework whether

a given network maintains oscillation over time in

response to any input sequence. This formulation

yields not only a novel and simple characterisation of

homeostasis but also provides a method to automati-

cally check homeostasis of a system using realisabil-

ity checkers (Jobstmann and Bloem, 2006; Jobstmann

et al., 2007; Filiot et al., 2009; Bloem et al., 2010).

Ito S., Hagihara S. and Yonezaki N..

A Qualitative Framework for Analysing Homeostasis in Gene Networks.

DOI: 10.5220/0004731400050016

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 5-16

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

௩

௪

Figure 1: Regulation effect.

Based on this formulation we analyse some homeo-

static properties of a number of small but tricky gene

networks.

This paper is organised as follows. Section 2 and

3 reviews the qualitative analysis method using LTL

(Ito et al., 2010) on that our work is grounded. In sec-

tion 4, we introduce the notion of realisability and for-

mulate homeostasis by this notion. Based on this for-

mulation, we show some example networks and anal-

yse homeostatic properties of them in section 5. Sec-

tion 6 discusses some related works. The ﬁnal section

offers conclusions and future directions.

2 LOGICAL

CONCEPTUALISATION OF

BEHAVIOURS

In gene regulation, a regulator is often inefﬁcient be-

low a threshold concentration, and its effect rapidly

increases above this threshold (Thomas and Kauff-

man, 2001). The sigmoid nature of gene regulation

is shown in Figure 1, where gene u activates v and

inhibits w. Each axis represents the concentration of

products for each gene.

Some important landmark concentration values

for u are 1) the basal level, 2) the level u

at which

u begins to affect v, and 3) the level u

at which u

begins to affect w. The values u

and u

are thresh-

olds of gene u. Whether genes are active or not can

be speciﬁed by the expression levels of their regula-

tor genes. If the concentration of u exceeds u

then v

is active (ON), and if the concentration of u exceeds

then w is not active (OFF). This switching view of

genes leads us an abstract representation of network

behaviours, transition systems.

Let us consider a simple network depicted in Fig-

ure 2, in which gene x activates gene y and receives

the positive input from the environment.

input

Figure 2: A simple example.

input

base

௫

௬

Figure 3: An example behaviour of the network in Figure 2.

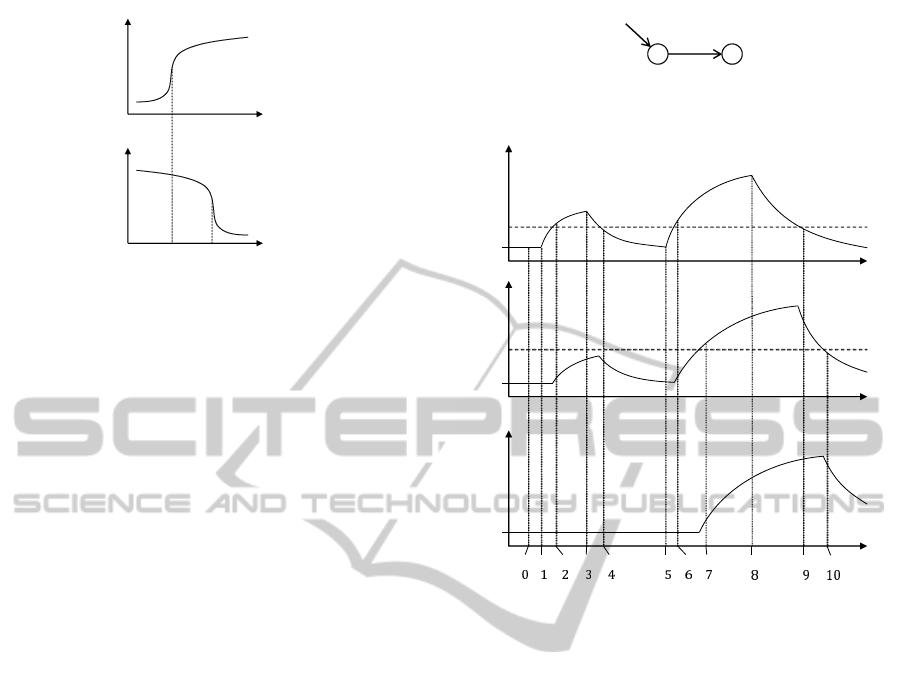
We consider the behaviour depicted in Figure 3 in

which e

is a threshold level of the input to activate

x and x

a threshold of x to activate y. At time t

the input, gene x and gene y are at basal level. At

time t

, the input to x is coming and the level begins

to increase. At time t

, since the level of input to x

exceeds e

, gene x is being expressed. At time t

, the

input to x is stopped and the level begins to decrease.

At time t

, since the level of input to x falls below e

gene x stops being expressed; that is, the level of x is

decreasing. At time t

the input to x is again coming

and at time t

gene x is being expressed since the input

level is over e

. At time t

, gene x is expressed over

, so gene y is being expressed. At time t

the input

to x is stopped and at time t

falls below e

so gene x

stops being expressed. At time t

, since gene x falls

below x

, gene y stops being expressed, after which

gene x and y stay at their basal level.

This behaviour can be represented as a transition

system in Figure 4. A transition system consists of

states (represented as circles) and transitions (repre-

sented as arrows). A state represents a current sta-

tus of the system, e.g. what genes are active or what

are the expression levels of genes. A transition rep-

resents a change of states. To describe status of the

system, we introduce logical propositions that repre-

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

݅݊

௫

݅݊

௫

݋݊

௫

݋݊

௫

݅݊

௫

݅݊

௫

݋݊

௫

݅݊

௫

݋݊

௫

௬

݋݊

௬

௫

݋݊

௫

௬

݋݊

௬

݋݊

௬

1 2 3 4 5 6 7 8 9 10

Figure 4: A Transition system corresponding to Figure 3.

sent whether genes are active or not (ON or OFF) and

whether concentrations of products of genes exceed

threshold values. In this network, we introduce the

propositions in

, on

, e

, and x

. The meaning of

each proposition is:

• on

, on

: whether gene x or y is active,

• in

: whether the input to gene x is coming,

• x

: whether the concentration of the products of

gene x exceeds the threshold x

• e

: whether the level of the input to gene x exceeds

the threshold e

Propositions depicted below each state in Figure 4

shows the status of it. For example, state 2 represents

the situation that the input to gene x is coming, the

level of input is above the threshold e

and gene x is

ON. We can observe that state 0 represents the situ-

ation at time t

, state 1 represents t

, ... and state 10

represents t

A single state transition can represent any length

of time, since the actual duration of the transition (in

real time) is immaterial

in this abstraction. There-

fore, the difference between t

−t

and t

−t

, the du-

ration of the input to x in Figure 3, is not captured

directly. We, however, can see that the latter duration

is longer by comparing the propositions in state 1 to

3 and in state 5 to 9: the latter duration is sufﬁciently

long for x to activate y.

Note that the real values of thresholds are also ir-

relevant. Propositions such as x

merely represent the

fact that the concentration of x is above the threshold

at which x affects y.

In this abstraction, behaviours are identiﬁed with

each other if they have the same transition system.

This abstraction seems rather simple but preserves es-

sential qualitative features of the dynamics (Snoussi

and Thomas, 1993; Thomas and Kauffman, 2001).

Any behaviour of gene networks can be abstracted

as transition systems. Sometimes, we need more

propositions for expression levels of genes besides

threshold values. We can introduce any number of

Symbols e

and x

are already used to represent the

thresholds but we can clearly distinguish them from the con-

text

This property is called speed independence (Rabi-

novich, 1998)

them. We will see an example of such extra proposi-

tions in section 5, in which we prepare two proposi-

tions for one activation of a gene to capture a level of

the activation.

3 MODELLING BEHAVIOURS OF

GENE NETWORKS IN LTL

3.1 Linear Temporal Logic

First we introduce linear temporal logic.

If A is a ﬁnite set, A

denotes the set of all inﬁ-

nite sequences on A. The i-th element of σ ∈ A

denoted by σ[i]. Let AP be a set of propositions. A

time structure is a sequence σ ∈ (2

)

where 2

the powerset of AP. The formulae in LTL are deﬁned

as follows.

• p ∈ AP is a formula.

• If φ and ψ are formulae, then ¬φ, φ∧ ψ, φ∨ψ and

φUψ are also formulae.

We introduce the following abbreviations: ⊥ ≡

p∧ ¬p for some p ∈ AP, ⊤ ≡ ¬⊥, φ → ψ ≡ ¬φ∨ψ,

φ ↔ ψ ≡ (φ → ψ) ∧ (ψ → φ), Fφ ≡ ⊤Uφ, Gφ ≡

¬F¬φ, and φWψ ≡ (φUψ)∨Gφ. We assume that ∧, ∨

and U binds more strongly than → and unary connec-

tives binds more strongly than binary ones.

Intuitively, ¬φ means ‘φ is not true’, φ∧ ψ means

’both φ and ψ are true’, φ ∨ ψ means ’φ or ψ is true’,

and φUψ means ‘φ continues to hold until ψ holds’. ⊥

is a false proposition and ⊤ is a true proposition. φ →

ψ means ’if φ is true then ψ is true’ and φ ↔ ψ means

’φ is true if and only if ψ is true’. Fφ means ‘φ holds at

some future time’, Gφ means ‘φ holds globally’, φWψ

is the ‘weak until’ operator in that ψ is not obliged to

hold, in which case φ must always hold. The formal

semantics are given below.

Let σ be a time structure and φ be a formula. We

write σ |= φ for φ is true in σ and we say σ satisﬁes φ.

The satisfaction relation |= is deﬁned as follows.

σ |= p iff p ∈ σ[0] for p ∈ AP

σ |= ¬φ iff σ 6|= φ

σ |= φ∧ψ iff σ |= φ and σ |= ψ

σ |= φ∨ψ iff σ |= φ or σ |= ψ

σ |= φUψ iff (∃i ≥ 0)(σ

|= ψ and

∀ j(0 ≤ j < i)σ

|= φ)

where σ

= σ[i]σ[i + 1]. . . , i.e. the i-th sufﬁx of σ.

An LTL formula φ is satisﬁable if there exists a time

structure σ such that σ |= φ.

AQualitativeFrameworkforAnalysingHomeostasisinGeneNetworks

x y

Figure 5: An example network.

3.2 Specifying Possible Behaviours of

Gene Networks in LTL

Now we review the method proposed in (Ito et al.,

2010) to model behaviours of a given network in lin-

ear temporal logic, using an example gene network

depicted in Figure 5.

In this network gene x activates gene y and gene y

inhibits gene x. Gene x has a positive environmental

input. Let x

be the threshold of gene x to activate

gene y, y

the threshold of gene y to inhibit gene x

and e

the threshold of the input to activate gene x.

To specify possible behaviours of this network, we

introduce the following propositions.

• on

, on

: whether gene x and y are ON respec-

tively.

• x

, y

: whether gene x and y are expressed beyond

the threshold x

and y

respectively.

• in

: whether the input to x is ON.

• e

: whether the positive input from the environ-

ment to x is beyond the threshold e

The basic principles for characterising behaviours

of a gene network are as follows:

• Genes are ON when their activators are expressed

beyond some thresholds.

• Genes are OFF when their inhibitors are ex-

pressed beyond some thresholds.

• If genes are ON, the concentrations of their prod-

ucts increase.

• If genes are OFF, the concentrations of their prod-

ucts decrease.

We express these principles in LTL using the

propositions introduced above.

Genes’ Activation and Inactivation. Gene y is

positively regulated by gene x. Thus gene y is ON

if gene x is expressed beyond the threshold x

, which

is the threshold of gene x to activate gene y. This can

be described as

G(x

↔ on

)

in LTL. Intuitively this formula says gene y is ON if,

and only if, gene x is expressed beyond x

due to pos-

itive regulation effect of gene x toward gene y. As

for gene x, it is negatively regulated by gene y and

has positive input from the environment. A condition

for activation and inactivation of such multi-regulated

genes depends on a function which merges the multi-

ple effects. We assume that gene x is ON if gene y is

not expressed beyond y

and the input from the envi-

ronment to gene x is beyond e

; that is, the negative

effect of gene y is not operating and the positive effect

of the input is operating. Then this can be described

G(e

∧ ¬y

→ on

This formula says that if the input level is beyond e

(i.e. proposition e

is true) and gene y is not expressed

beyond y

(i.e. proposition y

is false; ¬y

is true),

then gene x is ON (i.e. proposition on

is true).

For the inactivation of gene x, we have choices to

specify the rule. Let us assume that gene x is OFF

when the input from the environment is under e

and

gene y is expressed beyond y

, that is, the activation

to gene x is not operating and the inhibition to gene x

is operating, in which case gene x will surely be OFF.

This is speciﬁed as

G(¬e

∧ y

→ ¬on

). (1)

For another choice, let us assume that the negative

effect from gene y overpowers the positive input from

the environment. Then we write

G(y

→ ¬on

), (2)

which says that if the inhibition from gene y is oper-

ating, gene x becomes OFF regardless of the environ-

mental input to gene x. Yet another choice is

G(¬e

∨ y

→ ¬on

) (3)

which says that gene x is OFF when the positive in-

put is not effective or negative regulation from gene

y is effective. For example, although gene y is not

expressed beyond the threshold y

(i.e. the negative

effect of gene y is not effective), gene x is OFF if the

positive effect of the input is not effective.

We also have several options for the activation of

gene x. The choice depends on a situation (or assump-

tion) of a network under consideration.

Changes of Expression Levels of Genes over Time.

If gene x is ON, it begins to be expressed and in some

future it will reach the threshold for gene y unless

gene x becomes OFF. This can be described as

G(on

→ F(x

∨ ¬on

)).

This formula means ‘if gene x is ON, in some future

the expression level of gene x will be beyond x

, or

otherwise gene x will become off’. This situation is

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

௬

݋݊

௫

൓

௬

݋݊

௫

൓

௬

݋݊

௫

௬

݋݊

௫

൓

௬

൓݋݊

௫

൓

௬

൓݋݊

௫

൓

௬

(a) (b)

Figure 6: If gene x is ON, (a) the expression level of gene x

is over x

, or (b) gene x becomes OFF before gene x reaches

, where s

c is a time structure.

௬

݋݊

௫

௬

݋݊

௫

௬

݋݊

௫

௬

݋݊

௫

௬

൓݋݊

௫

௬

൓݋݊

௫

൓

௬

(a) (b)

Figure 7: If gene x is ON and the current expression level is

over x

, (a) the expression level of gene x keeps over x

, or

(b) gene x becomes OFF and as a result the expression level

may fall below x

depicted in Figure 6. If gene x is ON and expressed

beyond x

, it keeps the level until gene x is OFF. This

can be described as

G(on

∧ x

→ x

W¬on

This formula means ‘if gene x is ON and the current

expression level of gene x is over x

, gene x keeps its

level until gene x becomes OFF, or otherwise gene x

keeps its level always’. This situation is depicted in

Figure 7.

If gene x is OFF, its product decreases due to

degradation. Thus if gene x is OFF and the current

expression level of x is over x

, it will fall below x

some future unless x becomes ON again. This can be

speciﬁed as

G(¬on

→ F(¬x

∨ on

)).

If the expression level of gene x is under x

and x is

OFF then it keeps the level (i.e. it does not increase

and exceed x

) until x is ON. This can be speciﬁed as

G(¬on

∧ ¬x

→ ¬x

Won

We have similar formulae for gene y and the in-

put into gene x from the environment for increase and

decrease of them.

The conjunction of above formulae(i.e. joining by

∧ operator) is the speciﬁcation of possible behaviours

of the network. In other words, time structures which

satisfy the formula are possible behaviours of the net-

work.

This method for modelling behaviours of gene

regulatory networks can be contrasted to usual quan-

titative methods like ordinary differential equation

models. We qualitatively model gene regulatory net-

works by temporal logic formulae instead of quan-

titative analytical formulae. Note that we have sev-

eral possible temporal logic speciﬁcations for a sin-

gle network depending on order of threshold values,

functions for multi-regulations and how we capture

increase and decrease of expression of genes. Inter-

ested reader may wish to consult (Ito et al., 2010; Ito

et al., 2013b) for detail.

4 REALISABILITY AND

HOMEOSTASIS

In this section we discuss the connection between re-

active systems and gene networks. Based on this con-

nection, we formulate homeostasis of gene networks

by realisability of reactive systems.

A reactive system is deﬁned as a triple hX,Y, ri,

where X is a set of events caused by the environ-

ment, Y is a set of events caused by the system and

r : (2

)

→ 2

is a reaction function. The set (2

)

denotes the set of all ﬁnite sequences on subsets of

X, that is to say, ﬁnite sequences on a set of environ-

mental events. A reaction function determines how

the system reacts to environmental input sequences.

Reactive system is a natural formalisation of systems

which appropriately respond to requests from the en-

vironment. Systems controlling vending machines,

elevators, air trafﬁc and nuclear power plants are ex-

amples of reactive systems. Gene networks which re-

spond to inputs or stimulation from the environment

such as glucose increase, change of temperature or

blood pressure can also be considered as reactive sys-

tems.

A speciﬁcation of a reactive system stipulates how

it responds to inputs from the environment. For exam-

ple, for a controller of an elevator system, a speciﬁca-

tion will be e.g. ‘if the open button is pushed, the

door opens’ or ‘if a call button of a certain ﬂoor is

pushed, the lift will come to the ﬂoor’. It is impor-

tant for a speciﬁcation of a reactive system to satisfy

realisability (Pnueli and Rosner, 1989; Abadi et al.,

1989), which requires that there exists a reactive sys-

tem such that for any environmental inputs of any tim-

ing, it produces system events (i.e. responds) so that

it satisﬁes the speciﬁcation.

To verify a reactive system speciﬁcation, it should

be described in a language with formal and rigorous

AQualitativeFrameworkforAnalysingHomeostasisinGeneNetworks

semantics. Widespread research in specifying and de-

veloping reactive systems lead to the belief that tem-

poral logic is the useful tool for reasoning them (Bar-

ringer, 1987; Pnueli and Rosner, 1989; Abadi et al.,

1989; Vardi, 1995). LTL is known to be one of

many other formal languages suitable for this purpose

and several realisability checkers of LTL are available

(Jobstmann and Bloem, 2006; Jobstmann et al., 2007;

Filiot et al., 2009; Bloem et al., 2010).

Now we deﬁne the notion of realisability of LTL

speciﬁcations. Let AP be a set of atomic propositions

which is partitioned into X, a set of input propositions,

and Y, a set of output propositions. X corresponds to

input events and Y to output events. We denote a time

structure σ on AP as hx

, y

ihx

, y

i. . . where x

⊆ X,

⊆ Y and σ[i] = x

∪y

. Let φ be an LTL speciﬁcation.

We say hX,Y, φi is realisable if there exists a reactive

system RS = hX,Y, ri such that

∀ ˜x.behave

( ˜x) |= φ,

where ˜x ∈ (2

)

and behave

( ˜x) is the inﬁnite be-

haviour determined by RS, that is,

behave

( ˜x) = hx

, y

ihx

, y

i. . . ,

where ˜x = x

. . . and y

= r(x

. . . x

Intuitively φ is realisable if for any sequence of in-

put events there exists a system which produces out-

put events such that its behaviour satisﬁes φ.

Example 1. Let X = {push

open

, push

} and Y =

{door

open

}. The speciﬁcation

G(push

open

→ Fdoor

open

)

is realisable since there is a reactive system hX,Y, ri

with r( ¯xa) = {door

open

} where ¯x is any ﬁnite sequence

on 2

and a ⊇ {push

open

}. The speciﬁcation

G((push

open

→ Fdoor

open

)∧(push

→ ¬door

open

))

is not realisable since for input sequence

{push

open

, push

}

there is no output sequence

which satisﬁes the speciﬁcation.

Realisability can be interpreted as the ability of

a system to maintain its internal condition irrespec-

tive of environmental inputs. In the context of gene

networks, realisability can be naturally interpreted as

homeostasis. For example, a network for control-

ling glucose level responds to an environmental in-

puts such as glucose increase or decrease in a manner

to maintain its glucose level within a normal range. In

the framework described in section 3, behaviour spec-

iﬁcations of gene networks can be regarded as reactive

system speciﬁcations. Based on this connection, we

formulate homeostasis by realisability.

Let hI, O, φi be a behaviour speciﬁcation of a gene

network where I is the set of input propositions, O is

the set of output propositions and φ is an LTL for-

mula characterising possible behaviours of the net-

work. Let ψ be a certain biological property of the

network. A network property ψ is homeostatic in

this network if for any input sequence x

. . . there

exists a reaction function r such that the behaviour

σ = hx

, r(x

)ihx

, r(x

, x

)i. . . is a behaviour of the

network (i.e. σ |= φ) and σ also satisﬁes the property

ψ (i.e. σ |= ψ). Thus we have the following simple

deﬁnition of homeostasis:

Deﬁnition 1. A property ψ is homeostatic with re-

spect to a behaviour speciﬁcation hI, O, φi if φ∧ ψ is

realisable.

In this deﬁnition we consider responses of a sys-

tem not only to initial instantaneous inputs such as

dose-response relationship but also to any input se-

quences (e.g. inputs are oscillating or sustained),

which is difﬁcult to be captured by ordinary differ-

ential models. Moreover, we have any number of en-

vironmental inputs thus we can consider homeostasis

against compositive environmental inputs.

Based on the method described in section 3 and

this formulation, we can analyse homeostasis of gene

networks using realisability checkers. In the next sec-

tion, we demonstrate our method in analysing a num-

ber of small but tricky networks.

5 DEMONSTRATION: ANALYSIS

OF HOMEOSTASIS FOR

EXAMPLE NETWORKS

First we consider the network in Figure 5 again. The

network in Figure 5 is expected to have a function that

whenever gene x becomes ON, the expression of gene

x will be suppressed afterward. This function main-

tains the expression level of gene x to its normal range

(low level). Despite of the extreme situation that the

input to gene x is always ON, the expression of gene

x inevitably ceases due to the activation of gene y and

its negative effect on gene x. Therefore this function

is expected to be homeostatic. Now we formalise this

verbal and informal reasoning with our framework.

The property ‘whenever gene x becomes ON, the ex-

pression of gene x will be suppressed afterward’ is

formally stated in LTL as:

G(on

→ F(¬on

∧ ¬x

)). (4)

This formula says that the property ‘if on

is true, it

becomes false and gene x is suppressed below x

some future’ always holds. We check whether this

formula is realisable with respect to a behaviour spec-

iﬁcation introduced in section 3.2. There are 6 propo-

sitions on

, on

, x

, y

, in

and e

for this network. The

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

x y

+ -

Figure 8: The network in Figure 5 with a negative input for

gene y.

partition of input propositions and output propositions

are straightforward, that is, in

is the only input propo-

sition since the environment only controls the input to

gene x. Other propositions represent internal states

of the network. Note that the environment cannot

directly control the proposition e

, which represents

whether the level of the input exceeds e

. To exceed

the level e

, the environment needs to give the input

for a certain duration.

We had three options in the inactivation rule of

gene x, i.e. formulae (1),(2) and (3). In all choices the

property is realisable since even if in

is always true,

we need y

being false for the activation of gene x due

to the clause G(e

∧ ¬y

→ on

). If in

is always true,

gene x will be expressed beyond x

, and it induces

y’s expression. As a result, gene y can be expressed

beyond y

at which gene y inhibits gene x. Thus on

may not be always true. If we replace the clause for

the activation of gene x as G(e

→ on

), which says if

the input is effective gene x must be ON regardless of

the negative effect of gene y, then the property is not

realisable.

For realisability checking, we used Lily

(Jobst-

mann and Bloem, 2006) which is a tool for checking

realisability of LTL speciﬁcations. To use Lily, we

specify input propositions, output propositions and an

LTL formula. The result of checking (Yes or No) is

output to command-line and if it is YES, it also out-

puts a state diagram.

Now we assume gene y accepts negative input

from the environment (Figure 8). We have the extra

input proposition in

and output proposition e

. We

describe the activation rule for gene y as follows in

which gene y can be OFF by the negative input from

the environment:

G(¬e

∧ x

→ on

G(e

→ ¬on

Is the property (4) homeostatic with respect to this

behaviour speciﬁcation? The realisability checker an-

swers ’No’. The reason is that if the input for gene

y is always ON, gene y cannot be ON, therefore the

negative effect from gene y to gene x cannot be effec-

tive. In this input scenario gene x cannot become OFF

after gene x becomes ON.

http://www.iaik.tugraz.at/content/research/

design veriﬁcation/lily/

x y

Figure 9: A bistable switch.

Now we consider the next example depicted in

Figure 9. In this network we provide two thresholds

and y

for gene y. The threshold y

is the level

enough to activate gene x when the negative input

from the environment is not effective. The threshold

is the level enough to activate gene x regardless of

negative effect from the environment, that is, y

is the

threshold beyond which gene y overpowers the envi-

ronmental input. The behaviour speciﬁcation for this

network will be somewhat complicated. First, we de-

scribe the fact that the threshold y

is greater than y

which is simply described as follows:

G(y

→ y

which says ’if gene y is expressed beyond y

, it is also

beyond y

(since y

> y

)’. Note that the proposition

means ’gene y is expressed beyond the threshold

’.

The activation rules and inactivation rules for gene

x are as follows:

G(¬y

→ ¬on

), (5)

G(e

∧ y

∧ ¬y

→ ¬on

), (6)

G(¬e

∧ y

→ on

), (7)

G(y

→ on

). (8)

Formula (5) says that if gene y is under y

, gene

x is OFF regardless of the environmental input. For-

mula (6) says that if gene y is in between y

and y

but the negative input is effective, gene x is OFF. For-

mula (7) says that gene x is ON when negative input

is not effective and gene y is expressed over y

. For-

mula (8) says that gene x is ON when gene y is just

expressed over y

The activation rule for gene y is simple:

G(x

↔ on

)

The change of the expression level of gene y when

it is ON are described as follows:

G(on

→ F(y

∨ ¬on

)), (9)

G(on

∧ y

→ y

W¬on

), (10)

G(on

∧ y

→ y

W¬on

). (11)

Formula (9) says that if gene y is ON, it will reach

the ﬁrst threshold y

or otherwise it will become OFF.

Formula (10) says that if gene y is ON and the current

level is over the ﬁrst threshold y

, it will keep over y

AQualitativeFrameworkforAnalysingHomeostasisinGeneNetworks

(this means it can be expressed beyond y

), or other-

wise gene y becomes OFF. Formula (11) says that if

gene y is ON and the current level is over the highest

threshold y

, it keeps y

or otherwise it will become

OFF.

We have similar formulae for the change of the

expression level of gene y when it is OFF.

G(¬on

→ F(¬y

∨ on

)),

G(¬on

∧ ¬y

→ ¬y

Won

G(¬on

∧ ¬y

→ ¬y

Won

For the change of the expression level of gene x

and the environmental input we have similar formulae

except they have only one threshold.

We check the bistability of the expression of gene

x, that is to say, if gene x can always be ON or always

be OFF. These properties are described as follows:

Gon

, (12)

G¬on

. (13)

By using Lily, we checked that both properties are

really homeostatic. Informal reasoning for the ﬁrst

property (12) is as follows. Suppose that the input se-

quence such that the negative input to x is always ef-

fective, which is the best choice for the environment

to inactivate gene x. The system’s response to satisfy

the bistability is to start at a state in which both gene x

and y are ON and gene x and gene y are expressed be-

yond x

and y

, respectively. Since gene y is expressed

beyond y

, gene x can continue to be ON regardless

of negative input to x. The expression of gene y is

supported by the positive effect from gene x. For the

second property (13), we assume that the negative in-

put is always ineffective. The system’s response is

simply to start a state that both gene x and y is OFF

and gene x and y are expressed below x

and y

, re-

spectively. For x to be ON, we need y

being true but

the system can control gene y to be OFF since gene x

is OFF.

We expect both gene x and y are either ON or OFF

simultaneously. This can be checked by the following

properties:

Gon

∧ Gon

, (14)

G¬on

∧ G¬on

. (15)

Both properties are really homeostatic. Therefore

gene x and gene y are ‘interlocked’ in a sense.

We further investigate this ‘interlocking’ property.

Can gene x (and gene y) always be ON by its own?

That is to say, are the following properties homeo-

static?

Gon

∧ G¬on

, (16)

G¬on

∧ Gon

. (17)

x y

- -

Figure 10: A bistable switch with a negative input to gene

The answers are ’No’ for both properties. To keep

gene x being ON gene x must be expressed beyond

and this prevents gene y to be always OFF. Thus

the property (16) is not homeostatic. This property is

even not satisﬁable. That is to say, there is no input

sequence to satisfy the property (16). Conversely, to

keep gene y being ON gene x must be expressed be-

yond x

and this prevents gene x to be always OFF.

Thus the property (17) is not homeostatic and not sat-

isﬁable too.

Interestingly, provided gene y accepts a negative

input from the environment (Figure 10), the proper-

ties (12) and (13) are still homeostatic. Even if both

negative inputs are always effective, each gene can be

expressed thanks to the positive effect from the other

gene. We conﬁrmed the properties (12) and (13) are

really homeostatic with respect to the following be-

haviour speciﬁcation in which we have two thresholds

for gene x (only activation rules for gene y are shown):

G(¬x

→ ¬on

G(e

∧ x

∧ ¬x

→ ¬on

G(¬e

∧ x

→ on

G(x

→ on

Moreover, the properties (14) and (15) are still

homeostatic. The properties (16) and (17) are also

not homeostatic but are satisﬁable in contrast to the

previous case since if the environment appropriately

controls the inputs, gene y can be ON and OFF al-

ternately but keeps the expression level beyond y

that gene x can be ON indeﬁnitely.

The last examples are anti-stress networks (Zhang

and Andersen, 2007) depicted in Figure 11. The net-

works in Figure 11 control the upper right objects

to keep them within the tolerable ranges. Though

these networks are schematic, we are just interested in

the controlmechanisms which contributehomeostasis

against environmental stresses. Let us consider the

network of Figure 11 (c). If the amount of O

be-

comes low, the network tries to recover the level of

. The property can be described as follows:

G(¬o

→ Fo

)

In this formula we interpret proposition o

as ‘the

amount of O

is within the tolerable range’ so ¬o

means it deviates the tolerable range. The behaviour

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

Nrf2

Anti-electrophilic

Genes

Electrophile

Keap1

Electrophilic

stressor

(a)

HSF

HSP Genes

Misfolded

Proteins

Heat

(b)

Prolyl/asparaginyl

Hydroxylase

HIF

Anti-hypoxic

Genes

Hypoxia

(c)

Figure 11: Schematic representations of anti-stress gene

regulatory networks that meditate (a) electrophilic stress re-

sponse, (b) heat shock response and (c) hypoxic response.

Prolyl/asparaginyl

Hydroxylase

HIF

Anti-hypoxic

Genes

Hypoxia

Input

(c)

Figure 12: The network (c) with hypothetic negative inputs.

speciﬁcation of the network is obtained as usual

. We

checked the property is really homeostatic.

Now we have a question: is this homeostatic func-

tion broken by the assumption that anti-hypoxic genes

receive environmental negative input? (Fig. 12) To

check this hypothesis, we modiﬁed the behaviour

speciﬁcation in which anti-hypoxic genes receive a

negative input from the environment. The activation

rule for anti-hypoxic genes is modiﬁed considering

the negative input. The result of realisability check-

ing was ’No’. This analysis indicates that the home-

ostasis of this network may be broken by some envi-

We have ‘on’ propositions for each node and threshold

propositions for each edge.

ronmental factor which hinders the operations of anti-

hypoxic genes. Such analysis is difﬁcult by observing

dose-response relationship based on ordinary differ-

ential models.

The homeostatic properties for other two networks

are similarly checked. Basic network topologies are

almost the same and the modiﬁcation of network

speciﬁcations are minor.

6 RELATED WORK

In this section, we describe some other qualitative

methods for analysing biological systems.

BIOCHAM (Fages et al., 2004) is a language and

programming environment for modelling and simu-

lating biochemical systems, and checking their tem-

poral properties. Reactions are written as rules like

A+B=>C

, and simulations are performed by replac-

ing objects on the left-hand side with those on the

right-hand side. Since there are many possible rules

that can be applied in each state, there are many

possible successor states for each state depending

on the rule applied. After simulation, we have a

non-deterministic transition graph whose nodes are

possible states and edges are state transitions. The

set of possible behaviours of the simulation over-

approximates the set of all behaviours of the system

depending on the kinetic parameters. A biological

property is written in computation tree logic (CTL),

a type of branching time logic, and checked in the re-

sulting transition graph by the model checking tech-

nique (Clarke et al., 1999). In BIOCHAM, presence

or absence of objects is the only matter considered.

How we represent the interaction between biological

systems and environments in BIOCHAM is not pre-

sented, so it is unclear how we capture homeostasis in

BIOCHAM.

SMBioNet (Bernot et al., 2004) is a tool for for-

mally analysing temporal properties of gene regula-

tory networks. In SMBioNet, genes have concentra-

tion thresholds for activation or inhibition of each of

their regulating genes. A conﬁguration of systems is

represented as a vector of expression values, which

are segmented by threshold. For example, if a gene

has two thresholds, then it has three levels – 0, 1, and

2. Behaviours of a network are captured as a tran-

sition system on the vectors of values for genes in

the network. Temporal evolution of a system is de-

scribed by a transition function on the vectors. Tem-

poral properties are described in CTL, and veriﬁca-

tion of them is conducted by model checking on the

resulting transition systems. Since the models of SM-

BioNet are deterministic, it is not clear how to con-

AQualitativeFrameworkforAnalysingHomeostasisinGeneNetworks

sider any sequence of environmental inputs in SM-

BioNet.

GNA (de Jong et al., 2003) is a computational tool

for the modelling and simulation of gene regulatory

networks. GNA achieves simulation using piecewise

linear differential equation models and generates state

transition systems that represent possible behaviours

of networks. The qualitative dynamics of a system

are completely determined by inequality constraints

deﬁning the ordering between thresholds and stable

equilibria of the system. Network properties of in-

terest are checked automatically using model check-

ing (Batt et al., 2005). Since the models of GNA are

based on piecewise linear differential equation, inter-

actions between biological systems and environments

over time cannot be directly captured. How we take

this essential aspect into consideration by GNA is not

clear.

As we mentioned, our work is based on the

method proposed by Ito et al. (Ito et al., 2010). For a

behaviour speciﬁcation φ and a biological property ψ,

they check satisﬁability of the formula φ∧ψ to know

whether there is a behaviour which satisﬁes the prop-

erty, or check unsatisﬁability of φ ∧ ¬ψ to investigate

whether all behaviours satisfy the property. They did

not distinguish input propositions and output proposi-

tions. This means they only considered whether there

exist an input sequence to which a network can re-

spond without violating the biological property ψ.

7 CONCLUSIONS

In this paper we formulated the notion of homeosta-

sis in gene regulatory networks by realisability in re-

active systems. This formulation allows the auto-

matic analysis of homeostasis of gene regulatory net-

works using realisability checkers. We analysed sev-

eral networks with our method. In the analyses we can

easily ‘tweak’ a network (such as appending extra-

inputs from the environment) and observed whether

the homeostatic properties can be maintained. Such

ﬂexibility in analysing networks is an advantage of

our framework in the situation that we do not have

the deﬁnite network topologies. To test several hy-

pothetic networks, our method is more suitable than

quantitative approaches using ordinary differential

equation models.

There are several interesting future directions

based on this work. First is to ﬁnd more interest-

ing applications in real biological examples. In as-

sociation with this topic, we are interested in ‘con-

ditional’ homeostasis which means that under certain

constraints on input sequences, a property is homeo-

static. This can be easily formulated as follows. Let

I and O be the input and output propositions respec-

tively. Let hI, O, φi be a behavioural speciﬁcation and

ψ be a property. Let σ be an assumption about input

sequences e.g. ‘inputs to gene x and gene y come in-

ﬁnitely often but not simultaneously’. Then the prop-

erty ψ is conditionally homeostatic with respect to

hI, O, φi under a condition σ if hI, O, σ → φ ∧ ψi is

realisable. The motivation of this deﬁnition is that

in more realistic situation it is too strong to require a

system to respond to any input sequence.

The next topic is to develop a method to sug-

gest how we modify the model of a network when

an expected or observed property is not homeostatic

in a model. This problem is closely related to re-

ﬁnement of reactive system speciﬁcations (Aoshima

et al., 2001; Hagihara et al., 2009). We hope the

techniques developed so far for veriﬁcation of reac-

tive systems can be imported to analysis of gene net-

works.

Another important future work is to develop a

method to overcome high complexity in checking re-

alisability of LTL formulae. The complexity of real-

isability checking is doubly exponential in the length

of the given speciﬁcation (Pnueli and Rosner, 1989).

Thus it is intractable to directly apply our method to

large networks. To circumvent this theoretical limi-

tation we are interested in some approximate analysis

method (Ito et al., 2013b) or modular analysis method

(Ito et al., 2013a) in which a network is divided into

several subnetworks and analyse them individually.

The last topic is to extend our method with some

quantitative temporal logic (e.g. probability or real

time) (Tomita et al., 2011; Tomita et al., 2012) to en-

able quantitative analysis.

REFERENCES

Abadi, M., Lamport, L., and Wolper, P. (1989). Realiz-

able and unrealizable speciﬁcations of reactive sys-

tems. In ICALP ’89: Proceedings of the 16th Interna-

tional Colloquium on Automata, Languages and Pro-

gramming, volume 372 of LNCS, pages 1–17, Lon-

don, UK. Springer-Verlag.

Aoshima, T., Sakuma, K., and Yonezaki, N. (2001). An ef-

ﬁcient veriﬁcation procedure supporting evolution of

reactive system speciﬁcations. In Proceedings of the

4th International Workshop on Principles of Software

Evolution, IWPSE ’01, pages 182–185, New York,

NY, USA. ACM.

Barringer, H. (1987). Up and down the temporal way. The

Computer Journal, 30(2):134–148.

Barringer, H., Kuiper, R., and Pnueli, A. (1984). Now you

may compose temporal logic speciﬁcations. In Pro-

ceedings of the sixteenth annual ACM symposium on

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

Theory of computing, STOC ’84, pages 51–63, New

York, NY, USA. ACM.

Batt, G., Ropers, D., de Jong, H., Geiselmann, J., Ma-

teescu, R., Page, M., and Schneider, D. (2005). Vali-

dation of qualitative models of genetic regulatory net-

works by model checking : Analysis of the nutritional

stress response in Escherichia coli. Bioinformatics,

21(Suppl.1):i19–i28.

Bernot, G., Comet, J., Richard, A., and Guespin, J. (2004).

Application of formal methods to biological regula-

tory networks: extending Thomas’ asynchronous log-

ical approach with temporal logic. J. Theor. Biol.,

229(3):339–347.

Bloem, R., Cimatti, A., Greimel, K., Hofferek, G.,

K¨onighofer, R., Roveri, M., Schuppan, V., and See-

ber, R. (2010). RATSY – a new requirements analysis

tool with synthesis. In Proceedings of the 22nd inter-

national conference on Computer Aided Veriﬁcation,

volume 6174 of LNCS, pages 425–429, Berlin, Hei-

delberg. Springer-Verlag.

Clarke, E., Grumberg, O., and Peled, D. (1999). Model

Checking. MIT Press.

Croft, D., O’Kelly, G., Wu, G., Haw, R., Gillespie, M.,

Matthews, L., Caudy, M., Garapati, P., Gopinath, G.,

Jassal, B., Jupe, S., Kalatskaya, I., Mahajan, S., May,

B., Ndegwa, N., Schmidt, E., Shamovsky, V., Yung,

C., Birney, E., Hermjakob, H., D’Eustachio, P., and

Stein, L. (2011). Reactome: a database of reactions,

pathways and biological processes. Nucleic Acids Re-

search, 39(Database-Issue):691–697.

de Jong, H., Geiselmann, J., Hernandez, G., and Page, M.

(2003). Genetic network analyzer: Qualitative simu-

lation of genetic regulatory networks. Bioinformatics,

19(3):336–344.

Emerson, E. A. (1990). Temporal and modal logic. In

Handbook of Theoretical Computer Science, Volume

B: Formal Models and Sematics (B), pages 995–1072.

MIT Press.

Fages, F., Soliman, S., and Chabrier-Rivier, N. (2004).

Modelling and querying interaction networks in the

biochemical abstract machine BIOCHAM. J. Biol.

Phys. Chem., 4:64–73.

Filiot, E., Jin, N., and Raskin, J.-F. (2009). An antichain al-

gorithm for ltl realizability. In Proceedings of the 21st

International Conference on Computer Aided Veriﬁ-

cation, volume 5126 of LNCS, pages 263–277, Berlin,

Heidelberg. Springer-Verlag.

Hagihara, S., Kitamura, Y., Shimakawa, M., and Yonezaki,

N. (2009). Extracting environmental constraints to

make reactive system speciﬁcations realizable. In Pro-

ceedings of the 2009 16th Asia-Paciﬁc Software Engi-

neering Conference, APSEC ’09, pages 61–68, Wash-

ington, DC, USA. IEEE Computer Society.

Hagihara, S. and Yonezaki, N. (2006). Completeness of

veriﬁcation methods for approaching to realizable re-

active speciﬁcations. In Completeness of Veriﬁcation

methods for Approaching to Realizable Reactive Spec-

iﬁcations, volume 348, pages 242 – 257.

Ito, S., Ichinose, T., Shimakawa, M., Izumi, N., Hagihara,

S., and Yonezaki, N. (2013a). Modular analysis of

gene networks by linear temporal logic. J. Integrative

Bioinformatics, 10(2).

Ito, S., Ichinose, T., Shimakawa, M., Izumi, N., Hagihara,

S., and Yonezaki, N. (2013b). Qualitative analysis

of gene regulatory networks using network motifs.

In Proceedings of the 4th International Conference

on Bioinformatics Models, Methods and Algorithms

(BIOINFORMATICS2013), pages 15–24.

Ito, S., Izumi, N., Hagihara, S., and Yonezaki, N. (2010).

Qualitative analysis of gene regulatory networks by

satisﬁability checking of linear temporal logic. In Pro-

ceedings of the 10th IEEE International Conference

on Bioinformatics & Bioengineering, pages 232–237.

Jobstmann, B. and Bloem, R. (2006). Optimizations for

ltl synthesis. In Proceedings of the Formal Methods

in Computer Aided Design, FMCAD ’06, pages 117–

124, Washington, DC, USA. IEEE Computer Society.

Jobstmann, B., Galler, S., Weiglhofer, M., and Bloem, R.

(2007). Anzu: a tool for property synthesis. In Pro-

ceedings of the 19th international conference on Com-

puter aided veriﬁcation, volume 4590 of LNCS, pages

258–262, Berlin, Heidelberg. Springer-Verlag.

Kanehisa, M., Goto, S., Sato, Y., Furumichi, M., and Tan-

abe, M. (2011). KEGG for integration and interpreta-

tion of large-scale molecular data sets. Nucleic Acids

Res.

Karp, P. D., Riley, M., Paley, S. M., and Pellegrini-Toole, A.

(2002). The MetaCyc Database. Nucleic Acids Res.,

30(1):59–61.

Mori, R. and Yonezaki, N. (1993). Several realizability con-

cepts in reactive objects. In Information Modeling and

Knowledge Bases IV, pages 407–424.

Pnueli, A. and Rosner, R. (1989). On the synthesis of a re-

active module. In POPL ’89: Proceedings of the 16th

ACM SIGPLAN-SIGACT symposium on Principles of

programming languages, pages 179–190, New York,

NY, USA. ACM.

Rabinovich, A. (1998). On translations of temporal logic

of actions into monadic second-order logic. Theor.

Comput. Sci., 193:197–214.

Safran, M., Dalah, I., Alexander, J., Rosen, N., Iny Stein, T.,

Shmoish, M., Nativ, N., Bahir, I., Doniger, T., Krug,

H., Sirota-Madi, A., Olender, T., Golan, Y., Stelzer,

G., Harel, A., and Lancet, D. (2010). GeneCards

Version 3: the human gene integrator. Database,

2010(0):baq020+.

Snoussi, E. and Thomas, R. (1993). Logical identiﬁcation

of all steady states: the concept of feedback loop char-

acteristic states. B. MATH. BIOL., 55(5):973–991.

Thomas, R. and Kauffman, M. (2001). Multistationarity,

the basis of cell differentiation and memory. II. logical

analysis of regulatory networks in terms of feedback

circuits. CHAOS, 11(1):180–195.

Tomita, T., Hagihara, S., and Yonezaki, N. (2011). A proba-

bilistic temporal logic with frequency operators and its

model checking. In INFINITY, pages 79–93. EPTCS.

Tomita, T., Hiura, S., Hagihara, S., and Yonezaki, N.

(2012). A temporal logic with mean-payoff con-

straints. In Proceedings of the 14th international

conference on Formal Engineering Methods: formal

methods and software engineering, volume 7635 of

LNCS, pages 249–265, Berlin, Heidelberg. Springer-

Verlag.

AQualitativeFrameworkforAnalysingHomeostasisinGeneNetworks

Vanitha, V., Yamashita, K., Fukuzawa, K., and Yonezaki.,

N. (2000). A method for structuralisation of evo-

lutional speciﬁcations of reactive systems. In ICSE

2000, The Third International Workshop on Intelligent

Software Engineering (WISE3), pages 30 – 38.

Vardi, M. Y. (1995). An automata-theoretic approach to fair

realizability and synthesis. In Proceedings of the 7th

International Conference on Computer Aided Veriﬁ-

cation, volume 939 of LNCS, pages 267–278, Berlin,

Heidelberg. Springer-Verlag.

Wong-Toi, H. and Dill, D. L. (1991). Synthesizing pro-

cesses and schedulers from temporal speciﬁcations.

In Proceedings of the 2nd International Workshop on

Computer Aided Veriﬁcation, volume 531 of LNCS,

pages 272–281, London, UK, UK. Springer-Verlag.

Zhang, Q. and Andersen, M. E. (2007). Dose response rela-

tionship in anti-stress gene regulatory networks. PLoS

Comput. Biol., 3(3).

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms