Adaptation Schemes for Question's Level to be

Proposed by Intelligent Tutoring Systems

Rina Azoulay

, Esther David

, Dorit Hutzler

and Mireille Avigal

Department of Computer Science, Jerusalem College of Technology, Jerusalem 91160, Israel

Ashkelon Academic College, Ashkelon, 78211, Israel

Department of Computer Science, Jerusalem College of Technology, Jerusalem 91160, Israel

Computer Science Division, The Open University of Israel, Raanana, Israel

Keywords: Intelligent Tutoring Systems, Reinforcement Learning, Bayesian Inference.

Abstract: The main challenge in developing a good Intelligent Tutoring System (ITS) is suit the difficulty level of

questions and tasks to the current student's capabilities. According to state of the art, most ITS systems use

the Q-learning algorithm for this adaptation task. Our paper presents innovative results that compare the

performance of several methods, most of which have not been previously applied for ITS, to handle the

above challenge. In particular, to the best of our knowledge, this is the first attempt to apply the Bayesian

inference algorithm to question level matching in ITS. To identify the best adaptation scheme based on this

groundwork research, for the evaluation phase we used an artificial environment with simulated students.

The results were benchmarked with the optimal performance of the system, assuming the user model (abili-

ties) is completely known to the ITS. The results show that the best performing method ,in most of the envi-

ronments considered, is based on a Bayesian Inference, which achieved 90% or more of the optimal per-

formance .Our conclusion is that it may be worthwhile to integrate Bayesian inference based algorithms to

adapt questions to a student's level in ITS. Future work is required to apply these empirical results to envi-

ronments with real students.

1 INTRODUCTION

Intelligent Tutoring Systems (ITS) are based on

artificial intelligence methods (Woolf, 2009) to cus-

tomize instruction with respect to the student's capa-

bilities that dynamically change over the tutoring

period. To accomplish this, an ITS should contain

knowledge about the student's capabilities, termed

the student's model, and a set of pedagogical rules.

A critical characteristic of an ITS is the ability to

challenge students, without discouraging them due

to exaggerated challenges. Namely, on the one hand

the system should not provide questions to the stu-

dent that are too easy and leave him bored, while on

the other hand, the questions should not be too hard

to the point that they discourage the student from

using the system. In both of these extreme cases the

student will not realize its potential and therefore

will not benefit from using it. Therefore, we aimed

to construct an ITS that will match the hardest chal-

lenges the user can face and by doing so realize his

potential.

According to state of the art, most ITS systems make

use of the Q-learning algorithm for this adaptation

task. Our paper presents innovative results that com-

pare performances of several methods, most of

which have not been previously applied in ITS, to

handle this challenging adaptation task. In particu-

lar, to the best of our knowledge, this is the first

attempt to apply the Bayesian inference algorithm in

ITS for question level adaptation.

The leading principles involved in the develop-

ment of an efficient ITS include keeping track of

dynamically improving capabilities and knowledge,

and keeping the user active and satisfied. These are

achieved by considering the correctness of the an-

swers the student provides hitherto to the ITS. In

particular the ITS must choose a fixed number of

questions from a pre-prepared pull of questions to

present to the student. Obviously, the system is not

faced with a single decision for all the questions, but

instead question by question decisions, while taking

into account the history of the student's answers.

To enable a comparison between the various

245

Azoulay R., David E., Hutzler D. and Avigal M..

Adaptation Schemes for Question’s Level to be Proposed by Intelligent Tutoring Systems.

DOI: 10.5220/0004732402450255

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 245-255

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

proposed adaption schemes, we defined a utility

function to reflect the efficiency of each chosen

question. Specifically we considered the following

adapting schemes: (i) Q-learning (Sutton and Barto

2005, Rusell & Norvig 1995, Martin and Arroyo,

2004); (ii) Virtual Learning (Vreind, 1997); (iii)

Temporal Reasoning (Beck, Woolf and Beal 2000) ;

(iv) DVRL (Azoulay-Schwartz et al., 2013); (v)

Bayesian Inference (Conitzer and Garera, 2006); and

(vi) Gittins Based Method (Gittins, 1989). Most of

the algorithms have not been used for ITS, excluding

the Q-learning method which has been used for ITS,

as discussed in Section 2.

As this is a groundwork research to identify the

best adaptation scheme, at this stage of the study we

developed an artificial environment by simulating

students with ability distributions derived from a

normal distribution.

The performance of the various proposed meth-

ods were benchmarked with the optimal perfor-

mance of the system assuming the user model (abili-

ties) is completely known to the ITS. The results

show that the method that outperformed the others in

most of the environments we considered is based on

a Bayesian Inference which achieved more than 90%

of the optimal performance.

This paper is organized as follows. In Section 2

we provide a review of the current state of the art

methods used for choosing questions in ITS. In Sec-

tion 3 we present the ITS model, including the utility

function used in this study. In Section 4 we describe

the various adaption schemes, and present a detailed

description of the Bayesian inference algorithm

which we provide in Section 5. In Section 6 we de-

scribe the construction of the artificial environment

used for the evaluations and in Section 7 we present

the simulation results. Finally, we conclude and

discuss directions for future work in Section 8.

2 RELATED WORK

It is well known that a student learns much better by

one-on-one teaching methods than by common

classroom teaching. An Intelligent Tutoring System

(ITS) is one of the best instances of one-on-one

teaching (Woolf, 2009) that uses technology devel-

opment. A student who is supposed to learn a certain

topic by means of an ITS is assumed to do so by

solving problems given to him by the ITS.

The ITS evaluates a given answer by comparing

it to the predefined answer as it appears in its

knowledge base. The system keeps track of the us-

er's actions, and correspondingly builds and con-

stantly updates its student model. Moreover, it ob-

serves the topics that need more training and selects

the next question accordingly.

In this paper, we consider the way the student

model will be represented, how it will be used to

find the student's subsequent goals, and how it

should be updated according to the student's results.

In the current section, we survey several ITS sys-

tems that also contain a learning process to adapt to

the student's abilities.

Martin and Arroyo (Martin and Arroyo, 2004)

used Reinforcement Learning agents to dynamically

customize ITS systems to the student. The system

clusters students into learning levels, and chooses

appropriate hints for each student. The student’s

level is updated based on the answers they enter or

the hints they ask for. Their best success was by

using the e-greedy agent (e=0.1). Following Martin

and Arroyo, we also used a Q-learning algorithm

where the probability  of trying a non-optimal level,

was fixed at 0.1.

Iglesias et al. (Iglesias et al., 2008) proposed a

knowledge representation based on RL that allows

the ITS system to adapt the tutoring to students’

needs. The system uses the experience previously

acquired from interactions with other students with

similar learning characteristics. In contrast to Iglesi-

as et al., in our work the learning process is done

individually for each student, in order to learn the

level of each student.

Malpani et al. (Malpani, Ravindran and Murthy,

2009) present a Personalized Intelligent Tutoring

System that uses Reinforcement Learning techniques

to learn teaching rules and provide instructions to

students based on their needs. They used RL to teach

the tutor the optimal way of presenting the instruc-

tions to students. Their RL has two components, the

Critic and the Actor. The Critic follows Q-learning,

and the actor follows a Policy Gradient approach

with parameters representing the preference of the

choosing actions.

Sarma et al. (Sarma and Ravindran, 2007) devel-

oped an ITS system using RL to teach autistic stu-

dents, who are unable to communicate well with

others. The ITS aimed to teach pattern classification

problems. The student has to classify the pattern

(question) given. This classification is used to vali-

date an ANN, but does not teach real children. The

pedagogical module used in (Sarma and Ravindran,

2007) selects the appropriate action to teach students

by updating Q-values.

Finally, Beck et al. (Beck, Woolf and Beal,

2000)

constructed a learning agent that models the

student behavior in the ITS. Rather than focusing on

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

246

whether the student knows particular knowledge, the

learning agent determines the probability the student

will answer a problem correctly and how long it will

take him to generate his response. They used an RL

agent to produce a teaching policy that meets the

educational goals.

In this paper, we concentrate on the goal of se-

lecting the appropriate question level, with regards

to the current student model and our knowledge

about its past performance. For this goal, we com-

pared different learning schemes, most of which

have not been used for tutorial systems, and we

compared their results by means of simulation.

3 THE ITS MODEL

In the following section, we provide the ITS model

we developed. We detail the ITS process and the

utility function used to evaluate its performance.

The ITS process

We consider an ITS that provides a student with

questions. In particular, a specific student should

obtain a set of N questions. The simplified ITS pro-

cess is presented in Figure 1, and is based on 3 steps:

(1) an initialization step; (2) the process of choosing

the next appropriate question; (3) examination of the

student's answer and saving the information for the

future steps.

The simplified template used in Figure 1 can as-

sist in providing the details of the different schemes

used in the paper as well.

The ITS utility function

Clearly, we would like the student to succeed in

answering the questions correctly, but, in addition,

we would like the question to be of the highest level

possible.

The ITS utility function should reflect both crite-

ria. In this study, we provide the following two pos-

sible utility functions:

For each successful question utility function #1

considers its level: as the level of a successful ques-

tion is higher, the total utility is also higher.

Utility function #1:



question i=1..N

(level

| Q

was correctly answered)

Utility function #2 also considers the level of

questions, but also adds a constant reward for each

success, and a constant penalty for each failure, in

Figure 1: The simplified ITS process.

order to better represent the student's utility, which

decreases when it fails to answer questions.

Utility function #2:



question i=1..N

(level

+ C | question i correctly answered) –



question i=1..N

(C | question

i incorrectly answered).

Both functions consider the student's results for

each of the questions, 1..N. The motivation behind

these two functions is as follows:

Utility function #1 considers the advances in the

student's knowledge, thus it calculates the sum of

successful answers, while also considering their

levels. However, utility function #2 also considers

the preferences of the student himself, who does not

like to fail in answering queries, thus the utility

function adds a positive constant for each success

and reduces this constant as a penalty in cases of

failure.

To summarize, utility function #2 places more

importance on the success or failure event, by add-

ing a constant value or deducting a constant value

from the utility function, for each success or failure,

respectively.

Step 1: Initialize the student model

(utility function & beliefs/Q values).

Step 2:

a. Calculate next level of question

given the student model.

b. Choose a question given the

question level and present it to the

student.

Step 3:

a. Observe the student's answer

b. Check the answer.

c. Update the student model

The student observes the

question and tries to answer it

AdaptationSchemesforQuestion'sLeveltobeProposedbyIntelligentTutoringSystems

247

4 ALGORITHMS FOR

ADAPTING QUESTIONS TO

THE STUDENTS

In this section we provide a detailed description of

the various algorithms we propose for the challenge

of adapting the level of the next question that will be

given to the student. Note that all the proposed algo-

rithms aim to determine the level of the next ques-

tion, and given this, the ITS in turn should choose a

particular question of that level to present to the

student.

In this research we implemented and tested the

various algorithms we propose in order to identify

which has the best performance and therefore should

be integrated in the ITS for further investigation.

The algorithms are as follows.

1. Simple Q-learning algorithm (Harmon and Har-

mon 1997, Sarma 2007)

2. Temporal difference learning (TD) (Beck, Woolf

and Beal, 2000)

3. Virtual Learning algorithm. (Vriend, 1997)

4. DVRL (Azoulay-Schwartz et al., 2013)

5. Gittins Indices (Gittins, 1989)

6. Bayesian Learning (Conitzer and Garera, 2006)

assuming a normal distribution of the student's

level.

We proceed by providing further details for each

of the above algorithms.

1. Q-Learning

A Q-learning learning algorithm saves a value Q

for each pair of actions to be taken (in the classical

Q learning method, different states are considered,

but in our problem only one state exists). Given the

Q values, with a probability , the algorithm ex-

plores and randomly chooses an action, and with a

probability 1-, the algorithm exploits and chooses

the action with the highest Q value.

After the action is taken and the reward is ob-

served, the Q value of this state and action is updat-

ed using the following formula

Q(a)=

Q(a) +



[r + 



max

Q(a') - Q(a)] (1)

where  defines the speed of convergence of the Q

values, and  defines the discount ratio.

In our case, the actions are the possible ques-

tion's level. Each question's level is associated with a

certain Q value. Once the student provides an an-

swer, the relevant Q value is updated according to

the reward which indicates the success or failure in

answering the question.

Figure 2: The process of Q-based algorithms.

Figure 2 presents the Q-learning algorithm pro-

cess, whereby the figures of the other Q-based algo-

rithms can similarly be described.

2. TD learning algorithm

The TD learning algorithm is different than the Q

learning algorithm in the way the future reward is

calculated. In Sarsas' algorithm, which is a version

of the TD-learning algorithm, the updating rule uses

the following formula

Q(a)= Q(a) +



[ r + 



Q(a') - Q(a)] (2)

where a' is the action that is supposed to be taken

from this state, using the policy of choosing an ac-

tion taken by TD().

3. Virtual Learning algorithm

Virtual Learning is also similar to Q learning, but

the idea of virtual learning is that instead of learning

only on the basis of actions and payoffs actually

experienced, the algorithm can also learn by reason-

ing from the chosen action for other actions.

In our domain once a student succeeds in an-

swering a question, the Q learning of the current

level as well as the Q learning of the lower levels are

increased. Similarly, if a student fails to answer a

question the Q learning of the level of the current

question as well as the Q learning of the higher lev-

els are reduced.

Step 1: Initialize the utility function

and the Q values vector.

Step 2: Calculate the next level L:

With probability : L=random(1..5).

With probability 1-: L=arg max

Q(i).

b. Choose the next question given

level L.

Step 3: Observe the student's an-

swer and check it.

Update Q(a), where a=level, to be

Q(a)+



[r+



max

Q(a') - Q(a)]

The student observes the

question and tries to answer it

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

248

The student observes the

question and answers it.

4. DVRL

DVRL is similar to Virtual Learning, but once a

reward is received for the student's answer the, the

updating phase of the Q values relates not only to

the given question's level but also to the level of the

neighboring questions. Specifically, once a student

answers a question correctly, the Q learning of the

nearest higher level also increases, and when a stu-

dent fails to answer a question, the Q learning of the

nearest lower level also decreases.

5. Gittins Indices

Gittins (Gittins, 1989) developed a tractable

method for deciding which arm to choose, given N

possible arms, each with its own history. Gittins

calculated indices values which indicate the attrac-

tiveness of each arm as a function of its past success

and failures.

The indices calculated by Gittins consider the at-

tractiveness of each arm including future rewards

from exploring unknown arms. The indices for each

arm were calculated for the standard normal distri-

bution, and were provided in a table that can be used

to determine the optimal action for different combi-

nations of arms' success and failures and for differ-

ent values of the discount ratio over time. Moreo-

ver, in our study Gittins indices can be used to com-

pare the success rate of different levels, while also

considering the average and standard deviation of

the past results for each level, in the manner sug-

gested by (Azoulay-Schwartz, Kraus and Wilken-

feld, 2004), where Gittins indices is applied to mul-

tiple arms whereby each arm is normally distributed

with any value of  and . In particular, Algorithm 1

is used to choose an arm, given the sum[level] and

the std[level], which are the sum of rewards and the

standard deviation of rewards for each level, and

given GittinsIndex[n[level]] which is the Gittins

index for the number of past trials of this level for

the current student.

Algorithm 1: Choose next question using Gittins

indices

In other words, each level of questions is consid-

ered as an arm, and in each stage, Gittins indices are

calculated for each level, and the level with the

highest value of Gittins index is chosen.

Figure 3 presents the Gittins algorithm process

used in our study to choose the question level in ITS.

Figure 3: The Gittins algorithm process.

6. Bayesian Learning

Assuming a normal distribution of the student's

level, and given a particular student, the algorithm

can consider different parameters of the student level

distribution. Initially, the algorithm associates a

constant probability for each set of parameters (

and ).

In each step, the algorithm considers all possible

distributions of the student, and for each question's

level, the algorithm calculates the expected utility of

this level given all possible distribution of students,

and then it chooses the level with the highest ex-

pected utility. Once a question is chosen and the

student's response is observed, the probability of

each distribution of the student is updated using the

Bayesian rule.

Given the above list of algorithms, in the next

section we describe the results obtained by our simu-

lation, which compares the performance of the vari-

ous algorithms for artificial students.

Step 1:

a. Initialize the utility function, pro-

vide the Gittins indices table.

b. Initialize n[level]=0, sum[level=0

and sum2[level]=0 for each level.

Step 2:

a. Calculate the next level of question,

using algorithm 1.

b. Choose a question given the

question level and present it.

Step 3:

a. Observe the student answer and check

it. Calculate reward.

b. Update the following arrays:

n[level]=n[level]+1,

sum[level]=sum[level]+reward

sum2[level]=sum2[level]+reward

and std[level] for the chosen level.

Ifalevelwithn[level]<=2exists

Thenchooseit.

ChooseLevelwhichmaximizesvalue[level]

WhereValue[level]=

sum[level]/n[level]+

std[level]*GittinsIndex[n[level]]

AdaptationSchemesforQuestion'sLeveltobeProposedbyIntelligentTutoringSystems

249

The student observes the

question and answers it.

5 ADDITIONAL DETAILS ON

THE BAYESIAN LEARNING

ALGORITHM

In the following section we provide additional de-

tails on the Bayesian approach applied in the ITS

domain. In particular, it is assumed that a distribu-

tion exists from which the student's level is drawn in

any given time slot. Moreover, this distribution is

associated with an unknown mean and an unknown

standard deviation.

This is due to the fact that a certain student asso-

ciated with a mean level of 3, for example, can

sometimes succeed in answering questions from

level 4, and similarly can sometimes fail in answer-

ing questions from level 2.

The Algorithm's Details

In order to learn the student's level at each stage

of the simulation, for each student the algorithm

constructs a matrix of various possible mean inter-

vals and standard deviation intervals. In particular,

each row represents a certain mean interval of the

student's level and each column represents a certain

standard deviation interval such that each cell (i,j) in

the matrix stands for the probability that the given

student's level is of a mean between the upper limit

of the previous row and the upper limit of row i

assuming the standard deviation interval of column

In the initialization stage, each value in the ma-

trix is associated with an arbitrary probability such

that the sum of all the cells' probabilities is one.

Next, at each phase where a question is chosen and

the student provides an answer, each cell's probabil-

ity is updated according to the Bayesian rule. Final-

ly, formula 5 is used to determine the next level of

the question.

chosenLevel=Argmax

level=1..5







prob(





)*(pwins(level |





)*util (level)+

(1-pwins(level |





))*utilFailure). (3)

Where pwins(level |





) is the probability of a ques-

tion n from level level to be chosen, util (level) is the

utility from a successful answer to a question from

this level, and utilFail is the utility from failure to

answer a question from this level.

The explanation of the formula is as follows.

1. For each possible level, we review the entire

table, and calculate pwins(level |





), which is

the probability that a student with mean level



and a standard deviation



will be able to cor-

rectly answer a question of the current level

2. Given pwins(level |





), we calculate the ex-

pected utility from a question from level, if the

student distribution is normal with (





), where

pwins is multiplied by the success utility, and (1-

pwins) is multiplied by the failure utility.

3. Once this value is calculated for each possible

level, the level that achieves the highest expected

utility is chosen.

Figure 4 illustrates the Bayesian learning process

when used in ITS.

A Particular Example of the Bayesian Algorithm

Table 1 includes the initial beliefs for the ITS, as-

suming, for simplicity, that the mean and the stand-

ard deviation are assumed to be integer values be-

tween 0..5. The table is initialized as provided in

Table 1, where the probability of each pair of (





)

is equal, and the sum of probabilities is 1.

Table 1: Initial beliefs.





=0 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278



=1 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278



=2 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278



=3 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278



=4 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278



=5 0.0278 0.0278 0.0278 0.0278 0.0278 0.0278

Figure 4: The Bayesian algorithm process.

Step 1: Initialize the utility function,

Initialize the probability matrix

Prob(





)=1/(number-of-pairs).

Step 2:

a. Calculate the next level of question,

using formula 5.

b. Choose a question given the ques-

tion level and present it.

Step 3:

a. Observe the student's answer and

check it. Calculate the reward.

b. Calculate sumProb(level): the

total probability of level to win.

c. Use Bayesian rule:

Prob(





Prob(





)*pwins(level|





)

sumProb(level)

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

250

Given Table 1, the expected utility of each question's

level is provided in Table 2:

Table 2: The expected utility of each level given the initial

beliefs.

Level 1 2 3 4 5

Utility 0.686 1.13 1.31 1.26 1.01

For example, the utility of a question from level 2 is

as follows:





=0..5,



=0..5





)*pwins(2|x~N(





))*util(2)=





=0..5,



=0..5





)*pwins(2 |x~N(





))*2=1.13

Where util(2)=2 is the utility from the student suc-

cessfully answering a question from level 2.

Given Table 2, a question from level 3 is offered,

since its expected utility is the highest.

Now, suppose that the first student's threshold

was 4, thus the question is correctly answered by the

student.

Hence, the probability table should be updated ac-

cording to the Bayesian rule:

For each

=0..5,=0..5,

Prob(





Prob(





)*prob(x



3 |x~N(





))/sumProb(3)

Where sumProb is the probability of a question

level 3 to be chosen.

sumProb(x



3)=





=0..5,



=0..5





)*prob(x



3 |x~N(





)).

=0.437

For example, the probability of the student distribu-

tion to be mean 2 and std. 1 is:

Prob(

2,1)=0.0278*prob(x



3 |x~N(2,1))/0.437=

0.0278*0.159/0.437=0.0101

Table 3 shows the probabilities after the Bayesian

updating step.

Table 3: Beliefs after one updating step.





=0 0 0 0.00425 0.0101 0.0144 0.0174



=1 0 0.00145 0.0101 0.016 0.0196 0.0219



=2 0 0.0101 0.0196 0.0236 0.0255 0.0267



=3 0.0318 0.0318 0.0318 0.0318 0.0318 0.0318



=4 0.0636 0.0535 0.044 0.04 0.0381 0.0368



=5 0.0636 0.0621 0.0535 0.0476 0.044 0.0417

Given Table 3, the expected utility of each ques-

tion's level is calculated again, the next question is

chosen, the student's response is observed, and

again, an updating step is performed which updates

the probability table.

After explaining the Bayesian algorithm in de-

tail, we proceed by describing the simulated envi-

ronment used for our experimental study.



6 THE SIMULATED

ENVIRONMENT

Next, as this was groundwork research to identify

the best question level adaptation scheme, we pro-

posed an artificial environment with simulated stu-

dents for the evaluation phase.

For each question Qi, with a difficulty level of

Leveli, the student will either succeed or fail to an-

swer the question. The goal of the software is to

match appropriate questions to the students to max-

imize both (i) the number of correct answers and (ii)

the question's level presented to the student. For the

evaluation of the combination of these two maximi-

zation problems we proposed utility function #1, as

defined in Section 3.



i=1..N

(level

| Q

was correctly answered)

This utility function reflects the fact that the

higher a question's level and the more correct an-

swers there are, the higher the utility obtained. No-

tice, however that an incorrect answer provides zero

rewards.

The ITS model is defined as follows. For each

new student/user that starts to use ITS, no prelimi-

nary information is assumed. Therefore, the first

question presented to the new user should be arbi-

trarily determined by ITS. Once an answer is given

by the student, the adaptation algorithm should de-

cide the level of the next question to present based

on the history of the student's answers. Once the

student finishes using the ITS software the utility

value for the student is measured.

Given the assumptions above we now describe

the construction of the simulated students. We first

assume that a student with a certain level will not

always successfully answer questions of his or lower

level; similarly, he will not always incorrectly an-

swer questions of higher levels. Namely, the user's

level might be dependent on several conditions and

therefore may change with time.

However, in order to decide whether an artificial

student will answer a given question correctly or not,

a threshold level must be defined for him in order to

determine the level for which any harder question

will be answered incorrectly and for any easier or

equal level question he will answer correctly.

Second, we assume there are N questions that the

AdaptationSchemesforQuestion'sLeveltobeProposedbyIntelligentTutoringSystems

251

ITS will present to the student within the tutoring

period. Given these two assumptions we simulated a

certain student by drawing a certain mean value and

a certain standard deviation from the Normal distri-

bution for the student. Then we created a sequence

of N threshold levels. Namely, given this sequence,

for any question presented to this user we will com-

pare the question's level with the threshold level to

determine whether it will be answered correctly or

not.

For each simulated student, we ran each of the

algorithms described in section 3. Thus, we actually

tested each of the proposed algorithms on the same

set of randomized inputs. In the next section we

present the experimental results.

7 EXPERIMENTAL RESULTS

For comparison reasons, we first implemented each

of the proposed algorithms. Next, we created the

artificial environment by producing a set of simulat-

ed students.

For the Q learning, TD and VL algorithms, the

parameters (provided in Section 4) were set as:

=0.1, =0.95, =0.5. Note also that utility function

#1 is used in most of our experiments.

We ran simulations for an ITS, that aimed to pre-

sent the student with 10, 20, and 100 questions. In

particular, for each number of questions (10, 20, and

100), and for each randomly created student, we ran

each of the six proposed adaptation algorithms for

1000 runs. The simulation results are presented in

Table 4 and in Figure 5.

Table 4: The average utility, (standard deviation) and

successful rate obtained by different RL algorithms for 10,

20 and 100 questions.

100 questions 20 questions 10 questions Algorithm

115.479 (57.53)

77%

22.876 (11.92)

75%

10.826 (6.31)

74%

Q-Learning

115.685 (59.32)

78%

22.787 (12.03)

75%

10.853 (6.31)

74%

105.342 (53.32)

71%

22.211 (11.93)

73%

10.601 (6.26)

72%

Virtual

Learning

104.543 (53.67)

70%

21.435 (11.12)

70%

10.368 (5.92)

71%

DVRL

134.143 (74.16)

90%

23.105 (13.58)

76%

10.158 (6.13)

71%

Gittins

Indices

122.72 (74.16)

82%

24.074 (13.81)

79%

10.825 (6.76)

74%

Virtual

Gittins

Indices

137.458 (73.22)

92%

27.411 (15.54)

90%

13.244 (8.21)

90%

Bayesian

Inference

In each entry in the table there are three values

(upper left, upper right, and bottom). The upper-left

value represents the average utility achieved by the

given algorithm for the particular number of ques-

tions. The upper-right value (in parentheses) repre-

sents the standard deviation of that average. The

bottom value represents the ratio between the aver-

age utility obtained by the algorithm in the simulated

environment and the average utility obtained by the

ITS based on the student's known level of distribu-

tion at each time slot.

These results can be explained by the fact the Q-

learning algorithm's decision is based on the best

action achieved hitherto and a certain small proba-

bility of random choice while the Bayesian inference

algorithm considers several different normal distri-

butions of the student and therefore its performance

is much more accurate.

Figure 5: The average utility obtained by the different

algorithms as a function of the number of questions.

The results of the Gittins method were relatively

lower than the Bayesian algorithms, probably due to

the fact that the Gittins indices were calculated as-

suming independencies among the possible values,

and this assumption does not hold in our domain,

where the different levels are correlated. Neverthe-

less, the Gittins Indices' performance is relatively

high in comparison to most of the algorithms' per-

formances.

To summarize, when comparing the Gittins indi-

ces method and the Bayesian learning based algo-

rithm, we can note the following points:

1. Both methods assume normal distributed arms or

alternatives.

2. The Gittins indices takes into account future

rewards as a result of the exploration of new

arms, considering an infinite horizon scope, giv-

en a constant discount ratio, while the Bayesian

inference algorithm maximizes the expected util-

ity of the next step.

3. The Bayesian learning algorithm considers the

correlation between different alternatives, while

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

252

the Gittins based algorithm assumes independent

arms.

In fact, when comparing both methods, the Bayesian

based algorithm outperforms the Gittins based algo-

rithm, However, the Gittins Indices' performance is

relatively higher than most of the algorithms' per-

formances, given more than 10 steps. Moreover, the

Gittins algorithm is the best one when considering

high levels of improvement of the student level, as

illustrated in Figure 8.

Note also that if the normal distribution does not

hold, the UCB algorithm (Auer, Cesa-Bianchi and

Fischer, 2002) can be applied for multi armed bandit

processes. In contrast to Gittins method, the UCB

algorithm considers a finite set of actions, but again,

the alternative arms are assumed to be independent,

while in our study, a correlation does exists, as ex-

plained in point 3 above.

Next we compare the rate of successes in answer-

ing a question as shown in Figure 6. As observed,

the DVRL and the Q-learning methods achieve the

highest rate of success in answering question. But,

since they achieve a relatively low average of utility,

one can infer that these methods tend to offer easy

questions relative to the optimal level of questions

that should be provided.

Figure 6: The rate of questions that were successfully

answered as a function of the number of questions in the

simulation.

Note that the rate of success of the Bayesian can

also be increased by assigning higher weights for

correctly answering a question. For example, this

can be done by assigning a negative utility for a

question answered incorrectly, as provided in Utility

function #2, which is defined in Section 3:



question i=1..N

(level

+ C | question i was correctly answered) –



question i=1..N

(C | question

i was not correctly answered).

According to this utility function, for each cor-

rectly answered question the student receives a posi-

tive constant C (reward) in addition to the question's

level. However, for any incorrectly answered ques-

tion the student receives a constant negative value C

(penalty).

Consequently, next we compare all proposed algo-

rithms when the following utility function is used to

calculate the performance of the various algorithms

as presented in Figure 7.

Figure 7: The rate of questions correctly answered w.r.t.

all questions that were asked, as a function of the constant

C taken in the utility function (ITS with 50 questions).

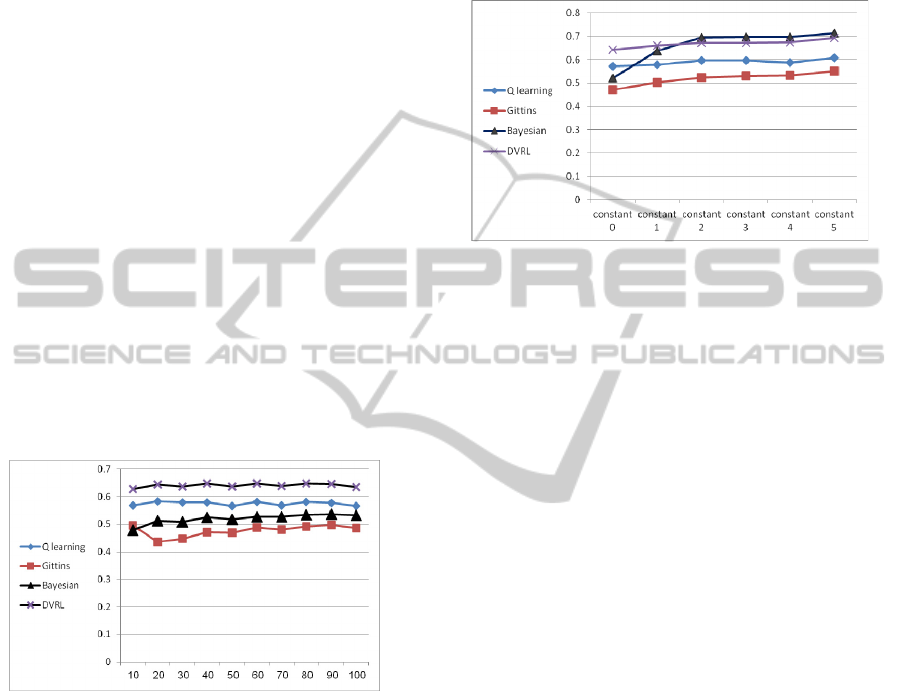
As can be seen in Figure 7, for the simulations

considering the above utility function with a con-

stant higher than 2 (i.e., the value of 2 for the reward

and -2 for the penalty), and with 50 questions a tu-

toring session, the Bayesian algorithm achieves the

highest accuracy level.

The explanation can be due to the fact that the

policy of the Q learning family algorithms, and in

particular the policy of DVRL, is careful, and for the

most part they prefer to choose the well-known suc-

cessful choice rather than explore new possibilities.

Thus, they chose relatively low level questions,

which achieve higher success rates but with lower

total utilities.

However, as the successfulness of question an-

swering has a higher effect on the utility function,

the Bayesian learning method, which aims to max-

imize the utility function, also suggests low level

questions to obtain higher utility values, and thus the

rate of successful questions increases respectively.

Thus we can conclude that the choice of the utili-

ty function has a great impact on the algorithms'

performances and further research should be con-

ducted in educational arena to verify which utility

function ideally represents the success of an ITS

when taking into account the teachers' and the stu-

dents' preferences that will allow the utmost effi-

ciency of the ITS.

Another interesting matter is the effect of stu-

dents who improve their abilities over time. In order

to test the performance of the different algorithms in

this case, we assumed that a mean threshold level for

AdaptationSchemesforQuestion'sLeveltobeProposedbyIntelligentTutoringSystems

253

each student will increase with constant rate  after

each step of the simulation.

Figure 8 demonstrates that for runs of 50 ques-

tions, where the mean level of the student is im-

proved each step by =0.05, and for more improve-

ment, the Gittins algorithm outperforms all other

algorithms, including the Bayesian inference meth-

od.

Figure 8: The algorithms' average utility for given im-

provements in the student's level during time.

However, an improvement level of d=0.05 means

that after 50 questions, a relative weak student (with

an average level of 2) will become an almost excel-

lent student (with an average level of 4.5), and in

real environments, such an improvement does not

occur so quickly.

The reason behind this lies in the fact that the

Gittins based algorithm may return to non beneficial

arms when their usage becomes relatively low (since

the Gittins indices depends on the usage of the arm),

and thus, the Gittins based algorithm does not ignore

the improvement of the student, and gives ITS the

ability to present harder questions as the student's

level improves. Future research is needed to include

the student's level of improvement in the model

considered by the Bayesian learning algorithm.

8 CONCLUSIONS

In this paper we examine different RL algorithms

that decide how to learn students' ability and how to

adapt the level of the question to the student's abil-

ity. We examined different algorithms, including Q

learning, TD, VRL, DVRL, Gittins' indices and

Bayesian inference, and we found that the Bayesian

inference based algorithm achieved the best results.

Moreover, the Q-learning based algorithm, named

DVRL, achieved the highest success rate.

The advantage of the Bayesian inference based

algorithm lie in the fact that it considers all the alter-

native distributions for each student, and updates its

beliefs regarding all the alternatives after each step.

The conclusion from this paper is that it may be

worthwhile to integrate the Bayesian inference based

algorithm as a Reinforcement Learning method in

future Intelligent Tutoring Systems.

However, these results are limited to artificial en-

vironments with simulated students. In future work

we intend to compare the Bayesian inference algo-

rithm using real data on the distribution of student

levels. Moreover, we intend to implement the Bayes-

ian inference based algorithm in a real ITS by prac-

ticing reading comprehension, to check its results on

real students, and compare the results obtained when

questions are chosen by the Bayesian inference algo-

rithms w.r.t. results obtained from a software provid-

ing random generated questions.

An additional area of research is to define a more

accurate utility function which will correctly reflect

the students' preferences from the automated soft-

ware.

Another direction of future work would be to take

into account the dynamic level of a student which

changes during the running of the ITS, and suggest

the appropriate model for the Bayesian algorithm to

handle this situation. This direction is important

when considering ITS which works with the same

students over a long period, since during the said

time period the student's level can change. Conse-

quently the appropriate adaptive algorithm should be

considered for such cases.

REFERENCES

Auer, P., Cesa-Bianchi, N. & Fischer, P., 2002, Finite-

time Analysis of the Multiarmed Bandit Problem, Ma-

chine Learning, 47, 235–256.

Azoulay-Schwartz, R., Katz, R. & Kraus, S. 2013, Effi-

cient Bidding Strategies for Cliff-Edge Problems, Au-

tonoumous agenst and multi-agent systems.

Azoulay-Schwartz, R., Kraus, S. & Wilkenfeld, J., 2004,

Explotation vs. Exploration in Ecommerce: Choosing

a Supplier in an Environment of Incomplete Infor-

mation, International Journal on Decision Support

Systems and Electronic Commerce 381, p. 1-18.

Beck, J. E., Woolf, B. P. & Beal, C. R. 2000, ADVISOR:

A machine learning architecture for intelligent tutor

construction. National Conference on Artificial Intel-

ligence.

Conitzer, V. & Garera, N., 2006, Learning algorithms for

online principal–agent problems and selling 1416

goods online, Proceedings of the International Con-

ference on Machine Learning, p. 209–216.

Gittins, J. C., 1989, Multi-armed Bandit Allocation Indi-

ces. John Wiley & Sons.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

254

Harmon, M. E. & Harmon, S. S., 1997, Reinforcement

Learning: A Tutorial. Publisher: Citeseer 1997. Vol-

ume: 21, Issue: 2.

Iglesias, A., Martínez, P., Aler, R. & Fernández, F. 2008,

Learning teaching strategies in an Adaptive and Intel-

ligent Educational System through Reinforcement

Learning. Applied Intelligence. Volume 31, Number 1.

p. 89-106.

Malpani, A., Ravindran, B., & Murthy, H., 2009, Person-

alized Intelligent Tutoring System Using Reinforce-

ment Learning. Twenty-Fourth International Florida

Artificial Intelligence Research Society Conferences.

Martin, K. N. & Arroyo, I., 2004, AgentX: Using Rein-

forcement Learning to Improve the Effectiveness of

Intelligent Tutoring Systems. Lecture Notes in Com-

puter Science, 2004, Volume 3220/2004, p. 564-572.

Rusell, S. & Norving, P., 1995, Artificial Intelligence, A

modern approach. Perntice hall, Inc.

Sarma, H., 2007, Intelligent Tutoring Systems Using Rein-

forcement Learning, A Thesis, Thesis Sreenivasa, In-

dian Institute of Technology, Madras.

Sarma, H., & Ravindran, B., 2007, Intelligent Tutoring

Systems using Reinforcement Learning to teach Autis-

tic students. Conference on Home/Community Orient-

ed ICT for the Next Billion (HOIT).

Sutton, R. S. & Barto, A. G., 2005, Reinforcement Learn-

ing: An Introduction. The MIT Press Cambridge, Mas-

sachusetts.

Vreind, N., 1997. Will reasoning improve learning? Eco-

nomics Letters, 55(1), p. 9–18.

Woolf, B. P., 2009, Building Intelligent Interactive Tutors

Student-centered strategies for revolutionizing e-

learning. Elsevier Inc.

AdaptationSchemesforQuestion'sLeveltobeProposedbyIntelligentTutoringSystems

255