
Nonparametric Discriminant Projections for Improved Myoelectric
Classification
Ernest N. Kamavuako
1
, Erik J. Scheme
2
and Kevin B. Englehart
2
1
Center for Sensory-Motor Interaction, Department of Health Science and Technology, Aalborg University,
Aalborg, Denmark
2
Institute of Biomedical Engineering, Department of Electrical and Computer Engineering, University of New Brunswick,
Fredericton, NB, Canada
Keywords: Pattern Recognition, Non-parametric Discriminant, kNN Classifiers, Myoelectric Classification.
Abstract: Linear discriminant analysis (LDA) is widely used for classification of myoelectric signals and it has been
shown to outperform simple classifiers such as k-Nearest Neighbour (kNN). However the normality
assumption of the LDA may cause its performance to decrease when the distribution of the feature space is
far from Gaussian. In this study we investigate whether nonparametric discriminant (NDA) projections in
combination with kNN classifiers can significantly decrease the classification error. Data sets based on both
surface and intramuscular electromyography (EMG) were used in order to solve classification problems of
up to 9 classes, including simultaneous movements. Results showed that in all data sets, the classification
error was significantly lower when using NDA projections compared with LDA.
1 INTRODUCTION
Linear Discriminant Analysis (LDA) is widely used
in classification of myoelectric signals for prosthetic
control. This is due to the fact that it is
computationally efficient and has been proven to
perform similarly to more advanced techniques
especially when the feature set is optimized
(Hargrove et al. 2007, Scheme et al. 2011). LDA
assumes that all classes of a training set have a
Gaussian distribution with a single shared
covariance, thus parameterizing it using the mean
and standard deviation only. When this assumption
is fulfilled and in case of simple classification
problems (limited number of classes), LDA provides
great performance even during real-time control
(Scheme et al. 2013). However in the case of more
complex classification problems, the performance of
LDA decays (Kamavuako et al. 2013). Several
extensions to the classical LDA have been proposed
in the literature such as Direct LDA (Yu and Yang,
2001), null space LDA (NLDA) (Chen et al. 2000),
orthogonal LDA (OLDA) (Ye 2005), uncorrelated
LDA (ULDA) (Ye et al. 2004), confidence base
LDA (Scheme et al. 2013), and so on.
Furthermore because LDA uses Fisher
projection, the actual number of features used is
bounded by the number of classes minus one.
Nonparametric discriminant (NDA) analysis
excludes the Gaussianity assumption; however it
requires a free parameter to be specified by the user,
which is the number of k- nearest neighbors (kNN).
NDA also removes the constraint on the number of
retained features. The determination of the kNN
makes it useful to be used in combination with k-
Nearest Neighbour classifier as previously shown
for face recognition (Li et al. 2009). This study
investigates whether the use of NDA can improve
the classification accuracy of myoelectric signals.
2 BACKGROUND
Nonparametric discriminant analysis (Fukunaga and
Mantock, 1983) is an extension of LDA originally
proposed by Fisher (Fisher, 1936). We will refer to
feature projection using LDA as Fisher discriminant
analysis (FDA). In this section FDA and two
versions of NDA are described. From a feature
extraction perspective, discriminant analysis is a tool
based on a criterion J and two square matrices
and
. These matrices generally represent the
scatter of sample vectors between different classes
for
, and within a class for
.
127
N. Kamavuako E., J. Scheme E. and B. Englehart K..
Nonparametric Discriminant Projections for Improved Myoelectric Classification.
DOI: 10.5220/0004732901270132
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 127-132
ISBN: 978-989-758-011-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2.1 Fisher Discriminant Analysis
FDA uses the parametric form of the scatter matrix
based on the Gaussian distribution assumption. The
within-class and between-class scatter matrices are
used to measure the class separability. If
equiprobable priors are assumed for classes, then
∙
∈
(1)
∙
(2)
where
denotes the mean of the class
, and
denotes the global sample mean.
The FDA is defined as the linear function
that maximizes the ratio of the determinant of
between-class matrix to that of the within-class
matrix as given in Eq. (3), which is mathematically
equivalent to the leading eigenvectors of
.
(3)
The number of extracted features is c – 1, because
the rank of S
b
is at most c – 1. The solution provided
by FDA is blind beyond second-order statistics. So
we cannot expect it to accurately indicate which
features should be extracted to preserve any complex
classification structure, especially for non-Gaussian
distributions. Furthermore because it assumes a
homogeneous variance and only the centers of
classes are taken into account for computing
between-class scatter matrix, it fails to capture the
boundary structure of classes effectively, which has
been shown to be essential in classification
(Fukunaga, 1990).
2.2 Nonparametric Discriminant
Analysis
Fukunaga and Mantock (1983) proposed a
nonparametric method for discriminant analysis in
an attempt to overcome the limitations of FDA for a
two-class problem. In NDA the between-class
scatter S
b
is of a nonparametric nature. This scatter
matrix is generally full rank, thus loosening the
bound on extracted feature dimensionality. For
myoelectric control purposes, discrimination
between many classes is usually desired. Li et al.
(2009) proposed an extension of the NDA to a
multiclass problem for face recognition as given in
Eq. (4). We will refer to this as NDA because only
the S
b
is of nonparametric nature.
,
,∙
∙
(4)
where ,, is the value of the weighting
function defined as
,,
,
,,
,
,
,
,
,
,
(5)
and
denotes the
feature vector of class ,α is a
parameter ranging from zero to infinity which
controls the changing speed of the weight with
respect to the distance ratio.
,
is the
Euclidean distance between two vectors. The local
kNN mean
is defined by
1
,
(6)
where
, is the
nearest neighbor from
class to the feature vector
.
The weighting function
,,
approaches 0.5 for
samples near the classification boundary and zero
for samples far away from the classification
boundary.
For NDA, the within-class matrix still has the
same form as FDA. Furthermore the NDA uses a
simple local mean instead of all the selected kNN
samples to compute the between-class scatter matrix
without considering the fact that different kNN
points contribute differently to the construction of
between-class scatter matrix (Li et al., 2009). Li et
al. (2009) proposed another extension of the NDA,
referred to as nonparametric feature analysis (NFA).
In NFA, the new nonparametric within-class scatter
matrix and between-class scatter matrix are given as
,
∙
,
(7)
,
,,∙
,
∙
,
(8)
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
128

where the weighting function in (5) is redefined as
,
,,
,
,,
,
,
,
,
,
,
(9)
In both cases (NDA and NFA), after computing the
and
or
and
the final NDA or
NFA features are eigenvectors of the matrix
∙
or
∙
for NDA and NFA
respectively. Contrary to FDA, which can only
extract at most c – 1 discriminant features, the NDA
and NFA inherently overcome the limitation by
making use of all samples in the construction of
between-class scatter matrix instead of using only
the class centers. Thus, for myoelectric
classification, optimal feature projections can be
found by tuning the following three parameters: the
number of local samples (kNN), the weighting
function parameter (α) and the numbers of retained
features (NRF) after projection as a means of
dimensionality reduction.
2.3 K-Nearest Neighbour Classifier
The NDA and NFA utilize information from the k-
nearest neighbors (kNN) in the construction of the
scatter matrices. A nonparametric classifier such as
the kNN classifier should be well suited for
classification of nonparametric projected features.
The kNN rule, first introduced by Fix and Hodges
(1951), is one of the most straightforward
nonparametric techniques. The basic principle
behind the kNN rule is that the most likely
assignment for a queried pattern is the class most
often represented by its bordering exemplars. In
addition to the standard kNN rule, we also tested an
extension to the kNN classifier referred to as the
local mean-based k-nearest neighbor algorithm
(LMKNN), which employs the local mean vector of
each class to classify query patterns (Mitani and
Hamamoto, 2006).
2.4 LMKNN Classifier
The LMKNN, as a successful extension of the kNN
rule, is a simple and robust classifier in cases where
the sample size is small. The goal of the LMKNN is
to overcome the negative effect of the existing
outliers in the training set (Gou et al., 2012). The
algorithm is summarized as follows:
1. Search the k nearest neighbors from set
of
each class
for the query pattern x. Let
, be the set of kNNs for x in the class
using the Euclidean distance metric.
2. Calculate the local mean from the class
as
1
,
3. Assign x to the class c if the distance between the
local mean vector for c and the query pattern in
Euclidean space is minimum.
argmin
3 METHODOLOGY
3.1 Subjects
Experiments were conducted with nine able-bodied
subjects (6 male/3 female, age range: 19 - 26 yrs).
The procedures were in accordance with the
Declaration of Helsinki and approved by the
University of New Brunswick’s research ethics
board. Subjects provided their written informed
consent prior to the experimental procedures. The
subjects had no history of any musculoskeletal
disorders.
3.2 Data Collection
Surface and intramuscular EMG were recorded
concurrently from the following muscles: flexor
carpi radialis (FCR), flexor digitorum superficialis
(FDS), extensor carpi radialis (ECR) and extensor
digitorum communis (EDC). Intramuscular wire
electrodes were made of Teflon-coated stainless
steel (A-M Systems, Carlsborg WA, diameter 50
µm) and were inserted into each muscle with a
sterile 25-gauge hypodermic needle. The insulated
wires were cut to expose 3 mm of the wire, in order
to capture more (less specific) EMG. The needle was
inserted, inclined approximately 45
o
, to a depth of
10 to 15 mm below the muscle fascia and then
removed to leave the wire electrodes inside the
muscle. Muscle identification and electrode position
were confirmed using an ultrasound scanner.
Intramuscular signals were analog bandpass filtered
between 0.1 and 4.4 KHz. Surface EMG was
recorded using four bipolar electrodes (Duo-trode
Ag-Ag/Cl, Myotronics, Inc.) placed no more than a
few millimeters proximal to the wire insertion points
so that they ostensibly recorded from the same
muscles as the wire electrodes. Surface EMG signals
were analog bandpass filtered between 10 – 500 Hz.
All signals were amplified (AnEMG12,
NonparametricDiscriminantProjectionsforImprovedMyoelectricClassification
129
OTbioelletronica, Torino, Italy), A/D converted
using 16 bits (NI-DAQ USB-6259), and sampled at
10 kHz. A reference electrode was placed at the
wrist.
3.3 Experimental Procedures
EMG signals were collected in two parts, during
unconstrained contractions corresponding to nine
classes of motion: Hand Open (HO), Hand Close
(HC), Wrist Flexion (WF), Wrist Extension (WE),
simultaneous HO+WF, HO+WE, HC+WF, HC+WE
and no motion. In the first part, four repetitions of 3s
were collected for each motion, during which the
unconstrained subjects dynamically ramped from a
low level contraction to a moderately hard level
(ramp data). In the second part, four repetitions of 3s
were collected for each motion, during which the
unconstrained subjects held a medium level
contraction to capture signals at a steady state (static
data). The experiment provided the following four
data sets processed separately: intramuscular ramp
data, surface ramp data, intramuscular static data,
and surface static data. Additionally, a previously
recorded data set from three transradial amputee
subjects, ranging in age from 25 to 45 (one acquired
and two congenital deficiencies) with six equally
spaced pairs of stainless steel surface electrodes was
used. Amputee subjects were prompted to elicit
contractions corresponding to the following five
classes of motion: WF, WE, WP, WS and no
motion. Four repetitions of 2 s were collected for
each motion during a ramp contraction. See (Scheme
et al., 2013) for more details.
3.4 Signal Processing
EMG signals were digitally high-pass filtered (3rd
order Butterworth filter) with a cutoff frequency at
20 Hz to attenuate movement artifacts. Four time-
domain features were extracted from overlapping
(by 32 ms) signal intervals of 160 ms in duration.
The following four time domain (TD) features were
computed on a per window basis: waveform length
(WL), mean absolute value (MAV), zero crossing
(ZC), slope-sign change (SSC). The feature space
was projected using FDA, NDA and NFA and
classified using KNN and LMKNN. Furthermore the
results were compared to the commonly used linear
discriminant analysis (LDA) classifier. For all cases,
data were processed using a four-fold validation
procedure.
Each fold consisted of assigning one repetition as
testing data and the remaining three repetitions as
training data; the mean of the four classification
errors was reported. To find the optimal projections,
the following range was used. The number of kNN
was varied from 2 to 50. Parameter α was limited to
0, 0.5, 1 and 2, 3. Higher α values were found to
decrease the performance during pilot analysis. NRF
was investigated from 20 to 100% of all the features.
For each case (KNN
raw
, KNN
fisher
, KNN
nda
,
KNN
nfa
, LMKNN
raw
, LMKNN
fisher
, LMKNN
nda
,
LMKNN
nfa
, LDA, SVM) a paired t-test was used to
compare that case with the case resulting in the
lowest classification error computed as the number
of misclassification divided by total number of
decisisons. P-values less than 0.05 were considered
significant.
4 RESULTS
Tables 1 and 2 summarize the results when using
kNN and LMKNN respectively. For every data set,
nonparametric projections performed significantly
better than when using raw features or Fisher
projections. Using kNN and LMKNN after
nonparametric projection performed significantly
better than LDA. Results obtained with LDA are
replicated in both Tables for clarity.
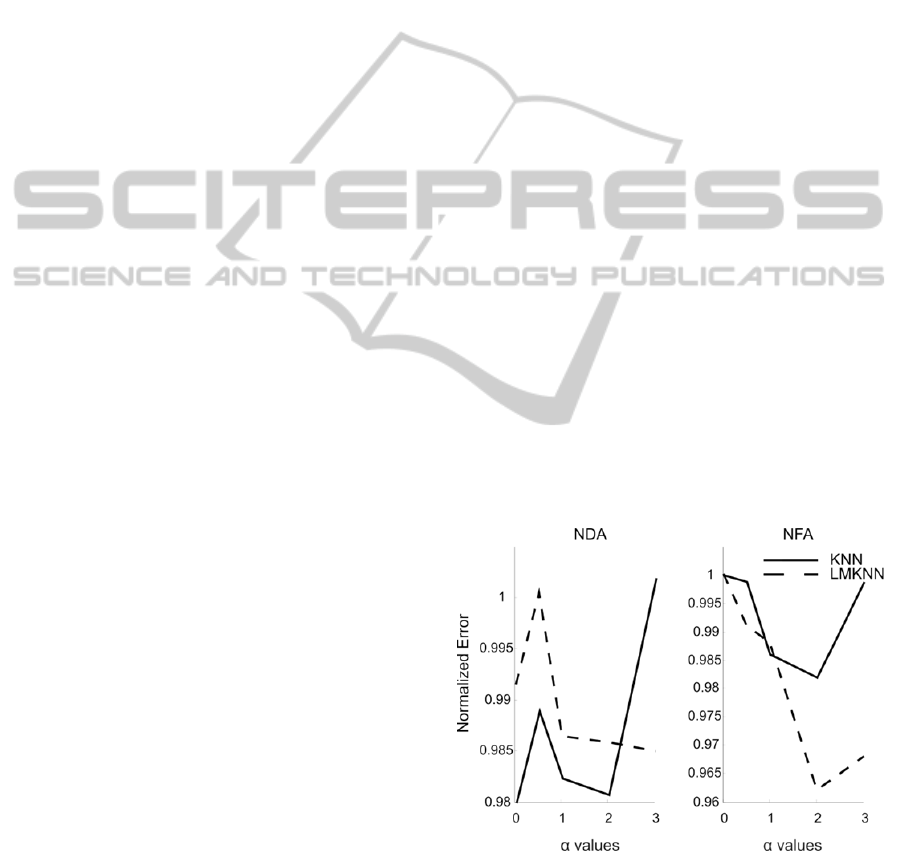
Figure 1 shows the performance of both NDA
and NFA with respect to α when kNN and the
number NRF are optimized, averaged over all
datasets. In most cases, the error associated with
varying α of is minimal; around 2.
Figure 1: Performance of NFA and NDA with respect to
alpha, which is the weighting function parameter. The
error is normalized with the maximum error for
visualization purposes.
For the range used in this study, the value of this
parameter seems not to affect the performance very
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
130
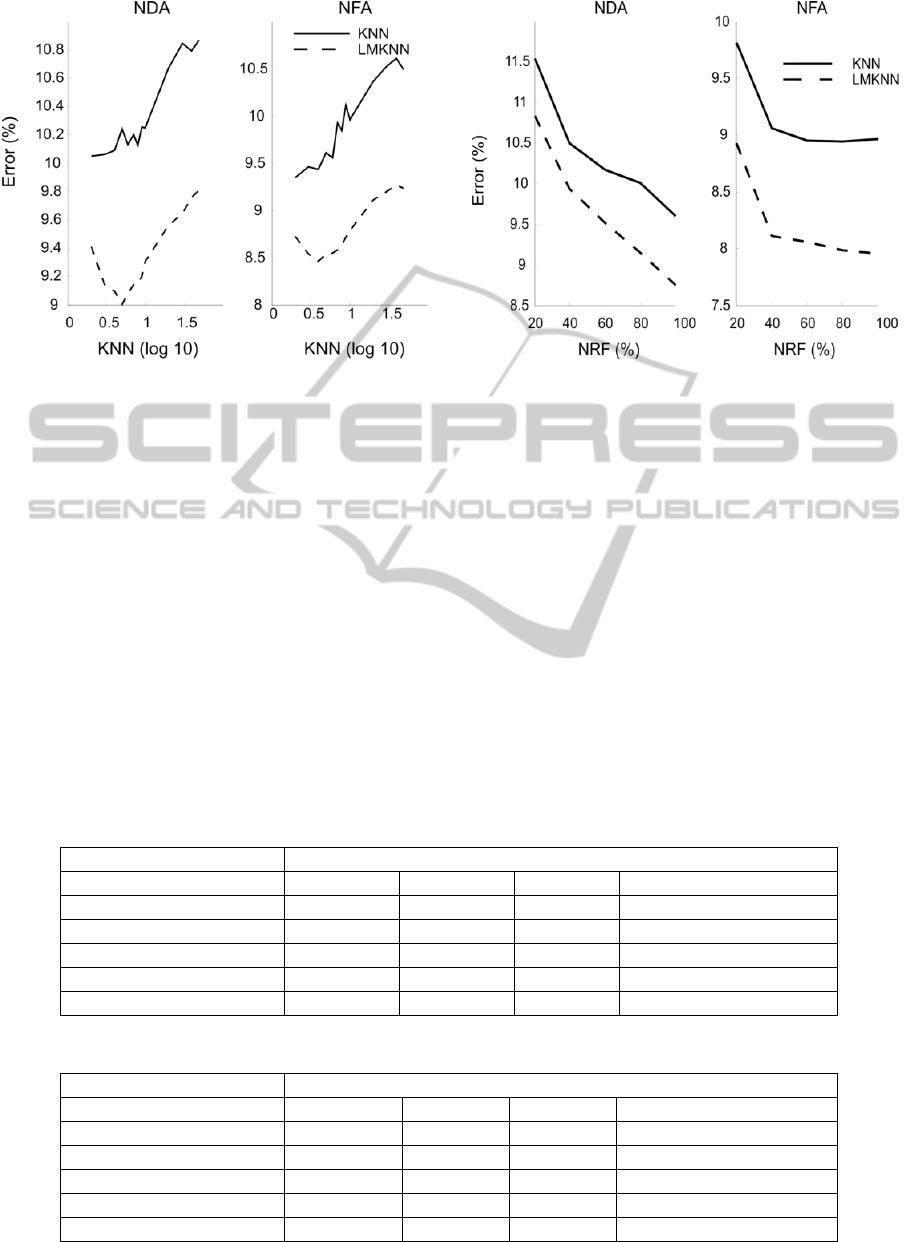
Figure 2: Performance of NDA and NFA with respect to
the kNN when alpha is fixed to 2.
much. Thus Figure 2 and 3 present the dependency
of error to kNN and NRF when α is fixed to 2.
Lower values of kNN are required for optimal
performance. NFA was found to need fewer features
than NDA. Thus when α is fixed and all the features
are used, kNN is the only remaining parameter to be
optimized.
5 DISCUSSIONS
The aim of this study was to investigate whether
nonparametric feature projections may improve
classification accuracy of myoelectric signals for
control purposes. Results showed that projecting the
Figure 3: Performance of NFA and NDA with respect to
the number of retained features (NRF) with fixed alpha.
features based on NFA and NDA did reduce
classification errors compared to the case when raw
features based on NFA and NDA did reduce
classification errors compared to the case when raw
features or Fisher projections are used with KNN
with KNN or LMKNN performed significantly
better than LDA classification alone. One drawback
with the use of nonparametric projections is that
three parameters must be optimized. Fortunately,
these results imply that only the number of KNN
samples is of major importance. In case of low
dimensionality of the feature space, all features can
be used and alpha parameters should be kept as low
and LMKNN classifiers. Furthermore, for every data
set used in this study, NFA and NDA in combination
Table 1: Classification errors obtained with KNN classifier.
Data set KNN
Fisher NDA NFA LDA
intramuscular ramp data 14.7 ± 2.0* 14.1 ± 2.2*
13.0 ± 1.8
17.8 ± 2.5*
intramuscular static data 9.0 ± 1.6* 7.8 ± 1.5
7.1 ± 1.5
12.6 ± 2.0*
surface ramp data 16.4 ± 2.5 15.4 ± 2.4
14.6 ± 1.9
19.1 ± 2.6*
surface static data 10.0 ± 1.9 9.5 ± 1.7
9.0 ± 1.6
12.2 ± 1.7*
amputee data 9.0 ± 2.4 9.4 ± 2.7
7.1 ± 2.0
9.6 ± 2.6
Table 2: Classification errors obtained with LMKNN classifier.
Data set LMKNN
Fisher NDA NFA LDA
intramuscular ramp data 14.5 ± 1.9* 13.2 ± 2.0
12.5 ± 1.9
17.8 ± 2.5*
intramuscular static data 8.7 ± 1.5* 7.3 ± 1.5
6.7 ± 1.5
12.6 ± 2.0*
surface ramp data 15.6 ± 2.5* 13.9 ± 2.3
13.5 ± 1.9
19.1 ± 2.6*
surface static data 9.4 ± 1.8 8.7 ± 1.5
8.6 ± 1.6
12.2 ± 1.7*
amputee data 9.4 ± 2.6 8.3 ± 2.3
6.2 ± 1.6
9.6 ± 2.6
NonparametricDiscriminantProjectionsforImprovedMyoelectricClassification
131

as possible (2 in this case). The shape of kNN-error
curve in the case of LMKNN motivates the use of an
optimization algorithm such as Deepest gradient that
will allow fast convergence to the minimum point.
Finding the number of k for kNN then becomes an
optimization problem that reduces computation time.
Another advantage of the NFA is the number of
features needed to achieve optimal minimal error.
From Figure 3, it can be considered that 40 % of the
features was sufficient in the case of NFA. Thus
with four channels times four features, the reduced
dimension is 6 – 7 for NFA compared to 8 for LDA.
The application of techniques presented here may be
useful for movement classification and realtime
control. However without optimization of the
parameters the techniques will be limited as training
time will be extremely long. For prosthetic control,
shortest training is desirable to improve user
satisfaction. Nevertheless although used extensively
for image processing, these techniques, their
performance for prosthetic control is limited. Most
the work are concentrated on parametric classifiers
that imposed normal distribution to the data.s In
conclusion, we have shown that nonparametric
projections in combination with kNN based
classifiers can significantly decrease myoelectric
classification error compared to the commonly used
LDA classification scheme.
ACKNOWLEDGEMENTS
This study was supported by Natural Sciences and
Engineering Research Council of Canada Discovery
Grant number 217354-10.
REFERENCES
Fukunaga, K., Mantock, J., 1983. Nonparametric
discriminant analysis. IEEE Trans. PAMI 5, 671–678.
Fisher R., 1936. The Use of Multiple Measures in
Taxonomic Problems. Annals of Eugenics, vol. 7, pp.
179-188.
Fukunaga K., Statistical Pattern Recognition. Academic
Press, 1990.
Li Z., Lin D., Tang X., 2009. Nonparametric Discriminant
Analysis for Face Recognition. IEEE Trans. Pattern
Analysis and machine intelligence 31(4): 755-761.
Fix E., Hodges JL., 1951. an important contribution to
nonparametric discriminant analysis and density
estimation. International Statistical Review, 57(3) pp.
233–247.
Mitani Y., Hamamoto Y., 2006. A local mean-based
nonparametric classifier. Pattern Recogn. Lett., 27,
1151–1159.
Gou J., Yi Z., Du L., Xiong T., 2012.. A Local Mean-
Based k-Nearest Centroid Neighbor Classifier. The
Computer Journal doi: 10.1093/comjnl/bxr131.
Scheme EJ., Hudgins BS., Englehart KB., 2013.
Confidence-based rejection for improved pattern
recognition myoelectric control. IEEE Trans Biomed
Eng. 60(6):1563-70.
Yu, H., Yang, J., 2001. A direct LDA algorithm for
highdimensional data with application to face
recognition. Pattern Recognition 34, 2067–2070.
Chen, L.F., Liao, H.Y.M., Ko, M.T., Lin, J.C., Yu, G.J.,
2000. A new LDA-based face recognition system
which can solve the small sample size problem.
Pattern Recognition 33, 1713–1726.
Ye, J., 2005. Characterization of a family of algorithms for
generalized discriminant analysis on undersampled
problems. Journal of Machine Learning Research 6,
483–502.
Ye, J., Janardan, R., Li, Q., Park, H., 2004. Feature
extraction via generalized uncorrelated linear
discriminant analysis. In: Proc. International
Conference on Machine Learning, pp. 895–902.
Scheme E., Englehart K., Hudgins B., 2011. Selective
Classification for Improved Robustness of Myoelectric
Control Under Nonideal Conditions. IEEE
Transaction on Biomedical Engineering, vol. 58, no.
6, pp. 1698-1705.
Kamavuako et al. 2013. Surface Versus Untargeted
Intramuscular EMG Based Classification of
Simultaneous and Dynamically Changing Movements.
IEEE Trans Neural Syst Rehabil Eng. in press.
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
132
