
Shape Similarity based Surface Registration
Manuel Frei and Simon Winkelbach
Institute for Robotics and Process Control, TU Braunschweig, Muehlenpfordtstr. 23, Braunschweig, Germany
Keywords:
Surface Registration, Scan Alignment, Self-similarity, Surface-based Feature, RANSAC, RANSAM, 3D
Puzzle.
Abstract:
In the last 20 years many approaches for the registration and localization of surfaces were developed. Most of
them generate solutions by minimizing point distances or maximizing contact areas between surface points.
Other algorithms try to detect corresponding points on the two surfaces by searching for points with same fea-
tures and align them. However, aligning and localizing self-similar surfaces or surfaces having large regions
with approximately constant curvature is still a complex problem.
In this paper a new algorithm for registration and matching of surfaces is introduced, which extends an ap-
proach maximizing the contact area between the surfaces by surface-based dissimilarity features and thereby
solves the problem of registering the problematic surfaces described above.
Our evaluation shows the great potential of our approach regarding efficiency, accuracy and robustness for
various applications like scan alignment, pottery assembly or bone reduction.
1 INTRODUCTION
Matching and registration of surfaces is an important
problem for many applications. Hereby the general
goal is the generation of a rigid body transformation
that aligns two surfaces. The field of applications in-
cludes registration of partially overlapping surfaces or
volumes, object recognition, object localization and
reconstruction of broken objects like broken pottery
or bone fractures in computer aided surgery. A review
of all published registration algorithms would go be-
yond the scope of this paper. Therefore we just give a
short summary of the most related work.
A standard algorithm for registration is the Itera-
tive Closest Point (ICP) algorithm, which aligns two
surfaces by iteratively searching for closest points and
calculating a transformation to align them (Besl and
McKay, 1992). Other ICP variants enhance the orig-
inal algorithm by using additional information like
texture (Papatheodorou and Rueckert, 2004), colour
(Johnson and Kang, 1997) or pseudo colour attributes
(Romero and Devy, 2008). However, the limitation
of the ICP algorithms is that an initial pose must be
known in advance.
Before performing a fine registration with ICP
usually a coarse registration has to be executed to find
an initial pose. Here two general procedures can be
differentiated.
The first class are algorithms registering surfaces
by searching for corresponding surface points with
characterizing features. Points with very similar sur-
face features probably correspond. These correspond-
ing points can then be used for the calculation of a
rigid transformation which aligns the two surfaces. In
general a feature can be any characterizing property
of a region or a point. They can be very complex as
spin images (Johnson and Hebert, 1999) or signatures
of histograms of orientations (Tombari et al., 2010)
whose advantage is that there are only few points on
the other surface with similar ones. Other approaches
use low-dimensional surface features like surface cur-
vatures (Yamany and Farag, 2002), edge points (Ser-
tel and
¨
Unsalan, 2006), 3d surface lines (Yao et al.,
2010) or surface integration based features (Gelfand
et al., 2005). Their advantage in respect to the com-
plex ones is the low complexity of computing, stor-
ing and comparing. However, with decreasing feature
complexity the difficulty of detecting correct point
correspondences especially increases when process-
ing surfaces being noisy or highly self-similar or hav-
ing large regions with nearly constant curvature.
The approaches belonging to the second class try
to find the best alignment by maximizing a quality
function in the parameter space of all rigid transfor-
mations between both surfaces. By testing many pa-
rameter combinations the optimal alignment of the
surfaces is generated. Whereas Hough Transform
based methods vote between all possible parame-
359
Frei M. and Winkelbach S..
Shape Similarity based Surface Registration.
DOI: 10.5220/0004733603590366
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 359-366
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

(a) (b) (c)
Figure 1: Cup fragments: (a) 4 fragments with 805 to 15721 vertices and convex hulls of 28.14 x 19.66 x 64.12 to 132.98 x
153.82 x 119.72 mm; (b) reassembled cup with eRANSAM; (c) matching results of approaches calculating the LCP.
ter combinations (Ballard, 1981), the Random Sam-
ple Consensus (RANSAC)-based approaches (Fis-
chler and Bolles, 1981) only evaluate parameter com-
binations being generated by randomly selecting data
points. However, because of the enormous storage
consumption and the high computation times the al-
gorithms aren’t applicable without any further im-
provements.
Therefore (Rusu et al., 2009) introduced a
RANSAC variant, Sample Consensus - Initial Align-
ment (SAC-IA), that reduces the number of consid-
ered surface points by detecting correspondence can-
didates with characterizing features (Fast Point Fea-
ture Histogram).
(Aiger et al., 2008) proposed a RANSAC variant
reducing the required number of transformation hy-
potheses for a good solution by detecting nearly con-
gruent coplanar 4-point sets on both surfaces.
Another RANSAC-based approach is the Random
Sample Matching (RANSAM) algorithm (Winkel-
bach et al., 2006). It also reduces the number of
required transformations compared to RANSAC by
detecting congruent 2-point sets on the two surfaces
with features being invariant under translation and ro-
tation and consequently is very fast. It can be applied
in many applications like the localization of objects
for an industrial bin picking system (Buchholz et al.,
2010), the localization of mobile robots (Iser et al.,
2008), the registration of scanned surfaces (Winkel-
bach et al., 2006) or the reconstruction of broken ob-
jects like bone fractures (Winkelbach et al., 2004). It
is robust to noise and outliers calculating the largest
common point set (LCP) of two surfaces and using
no surface features except surface normals. How-
ever, the registration problem of surfaces being highly
self-similar or having large areas with nearly constant
curvature can neither be solved by these approaches
without prior knowledge of surface shape or geome-
try (see Figure 1 (c)).
1.1 Contribution and Overview
In this paper we present the algorithm extended Ran-
dom Sample Matching (eRANSAM) which extends
RANSAM by integrating a surface-based, point-wise
dissimilarity feature and so combines the advantages
of algorithms calculating the LCP of two surfaces and
surface-based features. Thus we can handle a limi-
tation of most registration approaches, the matching
of surfaces having large regions with nearly constant
curvature, no or few feature points or being highly
self-similar. Since the generation of the dissimilarity
feature is robust against noise the whole registration
approach remains robust against noise. Another ad-
vantage of the algorithm is the fact that there is no re-
quired preprocessing on the data sets of the surfaces,
like removing points or smoothing the surface.
After having applied RANSAM or eRANSAM
the ICP algorithm can be used for refining the align-
ment results. However, all results presented in our
evaluation were obtained without an ICP pose refine-
ment.
In the following we describe the similarity fea-
ture and its generation, give an overview of the most
relevant RANSAM steps and show how to extend
RANSAM by the similarity feature. Finally we
present some registration results of eRANSAM for
various registration scenarios and compare them to
those of basic RANSAM and SAC-IA.
2 INTEGRATION OF A
DISSIMILARITY FEATURE
INTO RANSAM
RANSAM is an efficient and robust probabilistic
matching algorithm for finding a 4 ×4 homogeneous
transformation matrix T , which aligns two surfaces (A
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
360

and B) such that the LCP of the two surfaces is com-
puted. It is based on the well-known RANSAC ap-
proach, which is accelerated by a probabilistic birth-
day attack (Weisstein, 2008).
By using the birthday attack many potential pose
hypotheses are generated rapidly. The subsequent
evaluation of these likely poses is accelerated by a
Monte Carlo approximation whereby poor transfor-
mations are dropped early.
In this section eRANSAM is introduced which
combines RANSAM with a surface-based dissimilar-
ity feature. Therefore we first present the point-wise
dissimilarity feature and the calculation of the dis-
similarity weights. Second, we present some impor-
tant RANSAM steps, the generation of pose hypothe-
ses and the quality estimation of transformations, and
show how we can enhance them by integrating the
calculated weights.
But first we define some basics. Given the sets P
A
and P
B
of 3D point coordinates and the sets N
A
and N
B
of their corresponding 3D surface normals. We define
the combination of a 3D point coordinate and its cor-
responding surface normal in 3D as an oriented point
(6D parameter vector) (Johnson and Hebert, 1997)
and a pair of oriented points as a dipole. Addition-
ally in this paper we extend the 6D parameter vector
to a 7D parameter vector by adding one weight per
point from the sets W
A
and W
B
whose generation is
introduced in the following section:
A :=
{
u = [p
u
, n
u
, w
u
]
|
p
u
∈ P
A
, n
u
∈ N
A
, w
u
∈W
A
}
,
B :=
{
v = [p
v
, n
v
, w
v
]
|
p
v
∈ P
B
, n
v
∈ N
B
, w
v
∈W
B
}
.
(1)
Furthermore we define the boolean contact function
c(T, a, b) =
|
p
a
−T p
b
|
< ε
p
∧1−
n
T
a
H
i
n
b
< ε
n
(2)
which evaluates if two points a and b are in contact
to each other after being transformed into a common
coordinate system by the transformation T . The con-
stants ε
i
represent small tolerance values for a toler-
ated point distance and normal deviation depending
on noise and the point sampling resolution.
2.1 Dissimilarity Feature
In (Winkelbach et al., 2012) an approach for the gen-
eration of a shape-similarity rating for each surface
point is introduced. This algorithm assigns high sim-
ilarity values to those points or surface regions being
very similar to many surface regions of a given refer-
ence shape. By simply inverting the evaluation of this
approach we calculate a dissimilarity feature which is
illustrated by broken cup fragments in Figure 2.
Figure 2: Illustration of the dissimilarity of the cup frag-
ments (red represents high values, blue low values).
The algorithm consists of two steps, first gener-
ating potential alignments between source and refer-
ence shape and second calculating a dissimilarity rat-
ing depending on the generated transformations.
For the generation of a set of k potential match-
ing hypotheses H =
{
H
1
, H
2
, ...H
k
}
where H
i
is a
4 × 4 homogeneous transformation matrix we use
the RANSAM algorithm. However, any probabilis-
tic matching algorithm can be used generating partial
matches which are homogeneously distributed and
fulfil some conditions like a minimum number of con-
tact points.
In the second step for each surface point a ∈A the
subset
H(a) =
{
H
i
|
¬∃b ∈ B : c(H
i
, a, b)
}
⊆ H (3)
is calculated which is the set of all hypotheses where
a is not in contact with the reference surface B.
Now the proportion p(a) =
|
H(a)
|
|
H
|
can be regarded
as the probability that RANSAM doesn’t match sur-
face B in such a way that a point a is in contact with
it. Thus, it can be used as a measure for dissimilarity
between reference surface and the source surface.
In order to further increase the relevance of dis-
similar points in the registration process we calculate
dissimilarity weights
w
a
=
|
H(a)
|
2
(4)
by squaring the dissimilarity rating. They can be cal-
culated before executing the registration algorithm.
The runtime of registration scenarios can be re-
duced by ignoring points being highly self-similar us-
ing an automatically calculated threshold. We used
the Otsu threshold method (Otsu, 1979) which cate-
gorizes weights into two classes such that the intra-
class variance is minimized and the inter-class vari-
ance is maximized. The calculated threshold t is then
used for weight calculation:
w
a
=
(
|
H(a)
|
2
|
H(a)
|
> t,
0 otherwise
. (5)
A comparison of eRANSAM with and without thresh-
old usage can be found in our evaluation.
ShapeSimilaritybasedSurfaceRegistration
361

uv
u
p
v
p
v
n
u
n
uv
d
Figure 3: Geometric relations of a dipole being invariant
under rotation and translation.
2.2 Rapid Generation of Likely Pose
Hypotheses
RANSAM includes a very fast approach to find likely
pose hypotheses by assuming a contact between A and
B, e.g. a contact between dipoles. Such dipoles of A
and B, which are geometrically congruent, are can-
didates for contact points to be aligned. Geometrical
congruent means, that they have the same geometric
relations
rel(u, v) = (d
uv
, α, β, δ
uv
)
T
(6)
(see Figure 3) where d
uv
is the euclidean distance be-
tween point p
u
and p
v
, α is the angle between the nor-
mal n
u
and the line through p
u
and p
v
, β is the angle
between the normal n
v
and the line through p
u
and p
v
and δ
uv
is the angle between the normals n
u
and n
v
around the line through p
u
and p
v
.
The search for congruent dipoles is accelerated by ex-
ploiting the birthday attack. Therefore two 4D re-
lation tables (R
A
and R
B
) are used in which already
selected dipoles are stored using rel(u, v) as table in-
dices.
Instead of selecting dipoles of A and B randomly
(RANSAM) we use their weights W
A
and W
B
as se-
lection probability (eRANSAM). In this way points
having higher dissimilarity weights are selected more
often and so relevant matching hypotheses are gener-
ated more often. This results in the following loop:
1. Select a random dipole (a,c) ∈ A using w
a
and w
c
as selection probabilities and calculate rel(a, c).
2. Insert the dipole into the relation table R
A
:
R
A
[rel(a, c)] = (a, c).
3. Read out the same position of R
B
: (b, d) =
R
B
[rel(a, c)]. If there is an entry the new pose hy-
pothesis is calculated by bringing (a, c) and (b, d)
into contact.
4. Now the same procedure is done with the other
surface:
Select a random dipole (b,d) ∈B using w
b
and w
d
as selection probabilities and calculate rel(b, d).
5. Insert the dipole into the relation table R
B
:
R
B
[rel(b, d)] = (b, d).
6. Read out the same position of R
A
: (a, c) =
R
A
[rel(b, d)]. If there is an entry the new pose hy-
pothesis is calculated by bringing (a, c) and (b, d)
into contact.
These steps are repeated until the generated pose hy-
pothesis satisfies a certain condition, e.g. an achieved
sufficient quality or an exceeded predefined time
limit.
A simple approach for calculating the relative ho-
mogeneous transformation T aligning two dipoles is
given in (Winkelbach et al., 2006).
2.3 Weighted Random Sampling
As mentioned above lots of dipoles of A and B have
to be selected for generating an adequate number of
likely pose hypotheses. For this reason the random
sampling has to be very fast. As a tradeoff between
runtime and an accurate weighted random selection
the following quick heuristic algorithm is used in eR-
ANSAM where step 1 to 3 can be performed offline
and only step 4 has to be executed for each weighted
random sample of a point:
1. Sort the oriented points of A (B) by their weights
W
A
(W
B
).
2. Generate d
√
ne bins where n =
|
A
|
(n =
|
B
|
).
3. Fill the bins consecutively with the sorted points
in such a way that all bins have approximately the
same sum of weights
∑
n
i=1
w
i
d
√
ne
(first use the oriented
points with the highest dissimilarity rating).
4. Select two random numbers, use the first one to
select bin k (0 ≤k ≤d
√
ne) and the second one to
select a random oriented point of bin k.
In this way we obtain bins containing few oriented
points with high weights and bins containing lots of
oriented points having smaller weights.
Alternatively any algorithm performing a
weighted random sampling can be used, e.g. (Murray
et al., 2013).
2.4 Quality Estimation of Likely Pose
Hypotheses
The basic RANSAM algorithm estimates the quality
of a likely pose hypothesis by calculating the propor-
tion of overlapping area
Ω ≈
∑
n
i=1
w
B
(T, a
i
)
|
A
|
, (7)
where w
B
(T, a) is a function which returns 1 if the ori-
ented point a ∈ A is in contact with surface B after be-
ing transformed by T and 0 otherwise. RANSAM and
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
362

Table 1: Registration performance of 250 test runs: comparison of the RMSE in mm of corresponding vertices of the best pose,
RANSAM, SAC-IA, eRANSAM and eRANSAM with an Otsu threshold at dissimilarity weight calculation (eRANSAM
t
)
for various registration scenarios.
best pose RANSAM SAC-IA eRANSAM eRANSAM
t
object (Figure)
cup A+B (1)
cup A+C (1)
cup A+D (1)
cup C+D (1)
femur (5)
cup scans (6)
cylinder (7)
plane (8)
0.00
0.00
0.00
0.00
0.53
0.15
0.09
0.03
min med max
94.4 110 127
108 117 119
76.9 88.5 123
61.2 92.0 106
26.3 41.7 59.2
66.5 76.9 86.5
8.0 9.0 9.9
5.9 6.0 6.0
78.2
52.0
47.0
56.2
22.6
25.3
5.2
4.6
min med max
0.1 1.6 5.0
0.9 3.8 116
0.2 2.6 163
0.0 1.5 4.9
0.6 1.4 3.6
0.3 0.8 3.1
0.2 0.9 2.6
0.4 0.4 0.7
min med max
0.1 1.6 3.5
0.7 2.9 166
0.2 2.1 153
0.0 1.4 6.2
0.6 1.3 3.1
0.3 0.8 3.8
0.1 1.0 17.0
0.4 0.4 0.7
eRANSAM accelerate these computations by using a
k-d-tree to detect contact points and by performing an
efficient Monte Carlo strategy to drop transformations
with a weak forecasted matching quality early.
In eRANSAM we additionally use the precalcu-
lated weights to favour dissimilar points being in con-
tact over similar ones. Therefore we use the same
quality function (7) as RANSAM but we apply an-
other w
B
-function:
w
B
(T, a) =
(
w
a
·w
b
, ∃b ∈ B : c(T, a, b)
0, otherwise
. (8)
That’s because we can interpret the weight w
a
(w
b
)
of a point a (b) as the probability of his nonexistence
in the contact area between surface A and B. There-
fore the resulting probability of successfully aligned
points is given by the product of the probabilities of
the independent events w
a
and w
b
.
3 EXPERIMENTAL RESULTS
We applied our registration algorithm to various 3d
objects like potteries and bone fractures as well as to
3d scans and compared the generated results to those
of basic RANSAM and SAC-IA. All evaluations were
executed on an Intel Core 2 Quad with 2,83 GHz on
one single core. The runtime of eRANSAM was be-
tween 2 and 10 seconds depending on the number
of surface points of the datasets (10
4
to 10
5
points)
and the corresponding weights. Weight calculation
took additional 2 to 10 seconds for 100 hypotheses
(
|
H
|
= 100). In contrast to that the runtime of SAC-
IA was with 34 seconds to 8.5 minutes significantly
higher.
Since eRANSAM is a probabilistic approach we
performed 250 pairwise matches for each test object.
The common representation for registration results is
the mean error. However, it is only meaningful if
the values are normally distributed. In the evaluation
of eRANSAM the results aren’t normally distributed
and few outliers strongly influence the mean value.
Hence we present the registration results as the me-
dian, the minimum and the maximum quantiles of the
root mean squared error (RMSE) of correctly corre-
sponding points of the two surfaces.
Table 1 shows the results of some evaluated regis-
tration scenarios. It illustrates that RANSAM doesn’t
create correct alignments for any evaluated scenario
because the correct alignment doesn’t coincide with
the LCP of two surfaces in our scenarios. Further-
more it shows that SAC-IA neither creates correct
alignments for the evaluated scenarios and addition-
ally its registration runtime is very high. This is be-
cause there are no characterizing regions or points
on the surfaces, having approximately constant cur-
vature or being self-similar, that can be detected with
the FPFH feature. So the number of surface points
can’t be reduced drastically and so the LCP is still
not the correct registration result. Moreover, Table
1 shows that eRANSAM achieves correct and reli-
able results for all evaluated registration scenarios.
The few presented registration results having a high
RMSE are due to the limited runtime of the algo-
rithm. If the runtime was higher, better and similar
to the other solutions would be found (see also Fig-
ure 4). In this evaluation we only consider surfaces
being highly self-similar or having surfaces with a
nearly constant curvature and thus have a high vari-
ance in dissimilarity values. If a surface doesn’t have
such surface features the dissimilarity values are con-
stant for nearly all surface points. In such a case eR-
ANSAM achieves approximately the same registra-
tion results as basic RANSAM because no points be-
ing in contact are favoured.
3.1 3d Puzzle Problem
The characteristic of the 3d puzzle problem is the
matching of 3d objects, e.g. broken ones. Most al-
gorithms use complex segmentation techniques to de-
tect the fractured surface or try to detect feature points
(Huang et al., 2006) which is hardly possible consid-
ShapeSimilaritybasedSurfaceRegistration
363

0
10
20
30
40
50
60
70
80
90
0 2.5 5
RMSE [in mm]
time [in s]
Quantile 0% to 100%
Quantile 10% to 90%
Quantile 20% to 80%
Quantile 30% to 70%
Quantile 40% to 60%
Median
(a)
0
10
20
30
40
50
60
70
80
90
100
0 2.5 5
RMSE [in mm]
time [in s]
Quantile 0% to 100%
Quantile 10% to 90%
Quantile 20% to 80%
Quantile 30% to 70%
Quantile 40% to 60%
Median
(b)
0
5
10
15
20
25
30
35
40
45
0 2.5 5 7.5 10
RMSE [in mm]
time [in s]
σ = 0.0
σ = 0.1
σ = 0.25
σ = 0.5
σ = 1.0
(c)
Figure 4: Registration error (RMSE) over time of 250 test runs: (a) median and quantiles of eRANSAM results; (b) median
and quantiles of results of eRANSAM with threshold; (c) median RMSE of femur fragments with different additive noise.
Table 2: Registration results (RMSE in mm) for the femur fragments with additive noise after 5s.
eRANSAM eRANSAM
t
femur fragments with
no noise
σ = 0.1
σ = 0.25
σ = 0.5
σ = 1.0
min med max
0.6 1.4 3.6
0.7 1.7 4.0
0.8 1.9 5.8
0.9 2.5 33.3
1.9 9.6 36.3
min med max
0.6 1.3 3.1
0.8 1.6 3.7
0.6 1.5 3.9
0.7 1.8 4.6
1.9 7.6 35.5
(a) (b) (c)
(d) (e) (f)
Figure 5: Femur fragments: (a) Illustration of femur frag-
ments (35822 / 9402 vertices and convex hulls of 31.42 x
106.81 x 35.76 / 23.07 x 51.59 x 18.09 mm); (b),(e) simi-
larity (no noise/σ = 0.5); (c) matching result of eRANSAM;
(d),(f) femur fragments with additive noise (σ = 0.5/1.0).
ering weathered or splintered surfaces. By applying
eRANSAM we simply favour in the registration pro-
cess those surface regions which are detected by the
dissimilarity feature.
The femur fracture fragments (Figure 5) are re-
constructed from CT data and are used for several reg-
istration scenarios. First of all, the the two fragments
are matched by eRANSAM and the results are com-
pared to those of the RANSAM and SAC-IA algo-
rithms. While achieving wrong registration results by
using basic RANSAM or SAC-IA, eRANSAM cor-
rectly aligns them. In addition to that the runtime of
eRANSAM (and RANSAM) was 5 seconds and the
registration runtime of SAC-IA was with 89 seconds
much higher. The timing progress of eRANSAM of
the distance to the correct alignment is illustrated on
Figure 4 (a) and (b), where you can see that the me-
dian RMSE is below 2.5 mm already after 0.45 sec-
onds registration time. By additionally using an Otsu
threshold at dissimilarity weights calculation this reg-
istration error can already be achieved after 0.36 sec-
onds. Table 1 also apparently shows that the usage of
a threshold (e.g. Otsu) improves the registration re-
sults regarding accuracy. However it only accelerates
the registration process by decreasing the number of
potential selected points. Actually eRANSAM with-
out a threshold achieves results with a higher accuracy
but with a longer computation time. So the user has
to decide if he rather wants to have accurate results or
fast results which can be refined by ICP.
Exemplarily for all surfaces we present the perfor-
mance of eRANSAM at noisy input data for the fe-
mur fragments. Therefore we apply some zero-mean
Gaussian noise with various standard deviations (σ) to
the surfaces. Our evaluation shows that eRANSAM is
successful for surfaces with strong additive noise (see
Figure 4 (c)). Even in case of the highest, evaluated
noise level eRANSAM finds a solution that is good
enough for a subsequent ICP optimization.
Further we applied eRANSAM to broken cup
fragments and compared the results to RANSAM,
SAC-IA and eRANSAM with a threshold. These
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
364
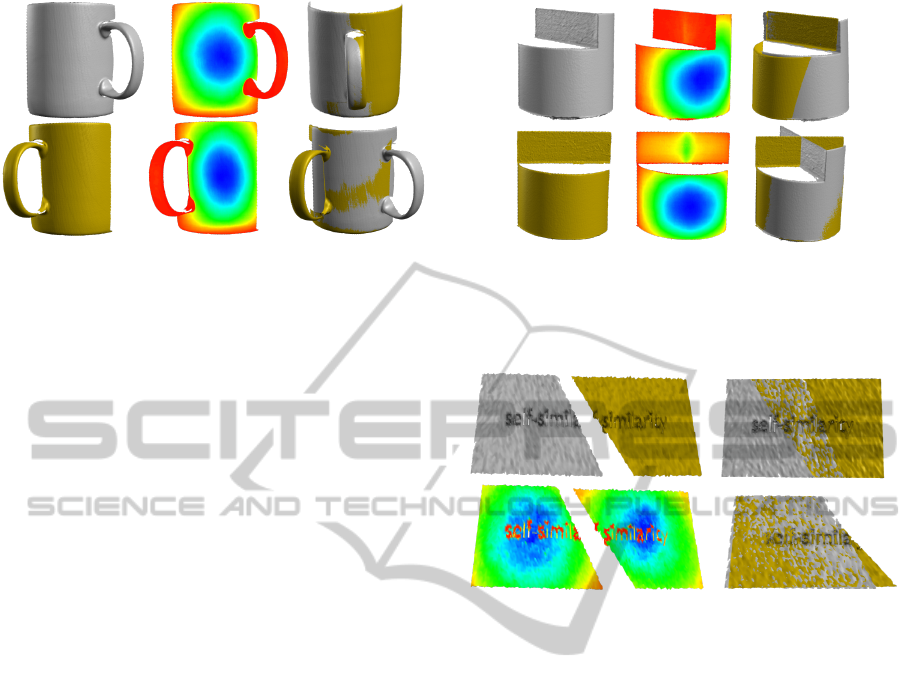
Figure 6: Illustration of cup scans (115505 / 110488 ver-
tices and 68.04 x 94.08 x 81.03 / 57.24 x 97.58 x 91.18
mm), their similarity, an eRANSAM matching result (right
top) and a wrong result with a LCP approach (right bottom).
are as well registration scenarios which could not be
solved by calculating the LCP (Figure 1). As our eval-
uation shows, eRANSAM is able to match all frag-
ments having a common fractured surface with a run-
time of 5 seconds and so the whole broken cup can
be restored. The runtime of SAC-IA achieving wrong
registration results was between 32 and 65 seconds.
3.2 Scan Registration
Another application area of eRANSAM is the regis-
tration of partly overlapping scans having large re-
gions with nearly constant curvature or being highly
self-similar. Our first test object is a cup (Figure
6) which is scanned from two different viewing di-
rections. In both scans the cup handle is visible.
However, because the cup body and the cup handle
have surfaces with nearly constant curvature it is dif-
ficult to detect feature points. Moreover the LCP of
the two scans isn’t the correct alignment either. eR-
ANSAM can solve even this complex registration sce-
nario since the cup handle is very dissimilar from
the body and therefore receives higher dissimilarity
weightings. eRANSAM isn’t only faster (10 seconds)
but also more accurate than SAC-IA (330 seconds).
Figure 7 illustrates another evaluated scenario for
scan registration, the alignment of two surfaces of
a cylinder-like object. Again the LCP approaches
lead to wrong registration results with runtimes of
10 (RANSAM) and 494 seconds (SAC-IA). Although
the scans don’t fit together correctly because of scan
deformations eRANSAM successfully aligns them
with a registration time of 10 seconds.
The final presented evaluation scenario is the reg-
istration of noisy, partly overlapping planes with few
dissimilar surface points (Figure 8). This is another
example where eRANSAM succeeds (2.5 seconds)
while LCP approaches (up to 221 seconds) fail.
Figure 7: Illustration of scans of a cylinder-like object
(50548 / 59052 vertices and 24.19 x 24.93 x 23.09 / 22.42 x
26.04 x 25.40 mm), their similarity, an eRANSAM match-
ing result (right top) and a wrong result with a LCP ap-
proach (right bottom).
Figure 8: Illustration of planes with distinctive text (5245
/ 8506 vertices and 15.05 x 2.19 x 10.00 / 16.83 x 2.18 x
10.00 mm), their similarity and an eRANSAM matching
result (right top) and a wrong result with a LCP approach
(right bottom).
4 CONCLUSIONS
In this paper we introduced eRANSAM, a new ap-
proach for the registration of two self-similar sur-
faces. Based on the RANSAM algorithm we use for
the calculation of the transformation aligning the sur-
faces additional characterizing information which de-
pend on a region-based dissimilarity feature. So we
combine the advantages of region-based surface fea-
tures and the robustness of the RANSAC-based algo-
rithms. The dissimilarity information are integrated
into RANSAM at two steps, the generation of likely
pose hypotheses by selecting surface points regarding
the dissimilarity and the quality estimation of likely
pose hypotheses where points being in contact are
weighted according to their dissimilarity values.
Our evaluation of eRANSAM achieved excellent
results. Although eRANSAM doesn’t require any
knowledge about the surface geometry, surface shape
or an initial pose it solves complex registration sce-
narios like registering self-similar surfaces in various
ShapeSimilaritybasedSurfaceRegistration
365

areas of application, e.g. scan alignment, reduc-
tion of bone fractures or assembly of pottery.
REFERENCES
Aiger, D., Mitra, N. J., and Cohen-Or, D. (2008). 4-points
congruent sets for robust pairwise surface registration.
ACM Trans. Graph., 27(3):1–10.
Ballard, D. (1981). Generalizing the hough transform to de-
tect arbitrary shapes. Pattern Recognition, 13(2):111
– 122.
Besl, P. and McKay, N. (1992). A method for registration
of 3-d shapes. IEEE Transactions on Pattern Analysis
and Machine Intelligence, 14(2):239–256.
Buchholz, D., Winkelbach, S., and Wahl, F. (2010).
Ransam for industrial bin-picking. In Proceedings of
ISR/Robotik 2010, pages 1–6.
Fischler, M. and Bolles, R. (1981). Random sample consen-
sus: A paradigm for model fitting with applications to
image analysis and automated cartography. Commu-
nunication of the Association for Computing Machin-
ery, 24(6):381–395.
Gelfand, N., Mitra, N. J., Guibas, L. J., and Pottmann, H.
(2005). Robust global registration. In Proceedings of
the third Eurographics symposium on Geometry pro-
cessing.
Huang, Q.-X., Fl
¨
ory, S., Gelfand, N., Hofer, M., and
Pottmann, H. (2006). Reassembling fractured ob-
jects by geometric matching. ACM Trans. Graph.,
25(3):569–578.
Iser, R., Spehr, J., Winkelbach, S., and Wahl, F. (2008). Mo-
bile robot localization using the fast random sample
matching approach. In Proceedings of Robotik 2008,
VDI-Berichte No. 2012, pages 163–166.
Johnson, A. and Hebert, M. (1997). Recognizing objects
by matching oriented points. In Proceedings of IEEE
Conference on Computer Vision and Pattern Recogni-
tion, 1997, pages 684–689.
Johnson, A. and Hebert, M. (1999). Using spin images
for efficient object recognition in cluttered 3d scenes.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 21(5):433–449.
Johnson, A. and Kang, S. B. (1997). Registration and inte-
gration of textured 3d data. In Proceedings of Intern.
Conference on Recent Advances in 3D Digital Imag-
ing and Modeling, 1997, pages 234–241.
Murray, L. M., Lee, A., and Jacob, P. E. (2013). Rethinking
resampling in the particle filter on graphics processing
units. ArXiv e-prints.
Otsu, N. (1979). A threshold selection method from gray-
level histograms. IEEE Transactions on Systems, Man
and Cybernetics, 9(1):62–66.
Papatheodorou, T. and Rueckert, D. (2004). Evaluation of
automatic 4d face recognition using surface and tex-
ture registration. In Proceedings of IEEE Intern. Con-
ference on Automatic Face and Gesture Recognition,
volume 6, pages 321–326.
Romero, F. and Devy, M. (2008). Registration by using a
pseudo color attribute. In Proceedings of Intern. Con-
ference on Pattern Recognition, volume 19, pages 1–
4.
Rusu, R., Blodow, N., and Beetz, M. (2009). Fast point
feature histograms (fpfh) for 3d registration. In Pro-
ceedings of IEEE Intern. Conference on Robotics and
Automation, pages 3212–3217.
Sertel, O. and
¨
Unsalan, C. (2006). Range image regis-
tration with edge detection in spherical coordinates.
In Proceedings of Intern. Conference on Multimedia
Content Representation, Classification and Security,
pages 745–752.
Tombari, F., Salti, S., and Stefano, L. (2010). Unique sig-
natures of histograms for local surface description. In
Proceedings of 11th European Conference on Com-
puter Vision, volume 6313, pages 356–369.
Weisstein, E. W. (2008). Birthday attack-from mathworld -
a wolfram web resource[online].
Winkelbach, S., Molkenstruck, S., and Wahl, F. (2006).
Low-cost laser range scanner and fast surface regis-
tration approach. Pattern Recognition (DAGM 2006),
Lecture Notes in Computer Science 4174, pages 718–
728.
Winkelbach, S., Rilk, M., Sch
¨
onfelder, C., and Wahl, F.
(2004). Fast random sample matching of 3d frag-
ments. Pattern Recognition (DAGM 2004), Lecture
Notes in Computer Science 3175, pages 129–136.
Winkelbach, S., Spehr, J., Buchholz, D., Rilk, M., and
Wahl, F. (2012). Shape (self-)similarity and dis-
similarity rating for segmentation and matching. In
Proceedings of Pattern Recognition (DAGM-OAGM
2012), Lecture Notes in Computer Science 7476,
pages 93–102.
Yamany, S. and Farag, A. (2002). Surface signatures: an
orientation independent free-form surface representa-
tion scheme for the purpose of objects registration and
matching. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 24(8):1105–1120.
Yao, J., Ruggeri, M., Taddei, P., and Sequeira, V. (2010).
Robust range image registration using 3d lines. In
Proceedings of IEEE Intern. Conference on Image
Processing, volume 17, pages 4321–4324.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
366
