A New Two-Degree-of-Freedom Space Heating Model for Demand

Response

Anita Sant’Anna

and Robert Bass

Embedded and Intelligent Systems Research Group, Halmstad University, Halmstad, Sweden

Department of Electrical & Computer Engineering, Portland State University, Portland, OR, U.S.A.

Keywords:

Space Heating, Demand Response, Thermal Comfort, Thermodynamic Model, Simulation.

Abstract:

In today’s fast changing electric utilities sector demand response (DR) programs are a relatively inexpensive

means of reducing peak demand and providing ancillary services. Advancements in embedded systems and

communication technologies are paving the way for more complex DR programs based on transactive control.

Such complex systems highlight the importance of modeling and simulation tools for studying and evaluating

the effects of different control strategies for DR. Considerable efforts have been directed at modeling thermo-

statically controlled appliances. These models however operate with only one degree of freedom, typically,

the thermal mass temperature. This paper proposes a two-degree-of-freedom residential space heating system

composed of a thermal storage unit and forced convection system. Simulation results demonstrate that such

system is better suited for maintaining thermal comfort and allows greater ﬂexibility for DR programs. The

performance of several control strategies are evaluated, as well as the effects of model and weather parameters

on thermal comfort and power consumption.

1 INTRODUCTION

The electric utilities sector currently faces a number

of challenges: how to manage electricity prices in an

unregulated market (Spees and Lave, 2007), how to

cope with more distributed and intermittent genera-

tion such as wind power (Kondoh et al., 2011), as

well as how to cope with ever increasing peak de-

mands (Ericson, 2009). Demand response (DR) pro-

grams are an effective means for alleviating such is-

sues. When consumers can respond in real time to

high electricity prices, they naturally tend to reduce

peak-time usage, and consequently help equalize de-

mand and prices (Spees and Lave, 2007). In addi-

tion, DR programs provide a more ﬂexible and efﬁ-

cient option for fast-response ancillary services (Kon-

doh et al., 2011).

Albadi et al. concisely summarized a hierarchy

of current incentive- and price-based utility DR pro-

grams (Albadi and El-Saadany, 2007). Incentive-

based residential programs often take the form of di-

rect control, wherein a utility can directly apply an

on/off duty cycle to customer appliances in order to

adjust aggregate customer demand. Often, such pro-

grams are used for load shedding during high-demand

periods. In return for taking part in such programs

customers are rewarded with an incentive, such as a

discount on their electricity bill. Incentive-based DR

has been considered in works such as (Mohsenian-

Rad et al., 2010).

Price-based programs, on the other hand, persuade

customers to change their electricity consumption be-

havior by adjusting prices throughout day. Price ad-

justments occur either in response to current demand

or are based on a predetermined time-of-use sched-

ule. Participating customers may therefore avoid

high electricity prices by modifying their behavior,

such as reducing consumption during peak-periods.

Price-based DR has been considered in works such as

(Fuller et al., 2011).

Current developments in embedded system tech-

nologies and communications make it possible to im-

plement home energy management (HEM) systems

that not only react to but also interact with the grid

through mechanisms like transactive control (Schnei-

der et al., 2011), (Chassin et al., 2008). In the future,

distributed HEM systems will be an integral part of

DR programs (Pipattanasomporn et al., 2012). Mod-

eling and simulation tools are essential in understand-

ing and evaluating the effects of different DR control

strategies prior to large scale deployment. In this con-

text, it is important to create residential load models

Sant’Anna A. and Bass R..

A New Two-Degree-of-Freedom Space Heating Model for Demand Response.

DOI: 10.5220/0004734600050013

In Proceedings of the 3rd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2014), pages 5-13

ISBN: 978-989-758-025-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

that simulate the physical behavior of appliances par-

ticipating in DR programs (Shao et al., 2013).

Thermostatically controlled appliances (TCA),

such as water heaters and HVAC systems, are of par-

ticular interests because they can store thermal en-

ergy. Intelligent control strategies can make use of

this storage capacity in order to avoid operating dur-

ing peak periods with little inconvenience to the cus-

tomer. A 2001 survey by the Ofﬁce of Energy Mar-

kets and End Use (RECS, 2001) reported that 9.1% of

household electricity consumption was due to water

heaters. Another considerable amount, 10.1%, was

due to space heating. Several pilot programs have

been conducted that employ hot water heaters as the

DR appliance, particularly in the U.S. states of Wash-

ington and Oregon (Kondoh et al., 2011), (Chassin

et al., 2008), (Diao et al., 2012), as well as in Norway

(Saele and Grande, 2011).

Considerable efforts have been directed to model-

ing thermostatically controlled loads. The thermody-

namic behaviors of electric water heaters and HVAC

system are normally described by differential equa-

tions (Lu, 2012), (Du and Lu, 2011), (Molina-Garcia

et al., 2011). Often, the system presents two behav-

iors: on or off. When the appliance is on, the temper-

ature of the thermal mass increases following a nega-

tive exponential curve (c − e

−τ

); when then appliance

is off, the temperature of the thermal mass decreases

exponentially (c + e

−τ

) (Lu et al., 2005). The time

constant τ relates to the thermal capacitance of the

thermal mass.

However, the above mentioned models present

only one degree of freedom (DoF) for control, typi-

cally, the desired indoor temperature or the minimum

and maximum acceptable temperatures for the ther-

mal mass (Pipattanasomporn et al., 2012). This pa-

per introduces a two-DoF space heating model com-

posed of a heat pump, a thermal storage unit (hot wa-

ter tank) and a forced convection system. The heat

pump transfers thermal energy to the thermal storage

and heats up the water. The hot water is circulated

through coiled pipes, transferring heat to it surround-

ing air, which is in turn circulated through the house

by the forced convection system. Such systems con-

tain, in effect, two thermal masses: the thermal stor-

age unit and the thermal mass of the house (air and

structures). These systems are not new, they are com-

mon in Canada and in Nordic countries, however, they

have not yet been considered in DR studies.

This paper demonstrates that two-DoF systems

are better adapted for maintaining thermal comfort

and allow greater ﬂexibility for DR programs. The

DR performance of the proposed system is compared

to a traditional one-DoF system through simulations.

The systems are evaluated with respect to their ability

to maintain indoor temperature within a comfortable

range (Peeters et al., 2009). Simple control strategies

are proposed for the forced convection system cou-

pled to on-off, and multistage compressors. Simula-

tion results show the importance of considering two-

DoF models for DR.

The contributions of this paper may be summa-

rized as follows.

• The description of a two-DoF heating system

model composed of an insulated thermal storage

unit and a forced convection system (FCS);

• The comparison and evaluation of two-DoF and

one-DoF systems for price-based DR;

• The evaluation of different control strategies for

two-DoF systems, and their effect on thermal

comfort for on/off, and multistage compressors as

well as three different weather proﬁles;

The remainder of the paper is organized as fol-

lows. Thermodynamic model and control strategies

are described in Section 2. Model and simulation pa-

rameters used for the study are explained in Section 3.

Simulation results are presented in Section 4 and dis-

cussed in Section 5. Finally, Section 6 concludes this

paper.

2 MODELS

2.1 Thermodynamic Model

The proposed system consists of:

• A rectangular volume with insulated walls repre-

senting the house.

• An insulated thermal energy storage unit (hot wa-

ter tank).

• A heat pump directly coupled to the thermal mass.

• A forced convection system (FCS) that transfers

heat from the thermal mass to the house.

This thermodynamic model can be represented as

a thermal circuit, as shown in Figure 1. The equiv-

alent mathematical model is shown in Equation (2),

where T

is the indoor temperature; T

is the ther-

mal mass temperature; and T

is the ambient outdoor

temperature. The mass of the water in the storage

tank is m

and its speciﬁc heat is C

. The heat

storage capacity of the house is represented by the

capacitance of value C

, which includes the heat

capacity of the air contained in the house as well as

it’s structure and materials. The heat conductivity be-

tween the thermal mass and the house is represented

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

Figure 1: Thermal circuit representation of the thermody-

namic model. T

is the indoor temperature; T

is the ther-

mal mass temperature; and T

is the ambient outdoor tem-

perature. The mass of the water in the storage tank is m

and its speciﬁc heat is C

. The heat storage capacity of

the house is represented by the capacitance of value C

which includes the heat capacity of the air contained in the

house as well as it’s structure and materials. The heat con-

ductivity between the thermal mass and the house is repre-

sented by Y

T M−H

, which depends on the heat transfer coef-

ﬁcient created by the FCS, Y

, and the thermal mass heat

loss, Y

, according to equation 1. The conductivity of the

house insulation is represented by K

; and

is the heat

pump’s thermal power output.

by Y

T M−H

, which depends on the heat transfer coefﬁ-

cient created by the FCS, Y

, and the thermal mass

heat loss, Y

, according to Equation 1. The conductiv-

ity of the house insulation is represented by K

; and

is the heat pump’s thermal power output.

It is worth noting that, if the conductivity between

the thermal mass and the house Y

T M−H

is kept con-

stant, this model is qualitatively no different from pre-

viously proposed models (Lu, 2012), (Du and Lu,

2011), (Molina-Garcia et al., 2011). However, by

considering an insulated thermal mass coupled with

a FCS, the indoor temperature is introduced as a new

degree of freedom, in addition to the temperature of

the thermal mass.

T M−H

= Y

(1)

− T

) −Y

TM-H

− T

)

(2a)

−Y

TM-H

− T

)

(2b)

2.2 Forced Convection System Model

and Control

Consider a FCS that can operate in two fan speed

modes, low and high. The two modes are modeled as

different heat transfer coefﬁcients between the ther-

mal mass and the house, Y

FC-low

and Y

FC-high

respec-

tively. The output of the FCS is controlled by a set of

if-then rules based on the ambient indoor temperature,

, as shown in Equation (3). The total heat transfer

between the thermal mass and the house is computed

from Equation 1.











0 if T

H-goal

FC-low

if T

H-goal

−1<T

≤T

H-goal

FC-high

if T

≤T

H-goal

−1

(3)

2.3 Heat Pump Model and Control

We consider a multistage heat pump capable of three

modes of operation: low, medium and high. The ther-

mal power supplied by each operation mode will be

referred to as

HP-low

HP-med

and

HP-high

respec-

tively.

In order to avoid modeling a short-cycled com-

pressor, we assume that the heat pump may not be

switched on and off in less than 5 minutes.

Operation is also affected by the demand response

program, which requires the pump to switch off dur-

ing peak periods, represented by the time-of-use rate

TUR

on-peak

Four different control scenarios are considered:

• Case I: A traditional one-DoF system where the

indoor temperature is directly coupled to the ther-

mal storage temperature, and consequently, to the

heat pump output. The heat transfer coefﬁcient

between the thermal mass and house is constant,

TM-H

= Y

FC-low

+ Y

. This scenario considers a

heat pump with only on/off operation. The heat

pump output is controlled based on the indoor

temperature as shown in Equation (4).

{

0 if T

H-goal

or TUR

on-peak

HP-high

if T

≤T

H-goal

−1

(4)

• Case II: A simple two-DoF system where the in-

door temperature and the thermal storage temper-

ature are controlled separately. The FCS is re-

sponsible for regulating the indoor temperature

and the heat pump is responsible for regulating the

thermal mass temperature. The heat pump is ei-

ther on or off, and its output is controlled based on

the thermal mass temperature as shown in Equa-

tion (5). The FCS operates as shown in Equa-

tion (3).

ANewTwo-Degree-of-FreedomSpaceHeatingModelforDemandResponse

{

0 if T

TM-goal

or TUR

on-peak

HP-high

if T

≤T

TM-goal

−2

(5)

• Case III: This scenario considers the previous

two-DoF system but with a multistage heat pump

that can operate in three different modes: low,

medium or high. The operation mode selection is

done through a collection of if-then rules based on

the thermal mass temperature as shown in Equa-

tion (6). The FCS operates as shown in Equa-

tion (3).











0 if T

TM-goal

or TUR

on-peak

HP-low

if T

TM-goal

−1<T

≤T

TM-goal

HP-med

if T

TM-goal

−3<T

≤T

TM-goal

−1

HP-high

≤T

TM-goal

−3

(6)

• Case IV: This ﬁnal scenario considers the pre-

vious two-DoF system with a multi-stage heat

pump. The heat pump output selection, however,

is done with the help of a PD controller as shown

in Equation (7). The FCS operates as shown in

Equation (3).

ctrl

= k

TM-goal

− T

) + k

(7a)











0 if

ctrl

≤

HP-low

or TUR

on-peak

HP-low

ctrl

≤

HP-med

ctrl

≤

HP-high

ctrl

HP-high

(7b)

2.4 Thermal Comfort

Acceptable upper and lower temperatures for residen-

tial buildings, as suggested by Peeters et al. (Peeters

et al., 2009), are given by Equations (8a) and (8b),

respectively, where T

is the indoor temperature, w is

the width of the comfort band in

◦

C, and α is a con-

stant ≤ 1. The study suggests that w = 5 and α = 0.7

incur in 90% acceptability. T

is computed as shown

in Equation (8c), where T

O−avrg

is the daily average

of the ambient outdoor temperature. The total time (in

hours) during which the indoor temperature is ourside

the comfort band, t

Disc

, can be computed as shown in

Equation (9), where i indicates each simulation time

step and J is the duration of the simulation time step in

seconds. Variations in temperature also affect thermal

comfort. Regarding cycling temperature, ASHRAE

standard 55-2004 (ANSI/ASHRAE 55-2004, 2004)

states that, if the peak variation exceeds 1.1

◦

C, the

rate of temperature change shall not exceed 2.2

◦

C/h.

upper

= T

+ wα (8a)

lower

= T

− w(1 − α) (8b)

= 20.4 + 0.06 T

O-avrg

(8c)

Disc(i) =

{

0 if T

lower

≤T

(i)≤T

upper

1 if T

(i)<T

lower

or T

(i)>T

upper

(9a)

Disc

3600

24(3600/J)

∑

i=1

Disc(i) (time in hours) (9b)

2.5 Power Usage and Cost Assessment

The electric power, P

, consumed by the heat pump

at every simulation time step, i, is computed us-

ing Equation (10), relating heat transfer to electrical

power consumption via the heat pump coefﬁcient of

performance (COP). The total cost, C

total

, for oper-

ating the system for one day can be computed based

on the time of use rates (TUR), as shown in Equa-

tion (11). Where J is the duration of the simulation

time step in seconds. Electricity consumption by the

FCS is not included in the cost analysis.

(i) =

(i)

COP(

(i),T

(i))

(10)

total

24(3600/J)

∑

i=1

(i)TUR(i)T (11)

3 SIMULATION SETTINGS

3.1 Model Parameters

We consider a 600 m

house (21188.8 cubic feet). The

heat capacity of the house, C

= 37968 kJ.K

−1

includes the heat capacity of its structure and vol-

ume of air. The heat capacity of the air con-

tained in the house was calculated from its vol-

ume, density (1.2041 kg.m

−3

), and speciﬁc heat

(1.005 kJ.kg

−1

). The heat capacity of the house

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

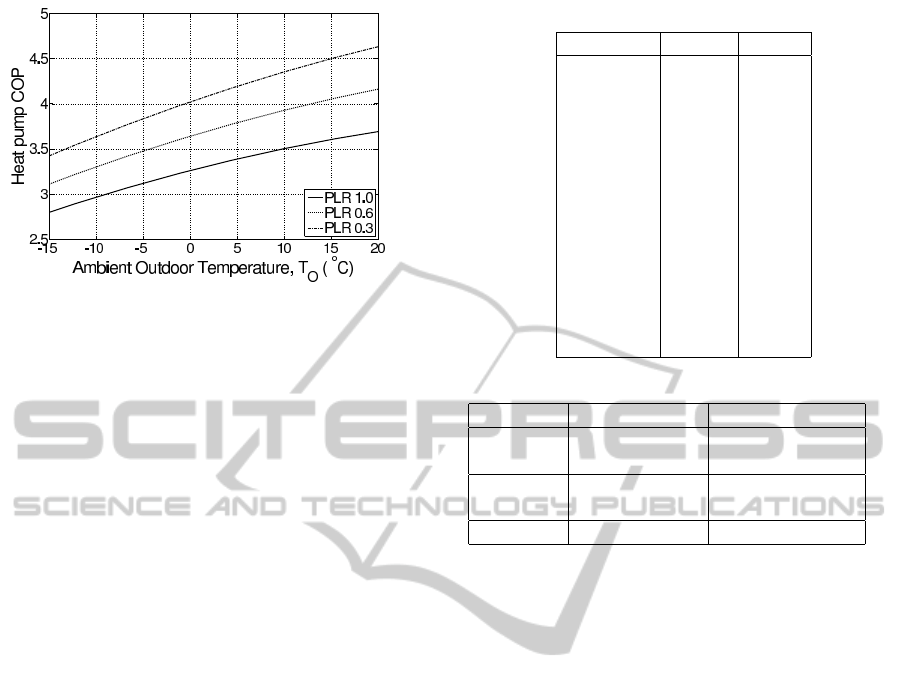
Figure 2: Heat pump coefﬁcient of performance (COP) as a

function of ambient outdoor temperature, T

, and part-load

ratio (PLR).

structure was calculated based on the method de-

scribed in (Olsen and Rode, 2008); considering Gyp-

sum plasterboard walls and ceilings 0.05 m thick, and

concrete and tile ﬂooring 0.1 m thick.

We consider a thermal storage unit of 150 gal-

lons (approximately 568 L). The thermal capacitance

of the thermal storage unit, C

= 2376 kJ.K

−1

was calculated from its volume, the density of wa-

ter (1.00 kg.L

−1

), and the speciﬁc heat of water

(4.185 kJ.kg

−1

). The thermal conductance of

the storage insulation, Y

= 0.003 kW.K

−1

, was calcu-

lated based on the typical electric water heater proper-

ties described in (DOE, 1998) (Table 8); considering

a cylindrical storage of 35 inches in diameter.

The heat transfer coefﬁcient related to the insu-

lating properties of the house, K

= 0.2530 kW.K

−1

derives from the surface area and thermal resistivity

of the home, and was calculated using the Oak Ridge

National Laboratory Online Simple Whole Wall R-

value Calculator (www.ornl.gov).

The heat transfer coefﬁcients used for the FCS,

TM-H

, was derive from Equation (2a), considering

there is no heat exchange with the outside, i.e. K

0; and the thermal mass is at a constant 65

◦

C. The

values for Y

FC-high

and Y

FC-low

were chosen so as to

increase the indoor temperature from 16 to 20

◦

C in

30 and 60 minutes respectively.

We consider a three-ton multistage heat pump,

adopting a COP model from Jeter et al. (Jeter et al.,

1987) that allows for COP to vary as a function

of both ambient outside temperature and compressor

speed. COP ranges represent a typical multi-speed

heat pump. The three operation modes,

HP-low

HP-med

and

HP-high

, correspond to 0.3, 0.6 and 1

part-load ratios (PLR) respectively. Figure 2 shows

the COP curves for each PLR.

The target indoor temperature, T

H-goal

, was 21

◦

This temperature is the approximate center of comfort

Table 1: Model parameters.

parameter value unit

2 376 kJ/K

37 968 kJ/K

0.2530 kW/K

FC-high

1.800 kW/K

FC-low

0.900 kW/K

0.003 kW/K

HP-low

3.15 kW

HP-med

6.30 kW

HP-high

10.5 kW

H-goal

◦

TM-goal

◦

1 kW/K

5 kJ/K

Table 2: Time of use rates for winter months.

time rate [cents/kWh]

on-peak

06:00 to 10:00

13.266

17:00 to 20:00

mid-peak

10:00 to 17:00

7.500

20:00 to 22:00

off-peak 22:00 to 06:00 4.422

range for the chosen weather proﬁles. The target ther-

mal mass temperature, T

TM-goal

, was 65

◦

C, which is

high enough to kill harmful bacteria in the water, but

not so high as to risk scalding in case of accident.

Model parameter values are summarized in Ta-

ble 1.

3.2 Simulation Parameters

The TUR reﬂect the winter rates in use by Portland

General Electric, as shown in Table 2, and were ap-

plied equally to all three locations. Three weather

proﬁles are considered: the average hourly tempera-

tures for January 1st in Portland, OR; Halmstad, Swe-

den; and Colorado Springs, CO; as shown in Figure 3.

Temperature control cases I through IV are simu-

lated for each of the three outdoor temperature pro-

ﬁles. The demand response program requires the

heat pump to switch off during peak time-of-use rates

(TUR). Total power usage and cost were calculated

for each scenario. Initial values for T

and T

were

21 and 65

◦

C respectively. The chosen simulation

time step J is 60 seconds, and the total simulation time

is 24 hours. Simulations are performed using Acumen

(www.acumen-language.org) (Taha et al., 2011), a

modeling language where models are deﬁned through

differential equations and simulations are generated

automatically.

ANewTwo-Degree-of-FreedomSpaceHeatingModelforDemandResponse

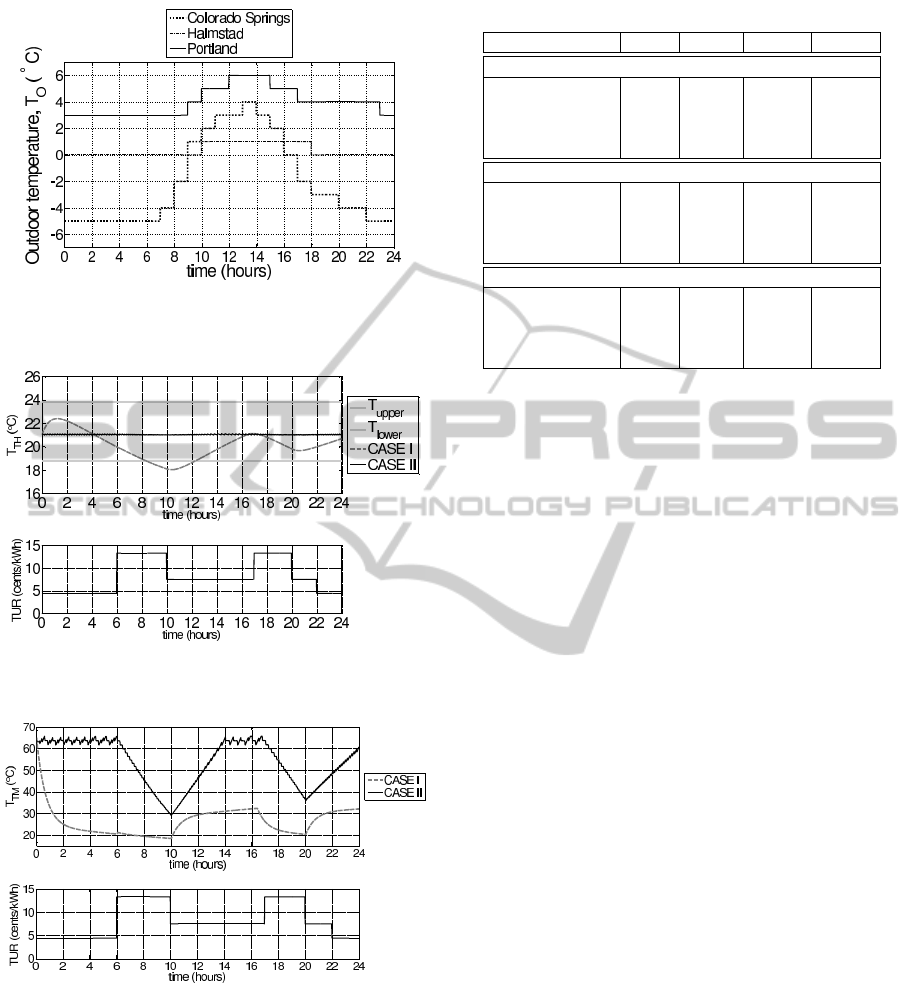
Figure 3: Weather proﬁles for Portland, Colorado Springs

and Halmstad. Average hourly outdoor temperature for the

month of January in each of the locations.

Figure 4: Indoor temperature, T

, and time-of-use rates

(TUR) for cases I and II, Colorado Springs weather proﬁle.

Figure 5: Thermal mass temperature, T

, and time-of-use

rates (TUR) for cases I and II, Colorado Springs weather

proﬁle.

4 RESULTS

Control cases I and II represent a typical one-DoF

system and the proposed two-DoF system respec-

tively, both under similar on/off control strategies.

The simulation results for indoor and thermal mass

temperature, contrasting these two cases under the

Table 3: Thermal comfort.

Case I Case II Case III Case IV

Colorado Springs

Disc

[hours] 4.02 0 0 0

mean T

[

◦

C] 20.11 21.02 21.02 21.01

cyclic ∆T

[

◦

C] 4.37 0.12 0.12 0.10

cyclic

[

◦

C/h] 0.58 - - -

Halmstad

Disc

[hours] 1.45 0 0 0

mean T

[

◦

C] 20.44 21.03 21.02 21.02

cyclic ∆T

[

◦

C] 3.79 0.12 0.12 0.10

cyclic

[

◦

C/h] 0.50 - - -

Portland

Disc

[hours] 0 0 0 0

mean T

[

◦

C] 20.66 21.04 21.03 21.03

cyclic ∆T

[

◦

C] 3.29 0.12 0.12 0.10

cyclic

[

◦

C/h] 0.60 - - -

Colorado Springs weather proﬁle, are shown in Fig-

ures 4 and 5 respectively. Very similar results were

obtained for simulations under Halmstad and Portland

weather proﬁles.

Results show that the response of the one-DoF

system (Case I) varies greatly and slowly. The in-

door temperature starts considerably high because the

initial thermal mass temperature is 65

◦

C. The ther-

mal mass temperature must decrease considerably in

order to maintain the indoor temperature within the

comfortable range. Another drawback of the one-DoF

system is that during peak-hours, when the heat pump

is off, the temperature of the house falls considerably

below the limits of thermal comfort Figure 4. The

additional DoF introduced by the FCS (Case II) al-

lows the thermal mass temperature to vary consider-

ably from 65 down to approximately 30

◦

C, Figure 5,

while the indoor temperature strays very little from

the goal temperature of 21

◦

C, Figure 4.

A summary of the indoor temperature results for

each of the simulated scenarios is shown in Table 3.

Note that the traditional one-DoF system simulated in

Case I results in indoor temperatures outside the com-

fortable limits for both Colorado Springs and Halm-

stad weather proﬁles. The two-DoF system simulated

in Cases II through IV, on the other hand, maintain the

indoor temperature very close to 21

◦

C with less than

0.2

◦

C of peak-to-peak cyclic variations.

Figure 6 shows the heat pump output, Q

, and

thermal mass temperature, T

, for cases II through

IV for the Colorado Springs weather proﬁle. In all

cases, the thermal mass temperature proﬁle is very

similar. Case II shows slightly larger cyclic oscilla-

tions due to the on/off duty cycles. The same pat-

terns were observed for simulations under Halmstad

and Portland weather proﬁles.

A summary of the thermal mass temperature be-

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

CASE IICASE IIICASE IV

Figure 6: Thermal mass temperature, T

, and heat pump

output, Q

, for cases II though IV, Colorado Springs

weather proﬁle.

Table 4: Thermal storage.

Case I Case II Case III Case IV

Colorado Springs

max T

[

◦

C] 65.00 65.69 65.00 65.00

min T

[

◦

C] 18.37 28.99 27.76 22.95

mean T

[

◦

C] 26.15 53.32 53.07 47.48

Halmstad

max T

[

◦

C] 65.00 65.78 65.00 65.00

min T

[

◦

C] 19.13 31.08 32.14 26.90

mean T

[

◦

C] 26.02 55.36 55.53 50.19

Portland

max T

[

◦

C] 65.00 65.78 65.14 65.00

min T

[

◦

C] 19.65 36.93 37.70 31.98

mean T

[

◦

C] 25.34 57.91 58.35 53.04

havior for all control cases is shown in Table 4. Note

that the mean temperatures for Case I are consider-

ably below the intended temperature of 65

◦

Table 5: Power consumption and cost.

Case I Case II Case III Case IV

Colorado Springs

Power [kWh] 33.447 41.940 42.806 40.935

Cost [USD] 2.31 2.56 2.63 2.56

Halmstad

Power [kWh] 30.312 37.726 42.806 35.858

Cost [USD] 2.07 2.40 2.63 2.31

Portland

Power [kWh] 23.543 29.505 30.364 28.502

Cost [USD] 1.57 1.90 1.94 1.85

Figure 7: Average thermal mass temperature versus cost

for control cases II, III, and IV. The gray box highlights

that cases I and II incur a cost of approximately 2,6 USD

to maintain a mean temperature of about 53

◦

C, whereas

case IV maintains the same mean temperature for only 1,85

USD. The clear box highlights that control cases II and III

are able to achieve an average temperature approximately

◦

C higher than case IV for an increased cost of less than

0,10 USD.

The power usages and costs for each simulated

scenarios are shown in Table 5. Case I consumes con-

siderably less energy than the other cases, however,

it does not fulﬁll the thermal comfort requirements.

Figure 7 shows a plot of mean thermal mass temper-

ature against cost for control cases II through IV un-

der all three weather proﬁles. The gray box in Fig-

ure 7 highlights that cases I and II incur a cost of ap-

proximately 2,6 USD to maintain a mean temperature

of about 53

◦

C, whereas case IV maintains the same

mean temperature for only 1,85 USD. Note also that

control cases II and III are able to achieve an aver-

age temperature approximately 5

◦

C higher than case

IV for an increased cost of less than 0,10 USD, high-

lighted by the clear box in Figure 7.

ANewTwo-Degree-of-FreedomSpaceHeatingModelforDemandResponse

5 DISCUSSION

The proposed two-degree-of-freedom system pro-

vides more ﬂexibility for DR programs. By decou-

pling the heat pump output from the indoor temper-

ature, the thermal storage can be used to store more

energy, as evidenced by the higher thermal mass tem-

peratures for Cases II through IV. The direct coupling

of the heat pump output and the indoor temperature in

Case I suggests that there is need for more advanced

predictive control strategies, speciﬁcally ones that can

pre-heat the structure in anticipation of peak time-of-

use rates or extreme weather. Such predictive control,

however, would not be able to cope with accidental

power loss or other unforeseeable issues. Having a

thermal storage, able to operate at higher tempera-

tures, makes the system more robust and more ﬂex-

ible.

Simulation results show that a heat pump operates

at maximum output when switching on immediately

after peak pricing hours end. This occurs because the

heat pump must compensate for the large thermal en-

ergy loss incurred during peak pricing hours. This

reconnection effect may increase power consumption

overall, and shift the peak periods instead of lessening

them. The effects of reconnecting appliances after a

forced disconnection has been studied, e.g. (Ericson,

2009), and control strategies have been designed to

minimize this reconnection effect for water heaters,

e.g. (Nehrir et al., 1999). In the case of space heating,

the reconnection spike may be reduced by making the

controller aware of current and predicted weather, or

pre-heating in anticipation of peak TUR. Reconnec-

tion costs and mitigating strategies will be investi-

gated in future works.

It is important to note that the control strategies

proposed here were not optimized in any way. Lower

goal temperatures for the thermal mass, for example,

are likely to result in lower power consumption. How-

ever, we implemented very simple and intuitive con-

trollers for the purpose of comparing different control

strategies that resulted in similar thermal mass and

house temperature proﬁles. There are many research

opportunities for optimization schemes that take into

account real-time pricing, weather predictions, and

other factors.

This paper investigates the behavior of single iso-

lated systems, where the only outside inputs were

weather and time-of-use rates. This facilitated an un-

derstanding of system properties. The next step is

to understand the impact of thousands of such sys-

tems being used for DR. Monte Carlo methods can be

used to simulate a large number of these systems with

slightly different parameters so as to model the slight

differences between real houses. However, in order to

develop a practical system model, parameters must be

validated against practical experiments. Future works

will focus on more realistic and large scale simula-

tions.

Customer willingness to participate in DR pro-

grams increases as the beneﬁts they derive exceed the

cost of the inconvenience (Fahrio

glu and Alvarado,

2000). Minimizing or eliminating discomforts should

lead to increased participation in such programs. De-

spite the simpliﬁcations made in this study, our re-

sults show that an insulted thermal storage unit cou-

pled to a heat pump and forced convection system

for space heating may be used in price-based demand

response programs without either compromising the

thermal comfort of the residents nor requiring they

modify their behavior by deferring consumption to a

later time period. This proposed system, therefore,

could be a means by which to increase participation

levels within utility DR programs.

6 CONCLUSION

Demand response programs are effective and rela-

tively inexpensive ways to cope with peak demands;

balance demand and generation; and stabilize elec-

tricity prices. Water heaters and HVAC systems

are commonly used for DR. This paper introduces a

space heating system composed of an insulated ther-

mal mass and forced convection system with two de-

grees of control freedom that can be used for DR. The

thermodynamic model was presented as well as four

different temperature control strategies. Simulations

were used to evaluate the performance of the sys-

tem based on thermal comfort and power consump-

tion in three different weather regions. Results show

that the FCS introduces an important degree of free-

dom that improves indoor temperature control while

at the same time allowing the temperature of the ther-

mal mass to vary more freely. The power consump-

tion of the system can vary greatly according to the

control strategy and the insulating properties of the

house. Future research avenues include investigat-

ing optimized control strategies that account for real-

time pricing, weather forecasts, occupancy patterns,

among others; and, investigating the aggregate de-

mand response of large numbers of homes equipped

with heat pumps, forced convection and controllable

thermal masses.

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

ACKNOWLEDGEMENTS

Partial funding for this research was provided by Port-

land General Electric (PGE). PGE played no role in

the design and analysis of the study, nor the interpre-

tation of ﬁndings. Nor did PGE participate in the writ-

ing of this report or the decision to submit this article

for publication.

REFERENCES

Albadi, M. and El-Saadany, E. (2007). Demand response

in electricity markets: An overview. In Power Engi-

neering Society General Meeting, 2007. IEEE, pages

1 –5.

ANSI/ASHRAE 55-2004 (2004). Thermal environmental

conditions for human occupancy. ASHRAE 55-2004.

ANSI Approved.

Chassin, D., Hammerstrom, D., and DeSteese, J. (2008).

The paciﬁc northwest demand response market

demonstration. In Power and Energy Society General

Meeting - Conversion and Delivery of Electrical En-

ergy in the 21st Century, pages 1–6.

Diao, R., Lu, S., Elizondo, M., Mayhorn, E., Zhang, Y.,

and Samaan, N. (2012). Electric water heater mod-

eling and control strategies for demand response. In

Power and Energy Society General Meeting, 2012

IEEE, pages 1 –8.

DOE (1998). Results and methodology of the engineering

analysis for residential water heater efﬁciency stan-

dards. US Department of Energy, Ofﬁce of Codes and

Standards.

Du, P. and Lu, N. (2011). Appliance commitment for house-

hold load scheduling. Smart Grid, IEEE Transactions

on, 2(2):411–419.

Ericson, T. (2009). Direct load control of residential water

heaters. Energy Policy, 37(9):3502 – 3512.

Fahrio

glu, M. and Alvarado, F. (2000). Designing incen-

tive compatible contracts for effective demand man-

agement. Power Systems, IEEE Transactions on,

15(4):1255 –1260.

Fuller, J., Schneider, K., and Chassin, D. (2011). Analy-

sis of residential demand response and double-auction

markets. In Power and Energy Society General Meet-

ing, 2011 IEEE, pages 1–7.

Jeter, S., Wepfer, W., Fadel, G., Cowden, N., and Dymek, A.

(1987). Variable speed drive heat pump performance.

Energy, 12(12):1289 – 1298.

Kondoh, J., Lu, N., and Hammerstrom, D. (2011). An eval-

uation of the water heater load potential for providing

regulation service. Power Systems, IEEE Transactions

on, 26(3):1309 –1316.

Lu, N. (2012). An evaluation of the hvac load potential for

providing load balancing service. Smart Grid, IEEE

Transactions on, 3(3):1263–1270.

Lu, N., Chassin, D., and Widergren, S. (2005). Model-

ing uncertainties in aggregated thermostatically con-

trolled loads using a state queueing model. Power Sys-

tems, IEEE Transactions on, 20(2):725–733.

Mohsenian-Rad, A.-H., Wong, V., Jatskevich, J., Schober,

R., and Leon-Garcia, A. (2010). Autonomous

demand-side management based on game-theoretic

energy consumption scheduling for the future smart

grid. Smart Grid, IEEE Transactions on, 1(3):320–

331.

Molina-Garcia, A., Kessler, M., Fuentes, J., and Gomez-

Lazaro, E. (2011). Probabilistic characterization of

thermostatically controlled loads to model the impact

of demand response programs. Power Systems, IEEE

Transactions on, 26(1):241–251.

Nehrir, M., LaMeres, B., and Gerez, V. (1999). A customer-

interactive electric water heater demand-side manage-

ment strategy using fuzzy logic. In Power Engineering

Society 1999 Winter Meeting, IEEE, volume 1, pages

433 –436 vol.1.

Olsen, L. and Rode, C. (2008). Heat capacity in relation

to the danish building regulation. In Proceedings of

the 8th Symposium on Building Physics in the Nordic

Countries: Selected papers, volume 3, pages 16–18.

Peeters, L., de Dear, R., Hensen, J., and D’haeseleer, W.

(2009). Thermal comfort in residential buildings:

Comfort values and scales for building energy simu-

lation. Applied Energy, 86(5):772 – 780.

Pipattanasomporn, M., Kuzlu, M., and Rahman, S. (2012).

An algorithm for intelligent home energy manage-

ment and demand response analysis. Smart Grid,

IEEE Transactions on, 3(4):2166–2173.

RECS (2001). Residential energy consumption surveys. US

Energy Information Administration, Ofﬁce of Energy

Markets and End Use.

Saele, H. and Grande, O. (2011). Demand response

from household customers: Experiences from a pilot

study in norway. Smart Grid, IEEE Transactions on,

2(1):102 –109.

Schneider, K., Fuller, J., and Chassin, D. (2011). Anal-

ysis of distribution level residential demand response.

In Power Systems Conference and Exposition (PSCE),

2011 IEEE/PES, pages 1–6.

Shao, S., Pipattanasomporn, M., and Rahman, S. (2013).

Development of physical-based demand response-

enabled residential load models. Power Systems, IEEE

Transactions on, 28(2):607–614.

Spees, K. and Lave, L. B. (2007). Demand response and

electricity market efﬁciency. The Electricity Journal,

20(3):69 – 85.

Taha, W., Brauner, P., Cartwright, R., Gaspes, V., Ames,

A., and Chapoutot, A. (2011). A core language for

executable models of cyber physical systems: work in

progress report. SIGBED Rev., 8(2):39–43.

ANewTwo-Degree-of-FreedomSpaceHeatingModelforDemandResponse