
Multi-objective Optimization for Characterization of Optical Flow
Methods
Jos
´
e Delpiano
1
, Luis Pizarro
2
, Rodrigo Verschae
3
and Javier Ruiz-del-Solar
4
1
School of Engineering and Applied Sciences, Universidad de los Andes, Mons.
´
Alvaro del Portillo 12.455, Santiago, Chile
2
Department of Computer Science, University College London, London, U.K.
3
Graduate School of Informatics, Kyoto University, Kyoto, Japan
4
Department of Electrical Engineering, Universidad de Chile, Santiago, Chile
Keywords:
Multi-objective Optimization, Optical Flow.
Abstract:
Optical flow methods are among the most accurate techniques for estimating displacement and velocity fields
in a number of applications that range from neuroscience to robotics. The performance of any optical flow
method will naturally depend on the configuration of its parameters. Beyond the standard practice of manual
(ad-hoc) selection of parameters for a specific application, in this article we propose a framework for auto-
matic parameter setting that allows searching for an approximated Pareto-optimal set of configurations in the
whole parameter space. This final Pareto front characterizes each specific method, enabling proper method
comparison. We define two performance criteria, namely the accuracy and speed of the optical flow methods.
1 INTRODUCTION
Optical flow (OF) has been applied widely to quan-
tify motion in computer vision problems. Specific
OF algorithms tend to be evaluated (for ranking or for
searching of optimal parameters) according to either
their accuracy, or their speed. However, when study-
ing the performance and computational requirements
of OF methods one can observe that some accurate
algorithms are not suitable for real-time applications.
For that reason, the evaluation and optimization of op-
tical flow algorithms according to both accuracy and
speed at the same time is very important for real world
applications, which have a constrained response time
or a high-accuracy requirement.
In general, when choosing a computer vision al-
gorithm for a specific application, very often an
accuracy-speed trade-off exists. In that case, a re-
searcher may take into account mainly two objectives:
algorithm error and execution time. When evaluating
the algorithm performance in a fixed image database,
the algorithm error and execution time are functions
of the algorithm parameters. In the optic flow litera-
ture, most papers do not consider the optimal selec-
tion of these parameters in a multi-objective manner.
They rather fine-tune the parameters manually, usu-
ally with the goal of minimizing either the error rate
or the processing time, basically leading to a single-
objective optimization of the algorithm. The main
disadvantage of the single-objective approach is that
the selection or combination of different objectives is
arbitrary. Therefore, the only methodology that can
give interesting results for the problem of accuracy-
speed optimization is multi-objective optimization.
When working with multi-objective optimization,
the aim is to improve at least one of the objectives
and not to get worse values in any of the other ob-
jectives. One extra advantage of multi-objective op-
timization is that the resulting set of solutions cor-
responds to an approximation of the Pareto front,
which contains information that is much richer than
the results of single-objective optimization. First, the
Pareto front can be used as a receiver operating curve
(ROC) of the optimized algorithms. This curve char-
acterizes each method and allows for comparison of
several methods. And second, one run of the opti-
mization algorithm gives information for different ap-
plications of the OF algorithm. That information in-
cludes the solution–parameter settings and accuracy-
speed statistics–for a family of speed-constrained and
accuracy-constrained problems.
Searching for the optimal parameter setting repre-
sents a large combinatorial problem that can be ap-
proached with evolutionary algorithms (B
¨
ack, 1996).
566
Delpiano J., Pizarro L., Verschae R. and Ruiz-del-Solar J..
Multi-objective Optimization for Characterization of Optical Flow Methods.
DOI: 10.5220/0004736305660573
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 566-573
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

In particular, we employ genetic algorithms (Gold-
berg, 1989) for this task. Genetic algorithms can solve
problems with multiple solutions. They do not require
objective function derivatives, thus they are easy to
implement and can cope with non-continuous prob-
lems. Standard genetic algorithms search the param-
eter space in an evolutive manner, considering only
one objective. To optimize several objectives concur-
rently we utilize an evolutionary multi-objective opti-
mization (EMO) strategy (Deb and Kumar, 1995). A
successful approach for EMO is named NSGA-II (an
improved non-dominated sorting genetic algorithm)
(Deb and Kumar, 1995; Deb et al., 2002). NSGA-II
has a fast approach for non-dominated solution sort-
ing and a smart criterion for diversity preservation.
Multi-objective optimization has been applied before
to other computer vision tasks, such as segmentation
(Everingham et al., 2006), face detection (Verschae
et al., 2005), tracking (Benlian and Zhiquan, 2007)
and 3D vision (Vite-Silva et al., 2007).
Optical flow is a vector field representing “appar-
ent velocities of movement of brightness patterns in
an image” (Horn and Schunck, 1981). Optical flow
algorithms tend to be evaluated (for ranking or for
searching of optimal parameters) according to either
accuracy (Barron et al., 1994)(Baker et al., 2011)
or speed (Changming and Sun, 2002)(Bruhn et al.,
2005a). By comparing methods in accuracy and speed
concurrently, it can be realized that some accurate al-
gorithms are not suitable for real-time applications.
Another important observation is the need for specific
hardware (graphic processing units) to obtain results
in very short execution times.
In the optical flow literature, most papers do not
consider the optimal selection of method parameters
in a multi-objective manner. They fine-tune the pa-
rameters manually instead. Some researchers have
developed stochastic/statistic methods for optical flow
parameter selection (Li and Huttenlocher, 2008)(Kra-
jsek and Mester, 2006)(Heas et al., 2012). They opti-
mize a posteriori probability or training loss in order
to find the best parameters. Then, they consider just
one objective and set aside execution time. An ex-
ception is found in (Salmen et al., 2011), where the
authors look for highly accurate and efficient OF al-
gorithms. However, they work with non-dense OF
methods and define efficiency as the number of flow
vectors found per frame. Thus, they are not consid-
ering algorithm speed. The present multi-objective
methodology is based on the speed-accuracy trade-off
observed in computer and biological vision (Chittka
et al., 2003).
In this article we explore multi-objective opti-
mization using NSGA-II (Deb et al., 2002) of the
combined local and global (CLG) method proposed
by Bruhn et al. (Bruhn et al., 2005b), which is a well-
known representative of the class of variational OF
methods. Nevertheless, our multi-objective optimiza-
tion strategy can be applied to tune the parameters of
any other optical flow method optimally, variational
or not. In general, the parameter space of an optical
flow method can be very large, which makes the opti-
mization task very challenging.
This work is structured as follows. Section 2 de-
scribes the variational optical flow method to be op-
timized and characterized in this paper. Section 3 re-
ports on the development of genetic algorithm-based
multi-objective optimization of optical flow. Sec-
tion 4 describes the experimental setup, reporting and
discussing the results. Section 5 gives some conclud-
ing remarks.
2 COMBINED LOCAL-GLOBAL
OPTICAL FLOW METHOD
The combined local-global (CLG) OF method (Bruhn
et al., 2005b) looks for a flow field w = (u,v,1)
T
on
the image space Ω that minimizes the functional
E(w) = E
similarity
+ αE
smoothness
(1)
where the term
E
similarity
=
Z
w
T
J
ρ
(∇
3
I)wdΩ (2)
represents the brightness constancy assumption,
based on the motion tensor J
ρ
(∇
3
I), given by K
ρ
∗
(∇
3
I∇
3
I
T
), a convolution with a Gaussian kernel
with parameter ρ, for image spatiotemporal deriva-
tives ∇
3
I = (I
x
,I
y
,I
t
). Image I is the result of convolu-
tion of the original image and kernel K
σ
. The second
term in the functional, related to requiring a smooth
flow field, is
E
smoothness
=
Z
|
∇u
|
2
+
|
∇v
|
2
dΩ (3)
It is also possible to use more general versions
of these two terms, to be able to get discontinuity-
preserving optical flow solutions (Bruhn, 2006):
E
similarity
=
Z
ψ
D
w
T
J
ρ
(∇
3
I)w
dΩ (4)
E
smoothness
=
Z
ψ
S
|
∇u
|
2
+
|
∇v
|
2
dΩ (5)
Quadratic penalization ψ
D
(s
2
) = ψ
S
(s
2
) = s
2
gives Equations (2) and (3) as a result. One option
for non-quadratic penalization is ψ
D
(s
2
) = ψ
S
(s
2
) =
Multi-objectiveOptimizationforCharacterizationofOpticalFlowMethods
567

√
s
2
+ ε
2
, a regularized version of the L
1
norm. It be-
haves as the L
1
norm for large values of s
2
, but has the
extra advantage of regularity.
The optimality condition for the minimization
problem is described by a system of non-linear par-
tial differential equations. The discretized version
of these equations can be solved using, for exam-
ple, Jacobi, Gauss-Seidel, successive over-relaxation
(SOR), or a full multi-grid (FMG) method, taking ad-
vantage of the fast high-frequency error removal fea-
ture of iterative methods for sparse linear systems.
In this work, we use a non-dyadic (image width and
height do not need to be a power of 2) linear multi-
grid algorithm following (Bruhn et al., 2005a; Briggs
et al., 2000).
3 PROPOSED METHODOLOGY
3.1 Evolutionary Multi-Objective
Optimization
Multi-objective optimization is a way of consider-
ing many objectives when looking for an optimum,
while avoiding arbitrarily combining/weighting them.
Furthermore, multi-objective optimization gives the
Pareto front for the optical flow method, which is a set
of the optimal settings for the given method. There-
fore, in our case it is a way of working with dif-
ferent applications of optical flow, both speed- and
accuracy-oriented. Choosing execution time and er-
ror as objectives, a set of parameter-space solutions
can be considered as optima. The concept of Pareto-
dominance has been shown to be very useful in order
to define that set of solutions.
A solution vector v = (v
1
,... ,v
N
ob j
), with v
i
the
solution for the i-th objective, is said to Pareto-
dominate a solution vector w if v
i
≤ w
i
, for every
i = 1,. . .,N
ob j
, and for at least one value of i, v
i
< w
i
.
A Pareto front is the set of all vectors that are not dom-
inated by any other vector.
A successful approach for EMO is named NSGA-
II (an improved non-dominated sorting genetic algo-
rithm) (Deb and Kumar, 1995; Deb et al., 2002).
NSGA-II has a fast approach for non-dominated solu-
tion sorting and a smart criterion for diversity preser-
vation.
NSGA-II sorts solutions as follows:
1. For each solution p, record the domination count
n
p
, i.e. the number of solutions which dominate
p. Store the set S
p
of solutions that p dominates.
The set of solutions with n
p
= 0 is the first non-
dominated front (their non-domination rank is 1).
2. For each solution p with n
p
= 0, reduce the
domination count of every solution q in S
p
by
one. Store solutions q which reached domina-
tion count 0 as a new non-dominated front (their
non-domination rank is one more than the previ-
ous non-dominated front).
3. Repeat step 2 for every new non-dominated front.
This algorithm preserves diversity of solutions.
A crowding measure is defined to quantify solution
diversity in a non-dominated front:
d
crowd
[i] =
N
ob j
∑
m=1
(p
i+1,m
−p
i−1,m
)/( f
max
m
− f
min
m
) (6)
with i = 2,..., l −1, where l is the number of solutions
and d
crowd
[1] = d
crowd
[l] = ∞. Here, p
i,m
is the i-th
solution value for objective m, after sorting solutions
using objective m. f
min
m
and f
max
m
are the minimum
and maximum values of objective m.
3.2 Optimization Methodology for
Optical Flow Performance
Given an OF method M, and an image database in-
cluding N
seq
image sequences {I
k,l
}
k=1,...,N
seq
;l=1,...,N
k
(total of N
DB
=
∑
N
seq
k=1
(N
k
− 1) image pairs), we
are interested in the average execution time T =
(1/N
DB
)
∑
k,l
f (p,I
k,l
,I
k,l+1
) and the average end-
point error AEE = (1/N
DB
)
∑
k,l
g(p,I
k,l
,I
k,l+1
) for the
evaluation of M over all image pairs I
k,l
,I
k,l+1
, both
functions of p, the parameter vector for method M.
Using the notation we have described in 3.1, the goal
is to find solution vectors v = (T,AEE), N
ob j
= 2, that
are not Pareto-dominated by any other solution.
Figure 1 shows a diagram for the application of
EMO to an OF method. In the diagram, an EMO al-
gorithm (NSGA-II in all the experiments shown here)
gives parameter vectors p to an OF method. The OF
method processes images I from sequences included
in an OF evaluation data set. This data set provides
ground truth flow (u
GT
,v
GT
) for evaluation of esti-
mated flow (u,v). The outputs are {p
opt
}, a set of
Pareto-optimal p-vectors, and accuracy-speed statis-
tics T, AAE.
Algorithm 1 describes this methodology in more
detail. The goal of this algorithm is to find an op-
timal Pareto front. The initial population is defined
randomly, according to parameter ranges specified by
the user. Then, each new population is initialized us-
ing binary tournament selection, binary recombina-
tion (crossover), and binary mutation (Deb and Ku-
mar, 1995; Deb et al., 2002). Previous and current
populations are combined and sorted according to
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
568

Figure 1: Diagram for Evolutionary Multi-Objective Optimization of Optical Flow Accuracy and Speed.
their non-domination rank and their crowding mea-
sure (Deb et al., 2002). Finally the N
ind
best indi-
viduals of the combined population are kept for cur-
rent generation. The non-domination rank and the
crowding measure are determined using the objective
values (accuracy-speed statistics in Figure 1, namely,
AEE and execution time T for the experiments in this
work).
The CLG OF parameters are α,ρ,σ, ε. The pa-
rameters to be varied for optimization are the regu-
larization parameter α, the derivative smoothing pa-
rameter ρ, and the image pre-smoothing parameter σ,
so for the experiments in this article, p = (α, ρ,σ).
Parameters ρ and σ affect AEE and the processing
time T . Their influence on AEE is clear. They also
influence T, because they determine the size of the
Gaussian filter used to smooth image intensities and
derivatives. The regularization parameter α affects
AEE clearly. A fixed value has been assigned to ε,
following (Bruhn, 2006). For the small set of ex-
periments with the SOR iterative solving method, we
will not vary the parameters related to the stopping
criteria. We are more interested in multilevel strate-
gies, such as the FMG solving method, which tends to
Pareto-dominate iterative methods in our experiments
and does not require stopping criteria.
4 EXPERIMENTAL RESULTS
This section describes the experimental setup and
results for optimization using sequences and ground
truth from the Middlebury data set (Baker et al.,
2011) (see Figure 2). The Middlebury data set
contains eight synthetic and laboratory sequences
with a dense ground truth.
Figure 2: Sample Images from the Middlebury Data Set.
Algorithm 1 : EMO of Optical Flow.
Input: u
gt
, ground truth optical flow of image se-
quences in the evaluation data set
Input: N
gen
, number of generations
Input: N
ind
, number of individuals in a generation
Input: N
seq
, number of image sequences in the eval-
uation data set
1: Initialize a parent population P
0
= {p
j
}
j=1,...,N
ind
2: Create an offspring population Q
0
(tournament
selection, recombination, and mutation)
3: for i = 1, ..., N
gen
do
4: Create a combined population R
i
= P
i
∪Q
i
including the parent population P
i
and the
offspring population Q
i
. Thus, population
R
i
has 2N
ind
individuals
5: Sort individuals from R
i
according to non-
domination rank (described in Section 3.1).
The result is the set F = {F
1
,F
2
,...} of all
the non-dominated fronts in R
i
6: Set P
i+1
=
/
0, f = 1
7: while Parent population is not yet filled,
|P
i+1
|+ |F
f
| ≤ N
ind
, with |P| the number of
elements in set P, do
8: Include f -th non-domination front in
the parent population, P
i+1
= P
i+1
∪F
f
9: Increment front index, f = f + 1
10: end while
11: Sort next front F
f
according to crowding
measure (described in Section 3.1).
12: Choose the best N
ind
individuals, P
i+1
=
P
i+1
∪F
f
[1 : (N
ind
−|P
i+1
|)]
13: Initialize population Q
i+1
(selection, muta-
tion, and crossover)
14: for j = 1,... ,N
ind
do
15: OpticalFlowEvaluation(p
j
), Algo-
rithm 2
16: end for
17: end for
Output: Global accuracy-speed (error-execution
time) statistics
Output: Pareto-optimal p-vectors {p
opt
}
Multi-objectiveOptimizationforCharacterizationofOpticalFlowMethods
569

Algorithm 2 : OpticalFlowEvaluation(p).
Input: u
gt
, ground truth optical flow of image se-
quences in the evaluation data set
Input: N
seq
, number of image sequences in the opti-
cal flow evaluation set
Input: p, parameter vector for the optical flow
method being studied
1: for k = 1,.. .,N
seq
do
2: Calculate optical flow for image sequence k
with parameters p, measure execution time.
3: Evaluate performance for image sequence k
using u
gt
4: end for
5: Calculate average error (AEE) and execution
time (T ) for the N
seq
image sequences
Output: Accuracy-speed (error-execution time)
statistics
Efficient genetic optimization requires user-
knowledge about the optimization problem. As a way
of providing that knowledge about multi-objective op-
timization of optical flow, we chose a wide range
for the parameters, containing parameter settings that
proved to perform well in preliminary experiments of
CLG optical flow. Minimum and maximum values for
discretization of parameters for the whole Middlebury
data set were configured so that α ∈ [0,10000], ρ ∈
[0,6] and σ ∈ [0,6]. Smaller parameter ranges were
chosen for previous experiments; as an example, for
some preliminary experiments with the Middlebury
data set, we selected α ∈ [650, 1100], ρ ∈ [0.1,4.5]
and σ ∈ [1,4].
Preliminary experiments were conducted with 32
and 64 individuals per generation. Results were sim-
ilar, so all experiments shown were run with popu-
lations of 32 individuals. Probability of crossover
was set to 0.9 and probability of mutation to 0.33
(1/n, with n = 3 the number of decision variables for
real-coded genetic algorithms)(see (Deb et al., 2002)).
Distribution indexes for crossover and mutation were
set to 20.
Two different sets of experiments were performed.
First, short experiments of 10 generations compared
successive over-relaxation (SOR) and full multi-grid
(FMG) solvers for the CLG optical flow method,
and then long experiments surveyed the convergence
of the optimization methodology when optimizing
CLG+FMG, the best performing (best accuracy and
speed) OF algorithm and solver, and tested the effect
of a larger parameter range.
Experiments were run on linux based PC’s with
Intel Core i7 CPU. Single-threaded optical flow meth-
ods were implemented in C/C++. However, in or-
der to take advantage of the multicore architecture we
had, genetic algorithm individuals were run in several
parallel threads, using OpenMP. A version of NSGA-
II C/C++ library (Deb et al., 2002) was modified to
run in parallel and used for EMO.
4.1 Middlebury Subset
For preliminary experiments, three image pairs
were selected: images 10 and 11 from sequences
Dimetrodon, Rubberwhale and Urban3 (see Figure 2),
and the proposed methodology was applied to that
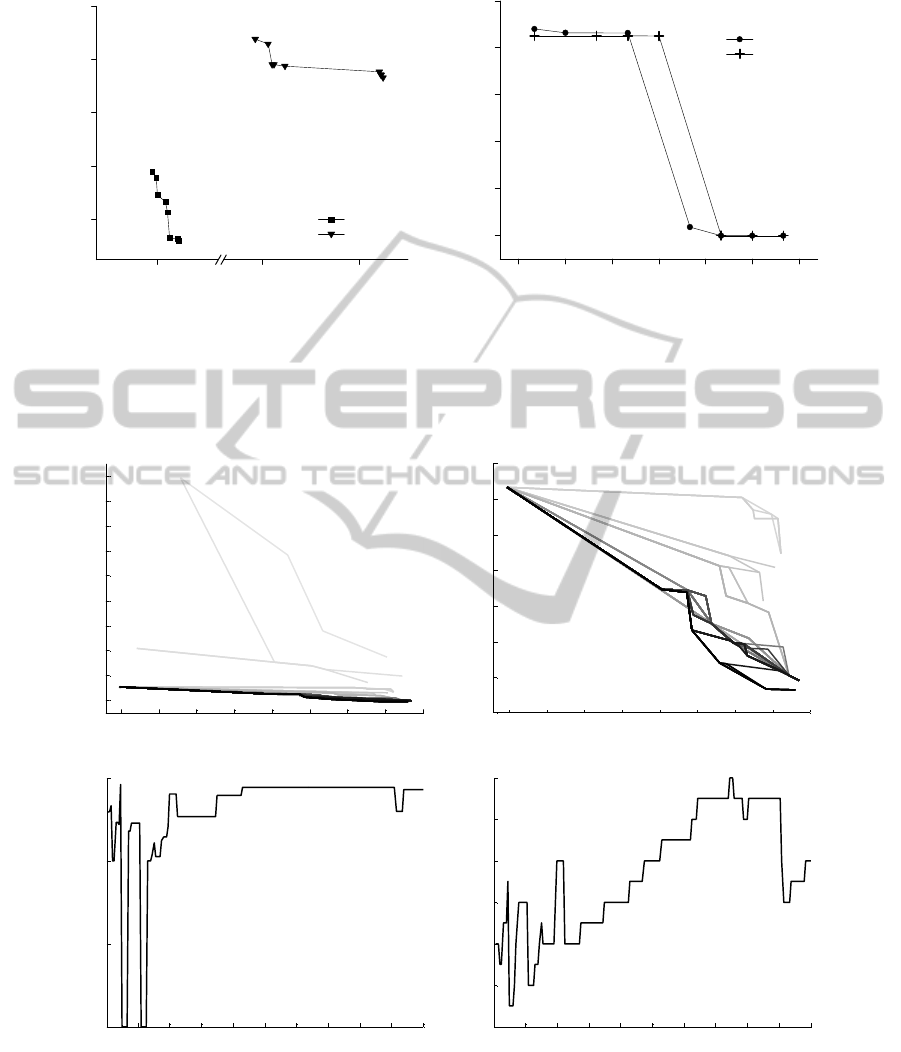
set. Figure 3(a) shows final Pareto fronts resulting
from EMO. Each Pareto front gives a characteriza-
tion of its corresponding method and the concept of
Pareto dominance can be applied for further analysis
of these results. Solutions related to the FMG solver
Pareto-dominate every SOR solution in the graph.
Then, the global Pareto front for both methods is the
FMG curve. Increasing the number of SOR iterations
would presumably give lower AEE values, and per-
haps a non-dominated solution, but with a very long
time spent in every execution. As a conclusion for
this figure, when working with images that are similar
to those in the database used, FMG solving methods
would be preferred over SOR.
Figure 3(b) presents two NSGA-II experiments
for the same OF algorithm and parameters. The
chosen OF algorithm is the best performing one
in the previous experiment (shorter experiments),
CLG+FMG. Both experiments were conducted with
60 generations and the same NSGA-II parameters.
Despite the randomness of genetic algorithms, most
of the measures converged to the same value or to
quite close values.
Figure 3(b) shows final Pareto fronts (accuracy-
speed plots) for both NSGA-II experiments. The
curves are very similar. The only slight difference
is a shift of less than 5 ms in two solutions. When
comparing these curves with Figure 3(a), an improve-
ment can be observed. These new curves dominate
the previous 10-generation experiment: every solu-
tion in these new experiments is faster (less execution
time) or equally as fast as all solutions in the previ-
ous run, and the minimum AEE obtained is less than
the previous minimum value. Although evident, the
difference between the results of the previous exper-
iment and these new ones is small enough and does
not suggest a change in the relative position of differ-
ent OF solving algorithms.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
570
a
b
500 7000 7500
2.12
2.14
2.16
2.18
2.20
Average End-Point Error (AEE) [pixels]
Execution Time [ms]
CLG - FMG
CLG - SOR
455 460 465 470 475 480 485
2.11
2.12
2.13
2.14
2.15
2.16
End-Point Error (AEE) [pixels]
Execution Time [ms]
Run 1
Run 2
Figure 3: Comparison of two different experiments of NSGA-II for the CLG OF algorithm with FMG solving method, bounds
for parameters as described in the text of the article. (a) Final Pareto front for CLG OF with FMG and SOR solvers, varying
the global OF regularization (α), derivative smoothing (ρ) and image pre-smoothing (σ), see Section 2. The execution time
axis was broken for better visualization. (b) Two experiments for the CLG OF algorithm with FMG solving method. Both
experiments were run with 60 generations of 32 individuals and the same NSGA-II parameters. Final Pareto fronts are shown.
Curves for one experiment are marked with plus signs (+) and curves for the other experiment use dots (.) as markers.
0.7 0.75 0.8 0.85 0.9 0.95 1 1.05 1.1
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
Execution Time [s]
Average End-Point Error (AEE - pixels)
0.7 0.75 0.8 0.85 0.9 0.95 1 1.05 1.1
1.99
2
2.01
2.02
2.03
2.04
2.05
2.06
Execution Time [s]
Average End-Point Error (AEE - pixels)
0 20 40 60 80 100 120 140 160 180 200
0
2
4
6
8
10
12
Generation
Archive Size
0 20 40 60 80 100 120 140 160 180 200
0
0.5
1
1.5
Generation
Crowding Measure
a
b
c
d
Figure 4: Evolution of execution time and error for the whole Middlebury database. (a) Evolution of the Pareto front in the
objective space. Black lines represent the final Pareto fronts. Solutions in each Pareto front are connected by line segments
for viewing purposes. The darkness of the gray levels decreases for earlier generations. (b) Detail from (a). (c) Crowding
measure evolution. (d) Archive size evolution.
Multi-objectiveOptimizationforCharacterizationofOpticalFlowMethods
571

4.2 Whole Middlebury Data Set
Figure 4 presents the evolution of solutions and
NSGA-II measures for the whole Middlebury data set
and for a long experiment (200 generations). Fig-
ures 4(a) and (b) show the Pareto fronts for even num-
bered generations. The gray level intensity is high
(light gray) for early generations and low (black) for
late generations. Solutions are connected by line seg-
ments to facilitate visual analysis. Many small and
a few large changes between generations can be ob-
served. Both the minimum execution time and AEE
were reduced. Figures 4(c-d) present the evolution
of NSGA-II measures. Every measure remained very
stable for the last tens of generations. Even the aver-
age AEE in the Pareto front (not shown) was reduced,
while preserving the crowding measure and increas-
ing the archive size.
Figure 5 shows the evolution of the Pareto fronts
for three combinations of optical flow functionals and
solving techniques. This figure gives an example of
the application of the proposed methodology to the
characterization and comparison of optical flow meth-
ods. A global Pareto front can be defined as the Pareto
front for all the solutions in this plot, even when these
solutions are related to different optical flow meth-
ods. The global Pareto front for these algorithms in-
cludes the Pareto front for CLG+FMG and part of
the Pareto front for RegL1CLG+SOR, a regularized
L
1
version of the CLG functional and SOR solving
method, see Section 2. Then, the CLG+SOR option
should not be chosen for any application. Depending
on the accuracy-speed requirements of each particu-
lar application, an operating point in the global Pareto
3
3.5
4
4.5
Point Error (AEE
- pixels)
CLG+FMG
CLG+SOR
RegL1CLG+SOR
0 5 10 15 20 25
1.5
2
2.5
3
Execution Time [s]
Average End-
Point Error (AEE
Figure 5: Evolution of the Pareto front for three combina-
tions of optical flow functionals and solving methods, when
applied to the whole Middlebury data set. The evolution of
the Pareto fronts for three different variants of optical flow
methods and solving techniques (CLG+FMG, CLG+SOR,
RegL1CLG+SOR) were given different colors, as shown in
the legend, and displayed on the same axes.
front should be chosen, either in the CLG+FMG or in
the RegL1CLG+SOR variants.
The overall running time of one optimization
experiment (200 generations, whole Middlebury
database, FMG solving method) was about three
hours. That experiment requires 6400 optical flow
evaluations. The resolution was 256 levels per param-
eter, then the equivalent brute force search would have
needed 16 million optical flow evaluations, more than
three orders of magnitude slower than our approach.
5 CONCLUSIONS
This article describes a strategy for optimizing the pa-
rameter setting of any optical flow method focusing
on two performance criteria, namely, the accuracy and
speed. The proposed methodology is based on evolu-
tionary multi-objective algorithms.
When choosing and adjusting an optical flow
method to a specific application, the design require-
ments for accuracy and speed are the keys to finding
the right method and its parameter configuration in
a graph of execution time versus error, showing op-
erating points for different methods. A straightfor-
ward way to do it would be finding a global Pareto
front of all methods and looking for those operating
points that fulfill the design requirements. In gen-
eral, the Pareto front of a first method/implementation
dominating the Pareto front of a second method–
understood as every point in the second curve being
dominated by at least one point in the first curve–
means the first method is better because it can achieve
lower error or execution time than any operating point
of the second method.
We have shown this analysis for two solvers of
the combined local and global (CLG) variational op-
tical flow method of Bruhn et al (Bruhn et al., 2005b).
Nevertheless, the proposed methodology can be uti-
lized to compare different optical flow methods and
to find their optimal operation points, i.e. parameter
settings.
This work shows experiments for the Middle-
bury optical flow evaluation data set. When ana-
lyzing the results, the following conclusions can be
reached: 1) The Pareto fronts for a multi-grid solving
method dominate the fronts related to the SOR solv-
ing method. 2) In spite of the randomness of genetic
algorithms, our tests show that the method converges.
The convergence time was a few orders of magnitude
faster than a brute force search. 3) The method effec-
tively reduces execution time and error, and gives a
receiver operating curve, where every operating point
is associated with a parameter setting.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
572

Finally, we would like to state that multi-objective
optical flow parameter optimization and characteri-
zation are needed for further development of optical
flow applications. It is perfectly reasonable to think
about Pareto-based optical flow rankings, assuming
some rules for fair result comparison. One solution
could be to allow researchers to run their experiments
on a common hardware platform. Current web-based
rankings can easily provide a graphical representation
of several objectives.
REFERENCES
B
¨
ack, T. (1996). Evolutionary algorithms in theory and
practice: evolution strategies, evolutionary program-
ming, genetic algorithms. Oxford University Press.
Baker, S., Scharstein, D., Lewis, J., Roth, S., Black, M.,
and Szeliski, R. (2011). A database and evaluation
methodology for optical flow. International Journal
of Computer Vision, 92:1–31.
Barron, J., Fleet, D., and Beauchemin, S. (1994). Perfor-
mance of optical flow techniques. International Jour-
nal of Computer Vision, 12(1):43–77.
Benlian, X. and Zhiquan, W. (2007). A multi-objective-
ACO-based data association method for bearings-only
multi-target tracking. Communications in Nonlinear
Science and Numerical Simulation, 12(8):1360–1369.
Briggs, W., Henson, V., and McCormick, S. (2000). A
Multigrid Tutorial. Society for Industrial and Applied
Mathematics.
Bruhn, A. (2006). Variational Optic Flow Computation, Ac-
curate Modelling and Efficient Numerics. Ph.D. dis-
sertation, Saarland University.
Bruhn, A., Weickert, J., Feddern, C., Kohlberger, T., and
Schn
¨
orr, C. (2005a). Variational optical flow compu-
tation in real time. IEEE Transactions on Image Pro-
cessing, 14(5):608–615.
Bruhn, A., Weickert, J., and Schn
¨
orr, C. (2005b). Lu-
cas/Kanade meets Horn/Schunck: Combining local
and global optic flow methods. International Journal
of Computer Vision, 61(3):1–21.
Changming and Sun (2002). Fast optical flow using 3D
shortest path techniques. Image and Vision Comput-
ing, 20(13-14):981–991.
Chittka, L., Dyer, A. G., Bock, F., and Dornhaus, A. (2003).
Psychophysics: Bees trade off foraging speed for ac-
curacy. Nature, 424(6947):388.
Deb, K. and Kumar, A. (1995). Real-coded genetic algo-
rithms with simulated binary crossover: Studies on
multimodel and multiobjective problems. Complex
Systems, 9(6):431–454.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).
A fast and elitist multiobjective genetic algorithm:
NSGA-II. IEEE Transactions on Evolutionary Com-
putation, 6(2):182–197.
Everingham, M., Muller, H., and Thomas, B. (2006). Evalu-
ating image segmentation algorithms using the pareto
front. In Heyden, A., Sparr, G., Nielsen, M., and Jo-
hansen, P., editors, Computer Vision - ECCV 2002,
volume 2353 of Lecture Notes in Computer Science,
pages 255–259. Springer Berlin / Heidelberg.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization, and Machine Learning. Addison-Wesley.
Heas, P., Herzet, C., and Memin, E. (2012). Bayesian
inference of models and hyperparameters for robust
optical-flow estimation. Image Processing, IEEE
Transactions on, 21(4):1437–1451.
Horn, B. K. and Schunck, B. G. (1981). Determining optical
flow. Artificial Intelligence, 17:185–203.
Krajsek, K. and Mester, R. (2006). A maximum likelihood
estimator for choosing the regularization parameters
in global optical flow methods. In Image Processing,
2006 IEEE International Conference on, pages 1081–
1084.
Li, Y. and Huttenlocher, D. (2008). Learning for optical
flow using stochastic optimization. In Forsyth, D.,
Torr, P., and Zisserman, A., editors, European Con-
ference on Computer Vision - ECCV 2008, volume
5303 of Lecture Notes in Computer Science, pages
379–391. Springer Berlin / Heidelberg.
Salmen, J., Caup, L., and Igel, C. (2011). Real-time estima-
tion of optical flow based on optimized Haar wavelet
features. In Evolutionary MultiCriterion Optimiza-
tion, pages 448–461. Springer.
Verschae, R., Ruiz-del-Solar, J., K
¨
oppen, M., and Garcia,
R. V. (2005). Improvement of a face detection sys-
tem by evolutionary multi-objective optimization. In
Proceedings of the Fifth International Conference on
Hybrid Intelligent Systems, pages 361–366, Washing-
ton, DC, USA. IEEE Computer Society.
Vite-Silva, I., Cruz-Cort
´
es, N., Toscano-Pulido, G., and
Fraga, L. G. (2007). Optimal triangulation in 3D com-
puter vision using a multi-objective evolutionary al-
gorithm. In Proceedings of the EvoWorkshops 2007:
Applications of Evolutionary Computing, pages 330–
339, Berlin, Heidelberg. Springer-Verlag.
Multi-objectiveOptimizationforCharacterizationofOpticalFlowMethods
573
