Statistical Identification of Co-regulatory Gene Modules using

Multiple ChIP-Seq Experiments

Xi Chen

, Xu Shi

, Ayesha N. Shajahan-Haq

, Leena Hilakivi-Clarke

Robert Clarke

2,3

and Jianhua Xuan

Department of Electrical and Computer Engineering, Virginia Tech, Arlington, VA 22203, U.S.A.

Lombardi Comprehensive Cancer Center, Department of Oncology, Georgetown University,

Washington, DC 20057, U.S.A.

Department of Physiology and Biophysics, Georgetown University, Washington, DC 20057, U.S.A.

Keywords: ChIP-Seq, TFBS, Target Genes, MCMC, Co-regulatory Modules.

Abstract: ChIP-Seq experiments provide accurate measurements of the regulatory roles of transcription factors (TFs)

under specific condition. Downstream target genes can be detected by analyzing the enriched TF binding

sites (TFBSs) in genes’ promoter regions. The location and statistical information of TFBSs make it

possible to evaluate the relative importance of each binding. Based on the assumption that the TFBSs of one

ChIP-Seq experiment follow the same specific location distribution, a statistical model is first proposed

using both location and significance information of peaks to weigh target genes. With genes’ binding scores

from different TFs, we merge them into a weighted binding matrix. A Markov Chain Monte Carlo (MCMC)

based approach is then applied to the binding matrix for co-regulatory module identification. We

demonstrate the efficiency of our statistical model on an ER-α ChIP-Seq dataset and further identify co-

regulatory modules by using eleven breast cancer related TFs from ENCODE ChIP-Seq datasets. The

results show that the TFs in individual module regulate common high score target genes; the association of

TFs is biologically meaningful, and the functional roles of TFs and target genes are consistent.

1 INTRODUCTION

Chromatin immunoprecipitation with massively

parallel DNA sequencing (ChIP-Seq) has greatly

advanced the regulation mechanism analysis by

identifying transcription factor binding sites

(TFBSs) of specific protein of interest (Park, 2009).

This technology helps biologists investigate that

how proteins interact with DNA to regulate gene

expression, which is essential for understanding

many biological processes and disease states.

Recently, to examine the principles of the human

cancer transcriptional regulatory network, many

ChIP-Seq experiments are being carried out in

various cancer cells to test hundreds of TFs under

different treatment conditions (Dunham et al., 2012;

Hurtado et al., 2011; Ross-Innes et al., 2010; Schultz

et al., 2010). With resources from the ENCODE

project (Dunham et al., 2012), researchers can now

investigate different TFs simultaneously under the

same cell type (Gerstein et al., 2012).

For ChIP-Seq data analysis, several motif searching

tools (Bailey et al., 2006; Heinz et al., 2010) are

widely used for both known motifs enrichment and

de novo motif discovery. In target gene annotation

(McLean et al., 2010; Salmon-Divon et al., 2010),

however, only the distance between the peak

location and the transcription starting site (TSS) of

its target gene is utilized to establish gene regulation.

As a result, over one thousand target genes are

obtained but no rank information provided. A

narrowed down gene list with fewer false positives

is desirable for biologists to perform further

validation. To tackle this issue existing in current

target gene identification, new methods utilizing

more information from the peak files are developed.

A reasonable assumption used in the TIP method

(Cheng et al., 2011) is that TFBSs in target genes’

promoter region would follow the same position-

specific probability distribution. But it is known that

only a portion of the TFBSs contain the TF

associated motifs, usually constituting 20 ~30% of

all peak files (Bailey et al., 2006; Heinz et al., 2010).

109

Chen X., Shi X., N. Shajahan-Haq A., Hilakivi-Clarke L., Clarke R. and Xuan J..

Statistical Identiﬁcation of Co-regulatory Gene Modules using Multiple ChIP-Seq Experiments.

DOI: 10.5220/0004736801090116

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 109-116

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

In that case, it is hard to assert that the TFBSs

without similar sequence pattern would follow the

same location-specific distribution. The false

positives in the peak files will contaminate observed

TFBS’s distribution. Furthermore, TIP only utilizes

each peak’s location information, regardless its

significance. The p-value of each peak indicates the

confidence of the current TFBS. If all the peaks

were treated equally when we generated the TFBS’s

location specific distribution, the low confident

peaks would lower the sensitivity of the target gene

identification. To improve these potential

weaknesses in TIP method, we proposed a more

rigorous hypothesis that the TFBSs containing

similar motifs should follow the same position-

specific distribution, and developed a statistical

model by incorporating peak’s both location and

statistics information to reveal the weight of each

gene. This approach offers a statistical inspection of

the binding relationship between enriched TFBSs

and associated target genes.

With the accumulation of ChIP-Seq data sets, we

can investigate the co-association among multiple

TFs and further identify co-regulatory modules.

Previous studies in location correlation of peak files

from multiple ChIP-Seq data sets provide evidence

for different TFs’ co-association (Gerstein et al.,

2012). The module identification is an on-going

topic for regulatory network analysis. Biclustering

methods (Turner et al., 2005) (Ihmels et al., 2004)

are widely used to provide multiple local optimal

solutions for module identification. They could

provide a quick view about the distribution of major

modules in a global picture. However, most

biclustering methods are unsupervised and use

different criteria to select final modules, therefore at

the gene level, the module size is not well controlled

and the results are provided without any rank

information regarding the difference among genes.

In this study, we further proposed a Markov

Chain Monte Carlo (MCMC) based approach to

investigate co-regulation mechanism. By clustering

the TFs into several candidate groups, a large

binding network is divided into several sub-

networks. Then, searching for multiple local optimal

modules in the entire binding network is equivalent

to identifying individual global optimal module in

each sub-network. In each sub-network, we used an

MCMC based approach to identify high confident

co-regulated genes. To overcome the over-fitting of

clustering methods, which actually provides non-

overlap TF clusters, we carried out a TF refinement

step by adding or deleting TFs randomly to highly

confident genes and checking the contribution of

each TF in our list to enforce co-regulation in

current module. By repeating these two steps for all

sub-networks, we identified a list of co-regulatory

modules with co-associated TFs and high confidence

target genes. Our method allows overlap among

modules at both TF and gene levels, which were not

included in earlier studies (Segal et al., 2003; Su et

al., 2010). To validate our method, we applied the

proposed scheme to analyse eleven breast cancer

related TFs’ ChIP-Seq datasets obtained from the

ENCODE project. Our computational results are

well supported by available biological literatures and

provide a detailed interpretation for the regulation

mechanism of selected TFs in breast cancer.

2 METHODS

First of all, for each TF’s ChIP-Seq experiment, we

calculated the target gene scores by using the peak

files reported by MACS, and generated gene

annotation file from GREAT (McLean et al., 2010).

A binding matrix is formed with binding scores as

units. Secondly, we applied affinity propagation

clustering (APC) (Frey and Dueck, 2007) to classify

the columns (TFs) of the matrix, and extracted sub-

networks with associated TFs and genes. Then, an

MCMC based approach was used to identify the

genes regulated by each cluster of TFs with high

score. Finally, after target gene selection, we applied

another round of sampling by adding or deleting TFs

dynamically to refine the regulators in each module.

2.1 Data Pre-processing

We downloaded the peak files processed by MACS

for the selected breast cancer TFs from the

ENCODE (http://genome.ucsc.edu/ENCODE/). The

information we extracted from these peak files

includes peak’s start, end, summit, summit height

and the significance p-value. To lower the impact of

false positive peaks, for each TF, we used HOMER

(Heinz et al., 2010) to isolate the peaks enriched by



Figure 1: Flowchart of the proposed approach for

regulatory module identification.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

110

TF associated motifs. For gene annotation, with user

specified upstream and downstream promoter

region, GREAT was used to generate peak

annotations with distance information.

2.2 Gene’s Binding Score Calculation

Given the input ChIP-Seq data, we proposed a

statistical model to evaluate each target gene’s

relative importance based on the observations from

specific TF’s ChIP-Seq data, as detailed in Eq. (1):



() 1

,| ,|

loca i

Gene peak input P Gene i input





(1)

where

() 1

loca i 

indicates that i-th base with

respect to TSS of g-th gene is covered by a peak.

Each peak is composed by several hundreds of bases

and each location follows the location specific

probability distribution. Thence, the probability for

each peak equals to the sum of the probability of all

the bases it covers. Further, considering the

conditional relationship of two steps, peak calling

and gene annotation, Eq. (1) can be extended as:









() 1

,| ,

loca i

Gene peak input P Gene i input P i input





(2)

There are two components for this joint

probability.

(|,)

P Gene i input

is the conditional

probability that g-th gene is a true target given by

the significant binding signal (peak) at i-th base.

While

(| )

i input

is the relative importance of i-th

base indicated by the TFBS location specific

distribution. Here the prior probability of P(input) is

set as constant value for all locations.

Probability

(|,)

P Gene i input

can be calculated by

the read depth at i-th base and its associated

significance score. The read depth h

(i) of i-th base

can be estimated by a triangle approximation as

shown in Fig. 2 and Eq. (3).

(a) (b)

Figure 2: Typical binding site locations with respect to

TSS: (a) TFBS occurs likely at upstream region with

~10kbps to TSS, (b) or downstream but close to TSS,

usually within 1kbps.

where RD

summit

is the reported peak height by peak

calling tool.

tart

ummit

and

end

, as shown in

()

summit

istart

D start i summit

summit start

end i

RD summit i end

end summit

























(3)

Fig. 2, are the start, summit and end positions of

each reported peak, respectively.

The significance p-value is actually a probability

and cannot be directly used. We used an exponential

distribution to fit the p-value as in Eq. (3) with λ=1.

For g-th gene, q

(i) is used to weight the read depth

(i) at i-th base as Eq. (4):

() exp[ ()]

p-value i q i







(4)

After the normalization with constant value C

(considering the maximum value of peak height and

q score), the conditional probability that g-th gene

can be linked with binding signal observed at i-th

base, which can be calculated as:





,()()/

ggg

P Gene i input h i q i C

(5)

Probability

(| )

i input

evaluates the prior

probability of i-th base according to the statistics of

read depth and significance of all peak files. To

generate location specific distribution, we pile up all

genes’ binding signals at i-th base with respect to the

TSS as Eq. (6).



() () () ()

gg gg

gig

Piinput h iq i h iq i



(6)

Compared to the TIP method, in our case the

binding signal at each location is associated with a

weight transformed from its significance. It will

lower the impact of false positive peaks in TFBS’s

distribution along the promoter region.

Given the TFBS distribution in Eq. (6) and

binding signals at each base, similar to Eq. (1), the

g-th gene’s regulatory score can be calculated as:



() 1

() ()

ggg

loca i

h i q i P i input





(7)

2.3 Module Identification

Module identification problem is to search for

multiple local optimal regulatory networks. In this

paper, we proposed an MCMC based scheme to

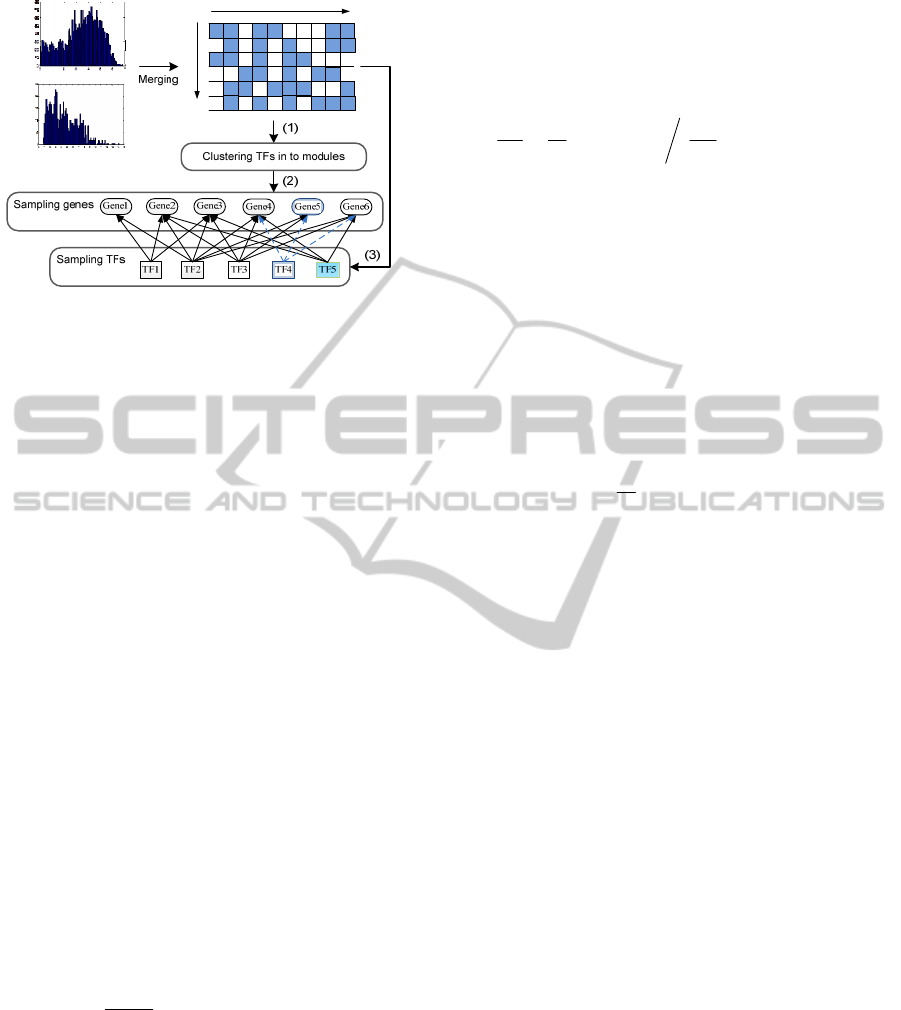
identify co-regulatory gene modules. As shown in

Fig. 3, there are three main steps: (1) use APC to

cluster TFs into candidate groups and generate initial

modules; (2) using MCMC to mimic the Markov

process at gene level in each module to identify high

confident co-regulated genes; (3) based on the genes

identified from (2), sampling all TFs to refine the

TFs in each module by adding new TFs or deleting

StatisticalIdentificationofCo-regulatoryGeneModulesusingMultipleChIP-SeqExperiments

111

Gene

Figure 3: Flowchart of regulatory module identification:

(1) TF clustering; (2) MCMC based gene identification;

(3) TF refinement by using sampling techniques. For

example, Gene 5 will be rejected during the MCMC

process due to its low gene score; in the TF refinement

step, TF 4 gets little support from the target level and it is

deleted; but TF 5, which is not covered by clustering

results for current module, is added because it also

regulates a large portion of genes in current module.

low confident ones. In this way, the multiple local

optimal solutions in the whole binding network are

equivalent to individual global optimal solution in

each associated sub-network.

In each module, during the MCMC process, each

state represents a sampled sub-network with fixed

up-stream regulators and sampled downstream

genes. According to Metropolis sampling algorithm,

for state transition, we proposed a new sub-network

by randomly adding or deleting one gene to current

sub-network. Then, we either accept the proposed

sub-network or keep current network by checking

whether the overall binding intensity is improved.

The state of Markov process is updated accordingly,

and we carry out next round of sampling. Finally,

the Markov process should converge to a sub-

network or a module with strongly co-regulated

genes.

For the m-th cluster with T

TFs, we define a

sub-network score as:

nnggt

Sfs









(8)

where f

is a binary vector with length of total gene

number G. In the n-th round of sampling, if g-th

gene is covered by current module, f

n,g

equals to 1,

otherwise it equals to 0. In Eq. (8), the sum of non-

zero units of f

is G

. Initially we randomly select G

genes and sub-network score is S

In the n-th round of MCMC process, a new sub-

network is proposed by randomly adding or deleting

one gene. The prior probability for adding or

deleting is 0.5. Whether such an adjustment

contributes to co-regulatory characteristic of current

module is determined by the acceptance criterion

defined as follows:

,, 1,,

11 11

ng gt n g gt

gt gt

fs f s





 



  

 

 

 

 

(9)

where S

and S

n-1

represent sub-module scores for

the proposed sub-module and current sub-module,

respectively. G

and G

n-1

are associated numbers of

genes. Here, if α is larger than 1, we accept the

proposed sub-module; else, we accept the proposed

module by probability α. If the proposed sub-module

is rejected, we directly set f

= f

n-1

for next round.

After N rounds of sampling, we generate a series





nN

. When N is large enough, the

posterior distribution condition on current module

for g-th gene is proportional to the count of its

appearance as F

during the MCMC process:





(10)

With selected top G

genes according to F

, we

used a sampling method to refine TFs. Using

clustering result as initial TF selection, in k-th

sampling, we randomly added a new TF or deleted a

current TF to current module. Similar to the

definition of Eq. (9), we determined whether the

proposed addition or deletion was accepted or not

according to the binding intensity in current module.

The result was recorded in vector h

. Finally, a series





hkK

were generated. For t-th TF, we

calculated sampling statistics H

by summing all h

k,t

The distribution of all TFs’ H score reflected the

contribution of each TF to the co-regulation in

current module. We adjusted the TFs by adding new

high score TFs and deleting low score ones. Our

method allows overlap at both gene and TF levels

among different modules. A common TF may

regulate different genes in several modules and

achieve distinct functional roles.

3 RESULTS

3.1 TFBS Location Distribution

Here, we present three TFBS distributions calculated

by our method and another TFBS distribution

calculated by TIP for comparison. By comparing the

distributions between Fig. 4(a) and Fig. 4(b), it can

be seen that MYC associated TFBSs share common

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

112

features in different environments (ovarian cancer

cell vs. breast cancer cell). In Fig. 4(a), the

distribution shows a high single sharp peak centred

on TSS, compared to a wider but still single peak at

the same location in Fig. 4(b). Different from MYC,

the ER-alpha’s distribution in Fig. 4(c) shows that

remote binding still has a high probability to occur

and plays important roles in target gene regulation.

Besides the main peak around TSS, another high

probability region appears around 500bps, which is

similar to Fig. 4(a). This observation shows that a

binding within a short range after TSS will also

activate the regulation. If we compare Fig. 4(c) with

the distribution generated by TIP in Fig. 4(d), our

distribution shows a higher probability near TSS and

that all the features such as high probability of

remote binding points are kept. It is well known that

most TFBSs bind close to TSS, i.e. within 2kbps.

But in Fig. 4(d), the distribution is more flat. The

sensitivity of TIP’s distribution is lower due to

assigning equal weight to low significant peaks, a

large portion of which is located far from TSS.

(a)

(b)

Figure 4: TFBS location specific probability distribution

from upstream -10k to downstream 1k with respect to

TSS: (a) MYC in ovarian cancer cell (in house data); (b)

MYC in MCF-7 breast cancer cell line from the Encode

project; (c) ER-alpha in MDA-MB-231 breast cancer cell

line (Stender, et al., 2010); (d) the same data as (c) but

calculated by the TIP method.

3.2 ER-α ChIP-Seq Data Validation

In this section, we utilized a human ER-α dataset

(Stender et al., 2010) to prove that target genes

identified by our method is not only intensely

regulated by the TF under investigation, but also

functional expressed. From the analysis done by

(Stender et al., 2010), we know that the ER-α

binding genes should have significant expression

change between wide type ER binding (ERwt) and

mutant ER binding (ERmut) conditions. We

calculated binding scores for 612 ERE motif

enriched genes by using our method and TIP,

respectively. We selected top 25%, 177 genes for

further comparisons.

Usually we have more confidence on the high

significant peak files. Thence, it is necessary to

check q scores of identified genes’ peaks (defined by

Eq. (4)). As shown in Fig. 5, our method utilizes

more significant peak files (the red bar) to identify

high score genes. And some relatively low

significant peaks are still used due to their high

location prior in the TFBS distribution. TIP misses

some highly significant peaks because a larger

number of low significant peaks are equally

weighted when the location distribution is generated.

The impact of false positive peaks is raised in TIP.

Figure 5: Significance score distribution of the binding

peaks used to identify high score target genes.

Figure 6: ER-α ChIP-Seq data analysis, heat map of

identified genes’ expression under two conditions.

There is still some gap to claim that the more

significant peaks that we used, the more strongly our

identified genes are regulated by the TF under

investigation. A true/functional binding will either

activate or inhibit its target gene’ expression.

Thence, in the second step, we have checked that

whether our identified target genes have significant

fold change when their upstream regulator ER-α is

1k0 -1k-2k-3k-4k-5k-6k-7k-8k-9k-10k

0.2

0.4

0.6

0.8

1.2

1.4

x 10

-3

bps

PDF

1k0 -1k-2k-3k-4k-5k-6k-7k-8 k-9k-10k

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

x 10

-3

bps

PDF

1k0-1k-2k-3k-4k-5k-6k-7k-8k-9k-10k

x 10

-4

bps

PDF

1k0-1k-2k-3k-4k-5k-6k-7k-8k-9k-10k

x 10

-4

bps

PDF

StatisticalIdentificationofCo-regulatoryGeneModulesusingMultipleChIP-SeqExperiments

113

muted. The heatmap of our identified genes’

expression profiles are shown in Fig. 6. It can be

seen that, most of the genes have significant fold

change between ERwt and ERmut conditions. We

compared the z-score distribution of our identified

top 177 genes, TIP identified top 177 genes, to all

612 candidate targets, respectively. Based on

Kolmogorov–Smirnov test, we observed that the

distribution of our results supported that it was a

significant subset with p-value 8.7e-3, while the p-

value of the genes identified by TIP was 4.1e-2. It is

evident that our identified genes are more

functionally expressed.

3.3 Co-regulatory Module

Identification

From ENCODE, we downloaded the ChIP-Seq data

of 11 breast cancer related TFs, which are carried

out on MCF7 breast cancer cell line, including

CEBPB, ELF1, EP300, FOXM1, GATA3, HAE2F1,

JUND, MAX, MYC, TCF4 and TCF12. Due to the

multiple possible motifs associated with some TFs,

with HOMER, we collected 36 motifs. Totally there

are 11,957 target genes annotated by GREAT with

upstream 10k and downstream 1k distance control.

After genes’ binding score calculation, we generated

a weighted binding matrix for module identification.

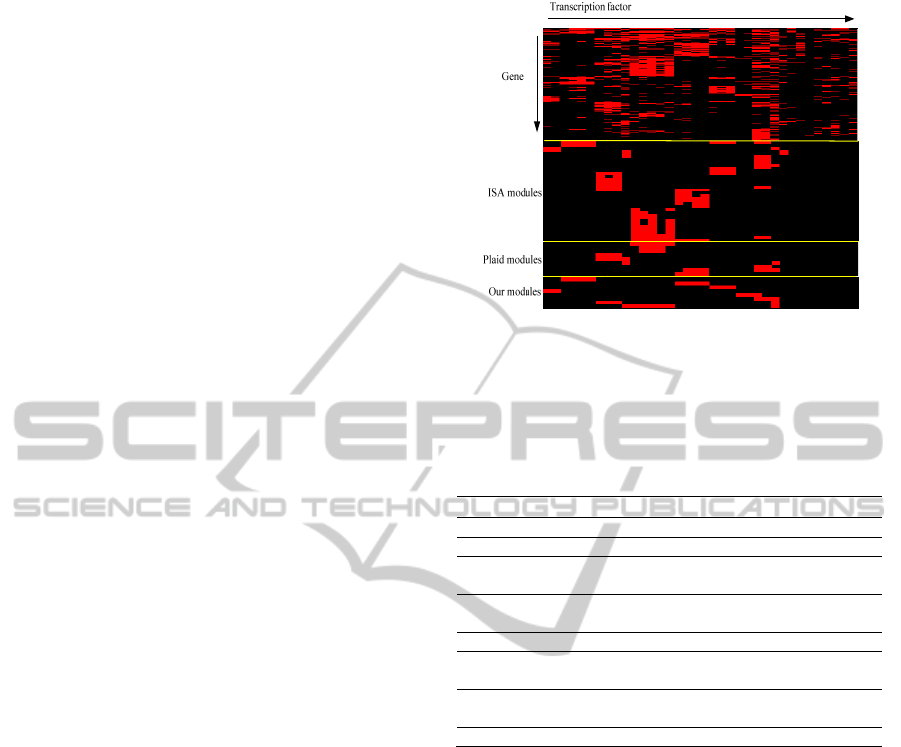
3.3.1 Comparison with Biclustering

To compare the performance of our module

identification method with that of biclustering

methods, we selected two widely used methods,

Plaid (Turner et al., 2005) and ISA (Ihmels et al.,

2004). Each method is carried out on the weighted

binding matrix, and finally, ISA, Plaid and our

method identify 36, 9 and 8 modules, respectively.

The overall binding pattern and three method’s

results are shown in Fig. 7, where the red unit

indicates binding occurrence. For our method, the

motif name and the number of genes identified in

each module are summarized in Table 1. The results

before and after TF refinement are presented as well.

In Fig. 7, it can be found that ISA is more

sensitive to the data matrix and provides quite

diverse biclustering results. We can see that there are

a lot of sub-modules in each dominant one.

Furthermore, its gene list is not well refined so that

the gene set in each module is too large to be further

investigated. The average number of genes is 1,923.

By comparing the results of ISA to the overall

binding pattern, the module containing TCF3 and

TCF4 is missed. Plaid provides isolated but

AP1

JUNAP1

GATA1

GATA4

GATA3

GATA2

E2F1

E2F4

E2F6

MYB

ELF1

GABPA

ELK1

ETS1

ELK4

MYC

cMYCL

cMYC

MAX

FOXA1L

FOXA2

FOXA1

TCF3

TCF4

AP2alpha

P2gamma

SP1

BMYB

STAT4

nMYC

TCF12

RMYB

CEBPAP1

CEBPB

NF1

FOXO1

Figure 7: Co-association patterns for multiple motifs and

identified modules of ISA, Plaid and our proposed

method.

Table 1: Summary of identified co-regulatory modules.

Module Gene* Motif name†

1 207/2200 AP1, JUNAP1, (TCF12)

2 588/4875 AP2alpha, AP2gamma, [SP1]

3 720/7961

ELF1 ELK1 ELK4 ETS1 GABPA

MYB [SP1] (FOXO1 BMYB)

4 610/4990

FOXA1 FOXA1L FOXA2

(CEBPAP1 CEBPB RMYB STAT4)

5 642/6466 E2F1, E2F4, E2F6, SP1

6 256/2849

GATA1, GATA2, GATA3, GATA4,

(NF1)

7 333/2775

MAX, MYC, cMYC, cMYCL,

(nMYC)

8 152/544 TCF3, TCF4, [AP2alpha]

*selected gene set/original gene set; † (.) denotes the deleted

TFs after sampling while [.] denotes the added TFs.

dominant modules. The number of genes in

individual module is 600 on average. It provides a

clear picture about the main modules with strong co-

regulation. However, it did miss some less dominant

but still important modules, i.e. modules 1, 4, 6 and

8 in Table 1. Our method not only captures all

important modules reported by ISA and Plaid, but it

also identifies their missed modules. TF refinement

plays quite an important role in the results

improvement. For example, without TF deletion, we

would include some noisy TFs like FOXO1 and

BMYB in module 3, which is not covered by

biclustering methods. ISA and Plaid also report that

AP2alpha and AP2gamma should be combined with

SP1 as a module, which is missed by clustering step.

Another significant advantage of our method is that

we can provide rank information in each module for

further gene selection.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

114

3.3.2 Result Interpretation

To better understand the regulation mechanism of

this breast cancer case study, we used functional

annotations to investigate co-regulatory modules, as

shown in Fig. 8. It is not strange that AP1 and

JUNAP1 are grouped together. It is known that

increased c-Jun activity is sufficient to trigger

apoptotic cell death (Bossy-Wetzel et al., 1997) and

plays an important role in the apoptosis pathway in

cancer (Bjornsti and Houghton, 2004). In module 2,

there is evidence for the co-existence of transcription

factors AP2 and SP1 in the promoter region of some

important genes in breast cancer (Liu et al., 2009).

ELF1, ELK1, ELK4, ETS1 and GABPA, a group of

ETS family TFs, are grouped with MYB and SP1 by

support of high score common genes in Module 3.

ETS1 activity is modulated by interactions with a

number of factors, including SP1 and MYB

(Wasylyk et al., 2002). FOXA1 and FOXA2 seem to

have at least in part redundant roles and modulate

the transcriptional activity of nuclear hormone

receptors (Bochkis et al., 2012). Module 5 is the

second largest module in this study. The fact that

promoters of growth and cell cycle regulated genes

frequently carry binding sites for transcription

factors of the E2F families and SP1 provides

evidence for what we observed in this module. DNA

repair, DNA replication and cell cycle are the top

functional groups enriched with p-value 4.75e-9,

1.59e-9 and 4.47e-6, respectively. This is consistent

to the report that E2F directly links cell cycle

progression with the coordinate regulation of genes

essential for both the synthesis of DNA as well as its

surveillance (Ren et al., 2002). Module 6 is

regulated by GATA family. While, in this data set,

the GATA related motifs are extracted from ChIP-

Seq file of GATA3, recently identified as one of the

three genes mutated in >10% of breast cancers.

Module 7 promotes a pair of well-known tumor

Figure 8: Identified 8 regulatory modules in the breast

cancer study.

related TFs, MYC and MAX. The transcriptionally

active MYC/MAX dimer promotes cell proliferation

as well as apoptosis (Amati and Land, 1994). In

Module 8 AP2alpha are combined with TCF3 and

TCF4 with high confidence. It is reported that AP-

2α inhibits β -catenin/TCF4 transcriptional activity

in colorectal cancer cells (Li and Dashwood, 2004),

might serve as a novel therapeutic target in cancers

with Wnt signalling.

4 DISCUSSIONS

In this study, we proposed a statistical method to

identify gene co-regulatory modules with multiple

ChIP-Seq experiments. However, the false positive

rate in genes identified from ChIP-Seq study still

needs some effort to improve. For example,

researchers are greatly interested in cancer

recurrence by using different technologies on

multiple data sets to compare different features of

genes in more than one treatment groups. A proper

way is to incorporate gene expression or RNA-Seq

data in the module identification process. With

multiple gene expression samples belonging to early

recurrence or late recurrence in cancer treatment, we

could identify co-regulated and differentially

expressed genes modules. This would link the

physical protein-DNA binding to functional

expression of target genes more intensely. Further, if

combined with time course expression data, it would

help us uncover the regulatory mechanism of

specific drug for cancer treatment.

5 CONCLUSIONS

In this study, we have developed a statistical scheme

to identify co-regulatory gene modules from

multiple ChIP-Seq experiments of TFs. We

developed a statistical model to calculate scores for

the target genes regulated by individual TF. The

TFBS distribution shows that it is condition specific

under different environment. Then, an MCMC

approach is proposed for co-regulatory module

identification. We have used a breast cancer case

study to show that our method is more advanced

than biclustering technology. Finally, through

functional annotations, it is shown that the identified

genes and TFs in each module are closely related by

their common functions, and different modules

participate in different functional roles in the

development of breast cancer.

StatisticalIdentificationofCo-regulatoryGeneModulesusingMultipleChIP-SeqExperiments

115

ACKNOWLEDGEMENTS

This work is supported in part by National Institutes

of Health (NIH) [CA149653, CA149147 and

CA164368].

REFERENCES

Amati, B. and Land, H. (1994) Myc-Max-Mad: a

transcription factor network controlling cell cycle

progression, differentiation and death, Current opinion

in genetics & development, 4, 102-108.

Bailey, T. L., et al. (2006) MEME: discovering and

analyzing DNA and protein sequence motifs, Nucleic

acids research, 34, W369-373.

Bjornsti, M. A. and Houghton, P. J. (2004) The TOR

pathway: a target for cancer therapy, Nature reviews.

Cancer, 4, 335-348.

Bochkis, I. M., et al. (2012) Genome-wide location

analysis reveals distinct transcriptional circuitry by

paralogous regulators Foxa1 and Foxa2, PLoS

genetics, 8, e1002770.

Bossy-Wetzel, E., Bakiri, L. and Yaniv, M. (1997)

Induction of apoptosis by the transcription factor c-

Jun, The EMBO journal, 16, 1695-1709.

Cheng, C., Min, R. and Gerstein, M. (2011) TIP: a

probabilistic method for identifying transcription

factor target genes from ChIP-seq binding profiles,

Bioinformatics, 27, 3221-3227.

Dunham, I., et al. (2012) An integrated encyclopedia of

DNA elements in the human genome, Nature, 489, 57-

74.

Frey, B. J. and Dueck, D. (2007) Clustering by passing

messages between data points, Science, 315, 972-976.

Gerstein, M. B., et al. (2012) Architecture of the human

regulatory network derived from ENCODE data,

Nature, 489, 91-100.

Heinz, S., et al. (2010) Simple combinations of lineage-

determining transcription factors prime cis-regulatory

elements required for macrophage and B cell

identities, Molecular cell, 38, 576-589.

Hurtado, A., et al. (2011) FOXA1 is a key determinant of

estrogen receptor function and endocrine response,

Nature genetics, 43, 27-33.

Ihmels, J., Bergmann, S. and Barkai, N. (2004) Defining

transcription modules using large-scale gene

expression data, Bioinformatics, 20, 1993-2003.

Li, Q. and Dashwood, R. H. (2004) Activator protein

2alpha associates with adenomatous polyposis

coli/beta-catenin and Inhibits beta-catenin/T-cell factor

transcriptional activity in colorectal cancer cells, The

Journal of biological chemistry, 279, 45669-45675.

Liu, R., et al. (2009) Transcription factor specificity

protein 1 (SP1) and activating protein 2alpha (AP-

2alpha) regulate expression of human KCTD10 gene

by binding to proximal region of promoter, The FEBS

journal, 276, 1114-1124.

McLean, C. Y., et al. (2010) GREAT improves functional

interpretation of cis-regulatory regions,

Nature

biotechnology, 28, 495-501.

Park, P. J. (2009) ChIP-seq: advantages and challenges of

a maturing technology, Nature reviews. Genetics, 10,

669-680.

Ren, B., et al. (2002) E2F integrates cell cycle progression

with DNA repair, replication, and G(2)/M

checkpoints, Genes & development, 16, 245-256.

Ross-Innes, C. S., et al. (2010) Cooperative interaction

between retinoic acid receptor-alpha and estrogen

receptor in breast cancer, Genes & development, 24,

171-182.

Salmon-Divon, M., et al. (2010) PeakAnalyzer: genome-

wide annotation of chromatin binding and

modification loci, BMC bioinformatics, 11, 415.

Schultz, D. J., et al. (2010) Anacardic acid inhibits

estrogen receptor alpha-DNA binding and reduces

target gene transcription and breast cancer cell

proliferation, Molecular cancer therapeutics, 9, 594-

605.

Segal, E., et al. (2003) Module networks: identifying

regulatory modules and their condition-specific

regulators from gene expression data, Nature genetics,

34, 166-176.

Stender, J. D., et al. (2010) Genome-wide analysis of

estrogen receptor alpha DNA binding and tethering

mechanisms identifies Runx1 as a novel tethering

factor in receptor-mediated transcriptional activation,

Molecular and cellular biology, 30, 3943-3955.

Su, J., Teichmann, S. A. and Down, T. A. (2010)

Assessing computational methods of cis-regulatory

module prediction, PLoS computational biology, 6,

e1001020.

Turner, H. L., et al. (2005) Biclustering models for

structured microarray data, IEEE/ACM transactions on

computational biology and bioinformatics / IEEE,

ACM, 2, 316-329.

Wasylyk, C., et al. (2002) Sp100 interacts with ETS-1 and

stimulates its transcriptional activity, Molecular and

cellular biology, 22, 2687-2702.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

116