Non-rigid Surface Registration using Cover Tree based Clustering

and Nearest Neighbor Search

Manal H. Alassaf

1, 2

, Yeny Yim

and James K. Hahn

Department of Computer Science, George Washington University, Washington DC, U.S.A.

Department of computer science, Taif University, Taif, Saudi Arabia

Samsung Electronics, Suwon, Geonggi-Do, Republic of Korea

Keywords: Non-rigid Registration, Iterative Closest Point Algorithm, ICP, Cover Tree, Clustering, Nearest Neighbor

Search.

Abstract: We propose a novel non-rigid registration method that computes the correspondences of two deformable

surfaces using the cover tree. The aim is to find the correct correspondences without landmark selection and

to reduce the computational complexity. The source surface S is initially aligned to the target surface T to

generate a cover tree from the densely distributed surface points. The cover tree is constructed by taking

into account the positions and normal vectors of the points and used for hierarchical clustering and nearest

neighbor search. The cover tree based clustering divides the two surfaces into several clusters based on the

geometric features, and each cluster on the source surface is transformed to its corresponding cluster on the

target. The nearest neighbor search from the cover tree reduces the search space for correspondence

computation, and the source surface is deformed to the target by optimizing the point pairs. The correct

correspondence of a given source point is determined by choosing one target point with the best

correspondence measure from the k nearest neighbors. The proposed energy function with Jacobian penalty

allows deforming the surface accurately and with less deformation folding.

1 INTRODUCTION

Iterative closest point algorithm (ICP) has been

widely used for registration of the surfaces (Besl and

McKay 1992; Zhang 1992). The ICP efficiently

calculates the transformation between two surfaces

by minimizing the Euclidean distance of the

correspondent point pairs. However, this distance

based measure can lead the optimization to the local

minima when the two surfaces are not close enough.

Another limitation of ICP algorithm is that it

requires searching all the points of a surface to

determine the best correspondence for a point of

another surface. Therefore, its time complexity is

O(n

The correspondence computation can be

accelerated using efficient nearest neighbor (NN)

search algorithms (Greenspan and Godin 2001). The

k-d tree has been widely used to limit the search

space to one set which is the nearest (Bentley 1975).

The k-d tree is a binary tree that is built by

repeatedly dividing the space into subspaces using

hyper planes. The k-d tree construction is simple and

it is quite efficient especially for low dimensional

data. However, its axis-aligned point division

regardless of point distribution can result in poor

search performance (Kumar et al. 2008). Greenspan

and Godins proposed a variant of k-d tree with

spherical triangular constraint that specifies the

neighborhood which lie within a sphere of radius 

(Greenspan and Godin 2001). Kumar et al. used the

vantage point tree (vp-tree) that divides the space by

using hyper shells with increasing radius instead of

using hyper planes (Kumar et al. 2008).

It is important to find the correct correspondence

as well as to accelerate the computation. To

determine the robust correspondences, Anguelov et

al. proposed a joint probabilistic model that enforces

the correlation between all correspondences in terms

of geodesic distance and penalizes the stretching and

twisting of the links between points (Anguelov et al.

2005). Huang et al. also constrained the geodesic

distances between points to be preserved by the

correspondences (Huang et al. 2008). They

initialized the candidate correspondences of all

points by finding the closest in Euclidean space and

579

H. Alassaf M., Yim Y. and K. Hahn J..

Non-rigid Surface Registration using Cover Tree based Clustering and Nearest Neighbor Search.

DOI: 10.5220/0004738405790587

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 579-587

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

feature space and pruned inconsistent mappings

based on the geodesic distance constraint.

In this paper, we propose an accurate non-rigid

ICP registration method that finds the correct

correspondences and reduces the computation

complexity with an efficient tree search. We address

the two challenges of the naïve ICP algorithm: the

optimization to the local minima and high time

complexity for correspondence computation. The

main idea of our method is to reduce the number of

possible correspondences from two surfaces by

using a hierarchical cover tree structure and find the

point pairs with the best correspondence measures.

A cover tree is constructed from the points of the

two surfaces which are target T and initially

matched source S. Given a point p on S, the

candidate corresponding points on T are determined

by traversing the cover tree and finding the nearest

neighbors from the tree instead of searching all the

points on T. This correspondence search is applied

for rigid ICP as well as non-rigid ICP. For rigid

registration, the nearest neighbors are determined by

dividing the tree nodes into several clusters. The

search space is limited to the leaf nodes of the

cluster which p belongs to. For non-rigid ICP, k-NN

search is performed on the tree to find the k-nearest

leaf nodes from T. We propose a correspondence

measure which takes into account local geometric

similarity.

For registration of the two surfaces, energy

minimization frameworks that minimize the distance

function between the surfaces have been proposed.

The distance energy function has been used to fit

one surface to another in conjunction with marker

error term between manually selected feature

correspondences. Allen et al. proposed a non-rigid

ICP algorithm that determines local affine

transformation per point by optimizing the distance

function (Allen et al. 2003). They added stiffness

term to force neighboring points to have similar

transformations and marker error term to avoid the

optimization to the local minima. Amberg et al.

optimized a similar energy function for fixed

stiffness and correspondences (Amberg et al. 2007).

They demonstrated accurate registration results for

the surface with a large missing region. Pauly et al.

optimized a distance function that calculated the sum

of the distances between a surface point and local

neighborhood of a point on another surface (Pauly et

al. 2005). Li et al. optimized the correspondence as

well as the deformation parameters (Li et al. 2008).

They also optimized a confidence weight of each

node in order to determine the correspondences

reliably and deal with the partial overlap problem of

the surfaces. In these related works, the stiffness

term has been effectively used to regularize the

deformation by minimizing the difference between

the deformation vectors of the adjacent points on the

surface. However, it does not deal with the problem

of the deformation folding which has the negative

Jacobian determinant of the deformation and results

in crossing of the adjacent deformation vectors.

To register the two surfaces with less

deformation folding while minimizing the distance

and stiffness, we propose a new energy function that

consists of the terms: fitting, stiffness, and Jacobian

penalty. The fitting term finds the deformation

vectors that minimize the error distances between

two corresponding point sets and the stiffness term

regularizes the deformation by minimizing the

difference between the deformation vectors of the

adjacent points on the surface. The Jacobian penalty

term penalizes negative Jacobian determinant of the

deformation (Rueckert et al. 2006). The Jacobian

matrix of the transformation has been applied to

guarantee the invertibility of the transformation

mainly for image registration (Vercauteren et al.

2009; Rohlfing et al. 2001). We adapt this penalty to

prevent the deformation folding on the surface.

The non-linear optimization of the two point sets

in the non-rigid registration of the surfaces is

computationally expensive since the number of

points on a surface is usually several thousands. For

efficient optimization, previous works proposed

reduced deformable models which divided the

surface into many small patches and transformed

them rigidly. (Huang et al. 2008; Li et al. 2008;

Chang and Zwicker 2009; Liu et al. 2009).

To closely match the two surfaces and thus

accelerate the optimization of the non-rigid ICP, we

propose a cluster-based locally rigid registration that

splits the two surfaces into clusters and transforms

each cluster on S to the corresponding cluster on T

by applying rigid ICP. All the points on T that

belong to the same cluster with the given source

point p considered in the corresponding cluster on T.

We refer to this registration method as a cluster-

based ICP. The previous reduced deformable models

have used regularly sampled points (Li et al. 2008;

Sumner et al. 2007), voxel grid structure (Chang and

Zwicker 2009), or clusters (Huang et al. 2008; Liu et

al. 2009). In the aspects of using the hierarchical

clustering for registration, our cluster-based ICP is

similar to that of (Huang et al. 2008; Liu et al. 2009).

However, our hierarchical clustering is based on

cover tree and our cluster-based ICP is applied to

initially match two input surfaces not for deformable

registration.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

580

2 METHOD

The non-rigid registration of the surfaces aims to

find the correct correspondences between S and T

and align S to T accurately by using the

correspondences. We propose a new non-rigid

registration method of the surface to achieve these

two goals. The proposed method consists of four

steps which are initial alignment, construction of the

cover tree, cluster-based ICP, and non-rigid ICP

registration. The two input surfaces are initially

matched by aligning the points with minimum z

depth, which are the positions of the nose tip in our

tested dataset, and scaling the surface S according to

the maximum ranges of the points on S and T. After

initial alignment, we construct a cover tree from the

points of both surfaces and use it for hierarchical

clustering and k-NN in the correspondence

computation of the cluster-based ICP and non-rigid

ICP, respectively. For the cluster-based ICP, we first

find the correspondence of each point on S among

the points in the same cluster which comes from T

and has the best correspondence measure. Once the

corresponding point sets on the two surfaces have

been determined, each cluster on S is locally

transformed to T by minimizing the error between

the two point sets. In the non-rigid ICP registration,

the candidate correspondences of a given point on S

are computed by looking for its k-NN in the cover

tree, which originate from T. A correct

correspondence is chosen by finding the best

correspondence measure among the k nearest points.

With the two correspondent point sets, the proposed

method deforms S to T by optimizing the energy

function that includes a fitting term, a stiffness term,

and a Jacobian penalty term.

2.1 Use of Cover Tree

The cover tree is a leveled tree where levels are

decreased as the tree is descended (Beygelzimer et

al. 2006). Each node in the tree corresponds to a

point in dataset P. Let P

denote the points of P at

level i. The cover tree has three properties of

nesting, covering, and separation. The nesting

property indicates that a point at a level i should

appear at all the levels beneath it. The covering

property satisfies the condition that the distance

between a point q in P

i-1

and its parent in P

is at

most 2

. The separation property meets the condition

that the distance between two distinct points at the

same level is at least 2

(Fig. 2).

The construction of the cover tree takes O(n)

space and O(c

n log n) time complexity. The time

complexity does not only depend on the number of

points of the dataset n, but also on the expansion

constant c. Expansion constant is defined as the ratio

of the points in a sphere with the maximum radius r

over the points in a sphere with the radius of r/2

(Beygelzimer et al. 2006).

In this paper, we adopt the cover tree data

structure for hierarchical clustering and k-NN

search. By using the cover tree with its nesting,

covering, and separation properties, the problem of

finding the correct correspondence in the ICP

registration is reduced from searching all the points

on T to searching a subset of the points. This subset

of the points is represented as a cluster of the points

within -radius for cluster-based ICP and as k

nearest points for non-rigid ICP.

2.1.1 Cover Tree Construction

using Distance and Surface Normal

Originally, the cover tree is constructed by taking

into account the distance between the points. Even

though the distance based cover tree can be used for

clustering points, it is difficult to obtain meaningful

clusters from surfaces that are not flat and have

complex geometric shapes. In order to subdivide the

surface into meaningful clusters such that the points

in each cluster have similar geometric features, we

extend the tree construction method by considering

the angular difference between the surface normal

vectors of the points as well as the Euclidean

distance between the points. We define our new

distance metric as a function f of two terms; one for

the Euclidian distance between two points x and y, d,

and the other for the angle θ between the normal

vectors, as described in f(x,y)=d(x,y)+λ(1-cosθ (x,y)).

As the angle θ increases, the value of the second

term increases which makes the value of f increase.

As a result, the two points are located far away from

each other in the cover tree. If the two points have

the same surface normal, only d affects the value of f

and the two points will be located in the cover tree

according to the distance. The parameter λ is a

weighting factor that controls the effect of the angle

θ. The value λ is determined according to the

features of the surface. As λ increases, the effect of

the second term becomes larger and the surface will

be clustered into points with similar geometric

features. However, setting λ to max can partition the

points that belong to one anatomical feature into

many clusters with respect to the normal variations

in that feature as shown in Fig. 3. We set λ to 0.05

experimentally to divide the surface into meaningful

clusters which correspond to anatomical features. By

Non-rigidSurfaceRegistrationusingCoverTreebasedClusteringandNearestNeighborSearch

581

using the function f in the tree construction, a parent

q for a new point p should satisfy the following

condition f(p,q) ≤ 2

. Here, i is the level of the cover

tree where q is located. The span of the cover tree,

including the number of levels, is affected by f. This

proposed function f satisfies the properties of a

distance function in a metric space.

2.1.2 The Use of the Cover Tree

for Hierarchical Clustering

After the cover tree is built from the points of the

two surfaces, the points are divided into k disjoint

clusters by cutting the tree at the level i with k nodes

such that each of the k nodes is a root of a sub-tree

and each sub-tree is considered a cluster as shown in

Fig. 2. As a result, each cluster denoted by C

rooted at its center, and the neighbor points within a

radius  

from the center correspond to the leaf

nodes of the sub-tree.

2.1.3 The Use of the Cover Tree for NN

The correspondence computation can be formulated

as a NN search problem in naïve ICP due to the fact

that it is based on the distance between the points.

the NN search problem, the dataset P of n points is

pre-processed such that one can find the nearest

neighbor point p of a given query point q with the

minimum distance d(q, p). The constructed cover

tree is used to find the k-NN points. Given a point

p ∊ P, the nearest points are determined by searching

the children list Q of p and finding a point with the

minimum error d(p,Q) =

min

∈

d(p,q). The error is

calculated with respect to the distance and angular

difference of the normal vectors. The exact k-NN

points are determined by sorting the errors between

p and q and finding the k points with the smallest

error. The NN search takes O(c

log n) time

(Beygelzimer et al. 2006).

2.2 Cluster-based ICP Registration

Rigid registration has been applied to compensate

the translational and rotational mismatch between

two surfaces. Recently, local rigid or affine

registration was used for reduced deformable model

(Chang and Zwicker 2009; Huang et al. 2008; Li et

al. 2008). By reducing the degrees of freedom for

optimization while considering the rigidity, S can be

deformed to T quickly and accurately. The proposed

cluster-based ICP method calculates the local rigid

transformations from several clusters which are

partial patches of the surfaces. It is used to provide a

good initial match for non-rigid registration.

2.2.1 Correspondence Computation

To find the correspondence of a point p on S among

the points on T, two surfaces are divided into

multiple clusters by cover tree based hierarchical

clustering described in Section 2.1.2. Only the points

in the same cluster with the p are considered as

candidates. For all candidate points q which come

from T, the correspondence measure is calculated

using E

Corr

as in Eq. 1 and the point with the

minimum measure E

Corr

is determined as the

correspondence of p:

IsometricNormalDistCorr

EEEqpE









),(

(1)

The first term E

Dist

is used to find the closest point

by calculating the Euclidean distance between two

points. The correspondence computation only using

Euclidean distance is not sufficient even though

rough correspondence is established by cover tree

based hierarchical clustering. To find more reliable

correspondence, we calculate two local geometric

measures. E

Normal

which is the angle between the

normal vectors is used to penalize the points in the

opposite surface direction. E

Isometric

is defined to

enforce the two corresponding points that have

similar connectivity with the adjacent points. This

measures the absolute difference between the length

of the connecting edges of p and that of the

connecting edges of q. The parameters, α and β,

control the effect of E

Normal

and E

Isometric

against E

Dist

As these parameters for local geometric features are

larger, the effect of E

Dist

decreases and the

determined corresponding point sets can slow down

the optimization. We set α and β to 0.05

experimentally in order to find the correspondence

that has similar geometric features while obtaining

the reasonable optimization performance.

2.2.2 Optimization

The transformation of each cluster is calculated by

minimizing the rigid registration error using Eq. 2,

where R and Tr are the rotation matrix and

translation vector, and p

and q

are the points on S

and T:







iiR

TrRqpE

)(

(2)

To reduce the discontinuity of the transformations

between clusters, the transformation of each point is

calculated by weighted averaging the rigid

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

582

transformations of the k nearest clusters. The weight

for each cluster is calculated in proportion to the

distance between the point and the center of each

cluster.

2.3 Non-rigid Registration

The proposed non-rigid ICP registration consists of

two steps. First, the correspondence of a given

source point is computed by searching k-NN in the

cover tree and finding a point with the minimum

correspondence measure. Second, once the two

corresponding point sets are determined, S is

deformed to T by minimizing the proposed energy

term so that the deformation is both accurate and

smooth, and has less deformation folding.

2.3.1 Correspondence Computation

For non-rigid registration of S to T, it is very

important to determine the correspondences reliably

and efficiently. To address this challenge, we

propose a method for correspondence computation

of non-rigid ICP registration. To find the

correspondence of a given point p on S, the search

space is limited to k-nearest points on T by using the

cover tree based k-NN search as described in

Section 2.1.3. Only k points which are the nearest

from p are considered as candidates. As k is larger,

more points are included as candidates and the

computation time of E

Corr

will increase. When k is

too small, possible candidates that might have the

best correspondence measure could be missed even

though the computation will be faster. We set k to 10

experimentally to find the best correspondence

among the sufficient number of candidates while

reducing the computation time. For all candidate

points, the correspondence measure is calculated

using Eq. (1) as described in Section 2.2.1, and the

point with the minimum measure E

Corr

is determined

as a correspondence.

2.3.2 Optimization

After determining two correspondent point sets from

S and T as P and P’, respectively, the points in P are

deformed to the points in P’. The deformation D is

calculated by minimizing the registration error E

described in Eq. 3:







JacobianSmoothFitiN

EEEE



(3)

The first term E

Fit

measures the accuracy of

alignment by calculating the distance between P’

and D(P). The second error term E

Smooth

regularizes

the deformation by minimizing the sum of

differences of the deformation between adjacent

points as shown in Eq. 4:







)(

)()())((

pNp

ijiSmooth

pDpDpDE

(4)

The third term E

Jacobian

regularizes the deformation

by assigning penalty to the points with the negative

Jacobian determinant. To impose penalty to the

points with negative Jacobian and avoid the folding

of the deformation, E

Jacobian

is defined by Eq. 5:

)))((1log())(( DJDetcpDE

iJacobian





(5)

where Det(J) is the determinant of the Jacobian

matrix J, and c is the constant that adjusts the effect

of the negative Jacobian term. The constant c is

proportional to the distance between p

and its

farthest neighbor. This Jacobian penalty term is

applied only for the points with the negative

Jacobian. To minimize E

between two

corresponding point sets, the Levenberg Marquardt

optimization algorithm is applied (Marquardt 1963).

γ and δ are the parameters that adjust the effect of

stiffness term and Jacobian term, respectively. If the

stiffness parameter γ is small, the optimization

converges quickly to the closest point based on the

fitting term. However, the surface mesh becomes

very irregular and bumpy. As γ is larger, the

deformation is smoother but the optimization

becomes slower and the surface may shrink. We set

γ to 1. The parameter δ for Jacobian term is set to 1

if the point has a negative Jacobian. Otherwise the

value is set to 0. The optimization ends when the

termination condition is met. If the reduced error

measure after each iteration i, E

- E

i-1

, is less than

5% of the error measure E

, it is considered that the

optimization converges to the optimum. By

penalizing the deformation with stiffness term and

Jacobian term, the proposed optimization regularizes

the deformation so that the deformed surface has

smooth deformation with less folding.

3 EVALUATION METHODS

To evaluate the proposed method, we tested three

different datasets; CT-simulated CT dataset, CT-

Kinect dataset, CT-CT dataset. For simulated

dataset, we extracted 3D surface from CT

(Computed Tomography) scans using Marching

Cube Algorithm (Lorensen and Cline 1987) and

Non-rigidSurfaceRegistrationusingCoverTreebasedClusteringandNearestNeighborSearch

583

used it as the source surface S. We simulated the

target surface T by warping the jaw and nose of S

using thin-plate spline warping (Bookstein 1989).

For CT-Kinect dataset, S was generated from the 2D

color image and depth map obtained from Microsoft

Kinect camera. A 3D surface with color was

generated from depth map by back-projecting the 2D

pixel positions. The surface T was extracted from

the CT scans. For CT-CT dataset, we extracted S

and T from two CT datasets which were acquired

from two different subjects. We also tested the

registration accuracy of noisy CT datasets in order to

demonstrate the robustness of the proposed method

to noisy dataset. Table 1 shows the number of points

in each tested dataset.

To demonstrate the effect of the proposed cover

tree-based clustering method, we compared our

clustering method with two k-means clustering

algorithms that initialize the cluster centers in

different ways. The first uses manually selected

initial centers (k-means manual) (Lloyd 1982) and

the second detects the centers automatically using k-

means++ algorithm (k-means++) (Arthur and

Vassilvitskii 2007).

To evaluate the effect of the proposed

correspondence computation using cover tree, we

compared the proposed method with the naïve ICP

algorithm, ICP algorithm with k-means manual, ICP

algorithm with k-means++ in aspects of the

registration accuracy. To compare the three

clustering methods in the same condition, we used

the same number of the clusters obtained from the

proposed clustering method for k-means manual and

k-means++ seeds number. The proposed method cut

the cover tree at depth equals to 3. We implemented

the naïve ICP algorithm that finds the

correspondence of a point p on S by searching the

point with the minimum distance from p among all

the points on T. For cluster-based registration, the k-

means manual and k-means++ clusters are used in

comparison with proposed method. For non-rigid

ICP correspondence, a cover tree based NN search

was applied to the results of the cluster-based ICP of

three different clustering algorithms along with

naïve ICP.

We visualized the color-coded error surfaces in

which the color of each surface point indicates its

own error measure. The point was colored red if the

depth of a point on T is closer than the depth of the

corresponding point on the deformed S. The point

was colored green in the opposite case.

4 RESULTS

Fig. 1 shows the result of the proposed registration

method for three different datasets. The first row

shows that the overall shape of S near jaw and nose

was deformed to the simulated surface T accurately.

The details of the surface such as lips and eyes were

not preserved due to the lower resolution of original

surface and the effect of stiffness term during

optimization. The second row shows the noisy

surface S acquired from Microsoft Kinect camera

was deformed to T closely. Even though the two

surfaces obtained from different subjects by

different devices have distinctively different nose

and mouth shapes, the color-coded error map shows

that entire face of S was deformed to T correctly.

There was a subtle difference between T and

deformed S near teeth and nose of the subject. The

third row shows that the two face surfaces acquired

from two different subjects were registered

accurately after applying the proposed method. The

surface S with open mouth and low nose tip was

deformed to the surface with closed mouth and high

nose tip that has little difference with T.

The registration errors of three methods with

clustering were lower than that of Naïve ICP. The

proposed method with cover tree led to the lowest

reduction rate against Naïve ICP. Especially in

Kinect-CT dataset with irregular point distribution,

the reduction rate of the proposed method was 28%

while those of k-means manual and k-means++ were

26% and 22%, respectively. There was no

significant difference in simulated CT and CT-CT

datasets which have relatively regular point

distributions. Fig. 4 shows the registration accuracy

of the noisy datasets compared to original dataset.

The registration errors of the k-means manual and k-

means++ increased in two noisy datasets, as opposed

to the cover tree method. The registration error

decreased in simulated dataset with the cover tree

method. Also, the increase of the error was the

smallest with cover tree in CT-CT dataset.

The proposed method which optimizes

Jacobian penalty term led to the smallest percentage

of the negative Jacobian in simulated dataset and

CT-CT datasets as shown in Table 2.

Table 3 shows the processing time for

clustering the points and finding correspondences by

using three different methods. The time for cover

tree based clustering was shorter than those for two

k-means clustering methods. Once the cover tree is

constructed in a pre-processing step, the proposed

clustering method only takes time for cutting the tree

at a specific level and labelling the points. While, k-

means manual and k-means++ require iterative

calculation of the distances until stabilization.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

584

5 CONCLUSIONS

In this study, we proposed a non-rigid surface

registration method which computes the

correspondence between two surfaces accurately and

efficiently. The cover tree based hierarchical

clustering and NN search were utilized to reduce the

search space for correspondence points in ICP. This

reduced the computational complexity of the

correspondence computation. In addition,

registration accuracy of the proposed method is

better than the methods using conventional

clustering, especially in the noisy dataset. The

proposed negative Jacobian term of energy function

led to registration with less deformation folding.

Extending cover tree construction to consider

orientation of the surface points introduced a hybrid

similarity measure for ICP that allows capturing

more reliable correspondence points.

A cover tree-based hierarchical clustering

reduced the search space of the correspondence

candidates of each point on S from all points on T to

only (1-c

)/(1-c

) of the points, where d is the depth

of the sub-tree that corresponds to a cluster.

Therefore, the complexity was reduced from O(n

)

to O(n(1-c

)/(1-c

)). Proof of this reduction can be

found in appendix 1. In addition, a cover tree-based

NN search found the k correspondence candidates of

every point on S from the points on T. The search

space of the correspondence computation for a point

was limited to k and the complexity was reduced to

O(c

n log n). The proposed cover tree based NN

search was not compared with the other NN search

algorithms such as k-d tree or v-p tree. In the future,

we consider doing this comparison.

We proposed an optimization function for non-

rigid ICP algorithm, including fitting term, stiffness

term, and Jacobian term. The proposed optimization

function with Jacobian penalty term regularized the

deformation so that the resulted surface has smooth

deformation with less folding. The results showed

that the proposed method led to the smallest ratio of

the negative Jacobian compared to the other non-

rigid ICP methods. The results also showed that the

ratio of the negative Jacobian was reduced by

incorporating proposed negative Jacobian term.

One interesting result was that the proposed

method showed the best results in CT-Kinect

datasets in aspects of registration accuracy and

percentage of the negative Jacobian. The Microsoft

Kinect camera has relatively poor perception

accuracy for the depth and thus the reconstructed

surface from the depth map was very noisy and

bumpy. This result demonstrated that the cover tree

based hierarchical clustering was suitable for the

noisy datasets. We improved the registration

accuracy by taking into account the distribution and

orientation of the point for tree construction.

REFERENCES

Allen, B., Curless, B., & Popović, Z., 2003. The space of

human body shapes: reconstruction and

parameterization from range scans. In ACM.

Amberg, B., Romdhani, S., & Vetter, T., 2007. Optimal

step nonrigid icp algorithms for surface registration. In

IEEE.

Anguelov, D., Srinivasan, P., Pang, H. C., Koller, D.,

Thrun, S., & Davis, J., 2005. The correlated

correspondence algorithm for unsupervised

registration of nonrigid surfaces. In Advances in

neural information processing systems.

Arthur, D., & Vassilvitskii, S., 2007. k-means++: The

advantages of careful seeding. In Society for Industrial

and Applied Mathematics.

Bentley, J. L., 1975. Multidimensional binary search trees

used for associative searching. In Communications of

the ACM.

Besl, P. J., & McKay, N. D., 1992. A method for

registration of 3-D shapes. In IEEE Transactions on

pattern analysis and machine intelligence.

Beygelzimer, A., Kakade, S., & Langford, J., 2006. Cover

trees for nearest neighbor. In ACM.

Bookstein, F. L. 1989. Principal warps: Thin-plate splines

and the decomposition of deformations. In IEEE

Transactions on Pattern Analysis and Machine

Intelligence.

Chang, W., & Zwicker, M., 2009. Range scan registration

using reduced deformable models. In Wiley Online

Library.

Greenspan, M., & Godin, G., 2001. A nearest neighbor

method for efficient ICP. In IEEE.

Huang, Q. X., Adams, B., Wicke, M., & Guibas, L. J.,

2008. NonRigid Registration Under Isometric

Deformations. In Wiley Online Library.

Kumar, N., Zhang, L., & Nayar, S., 2008. What is a good

nearest neighbors algorithm for finding similar patches

in images? In Computer Vision–ECCV.

Li, H., Sumner, R. W., & Pauly, M., 2008. Global

Correspondence Optimization for NonRigid

Registration of Depth Scans. In Wiley Online Library.

Liu, Y., Li, L., Xie, X., & Wei, B., 2009. Range image

registration using hierarchical segmentation and

clustering. In IEEE.

Lloyd, S., 1982. Least squares quantization in PCM. In

IEEE Transactions on Information Theory.

Lorensen, W. E., Cline, H. E. 1987. Marching cubes: A

high resolution 3D surface construction algorithm. In

ACM.

Marquardt, D. W., 1963. An algorithm for least-squares

estimation of nonlinear parameters. In Journal of the

society for Industrial and Applied Mathematics.

Non-rigidSurfaceRegistrationusingCoverTreebasedClusteringandNearestNeighborSearch

585

Microsoft Kinect. http://www.microsoft.com/presspass/

presskits/xbox/.

Pauly, M., Mitra, N. J., Giesen, J., Gross, M., & Guibas, L.

J., 2005. Example-based 3D scan completion. In

Eurographics Association.

Rohlfing, T., & Maurer Jr, C. R., 2001. Intensity-based

non-rigid registration using adaptive multilevel free-

form deformation with an incompressibility constraint.

In Medical Image Computing and Computer-Assisted

Intervention–MICCAI.

Rueckert, D., Aljabar, P., Heckemann, R. A., Hajnal, J. V.,

& Hammers, A., 2006. Diffeomorphic registration

using B-splines. In Medical Image Computing and

Computer-Assisted Intervention–MICCAI.

Sumner, R. W., Schmid, J., & Pauly, M., 2007. Embedded

deformation for shape manipulation. In ACM.

Vercauteren, T., Pennec, X., Perchant, A., & Ayache, N.,

2009. Diffeomorphic demons: Efficient non-

parametric image registration. In NeuroImage.

Zhang, Z., 1992. Iterative point matching for registration

of free-form curves and surfaces. In International

journal of computer vision.

APPENDIX

Claim 1: The correspondence computation using cover

tree-based hierarchical clustering reduces the time

complexity of Cluster-based ICP from O(n

) to O(n(1-

)/(1-c

)) where c is the expansion constant of the cover

tree and d is the depth of the sub-tree that corresponds to a

cluster.

Proof:

We know that each node in the cover tree has at most

children (Beygelzimer et al. 2006). Assume l is the

number of points in the largest cluster. Let’s assume the

worst case, when the constructed cover tree is balanced

and each node has exactly c

children. Cutting the cover

tree at level i with k nodes, each cluster contains one root

node of the sub-tree and all its decedent nodes in all the

lower levels from the level i down to the leaves level j. Let

d denote the depth of the sub-tree, i.e. d = j-i. The number

of the nodes in each cluster is calculated as follows: At

level i, d is 0 and each cluster has one root node. The total

number of nodes at level i is (c

)

=1. At the next level i-1,

d is 1 and each cluster has at most c

nodes which are the

children of the root node. The total number of nodes at

level i-1 is (c

)

= c

. As the level decreases by 1, d

increases by 1 and each cluster at each level has at most

)

nodes. Therefore, the total number of the nodes in a

cluster is calculated using Eq. (1).

Thus, the number of the nodes l in the largest cluster is

upper bounded by (1-c

)/(1-c

) and the time complexity

of ICP is upper bounded by O(n(1-c

)/(1-c

)) ■.

Figure 1: The registration results of the proposed method for simulated dataset (first row), Kinect-CT dataset (second row),

and CT-CT dataset. The initial source surfaces S (leftmost) were registered to the target surfaces T (3

column) by cluster-

based ICP and non-rigid ICP. The differences between the deformed surface (2

column) and the target were represented to

color-coded error map (4

column).

4404142 4

4d 4

() () () ...()

(1-c )/(1-c )

cc c c c



 





VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

586

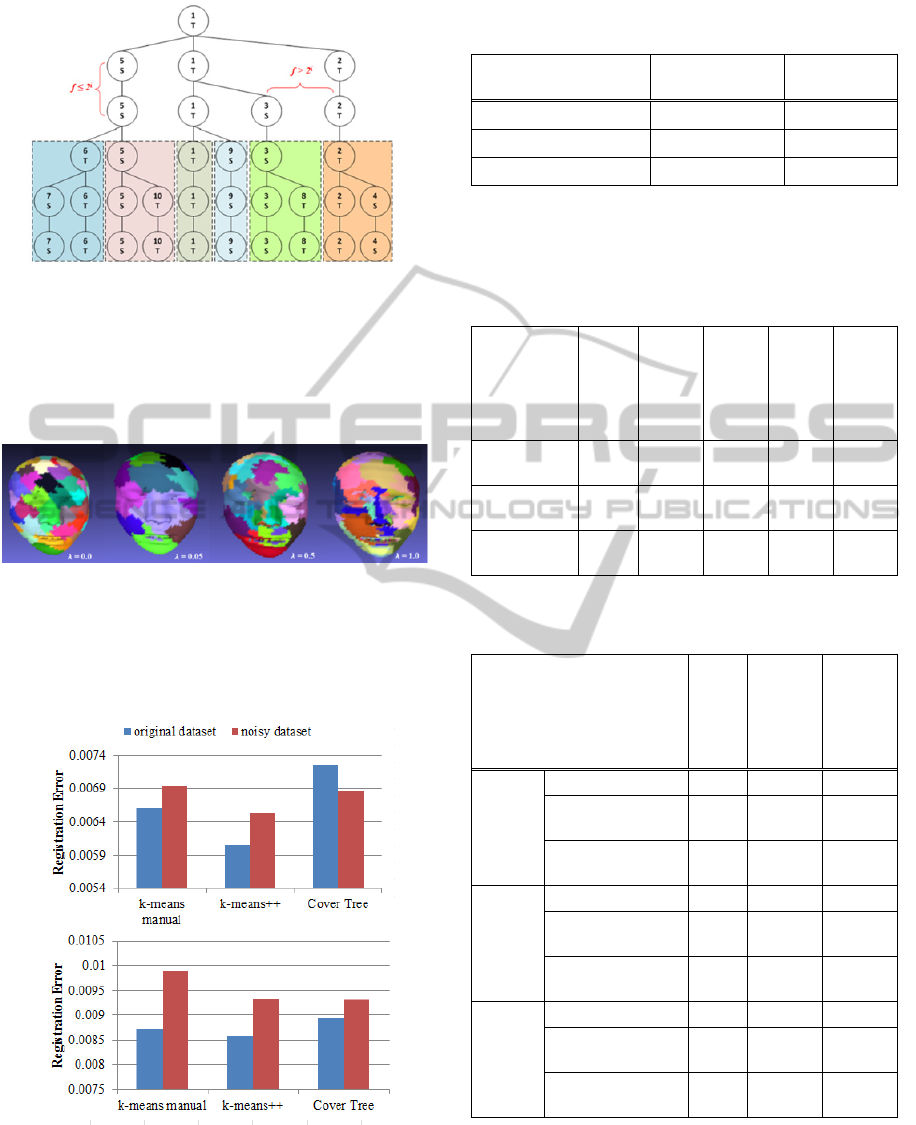
Figure 2: Example of clustering ten points using cover tree.

When we cut the tree at depth equals to 3, the ten points

are clustered into six clusters as indicated by shaded

squares. The points of each cluster correspond to the leaf

nodes of each sub-tree. The number and the character

written in each node indicate the order of insertion and the

original surface that this point belongs to, either T or S.

Figure 3: The effect of the λ weight of the angular term in

the cover tree construction can be shown by clustering at

depth equals to 3 in a face dataset. Left image: Traditional

cover tree constructed with distance only. Three images in

the right: Proposed cover tree construction with distance

and angular term with different λ weights.

Figure 4: The comparison of the registration accuracy

between original and noisy datasets: simulated dataset

(top) and CT-CT dataset (bottom).

Table 1: The number of surface points of the three tested

datasets.

Number of

points in S

Number of

points in T

Simulated CT Dataset 3067 2906

CT-Kinect Dataset 4591 3145

CT-CT Dataset 3145 4076

Table 2: The percentage of the points with negative

Jacobian when applying 4 different non-rigid ICP methods

to three datasets. The proposed method was tested with

and without applying Jacobian term by adjusting the

weighting factor δ.

(unit: %)

Naïve ICP

ICP with k-

means

manual

ICP with k-

means++

ICP with

cover tree

(

δ=0

)

ICP with

cover tree

(

δ=1

)

Simulated

CT Dataset

13.8 10.23 9.83 9.22 8.21

CT-Kinect

Dataset

19.98 15.09 16.67 10.97 11.16

CT-CT

Dataset

6.68 6.75 6.05 5.07 4.61

Table 3: Processing Time of Clustering and

Correspondence Computation.

(unit: sec)

k-means

manual

k-means++

Proposed

clustering

Simulated CT

Dataset

Clustering 2.153 1.857 0.936

Correspondence

(cluster-based ICP)

0.501 0.516 0.577

Correspondence

(non-rigid ICP)

69.68

212.645 81.370

CT-Kinect

Dataset

Clustering 1.185 0.921 0.671

Correspondence

(cluster-based ICP)

0.967 0.531 0.530

Correspondence

(non-rigid ICP)

309.5

150.104 107.547

CT-CT

Dataset

Clustering 1.560 2.714 0.686

Correspondence

(cluster-based ICP)

0.451 0.313 0.280

Correspondence

(non-rigid ICP)

122.0

75.926 78.405

Non-rigidSurfaceRegistrationusingCoverTreebasedClusteringandNearestNeighborSearch

587