
Assisting Navigation in Homogenous Fog
Mihai Negru and Sergiu Nedevschi
Computer Science Department, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
Keywords: Driving Assistance Systems, Fog Detection, Visibility Distance Estimation, Speed Recommendation.
Abstract: An important cause of road accidents is the reduced visibility due to the presence of fog or haze. For this
reason, there is a fundamental need for Advanced Driving Assistance Systems (ADAS) based on efficient
real time algorithms able to detect the presence of fog, estimate the fog’s density, determine the visibility
distance and inform the driver about the maximum speed that the vehicle should be traveling. Our solution
is an improvement over existing methods of detecting fog due to the temporal integration of the horizon line
and inflection point in the image. Our method performs in real time; approximately 50 frames per second. It
is based on a single in-vehicle camera and is able to detect day time fog in real time in a wide range of
scenarios, including urban scenarios.
1 INTRODUCTION
During the last decade a special attention was given
to advanced driving assistance systems. Nowadays
vehicles are equipped with active safety systems, in
order to reduce the number of traffic accidents. Thus
an important aspect, for avoiding accidents and
reducing the risk of accident, while driving, is the
ability of an advanced driving assistance system to
anticipate such risks and to notify the driver of the
hazardous situations. The National Highway Traffic
Safety Administration (NHTSA) states that the top
six most common causes of automobile crashes are:
distracted drivers, speeding, aggressive driving,
drunk driving, driver fatigue and weather
phenomena. In the case of driver inattention 80% of
accidents happen due to 3 seconds of distraction.
Even though there is a significant improvement in
road infrastructure the number of accidents caused
by extreme weather conditions is higher every year.
Among these conditions fog is considered to be the
most dangerous one because the visibility distance
decreases exponentially as fog density increases.
When the weather is affected by fog, drivers tend to
overestimate the visibility distances and drive with
excessive speed (Hautiere et al., 2006). For this
reason we developed a system for assisting the
driver in foggy situations. Our system is capable of
detecting the presence of fog in images, measuring
the visibility distance in such situations and
informing the driver about the maximum speed that
they should travel on the given road segment. An
important improvement of our method consists in
the fact that the horizon line and the inflection point
are detected frame-by-frame and then time filtered,
resulting in a very stable and reliable solution for fog
detection. Our solution performs in real time
(approximately 50 frames per second). It can be
ported easily on a modern smartphone or tablet,
making it an inexpensive and very accessible ADAS
solution. In addition the detection results could be
transmitted to a regional traffic information system
that gathers and distributes weather information in
real time.
2 RELATED WORK
Fog detection systems were studied in the past years
with the aim of detecting the presence of fog and
removing the fog effects from images. Pomerleau
(Pomerleau, 1997) estimates visibility in fog
conditions by means of contrast attenuation at road
markings in front of the vehicle. This approach
requires the presence and detection of road
markings. Another approach consists in the
combination of an in-vehicle camera and radar (Mori
et al., 2006). Based on Koschmieder’s law they
classify the fog density according to a visibility
feature of a preceding vehicle.
In (Bronte et al., 2009) a method for fog
detection based on the computation of the vanishing
619
Negru M. and Nedevschi S..
Assisting Navigation in Homogenous Fog.
DOI: 10.5220/0004740006190626
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 619-626
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

point is presented. The road lines are taken as
reference lines in order to compute the vanishing
point. After the vanishing point is found a
segmentation of the road and sky is performed. This
method is able to classify fog based on its density.
Object detection on foggy images is presented in
(Dong et al., 2011). The method uses a fixed camera
and performs object detection based on the
subtraction of the observed dense map and a
background depth map. The drawback of this
method is that it cannot be used in real traffic scenes,
where the background scenario is continuously
changing.
In (Pavlic et al., 2012) an approach based on
image descriptors and classification is used in order
to detect fog conditions. The image descriptors used
are Gabor Filters at different frequencies, scales and
orientations. The visibility distance estimation in fog
conditions is presented in (Hautiere et al., 2006).
Their algorithm is based on Koschmieder’s law and
is able to detect the visibility distance in day time
traffic scenarios. In order to assess if fog is present
in images they use a region growing procedure for
detecting the inflection point in the image. Knowing
the position of the inflection point and the horizon
line position (that is computed offline) they are able
to compute the visibility distance in the image.
Because accidents that happen during fog
conditions result in a high number of casualties,
there is a growing concern in providing assistance to
the drivers. One such approach was implemented by
the California Department of Transportation
(Berman et al., 2009). They have developed a fog
detection and warning system based on an array of
sensors able to detect fog. These sensors are
deployed every half mile on both direction of a
freeway. In addition this system is able to provide
drivers with information about the fog density and
the maximum speed that they should travel. The
information is displayed on Changeable Message
Signs. Although it is a very expensive system the
fact that the drivers are informed about the weather
conditions and speed limits reduced drastically the
number of accidents on this highway. Our intention
is to develop a more cost effective approach to the
problem of fog detection and to inform the driver
about the maximum speed on the given road
segment.
3 MODELING THE EFFECTS OF
FOG ON VISION
3.1 Koschmieder’s Law
In 1924, Koschmieder (Middleton, 1952) studied the
attenuation of luminance through the atmosphere
and proposed a relationship between the attenuation
of an object’s luminance L at distance d and the
luminance L
0
close to the object:
0
(1 )
kd kd
LLe L e
(1)
L
∞
is the atmospheric luminance and k is the
extinction coefficient. This equation states that the
luminance of an object seen through fog is
attenuated with an exponential factor e
-kd
; the
atmospheric veil obtained from daylight scattered by
fog between the object and the observer is expressed
by L
∞
(1-e
-kd
). By re-writing this equation and
dividing by L
∞
we obtain Duntley’s attenuation law
(Hautiere et al., 2006) that states that an object
having the contrast C
0
with the background is
perceived at distance d with contrast C:
0
0
()
kd kd
LL
CeCe
L
(2)
This law can be applied only in day light uniform
illumination conditions. From this expression the
meteorological visibility distance is derived (d
vis
):
“the greatest distance at which a black object, having
contrast (C
0
=1), of a suitable dimension can be seen
in the sky on the horizon”. In order for an object to
be barely visible, the International Commission on
Illumination has adopted a threshold for the contrast,
i.e. 5%. It results that:
13
log(0.05)
vis
d
kk
(3)
When dealing with images, the response function
of a camera can be applied to the Koschmieder’s
equation in order to model the mapping from scene
luminance to image intensity. Thus, the intensity
perceived in the image is the result of a function (f)
applied to equation (1):
1
kd kd
IfL Re A e
(4)
A
∞
is the sky intensity and R is the intrinsic pixel
intensity.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
620

3.2 Modelling the Camera in the
Vehicle Environment
Figure 1 presents a typical camera system mounted
inside a vehicle. The position of a pixel in the image
plane is given by its (u, v) coordinates, the position
of the optical center C is given by (u0, v0) and f
represents the focal length of the camera. Nowadays
cameras usually have square pixels, so the horizontal
pixel size tpu is equal to the vertical pixel size tpv,
(t
t
t
) thus we can introduce a new
constant denoted by αf/t
in order to express the
value of the focal length in pixels. The camera is
mounted at height H relative to the S(X, Y, Z)
coordinate system and θ represents the pitch angle.
Figure 1: The camera model in the vehicle environment.
From Figure 1 one can observe that the
horizontal line passing through the optical center
makes an angle θ with the z axis. Therefore it can be
expressed as:
0
tan
h
vv
(5)
In the case of a single camera, the flat world
hypothesis can be used to estimate the distance to
each line in the image (Negru and Nedevschi, 2013).
This hypothesis is used in the case of road scene
images, since a large part of an image is formed by
the road surface, which can be assumed to be planar.
So, the distance d of an image line v, can be
expressed by the following equation:
h
h
h
if v v
vv
d
if v v
(6)
Where
and v
h
represents the horizon line in
the image. The value of d from equation (6) will be
used in order to assess the visibility distance in fog
conditions.
4 METHOD DESCRIPTION
4.1 Estimation of the Visibility
Distance
In order to estimate the visibility distance we must
first examine the mathematical properties of the
Koschmieder’s law, presented in the previous
section. For estimating the extinction coefficient k
we must investigate the existence of an inflection
point in the image that will provide the basis for our
solution. By expressing d as in equation (6) and by
performing a change of variable, equation (4)
becomes:
(1 )
hh
kk
vv vv
IRe A e
(7)
If we take the derivative of I with respect to v,
taking into account that the camera response is a
linear function, one obtains:
2
()
h
k
vv
h
dI k
R
Ae
dv
vv
(8)
We know that objects tend to get obscured more
quickly when fog density increases. Moreover, the
maximum derivative decreases significantly and
deviates more substantially from the horizon line. So
the inflection point in the image can be found where
the derivative has a maximum value. By computing
again the derivative of I with respect to v, we get the
following equation:
2
3
()
2
h
k
vv
h
h
kRAdI k
e
dv v v
vv
(9)
Equation
0 has two possible solutions. We
search for a positive solution of k, so k=0 is not
acceptable. Thus the solution obtained is:
2( )
2
ih
i
vv
k
d
(10)
v
i
represents the position of the inflection point
in the image and d
i
represents its distance to the
camera.
If we are able to compute the position of the
inflection point and of the horizon line we can
compute the extinction coefficient from
Koschmieder’s law. If v
i
is greater than v
h
fog will
be detected in the image, otherwise we conclude that
there is no fog in the scene. From equations (3) and
(10) we can estimate the visibility distance in the
image:
AssistingNavigationinHomogenousFog
621
3
2( )
vis
ih
d
vv
(11)
Using this visibility distance and taking into
account the braking distances at various speeds, we
can infer the fog density and the maximum safe
driving speed of the vehicle should.
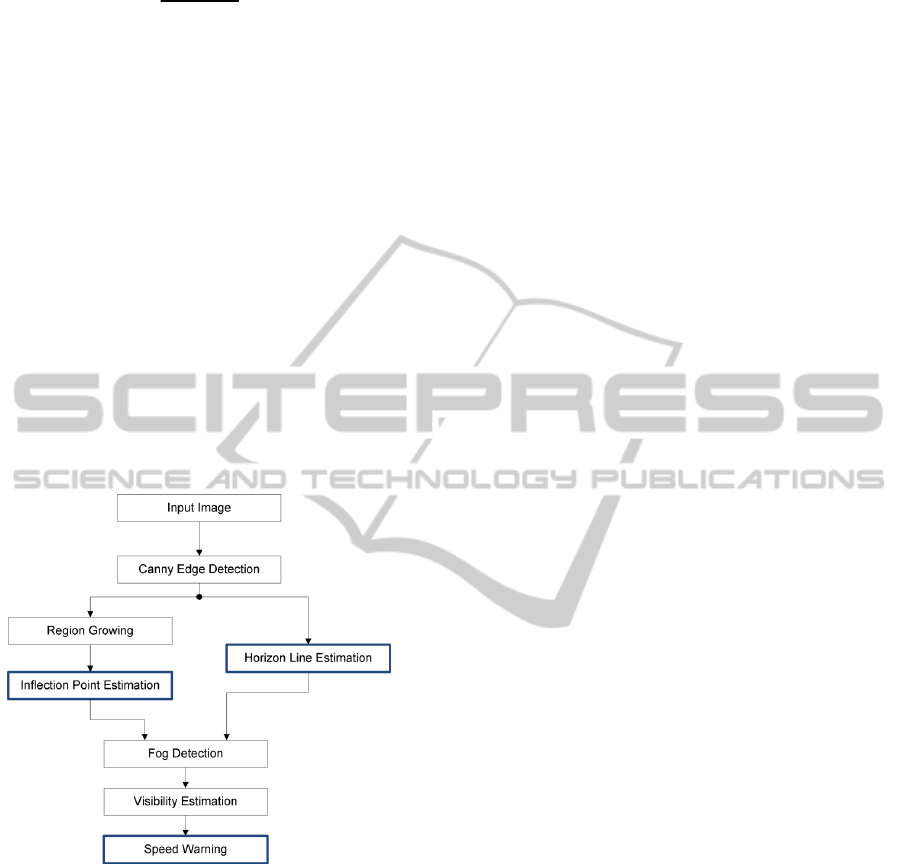
4.2 Algorithm Overview
The architecture of our framework is presented in
Figure 2. The main contributions of our work are in
the blue highlighted areas. Our method uses grey
scale images as input and is able to provide
information about the presence of fog in the image
and to estimate the maximum speed on the given
road segment. First we apply a Canny-Deriche edge
detector on the input image. Then we estimate the
horizon line and the inflection point in order to
assess whether fog is present in the image. If fog is
present in the image, then we perform visibility
estimation and speed warning recommendation.
Figure 2: System Architecture.
4.2.1 Horizon Line Estimation
Several methods can be employed for computing the
horizon line in the image. The first one relies on
using a simple calibration procedure to compute the
pitch angle of the camera (Hautiere et al., 2006). An
alternative, our choice, is to estimate the horizon line
based on the image features. This will ensure a
better result for the horizon line estimation in
different traffic situations.
The horizon line in the image will be detected by
finding the vanishing point of the painted quasi-
linear and parallel (in 3D) road features such as lane
markings. In (Bronte et al., 2009) only the two
longest lines are considered for finding the vanishing
point. We prefer a more statistical approach that uses
more lines and was previously used to find the
vanishing point of the 3D parallel lines from
pedestrian crossings (Se, 2000). The main steps for
the detection of the vanishing point are:
1. Select a set of relevant lines in the half lower
part of the image (road area). The Hough
accumulator was built from the edge points in the
interest area. The highest m peaks were selected
from the accumulator, and those that were having at
least n votes were validated as the relevant lines.
2. A RANdom SAmple Consensus (RANSAC)
approach is applied to find the largest subset of
relevant lines that pass through the same image
point. A number of K (=48 for a success probability
p=0.99 and percentage of good lines w=0.3) random
samples of two relevant lines are selected. For each
sample the intersection P of the two lines is
computed and consensus set is determined as the
subset of relevant lines that pass through P (within a
small circle around P). The sample having the
largest consensus set is selected.
3. The intersection points of each distinct pair of
lines from the largest consensus set are computed.
Finally, the vanishing point is computed as the
center of mass of the intersection points.
Figure 3 presents the results of applying the
horizon line detection process. The bottom image
presents only the detected Hough lines that form the
consensus set and their intersection points in green
colour.
Using this RANSAC approach for computing the
vanishing point provides an additional benefit. The
consensus score of the best pair of lines can be used
in a temporal scheme to deal with scenes that lack
painted lane markings: the vanishing point with the
highest consensus score is selected from the last N
frames. N can be chosen large enough to ensure the
car has travelled along multiple road segments. This
temporal integration makes the horizon line
detection algorithm more stable.
4.2.2 Region Growing
The region growing process follows the guidelines
presented in (Hautiere et al., 2006). The objective is
to find a region within the image that displays
minimal row to row gradient variation.
Starting from a seed point only the three pixels
above the current pixel are added to the region if
they satisfy the following constraints: the pixel does
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
622

Original Image Edge Image
Hough Image with the intersection points of the consensus
lines
Figure 3: Horizon Line estimation algorithm based on
Random Sample Consensus.
not belong to the region, it is not an edge point
and presents a similarity with the seed and the pixel
located below.
Original Image
Region Growing
Inflection Point Line Result
Figure 4: Region Growing and Inflection Point
Estimation.
4.2.3 Inflection Point Estimation
In order to compute the inflection point v
i
we must
first find the maximum band that crosses the region
from top to bottom (Hautiere et al., 2006). If we
cannot find such a band, then we can assume that
there is no fog in the image. Next we compute the
median value for each line of this band and we
smooth these values such that the obtained function
is strictly decreasing. We extract the local maxima
of the derivative of this function and compute the
values for k, R and A
∞
for these maxima. The point
that minimizes the square error between the model
and the measured curve is considered to be the
global inflection point v
i
of the image. Figure 4
illustrates the results for detecting the inflection
point line. The region growing result is displayed in
the top right image. The vertical band is presented
with blue and the smoothed median values in the
inflection point band are displayed with orange in
the bottom image. Finally, the inflection point line is
displayed in pink. In order to increase the robustness
of the inflection point computation, a temporal
scheme similar to the one for horizon line detection
is employed.
4.2.4 Fog Detection and Visibility Distance
Estimation
Once the horizon line v
h
and inflection point v
i
are computed, we can detect the presence of fog in
the image and we can estimate the visibility distance
d
vis
from equation (11). If the position of the
inflection point line is greater than the vertical
position of the horizon line we are able to detect fog
in the image. Based on the visibility distance
estimation we are able to classify fog into five
different categories presented in Table 1.
4.2.5 Speed Warning Recommendation
Many accidents that happen during fog conditions
are caused by excessive driving. For this reason a lot
of efforts have been made so that advanced driving
assistance systems will be able to provide good
maximum speeds for driving. A method for
determining variable speed limits taking into
account the geometry of the road, sight distance,
tyre-road friction and vehicle characteristics is
presented in (Jimenez et al., 2008). They construct
an Intelligent Speed Adaptation (ISA) system based
on a very detailed digital map. Although a lot of
information is implemented in the ISA, the system is
expensive and hard to retrofit on older vehicles. In
order to avoid any accidents in fog conditions we
consider that a “zero risk” approach would be more
cautious (Gallen et al., 2010). Thus we consider the
total stopping distance to be equal to the distance
travelled during the reaction time and the breaking
distance. So, for providing the driver with a good
recommendation of safe driving speed we consider
that the visibility distance d
vis
computed by our
method is given by the following equation
2
2
r
vis t r
v
dRv
gf
(12)
The first term of equation (12) represents the
AssistingNavigationinHomogenousFog
623
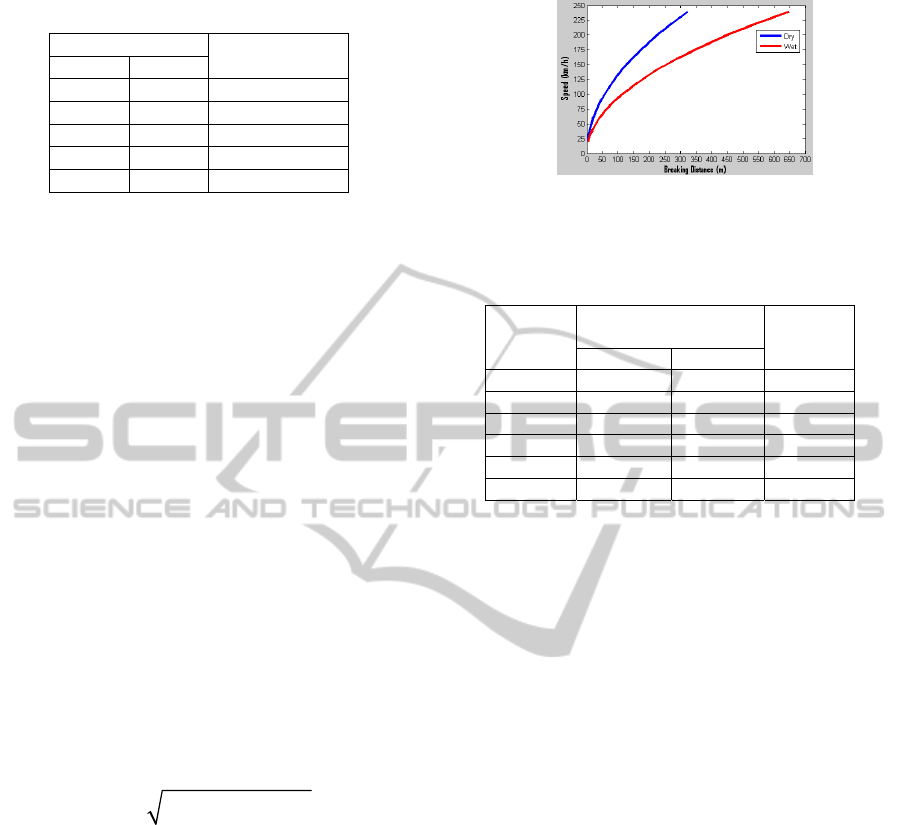
Table 1: Fog Categories.
Visibility distance
Fog
Category
Min Max
1000 m ∞ m No Fog
300 m 1000 m Low Fog
100 m 300 m Moderate Fog
50 m 100 m Dense Fog
0 m 50 m Very Dense Fog
distance travelled during the safety time margin
(including the reaction time of the driver), and the
second term is the braking distance. This is a generic
case formula and does not take into account the mass
of the vehicle and the performance of the vehicle’s
breaking and tire system.
R
t
is a time interval that includes the reaction
time of the driver and several seconds before a
possible accident may occur. Because we are
aiming to obtain a cost effective solution for
warning drivers about the speed that they should
travel during fog conditions and because we do
not take into account the geometry of the road
since we do not use an augmented digital map, we
have considered this interval to be equal to 5
seconds. This covers the interval of distracted
drivers’ inattention for most of the dangerous
events that might occur during fog conditions.
g is the gravitational acceleration, 9.8 m/s
2
f is the friction coefficient. For wet asphalt
we use a coefficient equal to 0.35.
v
r
denotes the recommended driving speed.
By solving equation (12) we obtain the following
positive solution for v
r
:
222
2
rt tvis
vgfRgfRgfd
(13)
Figure 5 represents a plot of the braking
distances on wet and dry asphalt according to the
speed of traveling. The friction coefficient for dry
asphalt was set to 0.7 and for wet asphalt to 0.35
(EnginneringToolbox).
Table 2 presents some maximum recommended
speeds according to the fog density and the visibility
distance measured by our algorithm. In addition we
show the braking distances on wet asphalt.
According to our model of computing the
recommended speed, the driver has enough time in
order to react and to break the vehicle in case of an
emergency or hazardous event.
Figure 5: Braking distance on dry and wet asphalt. These
values were computed with the following friction
coefficients: 0.7 for dry asphalt and 0.35 for wet asphalt.
Table 2: Speed Recommendations under Fog Conditions.
Visibility
distance
Maximum
Recommended speed
Braking
distance
m/s km/h
20 m 3.61 m/s 13 km/h 1.90 m
50 m 8.09 m/s 29 km/h 9.54 m
100 m 14.15 m/s 51 km/h 29.21 m
150 m 19.22 m/s 69 km/h 53.87 m
200 m 23.66 m/s 85 km/h 81.65 m
300 m 31.34 m/s 113 km/h 143.25 m
5 EXPERIMENTAL RESULTS
In order to assess our method we have synthetically
generated images using the GLSCENEINT
framework (Bota and Nedevschi, 2006). Then we
were able to add fog into these images using
Koschmieder’s equation, by considering A
∞
=255
and varying k from 0.01 to 0.15. Figure
6 presents
three scenarios for synthetic images. For k=0.03
(moderate fog in the image) we can observe that in
the first two scenarios the results are similar.
However, for the third scenario we are not able to
compute the inflection point, due to the presence of
the vehicles on the road. In the dense fog scenario (k
= 0.06) we are able to estimate the inflection point in
all three scenarios. For k=0.09 (dense fog situation),
we show the results for the second and third
scenario.
Figure 7 present the results of our fog detection
framework on real traffic images. These images
were acquired with a vehicle equipped with JAI-
A10-CL cameras during different fog conditions, in
the city of Cluj-Napoca. From top to bottom we
present different fog situations in accordance to the
fog categories presented in Table 1.
Table 3 presents the braking distances and the
necessary time for braking in the above four
scenarios. We can observe that the recommended
speed is accurate enough in order for the driver to
reduce the speed of the vehicle or even come to a
complete stop so as to avoid any collisions.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
624

Original Image Fog Image: k = 0.03 Result Fog Image: k = 0.06 Result
Original Image Fog Image: k = 0.03 Result Fog Image: k = 0.09 Result
Original Image Fog Image: k = 0.06 Result Fog Image: k = 0.09 Result
Figure 6: Results obtained on synthetic images. The blue horizontal line represents the horizon line, the pink line represents
the inflection point line and the two vertical blue lines delimit the vertical band. The black curve represents the smoothed
median values from the vertical band .The visibility distances and the maximum recommended speeds are displayed in
green on the resulting images.
Table 3: Braking distance in the presented scenarios.
Fog
Scenario
Max
Speed
Braking
Distance
Braking
Time
km/h m s
1. Low Fog
114.95 148.62 4.65
2. Moderate Fog
70.61 56.08 2.86
3. Dense Fog
43.26 21.04 1.75
4.Very Dense Fog
18.88 4.01 0.76
Our algorithm was implemented in C++ and was
tested on an i7 based PC running Windows
operating system. The synthetic images have a
resolution of 688 x 515 pixels and the average
processing time is of 21 ms. The real traffic images
were obtained with a JAI CV-A10CL camera. Their
resolution is 512 x 383 pixels and the average
processing time on one image is 18 ms.
6 CONCLUSIONS
In this paper we have presented a framework for
detecting fog in images grabbed from a moving
vehicle with the goal of assisting the driver with safe
speed recommendations and information about the
fog density and visibility distance in order to avoid
accidents.
Our algorithm is able to detect fog on roads that
are not very crowded or when the field of view of
the ego vehicle’s camera is not occluded by other
vehicles. One of our main contributions is the
continuous estimation of the horizon line by using
the RANSAC method and the temporal integration
based on the consensus score. This approach proves
to be very stable and provides accurate results when
comparing to the estimation of the horizon line by
using only the camera parameters (obtained during
the offline calibration). By using the temporal
filtering based on the consensus score, we are able to
detect the horizon line even in tough scenarios
where the lane markings are not visible, during
curves, when the vehicle passes over speed bumps or
even in situation where the road is not flat. Another
important contribution is the temporal integration of
the inflection point line. This provides us with the
mean of estimating the density of the fog even in the
situations where we are not able to detect the vertical
band after the region growing process. Thus we are
still able to provide the driver with the maximum
speed recommendation on the given road segment.
The algorithm used to estimate the maximum
speed in fog situations proves to be accurate enough
in order for the driver to reduce the driving speed as
to avoid any collision with other traffic participants.
ACKNOWLEDGEMENTS
This work has been supported by UEFISCDI
(Romanian National Research Agency) in the
CELTIC+ research project Co-operative Mobility
Services of the Future (COMOSEF).
AssistingNavigationinHomogenousFog
625

Original Image Result (Low Fog)
Original Image Result (Moderate Fog)
Original Image Result (Dense Fog)
Original Image Result (Very Dense Fog)
Figure 7: Results obtained on real traffic images. The
visibility distance and the maximum recommended speed
are written on the resulting images.
REFERENCES
Berman, M., Liu, J. & Justison, L. 2009. Caltrans Fog
Detection and Warning System. White Paper, ICX
technologies.
Bota, S. & Nedevschi, S. 2006. GLSCENEINT: A
Synthetic image generation tool for testing computer
vision systems. Proceedings of IEEE 2nd
International Conference on Intelligent Computer
Communication and Processing, Cluj-Napoca,
Romania. pp.
Bronte, S., Bergasa, L. M. & Alcantarilla, P. F. 2009. Fog
detection system based on computer vision techniques.
12th International IEEE Conference on Intelligent
Transportation Systems. pp. 1-6.
Dong, N., Jia, Z., Shao, J., Li, Z., Liu, F., Zhao, J. & Peng,
P.-Y. 2011. Adaptive Object Detection and Visibility
Improvement in Foggy Image.
Enginneringtoolbox. The Engineering Toolbox [Online].
Available: http://www.engineeringtoolbox.com/
friction-coefficients-d_778.html.
Gallen, R., Hautiere, N. & Glaser, S. 2010. Advisory
speed for Intelligent Speed Adaptation in adverse
conditions. 2010 IEEE Intelligent Vehicles
Symposium. pp. 107-114.
Hautiere, N., Tarel, J.-P., Lavenant, J. & Aubert, D. 2006.
Automatic fog detection and estimation of visibility
distance through use of an onboard camera. Machine
Vision and Applications, 17, pp. 8-20.
Jimenez, F., Aparicio, F. & Paez, J. 2008. Evaluation of
in-vehicle dynamic speed assistance in Spain:
algorithm and driver behaviour. Intelligent Transport
Systems, IET, 2, pp. 132-142.
Middleton, W. 1952. Vision through the atmosphere,
Toronto: University of Toronto Press.
Mori, K., Kato, T., Takahashi, T., Ide, I., Murase, H.,
Miyahara, T. & Tamatsu, Y. 2006. Visibility
Estimation in Foggy Conditions by In-Vehicle Camera
and Radar. Innovative Computing, Information and
Control, 2006. ICICIC '06. First International
Conference on. pp. 548-551.
Negru, M. & Nedevschi, S. 2013. Image based fog
detection and visibility estimation for driving
assistance systems. Intelligent Computer
Communication and Processing (ICCP), 2013 IEEE
International Conference on. pp. 163-168.
Pavlic, M., Belzner, H., Rigoll, G. & Ilic, S. 2012. Image
based fog detection in vehicles. 2012 IEEE Intelligent
Vehicles Symposium pp. 1132-1137.
Pomerleau, D. 1997. Visibility estimation from a moving
vehicle using the RALPH vision system. IEEE
Conference on Intelligent Transportation System. pp.
906-911.
Se, S. 2000. Zebra-crossing detection for the partially
sighted. IEEE Conference on Computer Vision and
Pattern Recognition. pp. 211-217 vol.2.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
626
