Detecting Events in Crowded Scenes using Tracklet Plots

Pau Climent-P

erez

, Alexandre Mauduit

, Dorothy N. Monekosso

and Paolo Remagnino

Robot Vision Team (RoViT), Kingston University, Penrhyn Road Campus,

KT1 2EE, Kingston upon Thames, U.K.

Department of Computing,

Ecole Nationale Sup

erieure d’Ing

enieurs de Caen (ENSICAEN), Caen, France

Engineering Design and Mathematics, University of the West of England, Bristol, U.K.

Keywords:

Tracklet Exploitation, Tracklet Plot, Bag-of-Words, Kmeans, Video Analytics, Crowd Analytics, Video

Surveillance.

Abstract:

The main contribution of this paper is a compact representation of the ‘short tracks’ or tracklets present in a

time window of a given video input, which allows to analyse and detect different crowd events. To proceed,

ﬁrst, tracklets are extracted from a time window using a particle ﬁlter multi-target tracker. After noise removal,

the tracklets are plotted into a square image by normalising their lengths to the size of the image. Different

histograms are then applied to this compact representation. Thus, different events in a crowd are detected via

a Bag-of-words modelling. Novel video sequences, can then be analysed to detect whether an abnormal or

chaotic situation is present. The whole algorithm is tested with our own dataset, also introduced in the paper.

1 INTRODUCTION

Automatic analysis of crowded scenes appears as a

need to reduce costs and improve people’s safety,

while reducing the burden of manual video surveil-

lance (Candamo et al., 2010; Davies et al., 1995).

Crowd analysis has received attention in the last

decade, and is of interest for a very wide range of

ﬁelds, as described in (Zhan et al., 2008; Jacques Ju-

nior et al., 2010).

There are different ways to approach crowd dy-

namics modelling. Many different scenes, ranging

from sparse scenes, with few individuals, to crowds,

all forming a continuum. This calls for a topology

of scenes, such as the one proposed by (Zhan et al.,

2008), with three levels: micro-, meso- and macro-

scopic which would be roughly equivalent to indi-

vidual, group or crowd levels. Topologies show the

human need for categorisation of situations, but this

does not mean that interaction among methods from

different levels cannot be possible.

In fact, in Thida et al. (Thida et al., 2013), the au-

thors state that approaches considered to be part of the

microscopic modelling (as it is the tracking of individ-

uals in a scene) can be used in a bottom-up approach,

which allows us to look at crowded situations from

the individual tracking perspective.

In this paper, we will present an idea based on

that concept. To do this, we obtain short tracks from

the people in the scene, and then use this informa-

tion and merge it into the ‘tracklet plot’, a feature

that will be described in Subsection 2.2. After that,

a bag of words modelling will extract the most com-

mon words, and their appearance frequencies in dif-

ferent situations (Section 2.3). We will also introduce

a novel dataset for crowded scene analysis from mul-

tiple views. Finally, the results for our method, as

well as the conclusions drawn will be presented in

Section 4.

1.1 Event Recognition and Tracklet

Exploitation

The work by Ballan et al. (Ballan et al., 2011) surveys

the ﬁeld of event recognition, from interest point de-

tectors and descriptors, to event modelling techniques

and knowledge management technologies. The au-

thors imply that the recognition of crowd events, and

the recognition of actions, performed by a single actor

using a single camera, have much in common, since

the event modelling techniques can be quite similar,

if not the same, regardless of the feature being used,

which will depend on the case.

Hu et al. (Hu et al., 2008) are able to extract

the dominant motion patterns of a video, by using

sparse optical ﬂow vectors as their tracklets, these

are then associated into motion patterns by a sink-

174

Climent-Pérez P., Mauduit A., N. Monekosso D. and Remagnino P..

Detecting Events in Crowded Scenes using Tracklet Plots.

DOI: 10.5220/0004742301740181

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 174-181

ISBN: 978-989-758-004-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

seeking process, followed by the construction of super

tracks which represent the dominant/collective mo-

tion patterns discovered. The authors obtain the dom-

inant motion patterns or trajectories, and these can be

used to detect deviations from the pattern. Neverthe-

less, other types of events cannot be detected. Las-

das et al. (Lasdas et al., 2012) use tracklets obtained

from a Kanade-Lucas-Tomasi (KLT) tracker, instead

of sparse ﬂow vectors. Furthermore, they enumerate

the desirable features of a motion summarisation sys-

tem to which the reader is referred.

Similarly, in G

arate et al. (Garate et al., 2009), the

authors track FAST points (Features from Accelerated

Segment Test) extracted from the bounding boxes of

objects detected via background subtraction. Density

is estimated in the image by superimposing a grid and

counting the number of FAST feature points in each

cell in the grid. Furthermore, the tracklets extracted

from the tracking of the FAST features are used to

detect dominant directions of motion.

On the other hand, Dee and Caplier (Dee and

Caplier, 2010) present an analysis of crowd events

based on histograms of motion direction (HMDs),

which, to some extent are similar to the tracklet plot,

except for the fact that the HMDs are obtained for

the whole video sequence, instead of smaller inter-

vals, as is done in this paper. Using small intervals al-

lows the analysis of particular situations happening at

a given moment in a long video, rather than analysing

the video as a whole.

2 METHODOLOGY

There are two main contributions in this paper. On the

one hand, a feature based on the compact representa-

tion of tracklets is presented (see Fig. 2 for examples).

On the other, a dataset for crowded scene analysis is

introduced. In this section, the ﬁrst contribution will

be explained.

The proposed feature enables the detection of

anomalous events in crowded scenarios. The tracklet

plot representation is, to some extent, similar to the

Motion History Images (MHI) introduced by Bobick

and Davis (Bobick and Davis, 2001), but instead, the

tracklet superimposition represents the density and or-

derliness of a particular interval: for instance, if all the

tracklets are parallel they will generate an area in the

image that is particularly bright (high intensity in a

narrow band), while a chaotic situation will be repre-

sented by an image which has no particular bright ar-

eas. Figure 1 shows an overview of the whole feature

extraction process, including also the training stage.

Video interval

of Δ frames

Inial boun-

ding boxes

Tracklets for

interval (TS)

Filtered

tracklets (FTS)

Tracklet plot

Histogram for

interval (h

s,int

)

Video se-

quence (S)

Bag-of-words training

s,1

s,2

s,3

s,4

s,5

...

Tracking

Noise

removal

Plong

Histogram

w1 w2 w3

Figure 1: Overview of the whole process up to Bag-of-

words training.

2.1 Tracking Multiple Targets

The ﬁrst step of the algorithm entails the extraction

of short tracks or tracklets. To do this, a tracking al-

gorithm needs to be employed. Most trackers need

an initialisation step, in which the moving objects or

people are detected. Once the algorithm has its ini-

tialisation seeds, the tracking then proceeds automat-

ically.

Furthermore, in our case, multiple targets need to

be tracked at the same time, in order to obtain the mo-

tion patterns of the whole scene. Thus, a multi-target

tracker, or a tracker running in parallel for each de-

tected individual must be used. In this step, a Particle

Filter based algorithm is used (P

erez et al., 2002), and

run in parallel for each of the individuals present in

the scene.

2.1.1 Tracklet Extraction

Since most trackers deal badly with tracking over long

periods of time, intervals of ∆ frames are used. Track-

let sets T S

n∆

are obtained for each interval, where

n is the interval number and so n · ∆ is the initial

frame for that tracklet set. These sets will contain

the tracklets for each individual being tracked dur-

ing the interval. At this point, the tracklet sets con-

sist of a series of 2D points for each individual; so

T S = {P

t=0

, ··· , P

∆−1

}, that is, for each frame t, P is

a set of 2D points, containing the centres of mass of

the bounding boxes of the people being tracked. It has

the form: P

= {c

, · ·· , c

}, where each c

represents

the center of mass of a tracked box with id i, and M

is the total amount of individuals in the scene for the

tracklet set T S.

Since the Particle Filter tracker yields a noisy out-

put due to the change in scale of the bounding boxes

that happens during tracking, a Kalman ﬁlter is ap-

plied to the sequences of centres of mass, so that

DetectingEventsinCrowdedScenesusingTrackletPlots

175

smoother tracklets are retrieved. By doing so, a se-

ries of ﬁltered tracklet sets FT S are obtained.

2.2 Feature Extraction

Feature extraction is performed in two steps. The ﬁrst

step consists of tracklet plotting. This step plots the

tracklets into a ﬁxed-size image, centered and nor-

malised (Sec. 2.2.1). Then, in the second step, a his-

togram is obtained from the image, which allows fur-

ther analysis of the individuals’ speed and direction

of motion (Sec. 2.2.2).

2.2.1 Tracklet Plotting

Once the tracklets have been ﬁltered, the compact rep-

resentation is obtained, namely the tracklet plot. To

do so, the tracklets in each set FT S are ﬁrst ﬁt into a

square image by normalising their lengths to the size

of the image. Each ﬁltered tracklet f t in the set is

assigned an equal weight:

weight =

I(max)

||FT S||

(1)

which is represented as an intensity value in the im-

age. Here, I(max) is the maximum intensity (255 for

8-bit images) and ||·|| denotes the number of elements

in the ﬁltered tracklet set FT S. Each tracklet is then

centered and superimposed in the tracklet plot, as it

is depicted in Fig. 2. It is worth noting that this rep-

resentation tracks global behaviour, and not situated

actions.

(a)

(b)

(c)

(d)

Figure 2: Example of different tracklet plots. a) Ordered

group of people walking at the same speed and direction; b)

a fast biker (b.2) and a slower pedestrian (b.1); c) Two peo-

ple walking in perpendicular directions; d) A chaotic situa-

tion, where people run away. Pictures are shown in inverted

colour and enhanced contrast.

2.2.2 Histogram Extraction

After the above process, a histogram can be extracted

from the tracklet plot. To do this, two methods are

proposed:

• Circular Histogram. This histogram takes con-

centric disc-shaped regions R into account, be-

ing R = r

0,ρ−1

, r

ρ,2ρ−1

, · ·· , r

nρ,max

a set of ranges,

where r

0,ρ

is a circular region around the centre of

the image with a radius of ρ, and max is the radius

of the image. The histogram for a given window

(of a sequence s) h

(s,win)

is then calculated as:

(s,win)

(r, I(x)) =

∑

∈r

I(p

) if I(p

) = I(x), ∀r ∈ R,

(2)

where each p

is a pixel in the region r. The

main advantage of this kind of histogram is that

it can control differences in velocity for the differ-

ent tracked individuals.

• Angle-distance Histogram. On the other hand,

a histogram based on sectors can be better to de-

tect the orderliness of a crowd, since it can de-

tect whether all the tracklets follow a particu-

lar direction of motion, or an small amount of

them, or the movement in the scene is chaotic,

with individuals running in many different direc-

tions. For this, sectors A are introduced, such that

A = α

0,γ−1

, · ·· , α

(n−1)γ,nγ

being γ the angle span

for each sector and with nγ = 2π. Thus, the equa-

tion for the histogram can be modiﬁed from (2),

to look like:

(s,win)

(α, r, I(x)) =

∑

∈(r,α)

I(p

) | I(p

) = I(x), (3)

for all r ∈ R and all α ∈ A.

Furthermore, two more histogram extraction

methods have been envisaged, each one based on the

two already presented, but with the particularity that

they have one fewer dimension (totalling 1 dimension

for the circular counterpart, and 2 dimensions for the

angle-distance). In these two modalities, the binning

in the intensity dimension is not performed; instead,

only the count of pixels in the plot that are not equal to

zero is kept. Different experiments have been carried

out, in order to establish which is the best histogram

modality to use (see Sec. 3).

Regardless of the method employed, all the his-

tograms h

(s,win)

are normalised to sum 1. Since the

method is applied to each window of a video se-

quence, sets of histograms H

can be obtained for each

sequence s in the set of video sequences for training.

Figure 3 shows the two main histogram modalities for

clarity; a) shows the circular histogram, with the dif-

ferent regions with their radius being multiples of ρ.

max depicts the maximum plot radius. In the same ﬁg-

ure, in b) the γ angle span is also shown, along with

the lines delimiting the sectors.

2.3 Bag of Words Modelling

To perform a modelling of the different crowd situa-

tions in the video input, a series of training video se-

quences S

train

are employed. Each sequence s has an

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

176

max

(a)

(b)

Figure 3: Example of the two main histogram extraction

modalities presented: a) circular histogram; b) polar his-

togram.

associated set of histograms H

. And h

(s,win)

denotes

the histogram for an interval (win) of sequence s.

A bag-of-words (BoW) modelling is applied to

the sequences (Sivic and Zisserman, 2003). This ap-

proach was ﬁrst used for the categorisation of docu-

ments in a corpus, and introduced the concept of a his-

togram of key word frequencies (Ballan et al., 2011).

In our case, a video is the analogue of a document;

the words in our documents will be tracklet plot his-

tograms; and the “key words” frequency histograms

for each document will be extracted by the BoW al-

gorithm as follows:

• Step 1. First, all the sequences of tracklet plot his-

tograms (H

) are taken, and the tracklet plot his-

tograms (h

(s,win)

) are fed into a k-Means cluster-

ing, regardless of the sequence they are originally

part of. This will return a ﬁxed number of cluster

representatives or key words (w).

• Step 2. These key words are used to generate key-

word sequences (W

), in which each of the original

words is replaced by the nearest key word from

Step 1.

– The distance to the a key word w is calculated

by the Jeffrey distance, as:

J(h

(s,win)

, w) =

KL(h

(s,win)

, w) + KL(w, h

(s,win)

)

(4)

where KL(·, ·) is the Kullback-Leibler distance

between the key word, or more generally for

two discrete probability distributions p, q:

KL(p, q) =

||p||

∑

i=1

, (5)

for all p

, q

| p

6= 0 and q

6= 0.

• Step 3. A histogram of key-word frequencies (η)

is obtained for each key-word sequence W

. Each

bin of this histogram is:

(w) =

||W

∑

x=1

δ(w, W

(x)), (6)

being

δ(w, W

(x)) =



1 if W

(x) = w,

0 otherwise.

(7)

• Step 4. All η

histograms are then normalised to

sum 1, this will make them invariant to sequence

length.

Once this process is ﬁnished, the model is trained,

and any future video input can be recognised by

means of the k-nearest neighbour (k-NN) algorithm.

3 EXPERIMENTATION

The algorithm described in the previous subsection

(Sec. 2.3), has been used to evaluate the performance

of the feature described in subsection 2.2. To do

so, ﬁrst a dataset was acquired. Then, a valida-

tion was performed, using a leave-one-sequence-out

cross-validation (LOOCV). In the next subsections,

the set-up is explained in more detail.

3.1 The Penrhyn Road Campus Dataset

A set of four cameras were placed in a building

adjoining the courtyard in the Penrhyn Road cam-

pus. Two cameras were installed on the second ﬂoor,

and two were placed on the fourth ﬂoor, all over-

looking the courtyard. A group of 20 actors per-

formed various stage group behaviours in the court-

yard, such as walking normally as one group, walking

normally as two crossing groups, walking in one di-

rection with some people abnormally deviating from

the trajectory followed by the rest, or simulating a

chaotic event where everybody runs away from a dan-

ger. These videos have been labelled into three cate-

gories, namely normal, abnormal and chaotic, re-

spectively. For the purpose of this work, 18 sequences

from one of the views are used. Table 1 summarises

the details of the dataset.

Table 1: Characteristics of the dataset.

Category Sequences

Normal 10

Abnormal 5

Chaotic 3

DetectingEventsinCrowdedScenesusingTrackletPlots

177

Figure 4: Example of a frame from a chaotic (panic event)

situation from the Penrhyn Road Courtyard dataset.

3.2 Testing Set-up and Validation

To test our method, a set of features (H) needs to be

obtained. It is a superset formed by all the sets of fea-

tures H

| s ∈ S, which in turn contain all the features

for all the intervals of sequence s: h

(s,win)

. The bag

of words modelling algorithm takes H as input and

yields a set of key-words w and the set of key-word

frequency histograms η (one per sequence: η

In order to validate our method, a leave-

one-sequence-out cross-validation (LOOCV) is em-

ployed. This process will take all the sequences ex-

cept for one, and create the training sequences set

train

= S −s

test

. Then H

train

is obtained as per the pro-

cess already described; subsequently, the BoW model

is trained. Then, the test sequence, s

test

is used to

check. This is done for all the folds, that is, by leaving

one sequence out for test at each fold.

All the steps through the process involve a num-

ber of parameter decisions, set as shown in Table 2.

The parameter iter is in reference to the number of

iterations that the k-Means algorithm is run during

the Bag-of-words model acquisition. The parameter

named reps is the number of times that the BoW is

run per test. Also, Table 3 is given, which shows the

bins used for the different histogram extraction meth-

ods employed.

Table 2: Parameters used for the validation of the method.

Parameter Value or range

∆ 50

plot radius 50

(s,win)

bins See Table 3

k-Means K 2–64

k-Means iter 1; 3

BoW reps 5; 15

Table 3: Size (as number of bins) for the histograms used.

Histogram Bins

Circular 6 × 255

Polar 8 × 6 × 255

Circular w/o int. 10

Polar w/o int. 8 × 6

4 RESULTS AND CONCLUSIONS

As said, different conﬁgurations have been tested. Ta-

ble 2 shows the values which have been used for each

of the parameters. These have been obtained experi-

mentally.

The k-Means clustering algorithm is prone to give

different results due to the random process related to

the cluster centre selection. As said, the variable iter

is related to the number of times the k-Means is run.

The clustering error is calculated each time, and the

clustering with the lower error is picked at the end

of the process. On the other hand, the Bag-of-Words

modelling can also be run multiple times (repetitions

or reps) with different k-Means centres, so that the

random initialisation problem is overcome.

Two different conﬁgurations have been tried, once

with iter = 3 and reps = 5; as well as iter = 1, and

reps = 15. Table 3 shows the size of the histograms

that have been used for the different modalities.

Figure 5 shows the results in a graphical form,

each of the series representing a different conﬁgura-

tion. Four series are shown in the ﬁgure. CI stands

for circular histogam, and LP stands for polar. Both

include intensity bins. The numbers next to the two

letters (CI or LP) correspond to the iterations of k-

Means (iter) and the repetitions of BoW (reps), re-

spectively.

Figures 6 and 7 show the behaviour of the algo-

rithm for the polar histogram that has been presented,

both without and with intensity bins respectively. It

is worth noting that the best result is achieved when

no intensity bins are used and reaches a maximum

success rate of 83% (K = 2). In the case of using

intensity bins, the maximum success rate is of 67%

(K = 2). Table 4 shows the maximum, mean and min-

imum success rates for the both modalities of polar

histogram.

Figures 8 and 9 show the behaviour of the algo-

rithm for the circular histogram that has been pre-

sented, both without and with intensity bins respec-

tively. In this case, the maximum success rates are

72.7% (K = 21), for the circular histogram without

intensity bins; and 61.6% (K = 7) for the histogram

with intensity bins. Table 5 shows the maximum,

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

178

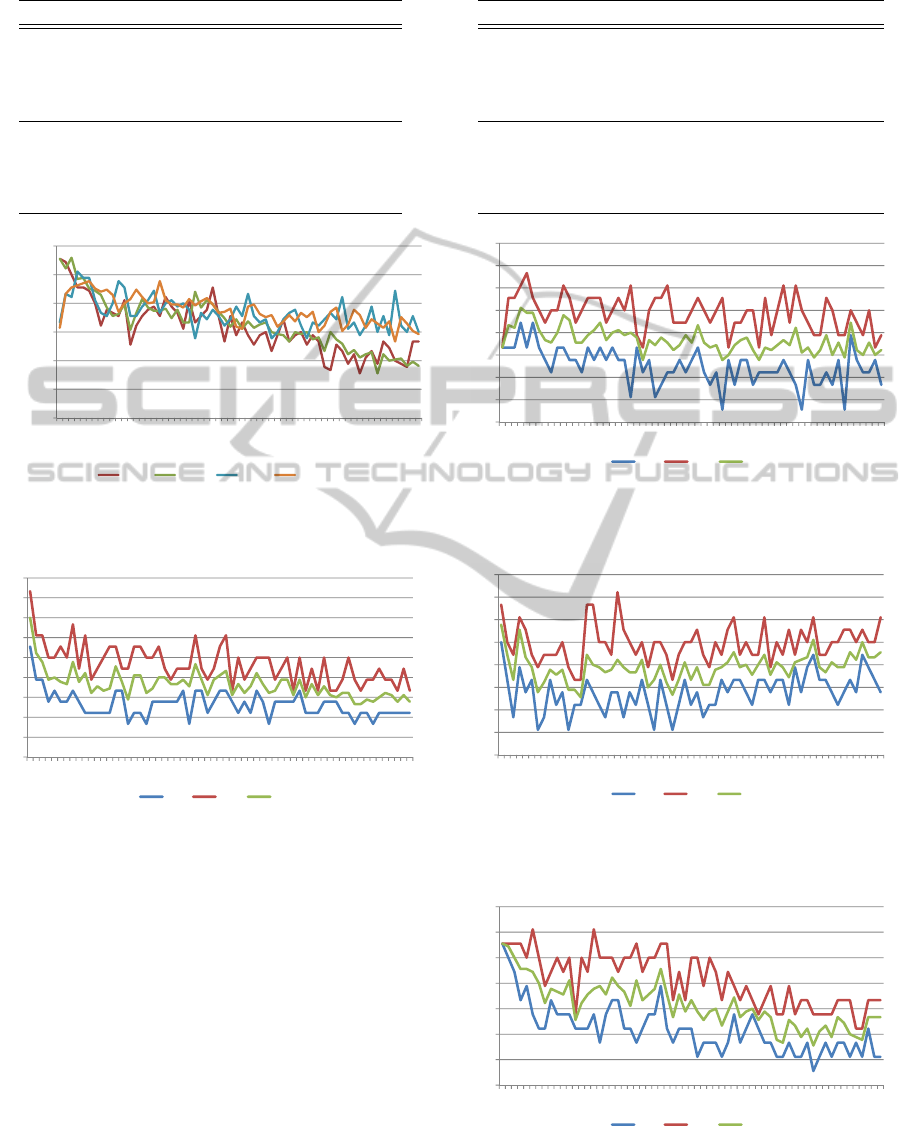
Table 4: Results for polar histograms.

Histogram Success % K

Polar

Lowest Min. 5.6% K = 51

Highest Max. 66.7% K = 6

Highest Mean. 51.5% K = 5

Polar w/o intensities

Lowest Min. 16.7% K = 18

Highest Max. 83.3% K = 2

Highest Mean. 70.0% K = 2

0,00%

10,00%

20,00%

30,00%

40,00%

50,00%

60,00%

2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62

Success rate (%)

Number of words (K)

CI 3,5 CI 1,15 LP 3,5 LP 1,15

Figure 5: Graphical view of the success rate for increas-

ing values of K, using polar and circular histograms (with

intensity bins).

2 8 14 20 26 32 38 44 50 56 62

min max avg

Figure 6: Maximum, mean and minimum success rates for

increasing values of K using the polar histogram (without

intensity values).

mean and minimum success rates for the both modal-

ities of circular histogram.

4.1 Discussion and Conclusions

A compact representation of the tracklets present in

a time window of a given video input has been pre-

sented. Tracklets are extracted from a time window

using a particle ﬁlter multi-target tracker. Noise is

then ﬁltered out, to obtain smooth tracklet trajecto-

ries. The tracklets are then plotted into a square

image, and a circular histogram is then applied to

this compact representation. Furthermore, a Bag-of-

words modelling has been employed over these fea-

Table 5: Results for circular histograms.

Histogram Success % K

Circular

Lowest Min. 5.6% K = 53

Highest Max. 61.6% K = 7

Highest Mean. 55.6% K = 2

Circular w/o intensities

Lowest Min. 11.1% K = 8

Highest Max. 72.2% K = 21

Highest Mean. 57.8% K = 2

2 8 14 20 26 32 38 44 50 56 62

min max avg

Figure 7: Maximum, mean and minimum success rates for

increasing values of K using the polar histogram (with in-

tensity values).

2 8 14 20 26 32 38 44 50 56 62

min max avg

Figure 8: Maximum, mean and minimum success rates for

increasing values of K using the circular histogram (without

intensity values).

2 8 14 20 26 32 38 44 50 56 62

min max avg

Figure 9: Maximum, mean and minimum success rates for

increasing values of K using the circular histogram (with

intensity values).

DetectingEventsinCrowdedScenesusingTrackletPlots

179

tures for crowd event recognition. Our method has

been validated by using a LOOCV cross-validation

on a novel dataset.

From the results, some conclusions can be drawn.

First, it can be seen that results are generally better

for lower values of K. This seems to be logical, since

there should be, at most, three or four different situa-

tions at a given moment in time; that is: normal, devi-

ations from normal and chaotic. Also, it can be seen

that results with histograms that do not take inten-

sity into account are better than their intensity-aware

counterparts. Finally, polar histogram seems to per-

form better than circular; which again, seems logical

due to the fact that the circular histogram does not

take orderliness into account.

It has to be noted that the dataset in use in this case

is a very challenging one, due to the presence of heavy

clutter due to objects in the scene (trees, benches...)

which complicates the tracking, which is the bottle-

neck of the process. A poor tracking result will al-

ways yield to worse results in general. Further work

needs to be carried out in this regard.

4.2 Future Work

In this section a series of immediate and future im-

provements are shown, which are considered to ame-

liorate the results.

As just said, the bottleneck of the whole process is

in the tracking. If the tracking fails, the tracklet plots

will not be representative of the situation in the scene.

For this reason, a good tracker is essential. Track-

ing perfectly and ﬂawlessly is still an open challenge

in the computer vision research community. Thus,

and since the aim of this work is not achieving bet-

ter tracking, ground truth data of the people could be

used to evaluate the tracklet plot histograms and the

bag-of-words modelling being applied. Another op-

tion would be using promising trackers such as the

recent work by Kwon et al. (Kwon and Lee, 2013).

Furthermore, testing our method on other datasets

is a pending task. Nevertheless, most existing datasets

are near-ﬁeld, and thus, ours seems more appropriate

for group and crowd analysis. Also, most of them pro-

vide video footage from a single view. Furthermore,

the types of situations present in our dataset, are not

always present in other publicly available datasets.

For instance, the UMN dataset

, would be the best

candidate to try our algorithm next. However, it has

two main drawbacks: ﬁrst, it includes scenes were

people wander, which is not considered ‘normal’ be-

haviour as deﬁned and used in this paper; second, it

http://mha.cs.umn.edu/proj events.shtml (Accessed:

Nov. 2013)

is single view, so planned extensions of our work for

multiple views could not be tested on it.

Finally, as just mentioned, future work also in-

cludes the use of video footage from multiple views.

To this end, information from all the available cam-

eras (four in our dataset) is to be combined and tested

either by a fusion method at the “feature level”, or

by merging by means of a “model-level” algorithm.

For the former, synchronised video is to be used, so

obtaining the features from the various video sources

simultaneously. The features are then fused by merg-

ing them into a longer feature. Dimensionality reduc-

tion techniques might be needed, since the features

are now much longer (i.e. four-fold) than the origi-

nal. In the latter, on the other hand, different models

for the different cameras are learnt, and then fusion

is performed afterwards, using a voting mechanism,

that in turn could assign weights to the different views

(e.g. by using an additional neural network layer).

ACKNOWLEDGEMENTS

This work has been supported by the European

Commission’s Seventh Framework Programme (FP7-

SEC-2011-1) under grant agreement N.

285320

(PROACTIVE project).

REFERENCES

Ballan, L., Bertini, M., Del Bimbo, A., Seidenari, L., and

Serra, G. (2011). Event detection and recognition for

semantic annotation of video. Multimedia Tools and

Applications, 51(1):279–302.

Bobick, A. and Davis, J. (2001). The recognition of human

movement using temporal templates. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

23(3):257–267.

Candamo, J., Shreve, M., Goldgof, D. B., Sapper, D. B.,

and Kasturi, R. (2010). Understanding Transit Scenes:

A Survey on Human Behavior-Recognition Algo-

rithms. IEEE Transactions on Transportation Sys-

tems, 11(1):206–224.

Davies, A., Yin, J., and Velastin, S. (1995). Crowd monitor-

ing using image processing. Electronics & Communi-

cation Engineering Journal, 7(1):34–47.

Dee, H. M. and Caplier, A. (2010). Crowd behaviour anal-

ysis using histograms of motion direction. In Im-

age Processing (ICIP), 2010 17th IEEE International

Conference on, pages 1545–1548. IEEE.

Garate, C., Bilinsky, P., and Bremond, F. (2009). Crowd

event recognition using hog tracker. In Performance

Evaluation of Tracking and Surveillance (PETS-

Winter), 2009 Twelfth IEEE International Workshop

on, pages 1–6.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

180

Hu, M., Ali, S., and Shah, M. (2008). Detecting global mo-

tion patterns in complex videos. In Pattern Recogni-

tion, 2008. ICPR 2008. 19th International Conference

on, pages 1–5. IEEE.

Jacques Junior, J., Raupp Musse, S., and Jung, C. (2010).

Crowd analysis using computer vision techniques.

Signal Processing Magazine, IEEE, 27(5):66–77.

Kwon, J. and Lee, K. (2013). Wang-Landau Monte Carlo-

based Tracking Methods for Abrupt Motions. Trans-

actions on Pattern Analysis and Machine Intelligence,

35(4):1011–1024.

Lasdas, V., Timofte, R., and Van Gool, L. (2012). Non-

parametric motion-priors for ﬂow understanding. In

Applications of Computer Vision (WACV), 2012 IEEE

Workshop on, pages 417–424. IEEE.

erez, P., Hue, C., Vermaak, J., and Gangnet, M. (2002).

Color-Based Probabilistic Tracking. In European

Conference on Computer Vision 2002, pages 661–675.

Sivic, J. and Zisserman, A. (2003). Video google: a text

retrieval approach to object matching in videos. In

Computer Vision, 2003. Proceedings. Ninth IEEE In-

ternational Conference on, pages 1470–1477 vol.2.

Thida, M., Yong, Y. L., Climent-P

erez, P., How-lung, E.,

and Remagnino, P. (2013). A Literature Review on

Video Analytics of Crowded Scenes. In Cavallaro,

A. and Atrey, P. K., editors, Intelligent Multimedia

Surveillance: Current Trends and Research, pages 1–

23. Springer (in press).

Zhan, B., Monekosso, D. N., Remagnino, P., Velastin, S. A.,

and Xu, L.-Q. (2008). Crowd analysis: a survey. Ma-

chine Vision and Applications, 19(5-6):345–357.

DetectingEventsinCrowdedScenesusingTrackletPlots

181