Key-point Detection with Multi-layer Center-surround Inhibition

Foti Coleca

, Sabrina Z

ırnovean

1,2

, Thomas K

aster

1,3

, Thomas Martinetz

and Erhardt Barth

Institute for Neuro- and Bioinformatics, University of L

ubeck, Ratzeburger Allee 160, L

ubeck 23562, Germany

University ”POLITEHNICA” of Bucures¸ti, Splaiul Independent¸ei 313, 060042, Bucures¸ti, Romania

Pattern Recognition Company GmbH, Innovations Campus L

ubeck, Maria-Goeppert-Straße 3, 23562 L

ubeck, Germany

Keywords:

Object Recognition, Pet Recognition, Sparse Representations, End-stopped Operators, Higher-order Decorre-

lation, Deep Multi-layer Networks.

Abstract:

We present a biologically inspired algorithm for key-point detection based on multi-layer and nonlinear center-

surround inhibition. A Bag-of-Visual-Words framework is used to evaluate the performance of the detector

on the Oxford III-T Pet Dataset for pet recognition. The results demonstrate an increased performance of our

algorithm compared to the SIFT key-point detector. We further improve the recognition rate by separately

training codebooks for the ON- and OFF-type key points. The results show that our key-point detection algo-

rithms outperform the SIFT detector by having a lower recognition-error rate over a whole range of different

key-point densities. Randomly selected key-points are also outperformed.

1 INTRODUCTION

Various object-recognition and tracking approaches

rely on the detection of object key-points (Lowe,

1999; Csurka et al., 2004). Regions around such

key-points are expected to contain the information

needed for matching and recognition. Although some

have argued that a dense sampling of randomly se-

lected points can replace or even outperform recog-

nition algorithms based on key-points (Nowak et al.,

2006), the beneﬁts of appropriate key-points and re-

lated saliency measures are obvious since they re-

duce the amount of information that needs to be pro-

cessed and often, as in many cases including ours,

lead to better recognition performance, see (Vig et al.,

2012a) for a recent example. The standard for key-

point detection is the SIFT algorithm, which selects

key-points as the local maxima of the Difference-of-

Gaussians (DoG) operator (Lowe, 1999).

We here show how SIFT key-point selection can

be improved by introducing a few biologically in-

spired extensions and new features. The DoG oper-

ator has been often used to model lateral inhibition, a

key feature of early visual processing. However, some

essential properties of biologically realistic lateral in-

hibition are usually ignored and it turns out that three

of them ﬁt our purpose of improving key-point selec-

tion. The ﬁrst property is that of nonlinearity, which is

here modeled as a simple one-way rectiﬁcation (clip-

ping) of the DoG. The second property is that of

ON/OFF separation, i.e. the distinct representation

of bright-on-dark versus dark-on-bright features. The

third property is that of multiple layers, i.e., the fact

that lateral inhibition occurs repeatedly in successive

layers of early visual processing. All these features

have been considered in (Barth and Zetzsche, 1998),

where the authors have shown that iterated and non-

linear lateral inhibition generates representations of

increasing sparseness and converges to end-stopped

representations, i.e., representations of only 2D fea-

tures like corners and junctions. In other words: the

linear DoG operator eliminates 0D regions, which are

uniform, and the iteration of the clipped DoG then

eliminates 1D regions, i.e., straight edges and lines.

This approach, however, has not been used for key-

point selection in the context of object recognition.

Operators that extract 2D features, called end-

stopped operators in vision, are thought to provide an

efﬁcient representation by eliminating redundancies

in images and videos (Zetzsche and Barth, 1990; Vig

et al., 2012b). This works well because 0D and 1D

regions are redundant in a geometrical sense (Mota

and Barth, 2000). Statistical approaches consider a

representation to be efﬁcient if statistical dependen-

cies in the signal are reduced. Linear operators such

as the DoG, however, can only decorrelate the signal

386

Coleca F., Zîrnovean S., Käster T., Martinetz T. and Barth E..

Key-point Detection with Multi-layer Center-surround Inhibition.

DOI: 10.5220/0004743103860393

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 386-393

ISBN: 978-989-758-003-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

and nonlinear operations such as those advocated in

(Zetzsche and Barth, 1990) are needed to deal with

higher-order dependencies. However, isotropic oper-

ators such as the DoG, even when combined with sim-

ple nonlinearities, are limited in their ability to deal

with higher-order dependencies.

Although the principle of iterating the nonlinear

DoG has been shown to provide 2D representations,

this insight was only supported by simulations. How-

ever, the computational power of linear-non-linear

(LNL) structures has been further analyzed in (Zet-

zsche and Nuding, 2007) and it has been shown how

LNL networks can reduce the statistical dependen-

cies in natural images. The idea is to learn the linear

part of the LNL sandwich, e.g., by PCA for decor-

relation, then apply a simple nonlinearity that would

introduce new correlations (since the nonlinearity can

map higher-order dependencies to second-order de-

pendencies), which can then be removed in the next

linear stage. These results can explain why the iter-

ation of the nonlinear DoG can progress towards re-

moving more and more redundancies.

More recently, deep learning algorithms have per-

formed very well in object-recognition tasks (Cires¸an

et al., 2010; Bengio, 2009; Hinton, 2007). The ﬁrst

layers of these deep multi-layer networks are meant

to provide efﬁcient representations and are trained

by unsupervised learning. When applied to natural

images, these algorithms often provide representa-

tions that exhibit an increasing degree of sparseness

as one proceeds from the ﬁrst to the subsequent lay-

ers. Based on the above considerations one can thus

interpret the multiple layers of the deep networks as

providing an increasing degree of higher-order decor-

relation, which reduce the statistical dependencies be-

tween the components of a representation vector. In

this context, one can interpret the iterated DoG pro-

posed here as an hard-wired implementation of a deep

multi-layer network where the linear decorrelating

operations are not learned but simply implemented as

a DoG.

Given the above considerations, we evaluate the

performance of our key-point detectors for different

numbers of layers and different numbers of selected

key-points. We use a Bag-of-Words approach on a

pet-recognition benchmark and the popular SIFT al-

gorithm as a base line.

2 SALIENCY OPERATORS

Key-points are usually selected randomly or accord-

ing to some saliency measure. We base our key-point

detection algorithm on the iterated nonlinear inhibi-

tion operator presented in (Barth and Zetzsche, 1998).

There it is shown how iterations of a simple nonlinear

operator can exhibit an increasing end-stopping be-

havior, making it an obvious candidate for key-point

detection. The balance between 1D and 2D features

that may lead to key points depends on the number of

iterations.

2.1 Multi-layer nonlinear inhibition

We deﬁne the nonlinear inhibition of a by b (a,b ∈ R)

N[N[a] − N[b]] (1)

where N[ ] is a nonlinearity in the form of half-wave

rectiﬁcation

N[x] = Max(x, 0). (2)

The multi-layer (iterated) nonlinear Difference-

of-Gaussian (INDoG) operator is deﬁned by taking a

and b to be the outputs of Gaussian low-pass ﬁlters of

different spatial extent:

i+1

= N[N[g

⊗ f

] − N[g

⊗ f

]]; i = 0, . . . , M (3)

where i is the layer index, ⊗ denotes convolution,

and g

, g

are Gaussian convolution kernels with vari-

ances σ

< σ

, the inhibitory ﬁlter being larger. Ini-

tially f

is equal to the image intensity.

2.2 ON/OFF Separation

As the INDoG operator exhibits responses only for

certain features (responds strongest at bright corners

and blobs, i.e. like an ON-type operator), one needs to

deﬁne a pair of operators in order to obtain ON/OFF

separation, i.e., distinct responses to bright and dark

features.

Accordingly, the CON operator is deﬁned as

i+1

= N[N[g

⊗ f

] − N[g

⊗ f

]]; i = 0, . . . , M (4)

while the COFF type operator is obtained by

= N[N[g

⊗ f

] − N[g

⊗ f

]]

i+1

= N[N[g

⊗ f

] − N[g

⊗ f

]]; i = 0, . . . , M

(5)

i.e. by reversing the inhibition at the ﬁrst iteration.

The responses of these operators on synthetic and

natural images over M = 8 iterations are shown in

Fig. 1. For the two squares, it can be seen how

the edge response gets progressively weaker and dis-

appears at the end, leaving only the corners to have

distinct peaks. In the natural image one can observe

the features becoming more separated over the itera-

tions. Larger features can be detected by running the

iterations in a DoG scale space, i.e., a collection of

different-scale responses are shown in Fig. 3.

Key-pointDetectionwithMulti-layerCenter-surroundInhibition

387

(a) (b) (c) (d) (e)

(f)

(g)

(h) (i)

(j)

Figure 1: Synthetic (a) and natural (f) images, and their ON/OFF responses (b)-(e), (g)-(j) after 1, 2, 4 and 8 iterations of the

INDoG algorithm on a single scale of the frame. Top row: squares are 100 × 100 pixels in size, taken from octave 2, scale 3

of the DoG scale space (σ

= 12.8, σ

= 16.08 pixels). Bottom row: picture size is 180 × 160 pixels, taken from octave 0,

scale 4 of the DoG scale space (σ

= 4.02, σ

= 5.05 pixels). The ON responses are shaded in white, and the OFF responses

in black.

3 PERFORMANCE EVALUATION

Evaluations of features are often done via a descriptor

repeatability or matching score (Mikolajczyk et al.,

2005). However, this is more suitable for key-point

detector evaluations used in image matching applica-

tions. In our case, we want to evaluate how much the

key-points contribute to object recognition and there-

fore use a object-recognition benchmark.

3.1 The Oxford III-T Pet Dataset

The dataset consists of 2371 pictures of cats and 4978

pictures of dogs. The images are further split into spe-

ciﬁc breeds, 25 of which are dogs and 12 are cats. The

images have been downloaded from various websites

on the Internet and therefore exhibit a high degree

of variation, the pets being photographed in various

poses, at different illumination levels, and the pictures

themselves being at different resolutions. Adding to

this is a high amount of intra-class variation due to the

different breed types being represented.

The dataset was used in (Parkhi et al., 2012) re-

sulting in recognition rates from 83% to 96% for cat-

versus-dog classiﬁcation. We do not use these as a

baseline, as their methods are not comparable with

ours (multiple regions are deﬁned which are densely

sampled, yelding a 20,000 dimensional feature vector

in the simplest approach). Also, although annotations

in the form of bounding boxes and pet silhouettes are

available, we do not use the additional data since we

only wish to asses the contribution of the different

types of key-points in general, and for a difﬁcult tasks.

(a) (b) (c)

Figure 2: Sample image from the Oxford III-T Pet Dataset,

along with face (b) and foreground/background/contour (c)

annotations.

3.2 Key-point Detectors

For evaluation, we compare our algorithm to Lowe’s

(Lowe, 1999) SIFT key-point detector as imple-

mented in the VLFeat (Vedaldi and Fulkerson, 2010)

library. The SIFT detector is also based on a DoG

scale-space analysis of the image, along with some

enhancements that suppress low contrast and straight-

edge responses. The SIFT keypoints that were used

in the evaluation were outputted by the unmodiﬁed

VLFeat package with the default parameters.

In order to make the comparison as close as possi-

ble, the INDoG detector was implemented as a mod-

iﬁcation of the open-source VLFeat package by re-

placing the usual DoG pyramid used in the SIFT de-

tector with our own INDoG CON/COFF frames and

skipping the principal curvature analysis for edge sup-

pression. The INDoG algorithm was run 4 times, for

1, 2, 4 and 8 iterations. As shown in Equations (4)

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

388

(a) (b) (c) (d) (e)

(f)

(g)

(h) (i)

(j)

Figure 3: Different scales of the ON/OFF responses on synthetic (a)-(d) and natural (f)-(i) images, and the key-points found

by the INDoG algorithm (the ﬁrst 100 as ordered by their magnitude). Both rows: frames are taken from iteration 4 of the

INDoG algorithm, at octaves 0, 1, 2 and 3, scale 4 of the DoG scale space (σ

= 4.03, σ

= 5.07 pixels, σ

s+1

= 2σ

and (5), the ﬁrst iteration is directly equivalent to the

SIFT algorithm, but without the edge suppression en-

hancements. All parameters, e.g., for the Gaussian

kernels, the numbers of scales etc. are the same as

the defaults used by the SIFT detector in all cases.

This way, the main differences between the SIFT key-

points and ours are the iterations (multiple layers) and

the ON/OFF separation, and we can study the effect of

the number of layers on the recognition performance.

As a control, we included randomly generated

key-points at strides of 4, 6, 8 and 10 pixels. The

randomly chosen key-points are used to extract SIFT

features of random scales ranging from 12 to 30 pixels

width per bin with the help of the VL Feat framework.

The orientation of the features is also calculated as in

the VL Feat framework implementation of the SIFT

features.

3.3 The Bag-of-Visual-Words

Framework

We evaluate the performance of our detector using a

Bag-of-Visual-Words (BoVW) framework. First, the

few images that are of excessive size (more than 1000

pixels horizontally or vertically) are discarded. The

positives (cats) and negatives (dogs) are randomized

and split into 80% training and 20% testing groups.

The detector is run on the images and the key-

points that have been found are ordered by their mag-

nitude. The total number of key-points is then limited

at 0.25% of the picture size for all detectors, the rest of

the key-points being discarded. Note that key-points

that return multiple orientation for the same location

are only counted as one towards the total number of

key-points allowed (i.e. only key-points at differing

locations are counted).

SIFT features are extracted at the key-point loca-

tions, using the rotation and scaling provided by the

detector for each key-point. In order to evaluate the

discriminative power of sparse key-points, a number

of subsets are created by discarding a portion of the

features, creating a total of 9 training/test sets con-

taining the top 100%, 50%, 30%, 20%, 10%, 5%, 3%,

2% and 1% key-points (as ordered by their magni-

tude) of the maximum number of allowed key-points

per frame.

The BoVW codebook is created using an online

K-means algorithm on all the extracted features in

each feature subset separately. The number of clusters

in each codebook was empirically set as the square

root of the number of key-points in that particular

subset (i.e. for 1 million key-points, which was ap-

proximately the allowed size of the full positive train-

ing set, we would set k = 1000). This codebook is

used to generate keyword histograms for each image

in the current set. The histograms are then normalized

with the l

norm and used in a support vector machine

(SVM) for training and classiﬁcation. We use a linear

kernel SVM with the softness parameter C set to 128

for all tests. This value has been chosen based on

several test runs, and it did not inﬂuence the relative

performance of the different methods tested here.

The above steps are repeated 5 times with a differ-

ent subset of the positive/negative images for a 5-fold

cross validation scheme, the resulting error rates be-

ing averaged at the end. Note that the codebooks are

generated from scratch for every set and subset sepa-

rately, no codebooks being reused at any point during

the performance evaluation.

3.4 Further Enhancements

There are many ways of enhancing the VBoW ap-

Key-pointDetectionwithMulti-layerCenter-surroundInhibition

389

Kept descriptors, %

Recognition rate, %

SIFT

INDOG 1 iteration

INDOG 2 iterations

INDOG 4 iterations

INDOG 8 iterations

Random sampling

100

(a)

Kept descriptors, %

Recognition rate, %

SIFT

INDOG 1 iteration

INDOG 2 iterations

INDOG 4 iterations

INDOG 8 iterations

Random sampling

100

(b)

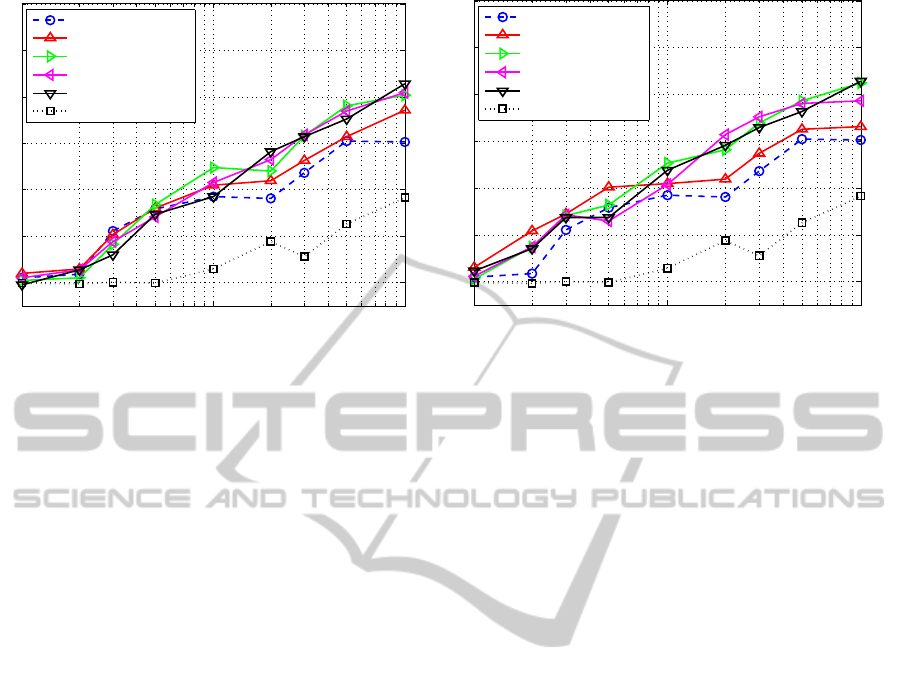
Figure 4: (a) Results for INDoG, SIFT and random key-point sampling at different key-point densities; (b) Results for the

INDoG algorithm with separate CON/COFF codebooks versus SIFT and random sampling (same as in (a)). The number of

key-points on the right (100%) is equal to 0.25% of the total number of pixels in the image.

proach, e.g. by improving the codebook creation step.

Here we propose a very simple extension, which is to

separate the ON- and OFF-type key-points, see Sec-

tion 2.2. This is implemented by separately training

two codebooks for the CON and COFF key-points.

We expect the recognition rate to improve due to the

additional information pertaining to the scene struc-

ture that was extracted at that particular key-point.

A further motivation for ON/OFF separation is that

ON/OFF streams are segregated in biological vision

systems.

As mentioned in section 3.1, the dataset contains

additional annotations such as bounding boxes and

pet silhouettes. An obvious improvement therefore

would be to restrict the codebook generation and

learning process only on the relevant portions of the

images, which has been shown to boost the recogni-

tion rate on this dataset (Parkhi et al., 2012). How-

ever, as we are interested in evaluating the overall per-

formance of the detectors in a general sense (i.e. with-

out a priori information about the object location), we

do not use these annotations.

4 RESULTS

The results are detailed in Table 1, together with

the variance (1σ) obtained by performing a ﬁve-way

cross validation (for clarity, error bars were not in-

cluded in Figure 4). Note that the average perfor-

mance of the INDoG algorithm surpasses the SIFT

key point detector as well as the random sampling

when using the maximum allowed number of key

points, and is more apparent at lower key point densi-

ties.

From Figure 4 it can be seen that, in general, the

recognition performance increases with the number

of key-points. When comparing the different curves,

one ﬁnds a signiﬁcant improvement due to the use of

several layers instead of just one layer of lateral in-

hibition, SIFT key points and randomly selected key

points are outperformed by multi-layer key-point de-

tectors. The right plot in Figure 4 demonstrates a

further improvement, which is obtained by separat-

ing the ON/OFF responses as describe in Sections 2.2

and 3.4. This improvement is also greater and more

consistent at lower key point densities, as seen in Ta-

ble 1.

In Figure 5 the spatial distribution of the found key

points is shown, within a typical example of an un-

cluttered picture from the dataset. It is interesting to

note that the key points found by the SIFT detector as

well as the ﬁrst iterations of the INDoG algorithm are

more spread throughout the picture, even in the uni-

form background area. In an uncluttered frame such

as the one shown, one could expect to see results sim-

ilar to the higher iterations of the INDoG algorithm,

i.e. key points concentrated on the object of interest,

as it exhibits the highest variations.

We can speculate that one of the reasons for the

increased performance would be the distribution of

key points on only the subjects in uncluttered frames,

i.e., the detector avoiding detection of key points in

uniform areas. Another reason might be an optimal

balance, controlled by the number of iterations, in the

allocation of key points to 1D and 2D features. Both

factors would lead to better codewords and an overall

improved performance of the BoVW framework.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

390

Table 1: Results for SIFT, INDoG 1, 2, 4, and 8 iterations (with and without CON/COFF separation) and random sampling.

The best results in each column are printed in bold type.

Descriptors kept 1% 2% 3% 5% 10% 20% 30% 50% 100%

SIFT 68.2% 68.3% 70.2% 71.1% 71.7% 71.6% 72.7% 74.1% 74.0%

±1σ 0.42 0.33 0.69 0.73 0.90 0.31 0.70 1.71 1.56

INDoG, 1 iteration 68.3% 68.6% 70.0% 71.2% 72.2% 72.3% 73.2% 74.3% 75.4%

±1σ 0.42 0.36 0.72 1.18 0.77 0.82 0.40 1.01 0.59

ON/OFF separation 68.6% 70.1% 70.9% 72.1% 72.2% 72.4% 73.5% 74.5% 74.6%

±1σ 0.32 0.89 0.46 0.87 0.88 1.80 1.17 0.81 1.30

INDoG, 2 iterations 68.1% 68.2% 69.7% 71.4% 72.9% 72.8% 74.3% 75.6% 76.0%

±1σ 0.22 0.10 0.44 0.75 1.17 1.13 0.81 1.16 1.17

ON/OFF separation 68.1% 69.5% 70.8% 71.3% 73.0% 73.6% 74.7% 75.7% 76.5%

±1σ 0.54 0.35 0.30 0.46 1.05 0.67 1.80 0.63 1.02

INDoG, 4 iterations 68.2% 68.5% 69.7% 70.8% 72.3% 73.2% 74.4% 75.4% 76.2%

±1σ 0.22 0.47 0.38 0.62 0.62 0.32 0.75 1.38 0.83

ON/OFF separation 68.2% 69.5% 70.9% 70.6% 72.1% 74.3% 75.0% 75.6% 75.7%

±1σ 0.33 0.58 0.70 0.54 0.47 0.45 0.84 0.41 1.10

INDoG, 8 iterations 67.9% 68.6% 69.2% 70.9% 71.7% 73.6% 74.3% 75.0% 76.6%

±1σ 0.53 0.65 0.55 0.60 1.02 0.72 0.87 1.35 1.01

ON/OFF separation 68.5% 69.4% 70.7% 70.7% 72.7% 73.8% 74.6% 75.3% 76.5%

±1σ 0.42 0.60 0.60 0.38 1.59 1.09 0.64 1.14 1.47

Random sampling 67.9% 67.9% 68.0% 68.0% 68.4% 70.1% 69.6% 70.7% 71.8%

±1σ 0.08 0.06 0.15 0.10 0.71 1.59 0.91 1.45 0.66

5 DISCUSSION

Although the improvements in performance relative

to SIFT key-points are not huge, our results show

that a very simple, biologically plausible, lateral-

inhibition scheme can be used successfully for key-

point detection. The computations have low com-

plexity and can be implemented as a parallel network.

Moreover, they can be implemented as neuromorphic

hardware on retina-like image sensors (Indiveri et al.,

2011), and it seems an interesting results that looping

the image through such a hardware will lead to key

points.

Unfortunately, as with other deep-networks, an

thorough analytical treatment and a deeper under-

standing of the nonlinear iterative computations is

currently missing and we therefore had to rely on

some heuristics, such as the notion of higher-order

decorrelation, to explain our results.

Various extensions and improvements are possi-

ble. As already suggested in (Barth and Zetzsche,

1998), one can replace the DoG with a RoG, i.e., a

ratio of Gaussians. The resulting INRoG is sensitive

to image contrast as opposed to difference in image

intensity. Furthermore, one can optimize the ratio be-

tween the two Gaussians, which has been here taken,

for better comparison, from the SIFT implementation,

although more stable results are obtained with a larger

surrounds (Barth and Zetzsche, 1998). Finally, exten-

sions to spatio-temporal DoGs, i.e., to moving images

are possible.

6 CONCLUSIONS

We have shown that the introduction of multiple lay-

ers provides a saliency measure and derived key-

points that enhance recognition performance relative

to just one layer of lateral inhibition. The enhance-

ment seems to be due to the fact that straight edges

are progressively suppressed as the number of layers

increases.

Key-pointDetectionwithMulti-layerCenter-surroundInhibition

391

Figure 5: Comparison between keypoints generated by SIFT (ﬁrst row) and the INDoG algorithm (next rows, from top to

bottom: 1, 2, 4 and 8 iterations). From left to right, the ﬁrst 20%, 50% and 100% of the maximum number of keypoints

allowed per image (deﬁned as 0.25% of the total number of pixels in the image, i.e. the same number of keypoints column-

wise), sorted by magnitude. The background picture has had its brightness and contrast lowered to facilite the viewing of the

keypoints.

Surprisingly, performance is enhanced relative to

the SIFT key-points, which use second order deriva-

tives and the determinant of the Hessian to suppress

straight edges in the saliency measure.

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

392

By using the arguments outlined in the Introduc-

tion, the role of the multiple layers can be under-

stood as a form of higher-order decorrelation of the

input, which leads to more efﬁcient representations

with increased sparseness and more representative

key-points.

ACKNOWLEDGEMENTS

This research is supported by the Graduate School for

Computing in Medicine and Life Sciences funded by

Germany’s Excellence Initiative [DFG GSC 235/1].

We thank the reviewers for their constructive com-

ments.

REFERENCES

Barth, E. and Zetzsche, C. (1998). Endstopped operators

based on iterated nonlinear center-surround inhibition.

In Human Vision and Electronic Imaging III, volume

3299 of Proc. SPIE, pages 67–78, Bellingham, WA.

Bengio, Y. (2009). Learning deep architectures for ai. Foun-

dations and trends

 in Machine Learning, 2(1):1–

127.

Cires¸an, D. C., Meier, U., Gambardella, L. M., and Schmid-

huber, J. (2010). Deep, big, simple neural nets for

handwritten digit recognition. Neural computation,

22(12):3207–3220.

Csurka, G., Dance, C., Fan, L., Willamowski, J., and Bray,

C. (2004). Visual categorization with bags of key-

points. In Workshop on statistical learning in com-

puter vision, ECCV, volume 1, page 22.

Hinton, G. E. (2007). Learning multiple layers of represen-

tation. Trends in cognitive sciences, 11(10):428–434.

Indiveri, G., Linares-Barranco, B., Hamilton, T., van

Schaik, A., Etienne-Cummings, R., Delbruck, T., Liu,

S.-C., Dudek, P., H

aﬂiger, P., Renaud, S., Schem-

mel, J., Cauwenberghs, G., Arthur, J., Hynna, K.,

Folowosele, F., Saighi, S., Serrano-Gotarredona, T.,

Wijekoon, J., Wang, Y., and Boahen, K. (2011). Neu-

romorphic silicon neuron circuits. Frontiers in Neuro-

science, 5:1–23.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Computer vision, 1999. The pro-

ceedings of the seventh IEEE international conference

on, volume 2, pages 1150–1157. Ieee.

Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A.,

Matas, J., Schaffalitzky, F., Kadir, T., and Van Gool,

L. (2005). A comparison of afﬁne region detectors.

International journal of computer vision, 65(1-2):43–

72.

Mota, C. and Barth, E. (2000). On the uniqueness of curva-

ture features. In Dynamische Perzeption, volume 9 of

Proceedings in Artiﬁcial Intelligence, pages 175–178,

oln. Inﬁx Verlag.

Nowak, E., Jurie, F., and Triggs, B. (2006). Sampling strate-

gies for bag-of-features image classiﬁcation. In Com-

puter Vision–ECCV 2006, pages 490–503. Springer.

Parkhi, O. M., Vedaldi, A., Zisserman, A., and Jawahar, C.

(2012). Cats and dogs. In Computer Vision and Pat-

tern Recognition (CVPR), 2012 IEEE Conference on,

pages 3498–3505. IEEE.

Vedaldi, A. and Fulkerson, B. (2010). Vlfeat: An open

and portable library of computer vision algorithms. In

Proceedings of the international conference on Multi-

media, pages 1469–1472. ACM.

Vig, E., Dorr, M., and Cox, D. (2012a). Saliency-based

selection of sparse descriptors for action recognition.

In Image Processing (ICIP), 2012 19th IEEE Interna-

tional Conference on, pages 1405 – 1408.

Vig, E., Dorr, M., Martinetz, T., and Barth, E. (2012b). In-

trinsic dimensionality predicts the saliency of natural

dynamic scenes. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 34(6):1080–1091.

Zetzsche, C. and Barth, E. (1990). Fundamental lim-

its of linear ﬁlters in the visual processing of two-

dimensional signals. Vision Research, 30:1111–1117.

Zetzsche, C. and Nuding, U. (2007). Nonlinear encoding in

multilayer LNL systems optimized for the represen-

tation of natural images. In Human Vision and Elec-

tronic Imaging XII, volume 6492 of Proc. SPIE, pages

649204–649204–22.

Key-pointDetectionwithMulti-layerCenter-surroundInhibition

393