
Evaluation of Color Spaces for Robust Image Segmentation
Alexander Jungmann, Jan Jatzkowski and Bernd Kleinjohann
Cooperative Computing & Communication Laboratory
University of Paderborn, Fuerstenallee 11, Paderborn, Germany
Keywords:
Image Processing, Color-based Segmentation, Color Spaces, Evaluation of Segmentation Results.
Abstract:
In this paper, we evaluate the robustness of our color-based segmentation approach in combination with dif-
ferent color spaces, namely RGB, L
∗
a
∗
b
∗
, HSV, and log-chromaticity (LCCS). For this purpose, we describe
our deterministic segmentation algorithm including its gradually transformation of pixel-precise image data
into a less error-prone and therefore more robust statistical representation in terms of moments. To investigate
the robustness of a specific segmentation setting, we introduce our evaluation framework that directly works
on the statistical representation. It is based on two different types of robustness measures, namely relative
and absolute robustness. While relative robustness measures stability of segmentation results over time, abso-
lute robustness measures stability regarding varying illumination by comparing results with ground truth data.
The significance of these robustness measures is shown by evaluating our segmentation approach with differ-
ent color spaces. For the evaluation process, an artificial scene was chosen as representative for application
scenarios based on artificial landmarks.
1 INTRODUCTION
Image segmentation refers to the problem of parti-
tioning a single image into regions of interest (ROI)
and a variety of techniques exists for region-based
segmentation (Freixenet et al., 2002). Each ROI de-
scribes a homogenous region where homogeneity is
measured, e.g., by means of features as color, texture,
or contours (Russell and Norvig, 2010). Which fea-
ture or combination of features is used to measure ho-
mogeneity depends on the goal of a certain computer
vision system, i.e. there is an ambiguous choice. Usu-
ally, a computer vision system includes object detec-
tion and recognition whose results are used for high
level applications. Features chosen for segmentation
depend on object characteristics that are assumed to
distinguish objects from their environment. Examples
from embedded systems domain are, e.g., driver as-
sistance systems for traffic sign recognition in the au-
tomotive domain (Mogelmose et al., 2012), obstacle
detection for behavior in robotics (Blas et al., 2008),
or face recognition in biometrics (Yang et al., 2009).
In this paper, we focus on color-based segmen-
tation for an efficient and robust object detection
within embedded systems. While efficiency is re-
lated to the implementation of our segmentation ap-
proach, robustness refers to stable segmentation re-
sults in presence of illumination variations and noise
over time. Since environmental illumination influ-
ences color perception, an evaluation of different
color spaces seems promising to achieve robustness.
Various color spaces exist, each aiming at provid-
ing special characteristics, e.g., regarding color dis-
tance, color description, or color ordering. While
some color spaces are based on the assumption
that each color is composed of three primary colors
(trichromatic theory; e.g. RGB, XYZ), other color
spaces aim at adapting human color perception (e.g.
HSV). Since color-based segmentation utilizes color
distances to measure homogeneity of image parti-
tions, the choice of color space has heavy impact on
segmentation results (Busin et al., 2009).
In this paper, we propose an efficient, color-based
segmentation approach. Furthermore, we present an
evaluation of this approach considering varying il-
lumination and different color spaces, namely RGB,
L
∗
a
∗
b
∗
, HSV, and LCCS. The goal of this evalua-
tion is to identify color spaces that provide robust re-
sults with our segmentation approach. Due to the ill-
posed nature of the segmentation problem, evaluation
of segmentation results is a hard challenge (Unnikr-
ishnan et al., 2007). On the one hand, results of an
entire vision system including segmentation typically
contain effects of post-processing steps and there-
fore do not allow to identify segmentation effects.
On the other hand, comparing segmentation results
648
Jungmann A., Jatzkowski J. and Kleinjohann B..
Evaluation of Color Spaces for Robust Image Segmentation.
DOI: 10.5220/0004743406480655
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 648-655
ISBN: 978-989-758-003-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

(a) RGB cube edges. (b) HSV color space. (c) L
∗
a
∗
b
∗
color space. (d) Log-chromaticity color space.
Figure 1: Visualization of colors from RGB cube edges within considered color spaces.
with ground truth data raises the question: What is
a ground truth segmentation? Considering these chal-
lenges of evaluating segmentation results, we propose
a relative and an absolute robustness measure within
our evaluation framework. By means of these values,
we aim at measuring robustness of segmentation re-
sults within a still scene sequence. In this context, ro-
bustness refers not only to constant regions over time
but also to constant regions at different illumination.
2 COLOR SPACES
Color spaces allow to describe a particular color by
means of basic components. The variety of color
spaces results from differences within these basic
components and many color spaces result from each
other by transformation. Hence, different color spaces
do not have to vary in their covered colors, but rather
differ in the order and scaling of colors. Depending
on the color space, this results in different distances
and distance relations between colors and therefore
effects color-based segmentation (cf. Section 5.1).
In this paper, we consider representatives of pri-
mary, luminance-chrominance, and perceptual color
space classes introduced in (Vandenbroucke et al.,
2003) as well as a variant of log-chromaticity color
space (LCCS) presented in (Finlayson et al., 2009).
RGB and XYZ are well known representatives of
primary color spaces. Since XYZ results from a lin-
ear transformation of RGB and RGB is most widely
used in color image segmentation (Busin et al., 2009),
we consider RGB. In RGB, color is described by its
percentage of the primary colors red, green, and blue.
Due to equidistant scaling of all three primary colors,
RGB color space describes a cube where the main di-
agonal represents gray values (Figure 1(a)).
The perceptual color space HSV describes a color
in cylinder coordinates by its hue, saturation, and a
luminance-inspired value (Szeliski, 2011). Hue is
described by the angle around the vertical axis with
complementary colors 180
◦
opposite one another; sat-
uration and value are usually ranged in [0,1] where
saturation S = 0 corresponds to shades of gray (Fig-
ure 1(b)). In fact, HSV and RGB are related to each
other by a non-linear transformation.
The luminance-chrominance color space L
∗
a
∗
b
∗
(also called CIELAB) was originally constructed by
International Commission on Illumination (CIE) with
a non-linear remapping of the primary XYZ color
space to describe differences of colors w.r.t. lumi-
nance and chrominance more perceptually uniform
(Szeliski, 2011). While a
∗
describes green and red
percentage of a color and b
∗
describes its blue and
yellow percentage, L
∗
represents luminance. Hence,
L
∗
-axis represents all levels of gray (Figure 1(c)).
Furthermore, we consider LCCS which results
from a logarithmic scaled projection of RGB color
space. In (Finlayson et al., 2009), LCCS is derived
based on assumptions of Lambertian reflectance,
Planckian lighting, and fairly narrow-band cam-
era sensors. In our evaluation we compute log-
chromaticity colors according to (Khanal et al., 2012):
(x,y) = (log (R/G),log(B/G)). (1)
Figure 1(d) shows a visualization of RGB cube edges
transformed to LCCS by Equation 1. Since projection
effects that one LCCS color represents various RGB
colors, e.g., the point of origin represents all gray val-
ues, this visualization is ambiguous.
3 IMAGE SEGMENTATION
The basic idea of image segmentation is to identify
contiguous blocks of pixels that are homogeneous
with respect to a pre-defined criterion. In our work,
we incorporate color as criterion of homogeneity.
3.1 Segmentation Algorithm
Our deterministic segmentation algorithm processes
an entire image row by row, starting at the topmost
row, at the leftmost pixel within each row. Contigu-
ous blocks of pixels with similar color are identified
and immediately extracted from the image. The algo-
rithm incorporates two major concepts. (1) Within a
EvaluationofColorSpacesforRobustImageSegmentation
649

(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 2: Segmentation example with exemplary intermediate steps. (a) Identified one region (solid) and one run (dashed)
in first row. (b) Identified five regions in first row. (c) Region growing step in second row. (d) Finished region growing step
in second row. (e) Started region growing step of second run. (f) Finished region growing step of second run. (g) Finished
region merging step. (h) Segmentation result. Five regions were identified, one pixel was skipped.
row, adjacent pixels with similar color are compactly
represented as run by means of run-length encoding.
(2) Across adjacent rows, a deterministic region grow-
ing and merging approach aggregates sets of runs with
similar color. Similarity of color depends on the un-
derlying color space and is measured by color space
specific heuristics (cf. Section 5.1).
3.1.1 Run Construction
A block of adjacent pixels with similar color values
within a row is compactly represented as run:
run
i
=
h
(x
1
,y
1
)
i
,l
i
i
, (2)
with (x
1
,y
1
)
i
being the coordinates of the left most
associated pixel P
1
i
and l
i
being the block’s length.
While processing a single row, adjacent pixels with
similar color are identified and stored as runs. A new
run is started when either a new row begins or after the
previous run was finalized. A current run is finalized,
when the end of the current row is reached or when
the color of the next pixel differs too much from the
representative color of the current run.
When starting a new run – let’s say run
i
– the co-
ordinates of the current pixel are stored to (x
1
,y
1
)
i
,
length l
i
is set to 1 and the color values of the current
pixel are saved as representative color values of run
i
.
The process of adding a new pixel to run
i
consists
of increasing length l
i
by 1 and recalculating the rep-
resentative color values of run
i
accordingly. A con-
structed run is discarded if its length is smaller than a
threshold value l
min
. After constructing a sufficiently
long run and before starting a new run, region grow-
ing and region merging takes place.
3.1.2 Region Growing by Aggregating Runs
Adjacent runs within the same row as well as across
adjacent rows are aggregated into a region if they have
similar color values. A region consists of a set of as-
sociated runs:
region
j
=
n
j
[
i=1
run
i
, (3)
with n
j
being the number of runs associated to
region
j
. Furthermore, each region possesses a rep-
resentative color that is calculated based on all asso-
ciated pixels.
A single run is initialized as new region if region
growing is not possible (Figure 2(a)) or if no adjacent
region with similar color values exists (Figure 2(b)).
The region merging step for a run run
i
starts at its left
most pixel position (x
1
,y
1
)
i
and looks up the region
which is associated with the pixel at the same column
in the previous row (Figure 2(c)). If such a region
– let’s say region
j
– exists and region
j
and run
i
have
similar color values, run
i
is added to region
j
by insert-
ing the run into the region’s set of runs (Figure 2(d)).
The representative color values of region
j
are updated
accordingly. The region growing process is finished
at this point since run
i
now belongs to region
j
and
cannot be added to any further adjacent region in the
previous row. Top adjacent regions that have not been
considered until now (like, e.g., the green and second
red region in Figure 2(f)) all are candidates for a final
region merging step.
If region
j
and run
i
do not have similar color val-
ues, the algorithm takes advantage of the run-length
encoding: all other pixels in the previous row belong-
ing to the same run are skipped (Figures 2(c)). By fol-
lowing this strategy, redundant comparisons are min-
imized.
3.1.3 Region Merging
The region merging step follows directly after a run
run
i
was added to a top adjacent region region
j
. Any
yet unconsidered regions are merged with region
j
if
their color values are similar. When merging region
j
with an adjacent region region
k
, region
k
’s set of runs
is added to region
j
’s set of runs while the color val-
ues of region
j
are updated accordingly (Figure 2(g)).
Again, the algorithm takes advantage of the run-
length encoding: regardless of whether region
j
could
be merged with a top adjacent region region
k
or not,
redundant comparisons can be minimized by skipping
all pixels belonging to the respective run (Figure 2(f)).
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
650

3.2 Robust Region Representation
Our segmentation algorithm produces a set of disjoint
regions. Each of them, in turn, consists of a set of
runs. For subsequent object detection steps, however,
the pixel precise image data representation in terms of
runs is inappropriate. In addition, pixel precise repre-
sentation is prone to stochastic errors such as image
noise. For that reason, we interpret a region and its
associated pixels as two-dimensional Gaussian distri-
bution in the image plane. Based on (Hu, 1962), the
distribution is described by two moments m
10
and m
01
of first order (corresponding to mean values m
x
and
m
y
) and three centralized moments µ
20
, µ
02
, and µ
11
of second order (corresponding to variances σ
2
x
and
σ
2
y
and covariance σ
xy
). We already showed in (Jung-
mann et al., 2012) how to efficiently compute these
moments by directly using the intermediate run-based
representation and how to derive additional attributes
such as center of mass or an equivalent elliptical disk.
Although assuming that pixels of a region are
Gaussian distributed, the true distribution may be
of arbitrary shape (like, e.g., the red region in Fig-
ure 2(h)). One approach for better approximating the
true distribution might be the incorporation of mo-
ments of higher order. In our work, however, we cur-
rently consider only moments up to second order.
4 EVALUATION FRAMEWORK
For evaluating the robustness of our segmentation ap-
proach in combination with different color spaces, we
set up the evaluation framework depicted in Figure 3.
The entire framework is divided into two main sec-
tions: the actual image segmentation process and the
evaluation process of the segmentation result.
The main component within the image segmenta-
tion section is our segmentation algorithm (cf. Sec-
tion 3). It consumes a single RGB image and pro-
duces a set of regions, each of them described in terms
of moments. The color space, in which the segmen-
tation process should take place, is selected in ad-
vance. For each selectable color space, a heuristic
for determining whether color values are similar, as
well as a calculation specification for averaging color
values are predefined. Each heuristic can be individu-
ally parametrized by means of thresholds. The nec-
essary color space transformation from the original
RGB color space into the selected color space is done
on-the-fly during the segmentation process by means
of an additional calculation specification.
The subsequent evaluation process can be divided
into two branches. Both of them use the regions pro-
duced by the segmentation process to evaluate the ro-
bustness of the current segmentation setting. The first
branch incorporates a tracking mechanism for eval-
uating relative robustness across consecutive images.
The second branch uses ground truth data to evaluate
absolute robustness for each frame individually.
4.1 Relative Robustness
Evaluating relative robustness of our segmentation al-
gorithm in combination with a selected color space
corresponds to evaluating how stable regions are de-
tected among consecutive frames without moving the
camera and without changes within the environment
(except of illumination changes). By doing so, we
want to estimate how good the different color spaces
can deal with image noise as well as different illumi-
nation conditions.
4.1.1 Region Tracking
We apply a deterministic tracking approach that es-
tablishes correspondences between regions of consec-
utive frames. The amount of established correspon-
dences is subsequently compared with the amount of
regions that were originally extracted by the segmen-
tation algorithm. The tracking algorithm was origi-
nally introduced in (Jungmann et al., 2010).
The main idea of the approach is to gradually re-
duce the amount of valid correspondences between
a region extracted from image I
t
and all regions ex-
tracted from image I
t−i
by applying heuristics with
respect to position, motion, size, and shape.
4.1.2 Evaluation
Let R
S
denote the set of regions extracted by the seg-
mentation algorithm. Furthermore, let R
T
denote the
set of successfully tracked regions detected by the
tracking algorithm. We define the relative robustness
κ
i
for a framework iteration i as
κ
i
=
|R
T
i
|
|R
S
i
|
. (4)
In order to get a meaningful value for the relative ro-
bustness, we consider a sliding window comprising
the last n framework iterations, and take the arith-
metic mean
κ =
1
n
n
∑
i=1
κ
i
=
1
n
n
∑
i=1
|R
T
i
|
|R
S
i
|
. (5)
If κ = 1, the current setting can be considered as
highly robust, since corresponding regions were de-
tected in each of the last n − 1 images. If κ = 0,
EvaluationofColorSpacesforRobustImageSegmentation
651

RGB
image
Segmentation
minimum run length
Averaging
regions
Heuristic
thresholds
Classification Evaluation
ground truth data
classified
regions
absolute
robustness λ
Tracking
parameters
Evaluation
tracked
regions
window length n
relative
robustness κ
result evaluationimage segmentation
Transformation
color space
window length n
min
l
τ
Figure 3: Our evaluation framework. It consists of a segmentation process and two evaluation branches for measuring relative
and absolute robustness of the applied color space in combination with our segmentation algorithm.
the segmentation results significantly differ in con-
secutive images and the current setting cannot be as-
sumed to be robust at all. Although R
T
may con-
tain regions with incorrect correspondences that dis-
tort the value of κ, we neglect an additional validation
step, but minimize the probability of wrongly estab-
lished correspondences by applying a highly restric-
tive parametrization to the tracking algorithm.
The final value of κ heavily depends on the
parametrization of the selected heuristic. For exam-
ple, by simple relaxing the heuristics’s thresholds as
much as possible, the entire image plane will be rep-
resented as a single region. Although the segmenta-
tion result is not useful for any further object detection
steps, the relative robustness will be maximal with
κ = 1. In short, κ alone is not sufficient for discussing
the overall robustness of a segmentation setting. For
that reason, we apply the additional evaluation branch
based on ground truth data.
4.2 Absolute Robustness
Evaluating relative robustness is done without any
foreknowledge. Evaluating absolute robustness, in
turn, is based on manually generated ground truth
data. By comparing segmentation results with ground
truth data, we estimate how robust a color space can
reproduce a desired result, e.g., under changing il-
lumination conditions. In our work, ground truth
data corresponds to a set of regions R
gt
represent-
ing a given structure within an image. Providing that
neither camera nor objects within the image area are
moved, ground truth data has not to be generated for
gt
region
(a)
m
region
gt
region
(b)
gt
A
m
A
overlap
A
(c)
Figure 4: Classification and evaluation: (a) regions that lie
within the boundaries of region
gt
are (b) merged into one
single region region
m
in order to (c) determine the overlap
between region
gt
and its related regions by means of their
bounding boxes.
each image individually but once for an entire se-
quence. Pixels belonging to the same region are la-
beled and subsequently used to calculate the region
representation in terms of moments (cf. Section 3.2).
4.2.1 Region Classification
The evaluation process is based on a non-exhaustive
classification step: an extracted region region
j
is as-
signed to a ground truth region region
gt
∈ R
gt
, if its
center of mass lies within the boundaries of region
gt
(cf. Figure 4(a)). More than one region may be as-
signed to region
gt
, while region
j
may also be assigned
to more than one ground truth region. Regions that are
assigned to the same ground truth region are merged
(cf. Figure 4(b)) by adding together the correspond-
ing moments. As result of the classification process,
each ground truth region region
gt
∈ R
gt
belongs to one
(possibly merged) region region
m
at the maximum.
4.2.2 Evaluation
The main idea of the evaluation step is to analyze the
overlap of a ground truth region region
gt
∈ R
gt
and
its associated region
m
. Instead of calculating a pixel-
precise value, we consider the overlap of the region’s
bounding boxes based on their equivalent elliptical
disks (cf. Figure 4(c)) and define the distance δ
gt,m
between those two regions as
δ
gt,m
= 1 −
2 · A
overlap
A
gt
+ A
m
, (6)
with A
m
being the area of region
m
’s bounding box, A
gt
being the area of region
gt
’s bounding box and A
overlap
being the overlapping area of both bounding boxes. If
region
gt
does not belong to any region
m
, the distance
has maximum possible value of 1. The absolute ro-
bustness λ
i
for a framework iteration i is then defined
as
λ
i
= 1 −
1
|R
gt
|
|R
gt
|
∑
k=1
δ
gt
k
,m
, (7)
with |R
gt
| denoting the total amount of ground truth
regions and δ
gt
k
,m
being the distance (6) of the k-th
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
652

(a) (b)
Figure 5: Color palette of 12 different colors: (a) original,
synthetic version, (b) printed and captured by camera.
ground truth region and its assigned region. As output
value λ, we consider the averaged absolute robustness
of the last n framework iterations:
λ =
1
n
n
∑
i=1
λ
i
. (8)
5 EXPERIMENTS
We evaluated the robustness of the four different color
spaces mentioned in Section 2 in combination with
our segmentation algorithm (Section 3.1) by consid-
ering 14 image sequences each consisting of 200 im-
ages. All sequences show exactly the same scene but
were acquired under different lighting conditions and
camera settings, respectively. The scene itself con-
sists of a palette of 12 different colors (Figure 5).
5.1 Color Space Specific Heuristics
We incorporated two different heuristics for deciding,
whether two color values are similar or not. Heuristic
h
1
is used for RGB and L
∗
a
∗
b
∗
. It determines sim-
ilarity of two color vectors ~µ and
~
ν by checking the
distance of each color channel individually:
h
1
(~µ,
~
ν,
~
τ) =
1 i f
|µ
1
− ν
1
| ≤ τ
1
∧
|µ
2
− ν
2
| ≤ τ
2
∧
|µ
3
− ν
3
| ≤ τ
3
0 else ,
(9)
with
~
τ being distinct threshold values. Heuristic h
2
is
used for HSV and LCCS. Contrary to h
1
, it checks the
distance of only two color channels individually:
h
2
(
~
υ,
~
ω,
~
τ) =
1 i f
|υ
1
− ω
1
− η| ≤ τ
1
∧ |υ
2
− ω
2
| ≤ τ
2
0 else ,
(10)
with
η =
360 i f |υ
1
− ω
1
| ≥ 180
0 else
(11)
being a correction value. Again,
~
τ denotes a vector of
distinct threshold values. In case of HSV color space,
the V channel is neglected. In case of LCCS, the
Cartesian coordinates (Equation 1) are transformed
into polar coordinates.
5.2 Framework Settings
The applied values for the different control values are
depicted in Table 1. The color space specific val-
ues for
~
τ were determined by feeding an image se-
quence with manually optimized camera parameters
and constant lighting conditions to the framework.
The threshold values were manually adjusted during
execution until the maximal possible sum κ+λ of rel-
ative and absolute robustness was identified.
Table 1: Static framework settings.
minimum run length l
min
= 5
window length n = 200
RGB thresholds (h
1
)
~
τ
RGB
= (13,14,8)
L
∗
a
∗
b
∗
thresholds (h
1
)
~
τ
L
∗
a
∗
b
∗
= (15,4,6)
HSV thresholds (h
2
)
~
τ
HSV
= (13,32)
LCCS thresholds (h
2
)
~
τ
LCCS
= (16,8)
5.3 Results
In Figure 6, relative and absolute robustness of the
14 different illuminated image scenes are plotted (cf.
short description in Table 2). Figure 6(a) shows
that relative robustness strongly differs not only be-
tween different sequences, but also for segmentation
with different color spaces applied to a single se-
quence. For sequences 1-7, where camera parameters
are manually optimized for human perception, κ is
in a high value range and differs maximal around 0.2
per sequence. This indicates that our segmentation
algorithm provides mostly equal regions over time
even at varying illumination (sequences 6 and 7). At
sequences 8-14 camera parameters are manipulated,
e.g., to get red, blue, or green cast. κ indicates that
these manipulations have heavy impact on segmenta-
tion results depending on the applied color space. At
blue cast in images, e.g., RGB and L
∗
a
∗
b
∗
get prob-
lems while segmentation results with HSV and LCCS
keep constant over time.
But relative robustness κ indicates only robustness
of segmented regions over time. It does not consider
whether segmentation results correspond to original
Table 2: Description of sequences considered at evaluation.
1 Manual optimized
camera parameters
8 Room light off; spot-
light from behind
2 Reduced brightness
(flickering appears)
9 Room light off; spot-
light from front
3 Reduced brightness 10 Red cast
4 Shadow 11 Blue cast
5 Spotlight 12 Green cast
6 Moving shadows 13 Minimum bright-
ness of camera
7 Moving spotlight 14 Maximum bright-
ness of camera
EvaluationofColorSpacesforRobustImageSegmentation
653
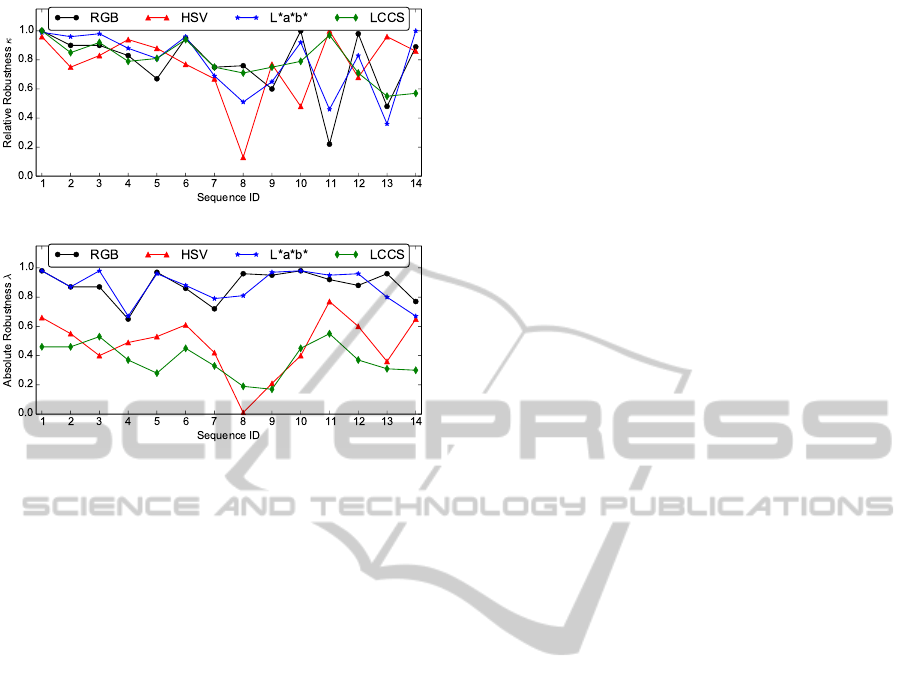
(a) Relative robustness κ.
(b) Absolute robustness λ.
Figure 6: Relative and absolute robustness results for all
sequences described in Table 2.
color segments, i.e. ground truth data. Hence, we
also have to consider absolute robustness λ depicted
in Figure 6(b). For our segmentation algorithm, it in-
dicates that robustness regarding segmentation of all
present colors under varying illumination is higher
using RGB or L
∗
a
∗
b
∗
than applying HSV or LCCS.
This is also confirmed by the examples shown in Fig-
ure 7. For the image scene with manual optimized
camera parameters (Figures 7(a)-7(e)), we notice that
usage of RGB or L
∗
a
∗
b
∗
provides separate regions for
each color of the palette. In contrast, segmentation
with HSV combines, e.g., the red and orange field as
well as the yellow and light green field. This might
be caused by the non-linear color-ordering within the
hue-axis where yellow is only represented by a small
angle range while red and green have a higher resolu-
tion in HSV (cf. Figure 1(b)). Using LCCS provides
an even less sophisticated segmentation result where,
e.g., orange, yellow, and light green are combined.
Figures 7(f)-7(o) show that changes in illumina-
tion affect the segmentation results of all considered
color spaces. Again, RGB provides best results and
L
∗
a
∗
b
∗
also performs well. Even though L
∗
a
∗
b
∗
re-
gions contain less segmented pixels, regions are simi-
lar to those of RGB. Within a vision system, results
of segmentation would be used for post-processing
steps, i.e. the representation of regions would be con-
sidered. Hence, results of segmentation with RGB
and L
∗
a
∗
b
∗
provide similar quality in the context of a
vision system. In contrast, results of HSV and LCCS
can, e.g., no longer cover the dark colors in presence
of shadow (white areas in Figures 7(h) and 7(j)). In
case of segmentation with HSV, this might be an im-
plementation issue because within HSV we do not
consider values positioned in a certain range around
the vertical axis of the color cylinder to avoid noised
gray values. Consequently, colors that appear almost
gray or even black were neglected by segmentation
using HSV. This has also negative effects regarding
the absolute robustness because the distance function
introduced in Equation 6 returns δ = 0 for these miss-
ing color fields.
In presence of an additional spotlight (Fig-
ures 7(k)-7(o)), the yellow field of the palette is too
much affected by reflections and therefore appears
almost white in the original image. Nevertheless,
segmentation with all considered color spaces except
LCCS extracts a region that at least partially covers
this area. Within segmentation using LCCS, all orig-
inally green and yellow color fields of the palette are
fused to one region with kind of mint green as average
color. Again, RGB and L
∗
a
∗
b
∗
provide best results.
6 CONCLUSIONS AND
OUTLOOK
In this paper, we presented our color-based segmen-
tation approach and evaluated its robustness in com-
bination with different color spaces. To investigate
the robustness of a specific segmentation setting, we
introduced our framework that directly works on our
statistical region representation. In this context, the
out-standing feature of the framework is the evalu-
ation of two different types of robustness: relative
robustness and absolute robustness. Relative robust-
ness is evaluated by tracking regions across consecu-
tive images, while absolute robustness is evaluated for
each frame individually based on manually generated
ground truth data.
With the evaluation of our segmentation algo-
rithm, on the one hand we proved the relative and
absolute robustness as a significant quantitative mea-
sure for robustness. On the other hand, we showed
that in our artificial setting the presented segmenta-
tion algorithm performs best using RGB color space.
Nevertheless, for some situations the segmentation
approach provided better results using other color
spaces like L
∗
a
∗
b
∗
or HSV.
In our future work, we want to use the evaluation
framework for automatically calibrating our segmen-
tation algorithm as well as adapting the threshold val-
ues used by our heuristics during execution time. Fur-
thermore, we want to switch from artificial scenes to
more realistic scenarios while appropriately adjusting
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
654

(a) Room light. (b) RGB. (c) HSV. (d) L
∗
a
∗
b
∗
. (e) LCCS.
(f) Shadow. (g) RGB. (h) HSV. (i) L
∗
a
∗
b
∗
. (j) LCCS.
(k) Spotlight. (l) RGB. (m) HSV. (n) L
∗
a
∗
b
∗
. (o) LCCS.
Figure 7: Original images and corresponding segmentation results using different color spaces. Images captured under room
light (a-e; sequence 1), with additional shadow (f-j; sequence 4), and with a spotlight (k-o; sequence 10).
the functionality of our evaluation framework, if nec-
essary. Aside from evaluating robustness of segmen-
tation results, we additionally intend to investigate if
the presented approach can be used for comparing im-
ages not on pixel level but on region level.
ACKNOWLEDGEMENTS
This work was partially supported by the German Research
Foundation (DFG) within the Collaborative Research Cen-
ter “On-The-Fly Computing” (SFB 901).
REFERENCES
Blas, M., Agrawal, M., Sundaresan, A., and Konolige, K.
(2008). Fast color/texture segmentation for outdoor
robots. In IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS), pages 4078–
4085.
Busin, L., Shi, J., Vandenbroucke, N., and Macaire, L.
(2009). Color space selection for color image segmen-
tation by spectral clustering. In IEEE International
Conference on Signal and Image Processing Applica-
tions (ICSIPA), pages 262–267.
Finlayson, G. D., Drew, M. S., and Lu, C. (2009). Entropy
minimization for shadow removal. Int. J. Comput. Vi-
sion, 85(1):35–57.
Freixenet, J., Mu
˜
noz, X., Raba, D., Mart
´
ı, J., and Cuf
´
ı,
X. (2002). Yet another survey on image segmenta-
tion: Region and boundary information integration. In
Proceedings of the 7th European Conference on Com-
puter Vision (ECCV), pages 408–422.
Hu, M.-K. (1962). Visual pattern recognition by moment
invariants. IEEE Transactions on Information Theory,
8(2):179–187.
Jungmann, A., Kleinjohann, B., Kleinjohann, L., and
Bieshaar, M. (2012). Efficient color-based image seg-
mentation and feature classification for image pro-
cessing in embedded systems. In Proceedings of the
4th International Conference on Resource Intensive
Applications and Services (INTENSIVE), pages 22–
29.
Jungmann, A., Stern, C., Kleinjohann, L., and Kleinjohann,
B. (2010). Increasing motion information by using
universal tracking of 2d-features. In Proceedings of
the 8th IEEE International Conference on Industrial
Informatics (INDIN), pages 511–516.
Khanal, B., Ali, S., and Sidib, D. (2012). Robust road
signs segmentation in color images. In Proceedings of
the 7th International Conference on Computer Vision
Theory and Applications (VISAPP), pages 307–310.
Mogelmose, A., Trivedi, M., and Moeslund, T. (2012).
Vision-based traffic sign detection and analysis for in-
telligent driver assistance systems: Perspectives and
survey. IEEE Transactions on Intelligent Transporta-
tion Systems, 13(4):1484–1497.
Russell, S. and Norvig, P. (2010). Artificial Intelligence - A
Modern Approach. Pearson, 3 edition.
Szeliski, R. (2011). Computer Vision - Algorithms a. Appli-
cations. Springer.
Unnikrishnan, R., Pantofaru, C., and Hebert, M. (2007). To-
ward objective evaluation of image segmentation al-
gorithms. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 29(6):929–944.
Vandenbroucke, N., Macaire, L., and Postaire, J.-G. (2003).
Color image segmentation by pixel classification in
an adapted hybrid color space: application to soccer
image analysis. Computer Vision and Image Under-
standing, 90(2):190–216.
Yang, U., Kim, B., and Sohn, K. (2009). Illumination in-
variant skin color segmentation. In 4th IEEE Con-
ference on Industrial Electronics and Applications
(ICIEA), pages 636–641.
EvaluationofColorSpacesforRobustImageSegmentation
655
