Force Directed Flow Map Layout
Alberto Debiasi, Bruno Simões and Raffaele De Amicis
Fondazione Graphitech, Via Alla Cascata 56/c, 28133, Trento, Italy
Keywords: Flow Maps, Force Directed Algorithm, GIS, Geovisualization.
Abstract: A flow map is a thematic map that is been used to emphasize the spatial pattern of one or more geographic
attributes. Although this kind of thematic maps is often drawn by hand, a few automatic computer
algorithms exist. In this research paper, we proposed a novel algorithm for the automatic generation of flow
maps that is theoretically grounded on physics’ laws to describe the motion and force of attraction or
repulsion between points. Properties associated to these laws are then used to merge different flows, as well
as for the improvement of the maps’ visual quality. Finally, we evaluate our work by generating a set of
flow maps and by doing a comparison with flow maps produced by existing algorithms.
1 INTRODUCTION
Geographic flows can represent the movement of
tangible objects (e.g. people, bank notes, and goods)
in geographical space, but also of intangible objects
(e.g. energy, ideas, and reputation). The functional
definition of 'flow' is ‘the continuous movement of
objects in one direction’ (Cambridge, 2013). The
quantification of movement (e.g. the number of
moving objects or the number of transitions) within
a flow is called 'flow magnitude' (Andrienko, et al.,
2007). The most frequent questions associated with
this kind of data are the following: where does the
flow start? Where does the flow arrive? Which is the
magnitude of the flow? And which is the magnitude
of flows that share the same destination?
An answer to these questions can be easily
deduced using visualization techniques like flow
maps. A flow map is a thematic map, which gives
emphasis to the spatial pattern of one or more
geographic attributes (Slocum, et al., 2009). In
particular, it shows the spatial distribution of
univariate geographic phenomena. Additional
properties of flow maps are: the flow magnitude is
represented as the width of each flow line, and the
sum of all flow line branches should add up to the
width of the flow line (Dent, 1990).
The first flow map was created by a cartographer
named Henry Drury Harness, in 1837, by showing
the transportation of passengers in Ireland. Since
then, this kind of thematic map is been used to
represent flow data. The success of this visualization
technique is due to its simple design and intuitive
understanding. Several years ago, a French
cartographer called Charles Joseph Minard
introduced one of the most popular flow maps
techniques which, for example, he used to represent
the movement of travelers on the principal railroads
of Europe in 1865, as well as the international
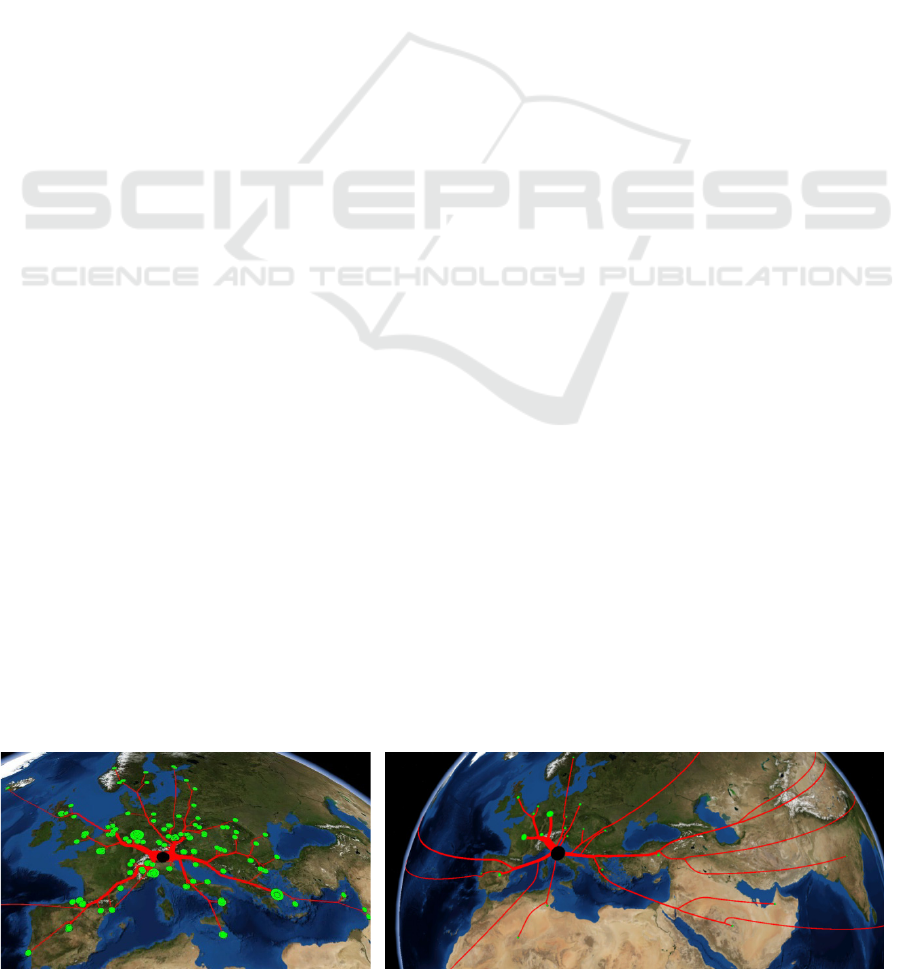
Figure 1: Flow maps: (left) Connections between Fondazione Graphitech and its partners (research centers, university,
companies). (right) Main exports of Italian goods in all over the world.
170
Debiasi A., Simões B. and De Amicis R..
Force Directed Flow Map Layout.
DOI: 10.5220/0004744601700177
In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 170-177
ISBN: 978-989-758-005-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
distribution of French wines, cotton and coal
(Friendly, 2000). Many of his works are still
available online (datavis.ca, 2013).
In flow maps, aggregation techniques can be of
valuable use because they reduce the visual clutter
(e.g. each flow is easier to trace). Additionally, they
enable the visualization of the magnitude of the
flows that share common destinations.
2 RELATED WORK
In this section we summarize the work done to
automatically generate flow maps, and then we
provide an overview of the force directed algorithms
in the field of graph drawing domain.
2.1 Algorithms for Automatic
Generation of Flow Maps
In this subsection we describe existent algorithms
for the automatic generation of flow maps.
Tobler in 1987 (Tobler, 1987) developed a computer
program called FlowMapper (Tools, 2001) used to
visualize migration maps; this mapper produces
generic maps without any optimization with respect
to the visualization of the data. For each flow, it
generates an arrow on the map with a width varying
accordingly to its magnitude. As the number of links
increases, it becomes increasingly difficult to
represent new flows without creating a visual clutter
(see
Figure
2a). Occlusion of trajectories produces
maps that are difficult to interpret unless some form
of generalization is applied.
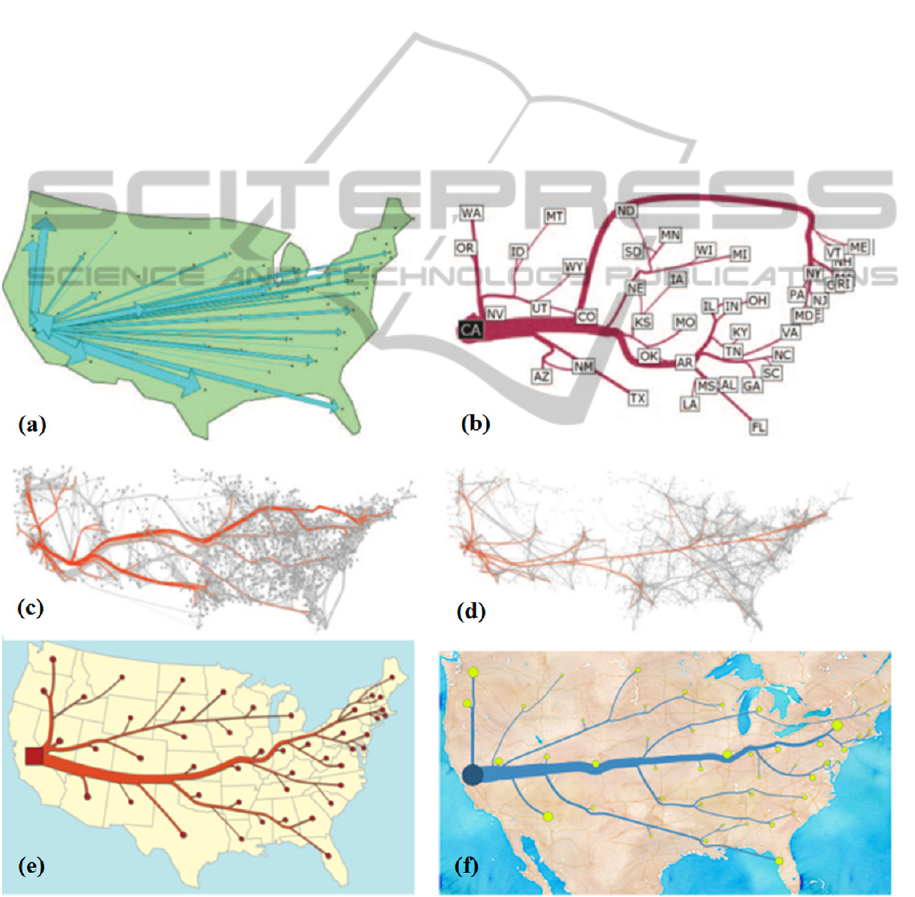
Figure 2: Different maps representing the migration from California in 1995-2000. (a) the first software that automatically
generate flow maps (Tools, 2001), (b) algorithm taking into account aggregation of flows (Phan, et al., 2005), (c) (d) the
force directed algorithms in graph drawing domain (Cui, et al., 2008), (Holten and Van Wijk, 2009), (e) the algorithm
based on spiral tree (Verbeek, et al., 2011), (f) the force directed algorithm described in this paper.
ForceDirectedFlowMapLayout
171

The main aspect of a flow map is the aggregation of
the flows. In 2005 Phan et al. (Phan, et al., 2005)
introduced a method to reduce the visual clutter by
merging the flows (see Figure 2b). The author used a
binary hierarchical clustering formulating the layout
in a simple and recursive manner. The advantage of
this algorithm is its Ο(n^2) time complexity, where
n is the total number of nodes used in the algorithm.
However this algorithm has a few limitations: during
the first step the nodes are moved if their proximity
is too small. Hence, it might lose the geographical
reference associated to each node. Furthermore, if
there are too many destination nodes in a small area,
by forcing binary splits introduces too many extra
routing nodes, which then leads to clutter.
Verbeek et al. (Verbeek, et al., 2011) describes a
method to overcome the aforementioned limitations
through the use of spiral trees. The authors used
spiral spline (Buchin, et al., 2011), which have
Ο log complexity, to generate maps that are
crossing-free. Another key property concerns the
weights of the leaves. If there are two flow maps
with the same origin and destinations but with
different magnitudes, then the layout of the flow
map will be represented differently. Moreover the
flow tree produced is constrained to avoid crossing
its own nodes, as well as user-specified obstacles
(see
Figure 2e). In order to have a high-quality map,
a quality function that takes into account the
obstacles, the smoothness, the angles and the
straightness, has to be minimized. The time required
to perform a flow map is mentioned in the paper as a
“couple of minutes”. Two limitations of this
algorithm are the complexity in the construction of
the tree structure and the non-intuitive body cost
function used to improve the aesthetic results.
2.2 Force-directed Techniques
The reduction of visual clutter has been studied
extensively in the graph drawing domain. A well-
studied class of approaches to overcome this
challenge is composed by force-directed algorithms.
In few words, in a force-directed algorithm the graph
is represented as a physical system of particles with
forces acting between them. At each iteration, the
energy of the system - defined as the sum of all the
forces that affects the particles – changes. The
algorithm halts when the local minimum of the
energy is found.
Eades et al. (Eades, 1984) introduced the idea of
replacing vertices by hinges and edges by springs.
Vertices are placed in a given initial positions, and
springs move the vertices to a minimal energy state
(i.e. the springs are compressed or extended as little
as possible). A few years later, similar methods were
introduced as an extension to this idea.
Kamada and Kawai's algorithm (Kamada and
Kawai, 1989) added the concept of an ideal distance:
the ideal distance between two vertices is
proportional to the length of the shortest path
between them.
Fruchterman et al. (Fruchterman and Reingold,
1991) presented a technique to draw general
undirected graphs according to some aesthetic
criteria, such as the distribution of the vertices in the
frame and the minimization of edge crossings. In
this case the forces are applied to each node of the
graph. Dwyer et al. proposed to add edge routing to
force-directed layouts (Dwyer, et al., 2007).
Cui et al. (Cui, et al., 2008) used a control mesh
that reflects the underlying control pattern reducing
the visual clutter (see
Figure 2c).
In the latter case Holten et al. (Holten and Van
Wijk, 2009) presented a force-directed algorithm in
which the edges are modeled as flexible springs that
can attract each other while node positions remain
fixed (see
Figure 2d). This algorithm works well in
aggregating edges of a generic graph. However the
generated graphs do not merge as quickly and
smoothly as hand-drawn flow maps.
Our work improves the algorithm proposed by
Holten et al. (Holten and Van Wijk, 2009) to
aggregate single origin flow tree.
3 SYSTEM DESIGN
The core of our algorithm focalizes on force-directed
techniques, following simple and intuitive concepts
that can be implemented in a few lines of code and
easily extended for possible improvements.
Figure 3: System diagram.
IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications
172

As mentioned in the section 0, algorithms to
automatically generate flow maps first create a flow
map tree and then use such structure to generate the
flow map. In this work, flows are generated directly
using a force-directed approach without creating a
tree structure at priori. The only structure necessary
is composed by the edges that start from the origin
and arrive to the target nodes.
This work has the objective of achieving
automatic generation of flow-maps, which are
created in a natural way, with high visual quality.
In particular we want to satisfy the following
aesthetic criteria, which are a common goal of
previous works as well (Phan, et al., 2005),
(Verbeek, et al., 2011):
1. The possibility of aggregate flows, reducing
the visual clutter.
2. The use of smooth curves for aesthetic
purposes.
3. The flow magnitude affects the layout of the
generated map; straight lines are correlated
to nodes with high magnitude.
4. The target nodes are not overlapped with
flows.
5. The flow is crossing-free.
In contrast to previous works, this paper presents
a novel force-directed algorithm to automatic
generate flows maps that satisfy the aforementioned
criteria and that is intuitive: imagine a pavement
with a set of elastic cords, tied on one side to a
common stake, and on the other side to different
strakes placed over the pavement. Every cord has a
different elasticity. In this example, we attempt to
aggregate these cords. Hence, we start from the
strake where all cords are tied and we try to bind
together near cords; those with higher elasticity are
dragged by the ones with less elasticity. However,
we have two criteria that are not satisfied: elastic
cords do not have smooth appearance and they
might collide with stakes. These are two issues of
our algorithm that shall be addressed in the
following sections.
The implemented method is divided in different
steps (see
Figure 3).
3.1 Basic Structure Generation
In order to aggregate flows that initially are straight
lines (see Figure 6a), we use a subdivision technique
to divide each flow line into a set of smaller
segments, hence creating new intermediate nodes.
However, not all initial flow lines end up with same
number of intermediate nodes. The number of
intermediate nodes generated for the flow is
proportional to the distance to the target. Each
intermediate node has an index, called “node index”
that defines the order. Nodes having the same “node
index” maintain the same distance from the origin
(see
Figure 6b). The idea is to aggregate the node
with the same “node index”.
At this step each intermediate node has one
father node and one child node. The flow magnitude
will be assigned to each intermediate node, thus each
intermediate node has the flow magnitude of its
flow.
Each intermediate node also knows which are the
two intermediate nodes with the same node index
that belong respectively to the previous and
following flow taking into account the clockwise
order. We define these two intermediate nodes as
“near nodes”.
3.2 Force-directed Algorithm
This phase is divided into two crucial steps,
executed every iteration.
3.2.1 Nodes Merging
This phase is responsible for the update of the flow
tree that becomes obsolete after merging the nodes,
having the same node index, the same father and
within a certain distance.
Another mandatory condition is that the two
nodes are “near nodes” with each other. In this way
crossing between flows cannot occur. This satisfies
the criterion 5, for example looking at the Figure 6
the nodes that belong to the flow N can only merge
with the nodes of flow M, as well as the nodes of the
flow Q. Meanwhile the nodes of the flow M can
merge both with the nodes of flow N and Q.
When the merge event occurs, the two nodes will
be removed and a new node is created to represent
their merge (see Figure 6c). The condition of having
the same father is required to maintain the
consistence of the tree structure. The new node will
inherit the behavior of the two nodes merged.
Additionally, its flow magnitude will be the sum of
the two node’s magnitudes. Hence, at each iteration
two or more intermediate nodes are aggregated,
reducing the number of nodes and updating the tree
structure. This step satisfies the aesthetic criterion 1.
In fact merging the nodes that compose the structure
implies the merging of the flows.
ForceDirectedFlowMapLayout
173
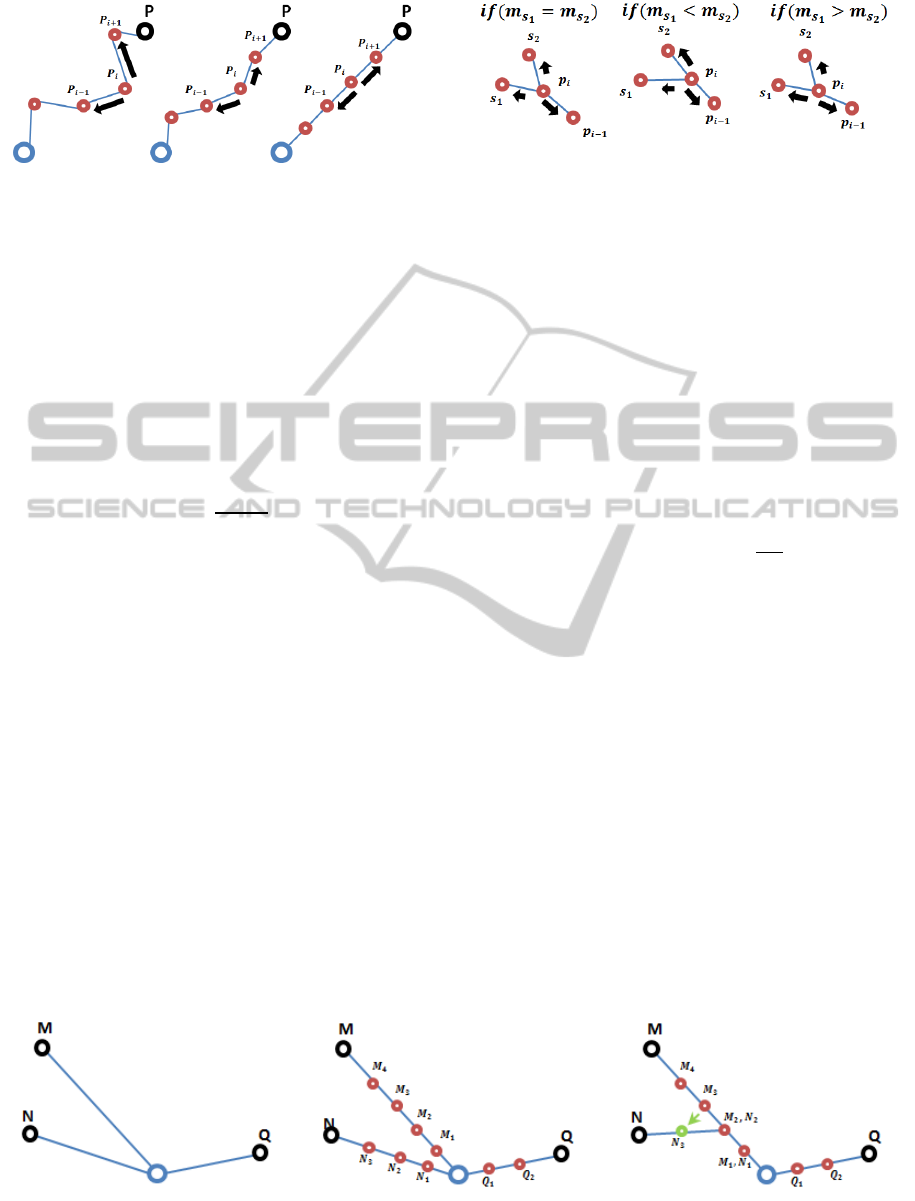
Figure 4: Stress force applied to the intermediate nodes of
a flow.
3.2.2 Nodes Moving
In this phase every intermediate node will interact
with zero, one or more other intermediate nodes.
The interaction is possible using different forces.
Electrostatic Force.
Attractive forces are calculated only between nodes
sharing the same index and father. This kind of force
is called electrostatic force and it is described by the
following equation:
,
‖
‖
(1)
where
is the vector representing the selected node
and
is the vector representing the interacting node
of index . The
notation means the unit vector of
meanwhile the
‖
‖
notation means the norm of .
The closer are two nodes and the higher will be the
force between them. However this formula takes
only in account the distance of the interacting nodes
and not their magnitude. Thus, we only apply the
force if the condition
is satisfied.
and
are respectively the magnitude of the node
and
.
Hence, nodes of smaller magnitude will be
attracted by nodes of higher magnitude.
Additionally, flows having higher magnitude will be
straighter than those one having lower magnitude.
Consequently, the aesthetic criterion 3, which states
"the flow magnitude affects the layout of the
generated map; straight lines are correlated to nodes
with high magnitude", is reached.
Figure 5: Different cases of stress force taking into
account the flow magnitude of child nodes.
Stress
Force.
In order to keep a homogeneous position from
the father node and from the child node, each node
applies a force to these nodes.
(2)
and
are respectively the vector
representing the father and the vector representing
the child of the node
. This is the force where each
node has one father and one child node. This force
tends to offset each node to a straight line formation
(see
Figure 4). When nodes have two or more child
nodes, we apply the following formula:
∑
∈
(3)
is the set of the children of the node
.
The node is moved towards the flow of higher
magnitude (see Figure 5).
is the magnitude of
the current node, that is, the sum of the magnitude of
all children.
is the magnitude of one child node.
In order to obtain smooth lines the stress force is
applied only if the force is greater than a threshold:
. This formula together with the
electrostatic force contributes to achieve the
aesthetic criterion 3 (see Figure 9).
For each iteration and pair of nodes, the force
that moves the node is equal to the sum of the
aforementioned forces.
Rejected Force.
After a certain number of iterations, an additional
force is used to avoid the overlapping of the
intermediate nodes with the target nodes.
Figure 6: Steps of the algorithm, (a) initial situation, (b) creation of the basic tree structure, (c) aggregation of nodes.
IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications
174
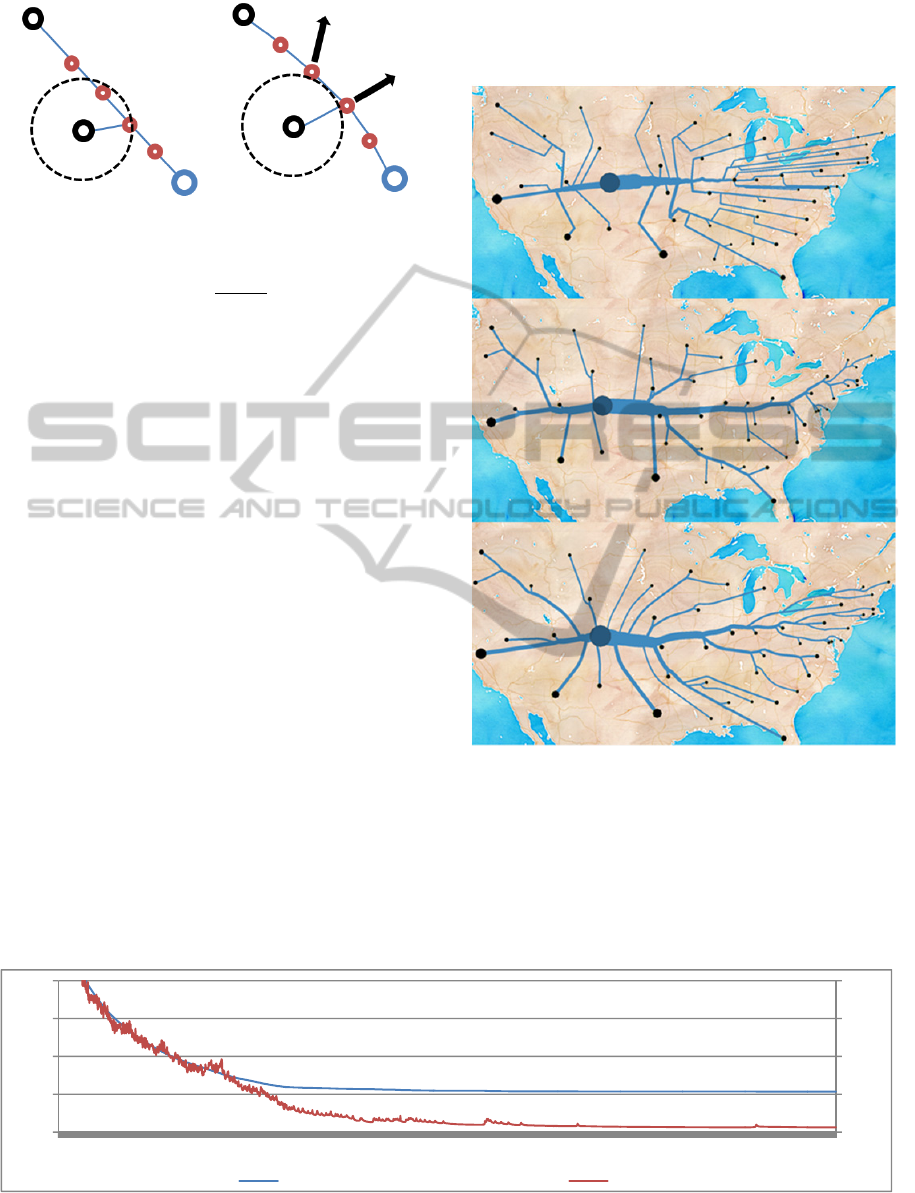
Figure 7: Rejected force applied to the intermediate nodes
of a flow.
,
‖
‖
(4)
This force is in magnitude equivalent to the
electrostatic force, but it has opposite direction (see
Figure
7). Moreover, only intermediate nodes near to
a certain distance are affected by this force. This
formula satisfies the aesthetic criterion 4 "The target
nodes are not overlapped with flows".
In this case, for each iteration and for each
couple of nodes, the following formula is calculated:
∑
,
∈
+
∑
,
∈
(5)
is the set of intermediate nodes that interact with
, i.e. they have the same index and the same father.
is the set containing all the target nodes. In order
to balance all the forces we introduce one constant
for each force. Finally, these are the two final
formula used by the algorithm, one with the rejected
force and the other without it:
∑
,
∈
+
∑
,
∈
(6)
∑
,
∈
+
(7)
and
are constants defined by the user.
can
be assigned as 2
since the reject force has to be
greater than the electrostatic force. The combination
of rejected force, electrostatic force and stressed
force creates ‘smooth’ flows despite its composition
by straight segments.
Figure 9: Flow maps of immigration from Colorado. On
top without the stress force, in the middle with the simple
electrostatic force using formula (3), on bottom the stress
force using a threshold, note in the last case as the main
flows are represented as smooth.
Figure 8: Chart showing the number of nodes (blue line, left axis) and the energy (red line, right axis) at every iteration (X
axis).
0
2
4
6
8
0
500
1000
1500
2000
1 501 1001 1501 2001
NumNodes Energy
ForceDirectedFlowMapLayout
175

Hence it fulfills the aesthetic criterion 2.
In this phase the displacements of all nodes are
calculated (accordingly with the forces) and then
these displacements are applied to the nodes.
3.3 Rendering Phase
To improve the visual appealing, we tested a few
rendering settings. First we represented flow lines
using parametric curves, in particular the natural
cubic spline (Spcath, 1974), using the intermediate
nodes with more than one child as control points.
However the result achieved was not satisfactory.
Therefore this phase is quite simple; a width line is
created from each node to its child. The thickness of
the line identifies the magnitude of its child.
Hence, this algorithm does not require the use of
parametric curves.
It is the sum of the forces and the high number of
nodes that generates a visual appealing result.
The size of the target nodes is proportional to the
flow magnitude.
4 RESULTS, DATASETS &
IMPLEMENTATION
Our program computes an optimal flow tree for most
maps in a couple of minutes on a system with 1.64
GHz and 2 GB of RAM. Flow trees are
automatically generated by our program without
requiring any user intervention.
The algorithm was initially developed using a 2D
Java canvas, but was later integrated in NASA
WorldWind (NASA, 2013).
The complexity of the algorithm is Ο
, where
is the number of iterations and is number of
nodes. To benchmark our algorithm, we decided to
use a few datasets. The results presented in this
section corresponds the dataset describing the
migration from California. We decided to pick this
dataset because we want to compare our results to
the ones of previous algorithms (see
Figure 2).
Accordingly with the initial number of 4176
intermediate nodes, it takes 227 seconds to have a
good result.
The chart in Figure 8 describes at each
interaction, the trend of the number of intermediate
nodes and the energy, that is, the sum of all the
forces, see formula (7). It is possible to notice that
the number of nodes is stable after 1200 iterations
meanwhile the energy is stable after 2300 iterations.
When the energy stability is reached, the algorithm
applies the rejected force, see formula (6). We apply
the rejected force at this stage because during the
first iterations this force can avoid the merging of
flows. This result and the time needed depend
mostly on two different factors: the number of initial
intermediate nodes and the constants used for the
different forces.
Another dataset describes the relation between
Fondazione Graphitech and its partners. The
magnitude defines the number of shared projects.
Moreover, the exports of Italian goods in all over the
World were also represented (see Figure 1).
5 CONCLUSION AND FUTURE
WORK
We have presented a force-directed algorithm for the
automatic generation of flow maps: by applying a
specific set of forces to the set of flow lines, we can
easily satisfy all criteria that characterize a well-
drawn flow map.
Additionally, we provide an evaluation of the
system that also shows that results are clearly much
better than in previous approaches.
There are a few aspects in this work that have
still margin for improvements. The performance can
be increased using the GPU (Frishman and Tal,
2007). A procedure to quantify the quality of the
visualization comparing the result with other
techniques should be performed. For example
measuring the amount of pixel-based overdraw and
empty space.
During the rendering phase an exhaustive study
has to be done to decide the more appropriate
parametric curve with high visual appealing.
At the moment the user has to define manually the
force factors; a possible improvement could be the
possibility to auto assign all the parameters
accordingly to the scale of the dataset.
Nowadays the users value the possibility to
interact with the maps. The force-directed algorithm
can be a powerful tool within such interactive
process. For example moving an intermediate node,
the others automatically are moved improving the
visual quality.
Additionally, this algorithm can be extended
taking into account more than one origin. The key
aspect will be the reduction of intersections between
flows.
IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications
176

ACKNOWLEDGEMENTS
This research has been supported by the European
Commission (EC) under the projects i-Scope (Grant
Agreement N. 297284) and SUNSHINE (Grant
Agreement N. 325161). The authors are solely
responsible this work which does not represent the
opinion of the EC. The EC is not responsible for any
use that might be made of information contained in
this paper.
REFERENCES
Andrienko, G., Andrienko, N. & Wrobel, S., 2007. Visual
analytics tools for analysis of movement data. ACM
SIGKDD Explorations Newsletter, 9(2), pp. 38-46.
Buchin, K., Speckmann, B. & Verbeek, K., 2011. Angle-
restricted steiner arborescences for flow map layout.
In: Algorithms and Computation. s.l.:Springer, pp.
250-259.
Cambridge, U., 2013. Cambridge Dictionaries Online.
[Online]
Available at: http://dictionary.cambridge.org
Cui, W. et al., 2008. Geometry-based edge clustering for
graph visualization. Visualization and Computer
Graphics, IEEE Transactions on, 14(6), pp. 1277-
1284.
datavis.ca, 2013. The Graphic Works of Charles Joseph
Minard. [Online]
Available at: http://www.datavis.ca/gallery/
minbib.php#Minard:1865e
[Accessed 11 September 2013].
Dent, B. D., 1990. Cartography: Thematic map design.
s.l.:WC Brown Dubuque, IA.
Dwyer, T., Marriott, K. & Wybrow, M., 2007. Integrating
edge routing into force-directed layout. s.l., s.n., pp. 8-19.
Eades, P., 1984. Heuristic for Graph Drawing. In: Congressus
Numerantium, vol. 42,. s.l.:s.n., pp. 149-160.
Friendly, M., 2000. Re-visions of Minard. Statistical
Computing \& Statistical Graphics Newsletter, 11(1), p. 1.
Frishman, Y. & Tal, A., 2007. Multi-level graph layout on
the GPU. Visualization and Computer Graphics, IEEE
Transactions on, 13(6), pp. 1310-1319.
Fruchterman, T. M. & Reingold, E. M., 1991. Graph
drawing by force-directed placement. Software:
Practice and experience, 21(11), pp. 1129-1164.
Holten, D. & Van Wijk, J. J., 2009. Force-Directed Edge
Bundling for Graph Visualization. s.l., s.n., pp. 983-
990.
Kamada, T. & Kawai, S., 1989. An algorithm for drawing
general undirected graphs. Inf. Process. Lett., #apr#,
31(1), pp. 7-15.
NASA, 2013. NASA WorldWind. [Online]
Available at: http://worldwind.arc.nasa.gov/java/
[Accessed 12 September 2013].
Phan, D., Xiao, L., Yeh, R. & Hanrahan, P., 2005. Flow
map layout. s.l., s.n., pp. 219-224.
Slocum, T. A., McMaster, R. B., Kessler, F. C. & Howard,
H. H., 2009. Thematic cartography and
geovisualization. s.l.:Pearson Prentice Hall Upper
Saddle River, NJ.
Spcath, H., 1974. Spline algorithms for curves and
surfaces. s.l.:Utilitas Mathematica Pub.(Winnipeg).
Tobler, W. R., 1987. Experiments in migration mapping
by computer. The American Cartographer, 14(2), pp.
155-163.
Tools, C.-S., 2001. Tobler’s Flow Mapper. s.l.:s.n.
Verbeek, K., Buchin, K. & Speckmann, B., 2011. Flow
map layout via spiral trees.. IEEE transactions on
visualization and computer graphics, 17(12), p. 2536.
ForceDirectedFlowMapLayout
177
