
Novel Parallel Algorithm for Object Recognition with the Ensemble
of Classifiers based on the Higher-Order Singular Value
Decomposition of Prototype Pattern Tensors
Bogusław Cyganek
1
and Katarzyna Socha
2
1
AGH University of Science and Technology, Al. Mickiewicza 30, 30-059 Kraków, Poland
2
The Strata Mechanics Research Institute, Polish Academy of Sciences, Reymonta 27, 30-059 Krakow, Poland
Keywords: Object Recognition, Tensor Processing, Higher-Order Singular Value Decomposition, Parallel Algorithms.
Abstract: In this paper a novel parallel algorithm for the tensor based classifiers for object recognition in digital
images is presented. Classification is performed with an ensemble of base classifiers, each operating in the
orthogonal subspaces obtained with the Higher-Order Singular Value Decomposition (HOSVD) of the
prototype pattern tensors. Parallelism of the system is realized through the functional and data
decompositions on different levels of computations. First, the parallel implementation of the HOSVD is
presented. Then, the second level of parallelism is gained by partitioning the input dataset. Each of the
partitions is used to train a separate tensor classifiers of the ensemble. Despite the computational speed-up
and lower memory requirements, also accuracy of the ensemble showed to be higher compared to a single
classifier. The method was tested in the context of object recognition in computer vision. The experiments
show high accuracy and accelerated performance both in the training and classification stages.
1 INTRODUCTION
Tensor based methods found great interest in pattern
recognition domain. In computer vision these were
also shown to provide excellent results in object
recognition (Vasillescu and Terzopoulos, 2002;
Savas, 2007; Cyganek, 2010). Tensor based methods
account for multidimensional nature of processed
data. However, the price for tensor processing and
decomposition, necessary for object recognition, is
high memory and computation time. Thus, important
is development of new parallel algorithms for tensor
processing which allow full exploitation of the
contemporary multi-core microprocessor. In this
paper we propose such a new parallel algorithm, as
will be discussed.
For different object recognition problems there
are many examples of classifiers which can achieve
either high accuracy or fast response (Duda, 2000).
However, the goal of reaching high accuracy and
response factors is easier with classifiers which
architecture naturally allows parallel processing. For
many real data classification tasks such requirements
can be accomplished with ensembles of classifiers,
which recently gained much attention (Kuncheva,
2005; Polikar, 2006; Cyganek, 2010). Such
ensembles usually rely on operation of a group of
cooperating classifiers. When cooperating in an
ensemble, despite their moderate individual
classification abilities, such a group frequently
shows superior accuracy compared to the more
complex but single classifiers (Kuncheva, 2005;
Polikar, 2006).
In this paper the problem of parallel
implementation of the ensemble composed of tensor
classifiers operating with the multi-dimensional data
is discussed. The system extends our previous work
on the problem of handwritten digits classification,
as well as road signs recognition. These showed high
accuracy using a serial software implementation
(Cyganek, 2010; Cyganek, 2012). In this paper we
present parallel versions of the mentioned
implementation.
In the proposed system, the member classifiers
perform subspace classification in the spaces
spanned by the bases obtained from the Higher-
Order Singular Value Decomposition (HOSVD) of
the prototype pattern tensors. The HOSVD classifier
shows good results when applied to multi
dimensional data, such as images (Vasilescu and
648
Cyganek B. and Socha K..
Novel Parallel Algorithm for Object Recognition with the Ensemble of Classifiers based on the Higher-Order Singular Value Decomposition of Prototype
Pattern Tensors.
DOI: 10.5220/0004745606480653
In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 648-653
ISBN: 978-989-758-004-8
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)
Terzopoulos, 2002; Cyganek, 2013). This is due to
tensor processing which allows separate control of
all intrinsic dimensions of data. Let us recall that in
the classical PCA-based classification method,
images are first vectorized and, in the result, the
obtained subspaces are spanned by vector bases
(Turk, 1991). Contrary to this, in the HOSVD
method the bases of the orthogonal pattern subspace
are spanned by the two-dimensional tensors
(images). In both methods, when classifying an
unknown pattern, these are projected onto the
subspaces of each of the trained class and the best
fitting projection is returned. However, in the tensor
case the bases are multidimensional. Nevertheless,
computation of tensor decompositions, such as the
HOSVD, is both time and memory demanding.
In the proposed system parallelism is obtained
through the functional and data decompositions on
different levels of computations. First, the parallel
implementation of the HOSVD is presented. Then,
the second level of parallelism relies on data
decomposition. For this purpose, the training dataset
is partitioned into smaller chunks, either by
clustering or bagging, as discussed in our previous
works (Cyganek, 2013). Each of the training data
partitions is then used to concurrently train a
corresponding separate tensor classifier of the
ensemble. Thanks to this, also memory requirements
for the training stage are greatly reduced. Last but
not least, the third possible level of parallelism is
obtained on the multi-class level since each of the
training classes can be trained independently of the
others. Parallel operation is also possible at the
response time of the system, since each subspace
projection can be also computed independently. The
experiments with the proposed system applied to the
problem of image recognition show high accuracy,
adjustable memory requirements, and accelerated
performance both in the training and response
stages.
2 MULTI-LEVEL PARALLEL
ARCHITECTURE OF THE
ENSEMBLE OF MULTI-CLASS
CLASSIFIERS
As already mentioned, tensor processing usually
results in high computational and memory demands.
The former can be alleviated by parallel
implementation of the specifically chosen parts of
the system, as will be discussed. In this approach we
exploit both strategies for parallel decompositions:
Data decomposition.
Functional decomposition.
However, in many real situations, parallel
processing of some software modules leads also to
higher memory demands. Therefore both aspects,
i.e. computational speed-up due to concurrency, as
well as memory requirements, need to be considered
together. These issues are addresses in the proposed
classification system.
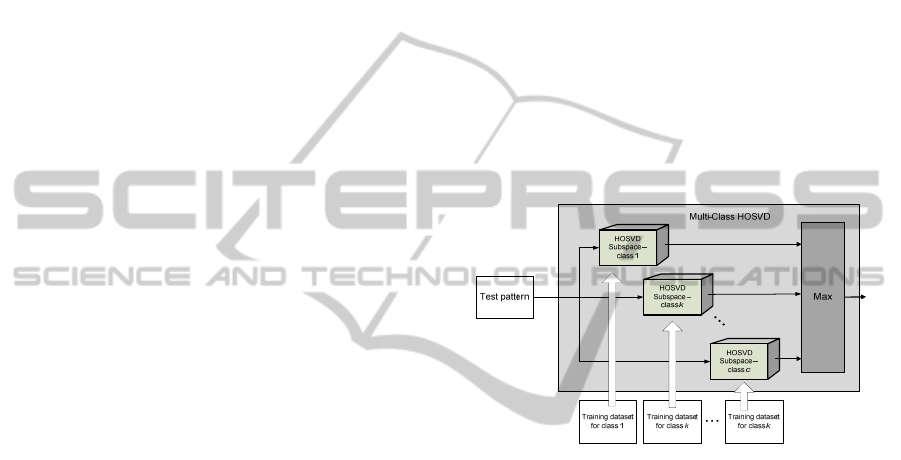
Figure 1 shows an architecture of a single multi-
class HOSVD based classifier. Each training dataset
of each class is used to build a separate tensor
subspace. During classification, a test pattern is
projected onto each of these subspaces to check the
closest class. Parallel operation of this module is
obtained due to the data decomposition, as well as
parallel implementation of the HOSVD algorithm, as
will be described.
Figure 1: Architecture of a HOSVD based single classifier
for multi-class classification. Each training dataset of each
class is used to build a separate tensor subspace. A test
pattern is projected onto each of the subspaces to check
the best fit. Parallel operation of this module can be
obtained due to data decomposition, as well as parallel
implementation of the HOSVD algorithm.
Figure 2 presents an extension to the system in
Figure 1. It is an ensemble composed of the multi-
class HOSVD classifiers. Each grayed block has a
structure as shown in Figure 1.
3 PARALLELIZATION OF THE
HOSVD SUBSPACE
CLASSIFIER
Tensors in data mining can be interpreted as
multidimensional arrays. Processing and analysis of
multi-dimensional data, such as images, builds well
into this framework. However, an analysis of data
content requires proper decomposition of pattern
tensors. One of the most popular decomposition
NovelParallelAlgorithmforObjectRecognitionwiththeEnsembleofClassifiersbasedontheHigher-OrderSingular
ValueDecompositionofPrototypePatternTensors
649

method is the HOSVD (Cichocki, 2009; Lathauwer,
1997; Lathauwer, 2000; Cyganek, 2013). It can be
used to build orthogonal spaces which can be then
used for pattern recognition in a way similar to the
subspace projection methods (Duda, 2000)(Turk,
1991). This procedure is briefly outlined in this
section. More information on tensors in signal
processing can be found in literature, e.g. (Cichocki,
2009; Lathauwer, 1997; Lathauwer, 2000; Cyganek,
2013; Cichocki, 2009).
Multi-Class
HOSVD
1
Multi-Class
HOSVD
i
Multi-Class
HOSVD
N
Classifier
Combiner
Data multiplexer (bagging, clustering)
ENSEMBLE OF HOSVD CLASSIFIERS
Test pattern
Data filtering (feature extraction)
Training dataset
for class 1
Training dataset
for class k
Training dataset
for class k
Figure 2: Architecture of the ensemble composed of the
multi-class HOSVD classifiers. Each base classifier has a
structure shown in Figure 1 (grayed blocks). Each member
multi-class classifier is trained with its partition of training
data from each class. Data partitions are obtained due to a
clustering or a bagging process.
In this section let us briefly present the main
concepts of tensors and their decomposition. The
first concept is the k-mode vector of a P-th order
tensor
12 P
NN N
. It is a vector obtained from
the elements of by changing only one index n
k
,
and keeping all other fixed. The second important
concept is the operation of the k-mode flattening of a
tensor. For a tensor , a result of its k-mode
flattening is the following matrix (Lathauwer, 1997;
Kolda, 2008)
12 1 1kkkP
NNNNN N
k
T
.
(1)
Now we can define the HOSVD decomposition.
For any P-dimensional tensor
12 mnP
NN N N N
, the HOSVD
decomposition allows to equivalently represent in
the following form (Lathauwer, 1997)
1122 PP
SS S
.
(2)
In (2) S
k
denote unitary matrices of dimensions
N
k
N
k
, which are called mode matrices. The tensor
12 mnP
NN N N N
is a core tensor which
fulfills properties of the sub-tensor orthogonality and
decreasing energy value (Lathauwer, 1997)(Kolda,
2008).
Lathauwer proposed a method of computation of
the HOSVD which is based on successive
application of the matrix SVD decompositions to the
flattened matrices of a given tensor (Lathauwer,
1997). The HOSVD decomposition algorithm for a
P-dimensional tensor is outlined in Figure 3. It
can be easily observed that computation of the
HOSVD requires a series of computations of the
SVD decompositions on flattened matrices. These
are independent versions (different modality) of the
input tensor. Therefore it is possible to run all these
SVD decompositions concurrently, which must be
synchronized on a barrier just before computation of
the core tensor in (8), however. Figure 3 shows the
algorithm for computation of the HOSVD. Its
grayed area can be run concurrently, as discussed.
Let us now observe that, thanks to the
commutative properties of the k-mode
multiplication, for each mode matrix S
i
in (2) the
following sum can be constructed
1
P
N
h
hPP
h
s
.
(3)
Further, it can be shown that tensors
1122 1 1hPP
SS S
(4)
in (3) constitute the basis tensors and s
h
P
are
columns of the unitary matrix S
P
(Lathauwer,
1997)(Lathauwer, 2000). Thus, they form an
orthogonal basis which spans a subspace. This
property is used to construct a HOSVD based
classifier (Savas, 2007; Cyganek, 2010).
In each subspace spanned by tensors
h
, pattern
recognition can be stated as a testing of a distance of
a given test pattern P
x
to its projections in each of
the spaces spanned by the set of the bases
h
in (4).
That is, the following optimization process needs to
be solved (Savas, 2007):
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
650

2
,
1
min
i
h
i
H
ii
xhh
ic
h
Q
cP
,
(5)
where the scalars c
i
h
denote unknown coordinates of
the pattern P
x
in the space spanned by
h
i
, and H≤N
P
denotes a number of chosen dominating
components. It can be further shown that to
minimize (5) we need to maximize the following
value (Savas, 2007; Cyganek, 2013)
2
1
ˆ
ˆ
ˆ
,
H
i
ihx
h
P
.
(6)
In other words, the (single) HOSVD based
classifier returns a class i for which its
i
from (6) is
the largest.
begin
for each k=1, …, P do
1. From Eq.(1) compute k-
mode flattened matrix T
k
of
tensor
2. Compute S
k
from the SVD
decomposition of T
k
T
kkkk
TSVD
(7)
end
Compute the core tensor from all
matrices S
k
11 22
TT T
PP
SS S
(8)
end
Figure 3: Algorithm for computation of the Higher-Order
Singular Value Decomposition of tensors of any
dimensions. The steps in gray can be executed
concurrently.
Each of the multi-class HOSVD blocks denotes a
single classification sub-system, as presented in
Figure 1. Each member multi-class classifier is
trained with its partition of training data from each
class. In the proposed system data partitions are
obtained due to the bagging process which also
showed to be superior to the clustering. However,
thanks to data partitions which are less numerous
than the whole training set, training of each of the
HOSVD member classifiers if possible on
computers with very limited memory. More details
on this can be found in our previous publication
(Cyganek, 2012).
4 IMPLEMENTATION AND
EXPERIMENTAL RESULTS
The presented method was implemented in C++,
supported by the DeRecLib software from
(Cyganek, 2013) and the OpenMP library for the
multicore processing (Chapman, 2008; OpenMP,
2013). The experiments were carried out on the
computer with 8 GB RAM and the Pentium® Quad
Core Q 820 microprocessor (eight cores due to the
hyper-threading technology (Intel, 2013)).
For the experiments the USPS dataset was used
which contains selected and preprocessed scans of
the handwritten digits (Hull, 1994)(LeCun, 1998), as
shown in Figure 4. Each test and train pattern is a
16
16 gray level image. The database is divided into
the training and testing partitions. The former counts
7291, and the latter 2007 patterns, respectively.
However, the bagging process was applied, as
described. In effect the training dataset is split into
smaller partitions. In this paper two partitions of 64
and 128 elements were used in experiments
(Cyganek, 2012).
Figure 4: Examples of the training (top) and test (bottom)
datasets from the USPS database (from data).
In our experiments parallelism on different levels
of computations were measured. Also, each parallel
realization was analyzed in the context of memory
requirements. The following parallel configurations
were built and analyzed:
1. Parallel version of the HOSVD algorithm (see
Figure 3).
2. Parallel construction of the HOSVD multi-
classifier shown in Figure 1 (i.e. each subspace
built concurrently).
3. Parallel training of the ensemble of multi-class
NovelParallelAlgorithmforObjectRecognitionwiththeEnsembleofClassifiersbasedontheHigher-OrderSingular
ValueDecompositionofPrototypePatternTensors
651
classifiers, shown in Figure 2 (i.e. each
member classifier trained concurrently with its
data partition).
4. Parallel run-time system response (formula (6)).
From the above, the version no. 1 resulted in a
speed-up ratio of 20-30%. This is due to two factors.
First reason is a relatively small number of parallel
threads since number of SVD computations in the
HOSVD algorithm (Figure 3) is equal to the tensor
valence P. In our case P=3 since the input tensors
consists of a number of 2D image prototypes. In
effect, despite a high number of computations, the
time overhead related to the thread launch makes the
whole operation less effective. The second factor
relates to a number of memory blocks allocated by
the SVD procedure in our framework. In a serial
implementation some of these allocations can be
reused which makes computations faster. However,
in the cases of higher order tensors, such as ten or
above, this way of parallelism can be considered
provide higher acceleration level than in the
presented experiments. This is also due to the fact
that the main tensor does not need to be copied.
Instead, it is accessed through the proxy objects,
each responsible for a different flattening mode.
This feature was implemented in our software
framework (Cyganek, 2013).
Because of the above, the two other parallel
processing options, no. 2 and 3, were analyzed.
These gave the best results, however when used
separately. Their concurrent application would result
in the nested parallelism which showed to be
ineffective in our system due to high thread
overhead (there are only eight cores). However, this
option can be used in systems with higher number of
cores or graphic processing units (GPU).
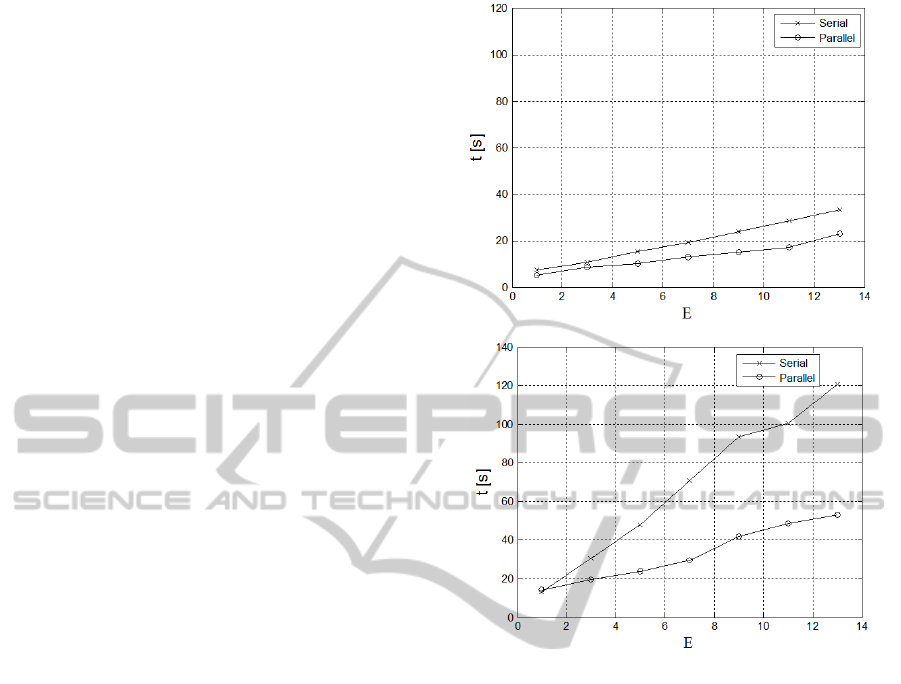
Figure 5 shows a speed-up ratio of the training
process in the serial and parallel implementations,
respectively. The plots are drawn for a different
number of member classifiers E in the ensemble and
different chunks of data from bagging. These are 64
chunks in Figure 5a, and 128 chunks in Figure 5b,
respectively. Analyzing the plots in Figure 5 we
noticed a two-times speed-up ratio in the OpenMP
implementation and with 8 cores. The speed-up ratio
is higher for larger chunks of data (128 in this case).
However, increasing numbers of data in the chunks
has its limits due to memory capacity (only 8 GB in
our system), as well as time for data transfers.
Nevertheless, the proposed data decomposition at
this level pave the way for parallel implementation.
Interestingly, application of many classifiers (an
ensemble) leads also to higher accuracy of the
Figure 5: System training speed-up ratio of the serial and
parallel implementations for different number of member
classifiers E in the ensemble and different chunks of data
from bagging: 64 chunks (upper), 128 chunks (lower).
system when compared to a single classifier. The
highest accuracy A=95% was obtained for E=13
member classifiers in the ensemble and 128 chunks
of data, as reported in our previous work (Cyganek,
2012). Nevertheless, the values of data in chunks
and classifiers in the ensemble need to be
determined experimentally since they depend on
type of used data.
Finally, parallel version no. 4 from the above list
was tested. It resulted in speed-up ratio of 10-15% in
the OpenMP software implementation. However,
after that the GPU implementation was implemented
and checked (CUDA platform) which resulted in a
speed-up ratio of 30-120 times depending on a size
of the base tensors
h
i
in (6). This option can be used
in demanding classification tasks with large base
tensors
h
i
, or in brute-force tasks in which patterns
are checked in each pixel position of an image, etc.
VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications
652

5 CONCLUSIONS
In this paper the parallel implementation of the
ensemble composed of classifiers operating with
multi-dimensional data is presented. The classifiers
of the ensemble are based on the Higher-Order
Singular Value Decomposition of the prototype
pattern tensors. Parallelism of the system is obtained
through the functional and data decompositions on
different levels of computations. As presented, the
first level of parallelism can be achieved by
functional decomposition of the SVD step in the
HOSVD algorithm. The second level of parallelism
is obtained by concurrent subspace construction for
each of the HOSVD classifiers. The third level of
parallelism is due to data decomposition with proper
partitioning of the input dataset (in our system this
was achieved by data bagging). The proposed
method also greatly limits memory requirements.
Finally, the response time of the system can be
significantly accelerated, which constitutes the
fourth level of parallelism in the presented
classification system. The experiments conducted on
image recognition show high accuracy and the
training speed-up ratio in order of 100-150% in the
multi-core operation. Despite the computational
advantages, also accuracy of the ensemble showed
to be higher than in the case of a single classifier.
ACKNOWLEDGEMENTS
This work was supported by the Polish National
Science Centre NCN, the grant no. DEC-
2011/01/B/ST6/01994, in the years 2013-2014.
REFERENCES
Cichocki, A., Zdunek, R., Amari, S., 2009. Nonnegative
Matrix and Tensor Factorization. IEEE Signal
Processing Magazine, Vol. 25, No. 1, pp. 142-145.
Chapman, B., Jost, G., Van Der Pas, A.R., 2008. Using
OpenMP. Portable Shared Memory Parallel
Programming. MIT Press.
Cyganek, B., 2010. An Analysis of the Road Signs
Classification Based on the Higher-Order Singular
Value Decomposition of the Deformable Pattern
Tensors, Lecture Notes in Computer Science, Vol.
6475, Springer, pp. 191–202.
Cyganek, B., 2011. Adding Parallelism to The Hybrid
Image Processing Library in Multi-Threading and
Multi-Core Systems. IEEE International Conference
on Networked Embedded Systems for Enterprise
Applications, pp. 103–110.
Cyganek, B., 2012. Ensemble of Tensor Classifiers Based
on The Higher-Order Singular Value Decomposition.
Lecture Notes in Artificial Intelligence, Vol. 7209,
Springer, pp. 578–589.
Cyganek, B., 2013. Object Detection in Digital Images.
Theory and Practice, Wiley.
Duda, R. O., Hart, P. E., Stork, D. G. 2000. Pattern
Classification. Wiley.
Hull, J., 1994. A Database for Handwritten Text
Recognition Research. IEEE Transactions on Pattern
Analysis and Machine Intelligence, Vol. 16, No. 5, pp.
550–554.
Intel, 2013. www.intel.com.
Kolda, T. G., Bader, B. W., 2008. Tensor Decompositions
and Applications. SIAM Review, Vol. 51, No. 3, pp.
455-500.
Kuncheva, L. I., 2005. Combining Pattern Classifiers.
Wiley.
Lathauwer de, L., 1997. Signal Processing Based on
Multilinear Algebra. PhD dissertation, Katholieke
Universiteit Leuve.
Lathauwer de, L., Moor de, B., Vandewalle, J., 2000. A
Multilinear Singular Value Decomposition. SIAM
Journal of Matrix Analysis and Applications, Vol. 21,
No. 4, pp. 1253-1278.
LeCun, Y., Bottou, L., Bengio, Y., Haffner, P., 1998.
Gradient-Based Learning Applied to Document
Recognition. Proceedings of the IEEE on Speech &
Image Processing. Vol. 86, No. 11, pp. 2278-2324.
OpenMP, 2013. www.openmp.org.
Polikar, R., 2006. Ensemble Based Systems in Decision
Making. IEEE Circuits and Systems Magazine. pp. 21-
45.
Savas, B., Eldén, L., 2007. Handwritten Digit
Classification Using Higher Order Singular Value.
Pattern Recognition, Vol. 40, No. 3, pp. 993-1003.
Turk, M., Pentland, A., 1991. Eigenfaces for Recognition.
Journal of Cognitive Neuroscience Vol. 3, No. 1, pp.
71–86.
Vasilescu, M.A.O., Terzopoulos, D., 2002. Multilinear
Analysis of Image Ensembles: TensorFaces, Lecture
Notes in Computer Science, Vol. 2350, Springer, pp.
447-460.
NovelParallelAlgorithmforObjectRecognitionwiththeEnsembleofClassifiersbasedontheHigher-OrderSingular
ValueDecompositionofPrototypePatternTensors
653
