Experiments Assessing Learning of Agent Behavior using Genetic

Programming with Multiple Trees

Takashi Ito, Kenichi Takahashi and Michimasa Inaba

Graduate School of Information Sciences, Hiroshima City University, Hiroshima, Japan

Keywords: Genetic Programming, Autonomous Agent, Conditional Probability, Island Model.

Abstract: In this paper, experiments to assess agent behavior learning are conducted to demonstrate the performance

of genetic programming (GP) with multiple trees. Using the methods, each has a chromosome representing

agent behavior as several trees. We have proposed two variants using the conditional probability and the

island model to improve the methods’ performance. In GP using the conditional probability, individuals

with high fitness values are used to produce conditional probability tables to generate individuals in the next

generation. In GP using the island model, the population is divided into two islands of individuals: one

island maintains diversity of individuals. The other emphasizes the accuracy of the solution. Moreover, this

paper improves methods to seek the optimal number of executions of each tree in an individual. Those

methods are applied to a garbage collection problem and a Santa Fe Trail problem. They are compared with

traditional GP, GP with control nodes, and genetic network programming (GNP) with control nodes.

Experimental results show that our methods are effective for improving the fitness.

1 INTRODUCTION

In the field of artificial intelligence, which aims at

modeling human intelligence, many researchers

have studied search algorithms to obtain agent

decisions and action rules to reach a goal.

Reinforcement learning and evolutionary learning

are representative means to learn agent behavior.

Evolutionary methods are known to be able to obtain

optimum rules for agent action in a broad search

space. Among evolutionary methods, genetic

programming (GP) and genetic network

programming (GNP) have been investigated eagerly

and widely (Koza, 1992; Hirasawa et al., 2001; Iba,

2002; Mesot et al., 2002; Tanji and Iba, 2010).

Genetic network programming (GNP) is also known

to able to find better solutions than genetic

programming (GP) can (Hirasawa et al., 2001; Iba,

2002). As an extensional method of GNP, GNP with

multi-start nodes and GNP with control nodes

(GNP

) have been proposed (Murata and

Nakamura, 2006; Eto et al., 2007). Although GNP

can search for better solutions than GNP can, GNP

has some shortcomings. For example, the readability

of GNP

is low because obtained rules are

expressed as a network. Moreover, the network

structure of GNP

corresponding to agent rules

tends not to be fully used. As a method to improve

readability, GP with control nodes (GP

) has been

proposed. In GP

, an individual consists of several

trees that express action rules (Minesaki, Ueda, and

Takahashi, 2009). Each tree is constructed with a

part of a network where the tree root node

corresponds to a control node of GNP

. The

GNP

network structure is divided into several

trees. Therefore, the GP

readability becomes

higher than that of GNP

. However, the GNP

ability is higher than that of GP

To improve the GP

ability, we have proposed

using conditional probabilities (GP

CN_CP

)

(Morioka, Ueda, and Takahashi, 2011) and the

island model (GP

CN_IL

) (Ito, Takahashi, and Inaba,

2013). We introduced conditional probabilities

between nodes to use their relations in individuals

with high fitness values. As a similar and more

general idea, frequent trees, i.e., subtrees that

frequently appear in the population, have been

proposed. Chunks of strongly related nodes are

regarded as frequent subtrees (Ono et al., 2012; Ono

et al., 2013). In GP

CN_CP

, individuals in the next

generation are generated using either genetic

operations or conditional probability tables, where

the conditional probability tables are updated using

264

Ito T., Takahashi K. and Inaba M..

Experiments Assessing Learning of Agent Behavior using Genetic Programming with Multiple Trees.

DOI: 10.5220/0004751402640271

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 264-271

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

individuals with high fitness values. Thereby,

CN_CP

can maintain the diversity of individuals

and can inherit the structures of excellent individuals

to the next generation with a high probability, where

the excellent individuals are the individuals that

have obtained appropriate rules for agent behavior in

the environment.

Additionally, we have used the island model to

promote diversity for overcoming local optima and

for improving the fitness because GP

has a

shortcoming: it tends to be trapped by local optima

(Iwashita and Iba, 2002). We designate GP

using

the island model GP

CN_IL

. In GP

CN_IL

, the population

is divided into two islands of individuals: One island

emphasizes maintenance of the diversity of

individuals. The other emphasizes improving fitness.

We designate the former as the diversity-oriented

island. The latter is the performance-oriented island.

The island model can be expected to prevent the

solution by GP

CN_IL

from reaching a local optimum

because GP

CN_IL

can emphasize two points such as

maintaining diversity and improving the fitness.

In this paper, we improve the method to seek the

optimal number of processing nodes activated per

tree (P) by gradually updating the value of P as

evolution proceeds. We designate GP

CN_CP

and

CN_IL

with the improved search method for P

CN_CP

(e) and GP

CN_IL

(e). We apply traditional

GNP

and GP

and our methods, GP

CN_CP

CN_IL

, GP

CN_CP

(e), and GP

CN_IL

(e) to a garbage

collection problem and Santa Fe Trail problem to

compare the performance. We use these problems

because the garbage collection problem and the

Santa Fe Trail are used to show the ability of GNP

and GP (Koza, 1992; Mesot et al., 2002; Eto et al.,

2007; Ono et al., 2013; Iwashita and Iba, 2002).

Although the symbolic regression problem exists as

another type of benchmark problem for GP and GNP,

we chose the garbage collection problem and the

Santa Fe Trail problem because the objective of this

paper is to obtain rules for agent actions. The former

is relatively easy, but the latter is difficult.

Experimentally obtained results are presented to

confirm the effectiveness of those methods.

2 GNP WITH CONTROL NODES

(GNP

)

GNP with control nodes (GNP

) has been proposed

as an extensional method of GNP; GNP

can

search for better solutions than GNP. Each

individual of GNP

has a network structure in

which nodes of three kinds are connected: control

nodes, branch nodes, and action nodes. Nodes of the

latter two kinds are also used in GNP. An example

of an individual of GNP

is presented in Figure 1.

The control node in GNP

controls the transition of

nodes that an agent refers to. Each control node has

a number representing the order of its execution. An

agent starts to refer to the node indicated by the

control node 1 and continues referring to nodes

according to the network connection until the

designated number of action nodes is executed.

Subsequently the agent refers to the control node

with the next number and carries out the node

designated by the control node. The agent refers to

the control node with the smallest number after the

control node with the largest number is processed.

Genetic operations of GNP

are only crossover and

change of node connection. The connection of

control nodes is not changed by genetic operations.

3 GENETIC PROGRAMMING

WITH CONTROL NODES

(GP

)

3.1 Genetic Programming with Control

Nodes (GP

)

To improve the readability of GNP

and to

maintain its efficiency, GP

has been proposed. An

example of an individual of GP

is depicted in

Figure 2. Individuals of GP

comprise several trees

which correspond to rules. The trees have numbers

corresponding to numbers of control nodes. The

number indicates the order in which an agent refers

to a tree. The trees correspond to networks starting

from control nodes of GNP

. The number of trees

in one individual, M (i.e. the number of control

nodes), is determined in advance. In the action phase

of autonomous agents, agents receive perceptual

information from the environment and determine

actions by referring to trees according to the tree

numbers.

A tree comprises terminal nodes and non-

terminal nodes. A terminal node denotes an action

that an agent can execute. A non-terminal node

denotes branch information by the perceptual

information. An agent refers to a tree with the

smallest number and carries out an action according

to the tree. When the number of actions that an agent

carries out using the tree exceeds a designated

number P, the agent refers to a tree with the next

number. The number P represents the number of

ExperimentsAssessingLearningofAgentBehaviorusingGeneticProgrammingwithMultipleTrees

265

Figure 1: Example of an individual of GNP

Figure 2: Example of an individual of GP

where the

number of trees is 4.

executions. After the tree with the largest number is

processed, the agent refers to the tree with the

smallest number.

The algorithm of GP

is the same as that of the

traditional GP. First, GP

performs the initial

generation of the population of individuals. Then, it

evaluates the fitness of each that has been generated.

If the condition to terminate processing is not met,

then it performs reproduction of the population of

individuals and genetic operations. It then generates

a population of individuals in the next generation.

Here, the condition to terminate processing is that

the number of generation becomes the designated

number of generations. Although the GP

individuals have several trees, the fitness is

evaluated for each individual, not for each tree.

Details of the genetic operations for GP

are

described in the next subsection.

3.2 Genetic Operations

Because one individual has several trees unlike

normal GP in GP with control nodes (GP

), for

each genetic operation an individual is selected at

random. then one tree is selected at random from the

selected individual. Each genetic operation is

applied to the selected tree.

3.2.1 Crossover

Crossover is the operation that exchanges subtrees in

trees of two parent individuals. First, two trees are

selected from two parent individuals respectively,

and nodes are selected at random for crossover from

all nodes of each tree. Second, subtrees whose root

nodes are the selected nodes are exchanged.

However, no crossover is executed when a tree

consists only of a root node.

3.2.2 Mutation

We use mutation of two kinds: a mutation-tree and a

mutation-node. A mutation-tree is an operation that

randomly selects one node from all nodes in a tree of

a parent individual and then replaces the subtree

subsequent to the selected node with a randomly

generated subtree. The mutation-node is the

operation that changes the content of the selected

node after selecting a node in a tree of a parent

individual. In mutation-node, if the selected node is

a non-terminal (terminal) node, then the node

content is replaced with another content of a non-

terminal (terminal) node. When any content of a

non-terminal node is changed, the edge number

might change. If the number of edges of a new

content becomes smaller, then the extra edges and

the succeeding subtrees are removed. However, if

the number of edges becomes larger, then randomly

generated subtrees are connected to the increased

edges.

3.2.3 Inversion

The inversion operation selects only a non-terminal

node at random from all nodes of a tree in a selected

individual, selects at random two child nodes. Then

it exchanges the subtrees that have the two child

nodes as the root nodes.

3.3 GP

using Conditional

Probabilities (GP

CN_CP

)

In GP

, a problem that the search ability is

insufficient exists. In order to utilize connections

among nodes of trees in individuals with high fitness

values, GP

using conditional probabilities

(GP

CN_CP

) has been proposed. The GP

CN_CP

algorithm is the following.

Individual

(

M=4

)

C1 C2 C3 C4

Identifier

Non-terminal node Terminal node

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

266

1: BEGIN

2: Generate initial population;

3: WHILE(i < N

) DO

4: Evaluate fitness;

5: WHILE(j < N

) DO

6: IF(Fit[j] >= T

) THEN

7: Add node counts to frequency

tables;

8: END IF

9: j++;

10: END DO

11: Build conditional probability

tables;

12: j=0;

13: WHILE(j < N

) DO

14: IF(j < N

) THEN

15: Generate an individual using

conditional probability tables;

16: ELSE

17: Generate an individual with

genetic operations;

18: END IF

19: j++;

20: END DO

21: i++;

22: END DO

23: END.

In the GP

CN_CP

algorithm, i and j respectively

denote the generation number and the individual

number. N

and N

respectively represent the

maximum generation number and the maximum

individual number. Moreover, Fit[j] is the fitness

value of individual j. T

stands for the fitness

threshold to build conditional probability tables, and

signifies the maximum number of individuals

generated using conditional probability tables.

CN_CP

differs from GP

in the way of

generating individuals for the next generation. In

CN_CP

, trees of individuals in the next generation

are generated using conditional probabilities in

addition to genetic operations. The conditional

probabilities are calculated from individuals with

high fitness values and are stored into conditional

probability tables for nodes.

Conditional probability tables are produced per

tree number using frequency tables that are produced

using individuals with high fitness values. We

expect to obtain action rules corresponding to roles.

First, frequency tables are made by counting the

frequency of child nodes attached to branching

edges for perceptual information of each

nonterminal node in trees of which the numbers are

the same over individuals. Additionally, we maintain

the diversity of individuals by inheriting frequency

tables of the previous generation at a constant rate to

the next generation. We update the values in the

frequency tables as follows.

























1α













α

(1)

Therein, F

(i) is the next frequency table for tree i,

(i) is the frequency table used in the previous

generation, and F

(i) is the frequency table

evaluated using only individuals of the current

generation. We designate



1α



as the inheritance

probability, where α∈



0,1



. The frequency table for

tree i in the current generation is calculated from

trees whose number is i in the individuals with high

fitness values in the current generation. We

designate the individuals with high fitness values as

elite individuals. We produce conditional probability

tables from the frequency tables.

We generate individuals using conditional

probabilities. In generating individuals using

conditional probabilities, the root node of a tree is

determined with the occurrence probability of each

node. Then, we determine child nodes of the root

node using the conditional probability table for the

root node. The decisions of child nodes using

conditional probabilities are repeated until a terminal

node is selected for the child node or until the depth

of the child node reaches the maximum depth

determined in advance. When the child node depth is

the maximum depth, a terminal node is selected for

the child node.

3.4 GP

using the Island Model

(GP

CN_IL

)

A shortcoming of traditional GP

is that it tends to

end the search with local optima when evolution

proceeds. We propose GP

using the island model

(GP

CN_IL

) as a method to improve the performance.

The objective of GP

CN_IL

is to increase the fitness

while maintaining the diversity. The island model is

a parallel distributed processing method which has

been proposed as an extension of the genetic

algorithm. In GP

CN_IL

in this study, individuals are

divided into two islands of individuals: the diversity-

oriented island and the performance-oriented island.

A flowchart of GP

CN_IL

is presented in Figure 3,

where N

represents the maximum generation

number. First, we generate an initial population.

Second, we evaluate the population of individuals

and perform migration, which is one feature of the

island model. Subsequently if the termination

condition is not satisfied, then we perform selection

and generate individuals of the next generation. The

termination condition is the same as GP

: when

the number of generations reaches the designated

number, the algorithm stops.

We preserve elite individuals and generate

individuals of the next generation by crossover in

ExperimentsAssessingLearningofAgentBehaviorusingGeneticProgrammingwithMultipleTrees

267

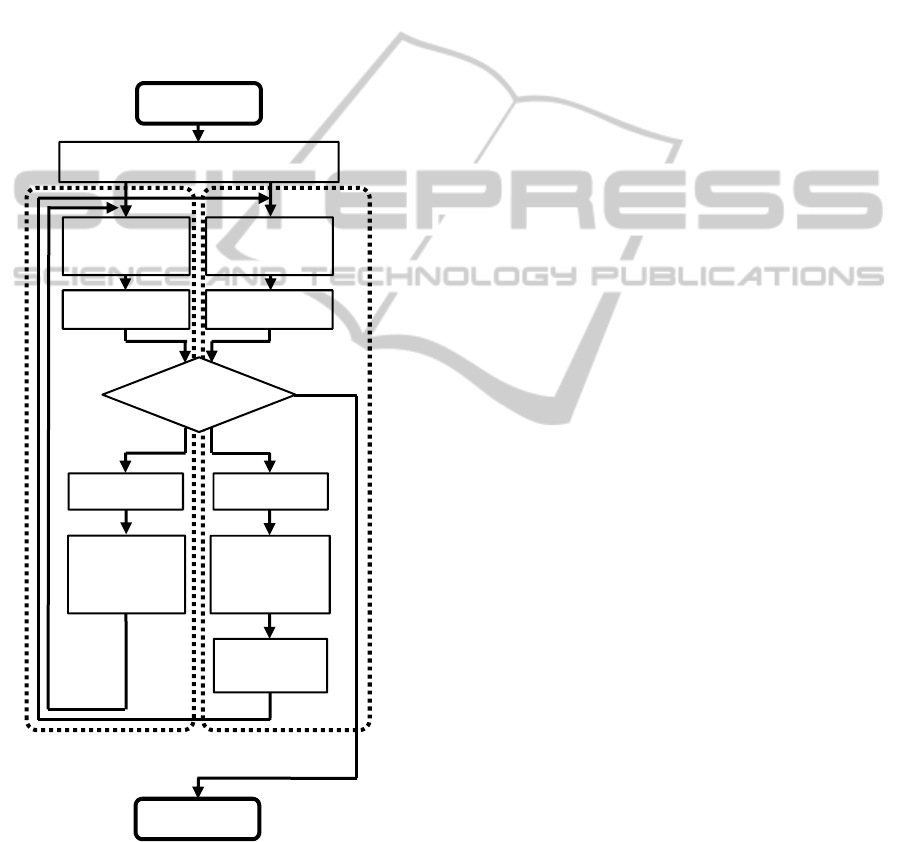
the performance-oriented island. However, in the

diversity-oriented island, we generate individuals of

the next generation by replacing some individuals

with randomly generated individuals and using

genetic operations. Crossover used in the

performance-oriented island is the depth-dependent

crossover (Ono et al., 2012). Unlike the normal

crossover, the depth-dependent crossover determines

a depth in the selected tree at random and then

selects a node for the crossover from nodes at that

depth. Consequently, a destructive crossover is

unlikely to occur. Individuals with high fitness

values are preserved (Iwashita and Iba, 2002).

Figure 3: Flowchart of GP

CN_IL

3.5 Search for the Optimal Value of P

We think that optimal values of the number of

control nodes (C) and the number of executions (P),

which is the number of action nodes repeatedly

processed in a tree differ according to the problem to

be solved and the size of action rules. Therefore, we

propose GP

(e), GP

CN_CP

(e), and GP

CN_IL

(e), which

are extensions of GP

, GP

CN_CP

, and GP

CN_IL

respectively, to obtain optimal values of P by

evolution. Let P

denote the value of P at generation

i. Then P is updated as follows.











(2)

In (2),  is the range for updating the value of P, and

=TotalSteps/C, where TotalSteps and C

respectively represent the maximum simulation steps

and the number of trees. For example, when

TotalSteps is 250, and an individual has two trees,

i.e. C=2, then the value of P

is selected as 125. The

value of  is chosen randomly between [-,+]. The

initial value of  is 12 for a garbage collection

problem and 16 for the Santa Fe Trail problem. The

values of  are decreased respectively to 1 at every

100 and 1,000 generations for the garbage collection

problem and the Santa Fe Trail problem. The value

is selected independently for each tree.

4 EXPERIMENTS

4.1 Garbage Collection Problem

The objective of a garbage collection problem is that

an agent picks up all pieces of trash scattered in the

field and carries them to a garbage dump site. An

example of the field of the garbage collection

problem is depicted in Figure 4. Field comprises a

two-dimensional lattice plane of the size 11×11 cells,

and the outermost cells are walls. The garbage

collection problem has one agent, ten pieces of trash,

and one dump site on the field. The agent can move

forward, turn left or right, or stay at each step. The

agent can also pick up a piece of trash by reaching

the cell where it exists and then can carry it to the

dump site. The maximum number of pieces of trash

that the agent can carry is assumed as two. We

prepare 10 environments generated by placing the

agent, trash, and the dump site at randomly selected

cells in advance. We define the fitness as the number

of total pieces of trash carried to the dump sites in

the 10 environments in 250 steps per environment.

Let N

denote the number of collected pieces of trash

in environment i. Then, the fitness value is

calculated as shown below.

Generate initial population

Selection

Genetic

erations

Start

Yes

Evaluation

of fitness

Evaluation

of fitness

Migration Migration

Selection

Depth-

dependent

crossover

Exchange with

random

individual

Performance-

oriented island

Diversity-

oriented island

Stop

Generation numbe

< N

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

268

Figure 4: Example of the field of a garbage collection

problem.

  







(3)

The maximum value of Fitness is 100. In

experiments, we measure the highest fitness value

obtained in a simulation run at each generation and

calculate the average of those fitness values obtained

through 30 simulation runs.

Table 1 presents the functions of non-terminal

nodes and terminal nodes in the garbage collection

problem. We have nodes of two kinds: 0 denotes

non-terminal nodes (branch nodes), and 1 denotes

terminal nodes (action nodes). Table 2, Table 3, and

Table 4 respectively show parameters of GNP

, GP

CN_CP

, and GP

CN_IL

used for experiments.

Figure 5 shows the change of the average fitness of

the garbage collection problem obtained for 1,000

generations. Therein, the vertical axis expresses the

fitness values; the horizontal axis expresses the

generation number. Figure 5 shows that GP

CN_CP

(e)

and GP

CN_IL

(e) show good performance in both the

maximum fitness and the evolution rate. GP

CN_CP

(e)

and GP

CN_IL

(e) are methods in which the optimal

value of P is sought. Consequently, the method to

obtain the optimal value of P is effective for

improving the performance.

Comparison of GP with GNP

shows that

GNP

has better capability than GP

. Comparison

of GP

with GP

CN_CP

shows the effectiveness of the

conditional probabilities. Moreover, comparison of

with GP

CN_IL

shows that the island model is

effective for improving the fitness, and that the

island model gives higher improvement than the

conditional probability tables do.

The experiments of the garbage collection

problem confirmed that using conditional

Table 1: Function of non-terminal nodes and terminal

nodes.

kind function (number of edges)

check the distance from the agent to the dump

site (3)

0 how many pieces of trash the agent has (3)

check the direction of the agent to the dump

site (8)

check the direction of the agent to the nearest

trash (9)

check the direction of the agent to the second

nearest trash (9)

1 move forward (1)

1 turn right (1)

1 turn left (1)

1 stay (1)

Table 2: Parameters of GNP

Maximum number of

generations

1,000

Population size 300

Number of nodes 18

Crossover probability of

nodes, P

0.1

Probability of changing

connection of nodes, P

0.01

Number of control nodes 10

Table 3: Parameters of GP

and GP

CN_CP

Maximum number of

generations

1,000

Population size 300

Tournament size 2

Elite number 1

Probability of mutation-

node, P

0.05

Probability of mutation-

tree, P

0.1

Crossover probability, P

0.8

Inversion probability, P

0.2

Number of population

generated by conditional

probability

Maximum depth of trees 6

Probability of changing

value of P, P

0.05

probabilities and the island models is effective. We

also ascertained that the readability of GP

higher than GNP

by examining the obtained trees

and the network.

4.2 Santa Fe Trail Problem

In the Santa Fe Trail problem, an agent must obtain

action rules to pick up all pieces of food in the field

agent

collection

place

trash

ExperimentsAssessingLearningofAgentBehaviorusingGeneticProgrammingwithMultipleTrees

269

Table 4: Parameters of GP

CN_IL

Performance-

oriented island

Diversity-

oriented island

Maximum

number of

generations

1,000

Population size 150 150

Tournament

size

4 2

Number of

elites

1 0

Probability of

mutation-node,

0 0.2

Probability of

mutation-tree,

0 0.1

Crossover

probability, P

1.0 0.8

Inversion

probability, P

0 0.1

Migration size 100

Maximum

depth of trees

Probability of

changing value

of P, P

0.05

Figure 5: Change of fitness of the garbage collection

problem obtained for 1,000 generations.

efficiently. The Santa Fe Trail problem field is

depicted in Figure 6. A two-dimensional lattice

plane comprises 32×32 cells. The Santa Fe Trail

problem has one agent and 89 pieces of food in the

field. The agent and the food are placed in

determined cells. The agent can move forward, turn

left or right, and stay in each step. Additionally, the

agent can pick up a piece of food by reaching the

Figure 6: Field of Santa Fe Trail problem.

Table 5: Function of non-terminal nodes and terminal

nodes.

kind function (number of edges)

0 if there is food ahead (2)

0 act X; then Y (2)

0 act X, then Y; then Z (3)

1 move forward (1)

1 turn right (1)

1 turn left (1)

cell in which it exists. We define the fitness as the

total number of pieces of food picked up in 400

steps. The maximum number of fitness is 89. The

population size is 500, and the maximum generation

number is 10,000. In experiments, we measure the

highest fitness value obtained in a simulation run at

each generation and calculate the average of those

fitness values obtained through 30 simulation runs.

Table 5 presents the functions of non-terminal

nodes and terminal nodes in the Santa Fe Trail

problem. We have nodes of two kinds: 0 denotes

non-terminal nodes (branch nodes), and 1 denotes

terminal nodes (action nodes).

Figure 7 shows the change of the average fitness

of the Santa Fe Trail problem obtained for 10,000

generations. Therein, the vertical axis expresses the

fitness values; the horizontal axis expresses the

generation number. Figure 7 shows that GP

CN_CP

and

CN_IL

show better performance than GP

in terms

of the maximum fitness and the evolution rate,

which indicates that the conditional probability

tables and the island model are effective to improve

the fitness. However, the fitness values of

CN_CP

(e) and GP

CN_IL

(e) are lower than those of

CN_CP

and GP

CN_IL

. The search method for the

optimum number of execution P does not work well

in this problem. We must examine the cause further.

In the experiment, the GNP

performance is

low because the PROG function is not implemented.

For the Santa Fe Trail problem, introducing the

conditional probability for generation of individuals

0,0

10,0

20,0

30,0

40,0

50,0

60,0

70,0

80,0

90,0

100,0

0 200 400 600 800 1000

GNP_CN

GP_CN

GP_CN(e)

GP_CNCP

GP_CNCP(e)

GP_CNIL

GP_CNIL(e)

Fitness

Generation

GNP

(e)

CN_CP

(e)

CN_IL

(e)

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

270

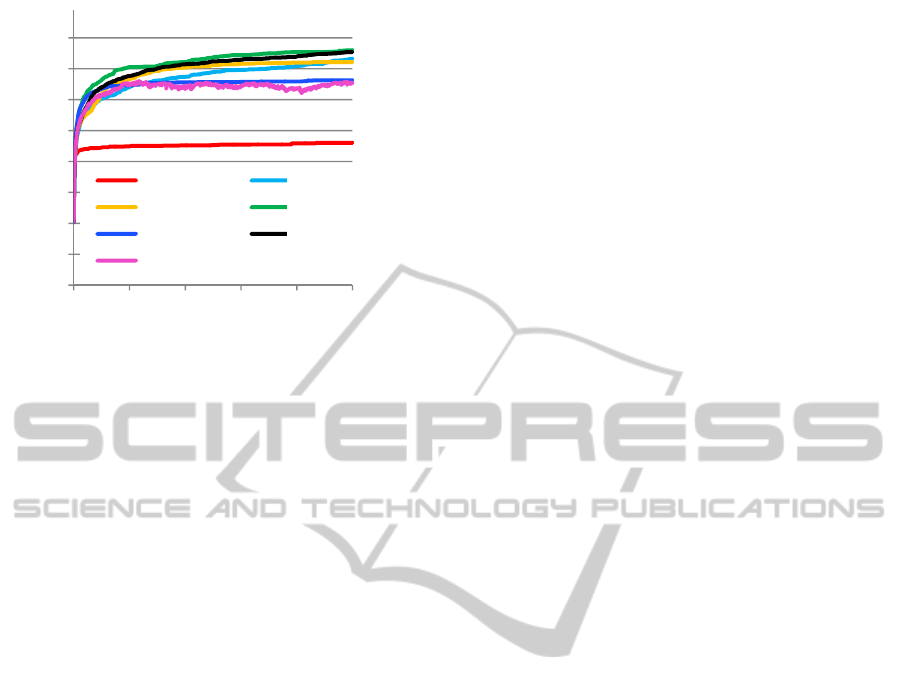
Figure 7: Change of fitness of Santa Fe Trail obtained for

10,000 generations.

and the island model also shows their effectiveness

to improve the fitness.

5 CONCLUSIONS

We applied our methods, GP

CN_CP

, GP

CN_IL

CN_CP

(e), and GP

CN_IL

(e) to a garbage collection

problem and the Santa Fe Trail problem, to assess

their performance. In those problems, our methods

show good performance in both the maximum

fitness and the evolution rate. The authors consider

that using conditional probabilities and the island

model prevented the solution from reaching a local

optimum. Additionally, results show that the method

to obtain the optimal value of P improves the fitness.

To improve the fitness of the sub-population of

CN_IL

, our future work will integrate the

conditional probability shown to be effective into

CN_IL

This research was in part supported by a

Hiroshima City University Grant for Special

Academic Research (General).

REFERENCES

Koza, J. R., 1992. Genetic Programming: On the

Programming of Computers by Natural Selection,

Cambridge, MA: MIT Press.

Hirasawa, K., Okubo, M., Katagiri, H., Hu, J., and Murata,

J., 2001. Comparison between Genetic Network

Programming and Genetic Programming Using

Evolution of Ant’s Behaviors, IEEJ Transactions on

Electronics, Information and System, Vol.121, No.6,

pp.1001-1009.

Iba, H., 2002. Genetic Algorithm, Igaku Shuppan. Japan.

Mesot, B., Sanchez, E., Pena, C.-A., and Perez-Uribe, A.,

2002. SOS++: Finding Smart Behaviors Using

Learning and Evolution, Eighth International

Conference on the Simulation and Synthesis of Living

Systems (Alife 8), Artificial Life 8, pp.264-273.

Tanji, M., and Iba, H., 2010. A New GP Recombination

Method Using Random Tree Sampling, IEEJ

Transactions on Electronics, Information and Systems,

Vol.130, No.5, pp.775-781.

Iba, H., 2002. Genetic Programming, University of Tokyo

Press.

Murata, T., and Nakamura, T., 2006. Multi-Start Node

Genetic Network Programming for Controlling

Multiple Agents, 2006 IEEE International Conference

on Systems, Man, and Cybernetics, Vol.3, pp.1927-

1932.

Eto, S., Mabu, S., Hirasawa, K., Huruzuki, T., 2007.

Genetic Network Programming with Control Nodes,

2007 IEEE Congress on Evolutionary Computation

(CEC2007), pp.1023-1028.

Minesaki, T., Ueda, H., and Takahashi, K., 2009.

Comparison experiment using Genetic Network

Programming, The Conference Program of the 2009

(60th) Chugoku-branch Joint Convention of Institutes

of Electrical and Information Engineers, p.546.

Morioka, T., Ueda, H., and Takahashi, K., 2011. Efficient

Evolutionary Learning of Agent Behavior by Genetic

Programming Using the Conditional Probabilities,

Proc. of 12

International Symposium on Advanced

Intelligent System 2011 (ISIS2011), pp.342-345.

Ito, T., Takahashi, K., Inaba, M., 2013. Improvement of

Genetic Programming with multiple trees, 2013 IEEE

SMC Hiroshima Chapter Young Researchers'

Workshop Proceedings, pp.9-12.

Ono, K., Hanada, Y., Shirakawa, K., Kumano, M., Kimura,

M., 2012. Depth-dependent crossover in genetic

programming with frequent trees, 2012 IEEE

International Conference on Systems, Man, and

Cybernetics, pp.359-363.

Ono, K., Hanada, Y., Kumano, M., Kimura, M., 2013.

Island model genetic programming based on frequent

trees, 2013 IEEE Conference on Evolutionary

Computation (CEC2013), pp.2988-2995.

Iwashita, M., and Iba, H., 2002. Parallel Distributed GP

with Immigrants Aging and Depth-dependent

Crossover, Transactions of Information Processing

Society of Japan, Vol.43, No.SIG10, pp.146-156.

0 2000 4000 6000 8000 10000

GNP_CN GP_CN

GP_Cne GP_CNCP

GP_CNCPe GP_CNIL

GP_CNILe

Fitness

Generation

GNP

(e)

CN_CP

(e)

CN_IL

(e)

CN_CP

CN_IL

ExperimentsAssessingLearningofAgentBehaviorusingGeneticProgrammingwithMultipleTrees

271