A Framework for 3D Object Identiﬁcation and Tracking

Georgios Chliveros

, Rui P. Figueiredo

, Plinio Moreno

Maria Pateraki

, Alexandre Bernardino

, Jose Santos-Victor

and Panos Trahanias

Instituto de Sistemas e Robotica, Instituto Superior Tecnico, Lisboa, Portugal

Institute of Computer Science, Foundation for Research and Technology Hellas, Heraklion, Greece

Keywords:

Object Tracking, Object Detection, Relative Pose Estimation, Robot Vision.

Abstract:

In this paper we present a framework for the estimation of the pose of an object in 3D space: from the

detection and subsequent recognition from a 3D point-cloud, to tracking in the 2D camera plane. The detection

process proposes a way to remove redundant features, which leads to signiﬁcant computational savings without

affecting identiﬁcation performance. The tracking process introduces a method that is less sensitive to outliers

and is able to perform in soft real-time. We present preliminary results that illustrate the effectiveness of the

approach both in terms of accuracy and computational speed.

1 INTRODUCTION

The identiﬁcation and subsequent relative pose track-

ing of objects in 3D space (6 degrees of freedom) is

an important problem in service robotics. Recently,

several software solutions have become available; e.g.

the case of ViSP

and BLORT

In ViSP, recognition is not taken into account.

This is the case with earlier works (Harris, 1992;

Koller et al., 1993), the reﬁnement of the estimated

object pose does not consider evaluation and/or pre-

diction of hypothesised object poses. In BLORT,

recognition and multiple pose hypotheses is consid-

ered via probabilistic frameworks; for example, in

(Azad et al., 2011; Choi and Christensen, 2012).

However, it assumes good pose priors which may lead

to losing track of the object.

In recent past, Drost et al. (Drost et al., 2010)

proposed an efﬁcient approach for detecting and sub-

sequent tracking. Given an object model, a descrip-

tion is extracted using point pair features, thus en-

coding the geometric relation between oriented point

pairs. The method is robust to sensor noise and out-

performs other feature-based state-of-the-art methods

like Spin Images (Johnson and Hebert, 1999) and

Tensors (Mian et al., 2006), in terms of robustness to

occlusion and clutter.

Tracking on a 2D camera plane can be performed

faster than those required in 3D space. Recently avail-

able low-cost range sensors (e.g. Kinect) can be used

http://www.irisa.fr/lagadic/visp/visp.html

http://users.acin.tuwien.ac.at/mzillich/?site=4

in such a way. However, for not affecting accuracy,

the pose hypotheses space is an important issue to

explore. This comes alongside the use of generated

model feature points which can reduce perspective-

n-point ambiguities in data association (Puppili and

Calway, 2006). Thus, issues that need addressing for

efﬁcient tracking are:

• reliably detect the object in question and identify

their model equivalent;

• by tracking the object, estimate and reﬁne its pose;

• suitable for online applications.

In this paper we introduce an approach under

which an object is recognized and its (initial) pose is

estimated through an acquired 3D point cloud (Sec-

tion 3). Identiﬁcation and initial pose estimation is

achieved via a fast extension (Figueiredo et al., 2013)

of Drost et al. (Drost et al., 2010) algorithm (Section

3). These serve as inputs to the tracking of the 6DoF

pose on the 2D camera plane using multiple hypothe-

ses (Chliveros et al., 2013) (Section 4). Preliminary

results for the described methods, are presented in

Section 5. Finally, some concluding remarks and fu-

ture work is provided in Section 6.

2 HYPOTHESES SPACE

As previously mentioned, the hypotheses space from

known 3D models is an important aspect for accuracy

and error compensation. We generate a representative

search space over rotations (α

+ δα

,α

+ δα

,α

672

Chliveros G., P. Figueiredo R., Moreno P., Pateraki M., Bernardino A., Santos-Victor J. and Trahanias P..

A Framework for 3D Object Identiﬁcation and Tracking.

DOI: 10.5220/0004751506720677

In Proceedings of the 9th International Conference on Computer Vision Theory and Applications (VISAPP-2014), pages 672-677

ISBN: 978-989-758-009-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

δα

). The term δα can be assigned as dictated by a

number of increment steps (N) over the full rotation

range (0,π) of the corresponding axis.

In the detection process case (see Section 3), all

retrieved pose hypotheses whose position and orien-

tation do not differ more than a predeﬁned threshold

are clustered together (Section 3.3).

Note that in order to deal with symmetry, before

clustering, we collapse all redundant hypotheses to a

single pose. This additional step removes the rota-

tional component around the object axis of symme-

try, ensuring that all redundant poses are gathered in

the same cluster. Thus, the process allocates less re-

sources, reduces the number of computations and be-

comes more stable.

In the tracking process case (see Section 4), new

hypotheses are generated only when the error of the

error minimisation step (see Section 4.2) exceeds a

predeﬁned threshold. However, the generation of

hypotheses is dictated within a short-term window.

That is to say, all pose hypotheses between all frames

within said time window are used as constraints in the

generation of new pose candidates. New pose candi-

dates are randomly sampled around the median of the

time-window retrieved poses (i.e. converged solution

of the minimisation step).

The uncertainty of tracking pose candidates is also

handled in Section 4.1. This is performed via a time-

window and is depicted by the covariance matrix S

In Section 4.2, the covariance matrix is updated, by

means of compensating re-projection errors (see Sec-

tion 4.2) (Haralick, 1994; Lourakis, 2010).

3 OBJECT DETECTION

An object description suitable for object identiﬁcation

and pose estimation is created through the analysis

of all possible permutations of surﬂet pairs. The ba-

sic units to describe surface shape are surﬂets (Wahl

et al., 2003) s = (p,n), where p represents sample

points in the surface and n are the associated surface

normals.

We consider rotationally symmetric objects,

where shape is invariant to rotations around a given

axis. We assume that the Z axis of the object’s refer-

ence frame is the axis of symmetry and the X-Y-Z Eu-

ler representation. We search for surﬂet pairs whose

aligning transformation is very close in translation,

roll and pitch. Similar surﬂet pairs are collapsed into

the same feature.

= kdk

Figure 1: Point Pair Feature.

3.1 Detection process

The identiﬁcation process consists of matching sur-

ﬂet pairs (s

) from a scene, to surﬂet pairs (s

)

extracted from a database of model objects.

For s

and s

being two surﬂets, the Point Pair

Feature (PPF) F ∈ F ⊂ R

is deﬁned as a 4-tuple

composed by the distance between the reference p

and secondary points p

, as well as the angle between

the normal of the reference point n

and the vector

d = |p

−p

|, the angle between the normal of the sec-

ondary point n

and d and, ﬁnally, the angle between

and n

as illustrated in Fig. 1.

This could be formally described by

F = PPF(s

) = ( f

, f

)

= (kdk,∠(n

,d),∠(n

)) (1)

3.2 Initial Pose Estimation

A set of reference surﬂets on the scene R

⊂ S is uni-

formly sampled from S and each of them is paired

with all the other surﬂets on the scene. The num-

ber of reference points is given by

= ξ

where

ξ ∈ [0; 1] is the reference points sampling ratio control

parameter.

For each scene surﬂet pair (s

) ∈ S

, PPF(s

)

is computed and set of similar model surﬂet pairs is

retrieved from the hash table. From every match be-

tween a scene surﬂet pair (s

) ∈ S

and a model sur-

ﬂet pair (s

) ∈ M

, one is able to compute the rigid

transformation that aligns the matched model with the

scene. This is done ﬁrst by computing the transfor-

mations T

m→g

and T

s→g

that align s

and s

, respec-

tively, to the object reference coordinate frame x axis,

and secondly by computing the rotation α around the

x axis that aligns p

with p

. The transformation that

aligns the model with the scene is then computed con-

sidering the ensuing expression:

m→s

= T

−1

s→g

R(α)T

m→g

(2)

The transformations T

m→g

and T

s→g

translate p

and p

, respectively, to the reference coordinate frame

origin and rotates their normals n

and n

onto the x

axis. After applying these two transformations, p

and p

are still misaligned. The transformation R(α)

AFrameworkfor3DObjectIdentificationandTracking

673

s→g

m→g

Figure 2: Pose acquisition by surﬂet pair aligment.

applies the ﬁnal rotation needed to align these two

points. The previous reasoning is depicted in Fig. 2.

The transformation expressed in eq. (2) can be

parametrized by a surﬂet on the model and a rotation

angle α. In (Drost et al., 2010), this pair (s

,α) is

mentioned as the local coordinates of the model with

respect to reference point s

3.3 Voting Scheme

This method uses a voting scheme similar to the GHT

for pose estimation. For each scene reference sur-

ﬂet, a two-dimensional accumulator array that repre-

sents the discrete space of local coordinates is cre-

ated. The number of rows, N

, is the same as the

number of model sample surﬂets

, and the number

of columns N

angle

is equal to the number of sample

steps of the rotation angle α.

A vote is placed in an accumulator array. The

position index corresponding to the local coordinates

,α) is incremented by 1. After pairing s

with all

, the highest peak (the position with more votes) in

the accumulator corresponds to the optimal local co-

ordinate.

4 TRACKING PROCESS

Given the detected model recognised by the detection

process (Section3.1) and the initial estimated pose

(Section 3.2), the tracking process in the 2D camera

frame can be instantiated.

For any pose s from a known model m

we extract

the 3D-to-2D projected feature model points

. The

set of model points are matched with image observed

feature points

. This is performed by employing

a nearest neighbour search by overlaying in the 2D

camera frame a uniform grid.

We query for each model feature points

and

ﬁnd the Euclidean distance for given image observed

feature points

. The image observed feature points

are produced from the contour and edges of the

model, as per method described in (Baltzakis and Ar-

gyros, 2009) and further extended in (Pateraki et al.,

2013).

The overall treatment of feature points (from ex-

traction to association) is much faster than other meth-

ods for associating contour points and has the addi-

tional beneﬁt of ﬁnding intersections in relatively dif-

ﬁcult to observe edges. The alternative of ﬁnding ap-

proximate nearest neighbours (Muja and Lowe, 2009)

would be computationally more expensive (Franklin,

2006). Uniform structures, which are optimized for

metrics in the Euclidean space E

(2)

, force query times

to be limited to O(N). Furthermore, this design

choice is not sensitive to noise and is capable of point

locations inclusion in planar graphs.

4.1 Pose Estimation

Our object pose estimation can be performed via point

correspondences C found between P = {

} and M =

{

} from an Iterative Closest Point (ICP) algorithm.

However, in the presence of noise and artifacts result-

ing, for example, from a cluttered background, the

ICP process can rapidly deteriorate.

This is not the case when using the Least Trimmed

Squares (LTS) estimator (Rousseeuw, 1984) in ICP

(TrICP; (Chetverikov et al., 2005)), since it allows

for the two point sets to contain unequal number of

points (i 6= j) and a percentage of points is offered in

a ‘trimming’ operation. The best possible alignment

between data / model sets is found by ‘sifting’ (e.g.

sorting) through nearest-neighbour combinations and

‘trimming’ (e.g. discarding) the less signiﬁcant pairs

(but not exceeding 50%). This is in an attempt to ﬁnd

the subset with lowest sum of individual Mahalanobis

distances, deﬁned as

i j

= (

−

)

+ S

)

−1

(

−

) (3)

where S

is the covariance, thus the uncertainty, on

the position of point feature

; and respectively for

, which depends on ‘outliers’ and thus the

feature space.

It should be noted that in practice the (robust) LTS

estimator and trimming does not guarantee the ab-

sence of outliers. Thus, we apply a non-linear re-

ﬁnement after the TrICP step to ensure that the inﬂu-

ence of outliers is further reduced; similarly to (Koller

et al., 1993; Fitzgibbon, 2003; Chliveros et al., 2013).

4.2 Error Minimisation

This minimisation step is performed in an effort to re-

duce the pose estimation errors that may arise from

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

674

outliers and abrupt camera motion, but more im-

portantly in order to initiate the generation of new

pose candidates; i.e. take into account issues of re-

initialisation.

The objective function can be formulated as a sum

of squares of a large number of nonlinear real-valued

factors:

= argmin

∑

i=1

||p

− f (s,m

)||

(4)

where f (·) is the function that projects the 3D

model points to the image plane, according to the

parametrised pose s, at translational terms (r

and rotational terms (α

,α

Equation 4 describes a non-linear minimisation

problem which can be solved via the Levenberg-

Marquardt (LM) algorithm. The Jacobians required

by LM were formulated analytically by performing

symbolic differentiation of the objective function.

5 RESULTS

To evaluate the accuracy and speed of the proposed

methods we have employed a set of tests ﬁrst for the

detection accuracy and then for the tracking perfor-

mance. As previously mentioned, the detection pro-

cess outputs the object model ID and its initial pose,

and the tracking process begins by accepting these as

inputs.

Evaluation of Detection

To evaluate the performance gains of the proposed

strategies to handle rotationally symmetries efﬁ-

ciently, in the presence of noisy visual sensors, we

created an experimental scenario similar to the one

referred in (Drost et al., 2010). In this experimental

scenario the models library comprises only one model

at a time and we generated 200 synthetic scenes con-

taining a single instance of a given model from the

ROS household objects library (see (Ciocarlie, )), on

a random pose. Before the down-sampling step, each

scene was corrupted by different levels of additive

Gaussian noise, with standard deviation σ propor-

tional to the model diameter diam(M). By using syn-

thetically generated scenes, we were able to compare

the algorithm pose results with a known ground truth.

During identiﬁcation we select 5% of the scene

points as reference points by setting ξ to 0.05. A

higher percentage would increase the robustness to

noise but also the recognition runtime. A recov-

ered pose was considered to be correct if the error

relative to the ground truth pose was smaller than

diameter(M)/10 for the position and 12 for the orien-

tation. We considered three different pose thresholds

(φ

and t

) to jointly represent features considered

redundant. Figure 3 shows recognition performance

results and speed gains for all the considered mod-

els and thresholds. When t

and φ

are both set to

0 (blue markers), no features are jointly represented.

Therefore the computational savings are only due to

collapsing of pose hypotheses around the axis of rota-

tional symmetry, during the pose clustering step. As

we increase the pose thresholds t

and φ

, we are

able to jointly represent more features and hence have

computational savings not only on the clustering but

also on the matching step.

For the tests with the cup model and pose thresh-

olds set to t

= 0.025 and φ

= 6

◦

(red markers),

we were able to discard 93.17% surﬂet pairs during

the creation of the model description, and reduce the

number of computations during pose detection. As

shown in Figure 3, the recognition rate drops slightly

for high levels of noise due to sampling effects, but

the recognition time performance increases signiﬁ-

cantly. For

≈ 5000, our method achieves iden-

tiﬁcation in time 300 times faster than (Drost et al.,

2010). However, the number of jointly represented

surﬂet pairs depends heavily on the object geomet-

ric conﬁguration. For objects whose shape has a

smaller radius relative to the axis of symmetry, and

also lower surﬂet density on the surface, less perfor-

mance gains can be achieved. For the tests compris-

ing the champagne glass model we were only able

to discard 55.33% surﬂet pairs (with t

= 0.025 and

= 6

◦

) during the creation of the model description,

and achieve no more than 3.5 times speed improve-

ments during recognition relatively to (Drost et al.,

2010).

Overall, we were able to obtain major improve-

ments on recognition speed. The latter does not have

signiﬁcant cost on recognition performance.

Evaluation of Tracking

In Table 1, quantitative analysis of our tracking

approach in a ‘cup’ (as a recognised) model se-

quence is provided. As a reference method, we

have used the default particle ﬁlter implementation of

BLORT’s software implementation. The experiments

performed provide representative cases for the max

number of hypotheses (depicted as ‘max hyp: n’) and

for corresponding number of minimisation iterations

allowed (depicted as ‘LM iter’).

The results of Table 1, illustrate that ‘growth time’

dependence for tracking the 6DoF pose of an object

is somewhat predictable and comparable in perfor-

mance to that of BLORT. It seems that the higher

AFrameworkfor3DObjectIdentificationandTracking

675

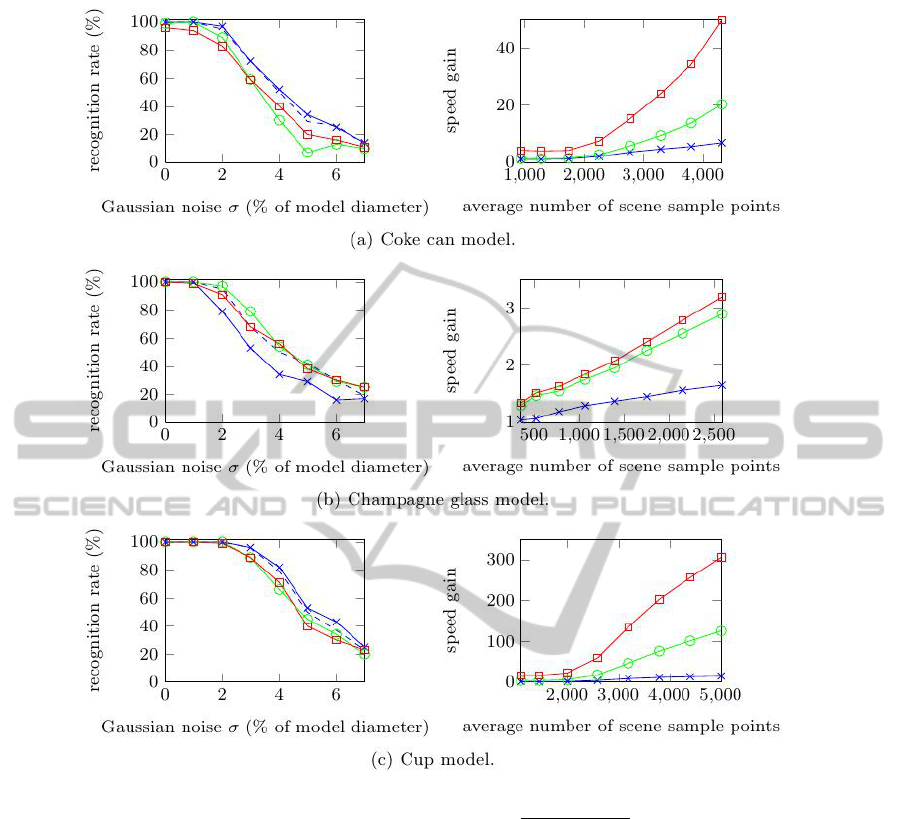
Figure 3: Comparison results of our approach (continuous lines) against the original method of Drost et al. (dashed lines),

with ξ = 0.05; Left: Recognition rate (%). Right: Time performance gain

Drost et al. runtime

Our runtime

Parameters: t

= 0, φ

= 0

◦

(blue markers), t

= 0.005, φ

= 1.2

◦

(green markers), t

= 0.025, φ

= 6

◦

(red markers).

the number of max hypotheses the higher the step in-

crease in terms of computational runtime. We note

that our implementation does not utilse hardware ac-

celaration. Optimisations are performed with re-

spect to custom matrix and array operations (based on

uBLAS and Lapack libraries). For completeness we

also report the computational time required by each

method.

Overall, our method is close to BLORT and for

this test case, it is applicable for on-line applications.

6 CONCLUDING REMARKS

In this paper we have suggested the use of a recogni-

tion method that uses its output as an input to a pose

tracking process. The savings in computational speed

do not affect recognition rates and tracking perfor-

mance. For the tests performed and results presented,

the combination of these two methods supports suit-

ability for online applications.

In future works we intent to perform further tests

on the framework’s accuracy (e.g. environmental con-

ditions). We also aim to exploring the effect certain

robot grasping strategies may have (e.g. object com-

ing out of the ﬁeld of view).

ACKNOWLEDGEMENTS

This work was partially supported by the European

Commission under contract number FP7-248258

(First-MM project).

VISAPP2014-InternationalConferenceonComputerVisionTheoryandApplications

676

Table 1: Results on MH3DOT tuning versus performance and accuracy. A ‘cup’ sequence and model is used with (partial)

ground truth data. As a reference for these test results we use the BLORT software implementation.

Total Error (952 frames) Time

Roll Pitch Yaw Scale (msec)

BLORT (max = 100) 11.1 11.7 3.5 2.3 141

MH3DOT (LM iter = 10) max hyp: n = 20 14.4 12.9 7.1 2.4 97

max hyp: n = 30 11.2 11.9 5.2 2.2 122

max hyp: n = 50 2.8 5.8 2.4 1.9 158

max hyp: n = 100

2.8 5.8 2.3 1.9 225

MH3DOT (LM iter = 20) max hyp: n = 20 13.9 11.5 6.5 2.1 103

max hyp: n = 30 9.8 7.7 4.4 1.9 179

max hyp: n = 50 2.7 5.8 2.3 1.8 254

max hyp: n = 100 2.7 5.6 2.3 1.8 335

REFERENCES

Azad, P., M

unch, D., Asfour, T., and Dillmann, R. (2011).

6-DoF model-based tracking of arbitrarily shaped 3D

objects. In IEEE Int. Conf. on Robotics and Automa-

tion, pages 5204–5209.

Baltzakis, H. and Argyros, A. (2009). Propagation of pixel

hypotheses for multiple objects tracking. In Advances

in Visual Computing, volume 5876 of Lecture Notes

in Computer Science, pages 140–149.

Chetverikov, D., Stepanov, D., , and Krsek, P. (2005).

Robust euclidean alignment of 3D point sets: the

trimmed iterative closest point algorithm. Image and

Vision Computing, 23:299–309.

Chliveros, G., Pateraki, M., and Trahanias, P. (2013). Ro-

bust multi-hypothesis 3d object pose tracking. In

Computer Vision Systems, volume 7963 of Lecture

Notes in Computer Science, pages 234–243.

Choi, C. and Christensen, H. I. (2012). Robust 3D vi-

sual tracking using particle ﬁltering on the special Eu-

clidean group: A combined approach of keypoint and

edge features. The International Journal of Robotics

Research, 31(4):498–519.

Ciocarlie, M. Household objects database. accessed 19-

July-2012.

Drost, B., Ulrich, M., Navab, N., and Ilic, S. (2010). Model

globally, match locally: Efﬁcient and robust 3d object

recognition. IEEE Transactions on Computer Vision

and Pattern Recognition (CVPR), pages 998 – 1005.

Figueiredo, R., Moreno, P., and Bernardino, A. (2013). Fast

3d object recognition of rotationally symmetric ob-

jects. In Pattern Recognition and Image Analysis,

volume 7887 of Lecture Notes in Computer Science,

pages 125–132.

Fitzgibbon, A. (2003). Robust registration of 2D and

3D point sets. Image and Vision Computing,

21(13):1145–1153.

Franklin, W. (2006). Nearest point query on 184,088,599

points with a uniform grid. Technical report, Rensse-

laer Polytechnic Institute, USA.

Haralick, R. (1994). Propagating covariance in computer

vision. In Proceedings of the 12th IAPR International

Conference on Pattern Recognition, volume 1, pages

493–498.

Harris, C. (1992). Tracking with rigid objects. MIT press.

Johnson, A. E. and Hebert, M. (1999). Using spin images

for efﬁcient object recognition in cluttered 3D scenes.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, pages 433–449.

Koller, D., Daniilidis, K., and Nagel, H. (1993). Model-

based object tracking in monocular image sequences

of road trafﬁc scenes. International Journal of Com-

puter Vision, 10:257–281.

Lourakis, M. (2010). Sparse non-linear least squares opti-

mization for geometric vision. In European Confer-

ence on Computer Vision, pages 43–56.

Mian, A. S., Bennamoun, M., and Owens, R. (2006). Three-

dimensional model-based object recognition and seg-

mentation in cluttered scenes. IEEE Transactions on

Pattern Anal. Mach. Intell, 28:1584–1601.

Muja, M. and Lowe, D. G. (2009). Fast approximate near-

est neighbors with automatic algorithm conﬁguration.

In Int. Conf. on Computer Vision Theory and Applica-

tions (VISAPP), pages 331–340.

Pateraki, M., Sigalas, M., Chliveros, G., and Trahanias, P.

(2013). Visual human-robot communication in social

settings. In IEEE Int. Conf. on Robotics and Automa-

tion.

Puppili, M. and Calway, A. (2006). Real time camera track-

ing using known 3D models and a particle ﬁlter. In

IEEE Int. Conf. on Pattern Recognition.

Rousseeuw, P. J. (1984). Least median of squares regres-

sion. Journal of the American Statistical Association,

79(388):871–880.

Wahl, E., Hillenbrand, U., and Hirzinger, G. (2003). Surﬂet-

pair-relation histograms: A statistical 3D-shape repre-

sentation for rapid classiﬁcation. 3D Digital Imaging

and Modeling, International Conference on, page 474.

AFrameworkfor3DObjectIdentificationandTracking

677