Shortest Path Challenging Problem

Context of Mobile Devices in Urban Area Considering Weakened GPS Signal and

Data Network Traffic

Philippe Lacomme

, Libo Ren

, Nicolay Tchernev

and Benjamin Vincent

Université Blaise Pascal (LIMOS UMR 6158) Campus des Cézeaux, 63173, Aubière, France

Université d’Auvergne (LIMOS UMR 6158), Campus des Cézeaux, 63173, Aubière, France

Keywords: Shortest Path, Mobile Device, Web Services.

Abstract: The shortest path problem is a well know routing problem which received a considerable amount of

attention for several decades. This problem is the cornerstone of any real-world routing problem including

the VRP or the Hub Location. The majority of efficient methods dedicated to these problems consist in

computing first the matric of shortest path between nodes. Furthermore, in recent years there has been a

revival of interest in the shortest path problem used in the context of various transportation engineering

applications. This paper relates to the conception of efficient routing algorithms tuned for mobility. More

precisely, it is targeted to the field of pedestrian mobility in an urban environment. In a mobile environment,

specific constraints as wireless network traffic disturbances must be taken into account. The architecture

that we tune for the project is based on an active monitoring system, which required new shortest path

calculation using the exposed web service API. The web service is performed when a specific constraint

appears or a new part of the path is required. Using of such architecture offers a new approach in

operational research algorithms and our contribution stands at the crossroads of optimization research

community and the web service community expectations.

1 INTRODUCTION

Distributed Computing Technologies and Web

services are growing rapidly in importance in

today’s computing environment and are already

widely accepted as industrial standards. By

combining modern computing technologies and

Operations Research, Optimization Services will

reach a larger audience informed of, and benefit

from, an increasing amount of OR software

implemented gaining gradual quality.

Moreover advances in digital electronics and

wireless communications have enabled the

development of low-cost Global Positioning

Systems (GPS) which can be used by pedestrian

mobility in urban environment. In wireless network

traffic, loss of connection due to network overload

and bad localization lead to a signiﬁcant increase in

travel times and a decrease in the probability of

being on-time at the ﬁnal destination.

Generally, pedestrians using GPS have a very

little knowledge on the path they walk. When the

GPS signal is broken, pedestrian can easily be lost

by taking a wrong direction or can be forced to wait

for GPS signal. Never mind the case, regarding

pedestrian needs, an inadequate paths planning can

lead to an "unfriendly walking environment" with

people feeling insecurity.

From a road safety viewpoint, pedestrians should

be provided with safe conditions where they avoid

being distracted by watching their GPS until the

signal returns. However, that cannot always be

achieved. A series of measures should be considered

to improve pedestrian safety and mobility.

Therefore, it is essential to use routing that

effectively respond to the wirelee network

disruptions and give high quality solutions within

acceptable calculation times. One important question

to be answered is how to use the level of online

information needed to obtain higher solution quality

with lower calculation times.

In this paper, we focus on the dynamic shortest

path problems with stochastic disruptions in the

wireless network. We are particulary interested in

networks where a single pedestrian has a certain

393

Lacomme P., Ren L., Tchernev N. and Vincent B..

Shortest Path Challenging Problem - Context of Mobile Devices in Urban Area Considering Weakened GPS Signal and Data Network Trafﬁc.

DOI: 10.5220/0004753403930400

In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 393-400

ISBN: 978-989-758-017-8

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

origin–destination pair. The pedestrian gets the real-

time information from the GPS at each node which

is an intersection of roads and/or streets. At every

intersection, the GPS determines the next road to

follow depending on the current state of the

pedestrian.

We concentrate more particularly on the design

of efficient routing algorithms tuned for pedestrian

mobility in an urban environment. The main

contributions of this paper are as follows: 1) we

develop a dynamic shortest path algorithm dedicated

to a mobility implementation; 2) we package this

operational research algorithm as a software service

based on Web services paradigm that facilitate

distributed computing; 3) next to this we design a

basic pedestrian system for Android using the

exposed web service API; 4) we test the efficiency

of our dynamic shortest path algorithm and copare

this to the optimal solutions find with Dijkstra

algorithm. The numerical results show that the

average gap is promizing.

The paper is organised as follows: the section 2

presents the context of this research. Section 3

descibes the system architecture for pedestrian

guidance system in an urban environment. An

example on the creation of a client is explained in

section 4. In Section 5, the numerical results and the

important insights are discussed before the

conclusion.

2 CONTEXT

2.1 Shortest Path

In recent years, there has been a revival of interest in

the shortest path problem for use in various

transportation-engineering applications. Without any

doubt it could be directly attributed to the recent

developments in Intelligent Transportation Systems

(ITS), particularly in the field of Route Guidance

System (RGS) and real time Automated Vehicle

Dispatching System (AVDS). In both cases, there is

a definite need to find the shortest paths from an

origin to a destination in a quick and accurate

manner.

In the above applications, the traditional optimal

shortest path algorithms often cannot be used

because in a large dense network the computation of

the shortest path can take a long time and is too

computationally intensive to be feasible for real-time

systems.

A number of heuristic search strategies have

been developed for increasing the computational

efficiency of shortest path search.

Most of these heuristic search strategies

originated in the artificial intelligence (AI) field

including but not limited to (Hart et al., 1968),

(Nilsson, 1971), (Pearl, 1984) where the shortest

path problem is used as a mechanism to validate the

effectiveness of these heuristics.

The current RGS field in both North America,

and Europe have generated renewed interest in using

heuristic algorithms to find shortest paths in a traffic

network for real-time vehicle routing operations.

(Guzolek and Koch, 1989) discussed how heuristic

search methods could be used in vehicle navigation

system. (Kuznetsov, 1993) debated applications of

an A* algorithm (ﬁrst proposed by Hart et al. 1968),

a bi-directional search method, and a hierarchical

search method.

Since then, a huge number of researchers have

followed the trend and tried to introduce a

worldwide strategy for improving the efficiency of

the shortest path search process. These efforts have

resulted in a large literature including a wide

spectrum of search strategies and mechanisms.

For a recent survey it is possible to refer to (Fu et

al., 2006) who proposes a state of the art and

examines the implementation and performance of

numerous heuristic algorithms. A recent survey of

(Garroppo et al., 2010) focuses on the multi-

constrained approximated shortest path algorithms

representing by recent publications of (Gubichev et

al., 2010) or (Willhalm, 2005).

2.2 Web Services

2.2.1 Historical Perspective

In recent decades, web services based solver servers

offered access to commercial or non-commercial

implementation of algorithms for solving non-linear

and linear problems. The well known formats as

MPS (Mathematical Programming System (IBM

1976)) and some others (MPL (Maximal Software,

2002), LINGO (Lindo Systems Inc, 2008), and

CAMPS (Lucas and Mitra, 1988)) specific to a given

solver are commonly used as a file format for

presenting and archiving linear programming (LP)

and mixed integer programming (MIP) problems.

Each client submits a text file which contains the

model and the data to a server. The results were sent

back to the client either via email or via a file which

could be downloaded from the server using the ftp or

http protocol. A comprehensive review of modelling

systems, formats and their features can be found in

(Dominguez-Ballesteros et al., 2002).

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

394

The design, development, implementation and

deployment of decision support systems have been

transformed by web based technologies. (Cohen et

al., 2001) give examples of web-based decision

support systems in Supply Chain Management,

Inventory Control or supplier management.

(Bhargava et al., 2007) reviews and summarises

recent technology developments, current usage of

Web-based DSS, and trends in the deployment of

such systems.

2.2.2 Definition and Standard

Web service is defined as a communication

techonologie between two devices over Internet. It

relies on the using of HTTP with an XML

serialization. Web services are characterized by their

great interoperability and extensibility due to the use

of XML, and they can then be combined in a loosely

coupled way in order to achieve complex operations

(Wang et al., 2004). During the last decade several

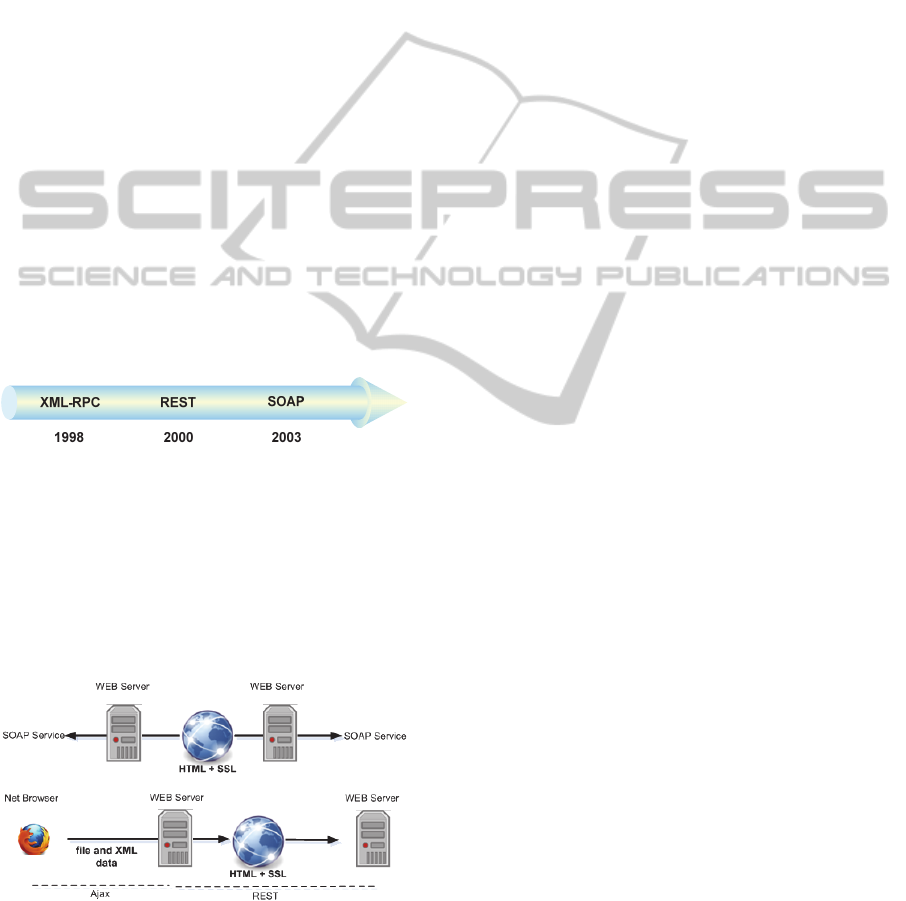
technologies have been used including: XML-RPC

(Remote Procedure Call), REST (REpresentational

State Transfer (Fielding 2002)) and lately SOAP

(Simple Object Access Protocol (Gudgin et al.,

2003) (Figure 1).

Figure 1: Client-Server architecture evolution.

According to W3C, the difference between

REST architecture and SOAP architecture concerns

the data exchange and the availability of some

language description which is a guaranty of an easy

to use and easy to spread web service (Figure 2). In

this paper, we are interested more particularly in

SOAP architecture.

Figure 2: Difference between REST and SOAP.

2.2.3 Soap Web Services

SOAP (Simple Object Access Protocol) is

fundamentally a stateless, one-way message

exchange paradigm that enables applications to

create more complex interaction patterns (e.g.,

request/response, request/multiple responses, etc.)

by combining one-way exchanges with features

provided by an underlying protocol and/or

application-specific information. SOAP provides

automatic discovery of the service and take

advantages of several languages and protocol wide

spread on the web:

 XML (eXtensible Mark-up Language) to

underlay representation format of the data

exchanged. The language is used to specify the

header and body elements of the SOAP message;

 WSDL (Web Service Definition Language) used

to described the public interface of the service

(Chinnici et al., 2007), i.e. computer-readable

description of Web services;

 UDDI (Universal Description, Discovery and

Integration) to register and spread a web service

(UDDI, 2002).

Messages must be carried by the SOAP and

formatted by the rules of it, and the description

(exposed interface) of the service must be deﬁned in

WSDL, i.e. the XML based language used to

describe and locate a SOAP web service).

3 SHORTEST PATH WEB

SERVICE

3.1 Proposed Web Service

The definition of the system architecture is based on

the SOAP Web Service definition that exposed 4

methods:

 Demarrer_Guidage is an asynchronous method

which starts the shortest path computation on the

server;

 TesterEtatDemande allow checking the state of

the execution of Demarrer_Guidage method

which returns 1 if the job is in progress, 0

otherwise;

 RecupererEtatGuidage permits to obtain the

shortest path computed;

 LireCodeRetour permits to decode a state code.

3.2 Network Data Source

The first step to compute a shortest path is to obtain

a real-world road network data. To do so, there

exist numerous sources including but not limited to

ShortestPathChallengingProblem-ContextofMobileDevicesinUrbanAreaConsideringWeakenedGPSSignaland

DataNetworkTraffic

395

Google Maps, ArcGis, Bing Maps, Mapquest, Via

Michelin and OpenStreetMap (OSM). Among them,

OSM has the great advantage to be an open-source

collaborative project that has reached 1 million users

in 2013. Around 30% of users have contributed to

OSM database. OSM consists of open data that are

freely available and it offers a data source for

researchers in the area of OR.

3.3 Proposed Shortest Path Algorithm

This paper aims to elaborate a dynamic shortest path

algorithm. As shown in Algorithm 1, the main loop

(lines 10-17) takes advantages of three

considerations:

 since it has been commonly recognized that the

computational effort required solving a generic

search grows faster than the size of the problem,

the original problem can be decomposed into

small sub-problems (lines 11-13), substantial

computational time saving can be achieved;

 the branch pruning techniques is considered. It

consists in discarding nodes from the scan

eligible nodes list after proving to be located out

of the assumed good solutions area (line 14). The

branch pruning algorithm maintains a strongly

limited set of eligible nodes as compared to A*

and provided a better complexity;

 a sub-goal based method (lines 15-16) can be

defined into a sub-problems especially for

shortest path problem in a road traffic network

where goals could be nodes or links located

between the origin and destination localization.

3.4 Integration of a Shortest Path

Algorithm into the Web Method

The web method Demarrer_Guidage is

asynchronous: it closes the communication

immediately and launches a long time process into a

thread. The main advantage is that one client can

continue its execution (Figure 3) in very short

delays.

The thread is linked to the client and more

precisely to the API Key which is used as session

identification. Into the thread the following

operations are achieved:

 The step 1 consists in verification of the API key

with the objective to check its validity and the

reach of maximal number of requests per day.

 The step 2 consists in downloading the road

network map from OpenStressMap using the

corresponding web service

(http://api.openstreetmap.org/).

 The step 3 consists in creation of the graph

representing the road network.

The step 4 is the computation of the shortest path

using the method Shortest_Path on the obtained

graph.

Algorithm 2 gives some details on the thread.

The procedure first checks the key and stops

immediately if the key is not valid (line 11). The line

12 consists in using the SOAP OSM API to obtain a

road network.

Line 13 involves extra web communication and

could be time consuming depending on the network

size. Line 14 consists in transforming the road

Algorithm 1: Shortest Path algorithm.

1. procedure Shortest_Path

2. Global parameters

3. L : sub-graph size

4. input parameters

5. G : the graph which models the urban network

6. Nx : initial nodes in the graph (pedestrian localization)

7. Ny : final nodes in the graph

8. output parameters

9. trip : set of nodes

10. begin

11. Compute the Euclidean distance from Nx to Ny

12. Compute the line equation from Nx to Ny

13. Define G'a subgraph around node Nx which models a sub-network around L meters

14. Reduce the number of nodes and arcs in G’

15. Determine N

out

the output node closest to the right intersection between the

line Nx_Ny and the border of rectangle including G’

16. Call Dijkstra algorithm to find shortest path in G’ between Nx and N

out

17. end

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

396

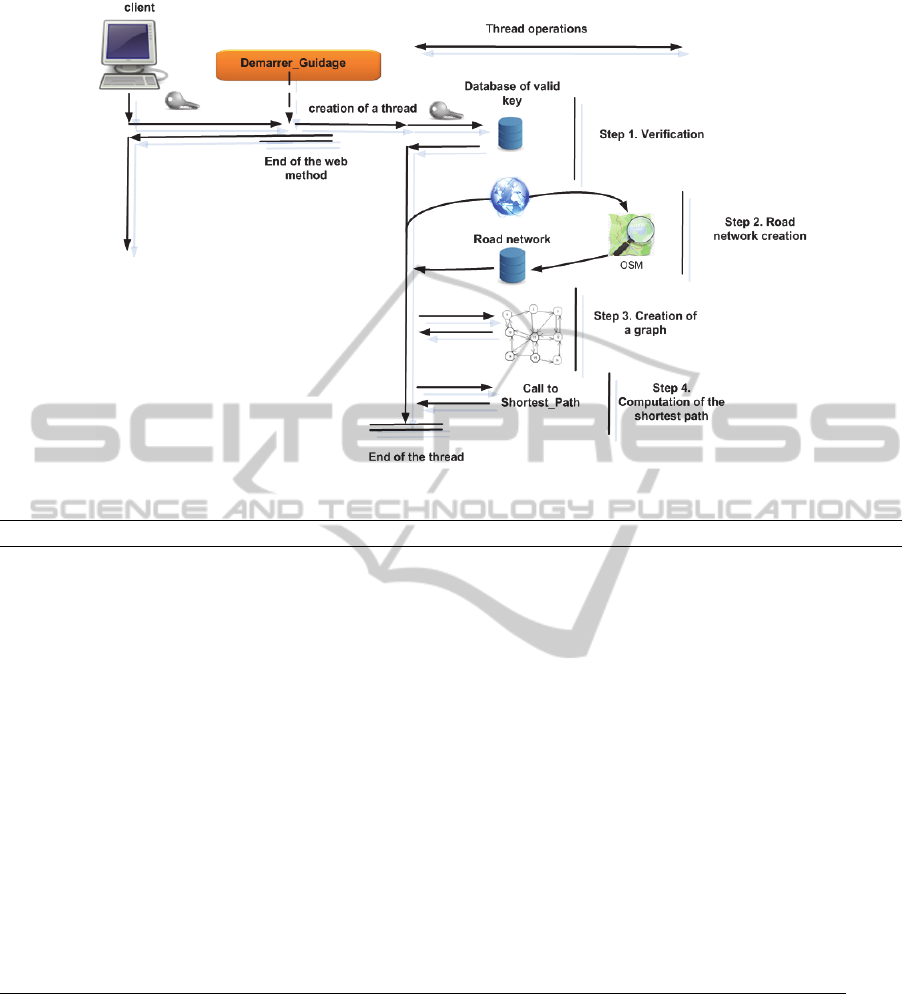
Figure 3: Web method Demarrer_guidage.

Algorithm 2: Thread_computation.

1. procedure Thread_computation

2. input parameters

3. G : the graph which modelize the urban network

4. (latx, longx) : the current position

5. (laty, longy) : the final position

6. Nx : initial nodes in the graph

7. Ny : final nodes in the graph

8. output parameters

9. trip : set of nodes

10. begin

11. call procedure Key_verification ()

12. if (key invalid) stop;

13. Connect to the mapquest web service and download the road network

14. Transform the road network into a graph (G)

15. Convert the position (latx, longx) into a node Nx in the graph

16. Convert the position (laty, longy) into a node Ny in the graph

17. Trip = call Shortest_Path (G, Nx, Ny)

18. T'= Convert trip into positions into the road network

19. return T'

20. end

network into a graph G. Line 15 consists in

conversion of position (latitude/longitude) into one

node in the graph. Note that this conversion could

require (according to the road network coding of

MapQuest) creation of new nodes. Similar remarks

hold for line 16. Line 17 consists in using the short

path procedure which provides a shortest path as a

sequence of nodes in G. The shortest path is then

transformed into a sequence of (latitude/longitude)

points on the road network.

3.5 Wireless Traffic Disturbances

In urban area mainly, the connection to the mobile

network depends on numerous parameters including

the internet provider quality equipment; the number

of users connected at the same time and modulation

of electromagnetic waves propagation. The last point

means that radio waves interact with the

environment though exotic physical mechanisms

including reflection, refraction, fast fading, slow

ShortestPathChallengingProblem-ContextofMobileDevicesinUrbanAreaConsideringWeakenedGPSSignaland

DataNetworkTraffic

397

fading and of course attenuation. Experts in wireless

networks stated it is impossible to predict the real-

life performances of such system one fully deployed

and that performances can be strongly modulated

especially in a mobile scenario.

The consequence is that mobile device

connection to a web service could be delayed or

impossible and could require conception of a mobile

solution where a graph is saved into the mobile

device allowing computation of a shortest path using

the mobile CPU only.

4 CONCEPTION OF CLIENT

USING WEB SERVICE

A client application using the proposed web service

contains three components: User interface, business

layer and SOAP layer. Among those three

components, SOAP layer could be created

automatically by a modern integrated development

environment.

The business layer can be divided into 3 steps to

make a demonstration of the different methods

execution:

Step 1. The client has to create a instance of the

class RecuperationDonnee and to define a

port assigned with

getRecuperationDonneePort .

Step 2. The client can access to the asynchrone

DemarrerGuidage method providing a valid

API key, and two (latitude/longitude)

positions.

Step 3. The client can periodically investigate if the

result is available or not using the

RecupererResultatGuidage method

providing only the key which is the session

identification.

With the objective to validate the principle and the

performance of the tune shortest path algorithm in

the real life conditions, an android application has

been created and it could be downloaded at: http://

www.isima.fr/~lacomme/ORWebServices/GPS4ped

estrian/source/Gps_android.apk

5 COMPUTATIONAL RESULTS

AND ANALYSIS

In this paragraph we present the performance of the

proposed dynamic shortest path algorithm in real

problem. The network corresponds to the urban

traffic system of Clermont-Ferrand city. Based on

these data, 27 instances were randomly generated.

The Origin and destination points are chosen such

that their distance corresponds to an hour walk (in

average 2,5km).

Two types of experiments have been performed.

The first one concerns the hypothesis that the

pedestrian does not deviate from the path proposed

by the algorithm (he never loses his way). The

second one concerns the hypothesis that the

pedestrian loses his path with a given probability.

The following notations are used in table 1 and 2:

N: instance number;

h*: optimal distance found by Dijkstra

algorithm (in meters) ;

h(p%): distance found by the proposed

algorithm with p probability that the

user loses its way (in meters);

Gap%: percentage deviation of optimal

solution;

I: number of algorithm iterations needed

to reach final destination;





, %: average distance from x executions of

27 instances (in meters).

Test results show that average gap from the optimal

solution is 5.62% and for 10 of instances the

algorithm found the optimal value.

Table 2 shows the results for the second

hypothesis: the pedestrian loses at each intersection

his way with a given probability p (p=1, 2, 5 and

10%). All results in table 2 are average values from

100 executions on the all 27 instances. Results prove

that the proposed algorithm has a promising

performance. The added distance is due to the

likelihood of pedestrian to lose his way. This

distance is near 7% the path in the case of

probability p=10%.

6 CONCLUDING REMARKS

The shortest path routing problem which is well-

known as a seminal problem in routing has been

chosen to study how constraints linked to mobility

push us into modifying routing algorithms to provide

efficient services. The Web services technologies

offer also to a community the possibility to reuse the

methods for a very small programming effort. The

Web Service paradigm is a new approach in

spreading operational research algorithms and our

contribution stands at the crossroads of optimization

research community and the web service community

expectations.

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

398

Figure 4

Example design of a client application using the Web service

Table 1: Test results for first hypothesis.

N° Origin point Destination point

*

0%

Gap % I

1 45.7581 3.1101 45.7780 3.0831 3629.80 3812.60

5.04

2 45.7792 3.1168 45.7580 3.0784 4509.11 5613.92

24.50

3 45.7848 3.1028 45.7746 3.0947 1639.40 1639.40

0.00

4 45.7890 3.0951 45.7704 3.1188 4047.20 4496.63

11.10

5 45.7780 3.1104 45.7884 3.0983 1866.19 1882.40

0.87

6 45.7751 3.0829 45.7710 3.0926 1245.82 1289.56

3.51

7 45.7701 3.0808 45.7801 3.1184 3278.60 3388.53

3.35

8 45.7821 3.0985 45.7636 3.1078 2737.98 2737.98

0.00

9 45.7705 3.0656 45.7651 3.0769 1525.79 1699.48

11.38

10 45.7819 3.1027 45.7647 3.0974 2417.21 3079.71

27.41

11 45.7590 3.1159 45.7856 3.0735 5440.46 5659.44

4.03

12 45.7789 3.0836 45.7823 3.1019 1789.43 1943.73

8.62

13 45.7890 3.1001 45.7707 3.0757 3383.98 3741.73

10.57

14 45.7683 3.1066 45.7816 3.1239 2750.92 2770.76

0.72

15 45.7645 3.1053 45.7812 3.0903 2529.81 2529.81

0.00

16 45.7728 3.0727 45.7662 3.0680 1260.14 1260.14

0.00

17 45.7805 3.1001 45.7763 3.0770 2074.18 2137.08

3.03

18 45.7592 3.0841 45.7777 3.0703 2588.66 2588.66

0.00

19 45.7620 3.1248 45.7612 3.0934 3033.87 3094.42

2.00

20 45.7691 3.1079 45.7879 3.0997 3103.75 3703.95

19.34

21 45.7773 3.0907 45.7877 3.0861 1677.82 1682.47

0.28

22 45.7764 3.0713 45.7664 3.0796 1454.39 1454.39

0.00

23 45.7725 3.0936 45.7668 3.1143 2047.18 2373.95

15.96

24 45.7613 3.0906 45.7867 3.0788 3356.14 3356.14

0.00

25 45.7682 3.0893 45.7654 3.0984 1127.62 1127.62

0.00

26 45.7654 3.0892 45.7654 3.0882 884.33 884.33

0.00

27 45.7659 3.1079 45.7804 3.0874 2594.19 2594.19

0.00

Avg. 2518.30 2686.78 5.62 9.22

Table 2: Test results for second hypothesis.

Value (m) GAP % Distance added (m) Standard deviation (m) I

*

2518,30 - - - 1

0%

2686,78 5,62 - - 9,22





100,1%

2704,57 6,32 17,79 58,87 9,39





100,2%

2725,76 7,18 38,98 88,18 9,55





100,5%

2783,59 9,49 96,81 139,47 10,12





100,10%

2896,78 13,96 210,00 206,35 11,20

ShortestPathChallengingProblem-ContextofMobileDevicesinUrbanAreaConsideringWeakenedGPSSignaland

DataNetworkTraffic

399

The first experimentation reported in this paper

pushes us into considering that complexity and proof

of optimality are not the only key of efficient

algorithms in the context of mobility but persuade us

that a valuable quality of service strongly depends of

a correct integration of components into a global

system.

Also, the following developments are suggested

for the future research; Besides Dijkstra’s algorithm,

other algorithms can also be applied in the dynamic

approach to improve the computational aspects of

the proposed algorithm.

REFERENCES

Bhargava, H. K., Power, D. J. and D. Sun, 2007, Progress

in Web-based decision support technologies, Decision

Support Systems, 43, pp. 1083-1095. 2007.

Chinnici R., J. Moreau, A. Ryman and S. Weerawarana

(Eds.), 2007, Web Services Description Language

(WSDL) Version 2.0 Part 1: Core Language, W3C

Proposed recommendation, May 23.

Cohen M. D., C. B. Kelly and A. L. Medaglia. 2001,

Decision support with web-enables software.

Interfaces. 31(2), pp. 109-129.

Dominguez-Ballesteros B., G. Mitra, C. Lucas and N.-S.

Koutsoukis, Modelling and solving environments for

Mathematical Programming (MP): a status review and

new directions, Journal of The Operational Research

Society. 53(10). pp. 1072-1092. 2002.

Fielding R.T. and R.N. Taylor. Principled design of the

modern web architecture, ACM Trans. Internet

Technol. (TOIT), 2(2), pp. 115–150. 2002.

Fu, L., Sun, D. and L. R. Rilett, Heuristic shortest path

algorithms for transportation applications: State of the

art, Computers & Operations Research 33, pp. 3324–

3343, 2006.

Garroppo, R., Giordano, S., Tavanti, L., 2010. A survey

on multi-constrained optimal path computation: Exact

and approximate algorithms, Computer Networks, 54,

pp. 3081–3107.

Guzolek J, Koch E. Real-time route planning in road

network. Proceedings of VINS, September 11–13,

1989. Toronto, Ontario, Canada, p. 165–9.

Gubichev,A. Bedathur, S., Seufert, S. and G. Weikum.

2010. Fast and Accurate Estimation of Shortest Paths

in Large Graphs. CIKM’10, October 26–30, Toronto,

Ontario, Canada.

Gudgin M., M. Hadley, N. Mendelsohn, J. J. Moreau and

H. Nielsen, SOAP version 1.2. Part 1. Messaging

framework, http://www.w3.org/TR/soap12-part1/,

2003.

Hart E. P., Nilsson N. J., Raphael B., 1968. A formal basis

for the heuristic determination of minimum cost paths.

IEEE Transaction, System Science and Cybernetics;

SSC-4(2):100–7.

IBM World Trade Corporation. IBM Mathematical

Programming System Extended /370 (MSPX/370):

Program Reference No. SH19-1095-1, New York

&Paris. Reference No. SH19-1095-1. 1976.

Kuznetsov T. High performance routing for IVHS. IVHS

America 3rd Annual Meeting, Washington, DC, April,

1993.

Lindo Systems Inc,. LINGO Modelling System Version

12.0. Manual. Chicago IL, USA: Lindo Systems Inc

Lindo Systems Inc. 2008.

Lucas C. and G. Mitra, Computer-assisted Mathematical-

Programming (Modelling) System—CAMPS, The

Computer Journal, 31(4), pp. 364-375. 1988.

Maximal Software, MPL Modelling System, Release 4.2,

2002.

Nilsson J. N. Problem-solving methods in artificial

intelligence. New York: McGraw-Hill; 1971.

Pearl J. Heuristics: intelligent search strategies for

computer problem solving. Addison-Wesley

Publishing Company; 1984.

UDDI Version 2.04 API Specification, UDDI Committee

Specification, 19 July 2002, available on

http://uddi.org/pubs/ProgrammersAPI_v2.htm.

Wang H., Huang, J. Z., Qub, Y. and J. Xia. Web services:

problems and future directions, Web Semantics:

Science, Services and Agents on the World Wide Web.

1 (3). pp. 309–320. 2004.

Kuznetsov T. High performance routing for IVHS. IVHS

America 3rd Annual Meeting, Washington, DC, April,

1993.

Willhalm. T., 2005. Engineering Shortest Paths and

Layout Algorithms for Large Graphs. Dissertation der

Universität Fridericiana zu Karlsruhe (TH).

ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems

400