Monitoring of Grinding Burn by AE and Vibration Signals

Rodolpho F. Godoy Neto

, Marcelo Marchi

, Cesar Martins

, Paulo R. Aguiar

and Eduardo Bianchi

Mechanical Department, School of Engineering, Univ. Estadual Paulista - UNESP,

Av. Luiz E.C. Coube, 14-01, 17033-0360, Bauru – SP, Brazil

Electrical Engineering Department, School of Engineering, Univ. Estadual Paulista - UNESP,

Av. Luiz E.C. Coube, 14-01, 17033-0360, Bauru – SP, Brazil

Keywords: Neural Network Application, Monitoring, Acoustic Emission, Grinding Process, Burn.

Abstract: The grinding process is widely used in surface finishing of steel parts and corresponds to one of the last

steps in the manufacturing process. Thus, it’s essential to have a reliable monitoring of this process. In

grinding of metals, the phenomenon of burn is one of the worst faults to be avoided. Therefore, a monitoring

system able to identify this phenomenon would be of great importance for the process. Thus, the aim of this

work is the monitoring of burn during the grinding process through an intelligent system that uses acoustic

emission (AE) and vibration signals as inputs. Tests were performed on a surface grinding machine,

workpiece SAE 1020 and aluminum oxide grinding wheel were used. The acquisition of the vibration

signals and AE was done by means of an oscilloscope with a sampling rate of 2MHz. By analyzing the

frequency spectra of these signals it was possible to determine the frequency bands that best characterized

the phenomenon of burn. These bands were used as inputs to an artificial neural networks capable of

classifying the surface condition of the part. The results of this study allowed characterizing the surface of

the work piece into three groups: No burn, burn and high surface roughness. The selected neural model has

produced good results for classifying the three patterns studied.

1 INTRODUCTION

Grinding is one of the most finishing processes used

in the manufacture of precision mechanical

components. It is the last stage in the manufacturing

chain, which is why it affords a high added value to

the end product. Despite its importance and

popularity, grinding still remains as one of the most

difficult and least understood processes in addition

to the function of solving the problems of time and

quality of the entire production sequence (Irani et al.

2005; Aguiar et al. 2010).

According to (Liao et al. 2008), grinding is one

of the most complicated process, mostly due to the

fact that a grinding operation is performed by a

grinding wheel which is composed of many tiny,

irregular shaped, and randomly positioned and

oriented abrasives (also called grits) bonded by some

medium. Thus, there are many variables that make it

difficult to choose the optimal parameters in a

simple way.

Since a reduction of the production costs and an

increase in the quality of the machined parts are

expected, the automated detection of the machining

process malfunctions has become of great interest

among scientists and industrialists. By the use of a

large variety of sensors, monitoring of machining

processes represents the prime step for reduction of

poor quality and hence a reduction of costs (Axinte

et al. 2004).

One of the most critical problems in the

intelligent grinding process implementation is the

automatic detection of surface burn in the parts. The

burn occurs during the cutting of the part by the

grinding wheel when the amount of energy

generated in the contact area produces an increase of

temperature enough to produce a change of phase in

the material. Such occurrence can visually be

observed by the bluish temper color on the part

surface (Aguiar et al. 2002). Grinding burn also has

an adverse effect on component in-service strength

and fatigue properties. When grinding becomes

abusive the grinding temperature can easily rise to

more than 800 C. Due to the effects of elevated

temperature, the surface of the workpiece may burn

and the deterioration of the surface becomes evident.

Workpiece burn during the grinding process is

272

F. Godoy Neto R., Marchi M., Martins C., R. Aguiar P. and Bianchi E..

Monitoring of Grinding Burn by AE and Vibration Signals.

DOI: 10.5220/0004753602720279

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 272-279

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

essentially an irreversible change in the

microstructure of a surface layer (Liu et al. 2005).

Therefore, the grinding burn control and monitoring

is of great interest to all industries dependent on the

grinding process, thus leading to a reduction in scrap

rate and production costs.

The main difficulty of controlling damages

caused in the grinding process is the lack of a

reliable method in supplying feedback in real time

during the process. Since the grinding process

causes intensive mechanical vibration and strong

acoustic emission, these signals can be picked up

easily and recorded by commercially available

instruments.

According to (Babel et al. 2013), in light of its

superior sensitivity to the multitude of fine dynamic

interactions between the wheel and the workpiece,

acoustic emission (AE) has emerged as a valuable

tool in a host of monitoring applications in grinding.

Typical examples include in-process wheel

mapping, and the sensing of wheel–work contact,

wheel loading, chatter and thermal damage. Still, the

authors report that in many applications, it suffices

to examine the signal in terms of time-averaged

indices, while others necessitate frequency domain

analyses of the raw AE signal, as the relevant

information is embedded in the spectral components

of the signal. In either case, due to the complex

nature of grinding processes, the challenge in the

effective and reliable application of AE lies in the

identification and interpretation of signatures

pertinent to the process responses that are of interest.

On the other hand, vibration is produced by

cyclic variations in the dynamic components of the

cutting forces, resulting from periodic wave

motions. The nature of vibration signals arising from

the metal cutting process incorporates free, forced,

periodic, and random types of vibration. Direct

measurement of vibration is difficult to achieve

because the vibration mode is frequency dependent.

Hence, related parameters are measured such as the

rate at which dynamic forces change per unit time

(acceleration) and the characteristics of the vibration

are derived from the patterns obtained (Dimla, Snr.

2002).

Several investigations have been carried out to

correlate vibration signals to the characteristics of

maching processes. For exemple, Yamamoto et al.

apud (Hassui & Diniz 2003) monitored the wheel

vibration (they fixed the sensor on the wheel

bearing) to detect the clogging of the wheel pores by

chips. Aiming towards this goal, they used adaptive

digital filters and created an index, based on the

outputs of these filters, called index of the signal

pattern. This index showed to have a good

relationship with the volume of chips clogged in the

wheel. (Hassui et al. 1998) proved that the RMS

signal of the workpiece vibration (they fixed the

sensor on the workpiece tailstock) presents better

relationship with wheel wear than acoustic emission.

Besides, the sensitivity of the vibration signal to

detect the wheel–workpiece moment of contact and

the moment of spark out end is as good as acoustic

emission sensitivity. (Hassui & Diniz 2003) tested

the ability of the vibration signal to follow the

changes of workpiece surface roughness and

circularity, in order to verify the possibility of using

it for the automatic definition of the dressing

moment.The results showed good correlation of

vibration signals with surface roughness and wheel

condition.

According to (Teti et al. 2010), it is generally

acknowledged that reliable process condition

monitoring based on a single signal feature (SF) is

not feasible. Therefore, the calculation of a sufficient

number of SFs related to the tool and/or process

conditions is a key issue in machining monitoring

systems. This is obtained through signal processing

methods that comprise pre-processing (filtering,

amplification, A/D conversion, and segmentation)

including, on occasion, signal transformation into

frequency or time–frequency domain (Fourier

transform, wavelet transform, etc).

One of the most used signal feature in maching

monitoring systems is the root mean square (RMS)

value, and it can be expressed as shown in equation









∆

















∆



(1)

where t is the integration time constant, and f

raw

the raw signal (Kim et al. 2001).

Thus, acoustic emission and vibration signals

have their own and interesting characteristics, which

adequately extracted and related to the studied

phenomena can provide valuable information to the

grinding process monitoring. This work aims at

monitoring workpiece burn during the grinding

process through neural modelling that uses features

of the acoustic emission (AE) and vibration signals

as inputs.

What makes this work distinguishible from

others is the use of vibration signal along with AE

signal. The former has not yet been employed in

grinding burn detection. Besides, study on frequency

domain for both signal that closely relates frequency

bands to bun, non burn and high surface roughness

MonitoringofGrindingBurnbyAEandVibrationSignals

273

values has not been carried out either. The selection

of frequency bands from the signal espectrum aims

to better extract the signal features for the classes

studied. Another contribuition of this work is related

to the types of classes, i.e., the models are able to

classify parts with high surface roughness values (no

visible burn), visible burn occurrence and normal

operation. It is worth mentioning that thermal

sensing, such as thermocouples inserted in the

workpiece or tool could produce good results as well

in monitoring the grinding burn. However, such

techniques are genererally invasive and, therefore,

infeaseble in most practical implementation.

2 NEURAL NETWORKS

IN MACHINING PROCESSES

According to (Teti et al. 2010), in monitoring and

control activities for modern untended

manufacturing systems, the role of cognitive

computing methods employed in the implementation

of intelligent sensors and sensorial systems is

fundamental. A conspicuous number of schemes,

techniques and paradigms have been used to develop

decision-making support systems functional to come

to a conclusion on machining process conditions

based on sensor signals data features. The cognitive

paradigms most frequently employed for the purpose

of sensor monitoring in machining, including neural

networks, fuzzy logic, genetic algorithms and hybrid

systems able to combine the capabilities of the

various cognitive methods.

Artificial neural networks (ANNs) are adaptive

and have parallel information-processing structures

with the ability to build functional relationships

between data and to provide powerful tools for

nonlinear, multidimensional interpolations. This

aspect of neural networks makes it possible to

capture and interpret the existing highly complex

nonlinear relationships between input and output

parameters that are frequently poorly understood. An

ANN is a system consisting of processing elements

(PE) with links between them. A certain

arrangement of the PEs and links produce a certain

ANN model, suitable for certain tasks (Ahmadzadeh

& Lundberg 2013).

Anns have been accepted as a very good tool that

can be applied to many nonlinear problems, where

finding solutions using traditional techniques are

cumbersome or impossible. Examples of applied

areas of nns include robotics, control, and system

identification. They have been successfully used in

condition monitoring and fault diagnosis in

machining processes. These applications have

usually used the pattern recognition approach

combined with the classification ability of anns

(marzi 2008).

Similar work on classification of grinding burn

can be found in (Spadotto et al. 2008), where the

authors perform only the classification of burn

degrees (slight burn, medium burn, severe burn and

non burn) of the part ground by using acoustic

emission and power signals statistics as inputs to the

neural network models. The results were good,

reaching a success rate of 93.5 % for model II,

which employs a statistic named DPO proposed by

(Aguiar et al. 2002), composed of the multiplication

between standard deviation of RMS AE and

maximum value of grinding power in the grinding

pass. Another similar work is presented by (Dotto et

al. 2003) in which a neural network model having

the RMS AE and grinding power as inputs is used to

classify burn and non burn condition of the parts

ground. Good response of the model can be

observed in the regions charts, where burning and

non burning occurrence were classified. The

investigation in (Kwak & Ha 2004) proposed a

diagnostic scheme of a grinding states (chatter,

vibration and grinding burn) by the neural network

using power and AE signals. The maximum

successful diagnosis was about 95 %. Other

investigations related to the topic of this work can

also be found. However, none of them has used the

vibration signal as well as verified the condition of

high surface roughness values of the work piece

ground.

3 MATERIALS AND METHODS

3.1 Experiments

The experimental tests were carried out in a surface

grinding machine. Each test consisted of a single

grinding pass across the workpiece length. Preceding

each test, a single-point diamond dresser performed

the dressing of the grinding wheel. Table 1 shows

the grinding condition of each test.

An acoustic emission sensor and a processing

signal unit, from Sensis manufacturer, model DM-

42, were employed in the tests. Also, a vibration

sensor, model 353B03 and a conditioning signal

unit, from PCB Piezotronic, were used. An

oscilloscope, model DL850, from Yokogawa,

collected both raw signals, at a sampling rate of 2

MHz. The sensors were fixed on the workpiece

holder and tested for good signal sensitivity and

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

274

without saturation.

Workpieces of SAE 1020 steel were ground with

an aluminum oxide grinding wheel, model 38A150-

LVH, from Norton, and cutting fluid was employed

(Emulsion water-oil of 4 %). The following grinding

parameters were used in the 13 tests: peripheral

speed of the grinding wheel – 30.78 m/s; workpiece

speed – 0.04 m/s; grinding wheel diameter – 326.64

mm; wheel width – 24.09 mm; workpiece

dimensions – 152.64 mm length and 13.01 mm

width. The schematic diagram in Figure 1 shows the

experimental test setup used in this work.

Figure 1: Experimental setup.

Following the experiments, the average surface

roughness (Ra) for each workiece was measured,

using a Taylor Hobson Surtronic 3+ precision

instrument. A sampling length of 1.6 mm and cut-off

of 0.8 mm were used, following the

recommendations of the ISO 4288-1996 standard.

Each workpiece surface length was equally divided

into 30 parts, where 3 surface roughness

measurements were taken from each part. Thus, the

mean value and standard deviation of each part were

calculated, allowing the assessment of the ground

workpiece regarding this important parameter. In

addition to the surface roughness measurements, the

visual inspection of each workpiece surface was

carefully carried out as well as all workpiece

surfaces were digitally photographed for further

analysis.

Table 1 shows information of the 13 tests, where

the cutting geometry means whether the grinding

wheel cut the workpiece in the conventional way,

i.e., flat geometry, or the workpiece was precisely

inclined to allow a ramp-cutting geometry. The latter

way, there are two cutting depths regarding the onset

and the end of the cutting, respectively. In Table 1,

HR stands for high surface roughness value, which

was so considered workpieces with this value higher

than 1.6 m and with no visible burn. Workpieces

with visible burn was considered as burn, and those

with no visible burn at all were classified as no burn.

Table 1: Information of the tests.

Test Cutting

Geometry

Depth of

Cut (m)

Surface

condition

Flat

10 No burn

2 20 No burn

3 30 Burn

4 40 Burn

5 40 No burn

6 30 No burn

7 20 No burn

8 10 No burn

9 20 No burn

10 30 No burn

11 55 HR

12 Ramp

20-70 HR

13 30-80 HR

3.2 Selection of Frequency Bands

and RMS Vectors

The data acquisition produced vector of 20 million

of samples for each machined workpiece. Subsets of

400,000 samples were selected from each test vector

and for each surface condition (No burn, burn and

high surface roughness) for further digital

processing. The data sets from the tests were

digitally processed in MATLAB. A study on the

signals spectra was performed in order to identify

frequency bands more strongly related to the burn

phenomenon in surface grinding. The Fast Fourier

Transform (FFT) algorithm was implemented in

MATLAB routine for each surface condition. The

RMS values of each signal (AE and vibration) were

used as reference to pick the right position from

which the 8192-block FFT, Hanning window, was

performed. The spectra for AE and vibration signals

are shown in Figure 2, where AE is within a

frequency range of 20 kHz to 300 kHz and vibration

of 1 kHz to 25 kHz, given by the sensors and

process characteristics. Frequency bands were then

selected from the spectrum of each signal, where

nine frequency bands were chosen for the AE signal

and six for the vibration signal, as shown in Figure 2

by the shade areas. The justification for frequency

band selection is based on obtaining the best feature

extraction that represents the classes studied (no

burn, burn, high surface roughness). The criterion

used in the frequency band selection was looking for

the frequency windows on which the magnitudes of

the signal for each class presented good differences.

MonitoringofGrindingBurnbyAEandVibrationSignals

275

Also, a minimum of overlapping among the three

classes spectra was sought. These frequency bands,

in kHz, are as following for AE: 40-51, 53-59, 62-

68, 71-78, 80-87, 95-104, 128-135, 160-170, and

176-186. The frequency bands selected, in kHz, for

vibration are: 1-3, 4-5, 6-8, 16-19, 20-21, and 22-25.

It is worth mentioning that there are other frequency

bands, which could be studied as well, but they will

be considered for further study.

Figure 2: Frequency spectra of three conditions and the

chosen frequency bands. (a) AE; (b) Vibration.

Three vectors of 400,000 samples each were

extracted from the raw signals (AE and vibration)

for each workpiece surface condition (no burn, burn,

and high roughness). This procedure was based on

three regions along a given ground workpiece,

which represented a certain surface condition.

Butterworth digital filters, order 6, for each

frequency band previously selected, were applied to

those vectors, and therefore new filtered vectors

were generated. The RMS values were obtained

using a block length of 2048 from the filtered

vectors for each workpiece surface condition.

Therefore, three RMS vectors were generated for

each surface condition from which the mean value

and standard deviation were calculated. Figure 3

depicts the procedure herein described. In this

figure, B1 to Bn stand for the frequency bands

selected for study.

3.3 Neural Network Models

Three types of MLP neural models were considered

for comparison in order to choose the best

classification model. Before building the NN

models, the analysis of the RMS values in function

of the frequency bands was carried out, and two

frequency bands for each signal (AE and vibration)

were selected for the models. Thus, the first NN

model consisted of 1 input (RMS values) and 3

outputs (No burn, burn, and high roughness), and it

was obtained by testing into the model each RMS

vector filtered out for the 4 frequency bands selected

previously. The second NN model was composed of

2 inputs (2 RMS values) and 3 outputs (as in the first

model), and it was obtained by testing two RMS

vectors into the model, as inputs, filtered out for the

4 frequency bands aforementioned. Finally, the third

model comprised of four RMS vectors at each

frequency band selected, as inputs, and 3 outputs (as

in the first and second models). An algorithm for

training and testing the models in MATLAB was

developed, where the number of neurons (5, 10, 15,

20 and 25) and hidden layers (1 to 3) were varied.

The Levenberg-Marquardt algorithm for training the

neural models was used. In addition, sigmoid

tangent activation function for the neurons of the

hidden layers and linear activation function for the

neurons of the output layer were found more

suitable.

Figure 4: RMS values as a function of frequency bands;

(a) AE; (b) vibration.

The input RMS vectors for training, testing and

validating the neural models were obtained by

dividing every RMS vector at each frequency band

selected into 200 equally parts. This was done for

both signals acquired (AE and vibration) in the 13

experimental tests. Therefore, a number of 2,600

samples for each RMS vector and for each

frequency band was obtained, resulting in the total

of 10,400 RMS values (4 frequency bands selected

and further described). Of course, depending on the

model considered, a different number of samples

will be used in the training process, as described

(a)

(b)

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

276

previously. The total data obtained from the

aforementioned procedure was then divided

randomly, with 60 % used for NN model training

and 20 % for validation. The remaining 20 % was

used to test the ANN to confirm its satisfactory

performance as well as to build the confusion

matrices of the models.

To train the MLP networks, ranges representing

the values 0 and 1 were defined. Thus, values

between -0.50 and 0.50 represent the output 0, while

values within the interval of 0.51 and 1.50 represent

the output 1.

4 RESULTS AND DISCUSSION

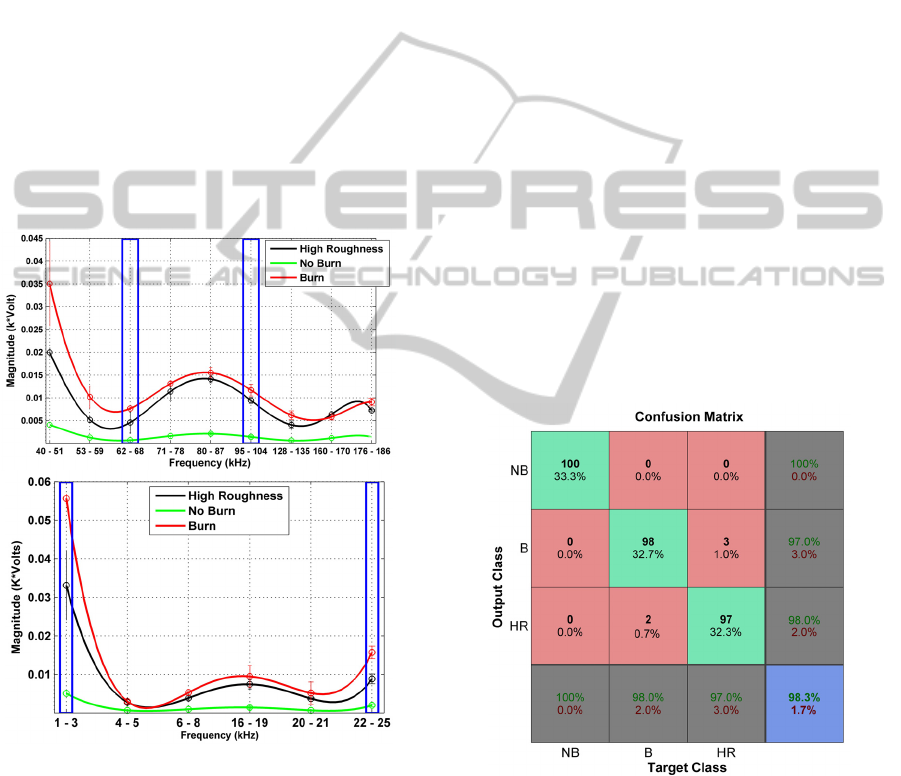
Figure 4(a) and 4(b) depicts the curves of the RMS

values for the nine and six frequency bands selected

for AE and vibration, respectively.

Figure 4: RMS values as a function of frequency bands;

(a) AE; (b) vibration.

The choice of the best frequency bands was based on

the observation of the signal magnitudes and

standard deviations at each frequency band. In other

words, a good situation was considered when the

signal magnitude increased according to the

following order of surface condition: no burn, high

roughness and burn. Also, the proximity of the

curves as well as the standard deviation were taken

into account, i.e., a small standard deviation and

non-overlapping of the curves were sought. Thus,

the frequency bands selected for the models were the

following: 62-68 kHz (B2 – AE), 95 kHz – 104 kHz

(B6 – AE), 1 kHz – 3 kHz (B1 – VIB), and 22 kHz –

25 kHz (B6 – VIB). These frequency bands are

indicated in Figure 4 as blue rectangles.

The results of the best neural models are

presented in Table 2, where it can be observed that

the combination of the AE and vibration signals in

the frequency bands selected (shown in Figure 4),

produced the best classification result (98.3 %) in

model A. Notwithstanding, the result of model 2

also shows a high level of classification (96.0 %).

Besides, model B has only 2 inputs, i.e., AE at 62

kHz - 68 kHz and vibration at 1 kHz – 3 kHz, which

is more suitable for hardware implementation.

Based on the results of models A and B, one can

argue that frequency band of 62 kHz – 68 kHz for

AE and 1 kHz – 3 kHz for vibration are good in the

feature extraction for this work.

Model C, however, presented a low success rate

of classification. That is due to the frequency bands

used in this model are not much representative of the

workpiece conditions.

Figure 5 shows the confusion matrix for model

A, which was obtained from 20 % of data set not

presented to the network-training phase.

Figure 5: Confusion Matrix for Model A (B=burn, NB=No

burn, HR=High roughness value).

It can be observed in the figure the good capacity of

pattern classification of the network, especially in

the class of no burn (NB) in which the success rate

of 100 % was achieved. The network, however, has

produced two false negatives for the burn class (B),

which were classified as high roughness (HR). Also,

three false negatives are observed for the high

(a)

(b)

MonitoringofGrindingBurnbyAEandVibrationSignals

277

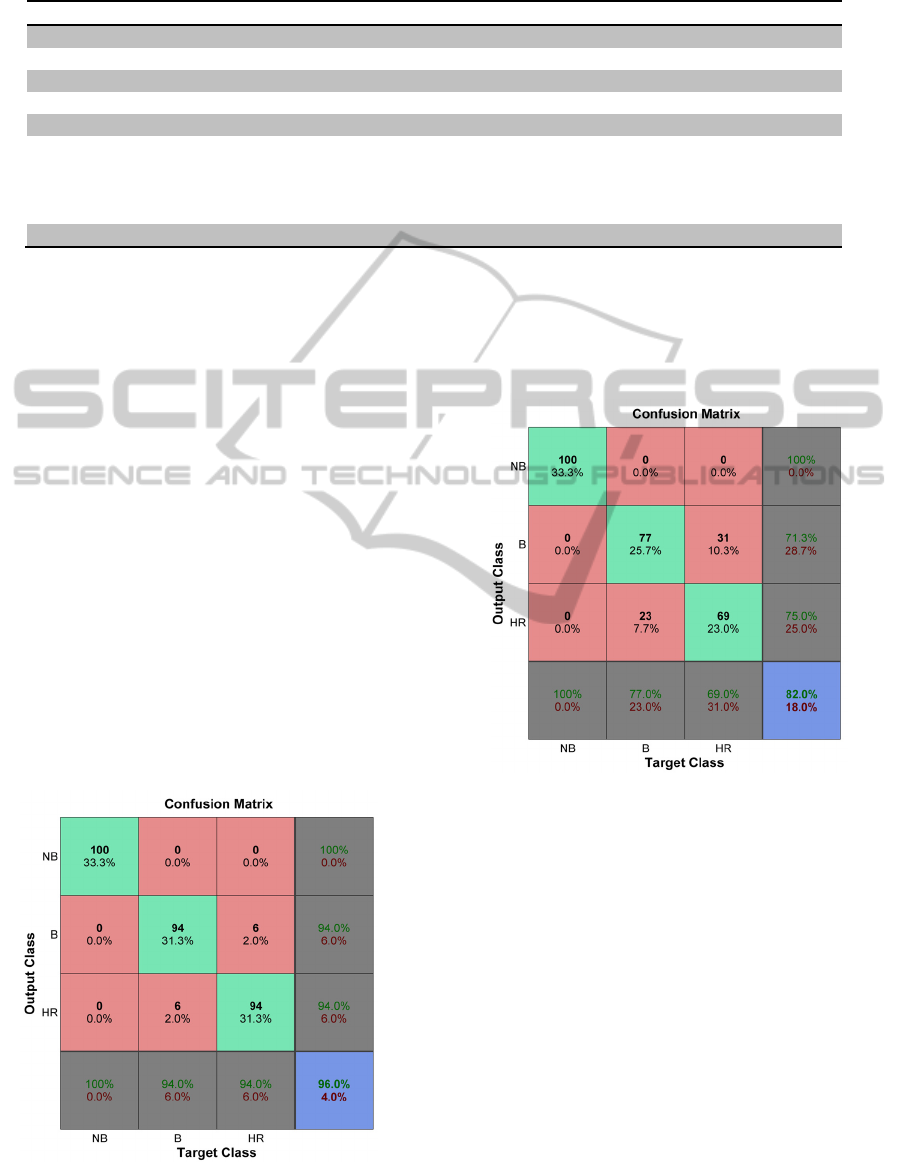
Table 2: Results of the best neural models.

Name Model A Model B Model C

Input Parameter Mean RMS value of AE and Vibration signals

Structure 10

–

5 25

–

0 3

–

Train. Function Levenber

arquardt Backpropa

ation

Max epochs 1000

Inputs 4 2 2

Frequency Bands

AE: 62kHz

–

68 kHz

95kHz – 104 kHz

VIB: 1kHz – 3kHz;

22kHz

–

25kHz

AE: 62kHz

–

68 kHz

VIB: 1kHz – 3kHz

AE: 95kHz

–

104 kHz

VIB: 22kHz – 25kHz

Overall Result 98.3 % 96.0 % 82.0 %

roughness class, which were classified as burn class.

Both kinds of errors could not be of concern in the

industrial environmental, since it would not

compromise the quality of the part being

manufactured.

The confusion matrix for model B is shown in

Figure 6. In this model, a greater number of false

negatives is observed for the same classes of model

A. On the other hand, this model has only two

inputs, which makes it more attractive for hardware

implementation.

The confusion matrix for model C is presented in

Figure 7, where one can clearly see the high number

of false negatives for both classes of burn and high

roughness. However, the success rate of 100 % for

no burn class was similarly achieved.

The models with one input have shown high

level of errors, and thus they were not presented.

Comparing the results of this work with the

investigations of (Kwak & Ha 2004) and (Spadotto

et al. 2008), it can be observed an improvement

in classifying the burn occurrence, i.e., model A

Figure 6: Confusion Matrix for Model B (B=burn, NB=No

burn, HR=High roughness value).

presented a success rate of 98.3 % against 95 % and

93.5 %, respectively. In addition, this investigation

adds an important class of high surface roughness to

the neural models, which becomes the monitoring

system even more effective.

Figure 7: Confusion Matrix for Model C (B=burn, NB=No

burn, HR=High roughness value).

5 CONCLUSIONS

The frequency content of the AE and vibration

signals showed different behavior for the three

surface conditions studied. Based on this analysis,

frequency bands could be selected for the neural

models, i.e., 62-68 kHz (B2 – AE), 95 kHz – 104

kHz (B6 – AE), 1 kHz – 3 kHz (B1 – VIB), and 22

kHz – 25 kHz (B6 – VIB).

The results showed that neural model A

presented a success rate of 98.3 %, which had the

four RMS inputs (2 AE and 2 VIB). However, a

small number of false negatives were observed in

the burn class as well as in the high roughness class,

which would not necessarily compromise the quality

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

278

of the part being manufactured. Also, model B

produced good results with a success rate of 96.0 %,

but an increased number of false negatives. This

model had only two inputs (1 AE and 1 VIB).

Nonetheless, the hardware implementation of model

B would be more interesting. Model C, however,

presented low success rate of classification and must

be discarded.

From model A and B, one can be argued that

frequency band of 62 kHz – 68 kHz for AE and 1

kHz – 3 kHz for vibration are good in the feature

extraction for this work.

As discussed in the previous section, the results

of this work have proved superior when compared

with the investigations of (Kwak & Ha 2004) and

(Spadotto et al. 2008). The extraction of the best

signals features from the spectra as well as the use of

vibration signal along with AE produced better

classification results.

Based on one of the best models obtained, it

would be possible to implement it into a hardware

that could provide information in real-time to

operator in order to make adjustments and possibly

avoid burning. In the case of burn classification has

been made, the part should be discarded.

ACKNOWLEDGEMENTS

The authors are indebted to FAPESP, CNPq and

CAPES, Brazilian agencies that have supported this

work. Also, thanks go to the NORTON Company,

from Saint Gobain Group, for donating the wheel.

REFERENCES

Aguiar, P.R., Bianchi, E.C. & Oliveira, J.F.G., 2002. A

method for burning detection in grinding process using

acoustic emission and effective electric power signals.

Manufacturing Systems, 31(3), pp.253–257.

Aguiar, P.R. De, Paula, W.C.F. De & Bianchi, E.C., 2010.

Analysis of Forecasting Capabilities of Ground

Surfaces Valuation Using Artificial Neural Networks.

J. of the Braz. Soc. of Mech. Sci. & Eng., XXXII(2),

pp.146–153.

Ahmadzadeh, F. & Lundberg, J., 2013. Remaining useful

life prediction of grinding mill liners using an artificial

neural network. Minerals Engineering, 53, pp.1–8.

Axinte, D. a et al., 2004. Process monitoring to assist the

workpiece surface quality in machining. International

Journal of Machine Tools and Manufacture, 44(10),

pp.1091–1108.

Babel, R., Koshy, P. & Weiss, M., 2013. Acoustic

emission spikes at workpiece edges in grinding: Origin

and applications. International Journal of Machine

Tools and Manufacture, 64, pp.96–101.

Dimla, Snr., D.E., 2002. The Correlation of Vibration

Signal Features to Cutting Tool Wear in a Metal

Turning Operation. The International Journal of

Advanced Manufacturing Technology, 19(10), pp.705–

713.

Dotto, F. et al., 2003. Automatic detection of thermal

damage in grinding process by artificial neural

network. Revista Escola de Minas, 56(4), pp.295–300.

Hassui, a. et al., 1998. Experimental evaluation on

grinding wheel wear through vibration and acoustic

emission. Wear, 217(1), pp.7–14.

Hassui, a. & Diniz, a. E., 2003. Correlating surface

roughness and vibration on plunge cylindrical grinding

of steel. International Journal of Machine Tools and

Manufacture, 43(8), pp.855–862.

Irani, R. a., Bauer, R.J. & Warkentin, a., 2005. A review

of cutting fluid application in the grinding process.

International Journal of Machine Tools and

Manufacture, 45(15), pp.1696–1705.

Kim, H.. et al., 2001. Process monitoring of centerless

grinding using acoustic emission. Journal of Materials

Processing Technology, 111(1-3), pp.273–278.

Kwak, J.-S. & Ha, M.-K., 2004. Neural network approach

for diagnosis of grinding operation by acoustic

emission and power signals. Journal of Materials

Processing Technology, 147(1), pp.65–71.

Liao, T.W. et al., 2008. Grinding wheel condition

monitoring with boosted minimum distance classifiers.

Mechanical Systems and Signal Processing, 22(1),

pp.217–232.

Liu, Q., Chen, X. & Gindy, N., 2005. Fuzzy pattern

recognition of AE signals for grinding burn.

International Journal of Machine Tools and

Manufacture, 45(7-8), pp.811–818.

Marzi, H., 2008. Modular Neural Network Architecture

for Precise Condition Monitoring. IEEE Transactions

on Instrumentation and Measurement, 57(4), pp.805–

812.

Spadotto, M.M. et al., 2008. Classification of burn degrees

in grinding by neural nets. In IASTED international

conference on artificial intelligence and applications.

Innsbruck: ACTA Press, pp. 1–6.

Teti, R. et al., 2010. Advanced monitoring of machining

operations.

CIRP Annals - Manufacturing Technology,

59(2), pp.717–739.

MonitoringofGrindingBurnbyAEandVibrationSignals

279