
Coverage and Goal Searching Behaviours of a Group of Agents
by a Special Single Query Roadmap
Its Benefits to Mutiple Query Roadmaps
Ali Nasri Nazif and Mohammad Torabi Rad
National Iranian Oil Company, Tehran, Iran
Keywords: Multi-agent, Single Query Roadmap, Coverage, Goal Searching.
Abstract: This paper tends to mainly target two different types of swarming behaviour in a 2D environment, namely
area coverage and goal searching within an environment occupied with obstacles. For such behaviours, we
introduce a roadmap (a tree) customized to behave well in multi-agent scenarios. We consider a variety of
situations and environments, and explain how the method we have proposed comes into operation under
such circumstances. A comparison is, also, made with respect to multiple query roadmaps.
1 INTRODUCTION
In our two former papers, Multi-Agent Area
Coverage Using a Single Query Roadmap (Nasri,
Davoodi and Pasquier, 2011) and Finding an
Unknown Goal in an Environment by a Group of
Agents (Nasri, Davoodi and Mohades, 2009), efforts
were made to introduce a new single-query roadmap
known as WMA-RRT which, is a form of graph,
spreads in free spaces of an environment, and is
applied to coordinate the movements of a group of
homogenous agents within the same environment.
What must be labelled as an important characteristic
of this roadmap is its construction on the basis of the
number of agents that do exist in the environment.
As a result, it is highly appropriate for multi-agent
scenarios. Further, as could be seen through the
following pages, such a roadmap plays the role of a
channel the agents employ to communicate.
The paper begins with an introduction on WMA-
RRT, and then it adheres to study coverage and goal
searching behaviours that benefit from the
constructed WMA-RRT in the environment. In brief,
the goal in coverage behaviour is to visually cover
an area by means of a group of agents, while the
primary aim in goal searchning behaviour is to find
an unknown goal by a group of agents in an
environment. Also in each part, experimental results
and comparision to multiple query roadmap methods
are presented.
2 WMA-RRT
Constructed in any given environment, a roadmap is
a graph able to capture the connectivity of free space
within the same environment. So far, two different
types of roadmaps have been introduced by
researchers, first of which is in demand of an
explicit representation of the workspace geometry.
Visibility Graphs as well as Generalized Voronoi
Diagrams could be named as cases belonging to this
group. However the roadmap introduced by the
paper falls in the second group which is constructed
based on sampling-based algorithms. They work by
generating sample points throughout the free space
of the environment and connecting them to build a
graph. There are two types of sampling planners:
multiple-query and single-query. In multiple-query
planners, in pre-processing phase, a roadmap is
constructed by simultaneously expanding some trees
from several randomly distributed starting points
and merging them to prepare the entire roadmap. It
is likely that the constructed roadmap is not
connected in a cluttered environment. Taking
multiple-query planners, PRM could be introduced
as the one most frequently used. (Kavaraki, Svestka,
Latombe and Overmars, 1996). The pre-processing
phase pertinent to multiple-query planners may be
occasionally very time consuming, but it is going to
answer many queries once the construction of the
roadmap has been completed.
Single-query planners, on the contrary, have
280
Nasri Nazif A. and Torabi Rad M..
Coverage and Goal Searching Behaviours of a Group of Agents by a Special Single Query Roadmap - Its Benefits to Mutiple Query Roadmaps.
DOI: 10.5220/0004753802800287
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 280-287
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

been introduced to handle situations in which it is
required to provide an answer to just a single query
as fast as possible. EST, Lazy RPM and RRT all
belong to this latter category of planners. Since the
planner introduced in this paper is a variation of
Rapidly-Exploring Random Tree (RRT) (Lavalle
and Kuffner, 2000), it is worth briefly explaining
how it operates.
The roadmap constructed by the RRT planner is
a tree which expands throughout the free space of a
given environment. This planner is probabilistically
complete, in other words, if the algorithm keeps
running for an adequate length of time, the
probability of covering every location of the
environment converges to one.
RRT construction algorithm is as follows: first a
uniform distribution is used to insert a sample point
qinit in the environment. When not colliding with any
obstacles, this sample point is added to the RRT tree
as its first node. In each iteration, another sample
point (
qrand) is randomly placed in the free space.
Then, among the previously added nodes, the nearest
neighbour node (
qnear) is selected for further
expansion. Next, a new node (qnew) is produced as a
result of moving the qnear by a predefined value
called step-size (ɛ) toward
qrand. Finally, if collision
free, the new node is added to the roadmap (Figure
1).
Figure 1: This figure illustrates how an RRT tree is
expanding given the current state of the tree.
Regardless of what swarming behaviour we are
going to contemplate, construction of WMA-RRT
begins by figuring out the location of the root of the
roadmap (Main Root) and continues by specifying
the adjacent nodes to the main root which we call
them Secondary Roots. The Secondary Roots are
exactly where the expansion of our tree starts.
We assume that at the beginning, all agents are
situated close to each other and can be surrounded
by a simple polygon. In order to build this polygon
in a way it could enclose all the agents, we apply
convex hull algorithm (Preparata and Hong, 1977).
The agents are considered as points in the
environment, thus the convex hull algorithm is able
to construct the minimal convex hull out of these
points, regardless of the obstacles in the
environment. We pick the point where the two
longest diameters of the polygon intersect as our
Main Root. In case that the intersection point is not
collision free, we will just replace the current longest
diameters by the next two ones.
Then it comes to assigning a particular node to
each agent. Here, the algorithm connects the agents’
initial locations to the Main Root and therefore some
edges are created. Our Secondary Roots are
produced by moving out a distance of at most ɛ in
the direction of these edges. Each of these
Secondary Roots is assigned to the corresponding
agents. From this point on, the algorithm works like
the RRT planner, but with two main differences.
First, in WMA-RRT all Secondary Roots are
considered as
qinit, in contrary to the RRT algorithm
in which we just have one
qinit that is inserted
randomly in the free space of the environment. The
second difference is that in WMA-RRT, our main
root is exempted from expansion. The tree expands
at a high pace, and it develops n sub-trees that we
assign as Branches, where n stands for the number
of agents in the environment.
3 SWARMING BEHAVIOURS
In this section, first we briefly discuss the works
formerly done on multi-agent systems, and then in
two different parts, we introduce our algorithms for
Coverage and Goal Searching behaviours using
WMA-RRT.
One of the earliest applications of multi-agent
systems is coordinating the movements of a group of
agents where each agent has its own starting point
and destination. There are two main approaches for
solving these kinds of problems: Centralized and
Decoupled.
In Centralized Planning, each agent is taken into
account as an end-effector of a multi-arm robot.
Paths for agents are planned simultaneously and
collisions between agents are self-collisions of the
robot’s arms. The main advantage of Centralized
Planning is completeness.
Decoupled Planning is less expensive than
Centralized Planning, but it is incomplete and it may
be unable to find a solution even if one does exist.
Swarm Intelligence, has recently been a source
of motivation for a lot of researches in multi-agent
systems. Swarm Intelligence is an AI technique
inspired by the collective behaviours observed in a
multitude of species which exhibit social life such as
ants and honey bees (Abraham and Guo, 2006).
ݍ
௧
ݍ
ݍ
௪
ݍ
ௗ
CoverageandGoalSearchingBehavioursofaGroupofAgentsbyaSpecialSingleQueryRoadmap-ItsBenefitsto
MutipleQueryRoadmaps
281

Coordinating a group of agents by employing
honeybees’ foraging behaviour has been one of the
earliest attempts in SI (Gordon and Wagner, 2003).
Also Bayazit uses a multiple-query roadmap as a
means of indirect communication between agents
(Bayazit, 2004).
Moreover, the swarming behaviour probably
observed in flocks of birds, schools of fish and sheep
herds motivated Reynolds to introduce a bio-
inspired technique to steer a group of rule-based
autonomous agents, called Boids (Reynolds, 1999).
Researchers have also used grid-based
approaches to deal with the area coverage problem.
Hazon and Kaminka, for example, proposed a
mechanism by decomposing the environment into
same size cells. Considering the initial positions of
the robots, they found a spanning tree of the free
cells which could be decomposed to some balanced
sub-trees. Finally each sub-tree was assigned to a
robot (Hazon and Kaminka, 2008).
3.1 Area Coverage
The area coverage problem deals with the use of one
or more agents to sweep or visually sense the free
space of an area.
The agents rely on the WMA-RRT roadmap to
move through the free space of the environment, and
also use it as a means of indirect communication as
shown later. WMA-RRT is considered a weighted
tree and the weight of the edges of the roadmap is
initialized to 0 at the starting point of the algorithm.
As described before, the tree has branches equal to
the number of agents. During the covering operation,
at least one agent is assigned to each branch. The
weight of the edges is updated while traversing the
roadmap.
All the information that the agents need in order
to do their job well in the environment is available
through the roadmap’s nodes. Our agents here are
simple autonomous entities capable of following
some explicit condition-action rules. They are utility
based agents, that is, each of them will try to
maximize its own utility function, which is defined
as the average over the weight of all traversed edges.
At the beginning of the mission, each agent is
assigned to independently find a branch, and keep
operating until the branch is thoroughly traversed.
Our main data structure, used by the agents
during the covering process, is an array of n trees,
where n represents the number of branches (agents)
in the environment.
Graph Brach[i]; 0 ≤ i ≤ n-1
The Graph itself is a class using two other
classes: Node and Arc. The agents use these classes
to gather information such as the outgoing edges of a
node and their corresponding weight.
Two arrays, Sync and Weight are the other data
structures that are used in our algorithm. Sync is
used to keep the number of active agents in each
branch:
Sync[i]; 0 ≤ i ≤ n-1
In other words, Sync[k] shows the number of
agents that are currently using branch[k] as their
exploration roadmap. As we will see, there may be
situations that more than one agent use the same
branch. At the beginning, all members of Sync array
have value of zero. Entering a specific branch such
as Branch[j], each agent increases the related value
of sync which is sync[j] by one (and decreases the
same value by one when it exits that branch).
The last array is Weight which is used to hold the
weight of the first edge of each branch (the edge that
connects the Main Root to the Secondary Root). As
we will see, the agents use this as a way to rapidly
exchange some information.
Weight[i] ; 0 ≤ i ≤ n-1
Figure 2 depicts a scenario with four agents a
few seconds after their mission has just started. As
can be seen, the first-coming edges of each branch
(four edges here) connect the Main Root to the
Secondary Roots. As soon as choosing an edge to
traverse, each agent increases the weight of it. The
first edge each agent begins to traverse is the starting
(first-coming) edge of its corresponding branch. As
a result, by increasing the weight of that edge, the
value of the corresponding item in array Weight
will
increase too. Also as can be seen in this figure, the
value of all members of sync array is equal to one,
because each agent starts exploring its dedicated
branch and by increasing the default value of the
corresponding array member from 0 to 1, shows that
it is active on that branch. It also has been mentioned
that our agents are utility based and they will try to
minimize the average weight of visited edges.
Therefore, the outgoing edge with the minimum
weight is nominated at each node for exploration,
since the heavier edges have been already visited
more, the lighter ones are reasonably preferred to be
selected here.
One of our aims is to return our agents to the
location where they have started their mission by the
time they have finished traversing their
corresponding branches. By choosing the outgoing
edge with minimum weight at each step, the agents
actually use a Depth-first search (DFS) to traverse
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
282
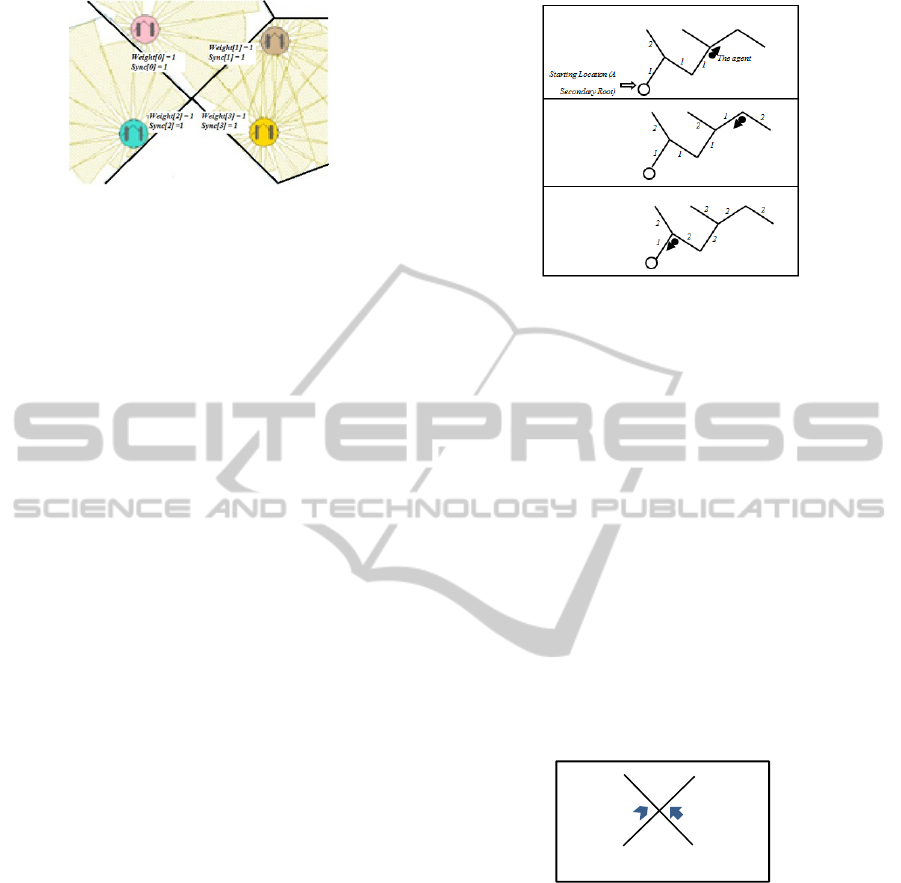
Figure 2: The values of items in arrays Sync and Weight a
few seconds after the start of the mission (all equal to 1).
the roadmap and this causes an automatic return of
the agents to their starting point. In fact in each
node, the edge with weight 1 shows the return path
to an agent as you can see in figure 3.
Because of the nature of the WMA-RRT
algorithm and the existence of various obstacles in
an environment, branches may differ in the number
of edges. It may cause the early return of some
agents to the origin while the other agents are still
working on their corresponding branches. In such
situations, an agent manages to maximize its
contribution by helping some other agents in their
exploration missions. In order to do that, it checks
the Weight array and chooses the member with the
minimum value such as Weight[k]. Then the
associated branch (here Branch[k]) is assigned to the
free agent in order to help the other agents working
on that branch to finish the exploration task.
Checking of the Weight array to choose its member
with minimum value is performed because of two
reasons: first, it shows the least traversed branch of
the roadmap by the other agents. Second, the agents
use this array to show the completion of traversing a
branch. When an agent returns to its origin, it has to
mark its traversed branch as completed to prevent
other agents from entering the same branch. This is
usually managed by assigning a special value (such
as a big number like 10000) to the corresponding
Weight member. Put it simply, checking the Weight
array enables an agent to avoid traversing a branch
which has been already explored by the other agents.
Even though a free agent can assist other
working agents, it may do more harm than good and
may trigger some problems. First, as provided
before, the agents use a DFS algorithm to traverse
their branch and the weight of the roadmap edges
causes an automatic return of the agents to the
origin. However, as the number of agents operating
in one branch exceeds one, the agents will be
paralyzed to find the return path inasmuch as the
other agents have already changed the weight
attributed to some edges of the roadmap.
Figure 3: Automatic return of an agent after traversing all
edges of its dedicated branch to its starting location.
In order to solve this problem, it is necessary for
each agent to have two copies of its branch,
dedicated and global. The global roadmap is shared
among all the active agents in a branch, but each
agent has its own dedicated roadmap, and agents do
not have access to each other’s dedicated roadmaps.
When an agent enters a branch, it makes a copy of
that branch’s global roadmap and, changes the
weight values belonging to its edges to zero. This
becomes that agent’s dedicated roadmap. The weight
of edges simultaneously alters in both roadmaps. By
default, agents use the global roadmap. Whenever
there are more than one agent in a branch, the agents
will reach a node for which all incoming and
outgoing edges have an equal weight. In that case,
the agents will use their dedicated roadmap to find
the return path.
Figure 4: The simultaneous arrival of two agents to a
node.
The second problem arises because the agents
have access to shared data. Consider the situation
shown in figure 4.
In figure 4, let’s imagine the situation in which
the right agent tends to choose the right edge (with
weight zero) for traversing, but prior to making any
change to its weight value, it come across with the
left agent that tries to choose the same edge. This
causes the exploration of a particular part of the
roadmap by more than one agent. To prevent such
an overlap, agents must have exclusive access to
shared data. Using the locking mechanism will
0
0
1
1
CoverageandGoalSearchingBehavioursofaGroupofAgentsbyaSpecialSingleQueryRoadmap-ItsBenefitsto
MutipleQueryRoadmaps
283

merely allow just one agent to access a specific
edge.
3.1.1 Experimental Results
We evaluated the introduced mechanism in a variety
of environments in order to examine the effects of
step size (distance between two nodes), number of
sample points and agents’ sensor range. All the
experiments were conducted in a Pentium 4 CPU
3.00GHz with 1 GB of RAM machine. In figure 5,
you can see a WMA-RRT roadmap constructed
based on 3 agents beside the covered areas by those
agents.
Figure 5: Left: WMA-RRT constructed based on three
agents. Right: The areas covered by those agents.
Table 1 summarizes the results of running our
proposed mechanism for covering the area
represented in figure 8.
Table 1: Percentage of the covered area for the
environment represented in figure 8.
Number
of Nodes
Step
Size
Number
of
Iterations
Agents’
Sensor
Range
Average
Coverage
Percentage
Coverage
Percentage
by Simple
PRM
Algorithm
400 20 10 r 74 71
400 20 10 2r 87 85
400 20 10 4r 90 90
400 20 10 Infinite 99 99
800 20 10 r 83 80
800 20 10 2r 88 84
800 20 10 4r 92 90
800 20 10 Infinite 99 99
200 40 10 r 88 86
200 40 10 2r 93 91
200 40 10 4r 95 94
200 40 10 Infinite 99 99
400 40 10 r 93 91
400 40 10 2r 95 94
400 40 10 4r 97 95
400 40 10 Infinite 99 99
800 40 10 r 97 93
800 40 10 2r 98 95
800 40 10 4r 99 98
800 40 10 Infinite 99 99
Table 1 bears testimony to the fact that our
proposed method is probabilistically complete. To
vividly clarify the point, it is possible to take a look
at the chart in figure 6; based on which increasing
the number of sample points improves the area
covered by the agents.
Figure 6: Area coverage percentage based on the number
of sample points (for step size=40 and sensor range=r).
3.1.2 Comparison with Multiple-Query
Roadmap based Methods
In addition to avoiding the extra time consumption
in the pre-processing phase of multiple-query
methods, there are also other benefits in using our
introduced method instead.
As mentioned before, one of the characteristics
of WMA-RRT roadmap is that it is a tree, and then
has no cycles. One of the problems with multiple-
query roadmaps is that the agents may get stuck in
roadmap loops. For example consider a simple
scenario with just one agent in figure 8.
As pictured in figure 7, after traversing two
triangular cycles, the agent returns to its staring
point, and it reaches a node with 4 outgoing edges
with the same weight. Because of the existence of
such cycles, it is quite common in multiple-query
roadmaps to observe a previously visited area being
re-traversed for multiple times. However, thanks to
the absence of any cycles in WMA-RRT, never does
such a phenomenon happen in our proposed method.
Figure 7: A multiple-query roadmap. An agent may get
stuck in a loop.
80
85
90
95
100
200 400 800
CoveragePercentage
1
1
1
1
1
1
1
I.
II.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
284
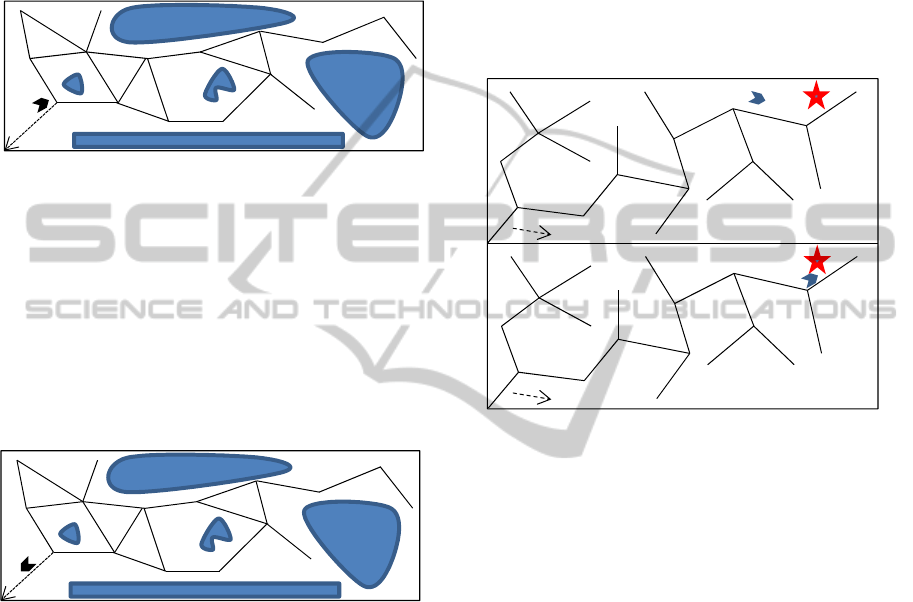
The second advantage of using WMA-RRT over a
multiple-query roadmap is that by the time the
exploration task of a certain part of the environment
has been completed, it is going to be confidently
flagged as “finished”. The multiple-query roadmaps,
however, does not enjoy the same level of certainty.
For example, consider the environment depicted in
figure 8.
Figure 8: An agent enters a part of an environment.
As illustrated, an agent is entering this part, yet
after traversing some edges of the roadmap, it
reaches a node in which all outgoing edges have the
same weight (figure 9). As the agent chooses an
edge which leads it to the outside of that part,
traversing that part remains uncompleted. After that,
other agents may enter the same part, and after
traversing some edges they leave that part. Thus,
none can say for sure if the exploration task of that
part has been fully accomplished.
Figure 9: The agent after traversing some edges of the
roadmap is leaving this part of the environment.
3.2 Goal Searching
The second swarming behaviour we are going to
investigate is goal searching in which the agents’
target is to find an unknown goal in an environment
and inform other agents of the location of that. In
this behaviour, the first agent that finds the goal has
to notify the other agents and those agents have to
move to the location of that goal. This behaviour is
used in scenarios in which there is a task and the
agents have to do it collaboratively with each other.
Exploring the environment to find the goal is
done like the previous behaviour, area coverage. The
only difference here is that the agents have to look
for the goal while exploring the environment. As
mentioned in the previous behaviour, the edges with
weight one lead the agents to the main root (starting
point). When an agent finds the goal, it has to inform
the other agents about the location. To do so, this
agent has to change the weight of all edges in its
branch (in global roadmap so that the other agents
will be able to see it) with value 1 to a special value
such as ½. Suppose that the agent that is working in
branch k finds the goal (figure 10). Changing the
weight of edges with value 1 to ½ will also alter the
value of item k in array Weight (Weight[k]) to ½
(see previous behaviour, area coverage).
Figure 10: An agent in branch k finds the goal (the star)
and by changing the edges’ weights with value 1 to ½
informs the other agents.
In this behaviour, all agents in each node have to
check the array Weight items. If they find an item
with value ½, they know that another agent has
already found the goal. When both agents are within
the same branch (branch k in our example), the
second agent uses the global roadmap and follows
the edges with weight 1 until it reaches an edge with
weight ½. After that, the edges with weight ½ lead
the agent to the location of the goal (figure 10). But
in cases the so-called second agent falls into a
different branch, it has to return to the main root and
after that by following the edges with weight ½, it
reaches the goal.
3.2.1 Experimental Results
We tested our algorithm for finding an unknown
goal based on WMA-RRT roadmap in different
environments. The result for finding the goal (the
star) in the environment in figure 11 has been
depicted in table 2.
Here, like the coverage behaviour, you can see the
effect of changing step size, the agents’ sensor range
1
1
1
1
Weight[k] = 1
Weight[k] = ½
1
1
1
2
1
1
1
2
2
2
1
½
½
½
½
½
½
½
½
2
2
2
2
I.
II.
CoverageandGoalSearchingBehavioursofaGroupofAgentsbyaSpecialSingleQueryRoadmap-ItsBenefitsto
MutipleQueryRoadmaps
285
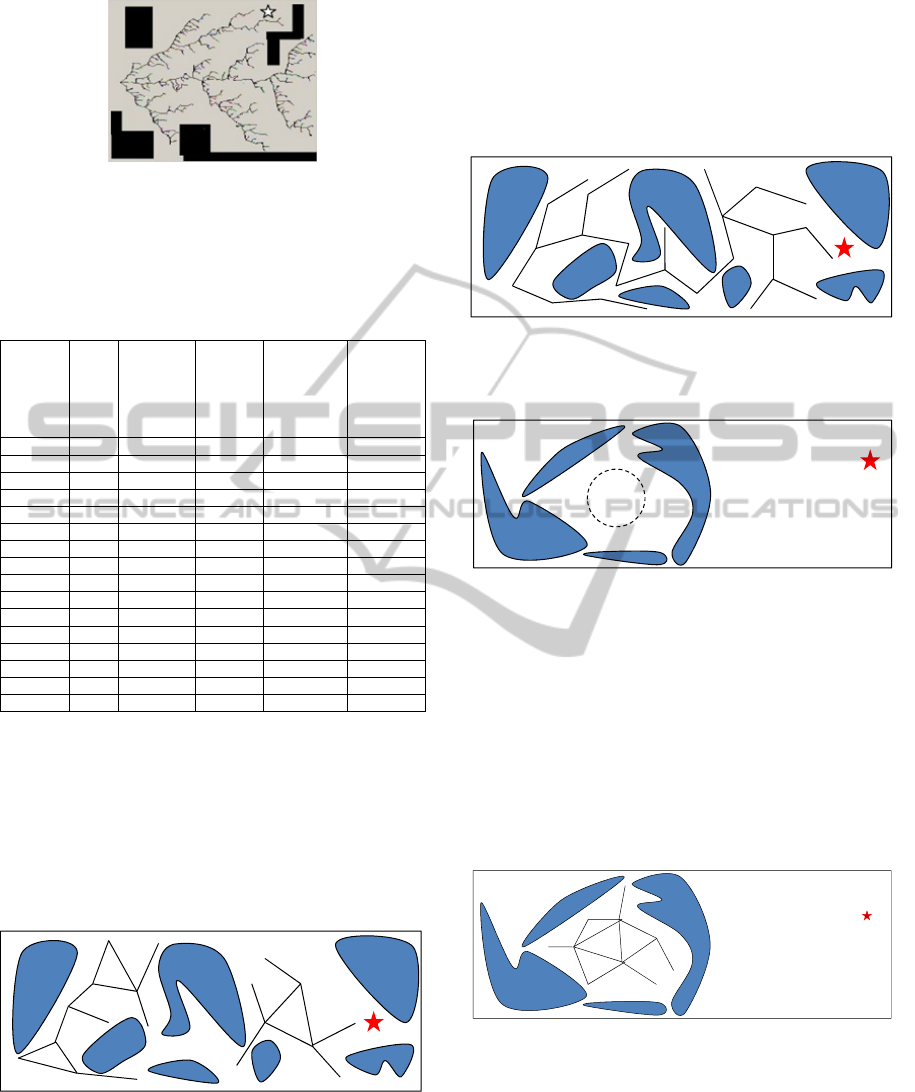
Figure 11: The aim of the agents here is to find the goal
(the star).
and the number of sample points on the results.
Table 2: Percentage of finding the goal by one of the
agents for the environment shown in figure 11.
Number
of Nodes
Step
Size
Number
of
Iterations
Agents’
Sensor
Range
Proportion
of
successful
runs
Proportion
of
successful
runs by
Simple
PRM
Algorithm
200 20 30 r 76 72
200 20 30 2r 83 80
200 20 30 4r 93 91
200 20 30 Infinite 100 100
400 20 30 R 87 85
400 20 30 2r 97 94
400 20 30 4r 100 100
400 20 30 Infinite 100 100
200 40 30 R 80 76
200 40 30 2r 93 91
200 40 30 4r 97 96
200 40 30 Infinite 100 100
400 40 30 r 100 100
400 40 30 2r 100 100
400 40 30 4r 100 100
400 40 30 Infinite 100 100
3.2.2 Comparison with Multiple-Query
Roadmap based Methods
One of the problems with multiple-query roadmaps
is that the constructed graph may be consisted of
some isolated components (figure 12). This usually
happens in cluttered environments. In these
situations the goal may be inaccessible to agents.
Figure 12: A PRM roadmap constructed in an
environment. This roadmap has two isolated components.
But as we previously explained, WMA-RRT has
just one connected component and we will never
face such problems (figure 13).
Even in scenarios that the goal is completely
inaccessible to the agents, our method behaves in a
better way than methods based on multiple-query
roadmaps (figure 14). In this figure, the agents have
been completely surrounded by some walls, so they
will never reach the goal.
Figure 13: A WMA-RRT roadmap constructed in an
environment. This roadmap has just one connected
component.
Figure 14: A situation in which the goal is inaccessible by
the agents.
In situations like this, it does not matter whether
we use WMA-RRT or a multiple-query roadmap
like PRM. In both cases, the agents will not be able
to find the goal. But in methods based on multiple-
query roadmaps, as there are cycles in the
constructed graph, the agents may get stuck in
infinite loops and they will never be able to
understand that the goal is inaccessible by using the
constructed roadmap (figure 15).
Figure 15: A multiple-query roadmap constructed in an
environment. The agents will never be able to find the
goal and they will get stuck in infinite loops.
But by using WMA-RRT as depicted in figure
16, the agents after traversing their branch return to
the origin and tag their branch as completed. In that
case, we understand that the goal is unreachable by
the agents, so by changing the starting location of
the agents to the outside of the surrounded obstacles,
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
286

Figure 16: A WMA-RRT roadmap constructed in the
environment. The agents will never be able to find the
goal, but they will find soon that the goal in unreachable.
one of the agents will finally be able to reach the
goal and inform the other agents (figure 17).
Figure 17: By changing the starting location of the agents,
one of them will find the goal.
4 CONCLUSIONS
In this paper, we discussed two of the most
important swarming behaviours, area coverage and
goal searching by using a special single-query
roadmap called WMA-RRT. WMA-RRT is used by
agents both as a roadmap and also as a
communication channel. The proposed method is
useful in situations in which there are some simple
agents, only capable of performing some simple
tasks and there are no communication devices
between them. The simplicity here means that the
agents do not have any special built-in memory to
memorize previously visited states and also they do
not need any communication devices to exchange
information. The only thing that they have is a
roadmap which is locally available to them. In future
works, we want to study another important
behaviour of agents “moving toward a goal”. In this
behaviour the agents move from a starting point to a
destination. We also would apply our algorithms to
3D environments. The effect of a calculated starting
configuration compared to a more improvised one
will also be discussed.
REFERENCES
Nasri Nazif, A., Davoodi, A., Pasquier, P., 2011. Multi-
Agent Area Coverage Using a Single Query Roadmap:
A Swarm Intelligence Approach. The First
International Workshop on Agent-based
Collaboration, Coordination and Decision Support.
Nagoya, Japan.
Nasri Nazif, A., Davoodi, A., Mohades, A., 2009. Finding
an Unknown Gaol in an Environment by a Group of
Agents. IEEE Symposium on Intelligent Agents.
Nashville, TN, United States.
Kavaraki, L., Svestka, P., Latombe, J., Overmars, J., 1996.
Probabilistic Roadmaps for Path Planning in High
Dimensional Configuration Space.
Lavalle, S., Kuffner, J., 2000. Rapidly-Exploring Random
Trees. In 4
th
Workshop on Algorithmic Foundations of
Robotics, Algorithmic and Computational Robotics:
New Directions, Pages 293-308.
Preparata, F., Hong, S., 1977. Convex Hull of Finite Set of
Points in Two and Three Dimensions. Common,
ACM, Pages 87-93.
Abraham, A., Guo, H., Liu, H., 2006. Swarm Intelligence:
Foundations, Perspectives and Applications. In Swarm
Intelligence Systems, Studies in Computational
Intelligence, Pages 3-25.
Bayazit, O. B., 2004. Roadmap-based flocking for
complex environments. In Proc. 10th Pacific
Conference on Computer Graphics and Applications,
PG02, pages 104-113.
Gordon, N., Wagner, I., Bruckstein, A., 2003. Discrete
Bee Dance Algorithm for Pattern Formation on a Grid.
In IEEE International Conference on Intelligent
Agents Technologies, Toronto, Canada, Pages 545-
549.
Reynolds, C., 1999. Steering behaviours for autonomous
characters. In Game Developers Conference.
Hazon, N., Kaminka, G., 2008. On redundancy, efficiency,
and robustness in coverage for multiple robots.
Robotics and Autonomous Systems.
The starting
location of
agents
CoverageandGoalSearchingBehavioursofaGroupofAgentsbyaSpecialSingleQueryRoadmap-ItsBenefitsto
MutipleQueryRoadmaps
287
