Automatic Polyp Detection using DSC Edge Detector and HOG Features
Himanshu Agrahari
1
, Yuji Iwahori
2
, M. K. Bhuyan
1
, Somnath Ghorai
1
, Himanshu Kohli
1
,
Robert J. Woodham
3
and Kunio Kasugai
4
1
Dept. of Electronics and Electrical Engineering, Indian Institute of Guwahati, Guwahati 781039, India
2
Dept. of Computer Science, Chubu University, Kasugai 487-8501, Japan
3
Dept. of Computer Science, University of British Columbia, Vancouver V6T 1Z4, Canada
4
Dept. of Gastroenterology, Aichi Medical University, Nagakute 480-1195, Japan
Keywords:
Endoscopy, Discrete Singular Convolution, Histogram of Oriented Gradients (HOG), Conic Fitting, Support
Vector Machine.
Abstract:
Endoscopy is a very powerful technology to examine the intestinal tract and to detect the presence of any
possible abnormalities like polyps, the main cause of cancer. This paper presents an edge based method for
polyp detection in endoscopic video images. It utilizes discrete singular convolution (DSC) algorithm for edge
detection/segmentation scheme, then by using conic fitting techniques (ellipse and hyperbola) potential candi-
dates are determined. These candidates are first rotated so as to make major axis in the x-axis direction, and
then classified as polyp or non-polyp by SVM classifier which is trained separately for ellipse and hyperbola
with HOG features.
1 INTRODUCTION
Medicine is an important area of application for com-
puter vision. Endoscopy allows medical practition-
ers to observe the interior of hollow organs and other
body cavities in a minimally invasive way. Diagnosis
involves both shape detection and the assessment of
tissue state. For example, a polyp is a pathological
condition directly related to geometrical shape. Diag-
nosis typically requires polyp removal and biopsy.
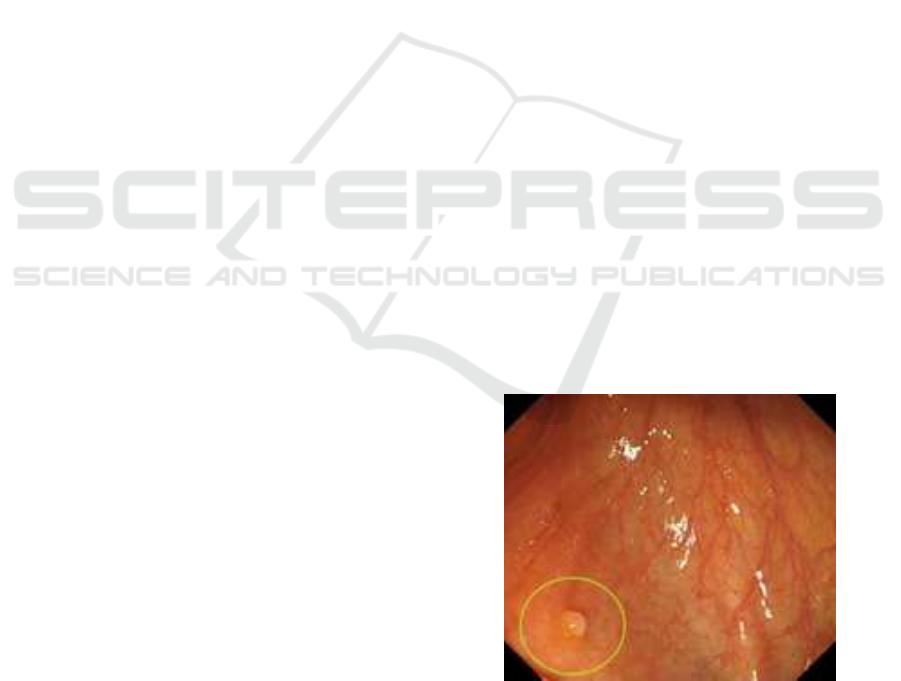
Polyps are abnormal growth of tissues from mu-
cous membrane (Fig.1). An early stage detection and
cure can save a human life as it develops into cancer
if undetected for a long time. It has been reported
that colorectal cancer is the second leading cause of
cancer-related deaths in U.S. (Parkerand Tong, 1997).
There are some previous approaches to extract
polyp candidate region from endoscope image.
Some work has used a patch-based approach
(Iakovidis and Maroulis, 2005)-(Alexandre and No-
bre, 2008). In (Iakovidis and Maroulis, 2005) and
(Karkanis and Iakovidis, 2003), patch features com-
puted are the Color Wavelet Covariance (CWC) and
the Local Binary Pattern (LBP). Candidate patches
are classified using an SVM. In (Alexandre and No-
bre, 2008), higher dimensional features of the RGB
color values and the XY position coordinates are used
Figure 1: Polyp shown inside the yellow circle.
leading to improved classification performance.
Performance of previous patch-based approaches
depends on the patch size. It is not straightforward to
detect polyps with differing sizes in an image. Fur-
ther, smaller polyps become quite sensitive to the fea-
tures used for detection. It is difficult to imagine how
to achieve robustness with a constant patch size.
Paper (Viana and Iwahori, 2013) proposes that So-
bel edge extraction technique has been used to detect
the edges and then classified the regions as polyp and
non-polyp using shape or geometric features like cir-
cularity, complexity, diameter etc. using SVM clas-
sifier. The presence of a lot of noise in endoscopic
495
Agrahari H., Iwahori Y., K. Bhuyan M., Ghorai S., Kohli H., J. Woodham R. and Kasugai K..
Automatic Polyp Detection using DSC Edge Detector and HOG Features.
DOI: 10.5220/0004756104950501
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 495-501
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

images results in the failure of typical edge detection
techniques such as Sobel.
Log Gabor filter has been used as segmentation
scheme (Karargyris and Bourbakis, 2009), in con-
junction with the SUSAN edge detector, geometric
information was used for classification after segmen-
tation.
Hessian filter was used to find the polyp candi-
dates then HOG features of the candidate regions
were computed for each component of the HSV color
space (Iwahori and Shinohara, 2013), where SVM
is introduced to classify the candidate region ex-
tracted by Hessian filter but this Hessian filter costs
much time for extracting candidate region with over-
detection.
In paper (Hwang and Oh, 2007), only elliptical
shape features are considered after edge detection. In
many cases, polyp could resemble more to a hyper-
bola than an ellipse and such cases leads to loss of
accuracy.
In this paper, DSC algorithm for edge detection,
a special class of DSC kernels as described in paper
(Hou and Wei, 2002) is used. Conic fitting is then ap-
plied to these edges to find the potential candidates,
which are then classified as polyps and non-polyps
by a SVM classifier which is trained separately for
ellipse and hyperbola with HOG features extracted
from DSC filtered images.
Our research is to classify the frames as polyp
and non-polyp and finally reducing physician’s work-
load by passing the frames having high probability for
polyp.
2 PROPOSED METHOD
The block diagram is shown in Fig.2 and this has been
divided into 4 major parts.
2.1 Dataset Preprocessing
2.1.1 Non-linear Filtering
Random variations in brightness or color decreases
the sensitivity of any algorithm. To tackle this, image
is first passed through non-linear filter like median fil-
ter. Here gray scale image is used.
2.1.2 Contrast Enhancement
In order to enhance the visibility of local details in an
image, CLAHE (Breckon and Solomon, 2011) is used
to improve image contrast. It is usually chosen over
Dataset preprocessing
DSC Edge Detector
Conic fitting and potential candidate
detection
Elliptic
Classification
Hyperbolic
HOG trained
SVM for ellipse
HOG trained
SVM for
hyperbola
Figure 2: Proposed Block Diagram.
simple Histogram Equalization because it can over-
come common problems like image saturation and
noise amplification.
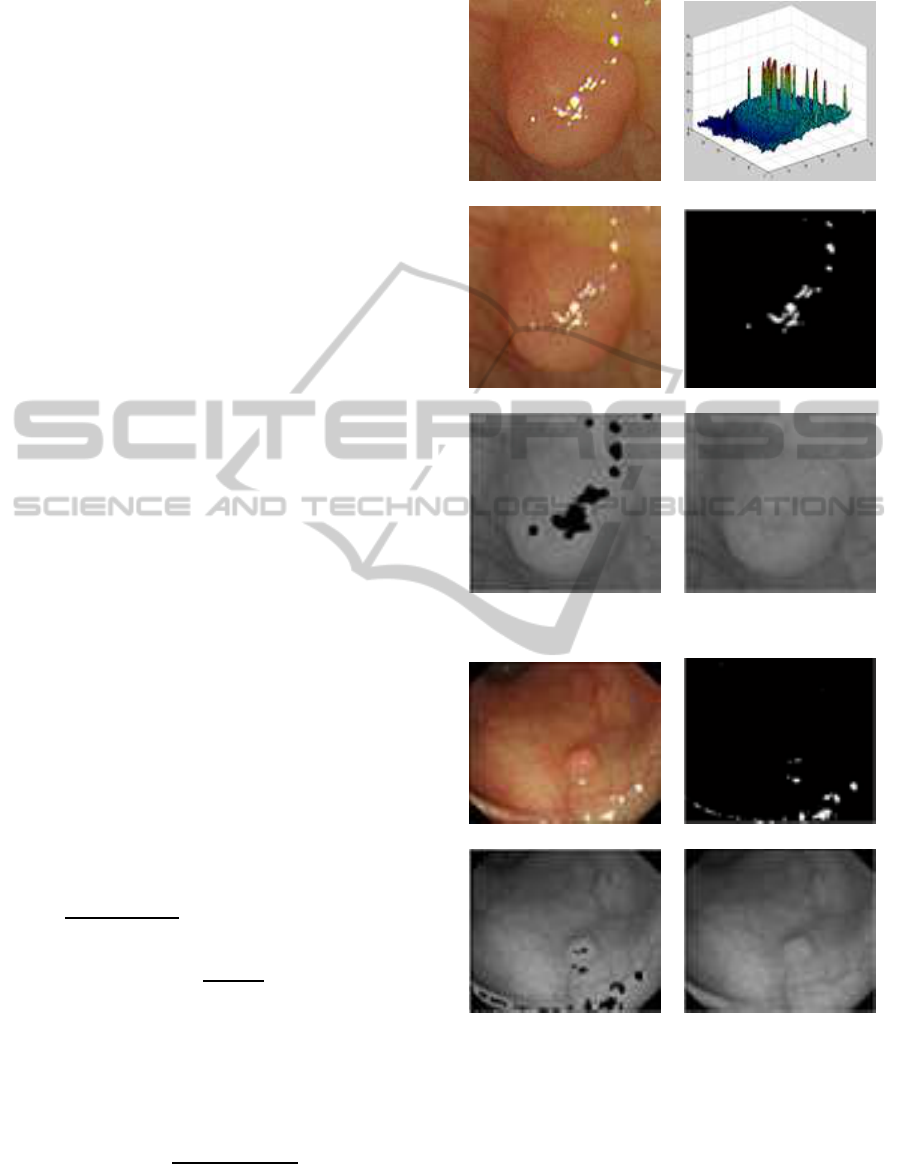
2.1.3 Specularity Removal
A polyp image obtained from conventionalendoscope
has both specular and diffused components. In medi-
cal image processing where details are so minute that
it is difficult to extract features, specular regions make
the process more difficult and inaccurate which re-
sults in loss of needful data. We cannot directly apply
our algorithms on these images. As we can see in
Fig.3(b), pixels having specularity show high peaks,
which eat-up the smooth and round property, which
are the basic conditions for our research. The imple-
mentation is based on (Shen and Cai, 2009). Spec-
ular components are detected and removed, and then
interpolation is done, which round off the values to
neighboring ones.
Let I be an RGB image with RGB value set per
pixel of the form V
R
, V
B
, V
G
. Using these values we
define certain terms on per pixel basis.
Terms:
V
min
= min(V
R
,V
B
,V
G
) (1)
V
mean
= mean(V
min
) (2)
V
std
= StandardDeviation(V
min
) (3)
T
v
= V
mean
+ k×V
std
(4)
where k = 0.5 suits most of the results
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
496
Calculation:
Find an offset t
p
such that:
t
p
= T
v
if V
min
> T
v
(5)
= V
min
else (6)
Find β which determines the specular component as:
β = V
min
− t
p
(7)
I
Specular
= 0.5β (8)
This specular component calculated is further di-
lated so that when it is subtracted from the original
image it does not give thin high intensity boundaries.
I
SpecularRemoved
= I − binary(I
Specular
) (9)
Now it can be seen this I
SpecularRemoved
has holes
which need to be covered. So holes are filled on the
basis of neighboring values. Use a spring metaphor.
Assumes springs (with a nominal length of zero) con-
nect each node with every neighbor (horizontally,ver-
tically and diagonally) since each node tries to be like
its neighbors,extrapolation is as a constant function
where this is consistent with the neighboring nodes.
As a result, specular removed leveled image is gener-
ated.
2.2 DSC Edge Detector
In this method, Discrete Singular Convolution (DSC)
for edge detection using particular class of DSC ker-
nels as described in (Hou and Wei, 2002) has been
used. To construct edge detectors, one dimensional,
n-th order DSC kernel of delta type is used:
δ
(n)
σ,α
(x− x
k
),n = 0,1,2,·· · (10)
where
δ
σ,α
=
sin(α)(x− x
k
)
(α)(x− x
k
)
e
−(x−x
k
)
2
/2σ
2
(σ > 0) (11)
δ
α
(x) =
sin(αx)
πx
(12)
and the superscript denotes the n-th order derivative.
Now δ
α
(x) is nothing but Shannon’s delta kernel
which correspondsto a family of ideal lowpass filters,
each having different bandwidth. Their correspond-
ing wavelet expressions ψ
α
(x) are band pass filters.
ψ
α
(x) =
sin2αx− sinαx
πx
(13)
The Fourier transformationof δ
α
(x) and ψ
α
(x) are
not differentiableso a regularization procedure is used
and the resulting DSC kernel in its discretized form is
(a) Original Image (b) Intensity Map
(c) Input Image (d) Specular Regions
(e) Gray Scale Image (f) Interpolated
without Specular Image
Component
(g) Input Image (h) Specular Regions
(i) Gray Scale Image (j) Interpolated
without Specular Image
Component
Figure 3: Specularity Removal.
expressed as δ
α,π
(x) whose Fourier transform is in-
finitely differentiable. . The derivatives δ
(n)
σ,α
(x
m
− x
k
)
(n=1,2,·· ·) are obtained by differentiation and can be
regarded as high pass or band pass filters depending
upon the value of the parameters. In this paper, the
AutomaticPolypDetectionusingDSCEdgeDetectorandHOGFeatures
497
first order derivatives have been used and these reg-
ularized filters are functions of Schwartz class which
have controlled residue amplitude at large values of x.
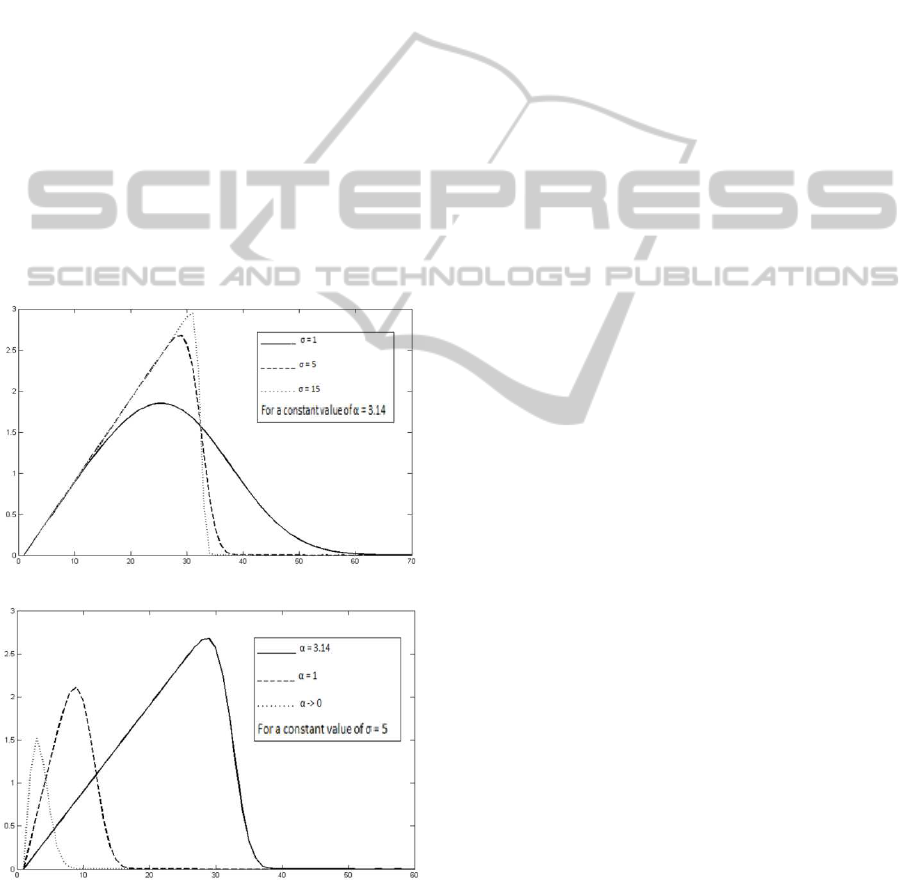
Fig.4 (a) illustrates the impact of parameter σ on
the filter in the frequency domain for a fixed value of
α. With the increase in value of σ the filter becomes
more localized in frequency domain and in time do-
main larger the value of σ, slower the filter will de-
cay. Fig.4 (b) shows the impact of α on the frequency
response of first order derivative for a fixed σ. In-
creasing the value of α moves the peak of frequency
response from the low frequency region to the higher.
So by balancing the values of σ and α in accordance
with the practical problem good results can be ob-
tained for example in case of high noise corruption
smaller values of α can be used. In case of polyp de-
tection in endoscopic images, the edge definition is
not very sharp as polyp and their neighboring areas
are similar in texture and there is a lot of noise in im-
ages so smaller values of α and σ should be used so as
to localize the frequency response at near about mid
frequency range.
(a) δ
(1)
σ,α
(x) for different values of σ
(b) δ
(1)
σ,α
(x) for different values of α
Figure 4: Frequency response of δ
(1)
σ,α
(x).
The 1st order fine scale DSC Edge Detector (DSCED)
is given by
DSCED
1
(x
i
,x
j
)
=
∑
W
n
k=−W
n
δ
(1)
(σ,α)
(x
i
− x
k
)I(x
k
,y
j
)
+
W
n
∑
l=−W
n
δ
(1)
(σ,α)
(y
j
− y
l
)I(x
i
,y
l
)
(14)
where I(x,y) is the intensity of input image.
Fig.5 shows a comparison between DSC filter and
Sobel operator. Before applying curve fitting tech-
nique, noises have to be removed. In case of typi-
cal edge detection techniques (Sobel in this case) de-
tected polyp boundaries are also similar to noise as in
Fig.5(a) and (c). Noise elimination results in the elim-
ination of polyp boundaries but not in case of DSC.
In some cases as in Fig.5(e) and (g), the polyp bound-
aries are not even detected in case of Sobel but are
detected well with DSC.
2.3 Conic Fitting and Potential
Candidate Detection
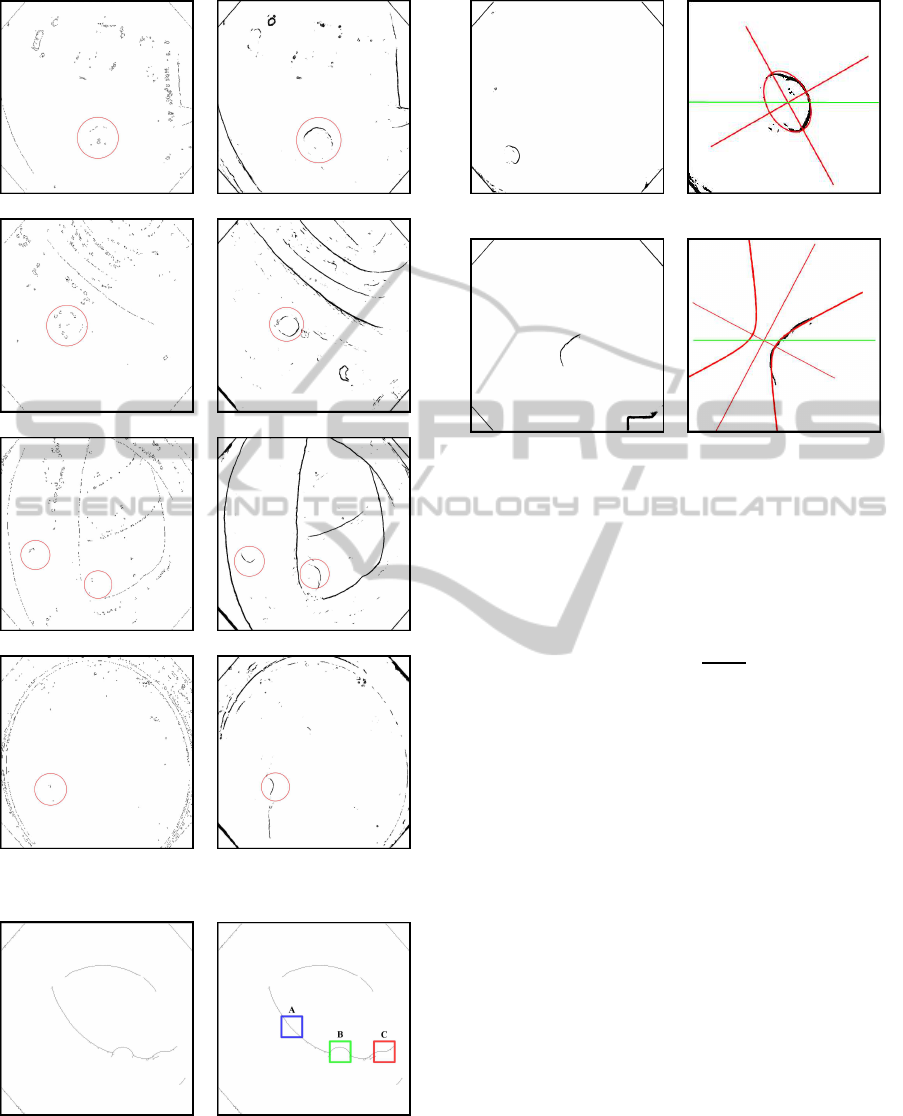
The extracted edges are of different sizes and orien-
tations. So the polyp could be a single edge or as a
part of a big edge (as shown in Fig.6 (b) green patch).
Both the cases are considered by uniformly picking
random points within a connected edge. The number
of points is proportionalto the length of the connected
component. Connected components with size greater
than a particular threshold are only considered. Now
for every picked point a square patch (160x160 pix-
els) is drawn around it with the point at the center.
Fig.6 (b) shows some of them. Now this square patch
is checked for which conic it represents better. The
process is performed on the basis of least square fit.
Fig.7 (b) and (d) show ellipse and hyperbola fit re-
spectively. Dividing this into class increases the clas-
sifier accuracy. All the geometric parameters (major
axis, minor axis, center, orientation angle) are calcu-
lated. The conic which satisfy the following condi-
tion:
(Majoraxis/Minoraxis) ≤ 2 (15)
are selected as potential candidates (in Fig.6 (b), B is
selected, but A and C are rejected) and are saved in
the respective groups of ellipse and hyperbola along
with data of orientation angle (which is used at the
time of classification).
2.4 HOG Feature Extraction and SVM
Classification
HOG Feature Extraction:
Patches finally obtained are rotated so as to bring
the major axis orientation to zero. Fig.7 (b) and (d)
show the rotated images. The HOG (Dalal and Triggs,
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
498
(a) Sobel (b) DSC
(c) Sobel (d) DSC
(e) Sobel (f) DSC
(g) Sobel (h) DSC
Figure 5: Result of Edge Map.
(a) Edge map of (b) uniformly selected
polyp image square patches
Figure 6: Square Patches.
2005) feature vectors are calculated. Rotation in-
creases the sensitivity of HOG features.
(a) Edge map of (b) best ellipse fit
polyp image
(c) Edge map of (d) best hyperbola fit
polyp image
Figure 7: Best Conic Fit.
Classification:
Support Vector Machine is used for classification.
The radial basis function (RBF) kernel type was used,
as expressed by the equation below:
K(x,x
′
) = e
−
kx−x
′
k
2
2σ
2
(16)
x and x
′
are two samples and σ is inversely pro-
portional to kernel width. SVM was trained sepa-
rately for Ellipse and Hyperbola. 140 positive images,
176 negative images for ellipse and 186 positive im-
ages, 286 negative images for hyperbola were used to
train the SVM. Each image was of 160 × 160 pix-
els. The dimensionality of the resulting HOG feature
vector was 168. The patches corresponding to ellipse
and hyperbola are classified separately with doubly
trained SVM.
3 EXPERIMENTAL RESULTS
In this section, we assess the effectiveness of the pro-
posed method using the set of 87 endoscopic images
taken from various patients. The set contains 50 polyp
images and 37 non-polyp images each of resolution
1000x1000 pixels. The images are first preprocessed
then gray scaled images are passed through DSC fil-
ter. We tried different combinations of (α, σ) values
like (0.4,1), (0.4,3), (0.8,1), (0.8,3), (1.5,1), (1.5,3)
and different widths 3,5,7,9 and out of these α=0.4,
σ=1 and width=9 were chosen by analyzing the time
AutomaticPolypDetectionusingDSCEdgeDetectorandHOGFeatures
499
complexity and the quality of edges obtained. The
DSC filtered image is then thresholded so as to get a
binary image. The threshold in this case is empiri-
cally determined as 8. A green circle is drawn when
a section of an edge is classified as polyp. In case
of polyp edges many intersecting circles are drawn in
close vicinity, because of selection of uniformly dis-
tributed random points for conic fitting mentioned in
the previous section. So we adopt a voting method.
In case of non intersecting circles, votes are not been
recorded. To get a polyp detected two or more circles
should intersect. Single circle vote is not counted.
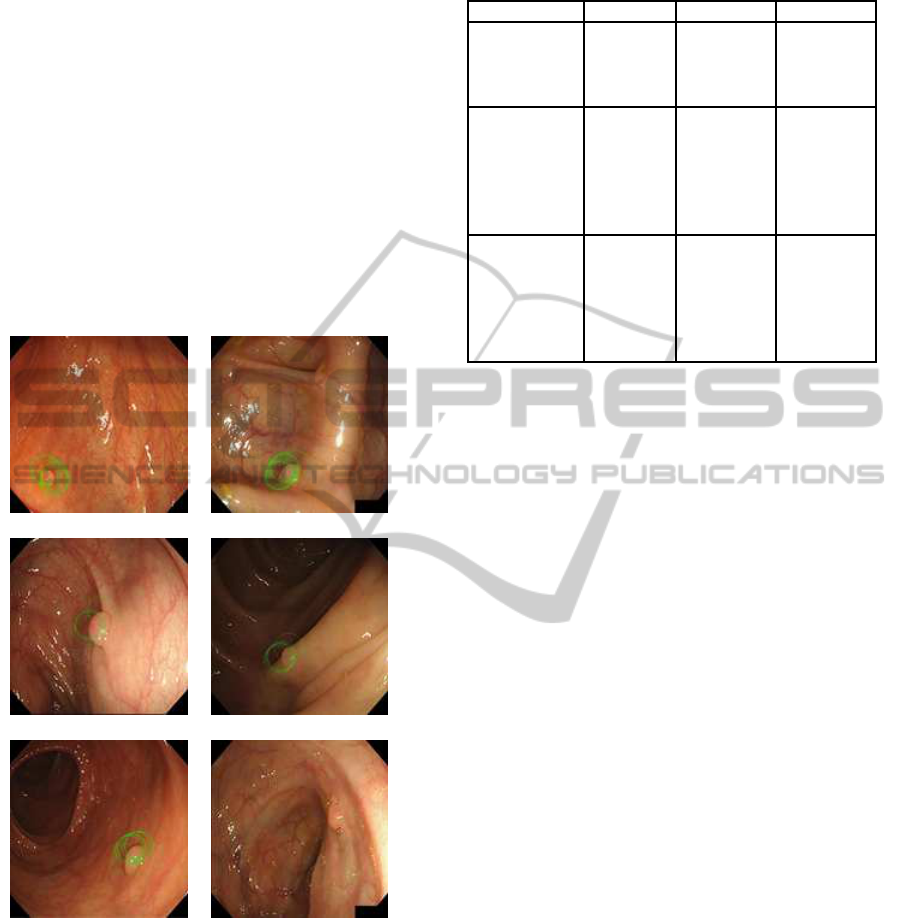
Fig.8 show the original endoscopic images, with
green circles marked at the area where polyp has been
detected.
(a) Identified Polyp (b) Identified Polyp
(c) Identified Polyp (d) Identified Polyp
(e) Identified Polyp (f) Missed Polyp
because of
single vote
Figure 8: Polyp Detection.
Accuracy, sensitivity and specificity are given in
Table 1.
4 CONCLUSIONS
In this paper a novel method for polyp detection has
been presented combining DSC edge detection with
Table 1: Classification Performance.
Method Accuracy Sensitivity Specificity
Only ellipse
fitting with
HOG over 52.87 % 74.00 % 24.32 %
DSC*
Ellipse and
hyperbola
fitting with
HOG over 50.57% 74.00 % 18.92%
original gray
scale image
(Proposed)
Ellipse and
hyperbola
fitting with 89.65 % 90.00 % 89.18 %
HOG over
DSC*
conic fitting (both ellipse and hyperbola) technique.
Classification is based on HOG features from DSC
filtered images. The power of the methodology lies in
the DSC edge detection technique. Proposed edge de-
tection is focused on the idea that due to the possible
presence of noise, the definition of image edge is not
sharp so finding edge by gradient methods becomes
an ill-posed problem. In case of endoscopic images,
the sources of noise are a lot, whether it is specular-
ity, blood vessels or saliva. Another problem lies in
the similarities of texture between polyp and its sur-
rounding regions. The DSC edge detection technique
is able to deal with these two problems which is clear
from experimental results and its comparison with So-
bel.
Results also show the advantage of including hy-
perbola with ellipse in conic fitting. Extracting HOG
features from DSC filtered images instead of origi-
nal image have resulted in higher accuracy after SVM
classification.
The experimental results shows that the over-
all methodology is quite promising and future work
should be extended to video sequences to perform
real-time detection.
ACKNOWLEDGEMENTS
This research was done while Himanshu Agrahari
visited Iwahori Lab. for his research internship and
they did B.Tech project at IIT Guwahati as the re-
search collaboration. Iwahori’s research is supported
by Japan Society for the Promotion of Science (JSPS)
Grant-in-Aid for Scientific Research (C) (23500228)
and Chubu University Grant. Woodham’s research is
supported by the Natural Sciences and Engineering
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
500

Research Council (NSERC).
REFERENCES
Alexandre, L. and Nobre, N. (2008). Color and position ver-
sus texture features for endoscopic polyp detection. In
Int. Conf. on BioMedical Engineering and Informatics
(BMEI), Vol.2, pp.38-42. IEEE.
Breckon, T. and Solomon, C. (2011). Fundamentals of digi-
tal image processing: a practical approach with exam-
ples in matlab. In Wiley-Blackwell, pp.76-79.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In IEEE CVPR, Vol.1,
pp.886-893.
Hou, Z. and Wei, G. (2002). A new approach to edge detec-
tion. In Pattern Recognition 35 (7), pp.1559-1570.
Hwang, S. and Oh, J. (2007). Polyp detection in
colonoscopy video using elliptical shape feature. In
Proc. of the Int. Conf. on Image Proc., pp. II-465 -
II-468.
Iakovidis, D. and Maroulis, D. (2005). A comparative
study of texture features for the discrimination of gas-
tric polyps in endoscopic video. In 18th IEEE Sym-
posium on Computer-Based Medical Systems, Vol.7,
No.3, pp.141-152. IEEE.
Iwahori, Y. and Shinohara, T. (2013). Automatic polyp de-
tection using hessian filter. In IAPR MVA2013, Health
and Life, 3-1, pp.21-247.
Karargyris, A. and Bourbakis, N. (2009). Identification of
polyps in wireless capsule endoscopy videos using log
gabor filters. In LiSSA, pp.143-147. LiSSA.
Karkanis, S. and Iakovidis, D. (2003). Computer-aided tu-
mor detection in endoscopic video using color wavelet
features. In IEEE Trans. on Information Technology in
Biomedicine. IEEE.
Parker, S. and Tong, T. (1997). Cancer statistics 1997. In
CA Cancer J. Clinicians, Vol.47, pp.5-27. Wiley.
Shen, H. and Cai, Q. (2009). Simple and efficient method
for specularity removal in an image. In Applied Op-
tics, 48(14), pp.2711-2719.
Viana, R. and Iwahori, Y. (2013). Automated polyp im-
age extraction from endoscope images. In Inter-
national Workshop on Advanced Image Technology
(IWAIT2013), pp.216-221. IWAIT.
AutomaticPolypDetectionusingDSCEdgeDetectorandHOGFeatures
501
