
Enhanced Kernel Uncorrelated Discriminant Nearest Feature Line
Analysis for Radar Target Recognition
Chunyu Wan, Xuelian Yu,Yun Zhou and Xuegang Wang
School of Electronic Engineering, University of Electronic Science and Technology of China, York, China
Keywords: Radar Target Recognition, Feature Extraction, Nearest Feature Line, Uncorrelated Constraint, Kernel
Technique.
Abstract: In this paper, a new subspace learning algorithm, called enhanced kernel uncorrelated discriminant nearest
feature line analysis (EKUDNFLA), is presented. The aim of EKUDNFLA is to seek a feature subspace
in which the within-class feature line (FL) distances are minimized and the between-class FL distances are
maximized simultaneously. At the same time, an uncorrelated constraint is imposed to get statistically
uncorrelated features, which contain minimum redundancy and ensure independence, and thus it is highly
desirable in many practical applications. Optimizing an objective function in a kernel feature space,
nonlinear features are extracted. In addition, a weighting coefficient is introduced to adjust the proportion
between within-class and between-class information to get an optimal effect. Experimental results on radar
target recognition with measured data demonstrate the effectiveness of the proposed method.
1 INTRODUCTION
Automatic target recognition (ATR) (Chen et al.,
2005) is a research topic of high interest in modern
radar technology. High resolution range profiles
(HRRP) contain rather detailed structural
information of a target, thus providing us with a
more reliable tool for ATR. One of the key problems
of radar target recognition using HRRP is how to
extract robust and effective features (Yu and Liu,
2008). Over the past few years, many classical
methods have been developed and applied to radar
target recognition successfully, such as principal
component analysis (PCA) (Turk and Pentland,
1991), linear discriminant analysis (LDA)
(Belhumenur et al., 1997), locality preserving
projections (LPP) (He et al., 2005), neighborhood
preserving projections (NPP) (Pang et al., 2005),
neighborhood preserving embedding (NPE) (He et
al., 2005) and etc. Although these methods have
achieved reasonably good performance for radar
target recognition, they cannot perform satisfactorily
when the number of training samples per class is
small.
In the NN-based classification, the representa-
tional capacity and the error rate depends on how the
prototypes are chosen to account for possible
variations and also how many prototypes are
available. In practical applications, only a small
number of training samples are available. In order to
expand the representational capacity of limited
training samples, Li et al. (1999) proposed nearest
feature line (NFL), which uses linear interpolation
and extrapolation between each pair of feature points
to cope with various changes. The classification is
done by using the minimum distance between the
feature point of the query and the FL’s. The
classification result also provides a quantitative
position number as a byproduct which can be used to
indicate the relative change between the query point
and the two associated training samples. Owing to
the excellent generalization capacity, NFL has been
successfully used to address many recognition
problems. However, it only used the NFL metric in
classification stage.
Over the past few years, some subspace learning
algorithms based on the idea of NFL have been
proposed. For instance, Zheng et al. (2006) proposed
nearest feature line-based nonparametric discrimi-
nant analysis (NFL-NDA), Pang et al. (2007) put
forward nearest feature line space (NFLspace). The
good properties are achieved by adopting the idea of
the nearest feature line to both subspace learning
stage and classification stage. Lu et al. (2010)
presented uncorrelated discriminant nearest feature
155
Wan C., Yu X., Zhou Y. and Wang X..
Enhanced Kernel Uncorrelated Discriminant Nearest Feature Line Analysis for Radar Target Recognition.
DOI: 10.5220/0004759701550160
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 155-160
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

line analysis (UDNFLA), and Yan et al. (2011)
proposed neighborhood discriminant nearest feature
line analysis (NDNFLA). Among these methods,
NFL-NDA and NFLspace only use the within-class
information and do not consider the between-class
information, which is deficient for subspace learning.
UDNFLA and NDNFLA use both within-class and
between-class information, but they all use linear
technique to compute the feature space, which is
inadequate to describe the complexity of real data
structure that is usually nonlinear. In addition, all of
them give the same emphasis on within-class and
between-class scatter matrix, which is not optimum
because the two matrices make different influence
on the recognition result.
Motivated by the above observations, we
propose in this paper a new nonlinear NFL-based
subspace learning method, called enhanced kernel
uncorrelated discriminant nearest feature line
analysis (EKUDNFLA), for radar target recognition.
Firstly, the data is nonlinearly mapped into an
implicit high dimensional feature space, in which the
data is as linearly separable as possible. Then,
proposed method minimized the within-class FL
distances and maximized the between-class FL
distances simultaneously, as more discriminant
information can be exploited. And meanwhile it
imposed an uncorrelated constraint to make the
extracted features statistically uncorrelated.
Uncorrelated features contain minimum redundancy
and ensure independence of features. They are
highly desirable in practical applications.
EKUDNFLA can exploit more discriminant
information and is more suitable for recognition
tasks. Kernel technique will be used to solve the
transformation matrix in the high dimensional
feature space. Finally, a weighting coefficient is
introduced into the objective function to get the
optimum proportion between the within-class and
between-class information.
2 NFL AND UDNFLA
2.1 NFL
Consider a data set
1
[, , ]
N
Xx x
in
D
R
.
Suppose that
m
x
and
n
x
are two samples coming
from the same class, the straight line passing through
the two samples is called a feature line (FL), denoted
as
mn
x
x
. The membership of query point
q
x
is
measured by the Euclidean distance between
q
x
and
its projection point
p
x
on the line
mn
x
x
, which is
termed as the FL distance and denoted as
qp
x
x
. The less the FL distance is, the more
probability that
q
x
belongs to the same class as
m
x
and
n
x
. The projection point (Pang, et al., 2007)
p
x
can be computed as below:
()
p
mnm
x
xxx
(1)
Where,
()()/()()
TT
qm nm nm nm
x
xxx xxxx
.
2.2 UDNFLA
The aim of UDNFLA is to find a projection matrix
V that maps each data point
i
x
to a lower
dimensional subspace
()
d
Rd D
by
T
ii
yVx
. The optimal transformation matrix V is
obtained by solving the following optimization
problem (Lu et al., 2010):
min ( ) ( )
s.t.
T
V
T
t
J
VtrVABV
VSV I
(2)
where,
1,()
(1 / )
T
N
ii
Pimnimn
imnPi
A N xx xx
,
1,()
(1 / )
T
N
ii
Rimnimn
imnRi
B N xx xx
,
()Pi
denotes the samples sharing the same class
label with
i
x
,
()Ri
denotes the samples with
different class label with
i
x
,
P
N
and
R
N
are the
numbers of samples in
()Pi
and
()Ri
, respectively.
The minimization of (2) can be converted to
solve the following generalized eigenvalue problem
()
t
ABv Sv
(3)
Let
1
,,
d
vv
be the eigenvectors of (3)
corresponding to the d smallest eigenvalues, then the
transformation matrix of UDNFLA is obtained by
1
[, , ]
d
Vv v
.
3 EKUDNFLA
As mentioned in section I, since UDNFLA is linear
method, it may not perform satisfactorily when the
data structure is highly nonlinear. Moreover, same
emphasis is laid on the within-class distances and
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
156

between-class distances, which is not optimum for
improving recognition performance.
In this section, we first extend the UDNFLA to
nonlinear form using kernel technique and yield
kernel uncorrelated discriminant nearest feature line
analysis (KUDNFLA), then it is modified with a
weighting coefficient, which finally gives rise to the
enhanced kernel uncorrelated discriminant nearest
feature line analysis (EKUDNFLA).
3.1 KUDNFLA
To begin with, the data set is mapped into an
implicit high-dimensional feature space F by using a
nonlinear function
:()
D
x
RxF
.
Then, in the feature space F, the projection of
()
i
x
onto the FL formed by
()
m
x
and
()
n
x
can be defined as:
,
() (() ())
(1 ) ( ) ( )
i
mn m n m
mn
x
xxx
xx
(4)
with
( ( ) ( )) ( ( ) ( ))
(()())(()())
() ( ),( ) ( )
() ( ),() ( )
T
im nm
T
nm nm
imnm
nmnm
x
xxx
x
xxx
xxx x
xxxx
(5)
where,
,
denotes inner product. By introducing
a kernel function,
12 1 2
(, ) (),( )kx x x x
, (5)
can be rewritten as:
(,) (,) (,) (,)
(,) (,) (,) (,)
in i m mn mm
nn nm mn mm
kx x kx x kx x kx x
kx x kx x kx x kx x
(6)
Now, in order to minimize the within-class FL
distances and maximize the between-class FL
distances simultaneously, we need to solve the
following minimization problem:
2
,
1, ()
2
,
1, ()
1
min ( ) ( )
1
()
()
N
TTi
imn
V
imnPi
P
N
TTi
imn
imnRi
R
T
wb
JV V x V x
N
VxVx
N
tr V S S V
(7)
where
w
S
and
b
S
are the within-class and between-
class FL distance scatter matrix, respectively, which
are defined as:
2
,
1, ()
,,
1, ()
1
()
1
() ()
N
i
wimn
imnPi
P
N
T
ii
imn imn
imnPi
P
Sxx
N
xx xx
N
(8)
2
,
1, ()
,,
1, ()
1
()
1
() ()
N
i
bimn
imnRi
R
N
T
ii
imnimn
imnRi
R
Sxx
N
xx xx
N
(9)
Next, to make the extracted features statistically
uncorrelated, the following uncorrelated constraint
(Yu and Wang, 2008) is considered:
T
t
VSV I
(10)
where,
1
1
() ()
T
N
tii
i
Sxmxm
N
is
the total scatter matrix in F,
with
1
1/ ( )
N
i
i
mN x
.
Combing (7) and (10), the KUDNFLA can be
formulated as the following constrained
minimization problem:
min ( )
T
t
T
wb
VSV I
tr V S S V
(11)
Since each column of V should lie in the span
of
12 n
( ),( ), ,( )
x
xx
, we can write
1, ,
11
(), , () ( )
NN
ii dii
ii
Vx xXA
(12)
where
,
(1,2,,)
ji
j
d
denotes the i-th entry
of the coefficient vector
j
, and
12
[, , , ]
Nd
d
A
R
.
Let
,
()
Ti
imn
QV x x
, and considering
(12) and (4), we have
() ()(1 )( ) ()
(1 )
TT
imn
T
imn
QA X x x x
A
(13)
where
,
1
1
()() (),(), , ( ),()
(,), ,( ,)
i
T
T
iiNi
T
iNi
Xx x x x x
kx x kx x
1
()( ) (, ), ,( , )
T
T
mmmNm
Xx kxx kxx
1
()() (, ), ,( , )
T
T
nnnNn
Xx kxx kxx
Then, we can get:
EnhancedKernelUncorrelatedDiscriminantNearestFeatureLineAnalysisforRadarTargetRecognition
157

,
1, ()
1, ()
,
1
()
1
()
N
TTi
wimn
imnPi
P
N
T
imnPi
P
TFL
w
T
i
i
mn
VSV V x x
N
QQ
N
AK A
xx V
(14)
TTFL
bb
VSV AK A
(15)
where
F
L
w
K
and
F
L
b
K
are called kernel within-class
and between-class FL distance scatter matrix,
respectively, with
1, ()
1
(1 )
(1 )
N
FL
wimn
imnPi
P
T
imn
K
N
(16)
1, ()
1
(1 )
(1 )
N
FL
bimn
imnRi
R
T
imn
K
N
(17)
Similarly, (10) is converted to
T
t
A
KA I
(18)
where
,
1
1
N
T
tii
i
K
cc
N
(19)
is kernel total scatter matrix,
with
1
1/
N
i
i
cN
.
Therefore, (11) becomes
min ( )
T
t
TFL FL
wb
AKA I
tr A K K A
(20)
3.2 EKUDNFLA
To further enhance the discrimination power of the
learned subspace, we introduce a weighting
coefficient β into (20) and give rise to the
EKUDNFLA algorithm:
min (1 )
TFL FL
wb
AKAI
T
t
tr A K K A
(21)
Where β is a constant between 0 and 1. Obviously, if
β=0.5 , the EKUDNFLA is reduced to KUDNFLA.
Generally speaking, the between-class FL
distances in the feature space F have been enlarged
by some extent, and more emphasis should be paid
on minimizing the within-class FL distances, so the
value of β should be greater than 0.5.
Finally, the constrained minimization problem
above is reduced to a generalized eigenvalue
problem:
(1 )
FL FL
wbt
K
KK
(22)
The matrix A is determined by eigenvectors
corresponding to the eigenvectors corresponding to
the d smallest nonzero eigenvalues of (22). Once A
is obtained, for any point
D
x
R
, it can be mapped
to a d-dimensional point z by:
()
TT
zV x A
(23)
Where
1
(,), ,( ,)
T
N
kx x kx x
.
4 EXPERIMENTS AND RESULTS
To evaluate the performance of the proposed
algorithm, two experiments were performed on radar
target recognition with measured HRRPs from three
flying airplanes, including An-26, Yark-42, and
Cessna Citation S/II. For each airplane, 260 profiles
over a wide range of aspects are adopted, and each
profile is preprocessed by energy normalization (Yu
and Wang, 2008).
In the first experiment, the performance of
EKUDNFLA is compared with two classical kernel
methods KPCA (Scholkopf, et al., 1998) and KFDA
(Mika, et al., 1999). The Gaussian
kernel
12 1 2
2
2
exp((, ) /σ )kx x x x
, is adopted, and
the parameter
σ
is empirically set as 0.2. For
EKUDNFLA, the parameter β should be greater than
0.5 as what is said above. It is difficult to determine
the optimal value of β analytically since it depends
on the original data. But we can get a value which is
optimal for our data experimentally with limited
training samples. We find that a relatively good and
stable result can be obtained if β is within the range
between 0.85 and 0.98. So, the parameter β is set as
0.9 in the following experiments. Since we only
focus on feature extraction, as for classification, the
nearest neighbor classifier using Euclidean distance
is employed for the sake of simplicity.
For each airplane, 26, 18 and 13 of all profiles
are used for training, respectively, and the remainder
for test. Table I tabulates the recognition rates
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
158
attained by each method with different number of
training samples per target (NTSPT).
As can be seen from Table I, the proposed
EKUDNFLA outperforms KPCA and KFDA with
gains of 9.58% and 2.29% when the NTSPT is only
13, and 13.63% and 2.06% when the NTSPT is 18.
and 10.69% and 0.01% when the NTSPT is
increased to 26. It indicates that the FL distance can
better characterize the geometrical structure of
samples than the conventional euclidean distance,
especially when the number of training samples per
class is small.
Table 1: Recognition rate (%) obtained by each method.
Method
Recognition rate (%)
26 18 13
KPCA 77.06 77.41 76.51
KFDA 87.74 88.98 83.80
EKUDNFLA 87.75 91.04 86.09
In the second experiment, we fix the NTSPT as 18.
Since the merit of EKUDNFLA stems from two
factors: kernel technique and weighting coefficient,
we also evaluated the performance when only one
factor is applied. Hence, we derived the kernel
uncorrelated discriminant nearest feature line
analysis (KUDNFLA) and enhanced uncorrelated
discriminant nearest feature line analysis (EUDNFL-
A), respectively. We have also compared EKUDNF-
LA with PCA, LDA, and two other NFL-based
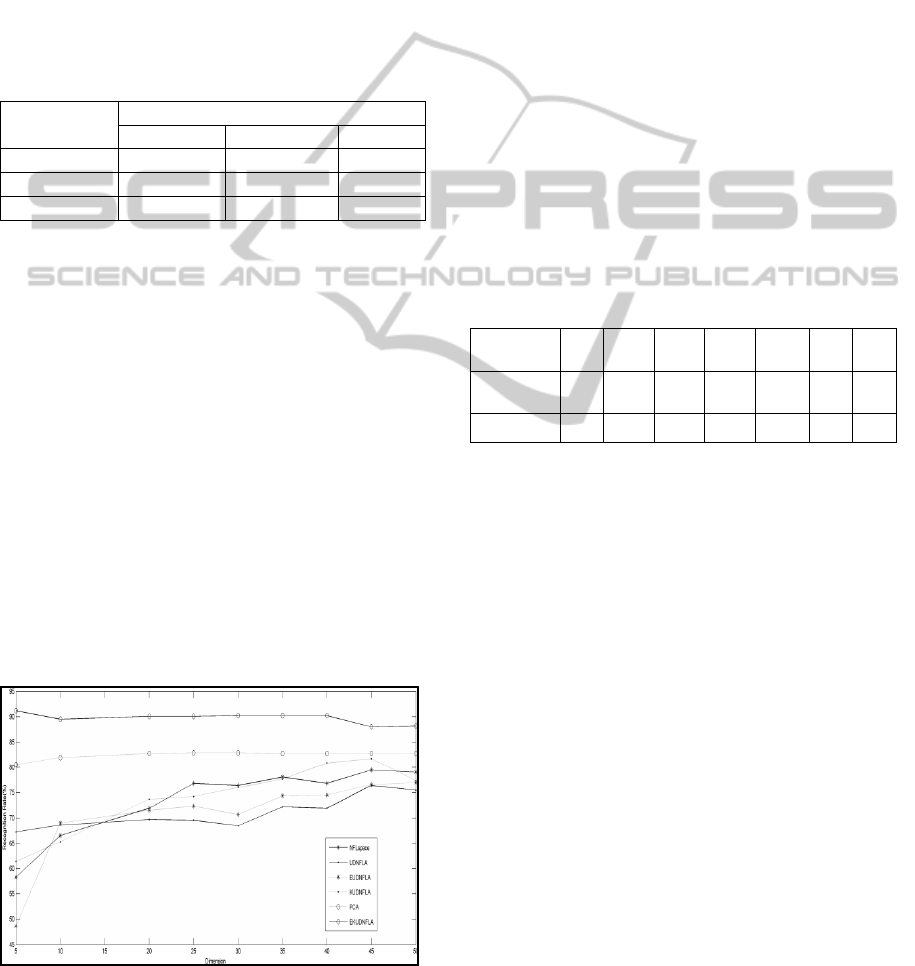
methods NFLspace and UDNFLA as well. Figure 1
shows the recognition rates versus feature
dimensions of all those methods mentioned above
except LDA, since the extracted feature deimension
is only 2 for our experiment. The top recognition
rates along with the corresponding dimensions
obtained by each method are listed in Table II. The
following observantions can be made from the
experimental results:
Figure 1: Recognition rates versus feature dimensions of
each method.
1) The proposed EKUDNFLA is overall superior to
all the other NFL metric subspace learning methods
involved in our experiments in terms of recognition
rate.
2) Compared with the linear NFL metric method
UDNFLA, KUDNFLA attains higher recognition
rate at almost each dimension. This is mainly
because KUDNFLA is a nonlinear method and the
kernel technique is helpful for improving its
discriminative power.
3) EKUDNFLA significantly outperforms
KUDNFLA in terms of recognition rate. It can be
attributed to the introduction of the weighting
coefficient, which gives more emphasis on
minimizing the within-class FL distances than
maximizing the between-class FL distance, so as to
use the within-class and between-class information
more effectively.
4) As we can see, the proposed EKUDNFLA also
outperforms conventional linear method PCA and
LDA with gains of 8.46% and 12.27%.
Table 2: Top recognition rate (%) and corresponding
dimension of each method.
Method
NFL
space
UD
NFLA
EUD
NFLA
KUD
NFLA
EKUD
NFLA
LDA PCA
Recognition
rate (%)
79.48 76.45 76.99 81.68 91.18 78.91 82.72
Dimension 45 45 50 45 5 2 45
5 CONCLUSIONS
We have proposed in this paper a new subspace
learning method, called enhanced kernel
uncorrelated discriminant nearest feature line
analysis (EKUDNFLA), for radar target recognition.
The method achieves good discrimination ability by
minimizing the within-class FL distances and
maximizing the between-class FL distances,
simultaneously. Furthermore, an uncorrelated
constraint is imposed to make the extracted features
statistically uncorrelated. Mapping the input data to
some high-dimensional feature space using the
kernel technique, nonlinear features are extracted. In
addition, weighting coefficient is introduced to
adjust the proportion between within-class and
between-class matrix. Experimental results on radar
target recognition with measured data show that
EKUDNFLA is overall superior to other NFL-based
methods in terms of recognition accuracy. And
compared with other conventional feature extraction
methods, like PCA, LDA, KPCA and KFDA,
EKUDNFLA also shows competitive performance.
EnhancedKernelUncorrelatedDiscriminantNearestFeatureLineAnalysisforRadarTargetRecognition
159

ACKNOWLEDGEMENTS
The authors would like to thank the anonymous
reviewers and editors for their helpful comments and
suggestions. This work is partially supported by the
National Natural Science Foundation of China (No.
61139003) and the China Postdoctoral Science
Foundation (No. 2013M531948).
REFERENCES
Chen, B., Liu, H.W., Bao, Z., 2005. PCA and kernel PCA
for radar high range resolution profiles recognition. In
the Proc. of 2005 IEEE International Radar
Conference. pp. 528-533.
Yu, X.L., Liu, B.Y., 2008. Optimal kernel discriminant
analysis for radar target recognition. In J. University of
Electronic Science and Technology of China, vol.37,
no.6, pp.883-885.
Turk, M., Pentland, A., 1991. Eigenfaces for recognition.
In J. Cogn. Neurosci.,vol. 3, no. 1, pp. 71-86.
Belhumenur, P.N., Hepanha, J.P., Kriegman, D.J.,1997.
Eigenfaces vs. Fisherface: Recognition using class
specific linear projection. In IEEE Trans. Pattern Anal.
Mach. Intell., vol. 19, no. 7, pp. 711-720.
He, X., Yan, S., Hu, Y., Niyogi, P., Zhang, H.J., 2005.
Face recognition using Laplacianface. In IEEE Trans.
Pattern Anal. Mach. Intell., vol. 27, no. 3, pp. 328–340.
Pang, Y.W., Zheng, L., Liu, Z.K., Yu, N.H., Li, H.Q.,
2005. A novel linear dimension reduction method. In
Proc. ICIC, pp. 117-125.
He, X.F., Cai, D., Yan, S.C., et al., 2005. Neighborhood
preserving embedding. In Proe. 10th IEEE Int. Conf.
ComputerVision, pp. 1208-1213.
Li, S., Lu, J.,1999. Face recognition using the nearest
feature line method. In IEEE Trans. Neural Networks,
vol. 10, no. 2, pp. 439-443.
Pang, Y., Yuan, Y., Li, X., 2007. Generalized nearest
feature line for subspace learning. In Electron. Lett.,
vol. 43, no. 20, pp. 1079–1080.
Zheng, Y.J., Yang, J.Y., Yang, J, Wu, X.J., Jin, Z., 2006.
Nearest neighbour line nonparametric discriminant
analysis for feature extraction. In Electron. Lett., vol.
42, no. 12, pp. 679-680.
Lu, J., Tan, Y.P., 2010. Uncorrelated discriminant nearest
feature line analysis for face recognition. In IEEE
Signal Process. Lett., vol. 17, no.2, pp. 185–188.
Yan, L., Pan, J.S., 2011. Neighborhood discriminant
nearest feature line analysis for face recognition. In
2nd Int. Conf. Innovations, pp. 345–348.
Yu, X.L., Wang, X.G., 2008. Uncorrelated discriminant
locality preserving projections. In IEEE Signal
Process. Lett., vol. 15, pp. 361–364.
Scholkopf, B., Smola, A., Muller, K.R., 1998.
Nonlinearcomponent analysis as a kernel eigenvalue
problem. In Neural Computation, vol. 10, no. 5, pp.
1299-1319.
Mika, S., Ratsch, G., Weston, J., et al., 1999. Fisher
discriminant analysis with kernels. In Proc IEEE Int.
Workshop on Neural Networks for Signal Processing
.Madison:Wisconsin, pp. 41-48.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
160
