On Metrics for Measuring Fragmentation of Federation over SPARQL

Endpoints

Nur Aini Rakhmawati, Marcel Karnstedt, Michael Hausenblas and Stefan Decker

INSIGHT Centre, National University of Ireland, Galway, Ireland

Keywords:

Linked Data, Data Distribution, Federated SPARQL Query, SPARQL Endpoint.

Abstract:

Processing a federated query in Linked Data is challenging because it needs to consider the number of sources,

the source locations as well as heterogeneous system such as hardware, software and data structure and distri-

bution. In this work, we investigate the relationship between the data distribution and the communication cost

in a federated SPARQL query framework. We introduce the spreading factor as a dataset metric for computing

the distribution of classes and properties throughout a set of data sources. To observe the relationship between

the spreading factor and the communication cost, we generate 9 datasets by using several data fragmentation

and allocation strategies. Our experimental results showed that the spreading factor is correlated with the com-

munication cost between a federated engine and the SPARQL endpoints . In terms of partitioning strategies,

partitioning triples based on the properties and classes can minimize the communication cost. However, such

partitioning can also reduce the performance of SPARQL endpoint within the federation framework.

1 INTRODUCTION

Processing a federated query in the Linked Data is

challenging because it needs to consider the number

of the sources, the source locations and heterogeneous

system such as the hardware, the software and the data

structure and the distribution. A federated SPARQL

query can be easily formulated by using the SERVICE

keyword. Nevertheless, determining the datasource

address that follows SERVICE keywords can be an

obstacle in writing a query because prior knowledge

data is required. To address this issue, several ap-

proaches (Rakhmawati et al., 2013) have been devel-

oped with the objective of hiding SERVICE keyword

and data sources location from the user. In these ap-

proaches, the federated engines receive a query from

the user, parse the query into sub queries, decide

the location of each sub query and distribute the sub

queries to the relevant sources. A sub query can be

delivered to more than one data source if the desired

answer occurs in the multiple sources. Thus, the dis-

tribution of the data can affect the federation perfor-

mance (Rakhmawati and Hausenblas, 2012). As an

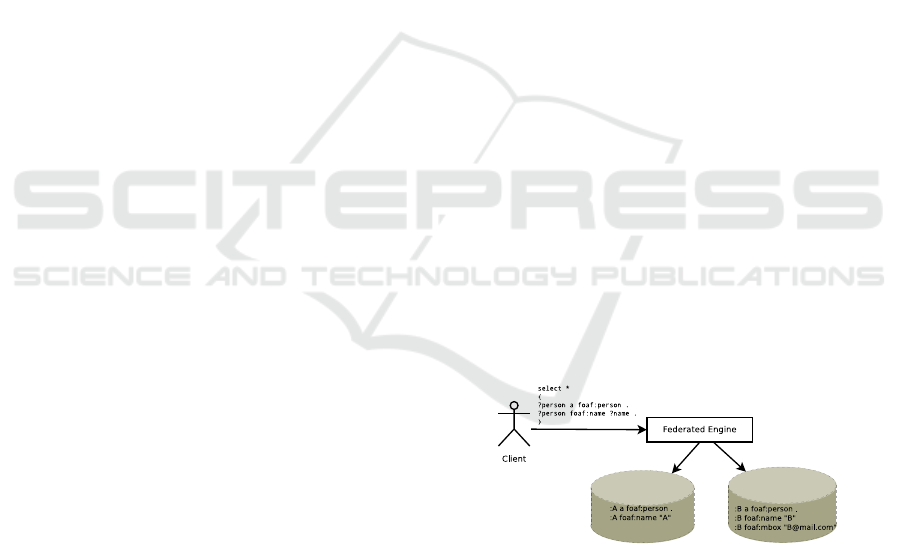
example, consider two datasets shown in Figure 1.

Each dataset contains a list of personal information

using the FOAF(http://xmlns.com/foaf/spec/) vocab-

ulary. If the user asks for the list of all person names,

the federated engine must send a query to all data-

Figure 1: Example of Federated SPARQL Query Involving

Many Datasets.

sources. Consequently, the communication cost be-

tween the federated engine and data sources would be

expensive.

In this study, we investigate the effect of data dis-

tribution on the federated engine performance. We

propose two composite metrics to calculate the pres-

ence of classes and properties across datasets. These

metrics can provide insight into the data distribu-

tion in the dataset which ultimately, it can determine

the communication cost between the federated en-

gine and SPARQL Endpoints. In order to evaluate

our metrics, we use several fragmentation and allo-

cation strategies to generate different shapes of data

distribution. After that, we run a static query set over

those data distributions. Our data distribution strate-

gies could be useful for benchmarking and controlled

systems such as organization system, but they can

not be address the problem in the federated Linked

119

Aini Rakhmawati N., Karnstedt M., Hausenblas M. and Decker S..

On Metrics for Measuring Fragmentation of Federation over SPARQL Endpoints.

DOI: 10.5220/0004760101190126

In Proceedings of the 10th International Conference on Web Information Systems and Technologies (WEBIST-2014), pages 119-126

ISBN: 978-989-758-023-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Open Data environmentbecause the Linked Data pub-

lisher has the power to control the dataset genera-

tion. The existing evaluations for assessing the feder-

ation over SPARQL endpoints (Montoya et al., 2012;

Schwarte et al., 2012) usually run their experiment

over different datasets and different query sets. In

fact, the performance of the federated engine is inﬂu-

enced by both dataset and query set. As a result, the

performance results may vary. For benchmarking, a

better comparison of federated engines performance

can made with either static query sets over different

datasets or static dataset with various query sets.

We only perform our observation on federation

over SPARQL endpoints. Query with a SERVICE

keyword is also out of the scope of our study be-

cause the query only goes to the speciﬁed source. In

other words, the data distribution does not inﬂuence

the performanceof the federation engine in that query.

Our contributions can be stated as follows: 1) We in-

vestigate the effects of data fragmentation and allo-

cation on the communication cost of the Federated

SPARQL query. 2) We introduce the spreading fac-

tor as a metric for calculating the distribution of data

across a dataset. In addition, we present the relation-

ship between the spreading factor and the communi-

cation cost of federated SPARQL queries. 3) Lastly,

we create datasets for evaluating the spreading factor

metric drawing from the real datasets. In particular,

we provide datasets and a dataset generator that can

be useful for benchmarking purpose.

2 RELATED WORKS

Primitive data metrics such as the number of triples,

the number of literals are not sufﬁciently represen-

tative to reveal the essential characteristics of the

datasets. Thus, Duan (Duan et al., 2011) introduced

a structuredness notion. Since this notion is applied

to a single RDF repository, it is not suitable for feder-

ated SPARQL queries which should consider the data

allocation in each repository as well as the number of

data sources involved in the dataset.

There are several data partitioning approaches for

RDF data clustering repository such as vertical parti-

tioning (Abadi et al., 2007) and Property Table par-

titioning (Huang et al., 2011). However, the commu-

nication in the RDF data clustering is totally differ-

ent than the communication in the federated SPARQL

query. In data clustering, several machines need

to communicate with each other in order to execute

a query, whereas in the federated SPARQL query,

there is no interaction amongst SPARQL endpoints.

The mediator has a role to communicate to each

SPARQL endpoint during query execution in the fed-

erated SPARQL query. Nevertheless, we apply RDF

data clustering strategies to generate the datasets for

evaluation.

The existing evaluations of the federation frame-

works used data partitioning in their experiment by

adopting data clustering strategies. Prasser (Prasser

et al., 2012) implemented three partitions: naturally-

partitioned, horizontally-partitioned and randomly-

partitioned. Fedbench(Schmidt et al., 2011) divided

the SP2B (Schmidt et al., 2009) dataset into sev-

eral partitions to run one of their evaluations. Our

prior work (Rakhmawati and Hausenblas, 2012) ob-

served the impact of data distribution on federated

query execution which particularly focus on the num-

ber of sources involved, the number of links and the

populated entities in several sources. In this work,

we extend our previous evaluation by implementing

more data partitioning schemes and we investigate

the effect of the distribution of classes and properties

throughout the dataset partitions on the performance

of federated SPARQL query.

3 SPREADING FACTOR OF

DATASET

Federated engines generally use a data catalogue to

predict the most relevant sources for a sub query.

The data catalogue mostly consists of a list of pred-

icates and classes. Apart from deciding the destina-

tion of the sub queries, a data catalogue can help fed-

erated engine generate set of query execution plans.

Hence, we consider computing the Spreading factor

of dataset to analyse the distribution of classes and

properties throughout the dataset. We initially deﬁne

the dataset used in this paper as follows:

Deﬁnition 1. Dataset D is a ﬁnite set of data sources

d. In the context of federation over SPARQL end-

points, d denotes a set of triple statements t that

can be accessed by a SPARQL endpoint. For each

SPARQL endpoint, there exists multiple RDF graphs.

In our work, we ignore the existence of graphs,

because we are only interested in the occurrences of

properties and classes in the SPARQL endpoint.

Deﬁnition 2. LetU be the set of all URIs, B be the set

of all BlankNodes, L be the set of all Literals, then a

triple t = (s, p,o) ∈ (U ∪ B) ×U × (U ∪ L∪ B) where

s is the subject, p is the predicate and o is the object

of triple t.

Later on, we determine the property and the class

in the dataset as follows:

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

120

Deﬁnition 3. Suppose d is a datasourcein the dataset

D, then the set P

(d, D) of properties p in the source

d is deﬁned as P

(d, D) = {p|∃(s, p, o) ∈ d ∧ d ∈ D}

and the set P(D) of properties p in the dataset D is

deﬁned as P(D) = {p|p ∈ P

(d, D) ∧ d ∈ D}

Deﬁnition 4. Suppose d is a datasourcein the dataset

D, then the set C

(d, D) of classes c in the source d

is deﬁned as C

(d, D) = {c|∃(s,rd ftype,c) ∈ d ∧ d ∈

D} and the set of classes c in the dataset D is deﬁned

as C(D) = {c|c ∈ C

(d, D) ∧ d ∈ D}

Given two datasets D = {d

} as shown in

Figure 1. Then P

,D) = {rdf:type,foaf:name},

,D) = P(D) = {rdf:type,foaf:name,foaf:mbox}

and C

,D) = C

,D) = C(D) = {foaf:person}.

3.1 Spreading Factor of Dataset

With the above deﬁnitions of class, property and

dataset, now we can describe how we calculate the

spreading factor. The spreading factor of the dataset

is based on whether or not classes and properties oc-

cur. Note that, we do not count the number of times

a class and property that are found in the source d be-

cause the federated engine usually relies on the pres-

ence of property in order to predict the data location

of a sub query. Given dataset D that contains a set

of datasets d, the normalizing number of occurrences

of properties in the Dataset D (OCP(D))is calculated

as follows: OCP(D) =

∑

∀d∈D

(d,D)|

|P(D)|×|D|

And the normal-

izing number of occurrences of classes in Dataset D

(OCC(D)) is computed as OCC(D) =

∑

∀d∈D

(d,D)|

|C(D)|×|D|

OCP(D) and OCC(D) have a range value from

zero to one. Inspired by the F-Measure function,

we combine OCP(D) and OCC(D) into a single met-

ric which is called the Spreading Factor Γ(D) of the

dataset D. Γ(D) =

(1+β

)OCP(D)×OCC(D)

×OCP(D)+OCC(D)

where β =

0.5

We assign β = 0.5 in order to put more stress on

properties than classes. The intuition is that the high-

est number of the query pattern delivered to SPARQL

endpoint mostly contains constant predicates (Arias

et al., 2011). Moreover, the number of distinct prop-

erties in the dataset is usually higher than the number

of distinct classes in the dataset. The high Γ value

indicates that the class and properties are spread out

over the dataset.

Look back at our previous example in which

we deﬁne P

,D), P

,D), P(D), C(D),

,D),C

,D), then we can calculate

OCP(D) =

2+3

3X2

= 0.833 and OCC(D) =

1+1

1X2

= 1.

Finally, we obtain Γ(D) = 1.172

3.2 Spreading Factor of Dataset

Associated with the Queryset

The spreading factor of a dataset reveals how the

whole of classes and properties are distributed over

the dataset. However, a query only consists of partial

properties and classes in the dataset. Thus, it is nec-

essary to quantify the spreading factor of the dataset

with respect to the queryset.

Deﬁnition 5. A query consists of set of triple patterns

τ which is formally deﬁned as τ(s, p,o) ∈ (U ∪V) ×

(U ∪V)× (U ∪L∪V) where V is a set of all variables.

Given a queryset Q = {q

,· · · ,q

}, the Q-

spreading factor γ of dataset D associated with query-

set Q is computed as γ(Q,D) =

∑

∀q∈Q

∑

∀τ∈q

OC(τ,D)

|Q|

where the occurrences of class and property for τ is

speciﬁed as

OC(τ, D) =











of D(o

,D)

|D|

if p

is rdf:type

∧o

/∈ V

pf D(p

,D)

|D|

if p

is not rdf:type

∧p

/∈ V

∑

∀d∈D

(d, D)|

|D|

otherwise

ofD(o, D) denotes the occurrences of object o in

the dataset D and pfD(p, D) denotes the occurrences

of predicate p in the dataset D which can be calculated

as follows: ofD(o, D) =

∑

∀d∈D

ofd(o, d, D) The oc-

currences of object o in the source d can be explained

as follows:

ofd(o, d, D) =



1 if o ∈ C

(d, D)

0 otherwise

pfD(p,D) =

∑

∀d∈D

pfd(p,d,D) The occurrence

of predicate p in the source d can be obtained from

the following formula:

pfd(p,d,D) =



1 if p ∈ P

(d, D)

0 otherwise

Consider an example, given a query

and a dataset as shown in Figure 1,

then OC(?person a foaf:person,D) = 1 and

OC(?person foaf:name ?name,D) = 1 because

foaf:person

and

foaf:name

are located in two data

sources. As a result, the q-Spreading factor γ(Q, D)

1+1

= 2

4 EVALUATION

We ran our evaluation on an Intel Xeon CPU X5650,

2.67GHz server with Ubuntu Linux 64-bit installed as

OnMetricsforMeasuringFragmentationofFederationoverSPARQLEndpoints

121

Listing 1: Dailymed Sample Triples.

dailymeddrug : 8 2 a dailymed : drug

dailymeddrug : 8 2 dailymed : a ct i v e i n g r e di e n t dail y m e d i n g :

Phenytoin

dailymeddrug : 8 2 r df s : la b e l ” D i l a n t in −125 ( Suspension ) ”

dailymeddrug :201 a dailymed : drug

dailymeddrug :201 dailymed : a c t i v e i ng r e d i e n t dail y m e d i n g :

Ethosuximide

dailymeddrug :201 r d f s : l a b el ” Za r o n t i n ( Capsule ) ”

dailymedorg : Parke−Davis a dailymed : o r ga n i za ti o n

dailymedorg : Parke−Davis r d f s : l a b e l ” Parke−Davis ”

dailymedorg : Parke−Davis dailymed : producesDrug

dailymeddrug : 8 2

dailymedorg : Parke−Davis dailymed : producesDrug

dailymeddrug :201

dailymeding : Ph eny t o i n a dailymed : i ng r e di e n ts

dailymeding : Ph eny t o i n rd f s : l ab e l ” Phenytoin”

dailymeding : Ethosuximide a dailymed : i n g r e d i e n ts

dailymeding : Ethosuximide r d f s : la b e l ” Ethosuximide ”

the Operating System and Fuseki 1.0 as the SPARQL

Endpoint server. For each dataset, we set up Fuseki

on different ports. We re-used the query set from our

previous work (Rakhmawati and Hausenblas, 2012).

We limited the query processing duration to one hour.

Each query was executed three times on two federa-

tion engines, namely SPLENDID (G¨orlitz and Staab,

2011) and DARQ (Quilitz and Leser, 2008). These

engines were chosen because SPLENDID employs

VoID(http://www.w3.org/TR/void/) as data catalogue

that contains a list of predicates and entities, while

DARQ has a list of predicates which is stored in the

Service Description(http://www.w3.org/TR/sparql11-

service-description/). Apart from using VoID,

SPLENDID also sends a SPARQL ASK query to de-

termine whether or not the source can potentially re-

turn the answer. We explain the details of our dataset

generation and metrics as follows:

4.1 Data Distribution

To determine the correlation between the commu-

nication cost of the federated SPARQL query and

the data distribution, we generate 9 datasets by di-

viding the Dailymed(http://wifo5-03.informatik.uni-

mannheim.de/dailymed/) into three partitions based

on following strategies:

4.1.1 Graph Partition

Inspired by data clustering for a single RDF storage

(Huang et al., 2011), we performed graph partition

over our dataset by using METIS (Karypis and Ku-

mar, 1998). The aim of this partition scheme is to

reduce the communication needed between machines

during the query execution process by storing the con-

nected components of the graph in the same machine.

We initially identify the connections of subject and

object in different triples. We only consider the URI

object which is also a subject in other triples. Intu-

itively, the reason is that the object which appears as

the subject in other triples can create a connection if

the triples are located in different dataset partitions.

V(D) denotes the set of pairs of subject and object that

are connected in the dataset D which can be formally

speciﬁed as V(D) = {(s, o)|∃s,o, p, p

′

∈ U : (s, p,o) ∈

D ∧ (o, p

′

) ∈ D

′

}. We assign a numeric identiﬁer

for each s,o ∈ V(D). After that, we create a list of se-

quential adjacent vertexes for each vertex then uses it

as input of METIS API. Run METIS to divide the ver-

texes and get a list of the partition number of vertexes

as output. Finally, we distribute each triple based on

the partition number of its subject and object. Con-

sider an example, given Listing 1 as a dataset sample,

then

V(D)={(dailymeddrug:82,

dailymeding:Phenytoin),(dailymeddrug:201,

dailymeding:Ethosuximide),(dailymedorg:Parke-Davis,

dailymeddrug:82),(dailymedorg:Parke-Davis,

dailymeddrug:201)}

Starting an identiﬁer value from one and increment

the identiﬁer later, we set the identiﬁer for daily-

meddrug:82 = 1, dailymeding:Phenytoin =2, dai-

lymeddrug:201=3, dailymeding:Ethosuximide=4 and

dailymedorg:Parke-Davis=5. After that, we can

create list of sequential adjacent vertexes V(D) is

{(2,5),1,(4,5),3,(1,3)}. Suppose that we divide the

sample of dataset into 2 partitions, then the output of

METIS partition is {1,1,2,2,1} where each value is

the partition number for each vertex. According to the

METIS output, we can say that dailymeddrug:82 be-

longs to partition 1, dailymeding:Phenytoin belongs

to partition 1, dailymeddrug:201 belongs to partition

2 and so on. In the end, we have two following parti-

tions:

Partition 1: all triples that contain dailymeddrug:82, daily-

meding:Phenytoin and dailymedorg:Parke-Davis

Partition 2: all triples that contain dailymeddrug:201 and

dailymeding:Ethosuximide

4.1.2 Entity Partition

The goal of this partition is to distribute the number of

entities evenly in each partition. Different classes can

be located in a single partition. However, the entities

of the same class should be grouped in the same parti-

tion until the number of entities reaches the maximum

number of entities for each source. We initially create

a list of the subjects along with its class (E(D)). The

set E(D) of pairs of subject and its class in the dataset

D is deﬁned as E(D) = {(s,o)|∃(s,rd ftype,o) ∈ D}

Then, we sort E(D) by its class o and store each pair

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

122

of the subject and object in a partition until the num-

ber of pairs of subject and object equals to the total

pairs of subject and object divided by the number of

partitions. After that, we distribute the remainders of

triples in the dataset based on the subject location.

Given Listing 1 as a dataset sample, then

E(D)={(dailymeddrug:82,dailymed:drug),(dailymeddrug:201

,dailymed:drug),(dailymedorg:Parke-Davis,dailymed:organization),

(dailymeding:Phenytoin,dailymed:ingredients),

(dailymeding:Ethosuximide,dailymed:ingredients)}

Suppose that we split the dataset into two parti-

tions, then the maximum number of entities for each

partition is

|E(D)|

numberof partitions

= 3 (ceiling 2.5).

We place dailymeddrug:82, dailymeddrug:201 and

dailymedorg:Parke-Davis in the partition 1 and store

the remainders of entities in the partition 2. As the

ﬁnal step, we distribute the related triples based on its

subject partition number.

4.1.3 Class Partition

Class Partition divides the dataset based on its classes.

The related triples that belong to one entity are placed

in the same machine. To begin with, we also create

E(D) which was used in Entity partition. Later, we

distribute each triple based on the subject class. ike

our previous entity partition example, we do the same

step to generate E(D). However, in the class partition,

we divide the dataset to three partitions since we have

three classes (dailymed:drug, dailymed:organization,

dailymed:ingredients).

4.1.4 Property Partition

Wilkinson(Wilkinson, 2006) introduced a method for

storing RDF data in traditional databases known as

Property Table (PT). There are two types of PT par-

titions: Clustered Property Table and Property-class

Table. In our property partition, we do not have

a Property class table because we treat all proper-

ties in the same manner. We place the triples that

have the same property in one data source. Be-

cause the number of properties in the dataset is gen-

erally high, we allow more than one property to

be stored in the same partition as long as we get

a balanced number of triples among the partitions.

Firstly, we group the triples based on its property.

Next, we store each group in a partition until the

number of partition triples is less than or equal to

the number of dataset triples divided by the num-

ber of partitions. For instance, given a dataset as

shown in Listing 1, then we have four properties:

rdf:type, dailymed:activeingredient,rdf:label and dai-

lymed:producesDrug. Suppose that we want to divide

the dataset into 2 partitions, then the maximum num-

ber of triples in each partition is

thenumberoftriples

thenumberof partitions

= 7. As the following step, we store the triples

based on its property as follows: Partition 1: ﬁve

triples with rdf:type property, two triples with dai-

lymed:activeingredient property and Partition 2: ﬁve

triples with rdfs:label property, two triples with daily-

med:producesDrug

4.1.5 Triples Partition

The federation framework performance is inﬂuenced

not only by the federated engine solely, but also de-

pends on the SPARQL Endpoints within the federa-

tion framework. In order to keep balanced workload

for SPARQL Endpoints, we split up the triples of each

source evenly because LUBM (Guo et al., 2005) men-

tioned that the number of triples can inﬂuence the per-

formance of a RDF repository. We created three triple

partition datasets (TD, TD2, TD3). TD is obtained

by partitioning the native Dailymed dataset into three

parts. TD2 and TD3 are generated by picking a ran-

dom starting point within the Dailymed dump ﬁle(by

picking a random line number).

4.1.6 Hybrid Partition

The Hybrid Partition is a partitioning method that

combines two or more previous partition strategies.

For instance, if the number of triples in a class is too

high, we can distribute the triples to another partition

to equalize the number of triples. Since the num-

ber of triples in each dataset of the Class Distribu-

tion CD are not equal, we create HD to distribute

the triples evenly. However, rdf:type property and

rdfs:label property are evenly through all partitions in

dataset HD2. This distribution is intended for balanc-

ing the workload amongst SPARQL Endpoints since

those properties are commonly used in our query set.

As shown in those ﬁgures, the classes and proper-

ties are distributed over most of the partitions in the

GD dataset. The PD has the lowest Spreading Fac-

tor among the dataset because each property occurs

in exactly one partition and only in one partition has a

set of triples that contains rdf:type. The dataset gener-

ation code and the generation results can be found at

DFedQ github(https://github.com/nurainir/DFedQ).

4.2 Metrics

To calculate the communication cost of the the fed-

erated SPARQL query, we compute the data transfer

OnMetricsforMeasuringFragmentationofFederationoverSPARQLEndpoints

123

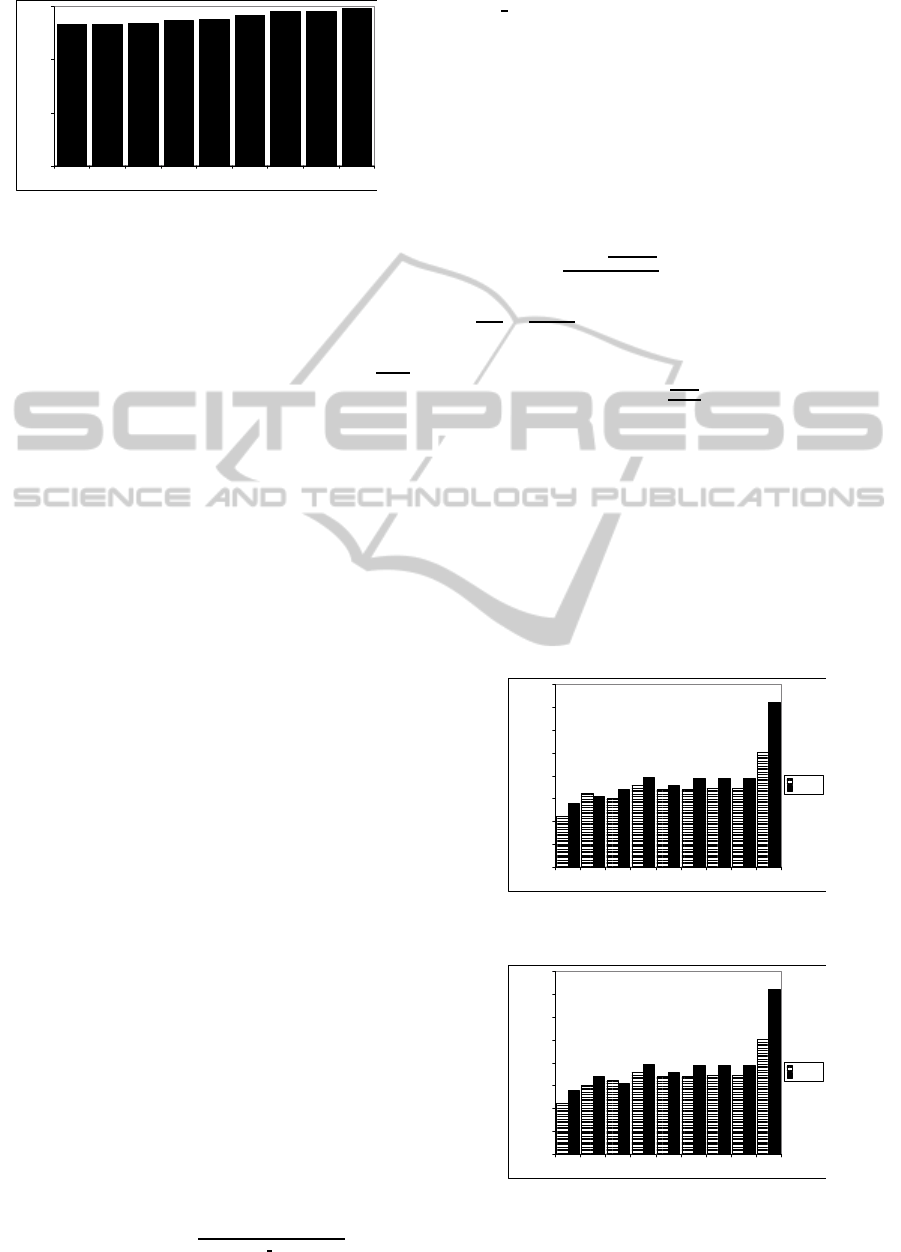
PD CD TD TD3 TD2 ED HD2 HD GD

Dataset Partitions

.000

.400

.800

1.200

Spreading Factor of The datasets

Figure 2: Spreading Factor of Dataset.

volume between the federated engine and SPARQL

Endpoints. The data transfer volume includes the

amount of data both sent and received by the me-

diator. Apart from capturing the data transmission,

we also measure the requests workload (RW) during

query execution. RW is calculated as RW =

T∗SS

where RQ refers to the number of requests sent by

the federated engine to all SPARQL Endpoints, T de-

notes the duration between when a query is received

by the federated engine and when its results starts to

be dispatched to the client and SS is the number of

selected sources. Furthermore, we also measure the

response time that is required by a federated engine

to execute a query.

For the sake of readability, we aggregate each per-

formance metric results into a single value. In or-

der to avoid trade-offs among queries, we assign a

weight to each query using the the variable counting

strategy from the ARQ Jena (Stocker and Seaborne,

2007). This weight indicate the complexity of the

query based on the selectivity of the variable posi-

tion and the impact of variables on the source selec-

tion process. The complexity of query can inﬂuence

the federation performance. Hence, we normalize

each performance metric result by dividing the met-

ric value with the weight of the associated query. In

the context of federated SPARQL queries, we set the

weight of the predicate variable equals to the weight

of the subject variable since most of the federated en-

gines rely on a list of predicates to decide the data

location. Note that, a triple pattern can contain more

than one variable. The details of the weight of subject

variable w

, predicate variable w

and object variable

for the triple pattern τ can be explained as follows:

(τ)=

(

3 if the subject of triple pattern τ ∈ V

0 otherwise

(τ)=

(

3 if the predicate of triple pattern τ ∈ V

0 otherwise

(τ)=

(

1 if the object of triple pattern τ ∈ V

0 otherwise

Finally, we can compute the weight of query

q: weight(q) =

∑

∀τ∈q

(τ)+w

(τ)+1

MAX COST

where

MAX

COST = 8 because if a triple pattern consists of

variablesthat are located in all positions, the weight of

the triple pattern is 8(3+3+1+1). By using the weight

of a query, we can align the query performance re-

sults afterwards. We do not create a composite metric

that combinesthe response time, the request workload

and the data transfer, but rather we calculate each per-

formance metric results individually. Given that Q is

a set of queries q in the evaluation and that m is a

set of performance metric results associated with the

queryset Q, then the ﬁnal metric µ for the evaluation

is µ(Q,m) =

∑

∀q∈Q

weight(q)

|Q|

For instances, the query in Figure 1 has a weight

3+1

3+1+1

= 1.125. Suppose that the volume of

data transmission during this query execution is 10

Mb and we only have one query in the queryset, then

µ(Q,m) can be calculated

1.125

= 8.88Mb.

5 RESULTS AND DISCUSSION

As seen in Figures 3 and 4, the data transmission

between DARQ and SPARQL Endpoints is higher

than the data transmission between SPLENDID and

SPARQL Endpoints. However, Figures 5 and 6 show

that the average requests workload in DARQ is less

than the average requests workload in SPLENDID.

PD CD TD TD3 TD2 ED HD2 HD GD

Dataset Partitions



















Figure 3: Average Data Transfer Volume Vs the Spreading

Factor of Datasets (order by the Spreading Factor value).

PD  CD TD3 TD2 ED HD2 HD GD

Dataset Partitions

0E+00

500E+03

1E+06

2E+06

3E+06

4E+06

Average Data Transmission (Bytes)

Splendid

DARQ

Figure 4: Average Data Transfer Volume Vs the Q-

Spreading Factor of Datasets associated with the Query-

set(order by the Spreading Factor value).

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

124

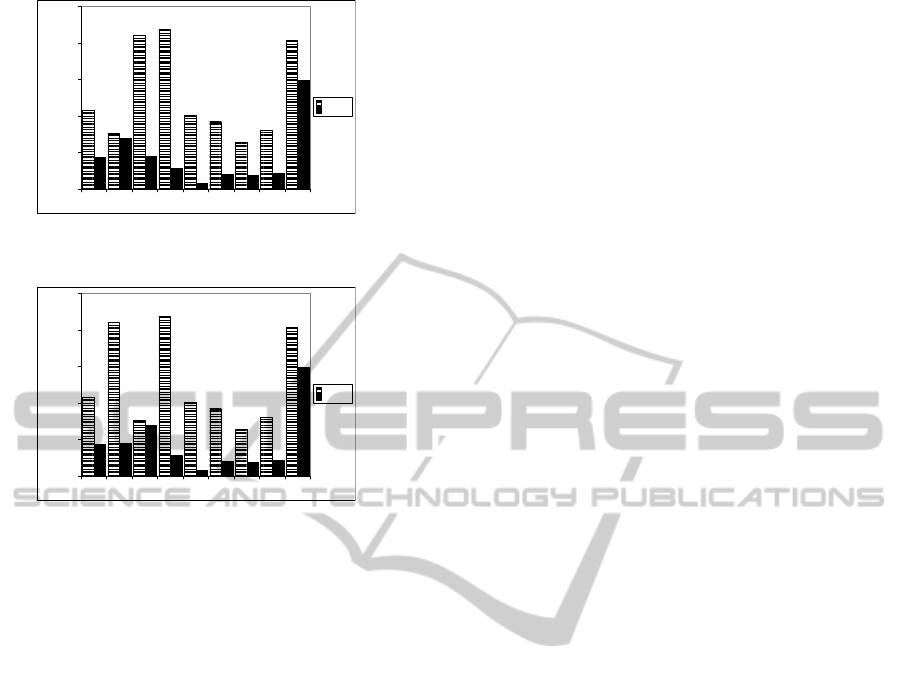
PD CD TD TD3 TD2 ED HD2 HD GD

Dataset Partitions

0E+00

5E+00

10E+00

15E+00

20E+00

25E+00

Average Requests Workload (Requests/Second)

Splendid

DARQ

Figure 5: Average Requests Workload Vs the Spreading

Factor of Datasets(order by the Spreading Factor value).

PD TD CD TD3 TD2 ED HD2 HD GD

Dataset Partitions

0E+00

5E+00

10E+00

15E+00

20E+00

25E+00

Average Requests Workload (Requests/Second)

Splendid

DARQ

Figure 6: Average Requests Workload Vs the Q-Spreading

Factor of Datasets associated with the Queryset(order by the

Spreading Factor value).

This is because DARQ never sends SPARQL ASK

queries in order to predict the most relevant source

for each sub query.

Overall, data transmission increases gradually in

line with the Spreading Factor of a dataset. However,

the data transmission rises dramatically for GD dis-

tribution. This indicates that in the context of Fed-

erated SPARQL queries, data clustering based on its

property and class is better than data clustering based

on related entities such as Graph Partition. The rea-

son behind this conclusion is that the source selec-

tion in federated query engine depends on classes and

properties occurrences. Furthermore, when the feder-

ated engines generate query plans, they use optimiza-

tion techniques based on the statistical predicates and

classes.

Although a small Spreading Factor can mini-

mize the communication cost, it can also reduce the

SPARQL Endpoint performance. As shown in Fig-

ure 5 and 6, a small Spreading Factor can lead to

the high number of requests received by SPARQL

Endpoint in one second because in the property dis-

tribution, the federated engine mostly sends differ-

ent query patterns to multiple datasource. More-

over, the SPARQL endpoint that stores the popular

predicates such as rdf:type and rdfs:label will receive

more requests than other SPARQL endpoints. Con-

sequently, this such condition can lead to incomplete

results because when overloaded, the SPARQL End-

point might reject requests (e.g Sindice SPARQL end-

point(http://sindice.com/)only allowsone client send-

ing one query per second). Poor performance is also

shown at the highest value of Spreading Factor of

the dataset (GD) because the entities are spread over

the dataset partitions. Hence, with the calculation of

the spreading factor of the dataset, the federated en-

gine can create a query optimization which attempts

to adapt the dataset characteristic that is shown from

the spreading factor value. For instance, if the dataset

has too small Spreading Factor, the federated engine

should maintain a timer to send several requests to the

same SPARQL endpoint in order to keep the sustain-

ability of the SPARQL endpoint as well as avoid the

incomplete answer.

6 CONCLUSION

We have implemented various data distribution strate-

gies to partition classes and properties over dataset

partitions. We introduced two notions of dataset met-

rics, namely the Spreading Factor of a dataset and

the Spreading Factor of a Dataset associated with the

query set. These metrics expose the distribution of

classes and properties over the dataset partitions. Our

experiment results revealed that the class and property

distribution effects on the communication cost be-

tween the federated engine and SPARQL endpoints.

However, it does not signiﬁcantly inﬂuence the re-

quest workload of a SPARQL endpoint. Partitioning

triples based on the properties and classes can mini-

mize the communication cost. However, such parti-

tioning can also reduce the performance of SPARQL

endpoints within the federation infrastructure. Fur-

ther, it can also inﬂuence the overall performance of

federation framework.

In future work, we will apply other dataset par-

titioning strategies and use more federated query

engines which have different characteristics from

DARQ and SPLENDID.

ACKNOWLEDGEMENTS

This publication has emanated from research con-

ducted with the ﬁnancial support of Science

Foundation Ireland (SFI) under Grant Number

SFI/12/RC/2289 and Indonesian Directorate General

of Higher Education. Thanks to Soheila for a great

discussion

OnMetricsforMeasuringFragmentationofFederationoverSPARQLEndpoints

125

REFERENCES

Abadi, D. J., Marcus, A., Madden, S. R., and Hollenbach,

K. (2007). Scalable semantic web data management

using vertical partitioning. In Proceedings of the 33rd

VLDB, VLDB ’07, pages 411–422. VLDB Endow-

ment.

Arias, M., Fern´andez, J. D., Mart´ınez-Prieto, M. A., and

de la Fuente, P. (2011). An empirical study of real-

world sparql queries. CoRR, abs/1103.5043.

Duan, S., Kementsietsidis, A., Srinivas, K., and Udrea, O.

(2011). Apples and oranges: a comparison of rdf

benchmarks and real rdf datasets. In ACM SIGMOD.

G¨orlitz, O. and Staab, S. (2011). SPLENDID: SPARQL

Endpoint Federation Exploiting VOID Descriptions.

In Proceedings of the 2nd International Workshop on

COLD, Bonn, Germany.

Guo, Y., Pan, Z., and Heﬂin, J. (2005). Lubm: A bench-

mark for owl knowledge base systems. Web Seman-

tics: Science, Services and Agents on the World Wide

Web, 3(2-3):158 – 182.

Huang, J., Abadi, D. J., and Ren, K. (2011). Scalable sparql

querying of large rdf graphs. PVLDB, 4(11):1123–

1134.

Karypis, G. and Kumar, V. (1998). A fast and high qual-

ity multilevel scheme for partitioning irregular graphs.

SIAM J. Sci. Comput., 20(1):359–392.

Montoya, G., Vidal, M.-E., Corcho,

O., Ruckhaus, E., and

Aranda, C. B. (2012). Benchmarking federated sparql

query engines: Are existing testbeds enough? In

ISWC(2), pages 313–324.

Prasser, F., Kemper, A., and Kuhn, K. A. (2012). Efﬁ-

cient distributed query processing for autonomous rdf

databases. EDBT ’12, pages 372–383, New York, NY,

USA. ACM.

Quilitz, B. and Leser, U. (2008). Querying distributed rdf

data sources with sparql. ESWC’08, pages 524–538,

Berlin, Heidelberg. Springer-Verlag.

Rakhmawati, N. A. and Hausenblas, M. (2012). On the

impact of data distribution in federated sparql queries.

In ICSC 2012, pages 255 –260.

Rakhmawati, N. A., Umbrich, J., Karnstedt, M., Hasnain,

A., and Hausenblas, M. (2013). Querying over feder-

ated sparql endpoints - a state of the art survey. CoRR,

abs/1306.1723.

Schmidt, M., Grlitz, O., Haase, P., Ladwig, G., Schwarte,

A., and Tran, T. (2011). Fedbench: A benchmark

suite for federated semantic data query processing. In

ISWC, volume 7031, pages 585–600. Springer.

Schmidt, M., Hornung, T., Lausen, G., and Pinkel, C.

(2009). Spˆ 2bench: a sparql performance benchmark.

In ICDE’09., pages 222–233. IEEE.

Schwarte, A., Haase, P., Schmidt, M., Hose, K., and

Schenkel, R. (2012). An experience report of large

scale federations. CoRR, abs/1210.5403.

Stocker, M. and Seaborne, A. (2007). Arqo: The architec-

ture for an arq static query optimizer.

Wilkinson, K. (2006). Jena property table implementation.

In In SSWS.

WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies

126