Increasing Self-consumption of Photovoltaic Electricity by Storing

Energy in Electric Vehicle using Smart Grid Technology in the

Residential Sector

A Model for Simulating Different Smart Grid Programs

M. J. van der Kam and W. G. J. H. M. van Sark

Copernicus Institute of Sustainable Development, Utrecht University, Utrecht, The Netherlands

Keywords: Smart Grid, Photovoltaic Electricity, Self-consumption, Electric Vehicle, Energy Storage.

Abstract: In this paper a model has been developed which intends to simulate the increase of self-consumption of

photovoltaic (PV)-power by storing energy in electric vehicle (EV) using smart grid technology in the

residential sector. Three different possible smart grid control algorithms for a micro-grid consisting of solar

panels, a household and an EV are presented that manage the (dis-)charging profile of an EV, either in real-

time or using linear optimization using predictions for PV-power and electricity demand. The different

control algorithms are simulated for a year using data for PV-power and electricity demand from the

Netherlands and one specific EV. Preliminary results of the model are presented, showing that all control

algorithms could significantly increase self-consumption and reduce peaks in electricity demand from the

main grid. Although the difference in performance of the control algorithms for self-consumption is

marginal, we find that linear optimization works better than the real-time algorithms for peak reduction.

1 INTRODUCTION

The worldwide increase of electricity demand poses

major challenges in the energy sector. Since 1971,

the final consumption of electricity has increased

four-fold to 60 PJ in 2010 (IEA, 2012) and is

expected to further increase due to growing global

population and welfare. Issues related to this

development include availability, cost and

environmental issues such as global warming and

depletion of resources. While the industrial sector

has the highest demand for electricity, demand in the

residential sector shows the highest increase in

Europe (Bertoldi and Atanusiu, 2008) and is

therefore an important sector for changes in

electricity provision and distribution.

Another important sector contributing to global

warming is the transport sector. Globally the

contributions of the transport sector to greenhouse

gas (GHG)-emissions amounted to nearly 20% in

2009 (Hoen et al., 2009). According to the European

Federation for Transport and Environment (2011)

emissions from the European transport sector

have increased by 29% since 1990.

Electric vehicles (EVs) are a promising

technology for reducing the environmental burden of

road transport (Essen, et al. 2011). If EV sales

increase it can be beneficial for reducing GHG-

emissions, but it also creates another issue;

electricity demand will increase even further. Also,

the typical charging pattern of EVs without a control

system coincides roughly with that of households

(E-laad, 2012), which is high in the morning and the

evening and low in the afternoon; it thus contributes

to existing peaks in electricity demand in the

residential sector.

PV technology can be part of the solution to

problems relating with electricity and transport,

since there are no emissions of greenhouse gasses

during electricity production. If PV electricity is

used to power EV’s, transport with EV will cause

even less or zero GHG emissions. An important

advantage of PV for the residential sector is its

scalability; even single households can use this

technology.

However, the mismatched production and load

curve for PV for domestic use poses a challenge. PV

installations produce most electricity around noon,

when solar insulation is high, while electricity

demand is usually low then. In addition, solar power

supply may be variable due to variations in cloud

coverage.

J. van der Kam M. and G. J. H. M. van Sark W..

Increasing Self-consumption of Photovoltaic Electricity by Storing Energy in Electric Vehicle using Smart Grid Technology in the Residential Sector - A

Model for Simulating Different Smart Grid Programs.

DOI: 10.5220/0004763000140020

In Proceedings of the 3rd International Conference on Smart Grids and Green IT Systems (SMARTGREENS-2014), pages 14-20

ISBN: 978-989-758-025-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Strategies to deal with these issues are for

instance demand response (DR) and electricity

storage (Castillo-Cagigal et al., 2011): in their paper

DR is defined as shifting load demand in order to

optimize electricity demand. Optimization goals are

for instance peak-shifting (flattening load demand

curve) or increasing self consumption (consumption

of locally produced electricity behind the meter) .

Smart grid technology combines the traditional

electricity grid or microgrid (a local, low-voltage

distritibution system) with information and

communication technologies in order to add

‘intelligence’ to the grid (Verbong et al., 2012). DR

is an essential aspect of smart grids, and is achieved

by turning appliances on and off within a certain

timeframe.

The main power grid can be used as virtual

storage for electricity. When supply is higher than

demand, electricity can be fed back and sold to the

grid and vice versa. This is an interesting option,

because in that case an expensive battery is not

needed. However, with increasing numbers of PV-

installations this strategy can become problematic,

because of the increased power transport over the

electricity grid. This will cause the need for more

investments in the grid in order to prevent overloads.

In response to this threat, several countries in Europe

have started implementing policies to stimulate self-

consumption (Castillo-Cagigal et al., 2011).

PV electricity could also be stored in EV

batteries. This way EVs can help increase self-

consumption. Furthermore, by using PV electricity

to power EVs GHG emissions for personal

transportation are reduced.

In this paper the potential of combining smart

grid technology with electricity storage in EVs for

increasing self-consumption in the residential sector

is investigated. This is done by creating a model of a

microgrid containing a household, solar panels and

an EV and simulating the effect on self-consumption

of PV-power of the system using smart grid

technology. The baseline for the potential is the

absence of a smart grid and is called “Uncontrolled

Charging”. The strategies investigated are “Real-

time Controlled Charging”, “Real-time Controlled

Charging and Discharging”, and “Linear

Programming”.

In section 2 the methodology is presented: it

includes the structure of the microgrid (2.1), the

proposed smart grid systems (2.2) and evaluation

method (2.3). In section 3 the first simulation results

are presented, analyzed and compared. Section 4

concludes the paper.

2 METHODOLOGY

The potential of increasing self-consumption by

storing PV energy in EVs is investigated by

performing computer simulations and evaluating the

results on performance indicators for self-

consumption and peak-reduction.

The basic input for the model is the total

electricity demand of households per time-step, the

supplied PV power per time-step and the technical

specifications and planned use (average trip

duration, distance and number of trips per week) of

the EVs. Based on these inputs the electricity

distribution for each time-step t is decided.

2.1 Micro-grid Model

The micro-grid contains a PV-installation, a

household with electricity demand, an EV and a

connection to the main grid; all elements are

connected. The PV-power and household electricity

demand are considered uncontrollable, Demand Side

Management is not taken into account here, while

the EV loading pattern is partly controllable and

partly uncontrollable (when energy is needed for

trips).

2.1.1 PV and Electricity Demand

The PV-installation provides electricity to the

microgrid. Data for PV-power profiles per time-step

is provided by Robin Berg from the company

LomboXnet. The dataset relates to a PV-installation

of 10 kWp in Utrecht, the Netherlands and is

available at hourly time resolution from July 6

2011 to December 31

2012. For this paper it is

assumed that the simulated household has 8 panels

of 250 Wp available, which leads to an estimated

annual yield of 1700 kWh assuming an annual yield

of 850 kWh/kWp, typical for the Netherlands.

The household has a certain electricity demand

profile that must be met at all times. Data for

household electricity demand is provided by Felix

Claessen and is based on measurements by Liander

(Claessen, 2012). The dataset relates to 400

households in the Netherlands and is available per

15 minutes for a week in February 2008. The weekly

data is repeated for a year multiplied by a factor per

week based on measurements from Liander in 2007.

In this research only the households are selected that

use 3500  20% kWh per year.

IncreasingSelf-consumptionofPhotovoltaicElectricitybyStoringEnergyinElectricVehicleusingSmartGrid

TechnologyintheResidentialSector-AModelforSimulatingDifferentSmartGridPrograms

2.1.2 Electric Vehicle

The battery of the EV is used as storage for excess

PV-power and energy can be extracted from it when

there is shortage of PV-power. The EV is also used

to make trips; energy needed to make trips is

considered inelastic demand and must be met at all

times. When an EV is on a trip it is not available to

exchange energy with the micro-grid. It is assumed

that on average three trips per week are made with

the EV, lasting between 4 and 8 hours, taking place

between 8:00 and 22:00 and using between 20% and

80% of the battery capacity.

Without a smart grid program, the EV, if

connected, will always charge until its full. This

strategie is called “Uncontrolled Charging” and is

represented by equation (1).

If E

t 1



 C

 t  t

 P

EV ,in



 P

EV ,in,max

(1)

With E

(t) the energy contained in EV-battery,

the battery capacity, t

the time-steps for which

the EV is at the loading station, P

EV,in

(t) the EV

charging power and P

EV,in,max

(t) the maximum EV

charging power.

One EV is simulated, with technical

specifications based on Tesla Model S (Tesla, 2013).

The technical specifications are presented in table 1.

With E

EV,min

the minimum energy in EV-battery,

EV,out,max

(t) the maximum EV discharging power

and η

EV,in

and η

EV,out

the

(dis-)charging efficiency.

Table 1: Technical specifications of simulated EV.

(kWh) 85

min

20% C

Energy consumption (kWh/km) 0.2

Typical range (km) 340

max

and P

out

max

(kW) 22



and



out

80%

2.2 Smart Grid Programs

In this section several control algorithms for

electricity distribution within the micro-grid are

proposed. All control algorithms require trips to be

planned in advance. The minimum amount of energy

in the battery is 20% allowing for short emergency

trips.

2.2.1 Real-time Controlled Charging

“Real-time controlled charging” uses the difference

between P

and P

load

for every time-step t. Based

on the energy content of the EV the loading pattern

is decided. In this algorithm, it is not possible to

extract energy from the EV in order to cover

electricity demand of the households.

First E

EV,req

, the minimum amount of energy in

the EV taking into account energy needed for trips

and maximum charging power, is defined in

equation (2).

If t  t 

EV ,trip

EV ,in,max

trip

















 E

EV ,req



EV ,trip

 P

EV ,in, max

 t

trip

 t



 E

EV,min

If t  t 

EV ,trip

EV ,in,max

trip













 E

EV ,req

 E

EV,min

(2)

With E

EV,trip

the total energy used for the trip and

trip

the start-time of the trip.

The loading pattern is then defined by equations

(3), (4), (5) and (6).

EV ,in







EV ,in,PV





 P

EV ,in ,grid





(3)

If P

load













t 1





 C

 t  t

P

EV ,in,PV







EV ,in



 P

load



(4)

If E









EV ,in,PV







EV ,req



 t t

P

EV,grid



 E

EV,req



 E

t 1



 P

EV ,in,PV



(5)

EV ,in







EV ,in,max

(6)

With P

EV,in,PV

(t) the PV-power used for charging

the EV, P

EV,in,grid

(t) the power from the main grid

used for charging the EV, P

(t) the available PV-

power and P

load

(t) the total load demand of the

household.

Equation (3) denotes that the EV is charged with

power from the PV-installations and from the grid. If

there is more PV-power than electricity demand, the

EV starts to charge until it is full or until there is no

more excess PV-power, see equation (4). The EV

only extracts energy from the grid when there is

shortage of PV-power in order to make a trip, see

equation (5). Finally, equation (6) makes sure the

total power into the EV cannot exceed the maximum

charging power.

2.2.2 Real-time Controlled Charging and

Discharging

This program uses the same equations as “real-time

controlled charging”, but is also able to extract

energy from the EV in order to cover electricity

demand of households. The additional equations are

presented in (7) and (8).

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

If P

load



 P



 E





 E

EV ,req



 t  t

 P

EV ,out







EV ,out

1

load



 P



(7)

EV ,out



 P

EV ,out ,max

(8)

2.2.3 Linear Programming

Increasing self-consumption of PV-power by

controlling the loading pattern of an EV can be

described as a linear optimization problem and

solved by using linear programming. Linear

programming is a method to solve constrained

optimization problems. Constrained optimization is

a technique used often in research on smart grids.

Recent examples are Guo et al. (2012), Silva et al.

(2012), Tanaka et al. (2011), González Vayá and

Andersson (2012).

The variables used in the linear program are

EV,in,PV

(t), P

EV,grid

(t), P

EV,out

(t), for every time-step t.

In order to maximize self-consumption, the PV-

power used to charge the EV is maximized. This

results in the following problem:

max P

EV ,in ,PV





(9)

subject to the following constraints:

 

,, ,, ,,

VinPV EVingrid EVinmax l

PtP tP tt 

(10)





,,,

V out EV out max l

tP tt

(11)



EV ,in

EV ,in,PV



 P

EV ,in,grid



t' 1







EV ,out

1

EV ,out



t' 1



 E

EV ,req



 E

EV ,trip



 E



, t  t

(12)



EV ,in

EV ,in,PV



 P

EV ,in,grid



t' 1







EV ,out

1

EV ,out



t' 1



 C



 E

EV ,trip



 E



, t  t

(13)

EV ,in,PV





 P





 P

load





, t  t

(14)

,out

 P

load



 P



, t  t

(15)

With dummy variable t’. Constraints (10) and

(11) ensure that the maximum (dis-)charging power

is not exceeded. Constraints (12) and (13) ensure

that the energy in the EV is sufficient for trips and

does not exceed the battery capacity. Constraints

(14) and (15) ensure that not more energy is (dis-

)charged then there is excess or shortage of PV-

power (when there is not enough PV-power for trips

energy is extracted from the grid). Furthermore, all

variables are non-negative.

Contrary to the real-time programs linear

programming is based on perfect information; all the

constraints are known for all time-steps t. However,

PV-supply and electricity demand are not known

exactly in advance. In order to provide realistic

prediction of how effective this program would be in

reality, some assumptions have been made. In this

paper, the method is called “realistic linear

programming”.

It is assumed that the calculations are made at

midnight and are based on the load pattern from the

previous day. An exception is made for weekends,

since weekend load demand differs significantly

from weekdays. However, the data is only available

for a week. Because of this predictions for Saturdays

will be based on data for Sundays and vice-versa.

The input for PV is based on PV-power predictions.

It is assumed that prediction deviates from the real

value with a standard deviation  of 10%. This

results in the following equations:

load , prediction







load ,real

t  24h



(16)

PV,prediction







PV,real



10%

(17)

The linear program is then executed with the

predicted values, while it is evaluated with the real

values.

2.3 Evaluation

All programs are simulated for each month of the

year. Based on the simulations the potential of

increasing self-consumption (SC) is calculated.

Self-consumption is defined as the relative amount

of PV-power for period T, with starting point T0,

used by either the households or the EV, see

equation (18).

SC T





min P





load



 P









t T0



(18)

A second indicator, relative peak reduction (RPR) is

also used for evaluation. RPR compares the

deviation from the average of the load demand for

the main grid P

grid,tot

(t), defined in equation (19),

with a control algorithm, denoted as P

grid,tot,control

(t),

to “uncontrolled charging”, denoted as P

grid,tot,no

control

(t), and is defined in equation (20):

IncreasingSelf-consumptionofPhotovoltaicElectricitybyStoringEnergyinElectricVehicleusingSmartGrid

TechnologyintheResidentialSector-AModelforSimulatingDifferentSmartGridPrograms

grid,tot



 P

load



 P



 P



(19)

RPR T





grid ,tot,control



 P

grid,tot,control



t T0



grid ,tot,no control



 P

grid,tot,no control



t T0



(20)

So for example, an RPR-score of 1 indicates no

relative peak reduction compared to “uncontrolled

charging”, a RPR-score of 0 means load demand is

totally flat for that day and a RPR-score above 1

would mean that there are higher peaks compared to

“uncontrolled charging”.

3 RESULTS

In this section, the first results from simulations are

shown. The results are based on 20 simulations per

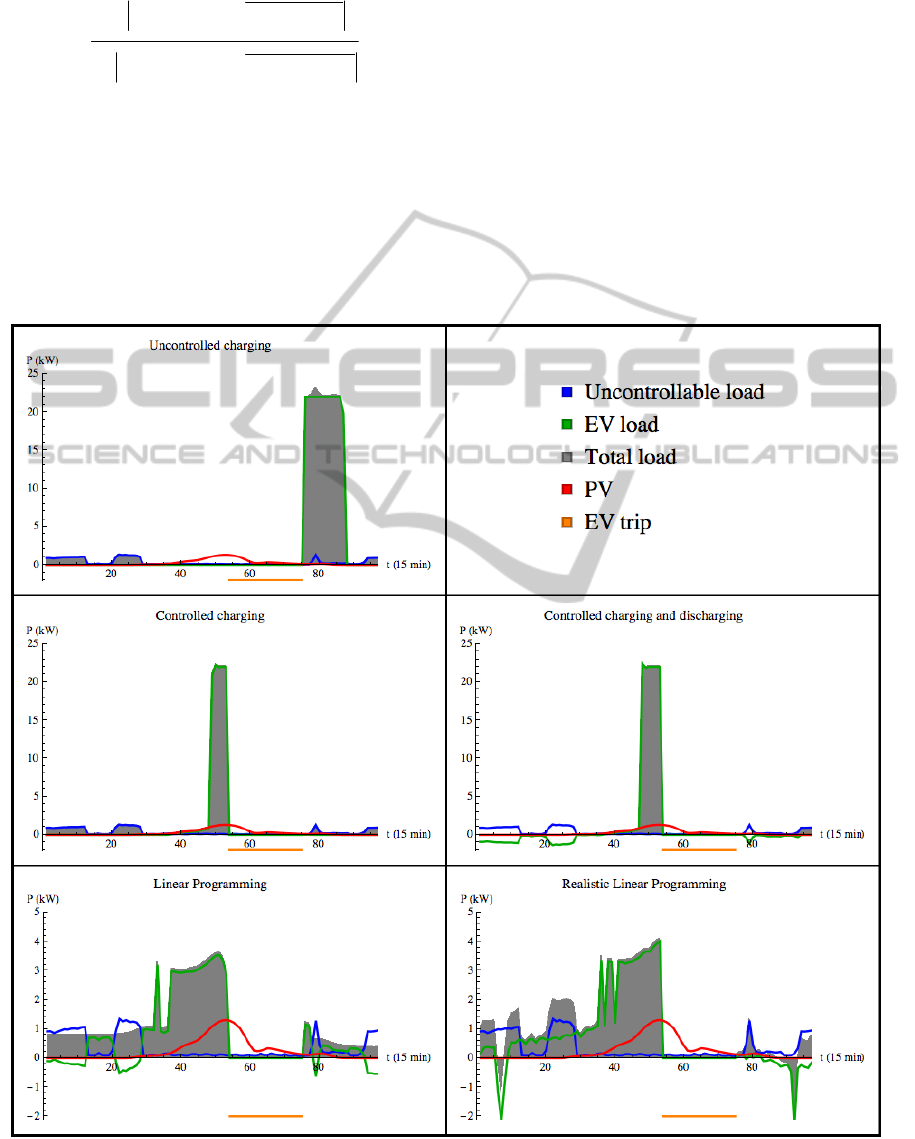
month for each smart grid program. In figure 1,

examples of individual runs for each program are

given. They are based on the same load and PV

profile and EV-trip.

In the case of “uncontrolled charging”, the EV

arrives home in the evening and starts charging

when there is no PV-power available. In the cases of

“Controlled charging” and “Controlled charging and

discharging” the EV only loads in times of excess

PV-power, but there is still a large peak in the

charging profile, since the EV needs to load much

Figure 1: Results of an individual full day run for each control algorithm. The orange bar shows the period during which the

EV is being used for a trip.

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems

Figure 2: Mean self-consumption and standard deviation of 100 simulations of each control algorithm for each month.

Figure 3: Mean peak reduction and standard deviation of 100 simulations of each control algorithm for each month.

more than there is PV-power available. Note that the

latter total load is very small outside the peak.

For both programs using linear optimization the

peaks in energy use are much smaller than for the

other programs, since the EV never charges at full

power, but at 20-25%. Because the requirements for

the trip are still exactly planned in the realistic case,

there are no problems for EV-use. However, it does

not perform as well as the idealistic case, since

electricity is fed back to the grid when it could by

used to cover load demand.

In figure 2, results from 100 24 hour simulations

per month for each program evaluated for self-

consumption are shown. It can be seen that even

though all systems perform much better than a

system without a smart grid, it is difficult to tell

which system performs best for self-consumption.

The differences between the programs are large

when compared for peak reduction (figure 3),

showing that “linear programming” flattens the load

demand for the main grid significantly better than

the real-time algorithms.

4 CONCLUSIONS

In this paper several control algorithms for

increasing self-consumption of PV-power in the

residential sector, using smart grid technology and

electricity storage in an EV, were proposed. The first

simulations show that all proposed systems could

IncreasingSelf-consumptionofPhotovoltaicElectricitybyStoringEnergyinElectricVehicleusingSmartGrid

TechnologyintheResidentialSector-AModelforSimulatingDifferentSmartGridPrograms

significantly increase self-consumption. Though the

systems have distinctive characteristics for the

resulting EV charging profile, it is unclear which

system performs best based on the proposed

indicator for self-consumption. In order to

investigate this issue, more simulations must be

carried out.

However, when evaluated on peak reduction, the

differences are much more clear. “Linear

programming” is superior to the real-time algorithms

for peak reduction.

As a follow-up of this paper, an extensive

sensitivity analysis will be performed for the

following parameters: (a) amount of solar panels

(kWp), (b) average yearly household electricity use,

and (e) the standard deviation in PV-power

predictions. Nevertheless, based on our preliminary

results, it is shown that a microgrid using smart grid

technology and electricity storage in an EV could

significantly increase self-consumption of PV-power

in the residential sector.

ACKNOWLEDGEMENTS

The authors would like to thank Robin Berg and

Floris Bruning from LomboXnet for providing the

data used for the PV- installations and Felix

Claessen for providing the electricity demand data

for households.

REFERENCES

Bertoldi, P., Atanasiu, B., 2008. Electricity consumption

and efficiency trends in the enlarged European Union;

Status Report 2006, Institute for Environment and

Sustainability.

Castillo-Cagigal, M., Caamaño-Martín, E., Matallans, E.,

Masa-Bote, D., Gutiérrez, A., Monasterio-Huelin, F.,

Jiménez-Leube, J., 2011. PV self-consumption

optimization with storage and Active DSM, for the

residential sector, Solar Energy, Vol. 85, pp 2338-

2348.

Claessen, F. N., 2012. Smart grid control; An analysis of

control systems within a Dutch residential microgrid

incorporating decentralised renewable energy

resources, M.Sc. Thesis, Universiteit Utrecht.

E-laad, 2012. Belastingprofiel van het net bij

laadtransacties op laadpalen van stiching e-laad;

periode: oktober 2011 t/m December 2011, graphic,

retrieved 11-9-2013 from.

http://www.e-laad.nl/uploads/files/nieuws-

2012/Oktober/grafiek2.jpg.

Essen, H. van, and Kampman, B., 2011. Impacts of

Electric Vehicles – Summary report, Delft: CE Delft.

González Vayá, M., Andersson, G., (2012), Centralized

and decentralized approaches to smart charging of

plug-in vehicles, IEEE.

Guo, Y., Pan, M., Fang, Y., (2012), Optimal power

management of residential customers in the smart

gird, IEEE, Transactions on Parallel and Distributed

Systems, Vol. 23, No. 9.

Hoen A., 2009. CO

emission reduction in transport:

Confronting medium-term and long-term options for

achieving climate targets in the Netherlands, The

Hague, Environmental Assessment Agency.

International Energy Agency, 2012. Key World Energy

Statistics, retrieved 27-2-2013 from http://www.iea.org/

publications/freepublications/publication/kwes.pdf.

Silva, M., Morais, H., Vale, Z., (2012), An integrated

approach for distributed energy resource short-term

scheduling in smart grids considering realistic power

system simulation, Energy Conversion and

Management, Vol. 64, pp 273-288.

Tanaka, K., Yoza, A., Ogimi, K., Yona, A., Snjyu, T.,

Funabashi, T., Kim, C., (2012), Optimal operation of

DC smart house system by controllable loads based on

smart grid topology, Renewable Energy, Vol. 39, pp

132-139.

Tesla, 2013. Tesla Model S technical specifications,

retrieved 5-3-2013 from www.teslamotors.com.

Verbong, G. P. J., Beemsterboer, S., Sengers, F., 2012.

Smart grids of smart users? Involving users in

developing a low carbon electricity economy, Energy

Policy, Vol. 52, pp 117-125.

SMARTGREENS2014-3rdInternationalConferenceonSmartGridsandGreenITSystems