
Applying Machine Learning Techniques to Baseball Pitch Prediction
Michael Hamilton
1
, Phuong Hoang
2
, Lori Layne
3
, Joseph Murray
2
, David Padgett
3
, Corey Stafford
4
and Hien Tran
2
1
Mathematics Department, Rutgers University, New Brunswick, New Jersey, U.S.A.
2
Department of Mathematics, North Carolina State University, Raleigh, North Carolina, U.S.A.
3
MIT Lincoln Laboratory, Lexington, Massachusetts, U.S.A.
4
Department of Applied Physics & Applied Mathematics, Columbia University, New York, New York, U.S.A.
Keywords:
Pitch Prediction, Feature Selection, ROC, Hypothesis Testing, Machine Learning.
Abstract:
Major League Baseball, a professional baseball league in the US and Canada, is one of the most popular sports
leagues in North America. Partially because of its popularity and the wide availability of data from games,
baseball has become the subject of significant statistical and mathematical analysis. Pitch analysis is especially
useful for helping a team better understand the pitch behavior it may face during a game, allowing the team
to develop a corresponding batting strategy to combat the predicted pitch behavior. We apply several common
machine learning classification methods to PITCH f/x data to classify pitches by type. We then extend the
classification task to prediction by utilizing features only known before a pitch is thrown. By performing
significant feature analysis and introducing a novel approach for feature selection, moderate improvement
over former results is achieved.
1 INTRODUCTION
Baseball is one of the most popular sports in North
America. In 2012, Major League Baseball (MLB)
had the highest season attendance of any American
sports league (MLB, 2012). Partially due to this pop-
ularity and the discrete nature of gameplay (allowing
easy recording of game statistics between plays) and
the long history of baseball data collection, baseball
has become the target of significant mathematical and
statistical analysis. Player performance, for example,
is often analyzed so baseball teams can modify their
roster (by drafting and trading players) to achieve the
best possible team configuration.
One area of statistical analysis of baseball that
has gained attention in the last decade is pitch anal-
ysis. To aid this study, baseball pitch data produced
by the PITCH f/x system is now widely available for
both public and private use. This data contains use-
ful information about each pitch; several character-
istics such as pitch speed, break angle, and type are
recorded. Because of the accessibility of large vol-
umes of data, both fans and professionals can perform
their own pitch studies, including sabermetrics anal-
ysis. Related pitch data analysis is available in the
literature. For example, Weinstein-Gould (Weinstein-
Gould, 2009) examines pitching strategy of major
league pitchers, specifically determining whether or
not pitchers (from a game theoretic approach) im-
plement optimally mixed strategies for handling bat-
ters. The research suggests that pitchers do mix op-
timally with respect to the pitch variable. In an eco-
nomic sense, this means that pitchers behave ratio-
nally relative to the result of any given pitch. An in-
teresting note from the author is that although MLB
pitchers are in the perfect position to utilize optimal
strategy mixing (compared to other research subjects
who have little motivation to optimally mix strate-
gies), “...experience, large monetary incentives, and
a competitive environment are not sufficient condi-
tions to compel players to play optimally.” Knowing
this, we obtain useful information about how pitchers
make decisions and (theoretically) which factors are
more important than others in prediction; by knowing
the results pitchers respond to (and the ones they don’t
respond to), it is possible reverse engineer this in-
formation and correspondingly tweak predictions for
maximal accuracy.
Count (number of balls and strikes in the current
at bat) is often cited as a basis for decisive strategy.
520
Hamilton M., Hoang P., Layne L., Murray J., Padget D., Stafford C. and Tran H..
Applying Machine Learning Techniques to Baseball Pitch Prediction.
DOI: 10.5220/0004763905200527
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 520-527
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

For example, Ganeshapillai and Guttag (Ganeshapil-
lai and Guttag, 2012) show that pitchers are much
more predictable in counts that favor the batter (usu-
ally more balls than strikes). Furthermore, Hopkins
and Magel (Hopkins and Magel, 2008) show a dis-
tinct effect of count on the slugging percentage of the
batter. More specifically, they show that average slug-
ging percentage is significantly lower in counts that
favor the pitcher; however, there is no significant dif-
ference in average slugging percentage (a weighted
measure of the on-base frequency of a batter) in neu-
tral counts or counts that favor the batter (Hopkins
and Magel, 2008). These results verify that count has
a significant effect on the pitcher-batter relationship,
and will thus be an important factor in pitch predic-
tion. Another interesting topic is pitch prediction,
which could have significant real-world applications
and potentially improve batter performance in base-
ball. One example of research on this topic is the work
by Ganeshapillai and Guttag (Ganeshapillai and Gut-
tag, 2012), who use a linear support vector machine
(SVM) to perform binary (fastball vs. nonfastball)
classification on pitches of unknown type. The SVM
is trained on PITCH f/x data from pitches in 2008 and
tested on data from 2009. Across all pitchers, an aver-
age prediction accuracy of roughly 70 percent is ob-
tained, though pitcher-specific accuracies vary.
In this paper we provide a machine learning ap-
proach to pitch prediction, using classification meth-
ods to predict pitch types. Our results build upon the
work in (Ganeshapillai and Guttag, 2012); however
we are able to improve performance by examining
different types of classification methods and by tak-
ing a pitcher adaptive approach to feature set selec-
tion. For more information about baseball itself, con-
sult the Appendix for a glossary of baseball terms.
2 METHODS
2.1 PITCH f/x Data
Our classifiers are trained and tested using PITCH f/x
data from all MLB games during the 2008 and 2009
seasons. Raw data is publicly available (Pitchf/x,
2013), though we use scraping methods to transform
the data into a suitable format. The data contains ap-
proximately 50 features (each represents some char-
acteristic of a pitch like speed or position); however,
we only use 18 features from the raw data and create
additional features that are relevant to prediction. For
example, some created features are: the percentage of
fastballs thrown in the previous inning, the velocity of
the previous pitch, strike result percentage of previous
pitch, and current game count (score). For a full list
of features used, see Appendix.
We apply classification methods to the data to pre-
dict pitches. On that note, it is important to clarify
a subtle distinction between pitch classification and
pitch prediction. The distinction is simply that clas-
sification uses post-pitch information about a pitch to
determine which type it is, whereas prediction uses
pre-pitch information to classify its type. For exam-
ple, we may use features like pitch speed and curve
angle to determine whether or not it was a fastball.
These features are not available pre-pitch; in that case
we use information about prior results from the same
scenario to judge which pitch can be expected.
The prediction process is performed as binary
classification (see section 2.2); all pitch types are
members of one of two classes (fastball and nonfast-
ball). We conduct prediction for all pitchers who had
at least 750 pitches in both 2008 and 2009. This spec-
ification results in a set of 236 pitchers. For each
pitcher, the data is further split by each count and,
with 12 count possibilities producing 2,832 smaller
subsets of data (one for each pitcher and count com-
bination). After performing feature selection (see sec-
tion 2.3) on each data subset, each classifier (see Ap-
pendix) is trained on each subset of data from 2008
and tested on each subset of data from 2009. The
average classification accuracy for each classifier is
computed for test points with a type confidence (one
feature in the PITCH f/x data that measures the con-
fidence level that the pitch type is correct) of at least
0.5.
2.2 Classification Methods
Classification is the process of taking an unlabeled
data observation and using some rule or decision-
making process to assign a label to it. Within the
scope of this research, classification represents deter-
mining the type of a pitch, i.e. given a pitch x with
characteristics x
i
, determine which pitch type (curve-
ball, fastball, slider, etc) x is. There are several clas-
sification methodologies one can use to accomplish
this task, here we used the methods of Support Vec-
tor Machine (SVM) and k−nearest neighbor (k-NN),
they are explained in full detail in (Theodoridis and
Koutroumbas, 2009).
2.3 Feature Selection Methods
The key differences between our approach and former
research (Ganeshapillai and Guttag, 2012) is the fea-
ture selection methodology. Rather than using a static
set of features, a different optimal set of features is
ApplyingMachineLearningTechniquestoBaseballPitchPrediction
521
used for each pitcher/count pair. This allows the algo-
rithm to adapt for optimal performance on each indi-
vidual subset of data.
In baseball there are a number of factors that in-
fluence the pitcher’s decision (consciously or uncon-
sciously). For example, one pitcher may not like to
throw curveballs during the daytime because the in-
creased visibility makes them easier to spot; how-
ever, another pitcher may not make his pitching de-
cisions based on the time of the game. In order to
maximize accuracy of a prediction model, one must
try to accommodate each of these factors. For exam-
ple, a pitcher may have particularly good control of a
certain pitch and thus favors that pitch, but how can
one create a feature to represent its favorability? One
could, for example, create a feature that measures the
pitcher’s success with a pitch since the beginning of
the season, or the previous game, or even the previous
batter faced. Which features would best capture the
true effect of his preference for that pitch? The an-
swer is that each of these approaches may be best in
different situations, so they all must be considered for
maximal accuracy. Pitchers have different dominant
pitches, strategies and experiences; in order to maxi-
mize accuracy our model must be adaptable to various
pitching situations.
Of course, simply adding many features to our
model is not necessarily the best choice because
we leave noise from situationally useless features
and suffer from curse of dimensionality issues. We
change our problem of predicting a pitch into pre-
dicting a pitch for each given pitcher in each given
count. We maximize accuracy by choosing (for each
pitcher/count pair) an optimal pool of features from
the entire available set. This allows us to maintain our
adaptive strategy while controlling dimensionality.
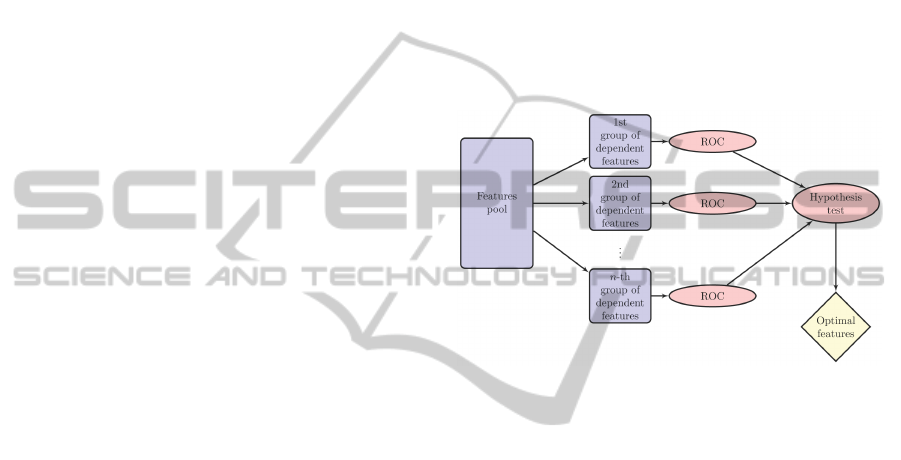
2.3.1 Feature Selection Implementation
As alluded to earlier, our feature selection scheme is
adaptive, finding a good feature set for each (pitcher,
count), e.g., (Rivera, 0-2). Our adaptive feature selec-
tion approach consists of 3 stages.
1. We create about 80 features (see the full list in the
Appendix). We then group all of our generated
features together into groups by similarity. Such
grouping might contain 4 to 12 similar features
such as accuracy over the last pitch, the last five
pitches, ten pitches, and accuracy over all pitches
in the last inning, etc.
2. We then compute the Receiver Operating Charac-
teristic (ROC) curve for each group of features,
then select the strongest one or two to move on to
the next stage. In practice, selecting only the best
feature provides worse prediction than selecting
the best two or three features. Hence at this stage,
the size of each group is reduced from 4 to 12 to
2 or 3.
3. We next remove all redundant features from our
final feature set. From our grouping, features are
taken based on their relative strength. There is
the possibility that a group of features might not
have good predictive power. In those cases, the
resulting set of features is pruned by conducting
hypothesis testing to measure significance of each
feature at the α = .01 level.
For a schematic diagram of our approach, see Figure
1.
Figure 1: Schematic diagram of the proposed features se-
lection.
2.3.2 ROC Curves
The Receiver Operating Characteristic (ROC) curve
are used for each individual feature in order to mea-
sure how useful a feature is in prediction. We cal-
culate this by measuring the area between the single
feature ROC curve and the line created by standard
guessing. This value of area tells us how much bet-
ter the feature is at distinguishing the two classes,
compared to standard guessing. These area values
are in the range of [0, 0.5), where a value of 0 rep-
resents no improvement over random guessing and
0.5 would represent perfect distinction between both
classes. For a more detailed description of the ROC
curve, see (Fawcett, 2006) and also Figure 2.
2.3.3 Hypothesis Testing
The ability of a feature to distinguish between two
classes can be determined using a hypothesis test.
Given any feature f , we compare µ
1
and µ
2
, the mean
values of f in Class 1 (fastballs) and Class 2 (nonfast-
balls), respectively. Then we consider
H
0
: µ
1
= µ
2
(1)
H
A
: µ
1
6= µ
2
(2)
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
522

Figure 2: The diagonal line represents the tradeoff between
true positive rate (sensitivity) and false positive rate by ran-
dom guessing. The curve represents a shift in this tradeoff
by using a given feature to assign class labels instead of
randomly guessing. In this case the shift represents an im-
provement in distinction between the two classes and the
region between the curve and line quantifies this improve-
ment.
and conduct a hypothesis test using the student’s t dis-
tribution. We compare the p-value of the test against
a significance level of α = .01. When the p-value is
less than α, we reject the null hypothesis and con-
clude that the studied feature means are different for
each class, meaning that the feature is significant in
separating the classes. In that sense, this test allows
us to remove features which have insignificant sepa-
ration power.
3 RESULTS
In this paper, we propose a new technique in the prob-
lem of baseball pitch prediction. Specifically, we
segment the prediction task by pitcher and count be-
cause each of these situations is different enough that
it would be a mistake to consider them equally. For
prediction by pitcher, we used data from 236 pitchers
(as noted in section 2.1). We then selected eight pitch-
ers from the 2008 and 2009 MLB regular seasons to
examine in details.
Table 1: Data for each pitcher.
Pitcher Training Size Test Size
Fuentes 919 798
Madson 975 958
Meche 2821 1822
Park 1309 1178
Rivera 797 850
Vaquez 2412 2721
Wakefield 2110 1573
Weathers 943 813
Table 1 describes the training and testing sets.
Data from 2008 season were used for training and
data from 2009 were used for testing. Table 2 depicts
the prediction accuracy among the eight pitchers as
compared across classifiers as well as naive guess. On
average, 79.76% of pitches are correctly predicted by
SVM-L and SVM-G classifiers while k-NN perform
slightly better, at 80.88% accurate. Furthermore, k-
NN is also a better choice in term of computational
speed, as noted in Table 3.
We compare the results of our prediction model
to a naive model that predicts simply by guessing a
pitcher’s most common pitch (either fastball or non-
fastball) from the training data and compute the im-
provement in accuracy in Table 4. The improvement
factor (percent), I, is calculated as follow:
I =
A
1
− A
0
A
0
× 100 (3)
where A
0
and A
1
denotes the accuracies of naive guess
and our model accordingly. The naive guess simply
return the most frequent pitch type thrown by each
pitcher, calculated from the training set (Ganeshapil-
lai and Guttag, 2012).
The average prediction accuracy of our model
over all 236 pitchers in 2009 season is 77.45%. Com-
pared to the naive model’s natural prediction accu-
racy, our model on average achieves 20.85% improve-
ment. In previous work (Ganeshapillai and Guttag,
2012), the average prediction accuracy of 2009 sea-
son is 70% with 18% improvement over the naive
model. It should be noted that previous work con-
siders 359 pitchers who threw at least 300 pitches in
both 2008 and 2009 seasons. In our study, we only
consider those pitchers that threw at least 750 pitches
in a season. This reduces the number of pitchers that
we considered to 236 pitchers.
In addition, we demonstrate the prediction accu-
racy of our model for each count situation. As illus-
trated in Figures 3 and 4, prediction accuracy is sig-
nificant higher in batter-favored counts and is approx-
imately equal in neutral and pitcher-favored counts.
We also calculate prediction accuracy for 2012
season, using training data from 2011 season or from
both 2010 and 2011 seasons. We again only select
pitchers who had at least 750 pitches in those seasons.
As shown in Table 5, the average pitch prediction ac-
curacy is about 75% in both cases (even though the
size of training data is double in the second case).
ApplyingMachineLearningTechniquestoBaseballPitchPrediction
523

Table 2: Prediction accuracy comparison (percents). Symbols: k-Nearest Neighbors (k-NN), Support Vector Machine with
linear kernel (SVM-L), Support Vector Machine with Gaussian kernel (SVM-G), Naive Guess (NG).
Classifier Fuentes Madson Meche Park Rivera Vaquez Wakefield Weathers Average
k-NN 80.15 81.85 72.73 70.31 93.51 72.50 100.00 76.01 80.88
SVM-L 78.38 77.23 74.83 72.40 89.44 72.50 95.50 77.76 79.76
SVM-G 76.74 79.38 74.17 71.88 90.14 73.05 96.33 76.38 79.76
NG 71.05 25.56 50.77 52.60 89.63 51.20 100.00 35.55 66.04
Table 3: CPU Times (seconds).
Classifier Fuentes Madson Meche Park Rivera Vaquez Wakefield Weathers Average
k-NN 0.3459 0.3479 0.3927 0.3566 0.4245 0.4137 0.4060 0.3480 0.3794
SVM-L 0.7357 0.5840 1.2616 0.7322 0.6441 1.1282 0.3057 0.5315 0.7408
SVM-G 0.3952 0.4076 0.7270 0.4591 0.4594 0.7248 0.5267 0.3641 0.5799
Figure 3: Prediction accuracy by count of 2009 season.
Figure 4: Prediction accuracy by count of 2012 season.
4 CONCLUSIONS AND FUTURE
WORK
Originally our scheme developed from consideration
of the factors that affect pitching decisions. For ex-
ample, the pitcher/batter handedness matchup is often
mentioned by sports experts as an effect, and it was
originally included in our model. However, it was
discovered that implementing segmentation of data
based on handedness has essentially no effect on the
Table 4: Improvement over Naive Guess (percents)
Pitcher Improvement Classifier
Fuentes 12.81 k-NN
Madson 22.01 k-NN
Meche 47.39 SVM-L
Park 37.62 SVM-L
Rivera 0.04 k-NN
Vaquez 42.68 SVM-G
Wakefield 0.00 k-NN
Weathers 118.73 SVM-L
prediction results. Thus, handedness is no longer im-
plemented as a further splitting criterion of the model,
but this component remains a considered feature. In
general, unnecessary data segmentations have nega-
tive impact solely because it reduce the size of train-
ing and testing data for classifiers to work with.
Most notable is our method of feature selection
which widely varies the set of features used in each
situation. Features that yield strong prediction in
some situations fail to provide any benefit in others.
In fact, it is interesting to note that in the 2008/2009
prediction scheme, every feature is used in at least one
situation and no feature is used in every situation.
It is also interesting to note that the most suc-
cessful classification algorithm of this model is sup-
ported by our feature selection technique. In general,
Bayesian classifiers rely on a feature independence
assumption, which is realistically not satisfied. How-
ever, our model survives this assumption because al-
though the features within each of the 6 groups are
highly dependent across groups. Thus the features
which are ultimately chosen are highly independent.
The model represents a significant improvement
over simple guessing. It is a useful tool for batting
coaches, batters, and others who wish to understand
the potential pitching implications of a given game
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
524

Table 5: Prediction model results for additional years. Note that percentage improvement is calculated on a per-pitcher basis
and then averaged overall.
Train Year(s) Test Year Naive Guessing Accuracy Our Model Accuracy Improvement
2011 2012 62.72 75.20 24.82
2010 and 2011 2012 62.97 75.27 24.07
scenario. For example, batters could theoretically use
this model to increase their batting average, assuming
that knowledge about a pitch’s type makes it easier
to hit. The model, for example, is especially useful
in certain intense game scenarios and achieves accu-
racy as high as 90 percent. It is in these game en-
vironments that batters can most effectively use this
model to translate knowledge into hits. Additionally,
it is interesting to note that in 0-2 counts where naive
guessing is least accurate, our model performs rela-
tively well.
Looking forward, much can be done to improve
the model. First, new features would be helpful.
There is much game information that we did not in-
clude in our model, such as batting averages, slugging
percentage per batter, stadium location, weather, and
others, which could help improve the prediction ac-
curacy of the model. One potential modification is
extension to multi-class classification. Currently, our
model makes a binary decision and decides if the next
pitch will be a fastball or not. It does not determine
what kind of fastball the pitch may be. However, this
task is much more difficult and would almost certainly
result in a decrease in accuracy. Further, prediction is
not limited to only the pitch type. For example, one
could consider the prediction problem of determining
where the pitch will be thrown (for example, a spe-
cific quadrant). Or it may be possible to predict, if
in the given situation a hit were to occur, where the
ball is likely to land. That information could be use-
ful to prepare the corresponding defensive player for
the impending flight of the ball.
ACKNOWLEDGEMENTS
This research was conducted with support from
NSA grant H98230-12-1-0299 and NSF grants DMS-
1063010 and DMS-0943855. We would like to thank
Jessica Gronsbell for her useful advice and Mr. Tom
Tippett, Director of Baseball Information Services for
the Boston Red Sox, for meeting with us to discuss
this research and providing us with useful feedback.
Also we would like to thank Minh Nhat Phan for help-
ing us scrape the PITCH f/x data.
REFERENCES
Fawcett, T. (2006). An introduction to ROC analysis. Pat-
tern recognition letters, 27(8):861–874.
Ganeshapillai, G. and Guttag, J. (2012). Predicting the next
pitch. In MIT Sloan Sports Analytics Conference.
Hopkins, T. and Magel, R. (2008). Slugging percentage
in differing baseball couns. Journal of Quantitative
Analysis in Sports, 4(2):1136.
MATLAB (2013). MATLAB documentation.
MLB (2012). Major league baseball attendance
records. Retrieved June 19, 2013 from htt p :
//espn.go.com/mlb/attendance/
/
year/2012.
Pitchf/x (2013). MLB pitch f/x data. Retrieved July, 2013
from htt p : //www.mlb.com.
SVM (2013). Support vector machines explained. Retrieved
July 3, 2013 from htt p : //www.tristan f letcher.co.uk.
Theodoridis, S. and Koutroumbas, K. (2009). Pattern
recognition, fourth edition. Academic Press, Burling-
ton, Mass., 4th edition.
Weinstein-Gould, J. (2009). Keeping the hitter off balance:
Mixed strategies in baseball. Journal of Quantitative
Analysis in Sports, 5(2):1173.
Wikipedia (2013). Wikipedia glossary of base-
ball. Retrieved July, 2013 from htt p :
//en.wikipedia.org/wiki/Glossary − o f − baseball.
APPENDIX
Generic (Original) Features
The original 18 useful features from the raw data.
1. At-bat-number: number of pitches recorded
against a specific batter.
2. Outs: number of outs during an at-bat.
3. Batter’s I.D.
4. Pitcher’s I.D.
5. Pitcher Handedness: pitching hand of pitcher, i.e
R = Right, L = Left.
6. Pitch-event: outcome of one pitch from the
pitcher’s perspective (ball, strike, hit-by-pitch,
foul, in-play, etc.)
7. Hitter-event: outcome of the at-bat from the
batter’s perspective (ground-out, double, single,
walk, etc.
8. Outcome.
ApplyingMachineLearningTechniquestoBaseballPitchPrediction
525

9. Pitch-type: classification of pitch type, i.e FF =
Four-seam Fastball, SL = Slider, etc.
10. Time-and-date
11. Start-speed: pitch speed, in miles per hours, mea-
sured from the initial position.
12. x-position: horizontal location of the pitch as it
crosses the home plate.
13. y-position: vertical location of the pitch as it
crosses the home plate.
14. On-first: binary column; display 1 if runner on
first, 0 otherwise.
15. On-second: binary column; display 1 if runner on
third, 0 otherwise.
16. On-third: binary column; display 1 if runner on
third, 0 otherwise.
17. Type-confidence: a rating corresponding to the
likelihood of the pitch type classification.
18. Ball-strike: display either ball or strike (not al-
ways clear from pitch-event).
Additional Features
From the original features above, we create the fol-
lowing features.
1. Inning
2. Lifetime percentage of fastballs thrown by pitcher
3. Previous 3 pitches: averages of horizontal and
vertical positions
4. Previous 3 pitches in specific count: horizontal
and vertical position averages
5. Player on first base, second base, and third base
(boolean)
6. Percentage of fastballs historically thrown to bat-
ter
7. Percentage of fastballs thrown in batter’s previous
at bat
8. Numeric score of result from previous meeting of
current pitcher and batter
9. Previous 3 pitches: fastball and nonfastball
combo, ball and strike combo
10. Previous 3 pitches in specific count: fastball and
nonfastball combo, ball and strike combo
11. Weighted base score
12. Velocity of previous pitch
13. Previous pitch in specific count: velocity
14. Percentage of fastballs over previous 5, 10, 15,
and 20 pitches
15. Number of base runners
16. Horizontal position of previous pitch thrown
17. Previous pitch in specific count: horizontal posi-
tion
18. Time (day/afternoon/night)
19. Vertical position of previous pitch thrown
20. Previous pitch in specific count: vertical position
21. Number of outs
22. Previous pitch: ball or strike (boolean)
23. Previous pitch in specific count: ball/strike
(boolean)
24. Percentage of fastballs thrown in last inning
pitched by pitcher
25. Previous pitch: pitch type
26. Previous pitch in specific count: pitch type
27. Percentage of fastballs over previous 5 pitches
thrown to specific batter
28. Strike result percentage (SRP) (a metric we cre-
ated that measures the percentage of strikes from
all pitches in the given situation) of fastballs
thrown in the previous inning
29. Previous pitch: fastball of nonfastball (boolean)
30. Previous pitch in specific count: fast-
ball/nonfastball (boolean)
31. Percentage of fastballs over previous 10 pitches
thrown to specific batter
32. SRP of nonfastballs thrown in previous inning
33. Previous 2 pitches: average of velocities
34. Previous 2 pitches in specific count: velocity av-
erage
35. Percentage of fastballs over previous 15 pitches
thrown to specific batter
36. Percentage of fastballs thrown in the previous
game pitched by pitcher
37. Previous 2 pitches: average of horizontal posi-
tions
38. Previous 2 pitches in specific count: horizontal
position average
39. Percentage of fastballs over previous 5 pitches
thrown in specific count
40. SRP of fastballs thrown in previous game
41. Previous 2 pitches: average of vertical positions
42. Previous 2 pitches in specific count: vertical posi-
tion average
43. Percentage of fastballs over previous 10 pitches
thrown in specific count
44. SRP of nonfastballs thrown in previous game
45. Previous 2 pitches: ball/strike combo
46. Previous 2 pitches in specific count: ball strike
and combo
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
526

47. Percentage of fastballs over previous 15 pitches
thrown in specific count
48. Percentage fastballs thrown in previous at bat
49. Previous 2 pitches: fastball/nonfastball combo
50. Previous 2 pitches in specific count: fastball and
nonfastball combo
51. SRP of previous 5 fastballs to specific batter
52. Numeric score for last at bat event
53. Previous 3 pitches: average of velocities
54. Previous 3 pitches in specific count: velocity av-
erage
55. SRP of previous 5 nonfastballs to specific batter
56. Batter handedness (boolean)
57. Cartesian quadrant for previous pitch
58. Cartesian quadrant average for previous 2 pitches
59. Cartesian quadrant average for previous 3 pitches
60. Fastball SRP over previous 5, 10, and 15 pitches
61. Nonfastball SRP over previous 5, 10, and 15
pitches
62. Cartesian quadrant for previous pitch in specific
count
63. Cartesian quadrant average for previous 2 pitches
in specific count
64. Cartesian quadrant average for previous 3 pitches
in specific count
Baseball Glossary and Info
Most of these definitions are obtained directly from
(Wikipedia, 2013).
1. Strike Zone: A box over the home plate which
defines the boundaries through which a pitch must
pass in order to count as a strike when the batter
does not swing. A pitch that does not cross the
plate through the strike zone is a ball.
2. Strike: When a batter swings at a pitch but fails to
hit it, when a batter does not swing at a pitch that
is thrown within the strike zone, when the ball is
hit foul and the strike count is less than 2 (a batter
cannot strike out on a foul ball, however he can
fly out), when a ball is bunted foul, regardless of
the strike count, when the ball touches the batter
as he swings at it, when the ball touches the batter
in the strike zone, or when the ball is a foul tip.
Three strikes and the batter is said to have struck
out.
3. Ball: When the batter does not swing at the pitch
and the pitch is outside the strike zone. If the bat-
ter accrues four balls in an at bat he gets a walk, a
free pass to first base.
4. Hit-By-Pitch: When the pitch hits the batters
body. The batter gets a free pass to first base, sim-
ilar to a walk.
5. Hit: When the batter makes contact with the pitch
and successfully reaches first, second or third
base. Types of hits include single (batter ends at
first base), doubles (batter ends at second base),
triple (batter ends at third base) and home-run.
6. Out: When a batter or base runner cannot, for
whatever reason, advance to the next base. Exam-
ples include striking out (batter can not advance to
first), grounding out, popping out and lining out.
7. Count: Is the number of balls and strikes during
an at bat. There are 12 possible counts spanning
every combination of 0-3 balls (4 balls is a walk)
and 0-2 strikes (3 strikes is a strikeout).
8. Run: When a base runner crosses home plate.
This is a point for that player’s team. The out-
come of a baseball game is determined by which
team has more runs at the end of nine Innings.
9. Inning: One of nine periods of playtime in a stan-
dard game.
10. Slugging Percentage: A measure of hitter power.
Defined as the average number of bases the hitter
earns per at bat.
11. Batting Average: The percentage of time the bat-
ter earns a hit.
12. At Bat : A series of pitches thrown by the pitcher
to one hitter resulting in a hit, a walk, or an out.
Classification Methods
Here we list the classifiers used in the experiment. For
more information about these classification methods,
consult the cited reference.
1. k-NN(s): k-nearest-neighbors algorithm (MAT-
LAB: knnsearch) with standardized Euclidean
distance metric (MATLAB, 2013).
2. SVM-L: Support Vector Machine with linear ker-
nel (SVM, 2013)
3. SVM-G: Support Vector Machine with RBF
(Gaussian) kernel (SVM, 2013)
ApplyingMachineLearningTechniquestoBaseballPitchPrediction
527
