
Handling Weighted Sequences Employing Inverted Files and Suffix Trees
Klev Diamanti
1
, Andreas Kanavos
2
, Christos Makris
2
and Thodoris Tokis
2
1
Science for Life Laboratory, Department of Cell and Molecular Biology, Uppsala University, Sweden
2
Department of Computer Engineering and Informatics, University of Patras, Greece
Keywords:
Searching and Browsing, Web Information Filtering and Retrieval, Text Mining, Indexing Structures, In-
verted Files, n-gram Indexing, Sequence Analysis and Assembly, Weighted Sequences, Weighted Suffix Trees.
Abstract:
In this paper, we address the problem of handling weighted sequences. This is by taking advantage of the
inverted files machinery and targeting text processing applications, where the involved documents cannot
be separated into words (such as texts representing biological sequences) or word separation is difficult and
involves extra linguistic knowledge (texts in Asian languages). Besides providing a handling of weighted
sequences using n-grams, we also provide a study of constructing space efficient n-gram inverted indexes.
The proposed techniques combine classic straightforward n-gram indexing, with the recently proposed two-
level n-gram inverted file technique. The final outcomes are new data structures for n-gram indexing, which
perform better in terms of space consumption than the existing ones. Our experimental results are encouraging
and depict that these techniques can surely handle n-gram indexes more space efficiently than already existing
methods.
1 INTRODUCTION
In this paper we focus on handling weighted se-
quences (Makris and Theodoridis, 2011). The diffe-
rence between weighted sequences and regular strings
is that in the former, we permit in each position the
appearance of more than one character, each with a
certain probability (Makris and Theodoridis, 2011).
Specifically, a weighted word w = w
1
w
2
· · · w
n
is a
sequence of positions, where each position w
i
consists
of a set of couples; each couple has the form (s, π
i
(s)),
where π
i
(s) is the probability of having the character
s at position i. Also, for every position w
i
, 1 ≤ i ≤ n,
∑
π
i
(s) = 1. Moreover, it is usually assumed that a
possible subword is worth the effort to be examined if
the probability of its existence is larger than 1/k; with
k being a user defined parameter. In order to han-
dle weighted sequences the Weighted Suffix Tree data
structure was implemented (Iliopoulos et al., 2006).
We consider this specific data strusture as a proper
suffix tree generalization.
The novelty in our approach is that for the first
time, we exploit inverted files and n-grams in the han-
dling of weighted sequences, thus providing an inter-
esting alternative to weighted suffix trees for a variety
of applications that involve weighted sequences. Our
approach is interesting since it offers interesting al-
ternatives to approaches using suffix arrays and suffix
trees with inverted files. This lacked in the bibliog-
raphy in contrast to traditional pattern search appli-
cations such as in search engines where both alter-
natives were offered (see for example (Puglisi et al.,
2006)). We do not delve into details of various pat-
tern matching operations but merely focus on how to
space efficiently transform weighted sequences into
normal and then handle them using the well known
technique of n-grams. Our target is not only at bio-
logical, but also at natural language applications. n-
grams are sequences of consecutive text elements (ei-
ther words or symbols); they are widely used in In-
formation Retrieval (Ogawa and Iwasaki, 1995), (Lee
and Ahn, 1996), (Navarro and Baeza-Yates, 1998),
(Millar et al., 2000), (Navarro et al., 2000), (Navarro
et al., 2001), (Gao et al., 2002), (Mayfield and Mc-
Namee, 2003), (Kim et al., 2007), (Yang et al., 2007),
especially in applications employing text that cannot
be separated into words.
The indexes produced with the n-gram inverted in-
dex technique, have a number of advantages. One of
them is that they work on any kind of sequences, even
if the sequence consists of words which have no prac-
tical meaning, such as DNA and protein sequences.
Moreover, the n-gram technique is language neutral
since it can be applied on different languages. Ano-
231
Diamanti K., Kanavos A., Makris C. and Tokis T..
Handling Weighted Sequences Employing Inverted Files and Suffix Trees.
DOI: 10.5220/0004788502310238
In Proceedings of the 10th International Conference on Web Information Systems and Technologies (WEBIST-2014), pages 231-238
ISBN: 978-989-758-024-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ther major benefit is that this indexing method is error-
tolerant, putting up with errors that occur during the
construction of the index; this is as it uses for its con-
struction, the 1-sliding technique.
Nevertheless, the n-gram inverted index has also
some drawbacks; the size tends to be very large and
the performance of queries tends to be inefficient.
This is the reason why a wide amount of research on
how to use this technique space efficiently has been
performed (Kim et al., 2005), (du Mouza et al., 2009),
(Tang et al., 2009).
In (Kim et al., 2005), an efficient method for con-
structing a two-level index is proposed. Specifically,
this method reduces significantly the size of the in-
dex and improves the query performance when com-
paring to the straightforward n-gram inverted index
technique; while preserving all the advantages of the
n-gram inverted index. This technique extracts sub-
strings of fixed length m from the original sequence
and then applies the classic n-gram technique on each
of those extracted substrings. As shown in (Kim et al.,
2005), this technique can provide significant space
improvements, but as it can be observed in our ex-
perimental results, when the original sequence is not
enough repetitive, the performance of this two-level
indexing technique deteriorates.
In detail, we propose three new techniques for
handling weighted sequences using n-grams index-
ing. We additionally propose a new framework for
space compaction aiming to face the aforementioned
space shortcomings of (Kim et al., 2005). In our
space efficient framework, instead of resorting to the
two-level indexing scheme, we judiciously select a set
of substrings of the initial sequences for the n-grams
of which, we employ the two-level indexing scheme;
while for the rest of them, we employ the straightfor-
ward one-level indexing scheme. The substrings are
selected based on the frequency of their appearance
in the whole document set. Also, the length of sub-
strings covering the initial sequence as well as the two
distinct variants of the algorithmic scheme (variant for
selecting these substrings employing a forest of suffix
trees and a variant for the generalized suffix tree) are
implemented and tested. It should be noted that these
generalized suffix trees are the weighted suffix trees
derived from the initial set of weighted sequences.
What is more, experiments on both synthetic and
real data are performed in order to validate the perfor-
mance of our constructions and the space reduction
that they offer. Our work can be considered both an
experimental research for the weighted sequences as
well as a survey for validating the space efficiency of
newly and previously proposed constructions in the
area of n-gram indexing.
The rest of the paper is organized as follows. In
section 2, the related work as well as the contribution
is presented. In section 3, we present the techniques
for handling weighted sequences. Subsequently, in
section 4, we describe our space compaction heuris-
tics. In following, section 5 presents a reference
to our experimental results. Finally, section 6 con-
cludes the paper and provides future steps and open
problems.
2 RELATED WORK AND
CONTRIBUTION
In (Christodoulakis et al., 2006), a set of efficient al-
gorithms for string problems, involving weighted se-
quences arising in the computational biology area,
were presented adapting traditional pattern matching
techniques to the weighted scenario. What is more, in
order to approximately match a pattern in a weighted
sequence, a method was presented in (Amir et al.,
2006) for the multiplicative model of probability esti-
mation. In particular, two different definitions for the
Hamming as well as for the edit distance, in weighted
sequences, were given. Furthermore, we should refer
to some more recent techniques (Zhang et al., 2010a),
(Zhang et al., 2010b), (Alatabbi et al., 2012), that be-
sides extending previous approaches, they also em-
ploy the Equivalence Class Tree for the problem at
hand. From these papers, special mentioning deserves
the work in (Zhang et al., 2010a), which generalizes
the approach in (Iliopoulos et al., 2006), so as to han-
dle effectively various approximate and exact pattern
matching problems in weighted sequences.
In addition, there is a connection with the pro-
babilistic suffix tree, which is basically a stochastic
model that employs a suffix tree as its index struc-
ture. This connection aims to represent compactly
the conditional distribution of probabilities for a set
of sequences. Each node of the corresponding proba-
bilistic suffix tree is associated with a probability vec-
tor that stores the probability distribution for the next
symbol, given the label of the node as the preceding
segment (Marsan and Sagot, 2000), (Sun et al., 2004).
In our work, we will mainly employ the pre-
processing techniques presented in (Iliopoulos et al.,
2006), where an efficient data structure for comput-
ing string regularities in weighted sequences was pre-
sented; this data structure is called Weighted Suffix
Tree. Our approach however can be also modified to
incorporate the techniques presented in (Zhang et al.,
2010a).
The main motivation for handling weighted se-
quences comes from Computational Molecular Bio-
WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies
232

logy. However, there are possible applications in
Cryptanalysis and musical texts (see for a discussion
but in this time for the related area of Indeterminate
Strings, which are strings having in positions, sets
of symbols, (Holub and Smyth, 2003), (Holub et al.,
2008)). In Cryptanalysis, undecoded symbols may
be modeled as set of letters with several probabili-
ties, while in music, single notes may match chords
or notes with several probabilities. In addition, our
representation of n-grams and our space compaction
heuristics are of general nature concerning the ef-
ficient handling of multilingual documents in web
search engines and general in information retrieval
applications.
Character n-grams are used especially in CJK
(Chinese, Japanese and Korean) languages, which by
nature cannot be easily separated into words. In these
languages, 2-gram indexing seems to work well. For
example in (Manning et al., 2008), it is mentioned
that in these languages, the characters are more like
syllables than letters and that most words are small in
numbers of characters; also, the word boundaries are
small and in these cases, it is better to use n-grams.
Moreover, n-grams are helpful in Optical Character
Recognition where the text is difficult to comprehend
and it is not possible to introduce word breaks. Ad-
ditionally, k-grams are useful in applications such as
wildcard queries and spelling correction.
3 ALGORITHMS
We initially describe the n-gram based techniques
for handling normal sequences, which are being pre-
sented in (Kim et al., 2005). Then we explain how
these can be adapted so that we can handle weighted
sequences. The algorithm proposed in (Kim et al.,
2005) tries to improve the straightforward inverted
file scheme that produces n-grams on the fly using a
sliding window; afterwards the algorithm stores them
in an inverted file by replacing it with a two-level
scheme, which is shown to be more space efficient.
In particular, this novel two-level scheme is based
on the following approach: (i) each of the initial se-
quences is processed and a set of substrings of length
m is extracted so as to overlap with each other by
n − 1 symbols, (ii) an inverted index (called back-
end index) for these substrings as well as the initial
sequence set, considering the substrings as distinct
words, are built, (iii) all the n-grams in each of the
substrings are extracted, (iv) an inverted index (called
front-index) is built, regarding the substrings as docu-
ments and the n-grams as words. This scheme, called
by its authors n-gram/2L, can be applied to any text
and in some cases, results to significant space reduc-
tion.
If the text can be partitioned into words (natural
language text), another scheme termed n-gram/2L-
v is provided. So, the subsequences are defined as
consecutive sequences of the text words, by exploi-
ting the intuitive remark that words exhibit repetitive-
ness in natural language text. Their experiments show
that when applied to natural text n-gram/2L-v, sample
space savings, compared to the initial technique, are
produced.
We attempt to adapt their techniques by present-
ing three algorithms for handling weighted sequences,
which are based in the exploitation of the technique
presented in (Kim et al., 2005); then we can adjust
them to the problem at hand.
3.1 1st Technique - Subsequences
Identification
In the first technique, we form separate sequences as
we split each weighted sequence into weighted sub-
strings; each one of length m. Each one of these
weighted substrings is used to produce normal sub-
strings by employing the normal substrings gene-
ration phase of (Iliopoulos et al., 2006) (p.267, algo-
rithm 2). In this phase, the generation of a substring
stops when its cumulative possibility has reached the
1/k threshold. The cumulative possibility is calcu-
lated by multiplying the relative probabilities of ap-
pearance of each character in every position. Each
produced substring is of maximum size m and for
every substring, we produce all the possible n-grams.
After this procedure, we store all the produced n-
grams in the n-gram/2L-v scheme.
Concerning the generation phase, all the positions
in the weighted sequences are thoroughly scanned
and at each branching position, a list of possible sub-
strings, starting from this position, is created. Then
moving from left to right, the current subwords are
extended by adding the same single character when-
ever a non-branching position is encountered; in con-
trast there is also a creation of new subwords at bran-
ching positions where potentially many choices are
supplied.
3.2 2nd Technique - On the fly n-grams
Identification
This technique is much simpler as we don’t need to
deploy all the generic sequences. Unlike the previous
technique, we just need to produce all the possible
n-grams and in following for each report, its corre-
sponding weighted sequences as well as their offsets.
HandlingWeightedSequencesEmployingInvertedFilesandSuffixTrees
233

As a matter of fact, we don’t have to form separate se-
quences, as in the previous approach, but instead only
split each generalized sequence into segments, each
of size m, and for each segment, just produce the re-
quested n-grams.
Hence, this particular scheme is by nature one-
level and we propose its use due its simplicity. Ho-
wever, as it will be highlighted in the experiments,
there are cases when the technique outperforms the
previous one in terms of space complexity.
4 SPACE EFFICIENT INVERTED
FILE IMPLEMENTATIONS FOR
NORMAL SEQUENCES
Our crucial remark is that, in order for the n-gram/2L
technique to provide space savings, the substrings,
where the initial sequences are separated, should ap-
pear a large number of times and should cover a broad
extent of the initial sequences, otherwise in case this
does not apply (e.g. if there is a large number of
unique substrings), then the space occupancy turns
out to increase instead of shrinking.
Hence, it would be preferable to use a hybrid
scheme instead of a two-level one; there we should
extract from the initial sequences, substrings that ap-
pear repetitively enough and cover a large extent of
the initial sequences. In following, for the specific
substrings, we will employ a two-level scheme; while
for the remaining parts of the sequences, we will use
the straightforward one-level representation. During
this separation, we elongate each selected substring
by n-1, as in (Kim et al., 2005).
So, as to achieve our goal and build a hybrid one
and two-level inverted index, we introduce three tech-
niques:
4.1 One Simple Technique
A variant of the algorithm described in (Kim et al.,
2005), called Hybrid indexing Algorithm version 0 -
hybrid(0), is implemented. In this implementation,
we decided to store the substrings of length m and of
a number of occurrences in the back-end inverted file
of the two-level scheme; provided that this number is
greater than a trigger. The user is asked to provide the
value of the trigger; the trigger is set equal to 1, for
the results presented in the corresponding section.
The substrings, occuring less or equal to the pro-
vided trigger, are just decomposed in their n-grams
and then saved in a one-level index. The substrings
stored in the two-level scheme, are also decomposed
in their n-grams, which we forward to the front-end
index of the two-level scheme.
4.2 Two Techniques based on Suffix
Trees
In these techniques, we locate substrings that (in con-
trast to hybrid(0)) can be of varying size, highly repe-
titive and cover a large extent of the initial sequences.
So as to locate them, we employ suffix trees (Mc-
Creight, 1976) that have been previously used in si-
milar problems (Gusfield, 1997) of locating frequent
substrings. In particular, we provide two different
variants in the implementation of our space efficient
heuristic schema. Those two distinct versions share a
common initial phase, while differing in their subse-
quent workings.
More analytically, we insert all the sequences in
a generalized suffix tree as described in (Gusfield,
1997) and in following we use this tree for counting
the repetitions of each substring of the stored docu-
ments. Note that if the sequences have been produced
by using mappings from weighted sequences, then the
produced suffix tree is similar to the weighted suffix
tree of the initial sequences. This operation is per-
formed during the building of the generalized suffix
tree; after that, each node of the tree keeps the in-
formation concerning the repetitions of the substrings
stored in it.
Subsequently, in each repetition, our algorithm
chooses a substring and a subset of each occurrence.
These two objects are in following included in the
two-level index. The selection procedure is described
as follows:
1. The substring needs to have a length equal or
greater than s; s is the least acceptable length of
a substring and constitutes a user defined parame-
ter at the start of the algorithm’s execution.
2. The substring has to be highly repetitive. This
means that it should have more than a specific
number of occurrences (trigger) in the set of in-
dexed documents; this trigger is also a user de-
fined parameter.
3. The appearances of the selected substring, which
are to be included in the two-level index, should
not overlap in more than half the length of the
subsequence; i.e. if the substring has a length
of 10 characters, consecutive appearances of this
substring should not overlap on more than 5 cha-
racters. By setting this criterion, we keep only the
discrete appearances of the selected substring.
After the end of the procedure, we have selected a
collection of substrings. We then sort this collection
WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies
234

Figure 1: Visualizing hybrid(1) and hybrid(2) techniques.
based on the total length of the original sequences that
the distinct occurrences cover (according to criterion
3). Furthermore, we select as best the occurrences
of specific subsequence that cover the majority of the
length of the initial sequences. We extract all these
substrings from the initial sequences, thus including
them in the two-level index. As a result, we have split
the initial sequences into a set of partitions that are
not included in the two-level index. Next, we elongate
them by n − 1, so as not to miss any n-gram; where n
is the n-gram length. Finally, we keep all these elon-
gated substrings in a list. As a result, we have per-
fomed the preprocessing step that allows us to follow
one out of two methods described below (see the pro-
cedure in Fig. 1):
(i) Hybrid Indexing Algorithm version 1 - hy-
brid(1). We construct for each elongated substring,
a separate suffix tree and process best utilizing the
same method as above. Then, our algorithm continues
executing the process for each suffix tree constructed
as cited above. This process is repeated as many times
as the user chooses at the beginning of the algorithm
execution.
(ii) Hybrid Indexing Algorithm version 2 - hy-
brid(2). We include all elongated substrings men-
tioned in a unified generalized suffix tree. In follo-
wing, our algorithm executes the process for the ge-
neralized suffix tree constructed. This process is re-
peated as many times as requested. Generally, the
more recursions we made, the better results we had;
however, because of the limited system resources, we
opted for 50 recursions in our experiments.
5 EXPERIMENTS
5.1 Experimental Setting
In our experiments, we used random weighted se-
quences to test our n-gram mapping techniques as
well as one file (of size 1 GB) containing Protein data
and DNA data to test our space compaction heuris-
tics. We also performed experiments with 10MB and
100MB with similar results. Due to lack of space,
only figures and comments from the 1GB data are pre-
sented in the main body of the article. Our experimen-
tal data were downloaded from the NCBI databases
(ftp://ftp.ncbi.nih.gov/genomes/). Furthermore, we
use initials to designate both m (length of substrings)
as well as the parameter s (size in bytes) in our space
compaction heuristics.
The computer system, where the experiments
were performed, was an Intel Core i5-2410M 2.3
GHz CPU with a 3GB (1x1GB and 1x2GB in 2xDual
Channel) RAM. The techniques we implemented and
applied on the experimental data mentioned above,
were:
1. Weighted Sequences Identification:
(i) Subsequences Identification,
(ii) On the fly n-grams Identification and
(iii) Offline Identification.
2. Space compaction heuristics:
(i) One-Level Inverted File (using the classic
straightforward technique),
(ii) Two-Level Inverted File (using the technique
in (Kim et al., 2005)),
(iii) Hybrid Inverted File using the Simple Tech-
nique - hybrid(0),
(iv) Hybrid Inverted File with separate suffix trees
- hybrid(1) and
(v) Hybrid Inverted File with a unified generalized
suffix tree - hybrid(2).
For our space compaction heuristics, we run all
techniques proposed in this paper (hybrid(0), hy-
brid(1) and hybrid(2)) in order to identify the most
space efficient solution available. So as to depict the
space compaction effectiveness of our approach, we
tried our approach on real data of significant size and
performed several experiments. As the experiments
show, our approach outstandingly reduces the space
complexity and stands by itself as a considerable im-
provement.
5.2 Weighted Sequences Results
As is depicted in Fig. 2, the offline approach is the
worst in the attained space complexity, as expected.
HandlingWeightedSequencesEmployingInvertedFilesandSuffixTrees
235
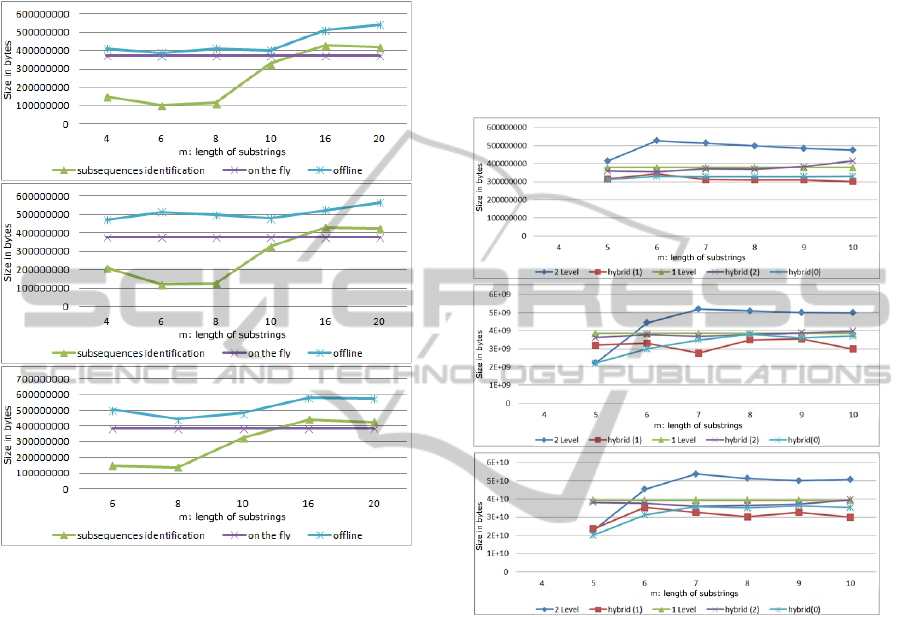
The reason is because all possible combinations of se-
quences are produced; not only those that are needed
by the two-level scheme. On the other hand, the of-
fline approach is more flexible since it can incorporate
different values of variables n and s.
Figure 2: Weighted Sequences 10MB for varying size of s
(a) n=2, (b) n=3 and (c) n=4.
With regards to the other two techniques, the on
the fly approach is the most robust and stable in per-
formance due to its fixed algorithmic behavior when
handling every possible input. The identification of
the subsequences, although better for small values of
s, behaves worse for larger values. This can be at-
tributed to the shortage of repetitions; being a vital
ingredient of the success of this method’s heuristic,
when the value of s is increasing.
5.3 Protein Data Results
In the performed experiments, we never needed to
make more than 50 recursions, as by this number we
got the best possible results from the index method.
Moreover, we ran experiments of substrings that have
length from 4 to 10, in order to demonstrate the im-
provements that the two-level technique produces to
the inverted file size.
Our hybrid(2) technique seems to be not as effi-
cient as hybrid(1) is. Although, it theoretically con-
siders the high repetitive sequence more efficiently
than the hybrid(1) technique, it does not seem to have
satisfactory results. A probable explanation could be
that using separate suffix trees, this method permits
more choices in the sequences that will be selected
for separate indexing than the Generalized suffix tree;
the latter demands the selection of the same substring
across different substrings. Furthermore, the tech-
nique is sensitive to the number of performed recur-
sions and needs a vast number of them to work effec-
tively.
Figure 3: Protein Data 1GB for varying size of s (a) n=2,
(b) n=3 and (c) n=4.
Another finding is that hybrid(0) technique is
quite similar to the two-level technique for substrings
with length 4 and 5 and after that, it is not as efficient
as our hybrid(1) technique. This behavior can be ex-
plained from the fact that this technique always takes
advantage of the positive characteristics of the two-
level techniques as long as it is better than one-level;
otherwise it resorts to the one-level.
Generally, in Protein data, our methods achieve
better results due to the fact that they take advan-
tage of the repetitiveness of the initial sequence even
when the number of the repetitions is quite low. This
is something that does not hold for the two-level
scheme, where the performance is clearly degraded.
5.4 DNA Data Results
In the results shown below, the maximum number of
recursions made, was fixed to 50 for each experiment.
WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies
236

In case of DNA data, we experimented for substrings
that have length from 4 to 13. We examined more
substring sizes so as to clarify the inefficiency of the
two-level technique when the repetitiveness becomes
lower. It is obvious that the two-level technique in-
creases the inverted file size produced, when the sub-
string length becomes larger than 11.
Analyzing the results presented in figure with
DNA data results, we can patently see that our hy-
brid(1) technique is not as efficient as the two-level
index. The reason for this inefficiency is that two-
level index takes advantage of the substrings of length
from 6 to 11, which seems to be highly repetitive in
the DNA sequences examined. As soon as the size
of the substring becomes lower than 6 or larger than
11, our method becomes obviously better. This oc-
curs because the DNA data file used, is not so highly
repetitive for subsequences of length <6 or >11.
Figure 4: DNA Data 1GB for varying size of s (a) n=2, (b)
n=3 and (c) n=4.
In cases when two-level technique performs bet-
ter than hybrid(1), we use hybrid(0) to store our data.
Hybrid(0) performs very similarly to two-level tech-
nique. The differences between the files produced by
those two techniques are considered to be negligible.
The reason why this phenomenon appears is due to
the highly repetitive nature of DNA data (the limited
alphabet) on limited size sequences.
As for our hybrid(2) method, we can clearly see
that this method seems to be inefficient, and works
worse than hybrid(1); this was something that was
also noted in Protein data and can be explained in a
similar way as previously mentioned. Perhaps a bet-
ter tuning of the involved algorithmic parameters and
a combination with hybrid(1) would result in a more
efficient scheme; but this is left as future work.
By choosing hybrid(0) or hybrid(1) techniques to
save the DNA data in inverted indexes, we are led to
very compact inverted file sizes. These sizes gener-
ally outperform or at least approximate the two-level
index efficacy.
In conclusion, our experiments clearly prove that
our techniques can significantly reduce space comple-
xity by handling n-gram indexes and can also stand as
considerable improvements.
6 GENERAL CONCLUSIONS
AND FUTURE WORK
In this article we presented a set of algorithmic tech-
niques for efficiently handling weighted sequences by
using inverted files. Also, these methods deal effec-
tively with weighted sequences using the n-gram ma-
chinery. Three techniques, which act as alternatives
to other techniques that mainly use suffix trees, were
presented. We furthermore completed our discussion
by presenting a general framework that can be em-
ployed so as to reduce the space complexity of the
two-level inverted files for n-grams.
In the future, we intend to experiment with var-
ious inverted file intersection algorithms (Culpepper
and Moffat, 2010), in order to test the time effi-
ciency of our scheme when handling such queries. We
could perhaps incorporate some extra data structures
as those in (Kaporis et al., 2003) as a well thought
out plan. Last but not least, we also plan to apply our
technique to natural language texts.
ACKNOWLEDGEMENTS
This research has been co-financed by the European
Union (European Social Fund - ESF) and Greek na-
tional funds through the Operational Program ”Edu-
cation and Lifelong Learning” of the National Strate-
gic Reference Framework (NSRF) - Research Fund-
ing Program: Thales. Investing in knowledge society
through the European Social Fund.
REFERENCES
Alatabbi, A., Crochemore, M., Iliopoulos, C. S., and
Okanlawon, T. A. (2012). Overlapping repetitions
HandlingWeightedSequencesEmployingInvertedFilesandSuffixTrees
237

in weighted sequence. In International Information
Technology Conference (CUBE), pp. 435-440.
Amir, A., Iliopoulos, C. S., Kapah, O., and Porat, E. (2006).
Approximate matching in weighted sequences. In
Combinatorial Pattern Matching (CPM), pp. 365376.
Christodoulakis, M., Iliopoulos, C. S., Mouchard, L.,
Perdikuri, K., Tsakalidis, A. K., and Tsichlas, K.
(2006). Computation of repetitions and regularities of
biologically weighted sequences. In Journal of Com-
putational Biology (JCB), Volume 13, pp. 1214-1231.
Culpepper, J. S. and Moffat, A. (2010). Efficient set inter-
section for inverted indexing. In ACM Transactions
on Information Systems (TOIS), Volume 29, Article 1.
du Mouza, C., Litwin, W., Rigaux, P., and Schwarz, T. J. E.
(2009). As-index: a structure for string search using
n-grams and algebraic signatures. In ACM Conference
on Information and Knowledge Management (CIKM),
pp. 295-304.
Gao, J., Goodman, J., Li, M., and Lee, K.-F. (2002). Effi-
cient set intersection for inverted indexing. In ACM
Transactions on Asian Language Information Pro-
cessing, Volume 1, Number 1, pp. 3-33.
Gusfield, D. (1997). Algorithms on Strings, Trees and Se-
quences: Computer Science and Computational Bio-
logy. Cambridge University Press.
Holub, J. and Smyth, W. F. (2003). Algorithms on indeter-
minate strings. In Australasian Workshop on Combi-
natorial Algorithms.
Holub, J., Smyth, W. F., and Wang, S. (2008). Fast pattern-
matching on indeterminate strings. In Journal of Dis-
crete Algorithms, Volume 6, pp. 37-50.
Iliopoulos, C. S., Makris, C., Panagis, Y., Perdikuri, K.,
Theodoridis, E., and Tsakalidis, A. K. (2006). The
weighted suffix tree: An efficient data structure for
handling molecular weighted sequences and its appli-
cations. In Fundamenta Informaticae (FUIN), Volume
71, pp. 259-277.
Kaporis, A. C., Makris, C., Sioutas, S., Tsakalidis, A. K.,
Tsichlas, K., and Zaroliagis, C. D. (2003). Improved
bounds for finger search on a ram. In ESA, Volume
2832, pp. 325-336.
Kim, M.-S., Whang, K.-Y., and Lee, J.-G. (2007). n-
gram/2l-approximation: a two-level n-gram inverted
index structure for approximate string matching. In
Computer Systems: Science and Engineering, Volume
22, Number 6.
Kim, M.-S., Whang, K.-Y., Lee, J.-G., and Lee, M.-J.
(2005). n-gram/2l: A space and time efficient two-
level n-gram inverted index structure. In Interna-
tional Conference on Very Large Databases (VLDB),
pp. 325-336.
Lee, J. H. and Ahn, J. S. (1996). Using n-grams for korean
text retrieval. In ACM SIGIR, pp. 216-224.
Makris, C. and Theodoridis, E. (2011). Algorithms in
Computational Molecular Biology: Techniques, Ap-
proaches and Applications. Wiley Series in Bioinfor-
matics.
Manning, C. D., Raghavan, P., and Schutze, H. (2008). In-
troduction to Information Retrieval. Cambridge Uni-
versity Press.
Marsan, L. and Sagot, M.-F. (2000). Extracting structured
motifs using a suffix tree - algorithms and application
to promoter consensus identification. In International
Conference on Research in Computational Molecular
Biology (RECOMB), pp. 210-219.
Mayfield, J. and McNamee, P. (2003). Single n-gram stem-
ming. In ACM SIGIR, pp. 415-416.
McCreight, E. M. (1976). A space-economical suffix
tree construction algorithm. In Journal of the ACM
(JACM), Volume 23, pp. 262-272.
Millar, E., Shen, D., Liu, J., and Nicholas, C. K. (2000).
Performance and scalability of a large-scale n-gram
based information retrieval system. In Journal of Dig-
ital Information, Volume 1, Number 5.
Navarro, G. and Baeza-Yates, R. A. (1998). A practical q-
gram index for text retrieval allowing errors. In CLEI
Electronic Journal, Volume 1, Number 2.
Navarro, G., Baeza-Yates, R. A., Sutinen, E., and Tarhio,
J. (2001). Indexing methods for approximate string
matching. In IEEE Data Engineering Bulletin, Volume
24, Number 4, pp. 19-27.
Navarro, G., Sutinen, E., Tanninen, J., and Tarhio, J. (2000).
Indexing text with approximate q-grams. In Combina-
torial Pattern Matching (CPM), pp. 350-363.
Ogawa, Y. and Iwasaki, M. (1995). A new character-
based indexing organization using frequency data for
japanese documents. In ACM SIGIR, pp. 121-129.
Puglisi, S. J., Smyth, W. F., and Turpin, A. (2006). Inverted
files versus suffix arrays for locating patterns in pri-
mary memory. In String Processing and Information
Retrieval (SPIRE), pp. 122-133.
Sun, Z., Yang, J., and Deogun, J. S. (2004). Misae: A new
approach for regulatory motif extraction. In Computa-
tional Systems Bioinformatics Conference (CSB), pp.
173-181.
Tang, N., Sidirourgos, L., and Boncz, P. A. (2009). Space-
economical partial gram indices for exact substring
matching. In ACM Conference on Information and
Knowledge Management (CIKM), pp. 285-294.
Yang, S., Zhu, H., Apostoli, A., and Cao, P. (2007). N-
gram statistics in english and chinese: Similarities and
differences. In International Conference on Semantic
Computing (ICSC), pp. 454-460.
Zhang, H., Guo, Q., and Iliopoulos, C. S. (2010a). An al-
gorithmic framework for motif discovery problems in
weighted sequences. In International Conference on
Algorithms and Complexity (CIAC), pp. 335-346.
Zhang, H., Guo, Q., and Iliopoulos, C. S. (2010b). Varieties
of regularities in weighted sequences. In Algorithmic
Aspects in Information and Management (AAIM), pp.
271-280.
WEBIST2014-InternationalConferenceonWebInformationSystemsandTechnologies
238
