A Controlled Study for Measuring Stress Induced Changes of Physiologic

Tremor with a Wearable Activity Sensor

udiger Zillmer, Brian Newby and Robert Treloar

Unilever R&D, Port Sunlight, Quarry Road East, Bebington CH63 3JW, U.K.

Keywords:

Activity Sensor, Accelerometer, Context Recognition, Emotional Stress, Tremor.

Abstract:

This work presents the results of a controlled study with the aim to quantify the effect of emotional stress

on physiologic tremor. A paced auditory addition test is utilized to induce emotional stress. The tremor is

measured by means of a wearable activity sensor (GENEA), were empirical mode decomposition is used to

extract the tremor signal. An autoregressive model and the fractal dimension of the signal are used to construct

tremor features. The result of an ANOVA test provides evidence that the stress condition increases the tremor

strength compared to the control. The observed changes of the spectral properties indicate that emotional stress

affects intentional tremor. These ﬁndings support the usage of wearable activity sensors for the investigation

of stress-related tremor changes and the evaluation of emotional context.

1 INTRODUCTION

At its simplest level, physiologic tremor can be said

to consist of two main components: mechanical and

centrally nervous driven (Elble, 1986; Hallet, 1998).

The contribution from each is still subject to de-

bate, and reported values in the literature concern-

ing this split may in part be due to the lack of stan-

dardization in experimental approach. Physiologic

tremor is present in everybody, but under particu-

lar conditions its amplitude may increase by over an

order of magnitude compared with standard physio-

logic tremor (Elble, 1986) which is referred to as en-

hanced physiologic tremor. Using an autoregressive

model and cross-spectral analysis it has been found

that enhanced tremor involves central structures (Tim-

mer et al., 2000). Factors which may instigate an

enhanced tremor state include fatigue, caffeine, and

stress.

Stress is an interesting context variable in the mea-

surement of human activity, as it affects the well-

being and the performance of the individual. Emo-

tional stress is usually assessed with the help of ques-

tionnaires. The quantiﬁcation of stress levels using

methods such as galvanic skin response, however, is

still a challenging task which requires high expertise

from the data analyst. With the advent of ubiquitous

computing, digital approaches have been tested which

involve mobile phone use patterns and speech analy-

sis (Lu et al., 2012). These methods allow the iden-

tiﬁcation of certain stress symptoms, while a quan-

tiﬁcation of stress levels is still elusive. Tremor, on

the other hand, is relatively easy to measure, as it is

well separated from the spectrum of voluntary move-

ments. The most commonly used objective measure-

ment techniques are accelerometry and Electromyog-

raphy (EMG) - or a combination of the two (Timmer

et al., 2000; Mansur et al., 2007; Godfrey et al., 2008).

In this paper we measure hand tremor by means of a

wearable accelerometer, and study the impact of emo-

tional stress on the tremor features. By means of be-

spoke processing and analysis methods we show that

the measurement of physiologic tremor by means of

wearable sensors promises to be an efﬁcient method

for the real-time assessment of emotional context.

2 THE STUDY

The most commonly used experimental approach to

measuring tremor is to record postural or resting

tremor using accelerometer sensors (Mansur et al.,

2007). This approach is adopted in the present study

which investigates the increase of the tremor ampli-

tude in healthy subjects exposed to emotional stress.

The study was designed as single blind study, ran-

domized with respect to a) the stress condition: a

paced auditory addition test (PASAT) (Tombaugh,

2006) and b) the control: listening to a piece of classi-

cal music (Rachmaninov adagios). The study design

178

Zillmer R., Newby B. and Treloar R..

A Controlled Study for Measuring Stress Induced Changes of Physiologic Tremor with a Wearable Activity Sensor.

DOI: 10.5220/0004789701780182

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 178-182

ISBN: 978-989-758-011-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

is summarized in Figure 1.

A total of 15 subjects (5 male and 10 female, age

25-35) with no pathologic tremor conditions were re-

cruited. All subjects were screened as per conﬁden-

tial medical questionnaire. During the test the pan-

ellist was seated, with the right arm placed on the

rest of their chair. The tremor response was mea-

sured by means of a 3-axis GENEA device attached

to the back of the subject’s hand. The GENEA is an

acceleration sensor developed by Unilever Discover

(Colworth, UK) which is now distributed by Activin-

sights Limited (Kimbolton, UK). The reliability and

performance of this sensor has been validated in sev-

eral studies (Esliger et al., 2011; Zhang et al., 2012).

The sensor is wireless, storing all measured data in a

ﬂash memory. Data download and initialization of the

sensor is accomplished by means of a bespoke hub.

During the exploratory analysis it was found that one

panellist is a potential outlier. An inspection of the

study records revealed that this panellist did not fol-

low the PASAT protocol - thus this panellist has been

removed from the subsequent analysis, leaving data

from 14 subjects (8 control, 6 intervention).

3 SIGNAL PROCESSING AND

FEATURE EXTRACTION

The accelerations were recorded with a sampling rate

of 80 Hz. For the following only the vertical acceler-

ation of the hand, a

, is considered. After smoothing

the signal by means of a moving average, the empiri-

cal mode decomposition (EMD) is used to extract the

tremor signal (see (de Lima et al., 2006)). Because

EMD employs an adaptive process to compute the

signal envelope, it is appropriate for the analysis of

nonstationary signals such as tremor. It is not a priori

clear which intrinsic mode functions (IMF) contain

the tremor signal. An inspection of the resulting fre-

quency spectra was used as a guide, whereupon it was

decided to use the sum of the ﬁrst two IMF as tremor

signal.

Typical tremor signals appear as noisy oscillations

with one or two dominating frequencies (see Fig. 2).

Such time series s(t) can be modelled by a damped

noise-driven oscillator model (Timmer et al., 2000).

To accomodate spectra with two peaks we adopt a 4th

order autoregressive model as follows:

s(t) = a

s(t − 1) + a

s(t − 2) + a

s(t − 3)

s(t − 4) + ξ(t) ;

(1)

where ξ(t) is the driving noise. A test using the partial

autocorrelation of the signals conﬁrmed the validity

of this model. The coefﬁcients a

reﬂect mechanical

properties of the hand and attached muscles, which is

not of interest here. The strength of the driving noise,

however, deﬁnes the amplitude of the tremorous oscil-

lations, which suggests to use the variance as measure

of the tremor strength:

SD = Var (ξ) . (2)

The noise variance is estimated by standard statistical

methods.

To measure changes of the tremor signal structure,

the fractal dimension FD for one dimensional time se-

ries can be used. This measure is related to the rough-

ness of the signal. The fractal dimension equals 1 for

smooth signals, however, for rough signals it takes

values between 1 and 2. It has been used success-

fully for the modelling and analysis of multi-scaled

random processes and ecological data (Halley et al.,

2004). A change of the fractal dimension may indi-

cate a change in the underlying mechanism of tremor

generation. For the computation of the fractal dimen-

sion we used the R package fractaldim, selecting the

madogram estimator (Gneiting et al., 2010).

4 RESULTS

Typical frequency (power) spectra of the tremor sig-

nal before and after the stress intervention are shown

in Figure 2 for the control and stress condition. The

effect of the the stress intervention is clearly visible,

resulting in an increase of the total power and an en-

hancement of lower frequencies around 6 Hz. In con-

trast, the control condition (listening to classical mu-

sic) leads to a reduction of the total power.

The effect of the stress intervention on the tremor

strength SD is compared with the control in the box-

plot Figure 3. Here SD

and SD

are the tremor

strength before (baseline) and after the intervention.

These results conﬁrm that the stress condition in-

creases the magnitude of SD, in contrast to the

control condition that tends to decrease the tremor

strength. In order to validate the effect of stress on

the tremor strength SD, ANOVA (analysis of vari-

ance) is used to quantify the difference between the

log-ratios log(SD

/SD

) of the stress and the con-

trol condition. The ANOVA, based on 1 and 12 de-

grees of freedom and F

1,12

= 8.34, results in a p-

value of 0.014, i.e., good evidence that the stress con-

dition indeed increases the strength of tremor. We

now consider the fractal dimension FD. As shown

in Figure 4, the stress condition leads to a decrease

of FD. Because the distributions of FD are slightly

skewed and have different variance for stress and con-

trol, we ﬁrst use the non-parametric Kruskal-Wallis

AControlledStudyforMeasuringStressInducedChangesofPhysiologicTremorwithaWearableActivitySensor

179

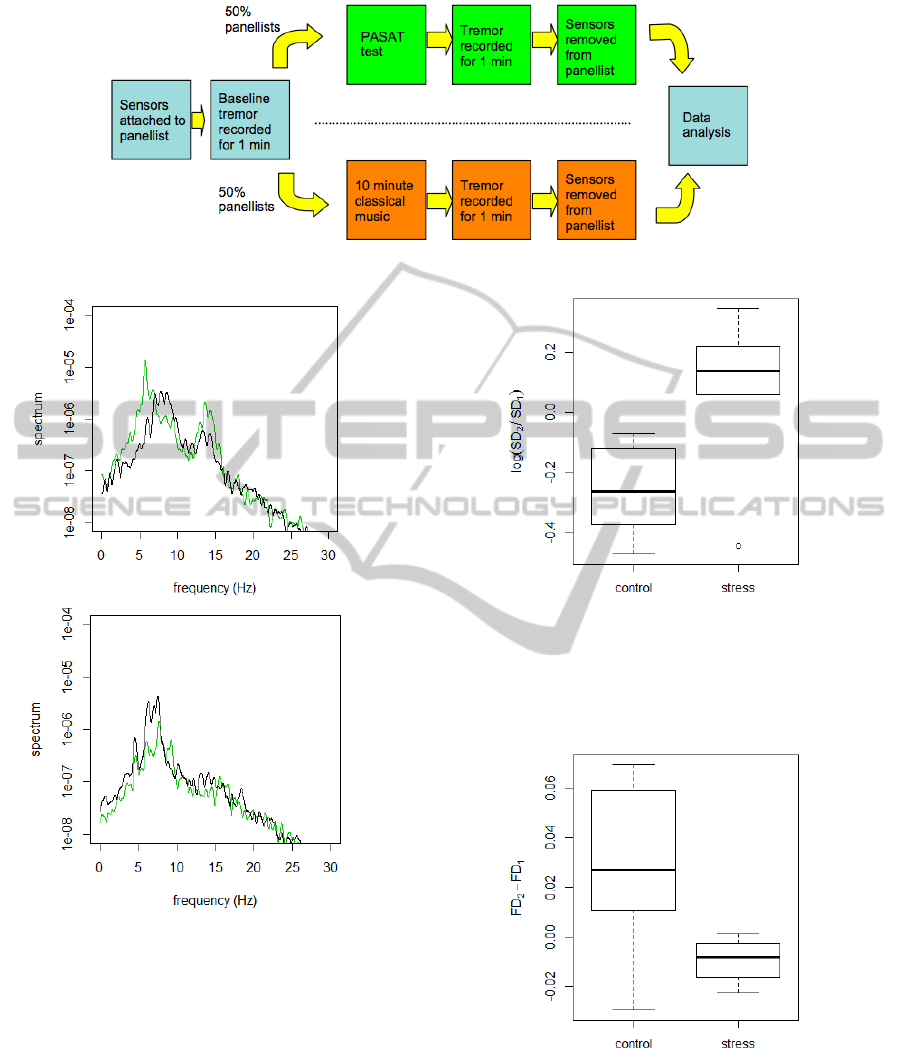
Figure 1: The design of the study to measure stress induced tremor.

Figure 2: The tremor frequency spectrum of a panellist who

was exposed to the stress (top panel) and control condition

(bottom panel). Shown is the spectrum before (black) and

after the intervention (green).

test (Kruskal and Wallis, 1952). The resulting statis-

tics are χ

= 4.82 on 1 degree of freedom and a p-

value of 0.028. Additionally we use Welch’s ANOVA

for unequal variances, which results in a p-value of

0.014. In summary, both methods give good evidence

that the stress condition decreases the roughness of

the tremor signal. It could be argued that the change

of the fractal dimension is related to changes of an

underlying low-dimensional dynamical system. In

order to test this hypothesis, signal surrogates were

Figure 3: Boxplot of the log-ratio, log(SD

/SD

), for the

control and stress (PASAT) condition. SD

and SD

are the

tremor strength before (baseline) and after the intervention.

The thick lines indicate the median while the lower and up-

per box edges indicate the 25th and the 75th percentile, re-

spectively.

Figure 4: Boxplot of the change of the fractal dimension for

the control and stress (PASAT) condition.

constructed by means of phase randomization. By

construction, the surrogates have the same frequency

spectrum as the original signal, while any dynamical

memory is removed by the randomisation step (Kantz

and Schreiber, 2005). The results for the surrogate

signals are shown in Figure 5. There is no signiﬁcant

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

180

Figure 5: Boxplot of the change of the fractal dimension as

computed from surrogate signals.

Figure 6: The average change of the normalised spectrum

for the control (black) and stress group (red).

change compared to Figure 4, which indicates that the

change of the signal roughness is related to changes of

a linear stochastic process (as modelled by Eq. (1)).

The decrease of the signal roughness should be re-

ﬂected in qualitative changes of the frequency spec-

tra. Indeed, as shown in Figure 2, the stress condition

leads to an increase of a low frequency peak around

6 Hz. To make this observation more precise, we

compute the average change of the spectrum as fol-

lows:

1. For each panellist compute the normalized spectra

and S

of the tremor signal before and after the

intervention, respectively.

2. Compute the average change of the log-spectrum,

mean[log(S

)], for the control and the stress

group.

The result shown in Figure 6 conﬁrms that the stress

condition enhances the power for low frequencies be-

tween 3-7 Hz.

5 CONCLUSIONS

We have presented the results of a controlled study

which investigates the change of physiologic tremor

as a result of emotional stress. Tremor was measured

by means of a wearable accelerometer attached to the

hand of the panellists. The stress group performed

an auditory addition test while the control group lis-

tened to classical music. To quantify the tremorous

oscillations we compute the strength of the driving

noise, estimated by an autoregressive model, and the

fractal dimension of the tremor signal. A comparison

of the signals recorded before and after the interven-

tion shows that stress leads to qualitative and quan-

titative changes of tremor. On the one hand, stress

increases the overall magnitude as measured by the

tremor strength. On the other, the fractal dimension

(roughness) of the signal decreases as a result of the

stress condition. Statistical tests conﬁrm the validity

of the observed changes. A test with surrogate sig-

nals shows that the change of the roughness can be

explained by parameter changes of a linear stochastic

process. The inspection of the change in the average

spectra reveals that the reduction in roughness is re-

lated to an increse of spectral power of low frequen-

cies between 3-7 Hz. This indicates that emotional

stress increases the magnitude of intentional tremor,

which has been observed in the same frequency range

(McAuley and Marsden, 2000).

Our results show that physiologic tremor, as mea-

sured by an accelerometer, is a marker of emotional

stress. However, although we observe statistically

signiﬁcant changes of mean quantities, there are con-

siderable variations between subjects. Thus, in order

to construct reliable stress scores based on accelerom-

eter data, the model has to be extended to allow for

additional factors such as age, gender and physiolog-

ical parameters. To this end, a larger study would be

required, which is beyond the scope of the pilot study

presented here.

Finally, the investigation was based on measure-

ments in a controlled lab environment. However, as

physiologic tremor occurs at relatively high frequen-

cies, its separation from voluntary activities appears

feasible even in real-life settings. Thus, the usage of

wearable activity sensors for the investigation of emo-

tional stress as well as for the evaluation of emotional

context is a promising topic for further research.

ACKNOWLEDGEMENTS

The authors are indebted to Sarah Paterson and Ian

Mahers who helped with the design and analysis of

AControlledStudyforMeasuringStressInducedChangesofPhysiologicTremorwithaWearableActivitySensor

181

the study.

REFERENCES

de Lima, E. R., Andrade, A., Pons, J., Kyberd, P., and Na-

suto, S. (2006). Empirical mode decomposition: a

novel technique for the study of tremor time series.

Med Bio Eng Comput., 44:569–582.

Elble, R. J. (1986). Physiologic and essential tremor. Neu-

rology, 36.

Esliger, D. W., Rowlands, A. V., Hurst, T. L., Catt, M.,

Murray, P., and Eston, R. G. (2011). Validation

of the genea accelerometer. Med Sci Sports Exerc.,

43(6):1085–1093.

Gneiting, T., Sevcikova, H., and Percival, D. (2010). Esti-

mators of fractal dimension: assessing the roughness

of times series and spatial data. Technical Report 577,

University of Washington, Department of Statistics,

University of Washington.

Godfrey, A., Conway, R., Meagher, D., and Olaighin, G.

(2008). Direct measurement of human movement by

accelerometry. Med Eng & Phys, 30:1364–1386.

Hallet, M. (1998). Overview of human tremor physiology.

Movement Disorders, 13:43–48.

Halley, J. M., Hartley, S., Kallimanis, A. S., Kunin, W. E.,

Lennon, J. J., and Sgardelis, S. P. (2004). Uses and

abuses of fractal methodology in ecology. Ecology

Letters, 7:254–271.

Kantz, H. and Schreiber, T. (2005). Nonlinear time series

analysis. Cambridge University Press, Cambridge,

2nd edition.

Kruskal, W. H. and Wallis, W. A. (1952). Use of ranks in

one-criterion variance analysis. Journal of the Ameri-

can Statistical Association, 47(260):583–621.

Lu, H., Frauendorfer, D., Rabbi, M., Mast, M. S., Chit-

taranjan, G. T., Campbell, A. T., Gatcia-Perez, D., and

Choudhury, T. (2012). Stresssense: detecting stress

in unconstrained acoustic environments using smart-

phones. In UbiComp 12, Proceedings of the 2012

ACM Conference on Ubiquitous Computing. ACM.

Mansur, P. H., Cury, L. K., Andrade, A. O., Pereira, A. A.,

Miotto, G. A., Soares, A. B., and Naves, E. L. (2007).

A review on techniques for tremor recording and

quantiﬁcation. Crit Rev Biomed Eng., 35(5):343–362.

McAuley, J. and Marsden, C. (2000). Physiological and

pathological tremors and rhythmic central motor con-

trol. Brain, 123:1545–1567.

Timmer, J., Lauk, M., H

außler, S., Radt, V., K

oster, B.,

Hellwig, B., Guschlbauer, B., L

ucking, C. H., Eichler,

M., and Deuschl, G. (2000). Cross-spectral analysis of

tremor time series. Int J Bif and Chaos, 10(11):2595–

2610.

Tombaugh, T. N. (2006). A comprehensive review of the

paced auditory serial addition test (pasat). Arch Clin

Neuropsychol., 21(1):53–76.

Zhang, S., Rowlands, A. V., Hurst, T. L., and Murray, P.

(2012). Physical activity classiﬁcation using the ge-

nea wrist worn accelerometer. Med Sci Sports Exerc.,

44(4):742–748.

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

182