Summarizing Genome-wide Phased Genotypes using Phased PC Plots

Sergio Torres-S

anchez, Nuria Medina-Medina and Mar

ıa M. Abad-Grau

Departmento de Lenguajes y Sistemas Inform

aticos, CITIC, University of Granada, Granada, Spain

Keywords:

Principal Component Analysis, Phased-genotype, Haplotype.

Abstract:

Ordination in reduced space such as principal component (PC) analysis and their visual representation in PC

plots may help to uncover important patterns among samples in highly dimensional data sets. When used

with data sets obtained from genome-wide genotyping, they may show biologically relevant relationships

among populations, such as population structure and admixture. Extending the PC analysis to genome-wide

phased genotypes may help to reveal different levels of inbreeding between or within populations as well as to

evaluate the quality of the haplotyping technique used. We have developed a method to perform PC analysis

to a data set of genome-wide phased genotypes and to plot results keeping information about individuals. The

method has been implemented in the computer program PCPhaser. To increase the method applicability and

reduce development time, PCPhaser implements the method through the transformation of the input data set by

segregating haplotypes and using software EIGENSOFT to perform PC analysis. Given this transformation,

the proposed method can be applied through any other software able to perform PCA, although PCPhaser will

be still required to draw the phased PC plots. PCPhaser is a linux-based software that can be downloaded from

http://bios.ugr.es/PCPhaser.

1 INTRODUCTION

Multivariate analyses, e.g. Principal Component

Analysis (PCA), may be used to reveal complex pat-

terns between samples such as population admixture

or structure from data sets composed of hundred thou-

sands genetic markers (Jombart et al., 2009; Novem-

bre et al., 2008; Lao et al., 2008; Wang et al., 2010).

In the case of PCA, which preserves the canonical Eu-

clidean distance among the samples, a geographical

resemblance of the genetic patterns when plotting the

ﬁrst two principal components has sometimes arisen

(Novembre et al., 2008; Lao et al., 2008; Wang et al.,

2010), revealing a linear isolation-by-distance model.

A PC plot is a 2D graph showing individual genetic

data reduced to two orthogonal vectors or principal

components.

Genotype-based PCA has been extended to

haplotype-based PCA (Brisbin, 2010), by considering

each copy of a chromosome as a separate data point

in the PC plot, when genome-wide phased genotypes

are truly known or computationally inferred.

In this work we provide a visual tool to show

genome-wide phasing results at individual level by

modifying the haplotype-based PC plots in order to

represent an individual i as a segment s

with end

points being the values of their two genome-wide hap-

lotypes for the two PCs shown in the plot.

The distance between the two haplotypes making

up an individual i, is represented by the length of the

segment s

and it may be considered as inversely pro-

portional to the relatedness or inbreeding of the two

haplotypes. In the extreme case of an individual with

exactly the same two genome-wide haplotypes, they

will be identical by descent (IBD), and the segment is

actually just a point.

Section 2 deﬁnes phased-PC plots and how they

can be computed. It also explains how the method

has been implemented in a software program called

PCPhaser (http://bios.gur.es/PCPhaser), and the data

transformation required for PCPhaser to be deﬁned

as a wrap for EIGENSOFT. In Section 3 we use our

implementation of this tool to provide some insight

into two different research topics: revealing different

levels of inbreeding in populations and evaluating the

quality of a haplotyping algorithm. Conclusions and

future work are explained in Section 4.

2 METHODS

Results obtained from multivariate analyses on ge-

130

Torres-Sánchez S., Medina-Medina N. and Abad-Grau M..

Summarizing Genome-wide Phased Genotypes using Phased PC Plots.

DOI: 10.5220/0004793501300135

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 130-135

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

netic data are sometimes difﬁcult to reproduce. The

main reasons for this discouraging fact are due to dif-

ferent initial transformations of data, such as allele

centering –subtracting the mean allele frequency from

all observations– and scaling –dividing each observa-

tion by allelewise values– and to the application of a

different method, such as Principal Coordinate Anal-

ysis (PCoA) (Pariset et al., 2003) while naming it as

PCA (Jombart et al., 2009).

We focused on PCA, as it is widely used, per-

formed on data sets of n binary markers like Single

Nucleotide Polymorphisms (SNPs). In the case of

more than two alleles, such as microarrays, data can

be transformed so that for each allele a marker will be

deﬁned (Patterson et al., 2006). We also focused on a

widely- used initial transformation consisting of allele

centering and a normalization step assuming Hardy-

Weinberg equilibrium (HWE) (Nicholson et al., 2002;

Patterson et al., 2006):

M(i, j) =

C(i, j) − µ( j)

( j)

HW E

C(i, j) − µ( j)

p( j)(1 − p( j))

(1)

with C(i, j) being the number of variant alleles –0,1

or 2 in binary markers– that an individual i has at

marker j, µ( j) being the column j mean, i.e., the

mean value of marker j among the m individuals in

the data set, p( j) an estimate of the underlying al-

lele frequency in autosomal data: p( j) = µ( j)/2 and

( j) the column j variance.

To extend the method to phased genotypes we ﬁrst

considered the data set as composed by 2 × m haplo-

types, i.e., each individual i, i = 1... m, having two

haplotypes h

, k = 1,2 and n markers j = 1 ... n so

that there will be 2 × m × n binary variables C

(i, j)

with values 0,1 at each marker j representing whether

the variant allele is present or not in haplotype h

individual i at marker j. We also deﬁned the simplest

transformation M

(i, j) performed on each haplotype

to be consistent with the common transformation

performed on genotypes referred above M(i, j), i.e., a

transformation for which the following property holds

for each individual i:

(i, j) + M

(i, j) = M(i, j), (2)

with h

and h

being the two haplotypes making up

the genotype of each individual i.

The transformation is deﬁned as:

(i, j) =

(i, j) − µ

( j)

, (3)

with µ

( j) and σ

( j) being respectively the column j

mean and variance, i.e., the mean and variance values

of marker j among the 2 × m haplotypes in the data

set.

It has to be noted that any other transformation

∗

(i, j) resulting in a linear relation with the trans-

formation M(i, j) performed on genotypes:

∗

(i, j) + M

∗

(i, j) = c

× M(i, j) + c

, (4)

with c

, c

being numeric constants, would not affect

the ﬁnal results in the PCA.

By considering the following expressions hold in

a data set with haplotypes of binary markers:

( j) = µ( j)/2 = p( j), (5)

2. the expression of the variance:

( j) =

∑

k,i

(i, j)

2 × m

− µ

( j)

∑

k,i

(i, j)

2 × m

−



∑

k,i

(i, j)

2 × m



( j) − µ

( j) = µ

( j)(1 − µ

( j)), (6)

C(i, j) = C

(i, j) +C

(i, j),∀i, j (7)

4. HWE:

p(g

) = p( j)

, p(g

) = (1 − p( j))

, p(g

) =

2p( j)(1 − p( j)) (8)

with p(g

) being an estimate of the underlying ho-

mozygous genotype frequency at marker j, p(g

)

an estimate of the wild-type homozygous geno-

type and p(g

) an estimate of the heterozygous

genotype,

our statement also holds:

M(i, j) =

HW E

(i, j) +C

(i, j) − µ( j)/2 − µ( j)/2

p( j)(1 − p( j))

(i, j) − µ( j)/2

p( j)(1 − p( j))

(i, j) − µ( j)/2

p( j)(1 − p( j))

(i, j) + M

(i, j). (9)

PCPhaser has been implemented as a set of macro

programs (bash shell) for Linux-like systems which

use EIGENSOFT (Patterson et al., 2006) to perform

PCA and gnuplot to draw the maps. Therefore, in-

stead of implementing our method from the scratch,

we performed a slightly different data transformation

∗

(i, j) = 2 × M

(i, j) (10)

in order to use EIGENSOFT with default parameters,

as it provides an easy and reasonably fast way to run a

SummarizingGenome-widePhasedGenotypesusingPhasedPCPlots

131

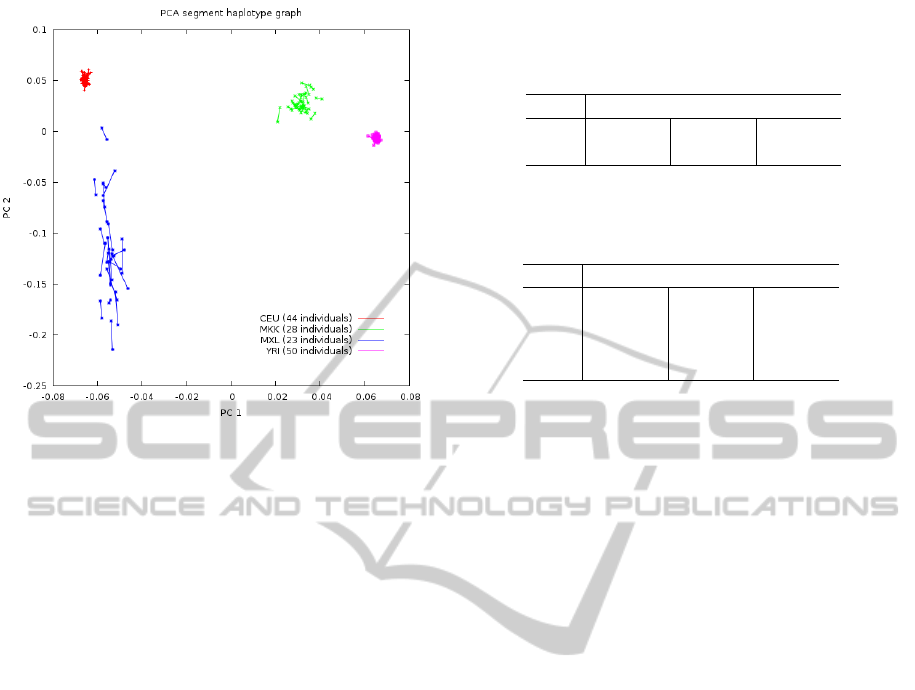
Figure 1: Phased-PC plot from HapMap samples, including

Utah residents with Northern and Western European ances-

try (CEU, red plus sign), Los Angeles residents with Mexi-

can ancestry (MXL, blue asterisks), Yoruban samples from

Ibadan (YRI, pink ﬁlled squares) and Maasai in Kinyawa

(MKK, green crosses) populations using quasi-true haplo-

types inferred from familial trios.

PCA over large data sets. Therefore, PCPhaser dupli-

cates the input genotype data in the makeped ﬁle, i.e.,

it splits each original line in the makeped ﬁle corre-

sponding to the phased genotype of an individual into

two lines, one for each haplotype, and duplicates each

allele.

Table 1 shows an example of the format of

phased genotypes for 3 SNPs and 2 individuals using

makeped (for clarity, no phenotype columns but indi-

vidual IDs are shown). The data transformation per-

formed by PCPhaser for these individuals and mark-

ers is shown in Table 2. As a result, two eigenvectors

will be produced for each individual, one for each

haplotype, which will be used by PCPhaser to draw

the segments in a phased-PC plot.

PCPhaser also allows to choose a subset of pop-

ulations to obtain the eigenvectors and the remaining

ones only to be projected on them.

As an example, Figure1 shows a phased-PC

plot produced by the method, implemented through

the software PCPhaser (http://bios.ugr.es/pcphaser).

Phased genotypes from half of the individuals pass-

ing quality control belonging to four different popula-

tions of the International Hapmap Project 3 (Hapmap

from now on) (HapMap-Consortium, 2003; HapMap-

Consortium, 2010) were randomly selected to be plot-

ted.

Table 1: Example of phased genotypes at three SNP mark-

ers for 2 individuals under the makeped format, for which

genotype-based PCA software programs (e.g. EIGEN-

SOFT) ignore the phase.

IND SNP #1 SNP #2 SNP #3

#1 C C A G C T

#2 C T G A T T

Table 2: Transformation performed by PCPhaser on phased

genotypes from Table 1 required by EIGENSOFT to carry

out phased-genotype PCA.

IND SNP #1 SNP #2 SNP #3

#1a C C A A C C

#1b C C G G T T

#2a C C G G T T

#2b T T A A T T

3 RESULTS

We have used this tool, implemented in the software

PCPhaser, to show its potential in two different re-

search lines, one related to population stratiﬁcation

and admixture and the other related to methods for

haplotype resolution.

3.1 Phased PC Plots Applied to

Population Stratiﬁcation and

Admixture

Phased-PC plots may be used (Figures 2 and 3) as a

tool to help uncover the level of inbreeding in differ-

ent populations. We used PCPhaser with two popu-

lations from the HapMap Project for which individ-

ual haplotypes are known –they use nuclear families

to obtain them accurately– and for which the large

difference in levels of inbreeding is already known:

MXL (30 trios, residents in Los Angeles, USA, with

Mexican ancestry) and CEU (30 trios, CEPH popula-

tion composed of Utah residents with ancestry from

Northern and Western Europe). Mexican is an ad-

mixed population with average genetic composition

of 60.70% European, 34.31% Asian (Amerindian)

and 4.99% African (Silva-Zolezzi et al., 2009) while

CEPH is a Caucasian population. From now on

we will refer to these known haplotypes as quasi-

true haplotypes since the phase cannot be completely

solved from familial trios. Thus, it remains unkown

in those positions in which all members of the family

are heterozygotic (Sebastiani et al., 2004).

To draw Figure 2 we randomly chose 44 parents

out of the 88 CEU parents from trio families avail-

able after the quality control performed by HapMap.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

132

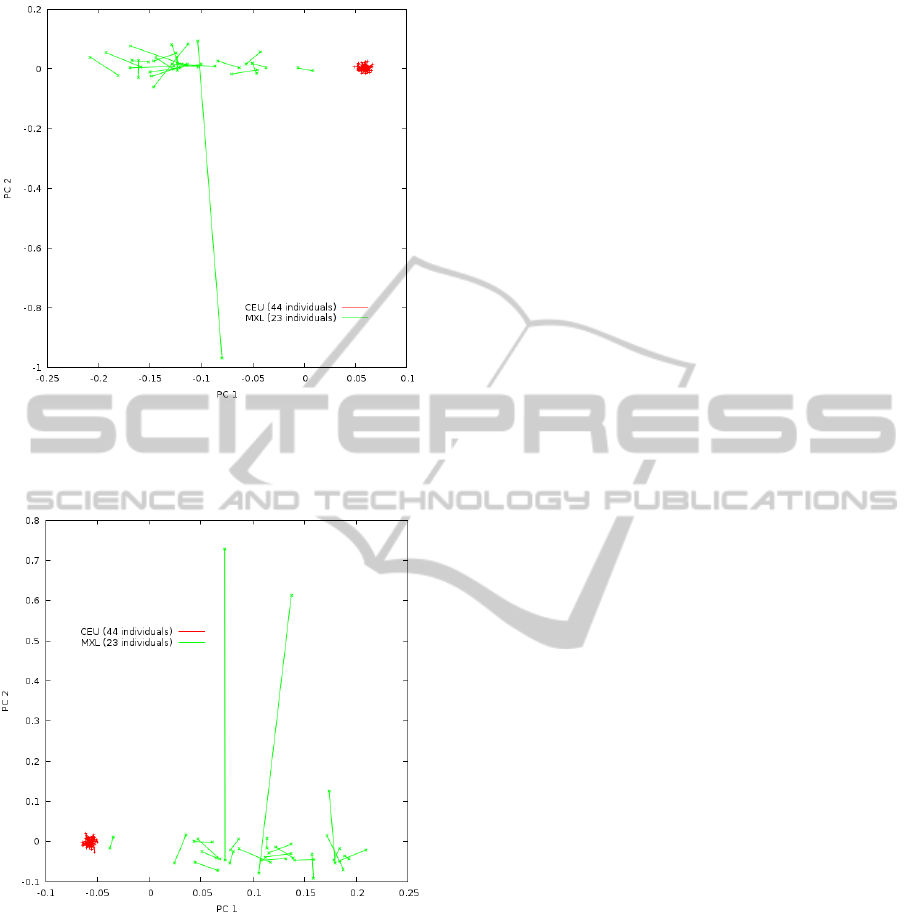
Figure 2: Phased-PC plot from HapMap MXL (green

crosses) and CEU (red plus sign) populations using quasi-

true haplotypes inferred from familial trios. The same sam-

ples used to learn the eigenvectors are plotted.

Figure 3: Phased-PC plot from HapMap MXL (green

crosses) and CEU (red plus sign) populations using quasi-

true haplotypes inferred from familial trios. Different sam-

ple subsets were used to learn the eigenvectors and to draw

the plot.

Similarly, we randomly chose 23 parents out of the

46 MXL parents from trio families available after the

quality control performed by HapMap. To draw Fig-

ure 3, once the eigenvectors were learned with the

chosen samples, the remaining samples were plotted

by projecting them on the learned eigenvectors. Both

ﬁgures show the phased-PC plots of the two ﬁrst PCs

drawn by PCPhaser. Each segment represents a sin-

gle individual with the end points representing the two

haplotypes.

It must be observed the large average difference in

the segment length between MXL and CEU popula-

tions.

It must also be observed how several segments

representing MXL individuals have similar direc-

tion from/to the cluster representing CEU individu-

als to/from large values of PC1, which may reﬂect

the large European and Amerindian genetic compo-

sition of Mexican population. There are one (Fig-

ure 2)/two (Figure 3) individuals with very long seg-

ments orthogonal to the cluster representing the CEU

population, which may reﬂect they have one parent

with African ancestry (as said above, only about 5%

of Mexican genetic ancestry is from Africa) and the

other having a most common Mexican mixture of Eu-

ropean and Amerindian ancestry.

3.2 Phased PC Plots to Show Accuracy

of Algorithms for Haplotype

Reconstruction

In the second example (Figures 4, 5, 6 and 7) we have

used the method to compare the average performance

of different phasing algorithms by plotting the ﬁrst 2

PCs for CEU (Figures 4 and 5) and MXL (Figures

6 and 7) populations. The main difference between

the four plots are due to the design used to perform

the analysis. Figures 4 and 6 use the same sample

subset to compute the eigenvectors and to draw the

plots, while Figures 5 and 7 use a different sample

subset to compute the eigenvectors and to draw the

plots.

In both approaches each drawn plot shows dif-

ferences between quasi-true haplotypes, two state-

of-the-art in silico methods: Beagle (Browning and

Browning, 2009) (Beagle, red plus signs) and Shape-

it (Delaneau et al., 2011) (Shapeit, green crosses)

and when haplotypes are randomly obtained, which

is equivalent to use unphased or genotype-based con-

ventional plots (Unphased, cyan ﬁlled squares).

When comparing Figures 4 and 6 it can be ob-

served how the average segment length in quasi-true

haplotypes (trios, blue asterisks) is larger in MXL

than in CEU. This is an expected result because of the

population admixture in MXL. Moreover, the advan-

tage of quasi-true haplotypes over the other methods

is clearer in MXL.

When comparing the two approaches, it can be ob-

served the large differences in the quasi-true haplo-

types (trios, blue asterisks): individual segments are

much shorter when the same samples were used to

learn the eigenvectors and to draw the plots. Con-

sidering how plot scaling changes between the plots,

SummarizingGenome-widePhasedGenotypesusingPhasedPCPlots

133

Figure 4: Phased-PC plot from CEU population using the

same panel to learn the eigenvectors and to draw the plot. 4

different methods are shown: (1) quasi-true haplotypes ob-

tained from trios (blue asterisks), Beagle (red plus signs),

Shapeit (green crosses), and random phasing (Unphased,

cyan ﬁlled squares).

Figure 5: Phased-PC plot from CEU population using an

independent panel to learn the eigenvectors. 4 different

methods are shown: (1) quasi-true haplotypes obtained

from trios (blue asterisks), Beagle (red plus signs), Shapeit

(green crosses), and random phasing (Unphased, cyan ﬁlled

squares).

this pattern is clearer in CEU. On the contrary, there

are very little differences in the other methods. This

result supports the use of the second approach since

it shows how differences increase between quasi-true

haplotypes and in-silico algorithms when an indepen-

dent sample subset was used to draw the plots.

All the plots support the idea that in-silico phas-

Figure 6: Phased-PC plot from MXL population using the

same panel to learn the eigenvectors and to draw the plot. 4

different methods are shown: (1) quasi-true haplotypes ob-

tained from trios (blue asterisks), Beagle (red plus signs),

Shapeit (green crosses), and random phasing (Unphased,

cyan ﬁlled squares).

Figure 7: Phased-PC plot from MXL population using

an independent panel to learn the eigenvectors. 4 differ-

ent methods are shown: (1) quasi-true haplotypes obtained

from trios (blue asterisks), Beagle (red plus signs), Shapeit

(green crosses), and random phasing (Unphased, cyan ﬁlled

squares).

ing methods are not accurate enough when used to

estimate long-range haplotypes, even if the algorithm

shows high accuracy rates for short-range haplotypes,

since phasing errors propagate along the chromosome

(Turner and Hurles, 2003). Moreover, when phase is

unknown or randomly solved, segments are actually

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

134

dots and there are no differences with the common

genotype-based PC plots.

When using the proposed method to compare ac-

curacy of different in-silico phasing algorithms, we

always need to know the true, or quasi-true, hap-

lotypes. Nowadays there are few publicly-available

data sets of true haplotypes from healthy individ-

uals. The most widely-used data sets come from

HapMap and includes quasi-true haplotypes, inferred

from familial trios, for Caucasians from Northwest

Europe (CEU), Africans from Nigeria (YRI), Kenya

(MKK, Maasai in Kinyawa) and a less-speciﬁc ori-

gin (ASW, African Ancestry in SW USA), and an ad-

mixed population (MXL, Mexican Ancestry in LA,

CA, USA). The more recent 1000 Genomes project

(Consortium’, 2010) does not include trios. There-

fore, for samples from other European or African re-

gions, or for Asian individuals it would be more difﬁ-

cult to ﬁnd out a large enough data set of true haplo-

types to apply the proposed method.

4 CONCLUSIONS

With this work we have extended the genotype-based

PC plots to use phased genotypes and we have shown

how phased-PC plots may shed new light to this kind

of graphs helping to understand not only population

drift, stratiﬁcation and admixture but also individual

genetic differences. Moreover, it may be used as a

by-view way to test accuracy of phasing methods at a

long-range haplotype level.

Based on phased-PC plots, we plan to design a

statistical test to compare accuracy between phased

genotypes returned by an in-silico phasing algorithm

and the true or quasi-true phased genotypes.

ACKNOWLEDGEMENTS

The authors were supported by projects CEI-

mic2013-2, CEI-IDi-2013-15, TIN2010-20900-C04-

1 and P08-TIC-03717 and the European Regional De-

velopment Fund (ERDF).

REFERENCES

Brisbin, A. (2010). Linkage analysis for categorical traits

and ancestry assignment in admixed individuals. PhD

thesis, Cornell University, Ithaca, New York.

Browning, B. L. and Browning, S. R. (2009). A uniﬁed ap-

proach to genotype imputation and haplotype-phase

inference for large data sets of trios and unrelated in-

dividuals. The American Journal of Human Genetics,

84(2):210–223.

Consortium’, T. . G. P. (2010). A map of human genome

variation from population-scale sequencing. Nature,

467:1061–73.

Delaneau, O., Marchini, J., and Zagury, J.-F. (2011). A

linear complexity phasing method for thousands of

genomes. Nature Methods, 9(2):179–81.

HapMap-Consortium, T. I. (2003). The international

hapmap project. Nature, 426:789–796.

HapMap-Consortium, T. I. (2010). Integrating common and

rare genetic variation in diverse human populations.

Nature, 467(7311):52–58.

Jombart, T., Pontier, D., and Dufour, A.-B. (2009). Ge-

netic markers in the playground of multivariate analy-

sis. Heredity, 102:330–41.

Lao, O., Lu, T. T., Nothnagel, M., et al. (2008). Correlation

between genetic and geographic structure in europe.

Curr. Bio., 18:1241–8.

Nicholson, G., Smith, A., Johnson, F., et al. (2002). As-

sessing population differentiation and isolation from

single-nucleotide polymorphism data. JRSS (B),

64:695–715.

Novembre, J., Toby, Bryc, K., et al. (2008). Genes mirror

geography within europe. Nature, 456(7218):98–101.

Pariset, L., Savarese, M., Cappuccio, I., and Valentini,

A. (2003). Use of microsatellites for genetic varia-

tion and imbreeding analysis in sarda sheep ﬂocks of

central italy. Journal of Animal Breeding Genetics,

120:425–32.

Patterson, N., Price, A. L., and Reich, D. (2006). Pop-

ulation structure and eigenanalysis. PLoS Genetics,

2(12):2074–93.

Sebastiani, P., Abad-Grau, M., Alpargu, G., and Ramoni,

M. F. (2004). Robust transmission/disequilibrium

test for incomplete family genotypes. Genetics,

168(4):2329–37.

Silva-Zolezzi, I., Hidalgo-Miranda, A., Estrada-Gil, J., et al.

(2009). Analysis of genomic diversity in mexican

mestizo populations to develop genomic medicine in

mexico. PNAS, 106(21):8611–16.

Turner, D. J. and Hurles, M. E. (2003). High-throughput

haplotype determiantion over long distances by haplo-

type fusion pcr and ligation haplotyping. Nature Pro-

tocols, 4:1771–83.

Wang, C., Szpiech, Z., Degnan, J., et al. (2010). Comparing

spatial maps of human population-genetic variation

using procrustes analysis. Stat. Appl. Genet. Molec.

Biol., 9(1):13.

SummarizingGenome-widePhasedGenotypesusingPhasedPCPlots

135