
Angle Measurements during 2D and 3D Movements of a Rigid Body
Model of Lower Limb
Comparison between Integral-based and Quaternion-based Methods
Takashi Watanabe
1
and Kento Ohashi
2
1
Graduate School of Biomedical Engineering, Tohoku University, Sendai, Japan
2
Graduate School of Engineering, Tohoku University, Sendai, Japan
Keywords: Angle, Inertial Sensor, Kalman Filter, Integral, Quaternion, Gait, Rehabilitation.
Abstract: Angle measurement system using inertial sensors was developed by our research group, in which lower
limb angles were calculated based on the integral of angular velocity using Kalman filter. The angle
calculation method was shown to be practical in measurement of angles in the sagittal plane during gait of
healthy subjects. In this paper, in order to realize practical measurements of 3 dimensional (3D) movements
with inertial sensors, the integral-based and the quaternion-based methods were tested in measurement of
2D movements in the sagittal plane and 3D movements of rigid body models of lower limb. The tested three
calculation methods, extended integral-based method, quaternion-based method proposed in this study and
simplified previous quaternion-based method, were suggested to measure the 2D movements with high
measurement accuracy. It was also suggested that there were no large difference in measurement of 2D and
3D movements between 3 methods. Visualization by stick figure animation of circumduction gait simulated
by a healthy subject also suggested that the angle calculation methods can be useful. It is expected to
improve measurement accuracies of 3D movements to those of 2D movements.
1 INTRODUCTION
Lower limb motor functions are important to prevent
bedridden and to make independence in daily living
and social participation. Therefore, motor disabled
persons or elderly people with decreased motor
function need rehabilitation training of their lower
limbs. In that rehabilitation, it is important to
evaluate a level of subject’s motor function in order
to make rehabilitation program and to instruct it.
Generally, therapists perform the evaluation of
motor function in rehabilitation by simple manual
methods such as watching movements, measurement
of the range of motion (ROM) with a manual
goniometer, or measurement of time and counting
the number of steps in 10 m walking test. Although
these simple, manual evaluation methods are
effective in limited space and time for rehabilitation
training, those evaluation results depend on
therapists. On the other hand, for quantitative and
objective evaluation of movements, motion
measurement system such as a camera-based system
or electric goniometers has been used. Rehabilitation
program proposed by the quantitative and objective
evaluations with motion measurement system is
expected to increase rehabilitation effect and to
decrease rehabilitation term. However, those motion
measurement systems are mainly used in research
works in laboratories, because these systems require
large space for setting the system and time-
consuming setup process, and are expensive.
Recently, use of inertial sensors (accelerometers
and gyroscopes) has been studied in measurement
and analysis of movements focusing on its shrinking
in size, low cost and easiness for settings. In
evaluation of motor functions, segment inclination
angles and joint angles have important information
for therapists and patients. Therefore, many studies
have been performed on measurement of joint angles
or segment tilt angles with inertial sensors (Tong
and Granat, 1999; Dejnabadi, et al., 2005; Findlow,
et al., 2008;, Cooper, et al., 2009; Sabatini, 2006;
Mazzà, et al., 2012.).
A motion measurement system using inertial
sensors has to give joint or segment inclination
angles calculating from angular velocities or
acceleration signals. In addition, measurement of
total lower limb movements such as simultaneous
35
Watanabe T. and Ohashi K..
Angle Measurements during 2D and 3D Movements of a Rigid Body Model of Lower Limb - Comparison between Integral-based and Quaternion-based
Methods.
DOI: 10.5220/0004793600350044
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 35-44
ISBN: 978-989-758-011-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

measurement of hip, knee and ankle joint angles is
required for clinical evaluation in rehabilitation
support. In our previous study, a joint angle
calculation method based on the integral of angular
velocity using Kalman filter was applied to all the
joint angles of the lower limbs. Measurement of gait
with healthy subjects suggested that the method can
be used practically in measurement of those angles
in the sagittal plane (Saito and Watanabe, 2011;
Watanabe, et al., 2011; Watanabe and Saito, 2011).
Angle measurement of 3-dimensional (3D)
movements has been required for evaluation of
motor function. For measurement of 3D angles with
inertial sensors, a method of using attitude angle
representation by quaternion was proposed (Sabatini,
2006). However, measurement of Euler angle was
tested in that study. On the other hand, the integral
of angular velocity can be expanded to measure 3D
movements, and it is possible to provide simply
angles in the sagittal plane and in the frontal plane.
The question focused in this paper was whether
there are any differences in angle measurement
between the integral-based method and the
quaternion based one or not. Therefore, this paper
aimed to evaluate angle measurement accuracy of
different calculation methods. For this purpose, a
Kalman filtering for angle calculation method using
quaternion was developed based on our integral-
based method. Then, a previous quaternion-based
method was modified to a simplified method for the
test. These 2 quaternion-based methods and an
extended integral-based method were evaluated in
measurements of angles during 2D movements in
the sagittal plane, and angles during 3D movements
in the sagittal and the frontal planes using rigid body
models that represented the lower limb. Finally, a
measured 3D movement during walking was tested
in recreating stick-figure animation.
2 ANGLE CALCULATION
METHODS
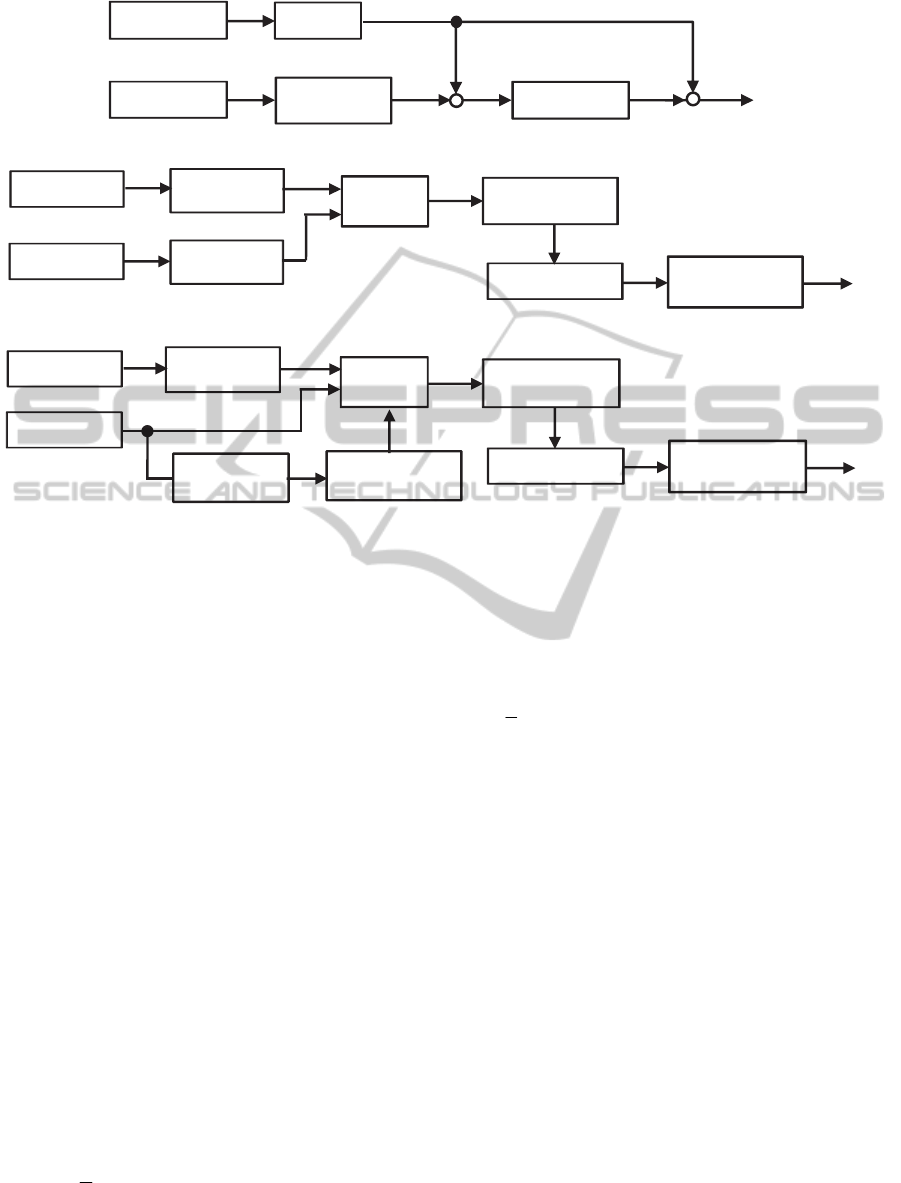
In this paper, three calculation methods shown in
Figure 1 were evaluated in angle measurement.
2.1 Extended Integral-based Method
Figure 1(a) shows outline of the integral-based
method of calculating segment inclination angle. In
this paper, the previous integral-based method
developed by our group was extended to calculate
angles in the sagittal and the frontal planes.
Basically, a segment inclination angle is
calculated by the integral of angular velocity (an
output of a gyroscope). Here, the calculated angle is
corrected by Kalman filter using angle measured
with an accelerometer (Watanabe and Saito, 2011).
Joint angles are calculated from 2 inclination angles
of the adjacent segments. That is, segment
inclination angle
)(t
inc
and joint angle
)(t
joint
are
calculated as follows:
)0()()(
0
inc
t
inc
dt
,
(1)
)()()(
21
ttt
incincjoint
,
(2)
where
)(t
shows angular velocity measured with a
gyroscope.
)0(
inc
is the initial joint angle calculated
from acceleration data. For instance, the angle in the
sagittal plane is calculated from acceleration signal,
x
a
and
z
a
, by following equation.
)0()0(tan)0(
1
xzinc
aa
(3)
Kalman filter estimates error in the angle calculated
from the output of a gyroscope (
ˆ
) by using the
difference between angles obtained by a gyroscope
and by an accelerometer (
y
). Then, angle (
ˆ
) is
calculated. That is,
)()(tan)(
)()()(
1
tatat
ttty
xzinc
accgyro
(4)
The state equation and the observation equation are
shown by using the error of the angle measured with
gyroscopes (
) and increment of bias offset for
one sampling period (
b
) as follows.
w
t
b
t
b
k
k
k
k
110
1
1
1
,
(5)
v
b
y
k
k
k
01
,
(6)
where
w
and
v
are errors in measurement with the
gyroscope and with the accelerometer, respectively.
Kalman filter repeats corrections (Equation (7))
and predictions (Equation (8)) as follows:
)
ˆ
(
ˆ
ˆ
ˆ
ˆ
2
1
kk
k
k
k
k
y
K
K
bb
,
(7)
k
k
k
k
b
t
b
ˆ
ˆ
10
1
ˆ
ˆ
1
1
,
(8)
where
1
K
and
2
K
are Kalman gain for
and
b
,
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
36
gyroscope
accelerometer
Kalman filter
integral
gyro
acc
y
ˆ
ˆ
conversion to
angle
ω
a
(a) Extended integral-based method
gyroscope
accelerometer
Kalman
filter
z
q
ˆ
calculation of
inclination angle
conversion to
quaternion
q
ˆ
rotation of vector
conversion to
rotation matrix
conversion to
quaternion
ω
a
(b) Proposed quaternion-based method
gyroscope
accelerometer
Kalman
filter
q
ˆ
calculation of
inclination angle
q
ˆ
conversion to
rotation matrix
rotation of vector
measurement
validation test
determination of
noise rate
conversion to
quaternion
ω
a
(c) Simplified previous quaternion-based method
Figure 1: Outline of tested angle calculation methods.
respectively. The hat upon a character and the
superscript minus represent estimated value and
predicted value, respectively. For the initial state,
0
ˆ
was set at zero and
0
ˆ
b
was set at the value at
the last measurement.
2.2 Proposed Quaternion-based
Method
Quaternion can be used to represent the attitude of
each segment of a rigid body. As shown in Figure
1(b), two quaternions are calculated from
acceleration and from angular velocity measured
with an inertial sensor. First, attitude angle
representation by quaternion is obtained from the
angular velocity. Then, Kalman filter was applied to
correct error using attitude angle representation by
quaternion obtained from the gravitational
acceleration.
Using the triaxial angular velocity
(, ,)
xyz
ω
,
quaternion
q
is propagated according to the
differential equation (Chou, 1992):
0
0
1
0
2
0
xyz
xzy
yz x
zy x
qq
(9)
The state equation is the time integration of
Equation (9), where
w
is the process noise in
measurement with a gyroscope.
wqq
kk
2
2
2
2
2
1
1
xkykzk
xkzkyk
ykzkxk
zkykxk
ttt
ttt
ttt
ttt
(10)
The observation equation is given by the following
equation, considering the observation noise
v
in
measurement with an accelerometer.
vIqvqz
kkk
1000
0100
0010
0001
,
(11)
where the observation vector is the quaternion-based
attitude representation
z
that is obtained from the
gravity acceleration. Then, correction and prediction
are represented by
)
ˆ
(
ˆˆ
kkkk
qzKqq
,
(12)
kk
qIq
ˆˆ
1
(13)
The quaternion-based attitude representation
z
can
be obtained by the followings (Favre, 2006).
AngleMeasurementsduring2Dand3DMovementsofaRigidBodyModelofLowerLimb-Comparisonbetween
Integral-basedandQuaternion-basedMethods
37

k
kkk
k
A
A
z
2
sin,
2
cos
,
(14)
where the angle
k
and axis of rotation
k
A
are
obtained from the inner and the cross products of a
measured acceleration vector
k
a
and the
acceleration vector defined as the initial attitude of
the sensor
0
a
. That is,
0
aa
kk
1
cos
(15)
0
aaA
kk
(16)
Using a rotation matrix calculated from the corrected
quaternion
k
q
ˆ
, longitudinal vector of each body
segment is rotated. Then, the rotated vector is
projected onto the sagittal and the frontal planes of
the global coordinate system. Inclination angles are
obtained from the inner product of those projected
vector and the unit vector of each plane.
2.3 Simplified Previous
Quaternion-based Method
The quaternion-based method of measurement of
Euler angle during human movements was
developed by Sabatini (Sabatini, 2006). In this
method, quaternion calculated from angular velocity
is corrected by Kalman filter using acceleration
signal and magnetic sensor signal. The acceleration
and the magnetic sensor signals are used as
observation signals directly. In addition, Kalman
gain is varied dynamically based on validation test
for those acceleration and magnetic sensor signals.
In this paper, the method was simplified
removing magnetic sensor as shown in Figure 1(c)
in order to compare the method under the same
condition using gyroscope and acceleration sensors.
3 EVALUATION OF ANGLE
CALCULATION METHODS
3.1 Measurement of 2D Movements
3.1.1 Experimental Method
A rigid body model of a duplex pendulum consisted
of steel prop body and L-type aluminium materials
corresponding to the thigh and the shank (Figure 2).
The hip and the knee joints can be moved smoothly
in a plane, while the hip joint position was fixed.
Two wireless inertial sensors (WAA-006,
Wireless Technologies) were attached on each L-
type material with double-sided adhesive tapes as
shown in Figure 2. The inertial sensor includes a 2-
axis gyroscope (ID-400, InvenSense for x and y
axes) and a 1-axis gyroscope (XV-3500CB, Seiko
Epson for z axis), and a 3-axis accelerometer
(H30CD, Hitachi Metals). The inertial sensor
communicates with a personal computer using
Bluetooth (Ver 2.0 + EDR, Class 2). Markers for the
optical motion measurement system (OPTOTRAK,
Northern Digital Inc.) were also attached on the L-
type materials with double-sided adhesive tapes in
order to measure reference angles for evaluation of
measurement accuracy.
thigh
shank
Inertial
sensor
thigh
shank
:OPTOTRAK marker
:Inertial sensor
Figure 2: Rigid body model of a duplex pendulum for 2D
movement measurements.
In angle measurements, the thigh was moved
manually for angular range of ±15, ±30, ±45, ±60,
and ±75 deg with cycle period of 2 s (0 deg means
the direction of the gravity). The cycle periods were
regulated manually by a metronome. The thigh was
moved referring to angle gauge, and the shank was
moved freely during the thigh movements. Since
prolonged measurements did not increase
measurement error in our previous tests (Watanabe
et al., 2011), the number of measurement trial was
increased (10 trials) with reducing measurement
time for each trial (35 s) in this paper.
The sensor signals and the marker positions were
measured simultaneously with a personal computer
at a sampling frequency of 100 Hz. Measured
acceleration signals were filtered with Butterworth
low-pass filter with the cut-off frequency of 20 Hz in
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
38

order to remove high frequency noise. Then,
inclination angles were calculated by the 3 methods
shown in Figure 1.
3.1.2 Results
An example of measured inclination angles are
shown in Figure 3. Although the simplified previous
quaternion-based method showed small difference
from angle waveforms obtained by other methods, it
seemed that angle waveforms obtained by all the 3
calculation method were almost same.
Measured angles were evaluated by root-mean-
square error (RMSE) and correlation coefficient
(CC) between the measured angle with sensor and
its reference signal obtained from camera based
motion analysis system. In the evaluation, the
difference in position between the sensors and
markers were removed by using the measured angle
at the beginning of the 1st measurement.
Figure 4 shows average values of the RMSE and
the CC of measured angles during 2D movement in
the sagittal plane. There were no large differences
between 3 calculation methods. However, the
integral-based method showed higher accuracy for
the thigh movements than the two quaternion-based
methods. The simplified previous quaternion-based
method increased the RMSE values and decreased
the CC values for the shank movements with angular
range of ±15 and ±75 deg in comparison to the
integral-based method.
3.2 Measurement of 3D Movements
3.2.1 Experimental Method
A wireless inertial sensor (WAA-010, Wireless
Technologies) was attached to the rigid body model
representing the thigh with the hip joint using a ball
joint with double-sided adhesive tapes as shown in
Figure 5. The inertial sensor includes a 3-axis
gyroscope (IDG-3200, InvenSense) and a 3-axis
accelerometer (ADXL345, Analog Devices). The
inertial sensor communicates with a personal
computer using Bluetooth (Ver 2.0 + EDR, Class 2).
Thigh movements of the rigid body model were
measured with the sensor and a camera based
motion analysis system (OPTOTRAK, Northern
Digital Inc.) simultaneously. All the data were
measured with a sampling frequency of 100 Hz, and
processed as same as that in the previous section.
The original position of the thigh part was in the
direction of the gravity. In the measurements, the
thigh part was moved repeatedly simulating the
circumduction gait. That is, the thigh part was
20 21 22 23 24 25 26 27
-80
-60
-40
-20
0
20
40
60
80
20 21 22 23 24 25 26 27
-80
-60
-40
-20
0
20
40
60
80
time [s]
time [s]
inclination angle of
the thigh part [deg]
inclination angle of
the shank part [deg]
proposed
quaternion method
integral method
simplified
previous method
reference
Figure 3: An example of measured inclination angles during 2D movements (±75 deg).
AngleMeasurementsduring2Dand3DMovementsofaRigidBodyModelofLowerLimb-Comparisonbetween
Integral-basedandQuaternion-basedMethods
39

RMSE [deg]
correlation coefficient
0
0.5
1
1.5
2
2.5
3
±15°±30°±45°±60°±75°
0.99
0.992
0.994
0.996
0.998
1
±15°±30°±45°±60°±75°
■integral method ■proposed quaternion method ■simplified p revious quaternion method
(a) thigh inclination angle
RMSE [deg]
correlation coefficient
■integral method ■proposed quaternion method ■simplified previous quaternion method
0
0.5
1
1.5
2
2.5
3
±15°±30°±45°±60°±75°
0.99
0.992
0.994
0.996
0.998
1
±15°±30°±45°±60°±75°
(b) shank inclination angle
Figure 4: Evaluation of angle calculation methods in measurement of 2D movements.
thigh
:OPTOTRAK marker
:Inertial sensor
Ball joint
Inertial sensor
Figure 5: Rigid body model used in measurement of
angles during 3D movements.
moved to flexed position of about 45 deg in the
sagittal plane through adducted position of about 45
deg in the frontal plane from the original position,
and then the thigh part was moved to the original
position by extension movement in the sagittal plane.
This movement was performed manually with a
cycle period of 2s, 4s or 8s. The sensor was facing
almost in the frontal plane during the movement.
The movement was performed repeatedly in a
measurement trial of 35 s. Five measurement trials
were performed for each condition of the cycle
period.
3.2.2 Results
Figure 6 shows an example of measured inclination
angles during 3D movements. Although the
inclination angles in the sagittal plane calculated by
3 calculation methods showed similar waveforms,
difference between calculated angles and the
reference angle was larger than those in
measurement of 2D movements. Calculated angles
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
40

10 11 12 13 14 15 16 17
-5
0
5
10
15
20
25
30
35
10 11 12 13 14 15 16 17
-5
0
5
10
15
20
25
30
35
time [s]
time [s]
inclination angle of
the thigh part [deg]
inclination angle of
the shank p art [deg]
proposed
quaternion method
integral method
simplified
previous method
reference
Figure 6: An example of measured inclination angles during 3D movements (2s of cycle period).
in the frontal plane showed larger difference than
that in 2D movements and the angle calculated by
the simplified previous method showed different
waveform from other 2 methods.
Figure 7 shows evaluation results for
measurements of 3D movements. In Figure 7(a),
average values of all the measurements of the shank
during the 2D movements were also shown. For the
angles in the sagittal plane, the measurement
accuracy of 3D movements decreased compared to
the 2D movement measurements. Then, the integral-
based method showed higher measurement accuracy
than the 2 quaternion-based methods. Values of CC
were low for the fast movement (2 s of cycle period).
For the angle in the frontal plane, the 2
quaternion based methods showed higher
measurement accuracy than the integral one. The
simplified previous method showed the smallest
RMSE values. However, variations of CC values of
the simplified quaternion method were larger in the
slow and fast movements than the proposed
quaternion method. In addition, for movements with
cycle period of 4 s, values of CC of all the 3
methods decreased, and variations of RMSE were
large.
4 DISCUSSIONS
The evaluation of measured angles with the rigid
body model showed that all the 3 methods measured
the angles in the sagittal plane during 2D
movements with average RMSE values less than 2.5
deg and with average correlation coefficients larger
than 0.996. For angles in the sagittal plane during
3D movements, average RMSE values were less
than about 3 deg and average CC values were larger
than 0.983. However, for angles in the frontal plane
during 3D movements, average RMSE values were
less than about 4 deg and its standard deviation was
less than about 1 deg. Although the measurement
accuracy was not so high for angles in the frontal
plane, it can improve manual measurement with
goniometer that is used with resolution larger than
about 5 deg, and it makes possible to measure angles
during movements in addition to measurement of
range of motion (ROM). These suggest that all the
tested 3 angle calculation methods can be practical
in measurement of movements. However, it is
expected to improve measurement accuracy for 3D
movements to those of the 2D movements.
Measurement accuracies of 2 quaternion
methods were lower than the integral-based method
for angles during the 2D movements in the sagittal
plane and for angles in the sagittal plane during 3D
movements. The simplified previous method showed
good accuracy for angles in the frontal plane in 3D
movement measurement. However, the differences
in the accuracy between calculation methods were
not so large. One of differences of the simplified
AngleMeasurementsduring2Dand3DMovementsofaRigidBodyModelofLowerLimb-Comparisonbetween
Integral-basedandQuaternion-basedMethods
41

RMSE [deg]
correlation coefficient
0
1
2
3
4
5
6
周期2s 周期4s 周期8s
2Dmotion
0.96
0.965
0.97
0.975
0.98
0.985
0.99
0.995
1
周期2s 周期4s 周期8s
2Dmotion
■integral method ■
p
roposed quaternion method ■simplified previous quaternion metho
d
2s 4s 8s 2D
2s 4s 8s 2D
(a) Sagittal plane
RMSE [deg]
correlation coefficient
0
1
2
3
4
5
6
周期2s 周期4s 周期8s
0.96
0.965
0.97
0.975
0.98
0.985
0.99
0.995
1
周期2s 周期4s 周期8s
■integral method ■proposed quaternion method ■simplified previous quaternion method
2s 4s 8s
2s 4s 8s
(b) Frontal plane
Figure 7: Evaluation of angle calculation methods in measurement of 3D movements.
previous quaternion method from other 2 methods is
to determine Kalman gain through measurement
validation test of acceleration signals. Although
Kalman gain can be varied dynamically during
measurement by this method, it is necessary to test
the validity of adjusting Kalman gain based on
measured acceleration signals. In our study, a
method of changing Kalman gain dynamically based
on magnitude of acceleration signal was not so
effective with the integral-based method (Teruyama
and Watanabe, 2013).
In order to test if current measurement accuracy
can be used for visualization of measured movement
or not, circumduction gait simulated by a healthy
subject was measured with the wearable inertial
sensor system developed by our research group
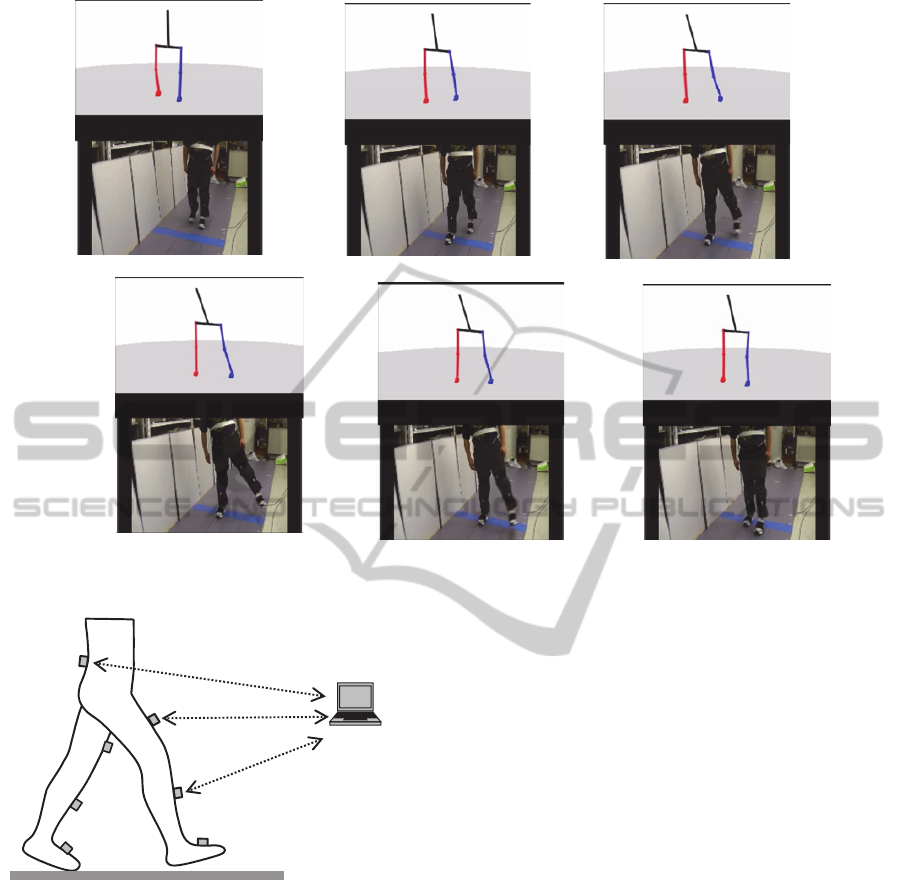
(Watanabe and Saito, 2011). The system consisted
of seven wireless inertial sensors (WAA-010,
Wireless Technologies) and a notebook computer
(Figure 8). Each sensor was attached on the body
with a stretchable band with hook and loop fastener
and a pocket for the sensor. The sensors are put
inside of the pocket and attached with the bands on
the feet, the shanks and the thighs of both legs, and
lumbar region as shown in Figure 8. Acceleration
and angular velocity signals of each sensor were
sampled with a frequency of 100Hz, and transmitted
to the PC via Bluetooth network and recorded.
Figure 9 shows an example of screenshots of stick
figure animation obtained from the software
developed by our research group (Watanabe and
Saito, 2011), in which the 3D angle measurements in
this study was implemented (simplified previous
quaternion-based method). By using angles in the
sagittal and the frontal planes, the stick figure
animation could represent the subject’s gait
movement appropriately. Although it is necessary to
evaluate measurement accuracy in human gait
measurement, it is expected that the calculated
angles can be effective for visualizing gait
movement measured with wearable inertial sensors.
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
42
(a)
(f)
(e)
(d)
(c)
(b)
Figure 9: Screenshots of stick figure animation recreated by angles in the sagittal and the frontal planes. From (a) to (f), the
subject walked forward.
PC
Bluetooth
Figure 8: Outline of the wearable inertial sensor system
developed by our group.
5 CONCLUSIONS
In this paper, the integral-based and the quaternion-
based angle calculation methods were compared in
angle measurements with the rigid body model.
Measurement of 2D movements in the sagittal plane
suggested that all the 3 methods can measure angles
with high measurement accuracy. For 3D
movements, although measurement accuracies of
those methods decreased compared to the
measurement of 2D movements, there were no large
difference in measurement accuracy between the 3
methods. Since the stick figure animation using
angles in the sagittal and the frontal planes showed
appropriately the measured circumduction gait, it
would be effective to use these angles calculation
methods. It is expected to improve measurement
accuracies for 3D movements to those of the 2D
movements.
ACKNOWLEDGEMENTS
This work was supported in part by the Ministry of
Education, Culture, Sports, Science and Technology
of Japan under a Grant-in-Aid for for challenging
Exploratory Research.
REFERENCES
Chou, J. C. K., 1992. Quaternion Kinematic and Dynamic
Differential Equations. IEEE Trans. Robotics
Automat., 8(1), 53-64.
Cooper, G., Sheret, I., McMillian, L., Siliverdis, K., Sha,
N., Hodgins, D., Kenney, L., Howard, D., 2009.
Inertial sensor-based knee flexion/extension angle
estimation. J. Biomech., 42, 2678-2685.
AngleMeasurementsduring2Dand3DMovementsofaRigidBodyModelofLowerLimb-Comparisonbetween
Integral-basedandQuaternion-basedMethods
43

Dejnabadi, H., Jolles, B. M., Aminian, K., 2005. A New
Approach to Accurate Measurement of Uniaxial Joint
Angles based on a Combination of Accelerometers
and Gyroscopes. IEEE Trans. Biomed. Eng., 52, 1478-
1484.
Favre, J., 2006. Quaternion-based Fusion of Gyroscopes
and Accelerometers to Improve 3D Angle
Measurement. Electronics Letters., 42(11), 612-614.
Findlow, A., Goulermas, J. Y., Nester, C., Howard, D.,
Kenney, L. P., 2008. Predicting Lower Limb Joint
Kinematics Using Wearable Motion Sensors. Gait
Posture, 28, 120-126.
Mazzà, C., Donati, M., McCamley, J., Picerno, P.,
Cappozzo, A., 2012. An Optimized Kalman Filter for
the Estimate of Trunk Orientation from Inertial
Sensors Data during Treadmill Walking. Gait &
Posture, 35(1), 138-142.
Sabatini, A. M., 2006. Quaternion-Based Extended
Kalman Filter for Determining Orientation by Inertial
and Magnetic Sensing. IEEE Trans. Biomed. Eng.,
53(7), 1346-1356.
Saito, H. and Watanabe, T., 2011. Kalman-filtering-based
Joint Angle Measurement with Wireless Wearable
Sensor System for Simplified Gait Analysis. IEICE
Trans. Inf. & Syst., E94-D, 1716-1720.
Teruyama, Y. and Watanabe, T., 2013. Effectiveness of
Variable-Gain Kalman Filter based on Angle Error
Calculated from Acceleration Signals in Lower Limb
Angle Measurement with Inertial Sensors. Comput.
Math. Methods Med. (in press).
Tong, K., Granat, M. H., 1999. A Practical Gait Analysis
System Using Gyroscopes. Med. Eng. Phys., 21, 87-
94.
Watanabe, T., Saito, H., Koike, E., Nitta, K., 2011. A
Preliminary Test of Measurement of Joint Angles and
Stride Length with Wireless Inertial Sensors for
Wearable Gait Evaluation System. Comput. Intel.
Neurosci., 2011, Article ID: 975193.
Watanabe, T. and Saito, H., 2011. Tests of Wireless
Wearable Sensor System in Joint Angle Measurement
of Lower Limbs. In Proc. 33rd. IEEE Eng. Med. Biol.,
5469-5472.
BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
44
