2D-0D Direct Capture of Carriers in Quantum Dot Lasers under

Optical Feedback

George Andre Pereira The

Depto of Teleinformatic Engineering, Federal University of Ceara, Campus do Pici s/n, Bl 725, Fortaleza, Brazil

Keywords: Quantum Dot Lasers, Lyapunov Exponents, Direct Capture.

Abstract: In this paper the operation of quantum dot lasers under optical feedback is studied on the basis of calculated

Lyapunov exponents of the dynamic multi-population rate-equations. Influence of the direct capture path for

the wetting layer carriers on the sensitivity to initial conditions is discussed. Results show that positive

exponents are achieved for different current injection scenarios, and that negative exponents are mainly due

to carriers in the dot confined states. Furthermore, existence of hiperchaos is obtained with both cascade and

direct capture models.

1 INTRODUCTION

Semiconductor quantum dot (QD) lasers have been

intensively studied in the last years because of their

potential compared to quantum well and bulk lasers,

as well as due to the particular properties associated

with the 3D confinement in the quantum dots, such

as the high differential gain which should lead to

reduced linewidth enhancement factor (LEF) and

low chirp. Essentially, the LEF or alpha-factor is a

parameter which measures the coupling between real

(phase) and immaginary (gain) parts of the complex

refractive index of the active material; any

fluctuation of phase or amplitude of the laser field

(due to spontaneous emission or even reflected back

light, for instance) induces relaxation oscillations,

changing the immaginary component of the

refractive index and, consequently, the real part as

well. This means that gain modulation (fluctuation

of immaginary component) leads to phase

modulation (real part) and, therefore spectral

broadening of the laser linewidth (chirp) is observed.

Many papers have indeed addressed this issue

and shown there is significant dependence of the

alpha-factor on both internal (carrier scattering

dynamics, wetting layer carrier population, etc.) and

external factors (cavity length, temperature) (Carrol,

2005 and 2006, Melnik, 2006). From the above

mentioned, the device becomes sensitive to out-of-

phase optical field, and even the coupling to optical

fiber could be a problem due to the delayed optical

field reflected back to the cavity (Gioannini, 2008a).

Literature has previously identified the 2D carriers

present in the wetting layer carrier as responsible for

most of the frequency fluctuation observed in

quantum dot lasers when subject to optical feedback

(Gioannini, 2008a and 2008b). Those works

revealed different operating regimes of quantum dot

lasers, ranging from stable to chaotic-like solutions

as the injection current increased, but did not

considered a more rigorous analysis to confirm the

existence of chaos. On the other side, more recently,

carriers of the wetting layer reservoir have also been

shown to influence the steady state of solitary edge-

emitting lasers when the scattering to 0D states has a

non-negligible dynamics (The, 2012), thus justifying

the inclusion of such direct capture of carriers in the

rate-equations. This scenario naturally motivates one

to investigate whether the existence of the 2D-0D

direct capture channel may influence the laser

regimes previously reported and how it differs to the

case in which only the cascade scattering takes

place. To accomplish with that, in the present work

the quantum dot laser response to current injection

with both cascade and direct capture models is

analyzed from the calculated Lyapunov exponents of

the dynamic system (Monteiro, 2002). Such

exponents (each one associated to a given state

variable) represent a measure of how the

hypervolume of an n-dimensional sphere (thinking

of the state space system representation) changes

with time, being therefore essential to confirm

chaotic dynamic.

212

Andre Pereira The G..

2D-0D Direct Capture of Carriers in Quantum Dot Lasers under Optical Feedback.

DOI: 10.5220/0004794902120217

In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 212-217

ISBN: 978-989-758-008-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

This paper is organized as follows: in the next

section the rate-equations based model to take into

account the delayed optical field and the direct

capture path is presented, and a discussion of the

Lyapunov exponents is added. In section III results

are presented and discussed. Finally, we draw the

conclusions.

2 MODELING

2.1 Rate-equations

The model here used is based on that of (The, 2012),

which considers separate dynamics for electron and

hole populations of InAs quantum dots inserted in

InGaAs quantum well, with GaAs separate

confinement heterostructure (SCH). In order to

correctly include the inhomogeneous dot size

distribution which takes place in the Stranski-

Krastanow growth technique, a multi-population

approach has been adopted (Rossetti, 2007); this

means that quantum dots of an ensemble are

separated into n small groups of dots similar in size,

thus leading to n equations for carrier number of

each confined state (GS, ES1 and ES2).

Furthermore, it contains the scattering channel of

carrier from the wetting layer to the confined states.

To highlight this, for what concerns carriers of the

conduction band, in the following only the

population equations for wetting layer, first-excited

and ground-state are respectively reported.







sw ws

w1 w0

n= +

tt t t

n ρ













(1)









 



2101

21 01

11 2

12 10

n ρ n ρ

n= +

n ρ

+n ρ n ρ

ttt

 



 





(2)

 



10 0

n ρ n ρ

n= +

n ρ

 





(3)

In the above equations,

is the SCH carrier

number and

is the carrier number of electrons in

the second-excited state. Terms inside the brackets

typed with greek

are the average occupation of

confined states (2 for ES2, 1 for ES1 and 0 for GS).

Terms in the denominator indicate the average time

constants for the various scattering mechanisms

between carriers of the conduction band; for

example,

is the average escape time from level 0

(GS) to energy level 1 (ES1), whereas

refers to

direct scattering from WL energy states to ES1

energy state. These scattering phenomena are

illustrated in Figure 1.

Figure 1: Schematic diagram of carrier dynamics in

conduction band. In dashed arrows the 2D-0D capture

channel.

In the valence band things are simpler, since hole

dynamics is governed by two equations only: one for

the dot states (index d) and one for holes in the SCH

(index s):

−

(4)

−

(5)

Notation of equations (4) and (5) is similar to the

previous ones, except that now they refer to holes,

and n

expresses the population of carriers in the

quantum dot and wetting layer altogether (2D and

0D holes constitute one ensemble). Term

I/e is the

mean number of holes injected per unit time in the

separate confinement heterostructure.

In the above equations non-radiative and

radiative recombination terms are omitted for

brevity.

The main difference between the model here

used and that of (The, 2012) is that the photon

equations for the cavity resonant modes have been

replaced by one equation for the internal electrical

field intensity,

and one for its phase, Φ. This

follows the classical Lang-Kobayashi model (Lang,

1980) used widely to study the effects of optical

feedback in semiconductor single-mode lasers (Otto,

2010; O'Brien, 2004). Here are the remaining two

equations:

2D-0DDirectCaptureofCarriersinQuantumDotLasersunderOpticalFeedback

213



2t 2n

cos

ph r

nES2 nES1 nGS

E= + +B

+g +g E

+k E t t w t + Δ t











(6)







sin

kE t t

Φ wt +Δ t

 



(7)

In the above equations

is the photon lifetime

in the laser cavity,

c is the free-space light velocity,

is the active material refractive index, k is the

intensity of feedback light,

is the angular

frequency of the solitary laser,

is the external

cavity roundtrip time and δf is the frequency chirp

calculated according to (Gioannini, 2007). Finally,

the terms inside the summation operator is the

material gain coupling cavity photons and carriers of

the ground-, first- and second-excited states.

2.2 Calculation of Lyapunov

Exponents

According to the theory of dynamical systems, only

nonlinear dissipative systems may experience

chaotic behavior, being chaos related to sensitivity

to initial conditions and characterized by a time

evolution towards a strange attractor in the phase

space (Monteiro, 2002). A widely used approach to

test sensitivity to initial conditions of nonlinear

systems and, therefore, conclude about the existence

of chaos requires the calculation of Lyapunov

exponents. Given a dynamic system with

p velocity

fields associated to state variables, there are two

requirements to be satisfied before concluding if the

process is chaotic:

a) at least one of the Lyapunov exponents

associated to the velocity equations is positive: this

is to guarantee divergence of adjacent trajectories

(those starting at slightly different initial

conditions);

b) the sum of all Lyapunov exponents associated

to the whole set of velocity field equations must be

negative: this is to ensure the system is dissipative

(and therefore phase space evolution towards a

strange attractor occurs).

In the present work the calculation of the Lyapunov

exponents is based on the following formula:









log

Fx+δ Fx

Λ =

N δ













(8)

In this expression,

N is the size of the discrete

time vector corresponding to the last time instants

of every simulation (transient is discarded), δ

is the

small deviation between two different initial

conditions and

F is the vector of state variables

representing the dynamical system.

3 RESULTS AND DISCUSSION

The model has been used to study the laser response

when it is subject to optical feedback, under

different current injection conditions. The device

considered is a 0.6 mm long edge-emitting device

emitting from the ground-state lasing line, at 1285

nm. This device has been chosen to allow for better

comprehension of already reported results,

especially the chaotic-like solutions which had not

been explained in terms of Lyapunov exponents

(Gioannini, 2008a and 2008b). Another goal of the

present analysis is to check whether the direct

capture carrier scattering phenomenon may

influence the conditions for chaos in the laser

device. Other parameters used in the simulations are

listed in Table 1.

Table 1: Quantum-dot material and laser parameters used.

Laser width: 4 microns QD density: 4.10

-2

Number of QD layers: 10 Energy separation (meV):

WL-ES2: 13 meV

ES2-ES1: 36 meV

ES1-GS: 37.3 meV

Internal loss: 1.5 cm

-1

Left/Right end-

reflectivity: 0.3/0.3

To accomplish with that, the following results

focus on the time-domain evolution of the Lyapunov

exponents. Figures 2 to 4 report for 150 mA, 300

mA and 600mA, respectively, in the top part the sum

of the Lyapunov exponents (for a total of 142

dynamic equations describing the laser under

feedback), and in the bottom the largest Lyapunov

exponent. First result is that at any of these injection

conditions there is always at least one positive

exponent and, besides, the whole sum of exponents

is always negative. This formally confirms,

therefore, that quantum dot lasers, as suggested by

previous theoretical and experimental works are

sensitive to feedback oscillations, entering chaotic

regime at different operating conditions.

Figures 2, 3 and 4 solid lines refer to results

obtained with a model including the direct capture

process, whereas dotted lines refer to a cascade

scattering based model. Simulation revealed two

interesting point about this: first, by comparison of

the largest Lyapunov exponent in Figures 2 and 4,

we see that at lower current injections higher

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

214

positive Lyapunov exponents are obtained when the

direct capture path is present, whereas at higher

electrical current levels the cascade model got higher

positive exponents. Since the positive Lyapunov

exponent is a measure of how fast two slightly

different initial conditions evolves to a divergence of

the velocity field, this result can be explained in

terms of the higher carrier density in the wetting

layer achieved with the cascade model (this is

because the direct capture represents an additional

drain for wetting layer carriers down to the dot

confined states).

Figure 2: Time evolution of Lyapunov exponents for 150

mA injection condition. Solid lines refer to direct capture

model and dotted lines to cascade only model.

Figure 3: Time evolution of Lyapunov exponents for 300

mA injection condition. Solid lines refer to direct capture

model and dotted lines to cascade only model.

Another important result in these figures is the

indication of hiperchaos in both direct capture and

cascade models, suggested by the existence, in

steady-state, of two positive Lyapunov exponents in

Figures 2 (solid lines, direct capture model) and 4

(dotted lines, cascade model).

To illustrate the sensitivity to initial conditions,

in Figure 5 it is shown the laser response in time-

domain, for a 150 mA driving current, when the

direct capture scattering process is included. Solid

line refers to the optical power evolution after a

certain initial condition, and the dotted line is the

same, except for a slight change in the initial

condition (from 10

-6

to 1.1 x 10

-6

) of some of the

state variables. Notice how the responses differ after

11000 integration steps.

Figure 4: Time evolution of Lyapunov exponents for 600

mA injection condition. Solid lines refer to direct capture

model and dotted lines to cascade only model.

Figure 5: Time-domain evolution of the photon number in

the laser cavity when the direct capture model is

considered. Dotted-line and solid-lines differ slightly in

the initial values for the state variables.

Finally, to complete this look at the Lyapunov

exponents, in Figure 6 the exponents associated to

the equations for carriers in the dot confined states

2D-0DDirectCaptureofCarriersinQuantumDotLasersunderOpticalFeedback

215

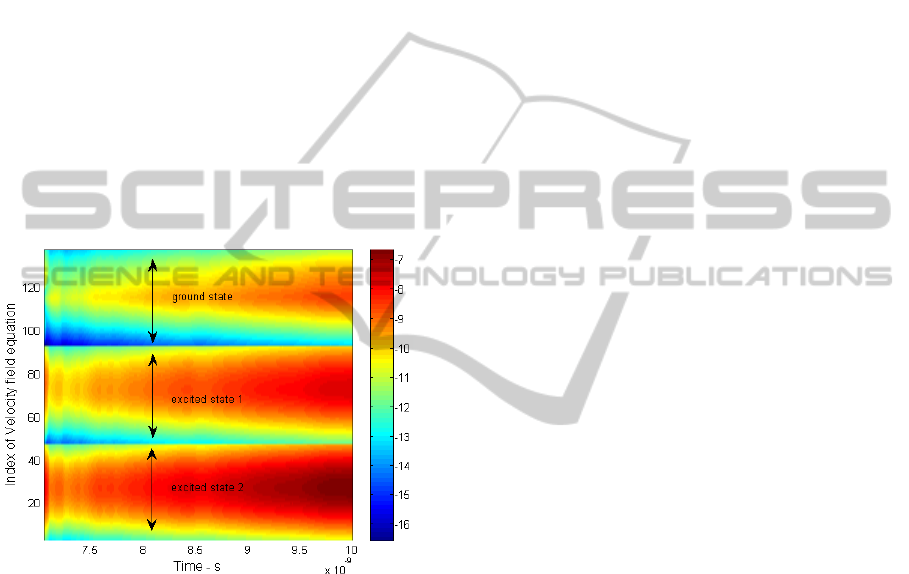
(ground-, first-excited and second-excited states) are

shown in color map. It refers again to the 150 mA

driving condition.

According to this figure we can see that the

exponents associated to the confined states are all

negative (thus being essential for the dissipative

feature of the system), and that there is a clear

dependence of the exponents on the quantum dot

grouping (carriers from the quantum dots more

likely in the ensemble lead to less negative

exponents). Additionally, if ES2 carriers are

compared to ES1 and GS ones, it can be pointed out

that carriers resonant with the spectral window of

lower material gain (that containing ES2 states)

contribute to less negative values of Lyapunov

exponents. This suggests that the way to get other

positive Lyapunov exponents is to operate with

shallow dots, favoring carrier escape up to wetting

layer, a scenario in which higher energy confined

states are less populated.

Figure 6: Time-domain evolution of the Lyapunov

exponents associated to the carrier number equations of

confined states. Color indicates magnitude of the

Lyapunov exponents.

4 CONCLUSIONS

In this work a numerical model for the direct capture

scattering process in quantum dot lasers under

optical feedback has been developed, and an

analysis of the possibility of chaotic operation has

been done after numerical calculation of the

Lyapunov exponents of the system.

Simulation results revealed that positive

Lyapunov exponents are achieved at different

driving conditions, for both direct capture and

cascade only models. Comparison between these

models showed different sensitivity to initial

conditions at different electrical driving levels: with

the direct capture included in the model, higher

positive exponents are obtained at lower currents,

and an inverse trend is obtained for the cascade

model.

Finally, results of the Lyapunov exponents

associated to the carriers in the dot confined states

showed that there is major tendency to negative

values and that the threshold of positive values may

be related to the spectrum window of lower material

gain.

ACKNOWLEDGEMENTS

Brazilian agency CNPq supported this work;

reference number 482393/2011-4.

REFERENCES

Carroll, O., Hegarty, S. P., Huyet, G., Corbett, B., 2005,

“Length dependence of feedback sensitivity of

InAs/GaAs quantum dot lasers,” Electronics Letters,

vol. 41, no. 16, pp. 39-40.

Carroll, O., O'Driscoll, I., Hegarty, S. P., Huyet, G.,

Houlihan, J., Viktorov, E. A., Mandel, P., 2006,

“Feedback induced instabilities in a quantum dot

semiconductor laser,” Optics Express, vol. 14, no 22,

pp. 10831-10837.

Gioannini, M., Montrosset, I., 2007, “Numerical analysis

of the frequency chirp in quantum-dot semiconductor

lasers,” IEEE J. Quantum Electron., vol. 43, no. 10,

pp. 941 – 949.

Gioannini, M., Al-Khursan, A. H., The, G. A. P.,

Montrosset, I., 2008a, “Simulation of quantum dot

lasers with weak external optical feedback,” The

Dynamics Days Europe, August 25-29, Delft.

Gioannini, M., The, G. A. P., Montrosset, I., 2008b,

“Multi-population rate equation simulation of quantum

dot semiconductor lasers with feedback,” 8th

International Conference on Numerical Simulation of

Optoelectronic Devices, September 1-5, Nottingham.

Lang, R., Kobayashi, K., 1980, “External optical

feedback effects on semiconductor injection laser

properties” IEEE J. Quantum Electron., vol. 16, no. 3,

pp. 347 – 355.

Melnik, S., Huyet, G., Uskov, A. V., 2006, “The linewidth

enhancement factor α of quantum dot semiconductor

lasers,” Optics Express, vol. 14, no. 7, pp. 2950-2955.

Monteiro, L. H. A., 2002, Sistemas Dinamicos, chapter 10,

Ed. Livraria da Fisica, Sao Paulo.

O'Brien, D., Hegarty, S. P., Huyet, G., Uskov, A. V.,

2004, “Sensitivity of quantum-dot semiconductor

lasers to optical feedback,” Optics Letters, vol. 29, no.

10, pp. 1072-1074.

PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology

216

Otto, C., Ludge, K., Scholl, E., 2010, “Modeling quantum

dot lasers with optical feedback: sensitivity of

bifurcation scenarios,” Physica Status Solidi B, vol.

247, no. 4, pp. 829-845.

Rossetti, M. et al, 2007, “Characterization and modeling

of broad spectrum InAs-GaAs quantum-dot

superluminescent diodes emitting at 1.2-1.3 um,”

IEEE J. Quantum Electron., vol. 43, no. 8.

The, G. A. P., 2012, “Rate-equations based model for the

2D-0D direct channel in quantum dot lasers,” 15o

Simposio Brasileiro de Micro-ondas e Optoeletronica,

August 5-8, Joao Pessoa.

2D-0DDirectCaptureofCarriersinQuantumDotLasersunderOpticalFeedback

217