Automated Generation of Geometry Questions for High School

Mathematics

Rahul Singhal

, Martin Henz

and Kevin McGee

School of Computing, National University of Singapore, Singapore, Singapore

Department of Communications and New Media, National University of Singapore, Singapore, Singapore

Keywords:

Automated Deduction, Graph-based Knowledge Representation.

Abstract:

We describe a framework that combines a combinatorial approach, pattern matching and automated deduction

to generate and solve geometry problems for high school mathematics. Such a system would help teachers

to quickly generate large numbers of questions on a geometry topic. Students can explore and revise speciﬁc

topics covered in classes and textbooks based on generated questions. The system can act as a personalized

instructor - it can generate problems that meet users speciﬁc weaknesses. This system may also help standard-

ize tests such as GMAT and SAT. Our novel methodology uses (i) a combinatorial approach for generating

geometric ﬁgures (ii) a pattern matching approach for generating questions and (iii) automated deduction to

generate new questions and solutions. By combining these methods, we are able to generate questions in-

volving ﬁnding or proving relationships between geometric objects based on a speciﬁcation of the geometry

objects, concepts and theorems to be covered by the questions. Experimental results show that a large number

of questions can be generated in a short time. We have tested our generated questions on an existing geometry

question solving software JGEX, verifying the validity of the generated questions.

1 INTRODUCTION

Geometry, the study of space and spatial relation-

ships, is an important and essential branch of the

mathematics curriculum at all grade levels. The study

of geometry develops logical reasoning and deduc-

tive thinking, which helps us expand both mentally

and mathematically. Children who develop a strong

sense of spatial relationships and who master the con-

cepts and language of geometry are better prepared

to learn number and measurement ideas, as well as

other advanced mathematical topics (National Coun-

cil of Teachers of Mathematics, 1989).

Euclidean geometry is a branch of mathematics

which deals with the study of plane and solid ﬁgures

on the basis of axioms and theorems employed by the

Greek mathematician Euclid. It is important to un-

derstand Euclidean geometry when studying a course

because geometry does not follow any set pattern. In

Euclidean geometry, one can only learn the axioms

and results proven from these axioms. The student

must apply these axioms with no set pattern or list of

steps for solving such questions. Therefore, a ques-

tion may have (possibly inﬁnitely) many solutions. To

practice the required problem solving skills, students

require a large number of different types of geome-

try questions on various concepts. Generally, text-

books and online sites provide a limited predeﬁned

number of questions for each topic. Once practiced,

these questions lose their purpose of enhancing stu-

dent thinking. The tedious and error-prone task of

generating high-quality questions challenges the re-

sources of teachers. Hence, there is a need for soft-

ware which assists both teachers and students to gen-

erate geometry questions and solutions.

The software can also act as a personalized in-

structor. It can generate questions that cover the re-

quired topic and meet the required level of student

proﬁciency. Apart from helping users, the framework

of generating questions has scientiﬁc contributions to

other research areas, such as Intelligent tutor systems

(ITS) and Massive Online Open Courses (MOOC).

Various research has been performed in automated

deduction of theorems at high school level in the ge-

ometry domain, although none with the goal of auto-

matic question generation. Instead, they mainly de-

mand users to generate the question with the help

of tools. In addition, they mainly focus on solving

and assessment of the questions. Our survey shows

that the currently available geometry systems, such as

Singhal R., Henz M. and McGee K..

Automated Generation of Geometry Questions for High School Mathematics.

DOI: 10.5220/0004795300140025

In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 14-25

ISBN: 978-989-758-021-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

JGEX, Geogebra, Cinderella and Sketchpad, are not

able to automatically generate questions of user spec-

iﬁed geometry topics.

The aim of this paper is to develop a framework

that can be used to generate geometry questions based

on speciﬁc inputs, such as geometry objects and theo-

rems to be involved in their solution. For a given set of

geometry objects, the algorithm can generate a large

set of questions along with their solutions. The so-

lutions will involve user desired theorems directly or

indirectly. Hence the framework can generate ques-

tions to test the theorem on various geometry objects

and concepts.

Our framework can generate questions involving

algebraic computations for a solution. Currently, we

restrict the relationships between quantitative enti-

ties to linear ones. Our framework has a predeﬁned

database of theorems and concepts which can be used

for generating questions. Given a set of user-selected

objects, our system can generate all possible ques-

tions using an existing database of concepts and theo-

rems.

The main contributions of this paper are as fol-

lows:

1. Our geometry question generator combines the

complementary strengths of a combinatorial ap-

proach, pattern matching and deductive reason-

ing. It can generate geometry questions which

were not possible previously.

2. A substantial evaluation is provided that demon-

strates the effectiveness of our generator. It can

generate various categories of the questions cov-

ered in the textbooks and questions asked in SAT

and GMAT.

3. A knowledge representation is described for ge-

ometry objects and predeﬁned theorems. This

representation helps in applying theorem informa-

tion within the generated questions.

2 RELATED WORK

In this section, we provide a general review of related

works. Computational research in the geometry do-

main started in the 19th century. However, lack of

question generating in geometry in the literature re-

quired a principled ab-initio approach in our work.

Researchers mainly focused on proving geometry

theorems. Broadly, geometric theorems are proven

using algebraic or non-algebraic methods. Algebraic

methods such as Wu’s method and Gr

obner bases

(GB) (Chou et al., 1994) generate algebraic equa-

tions from the given facts and relations. They involve

coordinate geometry and algebraic formulas to ﬁnd

new theorems. Hence, the proofs generated by these

methods are out of scope of high school mathematics

(Chou and Gao, 2001). Therefore, we are mainly in-

terested in the non-algebraic methods. Non-algebraic

methods for automatic discovery and proof of ge-

ometry theorems can be further divided into three

approaches: coordinate-free methods, formal logic

methods and search methods.

2.1 Coordinate-free Methods

These methods are applicable to constructive geom-

etry statements of equality. Various methods have

been proposed under this category, such as the area

method (Narboux, 2010; Chou et al., 2011), the full-

angle method (Chou et al., 2000; Wilson and Fleu-

riot, 2005), the complex number method, the vec-

tor method for Euclid plane geometry (Chou et al.,

2000), the volume method for Euclidean solid geom-

etry (Chou and Gao, 2001) and the argument method

for non-Euclidean geometry (Chou and Gao, 2001).

The area method was further improved and developed

into a computerized algorithm (Chou et al., 2000;

Chou and Gao, 2001). These methods can only be

applied in constructive geometry, which is outside the

scope of this paper.

2.2 Formal Logic Methods

Theorems in Tarski’s geometry were proven using

Interactive Theorem Prover (ITP) (McCharen et al.,

1976), albeit limited to several trivial theorems. ITP is

an interactive theorem prover based on the resolution

principle, which generates resolution style proofs that

resemble traditional proofs. In 1989, Quaife contin-

ued the work of McCharen with Otter (Quaife, 1989).

Otter is an automated theorem prover based on resolu-

tion. A series of tactics such as Hyper-resolution, UR-

resolution, paramodulation, support set and clause

weight can improve the resolution efﬁciency. In

2003, Meikle and Fleuriot developed Hilbert’s geom-

etry with the theorem prover Isabelle/Isar (Meikle and

Fleuriot, 2003), an interactive and/or semi-automated

theorem prover. The greatest disadvantage of formal

logic methods is their low reasoning efﬁciency (Jiang

and Zhang, 2012), caused by combinatorial explosion

of their search space.

2.3 Search Methods

Fundamentally, the search method is used in a rule-

based expert system, which includes a rule database,

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics

a fact database and a reasoning engine. The infer-

ence rules stored in the rule database include axioms,

theorems, lemmas, formula, deﬁnitions and algebraic

operation rules in geometry. Geometric facts stored in

the fact database include geometry predicates such as

angle bisector, equidistant points, parallel lines and

perpendicular lines. The reasoning engine deduces

new geometric facts by applying inference rules to the

facts database. There are three ways of performing

deduction search, namely forward chaining (Zhang

et al., 1996; Wilson and Fleuriot, 2005), backward

chaining (Wilson and Fleuriot, 2005), and bidirec-

tional chaining (Coelho and Pereira, 1986).

Forward chaining starts from the hypotheses and

rules and works towards the conclusion, while back-

ward chaining starts from the conclusion and works

towards the hypotheses through rules, and the bidirec-

tional chaining proceeds in both direction simultane-

ously. In 1975, Nevins proved geometry theorems via

bidirectional chaining (Nevins, 1975), and in 1986,

Coelho and Pereira developed a prover GEOM based

on bidirectional chaining (Coelho and Pereira, 1986).

Unlike Nevins, GEOM implemented backward chain-

ing in the reasoning process and only used forward

chaining to search congruent triangles hidden in the

diagram. In 1995, Chou, Gao, and Zhang described

an integration of a deductive database into the search

methods (Chou et al., 2000; Gao et al., 1998; Gao

et al., 1998; Chou and Gao, 2001). The deductive

database method can ﬁnd a ﬁxpoint for a given geom-

etry diagram, containing all properties of the geome-

try diagrams that can be deduced using a ﬁxed set of

geometry rules. They effectively controlled the size of

the facts database with structural deductive database

techniques.

Each search method has different advantages and

disadvantages. Forward chaining is always feasible,

but does not have an explicit reasoning goal. Back-

ward chaining has an explicit reasoning goal, but

sometimes lacks feasibility. The bidirectional chain-

ing method is feasible and has an explicit reasoning

goal, but is hard to implement. We are using forward

chaining in our framework as it is most suited for gen-

erating previously unknown quantities.

3 GEOMETRY QUESTION

SPECIFICATION

Mathematically a geometry question Q generated by

our system can be represented by a quintuple (Object

O, Concept C, Theorem T, Relationship R, Query type

qt) where:

• O ∈ (lines, triangles, square, circle, ... )

Figure 1: Connection of these components and knowledge

representations.

• C ∈ (perpendicular, parallel, midpoint, angle-

bisector, circumcircle...)

• T ∈ (Pythagorean theorem, similarity theorem,

various triangle-theorems, ...)

• R ∈ (syntactic, quantitative)

• qt ∈ (syntactic, quantitative)

In order to generate geometry questions, the user has

to provide a set of geometry objects O such as tri-

angles, squares, etc., and a set of concepts C which

the user wants the generated question to cover. Op-

tionally the user may select a set of theorems T to be

tested by the question. The relationship R can be ei-

ther syntactic such as perpendicular, parallel, etc., or

quantitative such as the length of an object, the ratio

of two quantities etc. The query type qt is the type

of generated question that can be asked to ﬁnd the

hidden relationship which can be calculated from the

given information.

4 FRAMEWORK

Our framework comprises three major components

along with the knowledge databases used for storing

input, geometry ﬁgures and a set of predeﬁned theo-

rems. Figure 1 shows the connection of these compo-

nents. The input consists of geometric objects, con-

cepts and theorems selected by the user. The input is

fed into the ﬁrst component, Generating Figure (GF).

This component is used for generation of geometric

ﬁgures from the input. Each ﬁgure constitutes a di-

agrammatic schema (DS) (Greeno et al., 1979) and

a set of unknown variables representing the relation-

ship between geometric objects. The geometric ﬁg-

ure is passed to the second component, Generating

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

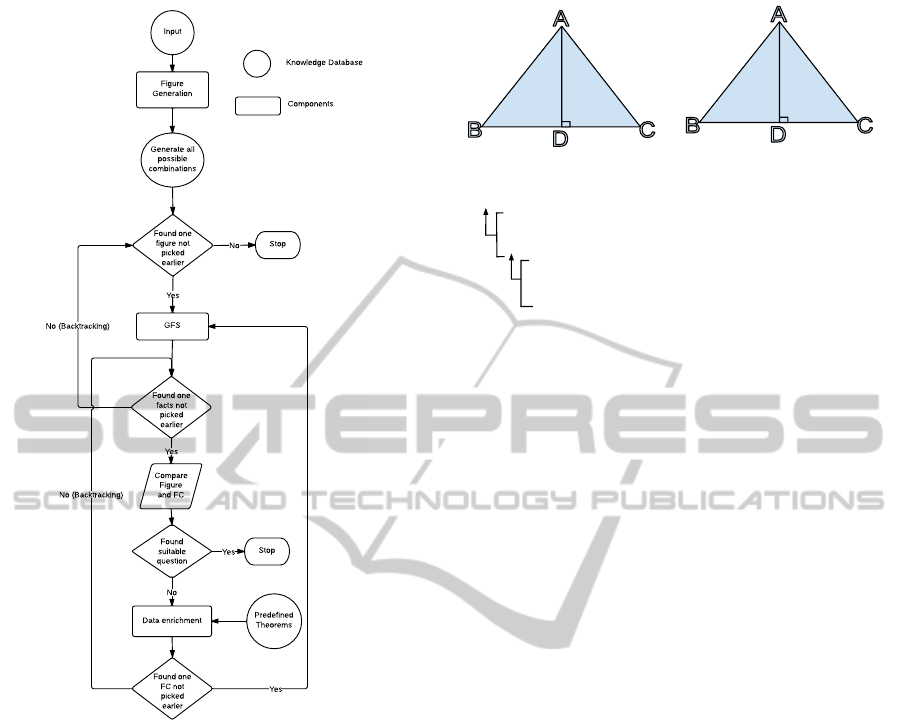
Figure 2: Flow diagram of the algorithm for generating

questions.

Facts and Solutions (GFS). This component is used

to ﬁnd values of the unknown variables representing

possible relationships to be asked by the generated

question. GFS makes use of the predeﬁned knowl-

edge database of axioms. It results in the formation

of a conﬁguration (Cfg) containing known values for

some relationships between its objects. New infor-

mation refers to the generation of suitable questions.

A question is considered suitable if it covers the es-

sential information such as a new fact and a proper

reasoning for the generated fact. Currently, the deci-

sion of suitability is taken manually by the user.If the

suitability conditions for the generated conﬁguration

(Cfg) are not met then conﬁguration is fed into the last

component, Generating data for the ﬁgure (GD). GD

assigns values to unknown variables of relationships.

Repeated processing by GD makes the questions gen-

erated from Cfg easier and easier, because the values

assigned by GD appear as given facts in the generated

questions. GD makes use of a predeﬁned set of the-

(a) (b)

length(B,D,7)

Pythagoras Theorem

length (A,B,10) (Given)

length (A,D,5) (Calculated)

Pythagoras Theorem

length (A,C,5) (Given)

length (D,C,4) (Given)

(c)

Figure 3: (a) The ﬁgure is generated by using triangle and

perpendicular as the geometry objects using the GF com-

ponent. (b) The data is generated for (a) using the GD com-

ponent. (c) The new fact and its derivation using the GFS

component is generated from the ﬁgure shown in (b).

orems and makes sure that the assignment results in

successful generation of geometry questions. FC gen-

erated from this component is again passed to GFS

component and this loop continues until a question is

found which meets suitability condition.

Along with these components, two knowledge

databases are used in the framework, namely the

Knowledge database for the generated ﬁgures (KF)

and the knowledge database for predeﬁned theorems

(KT). KF is generated dynamically during generation

of questions while KT is ﬁxed and can be modiﬁed

only after the algorithm terminates. KF is generated

and modiﬁed by the GF function, and GD requires

both KF and KT for generating data for the ﬁgure.

GFS has a set of axioms but no access to any knowl-

edge databases.

4.1 Algorithm

Figure 2 represents the ﬂowchart describing the al-

gorithm for generating geometric questions. Al-

gorithm 1 describes the ﬂowchart in further detail.

Here, we shall explain Algorithm 1 with the help of

an example. Figure 3 shows the step by step execu-

tion of the algorithm. We select the following input in

our example.

• Object: triangle and line segment

• Concept: perpendicular

• Theorem: Pythagorean Theorem

• Number of questions: 1

In the next subsections, we will describe each

knowledge database in detail, followed by the

three components and their interaction with these

databases.

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics

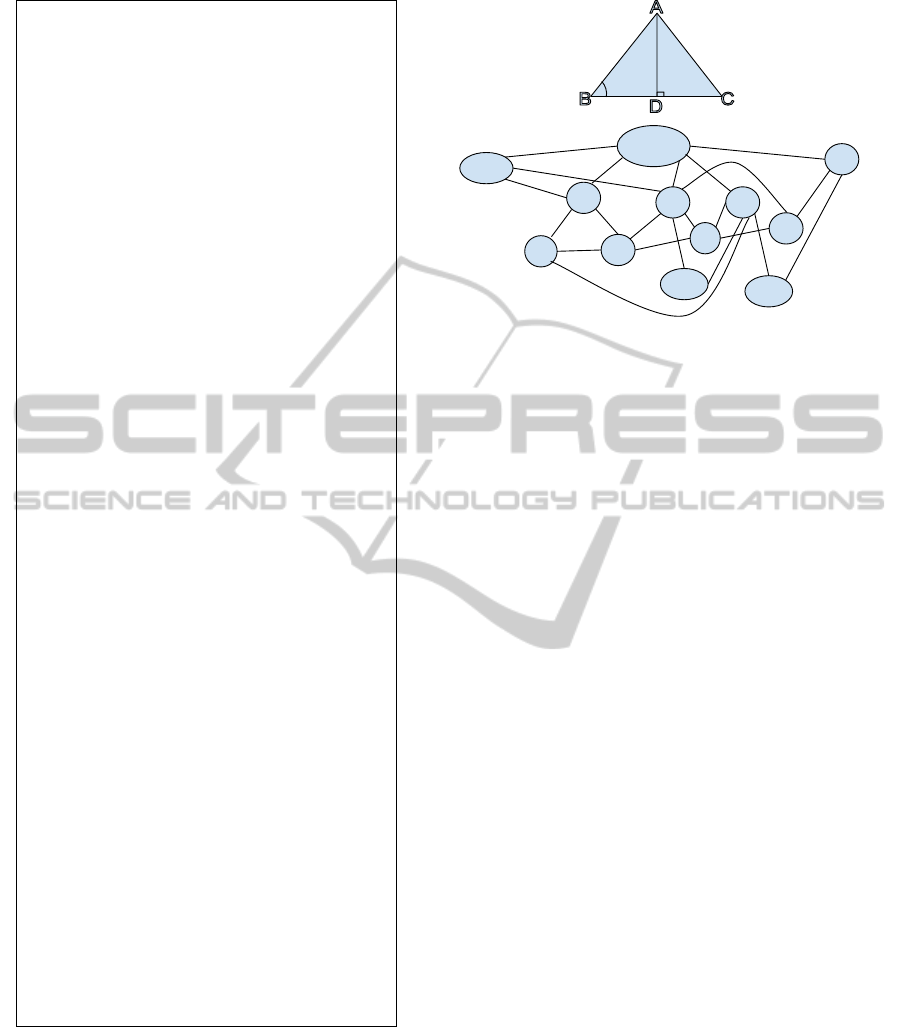
Data: User selects object(s), concept(s),

theorem(s) and the number of

questions to be generated.

Result: Question with single or multiple

solutions.

1. Generate all possible ﬁgures consisting

of geometry objects using GF function

from the given input.

2. Find one ﬁgure which has not been

picked earlier. If found, go to next step

else terminate.

3. Save this ﬁgure using KF knowledge

database.

4. Assign values to variables of ﬁgure

obtained in second step from the

predeﬁned knowledge database of

axioms through GFS function.

Conﬁgurations (Cfg) are generated

from this step.

5. Find one Cfg not picked earlier. If

found, goto next step. If not found,

backtracking to step 2.

6. Compare Cfg with the previously

stored ﬁgure.

7. If the comparison gives the desired

suitability then the Cfg is declared as a

generated question and the algorithm

stops. If the conditions are not met or

more number of questions are

required, go to the next step.

8. Conﬁguration Cfg obtained from GFS

is fed into the third component to

assign more unknown variables. It

makes use of KT, a predeﬁned

database of theorems.

9. From the conﬁgurations obtained from

GD, ﬁnd a new conﬁguration Cfg

which has not been chosen earlier. If

found, goto step 3. If all conﬁgurations

have been chosen earlier, goto step 5.

Algorithm 1: Algorithm for generating geometry

questions.

4.2 Knowledge Database for the Figure/

Figure Conﬁguration (KF)

KF contains the question ﬁgure and conﬁgurations

using a graph-based knowledge representation. The

Angle

ABC,

AB,

CA,

Triangle

ABC

Angle

ACB

Angle

CAD

HAS

CONTAIN

INDIRECTLY HAS

CONTAIN

HAS

(a)

(b)

CONTAIN

Figure 4: (a)The geometry ﬁgure and (b) Partially drawn

knowledge representation of (a).

nodes of our graph represent the geometric objects.

Two nodes can have multiple labeled arcs between

them, representing multiple relationships. In addition,

an arc can be bidirectional or unidirectional depend-

ing on the relationship between the nodes. Follow-

ing the example of the previous section, Figure 4(a)

shows the geometric ﬁgure: a triangle ABC is given

and AD is perpendicular to BC. Figure 4b shows its

partial representation in a graph format where we fo-

cus on the most important relations. Relationships

such as ”equal angle” and ”equal length”, which

require multiple objects/nodes, are represented by

nodes, e.g. , the relationship ”∠ABC” in Figure 4(b).

In addition, nodes of our graph store the value of

quantitative relationships. For example, the node

named ” Angle ABC ” stores the value of angle and

is connected to the two nodes representing sides AB

and BC.

KF is generated dynamically from the geometry

objects selected by the user. KF is initialized by the

GF component and later modiﬁcation is done accord-

ing to Algorithm 1 deﬁned in Section 4.1. Modiﬁca-

tion involves creation and deletion of nodes and arcs

between them.

4.3 Knowledge Database for Predeﬁned

Theorems (KT)

KT is a knowledge database which contains the pre-

deﬁned database of theorems. KT is used for assign-

ing values to the unknown variables of conﬁgurations

generated by the GF component. KT uses a graph-

based representation similar to KF. However the dif-

ference lies in the timing of generation. Unlike KF,

KT is generated before the system can generate ques-

tions and remains unchanged during the algorithm ex-

ecution. In order to use KT in the algorithm, some

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

Output1

Input2

Input1

Pythagorean

BC AB AC AC BC

HAS

INPUT

OUTPUT

CONTAIN

Figure 5: Representation used for generating data for the

given ﬁgure.

properties of theorems need to be known. Each theo-

rem can be applied to a particular geometry conﬁgura-

tion. Each theorem has certain inputs and outputs cor-

responding to inputs in the geometry conﬁguration.

Hence usage of a theorem requires assigning the vari-

ables of input and/or output. In KT, the information of

input and output for each theorem is stored along with

the geometric conﬁguration in which the theorem can

be applied. Nodes represent objects whereas arcs rep-

resent the input and output relationships. Input and

output are decided ofﬂine before the execution of the

algorithm and later used for assigning unknown vari-

ables to get a useful question. To illustrate the pro-

cess, the Pythagorean Theorem is taken as an exam-

ple in Figure 5. Given a triangle ABC, where ∠ABC

is 90

◦

, Figure 5 partially shows its usage of KT in

generating data. The node representing the side AB

has three arcs, two of which represent input and one

of which represents an output relationship. To use the

side AB as an input, the length of the sides AB and

BC or AC needs to be assigned. On the other hand,

to use side AB as an output, the length of sides AC

and BC needs to be given. By giving this as input or

output, we can be sure that the Pythagorean Theorem

will give a consistent result.

Now we are ready to describe the three compo-

nents which will use these knowledge databases to

generate questions and answers.

4.4 Generating Figure from the User

Input (GF)

This is the ﬁrst step executed by Algorithm 1 de-

scribed in Section 4.1. This component generates a

ﬁgure through the combination of a predeﬁned num-

ber of ways to combine geometric objects. Cur-

rently, we are focusing on triangles and line segments.

Hence our algorithm includes combinations in which

various triangles and lines can intersect. Furthermore,

we are currently limiting our algorithm to the inter-

section of two triangles. Adding more objects may

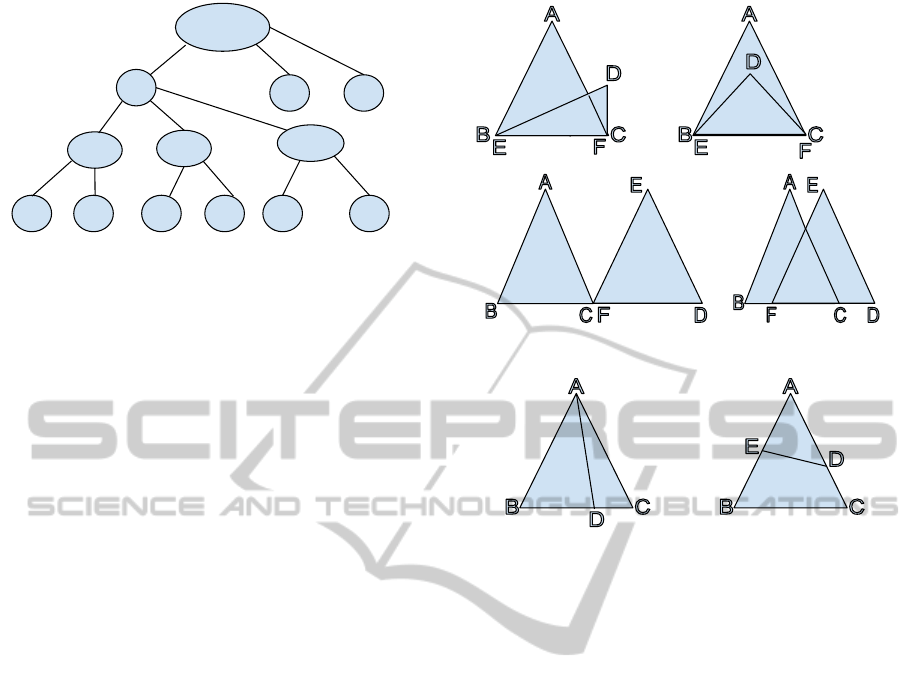
Figure 6: Some predeﬁned ways two triangle can intersect.

Figure 7: Some predeﬁned ways a triangle and a line can

intersect.

make the ﬁgure more complex, possibly leading to

unusual questions that are not commonly found in

textbooks. However there is no limitation on the in-

tersection of lines and triangles. Figure 6 shows some

of the possible ways of intersection of two triangles,

which have been taken into consideration while gen-

erating questions. Intersection of two triangles in-

cludes various cases such as two triangles sharing

common sides, common part of a side, common ver-

tex. Figure 7 shows the two ways in which a line

can intersect with a triangle. Figure 8 describes the

ﬂowchart for ﬁgure generation from the user-desired

input. It includes three functions for adding various

items such as objects, concepts and theorems. These

functions will add their respective items into the gen-

erated DS. For instance, addObject will add a new ob-

ject without removing the old one. Figure 9 shows an

example of adding a new object. Figure 10 shows

the same functions but for concept involvement in the

DS. Similar functions are used for adding theorems,

not discussed here.

The algorithm starts looking for DS in our knowl-

edge database, comprising of the user-desired input.

If DS is not found, then a DS is generated using the

addObject function, possibly resulting in several DS.

From the collection, a DS is picked and moved to the

next level of adding concepts to it. If each DS has

been picked, our algorithm terminates. The same ap-

proach is applied for concept addition in an existing

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics

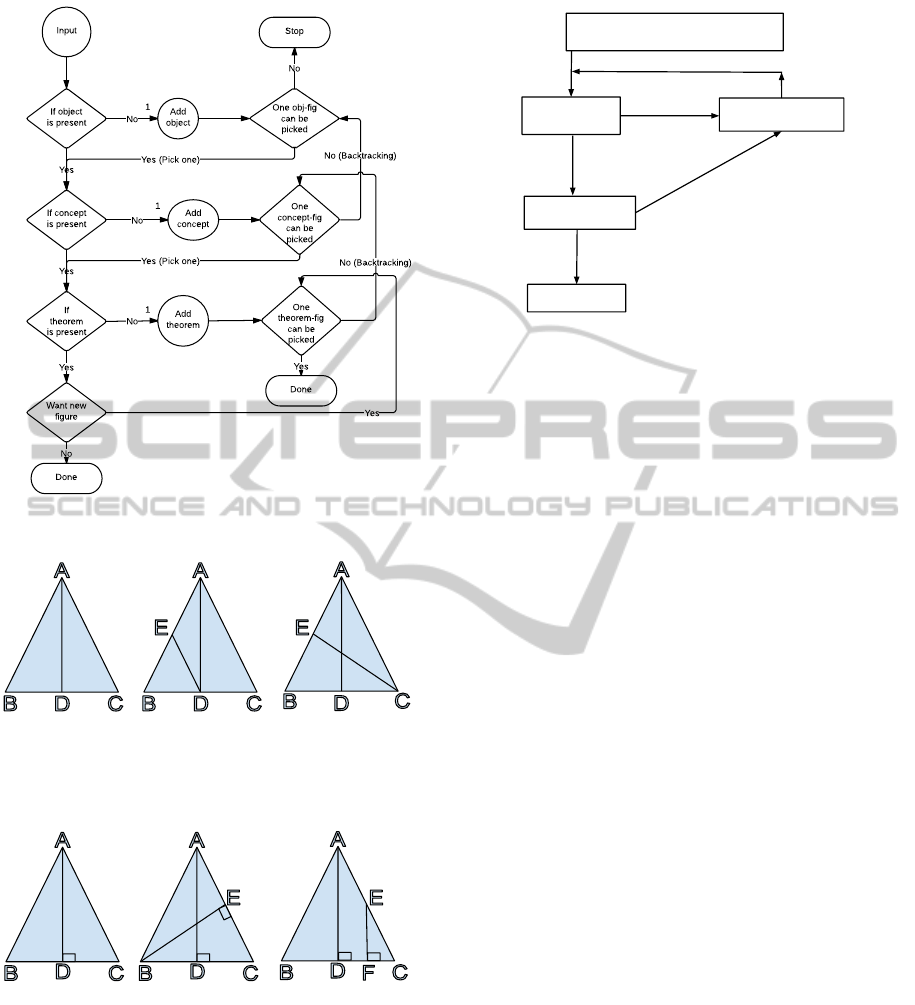
Figure 8: Working of GF component.

(a) (b) (c)

Figure 9: (a) Original ﬁgure; (b, c) ﬁgures resulting from

calling addObject function which adds one more line to the

conﬁguration.

(a) (b) (c)

Figure 10: (a) Original ﬁgure; (b, c) ﬁgures resulting from

calling addConcept function which adds one more concept

to the conﬁguration.

DS. However, in case all DS formed after concept ad-

dition have been picked, backtracking is performed

and a new DS is picked from the object-ﬁgures. A

similar approach is taken when all theorem-ﬁgures

have been picked, where backtracking leads to choos-

ing a new concept-ﬁgure from the previously gener-

ated collection.

Set hypothesis to be a new fact- list

New facts exist?

Reached a fixpoint

Forward Chaining

Terminate

Yes

Figure 11: Represents the approach used by GFS compo-

nent in ﬁnding new facts.

4.5 Generating Facts and Solutions

from the Conﬁguration (GFS)

This component is responsible for ﬁnding the val-

ues of unknown variables of the generated ﬁg-

ure/conﬁguration from the other two components.

This component acts as question generator and solver.

The unknown variables whose values have been found

represent the generated questions. The steps that

leads to ﬁnding the unknown variables represent the

solution. There can be many ways for ﬁnding the

values of the unknown variables. In such cases, this

component shows all solutions. For generating new

facts, it uses a predeﬁned database of theorems. The

difference between the theorem database of this com-

ponent and the previous two components lies in the

representation of theorems. In GFS, each theorem is

represented in the form of an axiom, while GQ and

GF represent theorems in the form of KT and KF, re-

spectively. In addition, GS includes a few basic al-

gebraic theorems, such as (a + b)

= a

+ b

+ 2ab,

which are not present in KT and KF. Such algebraic

theorems are used inside the axiom system for solving

and generating questions which involve algebra.

School Mathematics Study Group (SMSG) ax-

iomatic system is used, which is a combination of

Birkhoff’s and Hilbert’s axiom (Francis, 2002) sys-

tem. Figure 11 shows the ﬂow diagram of this ap-

proach. A ﬁxpoint is a state in which no new facts—in

our case, no new assignment of unknown variables—

can be deduced from the given facts (Chou et al.,

2011). For reaching a ﬁxpoint, forward chaining is

used to infer new facts from given facts and rules. The

rules used by our system are described in Prolog as

follows:

Q(x, n

) : −P

(x, n

)...P

(x, n

) (1)

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

(a)

length(B,C,10)

Apollonius Theorem

length (A, B, 8) (Given)

length (A, C, 6) (Given)

length (A, F, 5) (Calculated)

Pythagoras Theorem

length (A, E, 4) (Given)

length (F, E, 3) (Given)

(b)

Figure 12: (a)A question and its solution(b) involving mea-

surement of geometry objects which can be solved with our

rules.

which means

∀x[(P

(x, n

) ∧ ... ∧ P

(x, n

)) ⇒ Q(x, n

)] (2)

where n

, .., n

and n

represent numeric values. This

representation results in the storage of the integer/real

value of the geometry object in last argument of the

predicate. With the help of new rules, we can now

represent the facts related to dimensions of the ge-

ometric objects. Hence this representation of rules

can generate geometric questions, which involve mea-

surements of the geometric objects.

In addition, we have added predeﬁned algebraic

functions which can be used in rules. One instance of

our new rule is shown in Equation 3. The predicate

sq denotes the square function, which computes the

square of a and stores its value in b.

sq(a, b) (3)

Figure 12 shows an example which can be solved by

our rules. Given a triangle ABC, AE ⊥ BC, AB = 8,

AC = 6, AE = 4, FE = 3. our goal is to ﬁnd the

length of BC. Figure 12(b) provides a solution of

this question with the help of our new rules. In ad-

dition, these rules help to represent the basic theo-

rems which involve measurement values such as the

Pythagorean theorem, the Triangle Inequality theo-

rem and the side/angle ratio theorem in a triangle.

Hence it is possible to generate geometric questions

based on the above mentioned theorems. For instance,

the Pythagorean theorem can be represented in the

following way:

diff(X, C, 0) : −Triangle(a, b, c), sq(a, A), sq(b, B),

sq(c, C), sum(A, B, X ).

(4)

A trivial question which requires the Pythagorean the-

orem for solving would be as follows. Given a right

angle triangle and any two sides of the triangle, the

goal is to ﬁnd the third side.

Similarly, the Triangle Inequality Theorem can be

represented in the following way:

lessthan(X, 0) : −Triangle(a, b, c), length(a, A),

length(b, B), length(c, C),

sum(A, B, Z), diff(Z, C, X).

(5)

A trivial question from this theorem would be as fol-

lows. Given the length of any two sides of a triangle,

our goal is to ﬁnd the maximum value of the third side.

4.6 Generating New Conﬁgurations

from an Existing Conﬁguration

(GD)

Figure 13 explains the algorithm in the form of a

ﬂowchart. It starts with searching for user-selected

theorems. In case the user has not chosen any theo-

rem, a theorem is selected from the predeﬁned knowl-

edge database of theorems. However, our algorithm

terminates when all theorems have been selected once

for a given conﬁguration. After the theorem selection,

pattern matching on the theorem ﬁgure is performed.

If a matching pattern is found, a set of input and/or

output values are assigned to the chosen pattern. As-

signment is done with the help of a predeﬁned set of

theorems. In case the pattern is not found, a new the-

orem is chosen from KT and the whole process is re-

peated until we get the desired conﬁguration.

Depending on the requirements, several theorems

can be involved in a given conﬁguration. In addition,

it is possible to use a single theorem multiple times.

The method requires the concept of using the output

of one theorem as the input of another one. In this

way we can have all possible combinations of prede-

ﬁned theorems. Figure 14 shows an instance of as-

signing unknown variables. Figure 14b represents the

new data assigned to Figure 14a. It is generated with

the help of applying Pythagoras Theorem in triangle

ABE. The output is changed from BE to AE. Output

is considered the length of side calculated using the

Pythagoras Theorem from a given input. The input

and output for the Pythagoras Theorem is taken us-

ing KT. Figure 14c is generated by adding more data

in Figure 14a. New data is assigned by applying the

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics

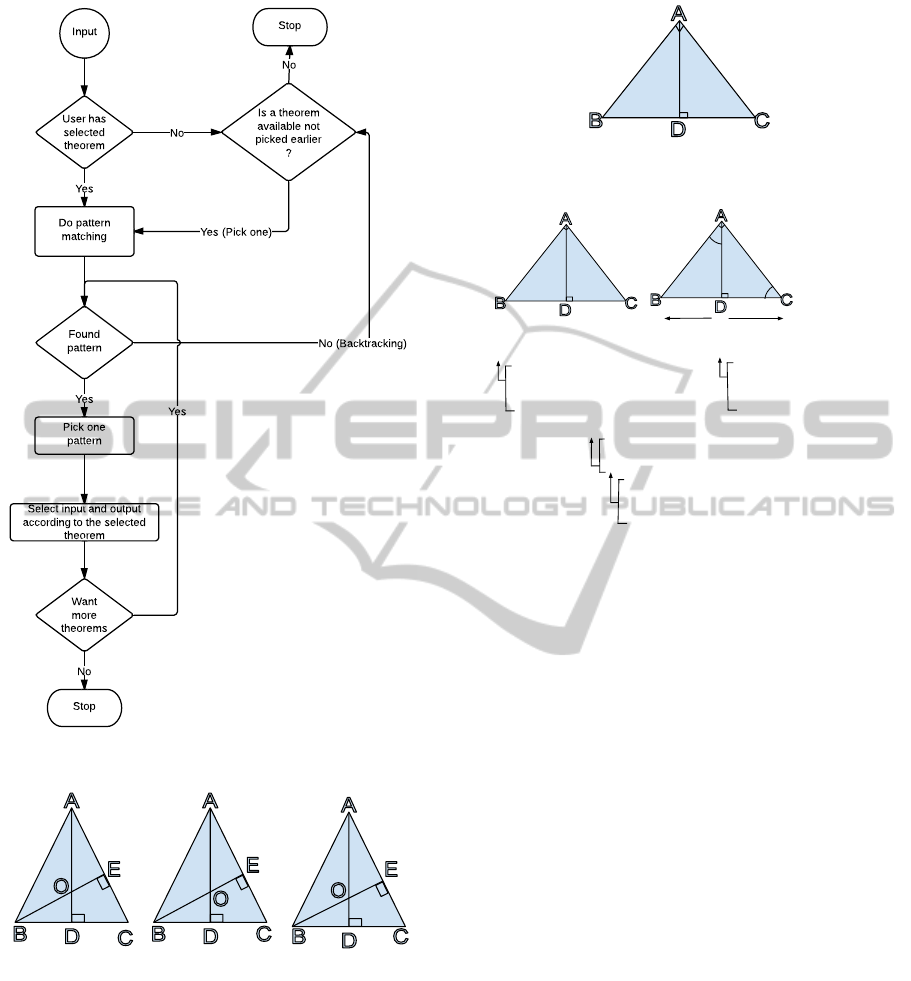
Figure 13: Working of GD algorithm.

(a)

(b)

(c)

Figure 14: (a) A ﬁgure and data is assigned to few geometry

objects. (b) Output of calling the changeData function. (c)

Result obtained by calling the addData function on (a).

Pythagoras Theorem in the triangle ADC. The theo-

rem requires two sides as input to generate one output.

Hence length of side EC is given.

In the above algorithm, it may happen that redun-

dant data is provided in the ﬁgure. Redundant data

refers to the values assigned to properties of some of

the geometric objects which are not required and can

be derived from the previously given data and prede-

9 16

Figure 15: An example in which redundant data is provided

in the given ﬁgure.

(a)

(b)

maxLength(B,C,sqroot(z

+ k

))

Inequality in trigonometry

length (D,B,kSinx) (Calculated in (d))

length (C,D,zCosx) (Calculated)

Trigonometry

perp (A,D,D,C) (Given)

length (A,C,z) (Given)

angle (A,C,C,D,x) (Given)

(c)

length (B,D,kSinx) (Calculated)

Trigonometry

perp (A,D,D,B)

length (A,B,k) (Calculated in (c))

angle (B,A,A,D,x) (Given)

length (B,A, k) (Calculated)

Similarity property

similarTriangle (D,A,C,A,B,C) (Calculated)

length (A,C,z) (Given)

areaRatio (D,A,C,A,B,C,1,y) (Given)

(d)

(e)

Area = y Area

Triangle ADC Triangle ABC

Figure 16: (a) The ﬁgure is generated by using triangle and

perpendicular as the geometry objects using the GF com-

ponent. (b) The data is generated for (a) using the GD com-

ponent such that the two triangles ADC and ADB become

similar. (c, d, e) The new fact and its derivation using the

GFS component is generated from the ﬁgure shown in (b).

ﬁned theorems. Figure 15 explains this situation with

the help of an example. In this ﬁgure, one data item is

redundant and any one of the length values can be re-

moved, since, by applying the similarity concept, the

third length can be derived from the other two lengths.

This type of reasoning may lead to an increase of the

difﬁculty level of the generated questions. This rea-

soning is added with the help of GFS, which is de-

scribed in Section 4.5.

Figure 13 contains non-deterministic decisions at

various steps. The non-deterministic selection of op-

tions can be avoided by adding more heuristics such

as ﬁxing the number and types of theorems to be in-

volved.

5 FURTHER EXAMPLES

This section explains our framework through more

examples covering various concepts and geometric

theorems.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

5.1 First Example

The input given in this question generation task is as

follows

• Object: triangle and line segment

• Concept: perpendicular

• Theorem: similarity, trigonometry and Inequality

• Number of questions: 1

The input given in the ﬁrst example covers the con-

cept of perpendicular lines. The generated questions

are required to make use of theorems involving simi-

larity of triangles, trigonometry and inequality. Fig-

ure 16 shows the step by step execution of the algo-

rithm for the given input. Figure 16a generates a con-

ﬁguration involving triangle and perpendicular ge-

ometry objects using the GF component. This ﬁgure

is generated by non-deterministically selecting a way

of generating perpendicular lines in a triangle from

our predeﬁned database.

Figure 16b is generated using GD component with

the help of KT in the ﬁgure 16a. There are various

ways of making two triangles similar. Firstly, this

component performs pattern matching to ﬁnd the suit-

able ways of making two triangles similar in the ex-

isting ﬁgure. Later, non-deterministically, it picks one

way of making triangles similar and generates data ac-

cordingly. Now GD component assigns data using the

trigonometry rules stored in the database. Currently,

the database is limited to the basic trigonometry rules

related to the sides and angles of a triangle. For exam-

ple, ”sin2θ = 2 sin θ cos θ” trigonometry rule does not

includes any sides and angles in a triangle. Hence, it

is not included in our database.

Figure 16c shows the new facts and the their rea-

soning generated using the GFS component. The new

fact is the new question and the reasoning is the solu-

tion of the generated question.

5.2 Second Example

The input given in this question generation task is as

follows

• Object: triangle and line segment

• Concept: parallel line

• Theorem: similarity and ratio of length of sides

• Number of questions: 1

The input given in the second example covers the con-

cept of parallel line. The generated questions are re-

quired to make use of theorems involving similarity

and ratio of length of sides of a triangle. Figure 17

shows the step by step execution of the algorithm for

(a) (b)

area (A,D,E, X/((c+1)

- 1)) (Calculated)

area (D,B,E,C, X) (Given)

ratioArea (A,D,E,D,B,E,C,1, (c+1)

- 1 )

Algebra

ratioArea (A,D,E,A,B,C,1, (c+1)

) (Calculated)

similarity theorem

similarTriangle (A,D,E, A, B,C) (Calculated)

ratioLength (A,D,A,B,1,c+1) (Calculated)

Algebra

ratioLength (A,D,D,B,1,c) (Given)

(c)

AD/ DB = 1/ c

Area DBCE = X

Find Area Triangle

ADE

Area = ?

Figure 17: (a) The ﬁgure is generated by using triangle and

parallel line as the geometry objects using the GF compo-

nent. (b) The data involving ratio of length of sides is gener-

ated for (a) using the GD component. (c) The new fact and

its derivation using the GFS component is generated from

the ﬁgure shown in (b).

the given input. Figure 17a generates a conﬁguration

involving triangle and parallel line geometry objects

using the GF component. Before generating similar-

ity of two triangles, it ﬁnds similar triangles in the

existing conﬁguration. It can be seen that the existing

conﬁgurations has similar triangles ADE and ABC.

Hence, there is no need to generate similar triangles.

Application of similarity theorem results in the gener-

ation of ratios of sides of length of two triangles. Fig-

ure 17b is generated using GD component with the

help of KT knowledge database. Figure 17c shows

the new facts and the their reasoning generated using

the GFS component. The new fact is the new ques-

tion and the reasoning is the solution of the generated

question.

5.3 Third Example

The input given in this question generation task is as

follows

• Object: triangle and line segment

• Concept: perpendicular and angle bisector

• Theorem: Sum of angle in a triangle

• Number of questions: 1

The input given in the third example covers the con-

cept of angle-bisector. The generated questions are

required to make use of theorems about sum of an-

gles in a triangle. Figure 18 shows the step by step

execution of the algorithm for the given input. Fig-

ure 18a generates a conﬁguration involving triangle

and perpendicular geometry objects using the GF

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics

(a) (b)

(c)

angle (B,O,O,D, 45 + (x/2)) (Calculated)

angle sum property

perp (D,A,D,B) (Given)

angle (D,B,B,E,C, 45- (x/2)) (Calculated)

angleBisector (B,E,C,B,A) (Given)

angle (A,B,B,C, 90-x ) (Calculated)

angle sum property

perp (A,D, D,C) (Given)

angle (E,C,C,D,x) (Given)

(d)

Find

angle BOD

Figure 18: (a) The ﬁgure is generated by using triangle and

perpendicular as the geometry objects using the GF compo-

nent. (b) Angle-bisector is added to (a) using the GF com-

ponent.(c) The data involving angles in a triangle is gener-

ated for (b) using the GD component. (d) The new fact and

its derivation using the GFS component is generated from

the ﬁgure shown in (c).

component. Figure 18b generates a new conﬁgura-

tion from (a) involving angle-bisector geometry ob-

ject. This ﬁgure is generated by non-deterministically

selecting a way of generating angle-bisector in a trian-

gle. The decision of generating perpendicular before

angle-bisector is taken randomly. Figure 18c is gener-

ated using GD component with the help of KT knowl-

edge database. There are many triangles in the exist-

ing conﬁguration. Hence, there are various ways of

assigning data to satisfy angle-sum property in these

triangles. GD component picks one triangle and gen-

erates the data accordingly. Figure 18d shows the new

facts and the their reasoning generated using the GFS

component. The new fact is the new question and the

reasoning is the solution of the generated question.

6 IMPLEMENTATION

Each component of our tool is implemented inde-

pendently, using state-of-the-art libraries and systems.

Various programming languages are used in the sys-

tem. C++ is used for performing calculations and

Python is used for implementation of the algorithms

used in GF and GD components. The algorithm

in GFS component is implemented using Constraint

Handling Rules (CHR) (Fr

uhwirth and Raiser, 2011).

CHR are used for generating new facts from the ax-

ioms and the given facts. In our implementation, we

use the CHR library provided by K.U.Leuven, on top

of SWI-Prolog (Schrijvers and Demoen, 2004). The

theorems used in GFS component are manually con-

verted in the format used by CHR library. For im-

plementing knowledge representation KF and KT, the

graph database Neo4j (Vicknair and Macias, 2010) is

(c)

X + 1

3x -2

(a) (b)

(d)

(e)

Figure 19: Generated questions based on ”triangle”, ”per-

pendicular” and ”Pythagorean Theorem” as input. Ques-

tions in ﬁgure(a-c)can be solved using Pythagorean Theo-

rem only. However, questions of ﬁgure (d) requires sim-

ilarity and ﬁgure (e) requires trigonometry for ﬁnding the

unknown value.

used. KF knowledge graph is used and modiﬁed by

all the components and ﬁnally represents the ques-

tion. Our knowledge databases such KT and prede-

ﬁned ways of intersection of geometric objects are

manually generated and stored before the questions

generation.

6.1 Experimental Results

The system can generate geometry questions using

the framework described in Section 4. Currently, our

knowledge database of objects contains line segments

and triangles. In addition, we have a predeﬁned set

of more than 100 theorems. The generated questions

cover ﬁve categories, e.g. similarity. Figure 19 shows

various questions generated by our system on select-

ing ”triangle” as object, ”perpendicular” as concept

and ”Pythagorean Theorem” as a theorem to be cov-

ered. The generated questions are tested using the

existing geometry solver tool JGEX (Gao and Lin,

2004). For testing in JGEX, the ﬁgure conﬁguration

is drawn manually by the user and the system is asked

to prove/ﬁnd a certain relationship. The tool is able to

prove/solve all the questions generated by our system.

Comparing the solutions generated by JGEX with the

solutions generated by our system, we found interest-

ing differences that may stem from different represen-

tations of geometric knowledge and reasoning tech-

niques and that deserve further investigation.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

7 CONCLUSION

In this paper, we provide a framework for the auto-

matic generation and solving of questions for high

school mathematics, speciﬁcally in the geometry do-

main. Our system is able to quickly generate large

numbers of questions on speciﬁc topics. Such a sys-

tem will help teachers reduce the time and effort

spent on the tedious and error-prone task of gener-

ating questions. Our work aims to develop an auto-

mated geometry question generation system that uses

a deductive approach for ﬁnding the relations between

mathematical concepts and for generating and prov-

ing these conjectures about concepts.

Future work can be carried in various directions.

An experiment needs to be performed in which the

generated problems would be placed in front of teach-

ers and let them guess which problem is from a text-

book and which one was generated from our algo-

rithm. Other major work would be generating ques-

tions according to the required difﬁculty level. An-

other improvement would be the addition of knowl-

edge by the user. Lastly, a GUI should be developed

in order to make it usable for teachers, students and

testers.

REFERENCES

Chou, S. C. and Gao, X. S. (2001). Handbook-of-

Automated-Reasoning. Elsevier and MIT Press.

Chou, S. C., Gao, X. S., and Zhang, J. Z. (1994). Machine

proofs in geometry: Automated production of read-

able proofs for geometry theorems.

Chou, S. C., Gao, X. S., and Zhang, J. Z. (2000). A de-

ductive database approach to automated geometry the-

orem proving and discovering. J. Autom. Reason.,

25(3):219–246.

Chou, S. C., Gao, X. S., and Zhang, J. Z. (2011). Area

method and automated reasoning in afﬁne geometries.

Coelho, H. and Pereira, L. (1986). Automated reasoning

in geometry theorem proving with prolog. Journal of

Automated Reasoning, 2(4):329–390.

Francis, G. (2002). Axiomatic systems for geometry.

uhwirth, T. and Raiser, F., editors (March 2011). Con-

straint Handling Rules: Compilation, Execution, and

Analysis.

Gao, X.-S. and Lin, Q. (2004). Mmp/geometer asoftware

package for automated geometric reasoning. In Win-

kler, F., editor, Automated Deduction in Geometry,

volume 2930 of Lecture Notes in Computer Science,

pages 44–66. Springer Berlin Heidelberg.

Gao, X. S., Zhu, C. C., and Huang, Y. (1998). Build-

ing dynamic mathematical models with geometry ex-

pert, i. geometric transformations, functions and plane

curves. In Proceedings of the Third Asian Technology

Conference in Mathematics.

Greeno, G., J., Magone, and Maria E. Chaiklin, S. (1979).

Theory of constructions and set in problem solving.

Memory and Cognition, 7:445–461.

Jiang, J. and Zhang, J. (2012). A review and prospect of

readable machine proofs for geometry theorems. Jour-

nal of Systems Science and Complexity, 25:802–820.

McCharen, J. D., Overbeek, R. A., and Wos, L. A. (1976).

Problems and experiments for and with automated

theorem-proving programs. IEEE Trans. Comput.,

25(8):773–782.

Meikle, L. and Fleuriot, J. (2003). , formalizing hilberts

grundlagen in isabelle/isar. In Theorem Proving in

Higher Order Logics.

Narboux, J. (2010). The area method: a recapitulation.

Journal of Automated Reasoning, 48:489–532.

National Council of Teachers of Mathematics (1989). Cur-

riculum and evaluation standards for school mathe-

matics.

Nevins, A. (1975). Plane geometry theorem proving using

forward chaining. Artiﬁcial Intelligence, 6(1):1–23.

Quaife, A. (1989). Automated development of tarskis ge-

ometry. Journal of Automated Reasoning, 5:97–118.

Schrijvers, T. and Demoen, B. (2004). The k.u.leuven chr

system: Implementation and application.

Vicknair, C. and Macias, M. (2010). A Comparison of a

Graph Database and a Relational Database.

Wilson, S. and Fleuriot, J. D. (2005). Combining dynamic

geometry, automated geometry theorem proving and

diagrammatic proofs. In European joint conference

on Theory And Practice of Software - ETAPS.

Zhang, J. Z., Gao, X. S., and Chou, S. C. (1996). The geo-

metric information search system by forward reason-

ing. Chinese Journal of Computers, 19(10):721727.

AutomatedGenerationofGeometryQuestionsforHighSchoolMathematics