
Knowledge Gradient for
Multi-objective Multi-armed Bandit Algorithms
Saba Q. Yahyaa, Madalina M. Drugan and Bernard Manderick
Department of Computer Science, Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussels, Belgium
Keywords:
Multi-armed Bandit Problems, Multi-objective Optimization, Knowledge Gradient Policy.
Abstract:
We extend knowledge gradient (KG) policy for the multi-objective, multi-armed bandits problem to effi-
ciently explore the Pareto optimal arms. We consider two partial order relationships to order the mean vec-
tors, i.e. Pareto and scalarized functions. Pareto KG finds the optimal arms using Pareto search, while the
scalarizations-KG transform the multi-objective arms into one-objective arm to find the optimal arms. To
measure the performance of the proposed algorithms, we propose three regret measures. We compare the per-
formance of knowledge gradient policy with UCB1 on a multi-objective multi-armed bandits problem, where
KG outperforms UCB1.
1 INTRODUCTION
The single-objective multi-armed bandits (MABs)
problem is a sequential Markov Decision Process
(MDP) of an agent that tries to optimize its decisions
while improving its knowledge on the arms. At each
time step t, the agent pulls one arm and receives re-
ward as a feedback signal. The reward that the agent
receives is independent from the past implementa-
tions and independent from all other arms. The re-
wards are drawn from a static distribution, e.g. normal
distributions N(µ,σ
2
), where µ is the true mean and
σ
2
is the variance. We assume that the true mean and
variance parameters are unknown to the agent. Thus,
by drawing each arm, the agent maintains estimations
of the true mean and the variance which are known as
ˆµ and
ˆ
σ
2
, respectively.
The goal of the agent is to minimize the loss of not
pulling the best arm i
∗
that has the maximum mean all
the time. The loss, or total expected regret, is defined
for any fixed time steps L as:
R
L
= Lµ
∗
−
L
∑
t=1
µ
t
(1)
where µ
∗
= max
i=1,···,|A|
µ
i
is the true mean of the
greedy (best) arm i
∗
and µ
t
is the true mean of the
selected arm i at time step t.
In the multi-armed bandits problem, at each time
step t, the agent either selects the arm that has
the maximum estimated mean (exploiting the greedy
arm), or selects one of the non-greedy arms in or-
der to be more confident about its estimations (ex-
ploring one of the available arms). This problem is
known as the trade-off between exploitation and ex-
ploration (Sutton and Barto, 1998). To overcome this
problem, (Yahyaa and Manderick, 2012) have com-
pared several action selection policies on the multi-
armed bandits problem (MABs) and have shown that
Knowledge Gradient (KG) policy (I.O. Ryzhov and
Frazier, 2011) outperforms other MABs techniques.
In this paper, we extend knowledge gradient
KG policy (I.O. Ryzhov and Frazier, 2011) to vec-
tor means, obtaining the Multi-Objective Knowledge
Gradient (MOKG). In the multi-objective setting,
there is a set of Pareto optimal arms that are incom-
parable, i.e. can not be classified using a designed
partial order relationship. Thus, the agent trades-
off the conflicting objectives (or dimensions) of the
mean vectors, the exploration (finding the Pareto front
set) and the exploitation (selecting fairly the optimal
arms).
The Pareto optimal arm set is found either by us-
ing: i) the Pareto partial order relationship (Zitzler
and et al., 2002), or ii) the scalarized functions (Eich-
felder, 2008). Pareto partial order finds the Pareto
front set by optimizing directly the multi-objective
space. The scalarized functions convert the multi-
objective space to a single-objective space, i.e. the
mean vectors are transformed in scalar values. There
are two types of scalarization functions, linear and
non-linear (or Chebyshev) functions. Linear scalar-
74
Q. Yahyaa S., M. Drugan M. and Manderick B..
Knowledge Gradient for Multi-objective Multi-armed Bandit Algorithms.
DOI: 10.5220/0004796600740083
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 74-83
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ization function is simple and intuitive but can not
find all the optimal arms in a non-convex Pareto front
set. In opposition, Chebyshev scalarization function
has an extra parameter to be tuned, however can find
all the optimal arms in a non-convex Pareto front
set. Recently, (Drugan and Nowe, 2013) have used
a multi-objective version of the Upper Confidence
Bound (UCB1) policy to find the Pareto optimal arm
set (exploring) and select fairly the optimal arms (ex-
ploiting), i.e. solve the trade-off problem in the Multi-
Objective, Multi-Armed Bandits (MOMABs) prob-
lem. We compare KG policy and UCB1 on the
MOMABs problem.
The rest of the paper is organized as follows. In
Section 2 we present background information on the
algorithms and the used notation. In Section 3 we in-
troduce multi-objective, multi-armed bandits frame-
work and upper confidence bound policy UCB1 in
multi-objective normal distributions bandits. In Sec-
tion 4 we introduce knowldge gradient (KG) pol-
icy and we propose Pareto knowldge gradient algo-
rithm, linear scalarized knowledge gradient across
arms algorithm, linear scalarized knowledge gradient
across dimensions algorithm, and Chebyshev scalar-
ized knowledge gradient algorithm. In Section 5 we
present scalarized multi-objective bandits. In Sec-
tion 6, we describe the experiments set up followed
by experimental results. Finally, we conclude and dis-
cuss future work.
2 BACKGROUND
In this section, we introduce the Pareto partial or-
der relationship, order relationships for scalarization
functions and regret performance measures of the
multi-objective, multi-armed bandits problem.
Let us consider the multi-objective, multi-armed
bandits (MOMABs) problem with |A|,|A| ≥ 2 arms
and with D objectives(or dimensions). Each objective
has a specific value and the objectives are conflicting
with each other. This means that the value of arm i can
be better than the value of arm j in one dimension and
worse than the value of arm j in other dimension.
2.1 The Pareto Partial Order
Relationship
Pareto partial order finds the Pareto optimal arm set
directly in the multi-objectivespace (Zitzler and et al.,
2002). Pareto partial order uses the following rela-
tionships between the mean vectors of two arms. We
use i and j to refer to the mean vector (estimated mean
vector or true mean vector) of arms i and j, respec-
tively:
1. Arm i dominates or is better than j, i ≻ j, if there
exists at least one dimension d for which i
d
≻ j
d
and for all other dimensions o we have i
o
j
o
.
2. Arm i weakly-dominates j, i j, if and only if
for all dimensions d, i.e. d = 1,··· ,D we have
i
d
j
d
.
3. Arm i is incomparable with j, i k j, if and only
if there exists at least one dimension d for which
i
d
≻ j
d
and there exists another dimension o for
which i
o
≺ j
o
.
4. Arm i is not dominated by j, j ⊁ i, if and only
if there exists at least one dimension d for which
j
d
≺ i
d
. This means that either i ≻ j or i k j.
Using the above relationships, the Pareto optimal arm
A
∗
set, A
∗
⊂ A be the set of arms that are not domi-
nated by all other arms. Then:
∀
a
∗
∈ A
∗
, and ∀
o
/∈ A
∗
(∀
o
∈ A), we have o ⊁ a
∗
Moreover, the Pareto optimal arms A
∗
are incom-
parable with each other. Then:
∀
a
∗
,b
∗
∈ A
∗
, we have a
∗
k b
∗
2.2 The Scalarized Functions Partial
Order Relationships
In general, scalarization functions convert the multi-
objective into single-objective optimization (Eich-
felder, 2008). However, solving a multi-objective op-
timization problem means finding the Pareto front set.
Thus, we need a set of scalarized functions S to gener-
ate a variety of elements belonging to the Pareto front
set. There are two types of scalarization functions that
weigh the mean vector, linear and non-linear (Cheby-
shev) scalarization functions.
The linear scalarization assigns to each value of
the mean vector of an arm i a weight w
d
and the result
is the sum of these weighted mean values. The linear
scalarized across mean vector is:
f
j
(µ
i
) = w
1
µ
1
i
+ ···+ w
D
µ
D
i
(2)
where (w
1
,··· ,w
D
) is a set of predefined weights
for the linear scalarized function j, j ∈ S, such that
∑
D
d=1
w
d
= 1 and µ
i
is the mean vector of arm i. The
linear scalarization is very popular because of its sim-
plicity. However, it can not find all the arms in the
Pareto optimal set A
∗
if the corresponding mean set is
a non-convex set.
The Chebyshev scalarization beside weights,
Chebyshev scalarization has a D-dimensional refer-
ence point, i.e. z = [z
1
,··· ,z
D
]
T
. The Chebyshev
KnowledgeGradientforMulti-objectiveMulti-armedBanditAlgorithms
75

scalarized can find all the arms in a non-convexPareto
mean front set by moving the reference point (Mietti-
nen, 1999). For maximization multi-objective multi-
armed bandits problem, the Chebyshev scalarization
is (Drugan and Nowe, 2013):
f
j
(µ
i
) = min
1≤d≤D
w
d
(µ
d
i
−z
d
), ∀
i
(3)
z
d
= min
1≤i≤A
µ
d
i
−ε
d
, ∀
d
where ε is a small value, ε > 0. The reference point z
is dominated by all the optimal mean vectors. Thus,
it is the minimum of the current mean vector minus ε
value.
After transforming the multi-objective problem to
single-objective problem, the scalarized functions se-
lect the arm that has the maximum function value:
i
∗
= max
1≤i≤A
f
j
(µ
i
)
2.3 The Regret Metrics
To measure the performance of the Pareto, scalar-
ized functions partial order relationships, (Drugan and
Nowe, 2013) have proposed three regret metric crite-
ria.
1. Pareto regret metric R
Pareto
measures the distance
between a mean vector of an arm i that is pulled
at time step t and the Pareto optimal mean set.
R
Pareto
is calculated by finding firstly the virtual
distance dis
∗
. The virtual distance dis
∗
is defined
as the minimum distance that is added to the mean
vector of the pulled arm µ
t
at time step t in each
dimension to create a virtual mean vector µ
∗
t
that
is incomparable with all the arms in Pareto set A
∗
,
where µ
∗
t
||µ
i
∀
i∈A
∗
as follows:
µ
∗
t
= µ
t
+ ε
∗
where ε
∗
is a vector, ε
∗
= [dis
∗,1
,··· ,dis
∗,D
]
T
.
Then, the Pareto regret R
Pareto
is:
R
Pareto
= dis(µ
t
,µ
∗
t
) = dis(ε
∗
,0) (4)
where dis, dis(µ
t
,µ
∗
t
) =
q
∑
D
d=1
(µ
∗
t
−µ
t
)
2
is the
Euclidean distance between the mean vector of
the virtual arm µ
∗
t
and the mean vector of the
pulled arm µ
t
at time step t. Thus, the regret of the
Pareto front is 0 for optimal arms, i.e. the mean of
the optimal arm coincides itself (dis
∗
= 0 for the
arms in the Pareto front set).
2. The scalarized regret metric measures the dis-
tance between the maximum value of a scalarized
function and the scalarized value of an arm that is
pulled at time step t. Scalarized regret is the dif-
ference between the maximum value for a scalar-
ized function f
j
which is either Chebyshev or lin-
ear on the set of arms A and the scalarized value
for an arm k that is pulled by the scalarized f
j
at
time step t,
R
scalarized
j
(t) = max
1≤i≤A
f
j
(µ
i
) − f
j
(µ
k
)(t) (5)
3. The unfairness regret metric is related to the vari-
ance in drawing all the optimal arms. The unfair-
ness regret of multi-objective, multi-armed ban-
dits problem is the variance of the times the arms
in A
∗
are pulled:
R
unf airness
(t) =
1
|A
∗
|
∑
i
∗
∈A
∗
(N
i
∗
(t) −N
|A
∗
|
(t))
2
(6)
where R
unf airness
(t) is the unfairness regret at time
step t, |A
∗
| is the number of optimal arms, N
i
∗
(t)
is the number of times an optimal arm i
∗
has been
selected at time step t and N
|A
∗
|
(t) is the number
of times the optimal arms, i
∗
= 1,··· , |A
∗
| have
been selected at time step t.
3 MOMABs FRAMEWORK
At each time step t, the agent selects one arm i
and receives a reward vector. The reward vector is
drawn from a normal distribution N(µ
i
,σ
2
i
), where
µ
i
= [µ
1
i
,··· ,µ
D
i
]
T
is the true mean vector and σ
i
=
[σ
1
i
,··· ,µ
D
i
]
T
is the standard deviation vector of arm
i, and T is the transpose.
The true mean and standard deviation vectors of
arms i are unknown to the agent. Thus, by drawing
each arm i, the agent estimates the mean vector ˆµ
i
and
the standard deviation vector
ˆ
σ
2
i
. The agent updates
the estimated mean ˆµ
i
and the estimated variance
ˆ
σ
2
in each dimension d as follows (Powell, 2007):
N
i+1
= N
i
+ 1 (7)
ˆµ
d
i+1
= (1−
1
N
i+1
) ˆµ
d
i
+
1
N
i+1
r
d
t+1
(8)
ˆ
σ
2,d
i+1
=
N
i+1
−2
N
i+1
−1
ˆ
σ
2,d
i
+
1
N
i+1
(r
d
t+1
− ˆµ
d
i
)
2
(9)
where N
i
is the number of times arm i has been se-
lected, ˆµ
d
i+1
is the updated estimated mean of arm i
for dimension d,
ˆ
σ
2,d
i+1
is the updated estimated vari-
ance of arm i for dimension d and r
d
t+1
is the collected
reward from arm i in the dimension d.
3.1 UCB1 in Normal MOMABs
In the single-obtimization bandits problem, upper
confidence bound UCB1 policy (P. Auer and Fischer,
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
76

2002) plays firstly each arm, then adds to the esti-
mated mean ˆµ of each arm i an exploration bound.
The exploration bound is an upper confidence bound
which depends on the number of times arm i has been
selected. UCB1 selects the optimal arm i
∗
that maxi-
mizes the function ˆµ
i
+
q
2ln(t)
N
i
as follows:
i
∗
= max
1≤i≤A
ˆµ
i
+
s
2ln(t)
N
i
where N
i
is the number of times arm i has been pulled.
In the multi-objective multi-armed bandits prob-
lem MOMABs with Bernoulli distributions, (Drugan
and Nowe, 2013) have extended UCB1 policy to find
the Pareto optimal arm set either by using UCB1 in
Pareto order relationship or in scalarized functions. In
this paper, we use UCB1 in the multi-objective multi-
armed bandits problem with normal distributions.
3.1.1 Pareto-UCB1 in Normal MOMABs
Pareto-UCB1 plays initially each arm i once. At each
time step t, it estimates the mean vector of each of
the multi-objective arms i, i.e. ˆµ
i
= [ˆµ
1
i
,··· , ˆµ
D
i
]
T
and
adds to each dimension an upper confidence bound.
Pareto-UCB1 uses a Pareto partial order relationships,
Section 2.1 to find the Pareto optimal arm set A
∗
P
UCB1
.
Thus, for all the non-optimal arms k /∈ A
∗
P
UCB1
there
exists a Pareto optimal arm j ∈A
∗
P
UCB1
that is not dom-
inated by the arms k:
ˆµ
k
+
s
2ln(t
4
p
D|A
∗
|)
N
k
⊁ ˆµ
j
+
s
2ln(t
4
p
D|A
∗
|)
N
j
Pareto-UCB1 selects uniformly, randomly one of
the arms in the set A
∗
P
UCB1
. The idea is to select most
of the times one of the optimal arm in the Pareto front
set, i ∈ A
∗
. An arm j /∈ A
∗
that is closer to the Pareto
front set according to metric measure is more selected
than the arm k /∈ A
∗
that is far from A
∗
.
3.1.2 Scalarized-UCB1 in Normal MOMABs
scalarized UCB1 adds an upper confidence bound to
the pulled arm under the scalarized function j. Each
scalarized function j has associated a predefined set
of weights, (w
1
,··· ,w
D
)
j
,
∑
D
d=1
w
d
= 1. The upper
bound depends on the number of times the scalarized
function j has been selected, N
j
and on the number of
times the arm i has been pulled N
j
i
under the scalar-
ized function j. Firstly, the scalarized UCB1 plays
each arm once and estimates the mean vector of each
arm, ˆµ
i
,i = 1, ··· , |A|. At each time step t, it pulls the
optimal arm i
∗
as follows:
i
∗
= max
1≤i≤A
f
j
(ˆµ
i
) +
s
2ln(N
j
)
N
j
i
!
where f
j
is either linear scalarized function, Equa-
tion 2, or Chebyshev scalarized function, Equation 3
with a predefined set of weights and ˆµ
i
is the estimated
mean vector of arm i.
4 MULTI OBJECTIVE
KNOWLEDGE GRADIENT
Knowledge gradient (KG) policy (I.O. Ryzhov and
Frazier, 2011) is an index policy that determines for
arm i the index V
KG
i
as follows:
V
KG
i
=
ˆ
¯
σ
i
∗x
−|
ˆµ
i
− max
j6=i, j∈|A|
ˆµ
j
ˆ
¯
σ
i
|
where
ˆ
¯
σ
i
=
ˆ
σ
i
/N
i
is the Root Mean Square Er-
ror (RMSE) of the estimated mean of an arm i.
The function x(ζ) = ζΦ(ζ) + φ(ζ) where φ(ζ) =
1
/
√
2π exp(
−ζ
/2) is the standard normal density and its
cumulative distribution is Φ(ζ) =
R
ζ
−∞
φ(ζ
′
)dζ
′
. KG
chooses the arm i with the largest V
KG
i
and it prefers
those arms about which comparativelylittle is known.
These arms are the ones whose distributions around
the estimate mean, ˆµ
i
have larger estimated standard
deviations,
ˆ
σ
i
. Thus, KG prefers an arm i over its al-
ternatives if its confidence in the estimate mean ˆµ
i
is
low. This policy trades-off between exploration and
exploitation by selecting its arm i
∗
KG
as follows:
i
∗
KG
= argmax
i∈|A|
ˆµ
i
+ (L−t)V
KG
i
(10)
where t is a time step and L is the horizon of experi-
ment which is the total number of plays that the agent
has. In (Yahyaa and Manderick, 2012), KG policy is
the competitive policy for the single-objective multi-
armed bandits problem according to the collected cu-
mulated average reward and average frequency of op-
timal selection performances. Moreover, KG policy
does not have any parameter to be tuned. Therefore,
we used KG policy in the MOMABs problem.
4.1 Pareto-KG Algorithm
Pareto order knowledge gradient (Pareto-KG) uses
the pareto partial order relationship (Zitzler and et al.,
2002) to order arms. The pseudocode of Pareto-KG
is given in Figure 1. At each time step t, Pareto-KG
calculates an exploration bound ExpB for each arm
a, (ExpB
a
= [ExpB
1
a
,··· ,ExpB
D
a
]
T
). The exploration
KnowledgeGradientforMulti-objectiveMulti-armedBanditAlgorithms
77

bound of arm a depends on the estimated mean of all
arms and on the estimated standard deviation of the
arm a. The exploration bound of arm a for dimension
d (ExpB
d
a
) is calculated as follows:
ExpB
d
a
= (L−t) ∗|A|D ∗v
d
a
v
d
a
=
ˆ
¯
σ
d
a
x
−|
ˆµ
d
a
− max
k6=a, k∈A
ˆµ
d
k
ˆ
¯
σ
d
a
|
, ∀
d∈D
where v
d
a
is the index of an arm a for dimension d, L
is the horizon of experiment which is the total num-
ber of time steps, |A| is the total number of arms, D
is the number of dimensions and
ˆ
¯
σ
d
a
is the root mean
square error of an arm for dimension d which equals
ˆ
σ
d
a
/
√
N
a
. N
a
is the number of times arm a has been
pulled. After computing the exploration bound for
each arm, Pareto-KG sums the exploration bound of
arm a with the corresponding estimated mean. Thus,
Pareto-KG selects the optimal arms i that are not dom-
inated by all other arms k,k ∈|A|(step: 4). Pareto-KG
chooses uniformly, randomly one of the optimal arms
in A
∗
P
KG
(step: 5). Where A
∗
P
KG
is a set that contains
Pareto optimal arms using KG policy. After pulling
the chosen arm i, Pareto-KG algorithm, updates the
estimated mean ˆµ
i
vector, the estimated standard de-
viation
ˆ
σ
2
i
vector, the number of times arm i is chosen
N
i
and computes the Pareto and the unfairness regrets.
1. Input: length of trajectory
L
;time step
t
;
number of arms
|A|
;number of dimensions
D
;
reward distribution
r ∼ N(µ,σ
2
r
)
.
2. Initialize: plays each arm
Initial
steps to
estimate mean vectors
ˆµ
i
= [ˆµ
1
i
, ···, ˆµ
D
i
]
T
;
standard deviation vectors
ˆ
σ
i
= [
ˆ
σ
1
i
, ···,
ˆ
σ
D
i
]
T
.
3. For
t = 1
to
L
4. Find the Pareto optimal arms set
A
∗
P
KG
such that
∀
i
∈ A
∗
P
KG
and
∀
j
/∈ A
∗
P
KG
ˆµ
j
+ ExpB
j
⊁ ˆµ
i
+ ExpB
i
5. Select
i
uniformly, randomly from
A
∗
P
KG
6. Observe: reward vector
r
i
,
r
i
= [r
1
i
, ···, r
D
i
]
T
7. Update:
ˆµ
i
;
ˆ
σ
i
;
N
i
← N
i
+ 1
8. Compute: the unfairness regret;Pareto regret
9. End for
10. Output: Unfairness regret, Pareto regret, N.
Figure 1: Algorithm: (Pareto-KG).
4.2 Scalarized-KG Algorithm
Scalarized knowledge gradient (scalarized-KG) func-
tions convert the multi-dimensions MABs to one-
dimension MABs and make use of the estimated mean
and estimated variance.
4.2.1 Linear Scalarized-KG Across Arms
Linear scalarized-KG across arms (LS1-KG) con-
verts immediately the multi-objective estimated mean
ˆµ
i
and estimated standard deviation
ˆ
σ
i
of each arm
to one-dimension, then computes the correspond-
ing exploration bound ExpB
i
. At each time step
t, LS1-KG weighs both the estimated mean vector,
i.e. ([ˆµ
1
i
,··· , ˆµ
D
i
]
T
) and estimated variance vector,
i.e. ([
ˆ
σ
2,1
i
,··· ,
ˆ
σ
2,D
i
]
T
) of each arm i, converts the
multi-dimension vectors to one-dimension by sum-
ming the elements of each vector. Thus, we have
one-dimension multi armed bandits problem. KG cal-
culates for each arm, an exploration bounds which
depends on all other arms and selects the arm that
has the maximum estimated mean plus exploration
bounds. LS1-KG is as follows:
eµ
i
= f
j
(ˆµ
i
) = w
1
ˆµ
1
i
+ ···+ w
D
ˆµ
D
i
∀i (11)
e
σ
2
i
= f
j
(
ˆ
σ
2
i
) = w
1
ˆ
σ
2,1
i
+ ···+ w
D
ˆ
σ
2,D
i
∀
i
(12)
e
¯
σ
2
i
=
e
σ
2
i
/N
i
∀
i
(13)
v
i
=
e
¯
σ
i
x
−|
eµ
i
− max
j6=i, j∈A
eµ
j
e
¯
σ
i
|
∀
i
(14)
where f
j
is a linear scalarization function that has
a predefined set of weight (w
1
,··· ,w
D
), eµ
i
,
e
σ
2
i
are
the modified estimated mean and variance of an arm
i, respectively which are one-dimension values and
e
¯
σ
2
i
is the modified RMSE of an arm i which is a
one-dimension value. v
i
is the KG index of an arm
i. x(ζ) = ζΦ(ζ) + φ(ζ) where Φ and φ are the cu-
mulative distribution and the density of the standard
normal density, respectively. Linear scalarized-KG
across arms selects the optimal arm i
∗
according to:
i
∗
LS
1
KG
= argmax
i=1,···,|A|
(eµ
i
+ ExpB
i
) (15)
= argmax
i=1,···,|A|
(eµ
i
+ (L−t) ∗|A|D ∗v
i
) (16)
where ExpB
i
is the exploration bound of arm i, |A| is
the number of arms, D is the number of dimension, L
is the horizon of an experiments, i.e. length of trajec-
tories and t is the time step.
4.2.2 Linear Scalarized-KG across Dimensions
Linear scalarized-KG across dimensions (LS2-KG)
computes the exploration bound ExpB
i
for each arm,
i.e. ExpB
i
= [ExpB
1
i
,··· ,ExpB
D
i
], adds the ExpB
i
to
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
78

the corresponding estimated mean vector ˆµ
i
, then con-
verts the multi-objective problem to one dimension.
At each time step t, LS2-KG computes exploration
bounds for all dimensions of each arm, sums the esti-
mated mean in each dimension with its corresponding
exploration bound, weighs each dimension, then con-
verts the multi-dimension to one-dimension value by
taking the summation over each vector of each arm.
Linear scalarized-KG across dimensions is as follows:
f
j
(ˆµ
i
) = w
1
(ˆµ
1
i
+ ExpB
1
i
) + ···+ w
D
(ˆµ
D
i
+ ExpB
D
i
)∀
i
(17)
where
ExpB
d
i
= (L−t) ∗|A|D∗v
d
i
, ∀
d∈D
v
d
i
=
ˆ
¯
σ
d
i
x
−|
ˆµ
d
i
− max
j6=i, j∈A
ˆµ
d
j
ˆ
¯
σ
d
i
|
, ∀
d∈D
|A| is the number of arms, L is the horizon of each
experiment, v
d
i
is the index of arm i for dimension d,
ˆµ
d
i
is the estimated mean for dimension d of arm i,
ˆ
¯
σ
d
i
is the RMSE of arm i for dimension d, ExpB
d
i
is
the exploration bound of arm i for dimension d and
x(ζ) = ζΦ(ζ) + φ(ζ) where Φ and φ are the cumu-
lative distribution and the density of the standard nor-
mal density, respectively. LS2-KG selects the optimal
arm i
∗
that has maximum f
j
(ˆµ
i
) as follows:
i
∗
LS
2
KG
= argmax
i=1,···,|A|
f
j
(ˆµ
i
)
4.2.3 Chebyshev Scalarized-KG
Chebyshev scalarized-KG (Cheb-KG) computes the
exploration bound of each arm in each dimension,
i.e. ExpB
i
= [ExpB
1
i
,··· ,ExpB
D
i
], then converts the
multi-objective problem to one-dimension problem.
Cheb-KG is as follows:
f
j
(ˆµ
i
) = min
1≤d≤D
w
d
(ˆµ
d
i
+ ExpB
d
i
−z
d
) ∀
i
(18)
where f
j
is a Chebyshev scalarization function that
has a predefined set of weights (w
1
,··· ,w
D
), ExpB
d
i
is the exploration bound of arm i for dimension d
which is calculated as follows:
ExpB
d
i
= (L−t) ∗|A|D∗v
d
i
, ∀
d∈D
v
d
i
=
ˆ
¯
σ
d
i
x
−|
ˆµ
d
i
− max
j6=i, j∈A
ˆµ
d
j
ˆ
¯
σ
d
i
|
, ∀
d∈D
And, z = [z
1
,··· ,z
D
]
T
is a reference point. For each
dimension d, the corresponding reference is the min-
imum of the current estimated means of all arms mi-
nus a small positive value, ε
d
> 0. The reference z
d
for dimension d is calculated as follows:
z
d
= min
1≤i≤|A|
ˆµ
d
i
−ε
d
, ∀
d
Cheb-KG selects the optimal arm i
∗
that has maxi-
mum f
j
(ˆµ
i
) as follows:
i
∗
Cheb−KG
= argmax
i=1,···,|A|
f
j
(ˆµ
i
)
5 THE SCALARIZED
MULTI-OBJECTIEVE BANDITS
The pseudocode of the scalarized MOMABs prob-
lem (Drugan and Nowe, 2013) is given in Fig-
ure 2. Given the type of the scalarized function
f, (f is either linear-scalarized-UCB1, Chebyshev-
scalarized-UCB1, linear scalarized-KG across arms,
linear scalarized-KG across dimensions or Cheby-
shev scalarized-KG) and the scalarized function set
( f
1
,··· , f
S
) where each scalarized function f
s
has
different weight set, w
s
= (w
1,s
,··· ,w
D,s
).
1. Input: length of trajectory
L
;reward vector
r ∼ N(µ,σ
2
r
)
;type of scalarized function
f
;set
of scalarized function
S = ( f
1
, ···, f
S
)
.
2. Initialize: For
s = 1
to
S
plays each arm
Initial
steps;
observe
(r
i
)
s
;
update:
N
s
← N
s
+ 1
;
N
s
i
← N
s
i
+ 1
;
(ˆµ
i
)
s
;
(
ˆ
σ
i
)
s
End
3. Repeat
4. Select a function
s
uniformly, randomly
5. Select the optimal arm
i
∗
that maximizes the
scalarized function
f
s
6. Observe: reward vector
r
i
∗
,
r
i
∗
= [r
1
i
∗
, ···, r
D
i
∗
]
T
7. Update:
ˆµ
i
∗
;
ˆ
σ
i
∗
;
N
s
i
∗
← N
s
i
∗
+ 1
;
N
s
← N
s
+ 1
8. Compute: unfairness regret;scalarized regret
9. Until
L
10. Output: Unfairness regret;Scalarized regret.
Figure 2: Algorithm: (Scalarized multi-objective function).
The algorithm in Figure 2 plays each arm of each
scalarized function f
s
, Initial plays (step: 2). N
s
is the number of times the scalarized function f
s
is
pulled and N
s
i
is the number of times the arm i un-
der the scalarized function f
s
is pulled. (r
i
)
s
is the
reward of the pulled arm i which is drawn from a nor-
mal distribution N(µ, σ
2
r
) where µ is the true mean and
σ
2
r
is the true variance of the reward. (ˆµ
i
)
s
and (
ˆ
σ
i
)
s
are the estimated mean and standard deviation vectors
of the arm i under the scalarized function s, respec-
tively. After initial playing, the algorithm chooses
randomly at uniform one of the scalarized function
(step: 4), selects the optimal arm i
∗
that maximizes
KnowledgeGradientforMulti-objectiveMulti-armedBanditAlgorithms
79

the type of this scalarized function (step: 5) and sim-
ulates the selected arm i
∗
. The estimated mean vector
(ˆµ
i
∗
)
s
, estimated standard deviation vector (
ˆ
σ
i
∗
)
s
, and
the number N
s
i
∗
of the selected arm and the number of
the pulled scalarized function are updated (step: 7).
This procedure is repeated until the end of playing L
steps which is the horizon of an experiment.
6 EXPERIMENTS
In this section, we experimentally compare Pareto-
UCB1, and Pareto-KG and we compare linear-
scalarized-UCB1, Chebyshev-scalarized-UCB1, lin-
ear scalarized-KG across arms, linear scalarized-KG
across dimensions, and Chebyshev scalarized-KG.
The performance measures are:
1. The percentage of time optimal arms are pulled,
i.e. the average of M experiments that optimal
arms are pulled.
2. The percentage of time each of the optimal arms
is drawn, i.e. the average of M experiments that
each one of the optimal arms is pulled.
3. The average regret at each time step which is the
average of M experiments.
4. The average unfairness regret at each time step
which is the average of M experiments.
We used the algorithm in Figure 2 for the scalar-
ized functions, and the algorithm in Figure 1 for the
Pareto-KG. To compute the Pareto regret, we need
to calculate the virtual distance. The virtual distance
dis
∗
that is added to the mean vector µ
t
of the pulled
arm at time step t (the pulled arm is not element in the
Pareto front (Pareto optimal arm) set A
∗
) can be calcu-
lated by firstly ranking all the Euclidean distance dis
between the mean vectors of the Pareto optimal arm
set and 0 as follows:
dis(µ
∗
1
,0) < dis(µ
∗
2
,0) < ··· < dis(µ
∗
|A
∗
|
,0)
dis
1
< dis
2
< ··· < dis
|A
∗
|
where 0 is a vector, 0 = [0
1
,··· ,0
D
]
T
. Secondly, find-
ing the minimum added distance dis
∗
which is calcu-
lated as follows:
dis
∗
= dis
1
−dis(µ
t
,0) (19)
where dis
1
is the Euclidean distance between 0 vector
and the Pareto optimal mean vector µ
∗
1
, and dis(µ
t
,0)
is the Euclidean distance between the mean vector
of the pulled arm that is not element in the Pareto
front set and vector 0. Then, add dis
∗
to the mean
vector of the pulled arm µ
t
to create a mean vector
that is element in the Pareto optimal mean set, i.e.
µ
∗
t
= µ
t
+ dis
∗
and check if µ
∗
t
is a virtual vector that
is incomparable with the Pareto front set. If µ
∗
t
is in-
comparable with the mean vectors of Pareto front set,
then dis
∗
is the virtual distance, calculate the regret.
Otherwise, reduce the added distance to find dis
∗
as
follows:
dis
∗
= (dis
1
−
dis
2
−dis
1
1
/D
) −dis(µ
t
,0)
where D is the number of dimensions. And, check if
dis
∗
creates µ
∗
t
that is incomparable with the Pareto
front set. If not reduce again the dis
∗
by using dis
3
instead of dis
2
and so on.
The number of experiments M is 1000. The hori-
zon of each experiment L is 1000. The rewards
of each arm i in each dimension d, d = 1, ··· ,D
are drawn from normal distribution N(µ
i
,σ
2
i,r
) where
µ
i
= [µ
1
i
,··· ,µ
D
i
]
T
is the true mean and σ
i,r
=
[σ
1
i,r
,··· ,σ
D
i,r
]
T
is the true standard deviation of the re-
ward. The true means and the true standard deviations
of arms are unknown parameters to the agent.
First of all, we used the same example in (Dru-
gan and Nowe, 2013) because it contains non-convex
mean vector set. The number of arms |A| equals 6,
the number of dimensions D equals 2. The stan-
dard deviation for arms in each dimension is either
equal and set to 1, 0.1, or 0.01 or different and gen-
erated from a uniform distribution over the closed
interval [0,1], i.e. taken from a normal distribu-
tion N(0.5,
1
/12). The true mean set vector is (µ
1
=
[0.55, 0.5]
T
, µ
2
= [0.53,0.51]
T
, µ
3
= [0.52,0.54]
T
,
µ
4
= [0.5,0.57]
T
, µ
5
= [0.51,0.51]
T
, µ
6
= [0.5, 0.5]
T
).
Note that the Pareto optimal arm set (Pareto front set)
is |A
∗
| = (a
∗
1
,a
∗
2
,a
∗
3
,a
∗
4
) where a
∗
i
refers to the op-
timal arm i
∗
. The suboptimal a
5
is not dominated
by the two optimal arms a
∗
1
and a
∗
4
, but a
∗
2
and a
∗
3
dominates a
5
while a
6
is dominated by all the other
mean vectors. For upper confidence bounce UCB1,
each arm is played initially one time, i.e. Initial = 1
as (Drugan and Nowe, 2013) (for Pareto-, linear-,
Chebyshev-UCB1), then the estimated mean of arms
are calculated and the scalarized or Pareto selection
is computed. Knowledge gradient KG needs the esti-
mated standard deviation for each arm,
ˆ
σ
i
, therefore,
each arm is either played initially 2 times, Initial = 2
which is the minimum number to estimate the stan-
dard deviation or each arm is considered unknown
until it is visited Initial times. If the arm is unknown,
then the estimated mean of that arm has a maximum
value, i.e. ˆµ
d
i
= max
d∈D
µ
d
j
, ∀
j, j∈|A|
and the estimated
standard deviation, i.e.
ˆ
σ
d
i
= max
d∈D
σ
d
j
, ∀
j, j∈|A|
to
increase the exploration of arms. We compare the
different setting for KG and found out that play-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
80
ing each arm initially 2 times, KG performance is
increased, therefore, we used this to compare with
UCB1. The number of Pareto optimal arms |A
∗
| is un-
known to the agent, therefore, |A
∗
| = 6. We consider
11 weight sets for the linear-, and Chebyshev-UCB1
and linear scalarized-KG across arms (LS1-KG),
linear scalarized-KG across dimensions (LS2-KG),
and Chebyshev-KG (Cheb-KG) functions, i.e. w =
{(1,0)
T
,(0.9, 0.1)
T
,··· ,(0.1,0.9)
T
,(0, 1)
T
}. For
Chebyshev-UCB1 and Chebyshev-KG, ε was gener-
ated uniformly, randomly, ε ∈ [0, 0.1].
Table 1 gives the average number ± the upper and
lower bounds of the confidence interval that the opti-
mal arms are selected in column A
∗
, the average num-
ber ± the upper and lower bounds of the confidence
interval that one of the optimal arm a
∗
is pulled in
columns a
∗
1
, a
∗
2
, a
∗
3
, and a
∗
4
using the scalarized func-
tions in column Functions.
Table 1 shows the number of selecting the op-
timal arms is increased by using knowledge gradi-
ent. Pareto-KG plays fairly the optimal arms. Al-
though ε set to a fixed value for all the scalarized
functions set ( j = 1, ··· , 11), Chebyshev-KG per-
forms better than the linear scalarization-KG across
arms (LS1-KG) and linear scalarization-KG across
dimensions (LS2-KG ) in playing fairly the optimal
arms. While, the performance of linear scalarized-
KG across arms (LS1-KG) in playing fairly the opti-
mal arms is as same as linear scalarized-KG across
dimensions (LS2-KG). Moreover, LS1-KG prefers
the optimal arms a
∗
4
and a
∗
3
then a
∗
1
and a
∗
2
and
LS2-KG prefers the optimal arms a
∗
1
and a
∗
2
then a
∗
4
and a
∗
3
. Pareto-UCB1 performs better than linear-
and Chebyshev-scalarization-UCB1, (LS-UCB1 and
Cheb-UCB1, respectively) according to the number
of selecting optimal arms. This is the same result
in (Drugan and Nowe, 2013) when the rewards are
drawn form Bernoulli distributions. Cheb-UCB1 per-
forms better than LS-UCB1 in selecting the optimal
arms. We also see that LS-UCB1 performs better
than LS1-KG and LS2-KG in playing fairly the op-
timal arms. And, Cheb-UCB1 performs better than
Cheb-KG in playing fairly the optimal arms. Figure 3
shows the average regret performances. The x-axis is
the horizon of each experiments and the y-axis is the
average of 1000 experiments. From Figure 3, we see
that how the regret performance is improved by us-
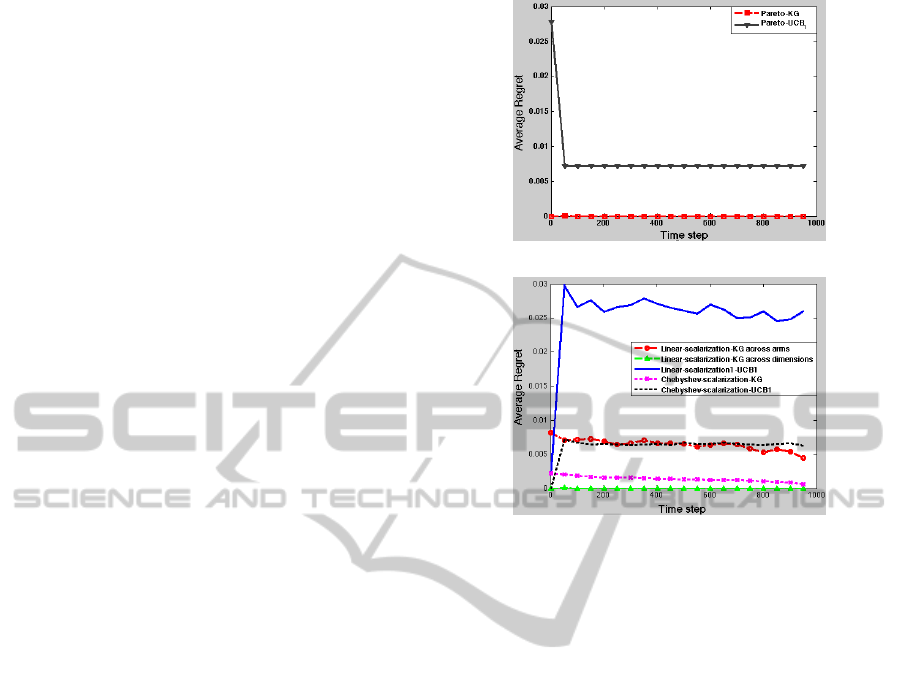
ing KG policy. Minimum Pareto regret is achieved by
using Pareto-KG in subfigure (a). Minimum scalar-
ized regret is achieved by using LS2-KG in subfig-
ure (b) and maximum regret is achieved by using
linear-scalarized-UCB1. From subfigure (b), we also
see Chebyshev-UCB1 performs better than linear-
scalarized-UCB1 and linear-scalarized-KG across di-
(a) Average Pareto regret performance
(b) Average scalarized regret performance
Figure 3: Average regret performance on bi-objective, 6-
armed bandit problems.
mensions performs better than linear scalarized-KG
across arms and Chebyshev scalarized-KG.
Secondly, we added another 14 arms to the previ-
ous example as (Drugan and Nowe, 2013). The added
arms are dominated by all other in A
∗
and have equal
mean vectors, i.e. µ
7
= ···µ
20
= [0.48,0.48]
T
. Fig-
ure 4 gives the average regret and the average un-
fairness regret performances of the Pareto-KG and
Pareto-UCB1. The x-axis is the horizon of each ex-
periments and the y-axis is the average of 1000 ex-
periments. Figure 4 shows the average regret perfor-
mance is improved by using Pareto-KG in subfigure
(a), while, the average unfairness performance in sub-
figure (b) is improved using Pareto-UCB1.
Thirdly, we added extra dimension to the previ-
ous example. The Pareto front set A
∗
contains 7
arms. Figure 5 gives the average regret performance
using σ
r
= 0.01. The y-axis is the average regret
performance and the x-axis is the horizon of exper-
iments. Figure 5 shows how the performance is im-
proved using KG policy in the MOMABs. Subfigure
a shows Pareto-KG performs Pareto UCB1. Subfig-
ure b shows best performance (the average regret is
decreased) for Chebyshev-KG and worst performance
for linear-UCB1. Chebyshev-UCB1 performs bet-
ter than linear-scalarized-KG across dimensions and
worse than linear-scalarized-KG across arms. And,
the Chebyshev scalarized- (KG and UCB1) is better
KnowledgeGradientforMulti-objectiveMulti-armedBanditAlgorithms
81
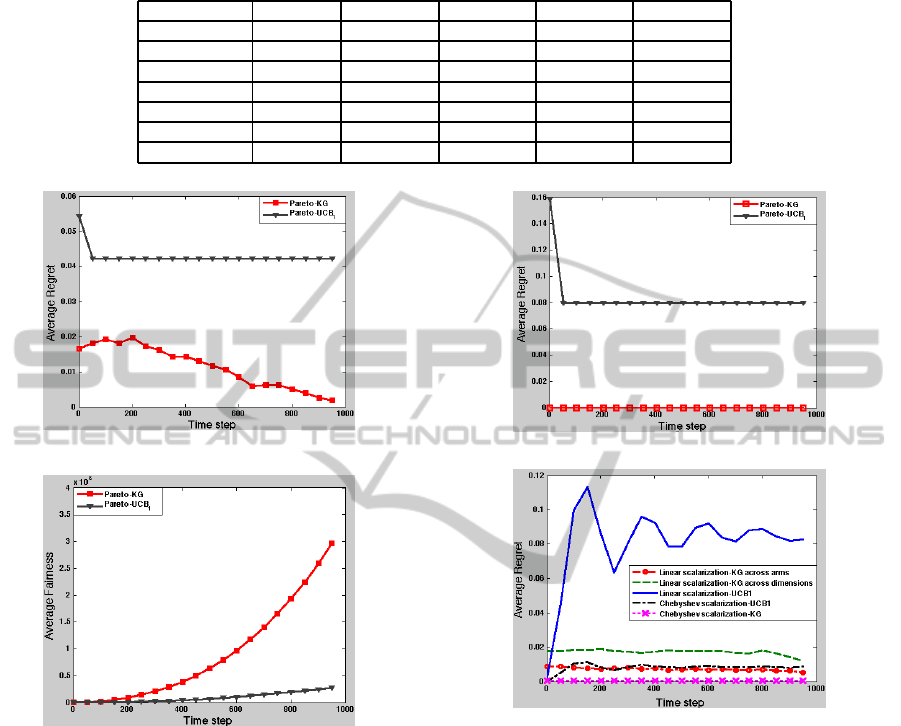
Table 1: Percentage of times optimal arms A
∗
are pulled and percentage of times each one of the optimal arm is pulled
performances on bi-objective MABs with number of arms |A| = 6 and the standard deviation of rewards are equal for each
arm i,i ∈A σ
i,r
= 0.01.
Functions A
∗
a
∗
1
a
∗
2
a
∗
3
a
∗
4
LS2-KG 999±.33 368±17.6 303±18.2 96±9.3 232±8.5
Pareto-KG 998±.02 250±.85 249±.87 250±.83 249±.82
LS1-KG 998±.04 222±9.7 122±7.4 301±14.4 353±12.2
Cheb-KG 998±.25 279±6 228±7 264±6 227±4.3
Pareto-UCB
1
714±.41 180±.3 163±.21 173±.23 198±.54
Cheb-UCB
1
677±.07 168±.08 166±.06 170±.06 173±.07
LS-UCB
1
669±.08 167±.06 168±.06 168±.06 166±.06
(a) Average regret performance.
(b) Average unfairness regret performance.
Figure 4: Performance comparison of Pareto-KG and
Pareto-UCB1on bi-objective MABs with 20 arms using
standard deviation of reward σ
r
= 0.1 for all arms. Sub-
figure (a) is the average regret performance and subfigure
(b) is the average unfairness regret performance.
than the linear scalarized- (KG and UCB1) according
to the regret performance.
Finally, we added extra 2 objectives in the previ-
ous triple-objective in order to compare the KG and
UCB1 performances on a more complex MOMABs
problem. Table 2 gives the average number ± the up-
per and lower bounds of the confidence interval that
the optimal arms are selected in column A
∗
, the av-
erage number ± the upper and lower bounds of the
confidence interval that one of the optimal arm a
∗
is
pulled in columns a
∗
1
,a
∗
2
,a
∗
3
,a
∗
4
,a
∗
5
,a
∗
6
, and a
∗
7
using
the scalarized functions in column Functions.
Table 2 shows the number of selecting the opti-
(a) Average Pareto regret performance
(b) Average scalarized regret performance
Figure 5: Average regret performance on triple-objective,
20-armed bandit problems.
mal arms is increased by using KG policy. Pareto-KG
outperforms Pareto-UCB1 in selecting and playing
fairly the optimal arms. Scalarized functions-KG out-
perform scalarized functions-UCB1 in selecting the
optimal arms, while scalarized functions-UCB1 out-
perform scalarized functions-KG in playing fairly the
optimal arms. LS1-KG (linear scalarized-KG across
arms) performs better than LS2-KG and Cheb-KG in
selecting the optimal arms. Cheb-KG performs bet-
ter than LS2-KG and worse than LS1-KG in select-
ing the optimal arms. LS2-KG performs better than
LS1-KG and Cheb-KG in playing fairly the optimal
arms and prefers playing a
∗
2
,a
∗
1
,a
∗
7
,a
∗
5
,a
∗
6
,a
∗
3
then a
∗
4
.
LS1-KG performs better than Cheb-KG and worse
than LS2-KG in playing fairly the optimal arms and
prefers a
∗
4
,a
∗
6
,a
∗
3
,a
∗
1
,a
∗
5
,a
∗
7
then a
∗
2
. Cheb-KG prefers
the optimal arms a
∗
1
,a
∗
6
,a
∗
3
,a
∗
5
,a
∗
2
,a
∗
4
, then a
∗
7
. LS-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
82

Table 2: Percentage of times optimal arms A
∗
are pulled and percentage of times each one of the optimal arm is pulled
performances on 5-objective MABs with number of arms |A| = 20 and the standard deviation of rewards are equal for each
arm i,i ∈A σ
i,r
= 0.01.
Functions A
∗
a
∗
1
a
∗
2
a
∗
3
a
∗
4
a
∗
5
a
∗
6
a
∗
7
LS1-KG 1000±0 143.1±6.273 76.6±4.566 154.1±7.459 195±7.633 135.8±7.25 164.8±8.353 130.6±6.336
Cheb-KG 999.7±.023 507.3±4.111 63.6 ±4.263 111.7±4.043 29.2±3.076 73.9±4.752 193.5±4.883 20.5±2.574
LS2-KG 601.1±8.993 109.2±6.439 121.8±6.827 57.9±4.454 57.1±4.093 79.3±5.668 79.1±5.536 96.7±6.271
Pareto-KG 571.3±3.54 81.4±.723 81.7±.738 81.6±.72 81.7±.72 81.9±.688 81.6±.72 81.4±.72
Pareto-UCB
1
455.1±.21 64.2±.095 60.3±.066 62.7±.073 69.1±.116 65.1±.076 65.1 ±.077 68.6±.114
LS-UCB
1
379.7±.278 53.9±.061 53.7±.063 54.5±.064 54.7±.064 54.4±.066 54.6±.068 53.9±.066
Cheb-UCB
1
367.9±.219 53.4±.073 54.1±.075 52.9±.073 52.7±.075 51.9±.074 51.6±.077 51.3±.077
UCB1 and Cheb-UCB1 play fairly the optimal arms,
while LS-UCB1 performs better than Cheb-UCB1 in
selecting the optimal arms.
From the above figures and tables, we conclude
that the average regret is decreased using KG pol-
icy in the MOMABs problem. Pareto-KG outper-
forms Pareto-UCB1 and scalarized functions-KG out-
perform scalarized functions-UCB1 according to the
average regret performance. While Pareto-UCB1 out-
performs Pareto-KG according to the unfairness re-
gret, where the unfairness regret is increased using
knowledge gradient policy. However, when the num-
ber of objective is increased Pareto-KG performs bet-
ter than Pareto-UCB1 in playing fairly the optimal
arms. According to the average regret performance,
Chebyshev scalarized-KG performs better than linear
scalarized-KG across arms and dimensions when the
number of arms is increased, while LS1-KG outper-
forms all other scalarization functions when the num-
ber of objectives is increased to 5.
7 CONCLUSIONS AND FUTURE
WORK
We presented multi-objective, multi-armed bandits
problem MOMABs, the regret measures in the
MOMABs and Pareto-UCB1, linear-UCB1, and
Chebyshev-UCB1. We also presented knowledge
gradient policy KG. We proposed Pareto-KG. We
also proposed two types of linear scalarized-KG (lin-
ear scalarized-KG across arms (LS1-KG) and lin-
ear scalarized-KG across dimensions (LS2-KG) and
Chebyshev-scalarized-KG. Finally we compared KG
and UCB1 and concluded that the average regret is
improved using KG policy in the MOMABs. Fu-
ture work must provide theoretical analysis for the
KG in MOMABs and must compare the family of up-
per confidence bound UCB1, and UCB1-Tuned poli-
cies (P. Auer and Fischer, 2002), and knowledge gra-
dient KG policy on the correlated MOMABs. and
must compare KG, UCB1, and UCB1-Tuned policies
in sequential ranking and selection (P.I. Frazier and
Dayanik, 2008) MOMABs.
REFERENCES
Drugan, M. and Nowe, A. (2013). Designing multi-
objective multi-armed bandits algorithms: A study. In
Proceedings of the International Joint Conference on
Neural Networks (IJCNN).
Eichfelder, G. (2008). Adaptive Scalarization Methods in
Multiobjective Optimization. Springer-Verlag Berlin
Heidelberg, 1st edition.
I.O. Ryzhov, W. P. and Frazier, P. (2011). The knowledge-
gradient policy for a general class of online learning
problems. Operation Research.
Miettinen, K. (1999). Nonlinear Multiobjective Optimiza-
tion. Springer, illustrated edition.
P. Auer, N. C.-B. and Fischer, P. (2002). Finite-time analysis
of the multiarmed bandit problem. Machine Learning,
47:235–256.
P.I. Frazier, W. P. and Dayanik, S. (2008). A knowledge-
gradient policy for sequential information collection.
SIAM J. Control and Optimization, 47(5):2410–2439.
Powell, W. B. (2007). Approximate Dynamic Program-
ming: Solving the Curses of Dimensionality. John
Wiley and Sons, New York, USA, 1st edition.
Sutton, R. and Barto, A. (1998). Reinforcement Learning:
An Introduction (Adaptive Computation and Machine
Learning). The MIT Press, Cambridge, MA, 1st edi-
tion.
Yahyaa, S. and Manderick, B. (2012). The exploration vs
exploitation trade-off in the multi-armed bandit prob-
lem: An empirical study. In Proceedings of the 20th
European Symposium on Artificial Neural Networks,
Computational Intelligence and Machine Learning
(ESANN). ESANN.
Zitzler, E. and et al. (2002). Performance assessment
of multiobjective optimizers: An analysis and re-
view. IEEE Transactions on Evolutionary Computa-
tion, 7:117–132.
KnowledgeGradientforMulti-objectiveMulti-armedBanditAlgorithms
83
