Validation of Numerical Simulation for Subdural Cortical

Stimulation

Using Spherical Phantoms and Anatomically Realistic Head Phantom

Jinmo jeong

, Donghyeon Kim

, Sangdo Jeong

, Jonghyun Lee

, Euiheon Chung

1,3

Sung Chan Jun

and Sohee Kim

1,3

Department of Medical System Engineering, Gwangju Institute of Science and Technology, Gwangju, South Korea

School of Information and communications, Gwangju Institute of Science and Technology, Gwangju, South Korea

School of Mechatronics, Gwangju Institute of Science and Technology, Gwangju, South Korea

Keywords: Cortical Stimulation, Numerical Simulation, Finite Element Method, Brain Phantom.

Abstract: The purpose of this study is to investigate the accuracy of numerical simulation for electric brain stimulation.

For this, we modelled brains using simple computational models with 2 and 3 shells, with and without

realistic head geometry, and performed numerical simulations using finite element method (FEM). The

corresponding head phantoms were constructed for the validation of simulation results. We implanted

stimulation electrodes in the head phantom, and measured the electric potential induced by the electrodes.

When comparing the electric potential obtained from numerical simulations and phantom experiments, both

results showed similar trend and amplitude, with a relative difference of 13.64% on average in the realistic

head model study. This result demonstrates that predicting the electric potential and its gradient (current

density) using computational simulation is reliable with reasonably small deviation from the actual

measurement.

1 INTRODUCTION

Electric brain stimulation (EBS) is known to be

useful in treating brain disorders: essential tremor,

chronic stroke, chronic pain, Parkinson’s disease,

movement disorder, refractory epilepsy, depression,

aphasia, and dystonia as an intervention therapy.

Although EBS is gaining a potential to treat brain

disorders and brain diseases, side effects (seizure

(Bezard et al., 1999)) and mechanisms of EBS are

obscure, and optimal stimulation parameters

(electrode position, amplitude, waveform, and

duration) remain unknown. Animal experiments and

computational studies are essential to answer these

questions. A computational study can provide the

information for estimating the effect of brain

stimulation by the implicit assumption that the

excitability of neurons is linearly proportional to the

magnitude of the current density (or electric field) in

the brain. (Wongsarnpigoon and Grill, 2012; Manola

et al., 2007) analysed the response of the neuron on

invasive brain stimulation with various stimulation

amplitudes and positions using a computational

brain model. (Opitz et al., 2013) generated an

individual brain model and showed a positive

correlation between fMRI and some simulation

results. In general, computational simulation results

are required to be validated. However, there have

been few papers on the validation of simulations.

(Wei and Grill 2005) built a phantom for the

validation of deep brain stimulation and compared

the simulation and phantom results. (Kim et al.,

2010) investigated the effect of head model,

conductivity condition, and position of stimulation

numerically, and constructed a head phantom for

verification. These studies made phantom models

and compared them with simulation results.

However, insufficient brain domain may lead to

ignore unwanted side effects, and using

oversimplified brain structures such as shell model

or smoothed cortex model may not inform the

precise effect of EBS.

The objective of this study is to investigate the

accuracy of the simulation for EBS (more

specifically subdural cortical stimulation (SuCS)).

For the study, we modelled simple sphere models

136

Jeong J., Kim D., Jeong S., Chung E., Jun S., Lee J. and Kim S..

Validation of Numerical Simulation for Subdural Cortical Stimulation - Using Spherical Phantoms and Anatomically Realistic Head Phantom.

DOI: 10.5220/0004796801360141

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 136-141

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

based on 2- and 3-shells and constructed the

corresponding head phantoms. Based on these

models, we implanted stimulation electrodes in the

head phantom, and measured the electric potential

induced by the electrodes. In the phantom modelling,

we used agarose/NaCl mixture to control the electric

conductivity and the shape of head phantom. In

addition, we made a computational brain model

based on a geometry obtained from magnetic

resonance imaging (MRI) and compared the

simulation and phantom experimental results.

2 METHODS

As the purpose of this study is to validate the

simulation for EBS, especially SuCS, the brain

geometries for simulation and phantom model were

identical. For comparison, we made 3 types of brain

models (2 shells, 3 shells, and 3 shells with realistic

brain geometry). We used similar isotropic

conductivity that was measured through experiments

in the human brain except the 2 shells model (Datta

et al. 2009). Figure 1 shows the schematic view of

each model.

2.1 Simulation Modelling

In general, EBS involves injecting into the brain the

direct electrical current or induced current by

voltage via electrode(s). Maxwell’s equation

explains such electrical behaviour within the brain;

thus, the following Laplace equation governs the

domain in our simulation model Ω:

Ω in 0V)(σ 

(1)

Here V and σ are an electrical potential and an

electrical conductivity in Ω, respectively. Assuming

that the electric flux through out of model Ω is

negligibly small (that is, insulated), the Neumann

boundary condition is applied on outer boundaries of

the model as follows:

outer

Ω on 0Jn 

(2)

where n and J are the normal vector to the boundary

and the current density, respectively. Further, the

Dirichlet boundary conditions are applied at the

cathode electrode surface ψ

cathode

in the model Ω and

anode electrode surface ψ

anode

as follows:

cathode

Ψon 0V 

(3)

anode

onVV 

(4)

where V

is an input voltage magnitude. We applied

simulation voltage V

as 5V in the 2 and 3 shell

models. Also, 1V simulation voltage was applied in

the 3 shell model with realistic brain geometry. To

obtain the solution for this numerical problem, we

used the finite element method (FEM). To solve the

boundary value problem using FEM, volume mesh

was generated in an adaptive way: we applied

volume constraint factor to each model component,

so that the mesh was coarse around simple

structures, while a finer mesh was used around

complex structures. The numbers of tetrahedron

elements were 2,189,812 for 2 shells model,

2,154,260 for 3 shells model, 3,026,529 for 3 shells

model with realistic brain geometry. The

convergence of stimulation’ results using finer

model was verified as 2 shells: 0.0098%, 3 shells:

0.0056% and 3 shells with realistic brain: 1.9%. Bi-

conjugate gradient stable solver with incomplete LU

preconditioner was used as the solver. All

simulations were done using COMSOL

Multiphysics 4.3 (COMSOL Inc Burlingtonm, MA).

2.2 Phantom Design and Measurement

For the purpose of validating simulation results, we

constructed the phantoms that correspond to each

simulation model. For modelling Sphere phantoms,

we used ‘mold’ to shape the model’s geometry.

Sphere based models (2 shells and 3 shells) were

made using commercially available plastic sphere

molds. To make a Sphere phantom with 2 and 3

shells, we assembled the phantom from inner layer

to outer layer. At first, the two plastic sphere molds

having different radius were prepared, then we filled

the inner sphere mold using agarose/NaCl mixture.

Figure 1: (a): Production process of the sphere phantom,

(b): Schematic of assembled brain phantom, (c) location of

the electrode, (d) The completed brain phantom.

ValidationofNumericalSimulationforSubduralCorticalStimulation-UsingSphericalPhantomsandAnatomically

RealisticHeadPhantom

137

After producing the inner layer, we put the mold of

the next outer layer in position and then filled with

agarose/NaCl mixture again. At second, we added

the outermost layer using the other plastic sphere

molds which is larger than other molds for make a 3

shells sphere phantom. Figure 1-(a) shows the

process of assembling the sphere phantom. Also, as

shown in Figure 1-(b), magnetic resonance images

(MRI) of human brain were used to generate a mold

for making the 3 shells model with realistic brain

geometry. The MRI data was segmented as skin (3

layer), skull and cerebrospinal fluid (CSF) (2nd

layer), and gray matter and white matter (1st layer).

Then based on the segmented data, we made the

mold using a 3D printer (Inspire 3D Printer, A450).

Figure 1 -(c, d) shows the model phantoms made of

3 shells and 3 shells with realistic brain geometry,

respectively. We placed two stimulation electrodes

for anode and cathode, respectively: the anode on

one side of the sphere and the cathode on the

opposite side of the first one. Especially, in the 3

shells model with realistic brain geometry, two

stimulation electrodes were placed on motor cortex

(figure 1-(c)) and a reference electrode was placed

on bottom of the model. A 5[V] DC voltage was

applied on each model using a function generator

(Agilent, E3631A) and the voltage was measured by

a digital multi-meter (Agilent, 34410A). Electric

potentials induced by the electrodes implanted in the

phantoms were measured at surface, 10mm depth,

and 2cm depth of each phantom and the measuring

points in 2 shells and 3 shells phantom was from 10°

to 170° with 10° interval (figure 2-(a, b)). 3 shells

model with realistic brain geometry had irregular

sensing points and is shown in figure 2-c.

2.3 Conductivity of Phantom Material

One of the methods to assign the conductivity of the

phantom is to adjust the NaCl concentration (mg/ml)

in agarose since the electrical conductivity of

agarose was controlled by changing the

concentration of NaCl((Wongsarnpigoon and Grill

2012; Manola et al., 2007)). In this study, powdered

agarose (Affymetrix, Agarose - LE) and NaCl were

mixed with deionized (DI) water. This solution

including agarose (2.6mg/ml), NaCl (DUKSAN,

Sodium Chloride) and DI water was stirred using a

magnetic stir bar and poured into a regular

hexahedron mold. The dimensions of the mold were

74 mm of length, 25 mm of width and 2.4 mm of

length. The resistance of completed agarose/NaCl

mixture was measured by an impedance

measurement system (Gamry, Reference 600) for

identifying the conductivity of agarose with NaCl,

and then we calculated the conductivity using

equation.





ΩΑℓ/ σ





(5)

Here σ, ℓ, and A is conductivity [S/m], length [m],

and area [m

], respectively. Ω is the measured

resistance [ohm]. Thus, the ratio of NaCl

concentration to agarose was estimated and adjusted

to mimic the conductivity of the phantom similar to

that of the human brain.

Table 1 shows the conductivities of each layer in

the phantoms used in this study. The assigned

conductivity for 2 shells was not like actual brain

conductivity. However, the other models had similar

isotropic conductivity that was measured through

experiments in the human brain (Datta et al., 2009).

Figure 2: (a, b): Schematic view of 2 shells and 3shells sphere phantom model, (c): Schematic view of brain phantom model.

The numbers on (c) represents sensing points.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

138

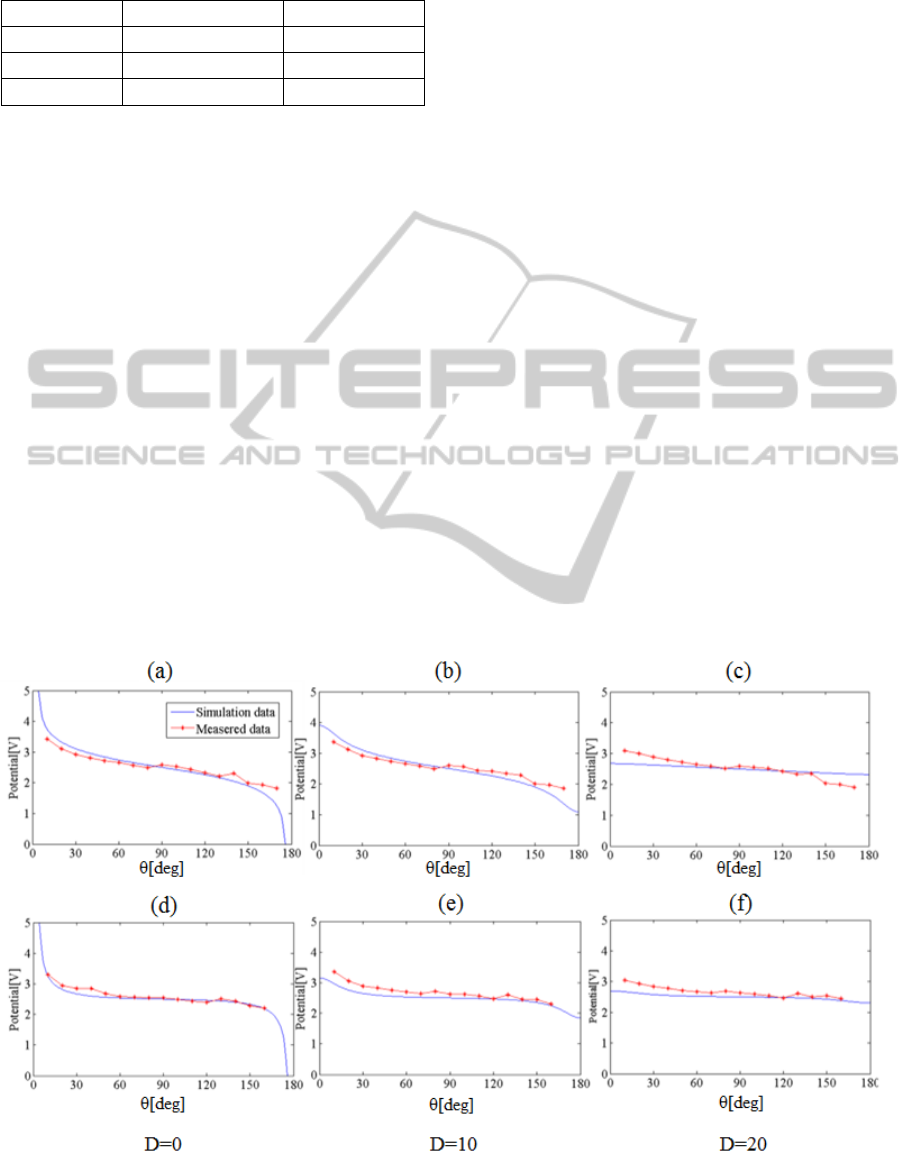
Table 1: The conductivity of each spherical phantom and

simulation model (1

layer is central part).

2 shells 3 shells

layer 0.012 [S/m] 0.214 [S/m]

layer 0.28 [S/m] 0.012 [S/m]

layer - 0.470 [S/m]

3 RESULTS

3.1 Sphere Phantom Results versus

Simulation Results

Figure 3-(a-c) shows the result of numerical

simulation and phantom experiment using 2 shells

sphere model. When we measured the electric

potential with polar angles from 10° to 170° on a

basis of the center of shells with 10° interval, the

slope of electric potential was steep around the

electrodes and flat far away from the electrodes.

Also, there was small variation in electric potential

when measured at points deep inside the brain model.

Overall behaviour between simulation and phantom

experiment were similar and the relative difference

was quite low (4.68% on average). Even in the

steepest area (θ: 0~30°, d: 0~10mm), the phantom

experimental result was in good agreement with the

result of simulation. Furthermore, when a more

complicated 3-shells brain model was used, we

could see a relative difference of 7.18% on average

between the simulation and experimental results,

obtained at 3 different depths, as shown in figure 3-

(d-f). When comparing the simulation results of 2

shells and 3 shells sphere models, there was a

difference in magnitude of electric potential of

0.21[V] on average. However, they showed the same

shape of curve. The difference between the result of

simulation and phantom experiment was within

8.82%.

3.2 Realistic Head Results versus

Simulation Results

Figure 4 shows the electric potential at 13 different

points on surface of the head model, 10mm depth,

and 20mm depth obtained from the simulation and

phantom experiment. Most of the electric potential

from both simulation and experimental results was

around 0.87[V]. Also, from simulation, the electric

potential in the upper area of model (around

implanted electrodes; sensing point 9, 10, 11, 12,

and 13) was higher, 0.90[V] on average, when

compared to other measurement points where

0.86[V] on average was obtained. From phantom

experiment, however, the potentials at point 11, 12,

and 13 were below the average potential: potential at

point 11 was 0.86[V], 0.81[V] at point 12, and

0.84[V] at point 13 while the average potential was

0.87[V] along the depth). The average relative

Figure 3 Above: Results of the comparative experiment using 2 shells sphere model, (a): surface (b): 10mm (c): 20mm,

Below: Results of the comparative experiment using 3 shells sphere model, (d): surface (e): 10mm (f): 20mm.

ValidationofNumericalSimulationforSubduralCorticalStimulation-UsingSphericalPhantomsandAnatomically

RealisticHeadPhantom

139

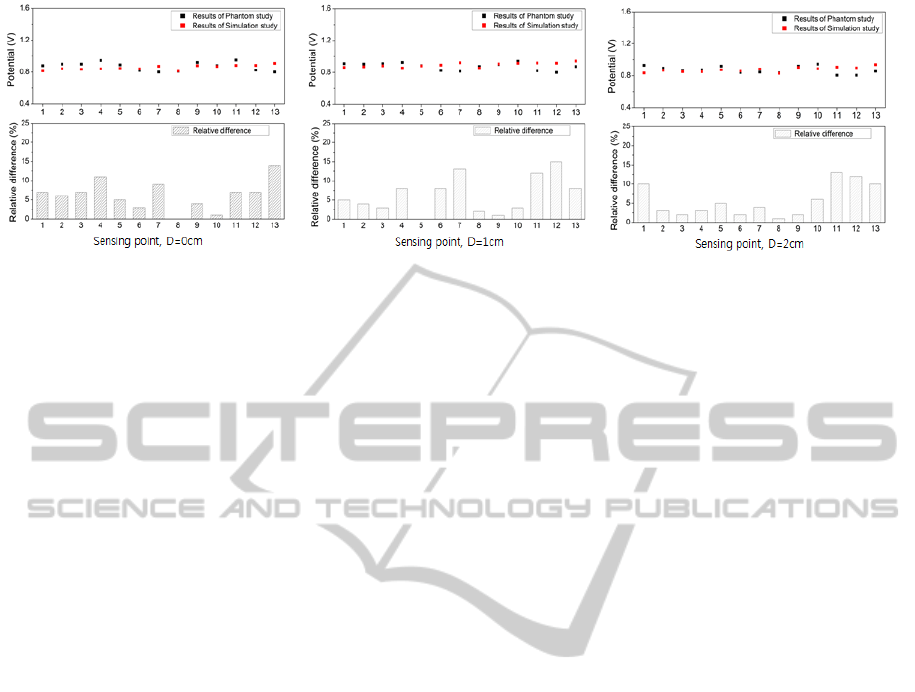
Figure 4: Results of the comparative experiment using brain model, (a): surface (b): 10mm (c): 20 mm.

difference between the results was 6.02%. Relatively

higher differences were observed at the points 11, 12,

and 13: 10.60%, 11.03%, and 10.33% on average

with depth, respectively. When considering relative

difference with respect to the depth of measurement,

there was little difference among the potentials

obtained at different depths (surface: 6.23%; 10mm:

5.57%; 3cm: 6.19%).

4 DISCUSSION

We performed a number of brain phantom studies to

evaluate the accuracy of numerical simulation for

EBS. All the results (2 and 3 layer sphere models,

and 3 shells with realistic head geometry) showed

good agreements in electric potential between

simulation and phantom experiments (average

relative difference: 4.57% in 2 shells; 7.09% in 3

shells; 6.03% in 3 shells with realistic geometry) and

the trend of voltage between simulation and

phantom study was similar among results.

In relative difference view, it was low at between

electrodes and high at around anode and cathode

(around anode: 8.43%, between electrodes: 4.10%,

and around cathode: 9.85% in average with models

and depth) when we examined the relative difference

between simulation and experiment according to

different measurement points in 2 shells and 3 shells

models (polar angles: from 0° to 30°, between

electrodes: 40° to 140°, around cathode: 150° to

180°). Also, these differences are even seen in the 3

shells model with realistic brain geometry. From the

result of simulation using 3 shells with realistic brain

geometry, we could see the higher potential at point

9, 10, 11, 12, and 13 because of its position and

these points have higher relative difference than the

other points. Although, there was little difference

between simulation and phantom experimental

results, there were several limitations for validating

simulation results. First, due to a small displacement

of measuring point, there was a larger relative

difference around electrode. So far, there are reports

which tried to measure electric potential on

phantom. However, they reported the accuracy of

measured electric potential was not good because of

poor spatial control over placement of the measuring

sensor (Jung et al., 2013; Suesserman et al., 1991).

To overcome the problem, coordinate-based

measuring machine is needed. As well, generated

water screen arising in the phantom model due to

solidification of agarose/NaCl mixture has another

possibility for the difference between the simulation

and experimental results. Second, in the 3 shells

with realistic geometry phantom, the variation of

electric potential at sensing point evaluated by

numerical stimulation was not big; also the variation

of electric potential at sensing point measured by

phantom was not big. Both results mean that we

chose measuring sensing points having similar

electrical potential. To compare the both results as

aspect of validation for result of simulation, choice

the sensing points set which having big variance is

very important. As a further study, thus, we are

working on the measurements with the realistic head

phantom focusing on the vicinity of stimulation

electrodes where the gradient of potential is large as

the target region of stimulation is generally near

stimulation electrode. Furthermore similar phantom

study with varying dynamic voltage or current

instead of applying static voltage or current would

provide more insight into the realistic electrical

stimulation practice.

5 CONCLUSIONS

In this paper, we systematically compared numerical

simulation and experimental phantom results to

validate simulation tools for subdural cortical

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

140

stimulation. Based on our results, we could see good

agreements between simulated and measured

electrical potential in both simple spherical phantom

and realistic head phantom experiments. These

results provide a convincing justification for

investigating the effects of EBS using computational

models.

ACKNOWLEDGEMENTS

This work was supported by the Institute of Medical

System Engineering (iMSE) in the GIST.

REFERENCES

Bezard, E. et al., 1999. Cortical Stimulation and Epileptic

Seizure: A Study of the Potential Risk in Primates.

Neurosurgery, 45(2).

Datta, A. et al., 2009. Gyri -precise head model of

transcranial DC stimulation: Improved spatial focality

using a ring electrode versus conventional rectangular

pad. Brain stimulation, 2(4), pp.201–207.

Jung, Y. et al., 2013. An image-guided transcranial direct

current stimulation system: a pilot phantom study.

Physiological measurement, 937.

Kim, D.-H. et al., 2010. Distortion of the electric field

distribution induced in the brain during transcranial

magnetic stimulation. IET Science, Measurement &

Technology, 4(1), p.12.

Manola, L. et al., 2007. Anodal vs cathodal stimulation of

motor cortex: A modeling study. Clinical

Neurophysiology, 118(2), pp.464–474.

Opitz, A. et al., 2013. Physiological observations validate

finite element models for estimating subject-specific

electric field distributions induced by transcranial

magnetic stimulation of the human motor cortex.

NeuroImage, 81, pp.253–64.

Suesserman, M. F., Spelman, F. a & Rubinstein, J.T., 1991.

In vitro measurement and characterization of current

density profiles produced by non-recessed, simple

recessed, and radially varying recessed stimulating

electrodes. IEEE transactions on bio-medical

engineering, 38(5), pp.401–8.

Wei, X. F. & Grill, W. M., 2005. Current density

distributions, field distributions and impedance

analysis of segmented deep brain stimulation

electrodes. Journal of neural engineering, 2(4),

pp.139–47.

Wongsarnpigoon, A. & Grill, W. M., 2012. Computer-

based model of epidural motor cortex stimulation:

effects of electrode position and geometry on

activation of cortical neurons. Clinical

neurophysiology : official journal of the International

Federation of Clinical Neurophysiology, 123(1),

pp.160–72.

ValidationofNumericalSimulationforSubduralCorticalStimulation-UsingSphericalPhantomsandAnatomically

RealisticHeadPhantom

141