Identiﬁcation of Gait Events using Expert Knowledge and Continuous

Wavelet Transform Analysis

Siddhartha Khandelwal and Nicholas Wickstr¨om

Intelligent Systems Laboratory, Halmstad University, Box 823, SE-301 18, Halmstad, Sweden

Keywords:

Gait Event Detection, Wavelet Analysis, Accelerometers, Outdoor Walking, Continuous Wavelet Transform.

Abstract:

Many gait analysis applications involve long-term or continuous monitoring which require gait measurements

to be taken outdoors. Wearable inertial sensors like accelerometers have become popular for such applications

as they are miniature, low-powered and inexpensive but with the drawback that they are prone to noise and re-

quire robust algorithms for precise identiﬁcation of gait events. However, most gait event detection algorithms

have been developed by simulating physical world environments inside controlled laboratories. In this paper,

we propose a novel algorithm that robustly and efﬁciently identiﬁes gait events from accelerometer signals

collected during both, indoor and outdoor walking of healthy subjects. The proposed method makes adept

use of prior knowledge of walking gait characteristics, referred to as expert knowledge, in conjunction with

continuous wavelet transform analysis to detect gait events of heel strike and toe off. It was observed that in

comparison to indoor, the outdoor walking acceleration signals were of poorer quality and highly corrupted

with noise. The proposed algorithm presents an automated way to effectively analyze such noisy signals in

order to identify gait events.

1 INTRODUCTION

Gait is generally deﬁned as the manner or way of

walking. The healthy locomotor system integrates in-

put from the motor cortex, cerebellum, and the basal

ganglia, as well as feedback from visual, vestibular

and proprioceptive sensors to produce controlled mo-

tor commands that result in coordinated muscle ﬁr-

ings and limb movements (Hausdorff, 2007). This

multi-levelneural-locomotorcontrol system produces

a stable gait and a highly consistent walking pattern

while improper co-ordination may lead to deviations

from normal gait behavior resulting in unstable gait.

Gait analysis involves measuring and understanding

various parameters of gait to interpret and draw con-

clusions on physiological, pathological and psycho-

logical factors modulating healthy or unhealthy gait.

In recent years, technological advances have made it

possible to develop better techniques for gait anal-

ysis and as such its applications have grown mani-

fold. It can be used to design and optimize functional

electrical stimulation (FES) systems (Williamson and

Andrews, 2000; Mansﬁeld and Lyons, 2003), clini-

cal tool for diagnosis and severity analysis of neuro-

physiological disorders and impairments (Socie et al.,

2013), elucidate the working of our neuro-locomotory

system (Hausdorff, 2007), assess the quality of gait of

amputees and rehabilitating patients (Aminian et al.,

2004; Selles et al., 2005), recognize different walking

behaviors (Hafner and Bachmann, 2008), predict and

evaluate the risk of falls in older adults (Reelick et al.,

2009; Callisaya et al., 2010) and many more.

Gait is comprised of sequential gait cycles and

each such gait cycle is composed of a sequence of

events that mark the transition from one gait phase

to another (Rueterbories et al., 2010). In the tempo-

ral domain, gait events are expressed as a function of

time while in the spatial domain, gait movements are

expressed as a function of the orientation of the limbs

and joints. In terms of temporal domain parameters,

the two most relevant events in a normal gait cycle are

the initial heel contact or heel strike (HS) and termi-

nal contact or toe off (TO). Both these key events are

widely used in gait analysis because of the aforemen-

tioned applications and the fact that other temporal

parameters like swing, stance and stride time can be

directly computed from them. Thus detecting HS and

TO accurately is of vital importance in clinical gait

analysis and many sensors have been used to this end.

Force plates and camera-based motion capture

(mocap) systems are considered as the “gold stan-

dard” or reference for identifying gait events (Miller,

197

Khandelwal S. and Wickström N..

Identiﬁcation of Gait Events using Expert Knowledge and Continuous Wavelet Transform Analysis.

DOI: 10.5220/0004799801970204

In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2014), pages 197-204

ISBN: 978-989-758-011-6

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2009; Desailly et al., 2009). Force plates capture

the ground reaction force caused by the pressure ex-

erted by the foot on them. Thus by applying simple

thresholds on the recorded force, individual events of

HS and TO can be precisely identiﬁed (Mills et al.,

2007). Camera-based mocap systems track markers

that are placed on the body (Hanlon and Anderson,

2009; Aung et al., 2013). Generally, a laboratory

setup consists of a pair of force plates (one for each

foot) that is used concurrently with the mocap sys-

tem. Though these devices provide relatively pre-

cise measurements, they are highly expensive, immo-

bile and require competence in maintenance, opera-

tion and execution. The fact that they record the infor-

mation of only a couple of steps renders them inade-

quate for applications that need long-term or continu-

ous gait monitoring. For example, some authors have

hypothesized that in-coordination between the neu-

ral and locomotor control systems results in speciﬁc

gait patterns which can be used for analyzing neuro-

physiological disorder patients (Stolze et al., 2004;

Hausdorff, 2007) or older adults that have a fear of

falling (Herman et al., 2005; Reelick et al., 2009).

These applications would essentially require mobile

sensors and robust gait analysis algorithms for day-

to-day monitoring of such patients.

Pressure sensitive mats and foot switches provide

the option of being used outside the laboratory for

measuring gait events. The pressure sensitive mat

(e.g.GaitRite) consists of a grid of pressure sensors

that can be few meters in length (McDonough et al.,

2001). Foot switches like force sensitive resistors can

be attached at various positions below the feet or in-

soles of the shoe (Williamson and Andrews, 2000;

Aminian et al., 2002; Lau and Tong, 2008). How-

ever there have been studies to show that they are less

reliable and not durable over longer periods (Mans-

ﬁeld and Lyons, 2003) and cannot differentiate be-

tween foot load changes due to walking and those

caused by weight shifting for non-walking tasks (Pap-

pas et al., 2001). Hence, from a long-term perspec-

tive, they might not be convenient for outdoor use in

daily life and be prone to mechanical failures. More-

over, these sensors provide only temporal information

and thus restrict the scope for any further analysis in-

volving spatial parameters of gait.

Consequently, for such long-term gait monitor-

ing and daily life applications, an alternative is to

use wearable inertial sensors like accelerometers and

gyroscopes. Advancements in MEMS technology

have made them miniature, low-powered, durable, in-

expensive, highly mobile and readily available (Ka-

vanagh and Menz, 2008). In recent years, many

gait event identiﬁcation algorithms have been devel-

oped using inertial sensors (Rueterbories et al., 2010).

While some have used gyroscopes (Pappas et al.,

2001; Aminian et al., 2002; Lee and Park, 2011),

others have found it appropriate to use accelerome-

ters (Williamson and Andrews, 2000; Mansﬁeld and

Lyons, 2003; Selles et al., 2005; Hanlon and Ander-

son, 2009; Sant’Anna and Wickstr¨om, 2010; Aung

et al., 2013). A major drawback of using inertial

sensors is that they provide highly noisy information

and thus require very robust algorithms for gait anal-

ysis. Based on the quality and type of information

they provide, some authors have discussed the pros

and cons of using either accelerometers or gyroscopes

(Aminian et al., 2002; Lau and Tong, 2008) though it

must be noted that these sensors are used and well re-

searched in other ﬁelds like aerospace and humanoids

(Khandelwal and Chevallereau, 2013). In the con-

text of gait event analysis, accelerometers seem to

be a better choice than gyroscopes for developing

automated gait event identiﬁcation systems. Sudden

movements like jerks or turns during walking would

cause large gyro drift errors. Furthermore, gyroscopes

have high power consumption, long reaction time and

are very sensitive to temperature effects limiting their

long-term outdoor use (Tan and Park, 2005; Wood-

man, 2007). Accelerometers, on the other hand, suf-

fer from noise due to mechanical vibrations and cali-

bration errors but these do not diverge in time and in

many cases can be handled effectively.

Recently, many methods have been developed

for identifying gait events only from accelerometer

data. Some of these algorithms apply different tech-

niques to analyze signals obtained from individual

accelerometer axis (Williamson and Andrews, 2000;

Mansﬁeld and Lyons, 2003; Selles et al., 2005; Tor-

realba et al., 2010). Hence, at the beginning of the

experiment, the accelerometer is positioned in some

speciﬁc orientation such that each accelerometer axis

is aligned with some pre-deﬁned limb axis and the

assumption is made that the accelerometer shall stay

statically positioned during the entire movement of

the experiment. Otherwise, either the axis alignment

should be readjusted frequently or the exact orien-

tation of the accelerometer must be known through-

out the experiment (which might be difﬁcult to es-

timate) to compensate for the misalignment of the

axes. A possible alternative could be to analyze the

resultant accelerometer signal instead as it is invari-

ant to individual axis alignment. Some other meth-

ods use machine learning techniques (Williamson and

Andrews, 2000; Aung et al., 2013) but the difﬁculty

with such algorithms is that they depend on labeled

training data and the addition or exclusion of any

parameter would require re-training the entire algo-

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

198

rithm. In recent years, wavelet transforms are being

increasingly used to develop gait event detection al-

gorithms (Aminian et al., 2002; Forsman et al., 2009;

Gouwanda and Senanayake, 2009; Aung et al., 2013)

as it supports simultaneous time frequency analysis

of non-stationary signals and have been shown to be

robust among peak detection algorithms (Yang et al.,

2009). Additionally, baseline trends can be implic-

itly removed and no preprocessing of the signal is re-

quired (Du et al., 2006). All methods and techniques

that were reviewed in this paper have been developed

by ‘simulating a physical world environment inside a

controlled laboratory’. Therefore there is a need for

a robust algorithm that can identify gait events from

acceleration signals collected in the ‘outdoor environ-

ment’.

This paper proposes a novel algorithm for the ro-

bust identiﬁcation of gait events from accelerome-

ter data collected during indoor and outdoor walk-

ing. The developed method combines the knowl-

edge about some known gait characteristics referred

to as expert knowledge (EK) with continuous wavelet

transform (CWT) analysis of the resultant accelerom-

eter signal. The proposed method is applied on an

indoor walking dataset to evaluate its efﬁciency and

accuracy. The robustness of the algorithm is evalu-

ated by applying it on outdoor walking signals and

comparing the mean stride time calculated from the

left and right legs of each subject. Since the outdoor

walking signals were of poorer quality and noisier

than indoor, further analysis was required to identify

the gait events. The rest of this paper is organized into

four sections. Sections 2 & 3 describe the data collec-

tion procedure and the developed algorithm, respec-

tively. Section 4 presents the results while Section 5

concludes this paper and discusses future work.

2 EXPERIMENTS

Fifteen healthy volunteers participated in the experi-

ments with informed prior consent. Each subject had

two Shimmer (3-axis) accelerometers (sampling at

128 Hz) attached to both their ankles, just above their

lateral malleolus. Velcro straps were used to keep the

sensors in place. The subjects were instructed to walk

for about 25 minutes at their preferred walking speed

on an outdoor street which was not absolutely ﬂat and

made of asphalt concrete. The proposed method was

also applied on a previously published dataset which

was collected from 6 subjects walking inside a labo-

ratory (Sant’Anna and Wickstr¨om, 2010). The exper-

iment used two Shimmer 3-axis accelerometers (sam-

pling at 50 Hz) positioned at the ankles and a 6m

long Gold GaitRite pressure sensitive mat (sampling

at 60 Hz) which had its own software for detecting

HS and TO. The pressure mat data was used as the

ground truth. All analysis was performed in MAT-

LAB (MathWorks, Natick, Massachusetts, USA).

3 METHODOLOGY

3.1 Continuous Wavelet Transform

The wavelet transform produces a time frequency de-

composition of the signal which separates individual

signal components more effectively than the short-

time Fourier transform. The ability to give the time

localization of the spectral components in a non-

stationary signal has rendered it a powerful tool for

processing of biosignals like EEG, EMG and ECG

(Raﬁee et al., 2011). Wavelet transforms can be

mainly divided into discrete and continuous forms.

The former operates over scales and positions based

on powers of two making it non-redundant, computa-

tionally more efﬁcient and sufﬁcient for reconstruc-

tion of signal. The latter allows transforms at all

scales and positions, thus maintaining all information

without down-sampling which makes it appropriate

for tasks like peak detection (Du et al., 2006) and pat-

tern matching. The Continuous Wavelet Transform or

CWT of a signal, x(t), is given as:

CWT(a, b) =

√

+∞

−∞

x(t)ψ

∗

(

t −b

)dt (1)

where ψ

∗

(t) is the complex conjugate of the wavelet

function ψ(t) and a and b are the dilation and loca-

tion parameters of the wavelet, respectively (Mallat,

1999). ψ(t), usually termed the mother wavelet func-

tion, must satisfy certain mathematical criteria like ﬁ-

nite energy and no zero-frequency component to be

admissible (Addison, 2005). The dilation or scale

is inversely proportional to the spectral components.

Low scales or high frequencies provide more local in-

formation while high scales or low frequencies pro-

vide relatively more global information about the sig-

nal. This multi-resolution property of CWT makes it

appropriate for gait analysis.

3.2 Expert Knowledge

There are some characteristics that are particular to

gait signals which is used in conjunction with CWT

analysis to develop the proposed algorithm. These

known gait characteristics, namely, EK

1,2,3

are enu-

merated below:

IdentificationofGaitEventsusingExpertKnowledgeandContinuousWaveletTransformAnalysis

199

1. For a subject walking at their preferred walking

speed, the shape of the HS regions in the resultant

accelerometer signal have consistency throughout

the signal as shown in Figure 1a. TO regions have

a similar consistency but their peaks are lower

than HS because normally the heel strikes the

ground with higher force compared to the toe lift-

ing off the ground.

2. The activity of walking cannot be done at arbi-

trarily high speeds. There is an upper bound in

the frequencies that are generated during walking.

3. This is an extension of EK

. During walking

at preferred walking speed, the velocity might

change with fairly consistent stride time but there

is no random high jump in speed from one step to

the other. For example if one step is taken at x m/s

then the following next step cannot be at 1.5x m/s

for a ‘normal’ walk.

Each of these facts are utilized to develop the pro-

posed method. Figure 1a shows the resultant accel-

eration signal that is calculated from the individual

accelerations from each axis of the 3-axis accelerom-

eter. EK

is used to choose the mother wavelet that is

applied to this resultant acceleration signal. The CWT

gives continuous wavelet coefﬁcients which illustrate

how well a wavelet function correlates with a speciﬁc

signal. Thus greater the correlation, higher will be

the CWT coefﬁcients and vice-versa. The wavelet

‘symlet-4’ (sym4) is chosen as the mother wavelet

function ψ(t) which is near symmetric and orthog-

onal (Figure 1b). Sym4 wavelet highly matches or

correlates with the HS regions giving sharper peaks

at higher scales (called ridges) more than the TO

regions, thus providing a better separation between

them at the same scales. EK

is used to choose the

appropriate scales for further analysis. As shown in

Figure 2, the information on lower scales corresponds

to high frequency noise and artifacts which can be ex-

0 100 200 300 400 500

Sample no.

Amplitude

Resultant Acceleration signal

HS HS HS HS

TO TO TOTO

0 2 4 6

0.5

Scaling function − sym4

0 2 4 6

−1

−0.5

0.5

1.5

Wavelet function − sym4

Figure 1: (a) HS and TO regions in the resultant accelera-

tion signal from outdoor walking. (b) Scaling and wavelet

functions of sym4 wavelet.

Figure 2: CWT coefﬁcients of the resultant acc. signal.

cluded. This is one of the many advantages of CWT

analysis as no pre-processing of the signal like noise

ﬁltering or smoothing is required. The scales that

are chosen for further analysis are where the CWT

coefﬁcients for the matched HS region are high and

form sharp ridges. In this case, as shown in Figure

2, the CWT coefﬁcients are very high between scales

40 to 80. Thus they are chosen for further analysis

and these scale bounds are applied to the resultant ac-

celeration signals of all subjects. EK

is used in the

statistical diagnosis of stride time to automatically de-

tect the inconsistent HS and TO regions (explained in

Section 3.3.2 and 3.3.3).

3.3 Identiﬁcation of Gait Events

3.3.1 Detecting the good HS

According to Eq.1, the CWT of the acceleration sig-

nal results in a CWT coefﬁcients matrix or CCM that

is based on the scale and location parameters of the

sym4 wavelet. Each row of this matrix corresponds

to a chosen scale of the wavelet while each column

corresponds to that sample of the acceleration signal

where the wavelet is positioned or located. Thus an

element in this matrix represents the correlation be-

tween the wavelet and a signal sample at a givenscale.

The CCM matrix has a size mxn where m is the total

number of chosen scales and n is the total length of

the vector of the samples of the acceleration signal.

The maximum coefﬁcient value in each column of the

CCM matrix represents the best matching for that sig-

nal sample from all chosen scales. A vector MC

1xn

deﬁned which contains the maximum coefﬁcient val-

ues from all n columns. A rough envelope (RE) of the

HS regions is obtained by subtracting the mean of MC

from MC and retaining all non-negative values from

the result (refer Figure 3a):

1xn

(

MC−

MC if MC −MC ≥ 0

0 if MC−MC < 0

(2)

where MC = max(CCM) and MC = mean(MC).

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

200

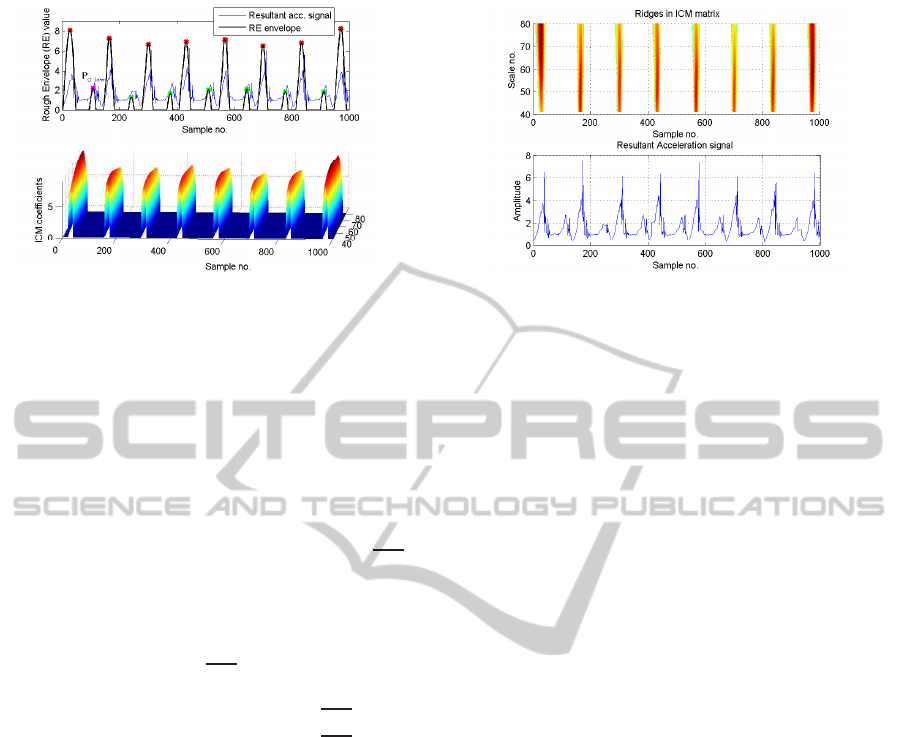
Figure 3: (a) Rough envelope (RE) of the HS and TO re-

gions. Red and green dots represent peaks that belong to

the C

high

and C

low

clusters respectively. The magenta dot

represents P

C−low

. (b) Coefﬁcients of the ICM matrix.

Then all local maxima points or peaks in the rough

envelope are found and separated into two clusters us-

ing k-means clustering. One cluster, C

high

, comprises

high-valued peaks located in the HS regions while the

other cluster, C

low

, comprises low-valued peaks from

the TO regions (Figure 3a). The peak with the highest

value in the C

low

cluster is identiﬁed and labeled as

C−low

. All coefﬁcients greater than (P

C−low

MC)

in the CWT coefﬁcients matrix would approximately

correspond to only the HS regions. Thus an interme-

diate coefﬁcients matrix (ICM

mxn

) is created from the

original CWT coefﬁcients matrix by setting all coef-

ﬁcients less than (P

C−low

MC) to zero:

ICM =

(

CCM if CCM > (P

C−low

MC)

0 if CCM 6 (P

C−low

+ MC)

(3)

The ICM coefﬁcients (shown in Figure 3b) rep-

resent the probable HS event with sharp ridges. By

computing the local maxima along the columns in the

ICM matrix, the ridges that correspond to the occur-

rence of HS events are obtained, as shown in Figure 4.

The mean of local maxima points making each ridge

in the ICM matrix gives the good HS events in the

resultant acceleration signal. For a good quality sig-

nal with a high signal to noise ratio (SNR), all HSs

will probably be identiﬁed in this step which was the

case with the indoor walking dataset. However, the

acceleration signals collected during outdoor walking

were highly noisy with poor SNR. For such signals,

it is observed that few HS and TO regions are irregu-

larly shaped, i.e. they look different from the regular

HS and TO regions due to signal corruption, sampling

effects or other factors inﬂuencing noise (some exam-

ples are shown in Figures 5 and 6). Due to their irreg-

ular and inconsistent shape, these noisy HS regions

do not match with the sym4 wavelet as much as the

other regular HS regions and lead to lower peaks that

Figure 4: Ridges in the ICM matrix that correspond to HS.

do not fall in the C

high

cluster. As a result, the ridges

corresponding to these noisy HSs do not appear in the

ICM matrix and are undetected in this step. Similarly

it might be that the noisy TO regions might get in-

correctly identiﬁed as HS due to high peaks that fall

in the C

high

cluster. Using EK

, a statistical analysis

of stride time allows us to automatically detect these

irregular HS and TO regions and identify them cor-

rectly. Henceforth the terms ‘noisy HS’ and ‘noisy

TO’ are used to represent the HSs that were unde-

tected and TOs that were misidentiﬁed as HSs, in this

step, respectively.

3.3.2 Locating the Noisy HS Events

The ridges corresponding to the noisy HS regions go

undetected in the previous step. An automated way to

ﬁnd these missed HSs is by statistically investigating

stride time. Stride time is deﬁned as the periodic time

between any two gait events such as HS. Using EK

2,3

it can be deduced that the stride time values which are

greater than 1.5 times the median stride time (appear

as high outliers in the boxplot of stride time in Figure

5) correspond to the noisy HSs. From each of these

high outliers, the HS event before and after the missed

HS event can be identiﬁed by referring to the vector

of good HSs obtained in Section 3.3.1. A temporal

boundary can be set to search for the missed ridges of

the noisy HSs in the CCM matrix:

bound

low

= HS

bef ore

+ Q1

bound

high

= HS

after

+ Q3 (4)

where HS

bef ore

and HS

after

are the HS events before

and after the missed HS and Q1 and Q3 are the 1st

and 3rd quartiles of stride time. The mean of the local

maxima points making each of these missed ridges in

the CCM matrix gives the location of the noisy HS

events which are appended to the vector of HSs. The

stride time is recomputed at the end of this step.

IdentificationofGaitEventsusingExpertKnowledgeandContinuousWaveletTransformAnalysis

201

0 100 200 300

Examples of noisy HS regions

Amplitude

Time (in samples)

0 100 200 300

Amplitude

Time (in samples)

100

150

200

250

300

Stride time (in samples) after

detecting the good HSs

Figure 5: Examples of noisy HS regions (circled in red) that

can be statistically detected from stride time.

3.3.3 Removing the Noisy TO Events

As explained in Section 3.3.1, the noisy TOs are the

ones which have been misidentiﬁed as HS and can be

automatically detected and removed in a similar sta-

tistical fashion as above using EK

and stride time.

Figure 6 shows the boxplot of stride time. The noisy

TOs lie in the cluster of outliers below the lower

whisker of stride time. These outliers correspond to

stride time values below (Q1−1.5∗IQR) where Q1

is the ﬁrst quartile and IQR is the interquartile range

of stride time. A noisy TO always give rise to a con-

secutive outlier pair among these low outliers. Such a

pair consists of one outlier which corresponds to the

distance between the previous HS and the noisy TO

and the other outlier which corresponds to the dis-

tance between this same noisy TO and the next HS.

This pair of outliers would be indexed consecutively

in the vector of HSs because they occur one after the

other as shown in Figure 6. Thus by identifying such

outlier pairs, the noisy TOs that have been misidenti-

ﬁed as HSs are removed from the vector of detected

HSs.

3.3.4 Final HS and TO Events

At the end of executing the previous three steps, the

conclusive HS events are obtained in the given accel-

eration signal. The TOs are detected by looking for

0 100 200

Example of noisy TO region

Time (in samples)

Amplitude

120

150

Stride time (in samples) after

locating the noisy HSs

Figure 6: Example of noisy TO region (circled in red) that

creates an outlier pair in the boxplot of stride time.

the ridges between two HSs in the CCM matrix that

are created by matching of the wavelet with TO re-

gions (Figure 2) .

4 RESULTS

Section 3 presents a four step procedure to systemati-

cally identify the gait events of HS and TO:

1. Detect the good HS events: Identiﬁes the HS from

the ridges in the ICM matrix that correspond to

the consistent and regularly shaped HS regions.

Stride time is computed at the end of this step.

2. Locate the noisy HS events: Detects the missed

HS events in step 1 (that correspond to the irreg-

ularly shaped noisy HS regions) by searching for

the missed ridges in CCM matrix within the de-

ﬁned temporal bounds.

3. Remove TO incorrectly identiﬁed as HS: Detects

and removes the irregularly shaped TO regions

misidentiﬁed as HS in step 1, by identifying lower

outlier pairs in stride time values that are consec-

utively indexed in the vector of HSs.

4. Final HS and TO events: Conclusive HS and TO

events in the given acceleration signal.

Figure 4 corresponds to step 1 while Figure 7

shows the stride time at the execution of steps 2, 3 and

4; by applying the proposed method on a subject’s ac-

celerometer signal from outdoor walking. The noisy

HSs and TOs are seen as long spikes which subse-

quently get removed after the execution of each step.

The developed algorithm was ﬁrst applied on an

indoor walking dataset consisting of 6 subjects. Since

these signals had high SNR, steps 1 and 4 were suf-

ﬁcient to detect the HS and TO of all subjects. Table

1 shows the mean absolute error and standard devia-

tion in detecting HS and TO using the proposed al-

gorithm in comparison with the results of symbolic

approach and peak detection reported in (Sant’Anna

0 700 1400

Step 2: Locate the noisy HS events

0 700 1400

Stride time (seconds)

Step 3: Remove TO incorrectly identied as HS

0 700 1400

No. of steps taken (while walking)

Step 4: Final HS and TO events

0.5

1.5

2 3 4

Stride time (sec.) at each step

Figure 7: Stride time (seconds) at steps 2, 3 and 4 while

processing an outdoor walking acceleration signal.

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

202

and Wickstr¨om, 2010), that were applied to the same

dataset. The errors were calculated by comparing the

detected gait events with the ground truth. In the pro-

posed method there was a constant bias of 5 samples

between the identiﬁed TO in the signal and the ground

truth given by the pressure mat. This could be due

to the fact that the pressure mat registers a TO when

the toe leaves the mat to enter the swing phase while

the proposed algorithm detects the TO when the toe

presses against the ground just before the lift, during

which there is highest resultant acceleration in the TO

region. This constant bias has been removed while

computing the mean absolute error and standard de-

viation of TO presented in Table 1.

The developed algorithm was then applied to the

outdoor walking data consisting of 15 subjects. Since

these signals had poor SNR, all steps were required to

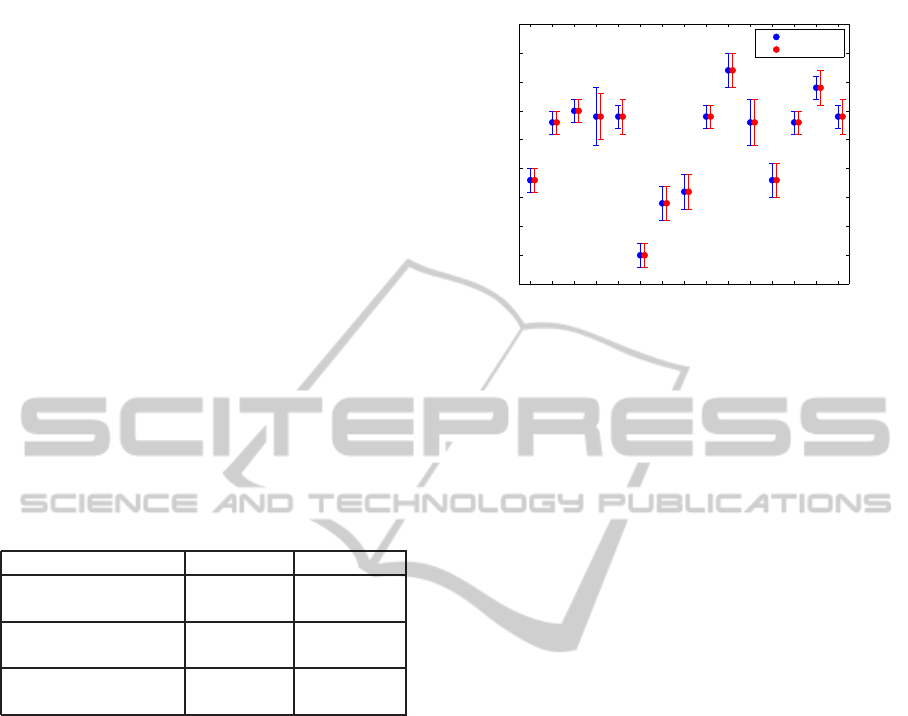
detect the gait events. Figure 8 shows the mean and

standard deviation of stride time computed for the left

and right leg of each subject for outdoor walking.

Table 1: Mean absolute error (MAE) and standard deviation

(SD) in seconds for different methods applied on the indoor

walking dataset of six subjects.

Method Gait Event MAE (SD)

Proposed Method

HS 0.03 (0.01)

TO 0.01 (0.01)

Symbolic Approach

HS 0.05 (0.04)

TO 0.03 (0.04)

Peak Detection

HS 0.07 (0.10)

TO 0.03 (0.03)

5 CONCLUSIONS & DISCUSSION

Most previous methods on gait event detection have

been developed for data collected indoors during con-

trolled lab experiments that provide gait events for

only a couple of steps. This paper presents a novel

algorithm which combines known gait characteris-

tics with wavelet analysis to robustly identify the gait

events, HS and TO, from accelerometer signals col-

lected in indoor as well as outdoor walking. The de-

veloped method uses resultant accelerometer signal

which eliminates the need to know the speciﬁc ori-

entation or alignment of the sensor. For indoor walk-

ing, the proposed algorithm detects gait events with

higher accuracy (Table 1) in comparison to the results

of symbolic approach and peak detection method re-

ported in (Sant’Anna and Wickstr¨om, 2010). Steps 1

and 4 were sufﬁcient to identify the gait events of all

subjects indicating that the data has high SNR.

Analyzing the noisy HSs and TOs in the accel-

eration signals of the outdoor data (examples shown

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15

0.8

0.85

0.9

0.95

1.05

1.1

1.15

1.2

1.25

Subject No.

Mean stride time (seconds)

Mean stride time (sec.) and standard deviation for Outdoor Walking

Left Foot

Right Foot

Figure 8: Mean stride time (sec.) and standard deviation for

left and right foot of all 15 subjects for outdoor walking.

in Figure 5 and 6) reveals that it has a much lower

SNR in comparison to the indoor data. The extra steps

needed to detect gait events from outdoor data indi-

cate the uncertainty in applying existing algorithms

developed by using indoor data with high SNR. Due

to lack of foot switches during outdoor walking ex-

periments, the detected gait events could not be com-

pared to ground truth. However, for a healthy subject

walking at their preferred walking speed, the stride

time of both feet should be similar with analogous

mean stride time as presented in Figure 8; thus sub-

stantiating the robustness of the proposed algorithm.

This makes it useful for long-term and continuous

gait monitoring applications. Using foot switches as

ground truth and performing the analysis in real-time

are considered for future work.

The use of gait expert knowledge in the algorithm

allows a robust analysis. Depending on the quality of

the acquired signal and the desired application, it al-

lows the user to decide to either skip or execute steps

2 and 3 (Section 4). This encourages the future pos-

sibility to adapt the proposed methodology to other

types of data and complex gait. Additionally, each of

the four steps of the proposed algorithm provide an

insight into the quality of the collected accelerome-

ter signal which can be further analyzed to deﬁne a

‘data quality index’. This could prove useful to clin-

icians and researchers to determine the utility of the

collected data and run diagnostics accordingly.

REFERENCES

Addison, P. S. (2005). Wavelet transforms and the ECG:

A review. Physiological Measurement, 26(5):R155–

R199.

Aminian, K. et al. (2002). Spatio-temporal parameters of

gait measured by an ambulatory system using minia-

IdentificationofGaitEventsusingExpertKnowledgeandContinuousWaveletTransformAnalysis

203

ture gyroscopes. Journal of Biomechanics, 35(5):689–

699.

Aminian, K. et al. (2004). Evaluation of an ambulatory sys-

tem for gait analysis in hip osteoarthritis and after total

hip replacement. Gait & Posture, 20(1):102–107.

Aung, M. et al. (2013). Automated detection of instanta-

neous gait events using time frequency analysis and

manifold embedding. IEEE Transactions on Neural

Systems and Rehabilitation Engineering.

Callisaya, M. L. et al. (2010). Ageing and gait variability

a population-based study of older people. Age and

Ageing, 39(2):191–197.

Desailly, E. et al. (2009). Foot contact event detection using

kinematic data in cerebral palsy children and normal

adults gait. Gait & Posture, 29(1):76 – 80.

Du, P. et al. (2006). Improved peak detection in mass spec-

trum by incorporating continuous wavelet transform-

based pattern matching. Bioinformatics, 22(17):2059–

2065.

Forsman, P. et al. (2009). Wavelet analysis to detect gait

events. In EMBC, pages 424–427.

Gouwanda, D. and Senanayake, S. (2009). Applica-

tion of hybrid multi-resolution wavelet decomposition

method in detecting human walking gait events. In

SOCPAR, pages 580–585.

Hafner, V. and Bachmann, F. (2008). Human-humanoid

walking gait recognition. In Humanoids 2008, pages

598–602.

Hanlon, M. and Anderson, R. (2009). Real-time gait event

detection using wearable sensors. Gait & Posture,

30(4):523–527.

Hausdorff, J. M. (2007). Gait dynamics, fractals and

falls: Finding meaning in the stride-to-stride ﬂuctu-

ations of human walking. Human Movement Science,

26(4):555–589.

Herman, T. et al. (2005). Gait instability and fractal dy-

namics of older adults with a cautious gait: why do

certain older adults walk fearfully? Gait & Posture,

21(2):178–185.

Kavanagh, J. J. and Menz, H. B. (2008). Accelerometry: A

technique for quantifying movement patterns during

walking. Gait & Posture, 28(1):1–15.

Khandelwal, S. and Chevallereau, C. (2013). Estimation

of the trunk attitude of a humanoid by data fusion of

inertial sensors and joint encoders. In CLAWAR, pages

822–830.

Lau, H. and Tong, K. (2008). The reliability of using ac-

celerometer and gyroscope for gait event identiﬁca-

tion on persons with dropped foot. Gait & Posture,

27(2):248–257.

Lee, J. and Park, E. (2011). Quasi real-time gait event detec-

tion using shank-attached gyroscopes. Medical & Bi-

ological Engineering & Computing, 49(6):707–712.

Mallat, S. (1999). A wavelet tour of signal processing. Aca-

demic Press.

Mansﬁeld, A. and Lyons, G. M. (2003). The use of ac-

celerometry to detect heel contact events for use as a

sensor in FES assisted walking. Medical Engineering

& Physics, 25(10):879–885.

McDonough, A. L. et al. (2001). The validity and reliability

of the GAITRite system’s measurements: A prelimi-

nary evaluation. Archives of Physical Medicine and

Rehabilitation, 82(3):419–425.

Miller, A. (2009). Gait event detection using a multilayer

neural network. Gait & Posture, 29(4):542–545.

Mills, P. M. et al. (2007). Agreement between footswitch

and ground reaction force techniques for identifying

gait events: Inter-session repeatability and the effect

of walking speed. Gait & Posture, 26(2):323–326.

Pappas, I. et al. (2001). A reliable gait phase detection sys-

tem. IEEE Transactions on Neural Systems and Reha-

bilitation Engineering, 9(2):113–125.

Raﬁee, J. et al. (2011). Wavelet basis functions in biomed-

ical signal processing. Expert Systems with Applica-

tions, 38(5):6190–6201.

Reelick, M. F. et al. (2009). The inﬂuence of fear of falling

on gait and balance in older people. Age and Ageing,

38(4):435–440.

Rueterbories, J. et al. (2010). Methods for gait event de-

tection and analysis in ambulatory systems. Medical

Engineering & Physics, 32(6):545–552.

Sant’Anna, A. and Wickstr¨om, N. (2010). A symbol-based

approach to gait analysis from acceleration signals:

Identiﬁcation and detection of gait events and a new

measure of gait symmetry. IEEE Transactions on

Information Technology in Biomedicine, 14(5):1180–

1187.

Selles, R. et al. (2005). Automated estimation of initial

and terminal contact timing using accelerometers; de-

velopment and validation in transtibial amputees and

controls. IEEE Transactions on Neural Systems and

Rehabilitation Engineering, 13(1):81–88.

Socie, M. J. et al. (2013). Gait variability and disability in

multiple sclerosis. Gait & Posture, 38(1):51–55.

Stolze, H. et al. (2004). Falls in frequent neurological dis-

eases. Journal of Neurology, 251(1):79–84.

Tan, C. W. and Park, S. (2005). Design of accelerometer-

based inertial navigation systems. IEEE Transactions

on Instrumentation and Measurement, 54(6):2520–

2530.

Torrealba, R. et al. (2010). Statistics-based technique for

automated detection of gait events from accelerometer

signals. Electronics Letters, 46(22):1483–1485.

Williamson, R. and Andrews, B. (2000). Gait event detec-

tion for FES using accelerometers and supervised ma-

chine learning. IEEE Transactions on Rehabilitation

Engineering, 8(3):312–319.

Woodman, O. J. (2007). An introduction to inertial naviga-

tion. Technical report, Univ. of Cambridge.

Yang, C. et al. (2009). Comparison of public peak detection

algorithms for MALDI mass spectrometry data analy-

sis. BMC Bioinformatics, 10(1):4.

BIOSIGNALS2014-InternationalConferenceonBio-inspiredSystemsandSignalProcessing

204