Finding Coherent Regions in PET Images for the Diagnosis of

Alzheimer’s Disease

Helena Aidos, Jo˜ao Duarte and Ana Fred

Instituto de Telecomunicac¸˜oes, Instituto Superior T´ecnico, Lisbon, Portugal

Keywords:

Support Vector Machines, ROI, Feature Extraction, Image Segmentation, Mutual Information.

Abstract:

Alzheimer’s disease is a type of dementia that mainly affects elderly people, with unknown causes and no

effective treatment up to date. The diagnosis of this disease in an earlier stage is crucial to improve patients’

life quality. Current techniques focus on the analysis of neuroimages, like FDG-PET or MRI, to ﬁnd changes

in the brain activity. While high accuracies can be obtained by combining the analysis of several types of

neuroimages, they are expensive and not always available for medical analysis. Achieving similar results using

only 3-D FDG-PET scans is therefore of huge importance. While directly applying classiﬁers to the FDG-PET

scan voxel intensities can lead to good prediction accuracies, it results in a problem that suffers from the curse

of dimensionality. This paper thus proposes a methodology to identify regions of interest by segmenting

3-D FDG-PET scans and extracting features that represent each of those regions of interest, reducing the

dimensionality of the space. Experimental results show that the proposed methodology outperforms the one

using voxel intensities despite only a small number of features is needed to achieve that result.

1 INTRODUCTION

One of the most common forms of dementia is

Alzheimer’s disease (AD), a progressive brain dis-

order that has no known cause or cure. It is a dis-

ease that slowly leads to memory loss, confusion, im-

paired judgment, personality changes, disorientation

and the inability to communicate. An early detec-

tion is very important for an effective treatment, espe-

cially in the Mild Cognitive Impairment (MCI) stage,

to slow down the progress of the symptoms and to im-

prove patients’ life quality. MCI is a condition where

a person has mild changes in thinking abilities, but it

does not affect daily life activities. People with MCI

are more likely to develop AD, even though recent

studies suggest that a person with MCI may revert

back to normal cognition on its own (Alzheimer’s As-

sociation, 2013).

Neuroimages allow the identiﬁcation of brain

changes and have been used for automated diagno-

sis of AD and MCI (Silveira and Marques, 2010; Ye

et al., 2012). Due to the high variability of the pat-

tern of brain degeneration in AD and MCI, the analy-

sis of brain images is a very difﬁcult task. Moreover,

attempts are being made to develop tools to automat-

ically analyze the images and, consequently, diagno-

sis AD and MCI conditions (Morgado et al., 2013;

Ram´ırez et al., 2013).

Most of the techniques developed have focused

on analyzing small parts of the brain like hippocam-

pus (Gerardin et al., 2009) or the gray matter volume

(Fan et al., 2008). However, these techniques have

some limitations by the fact that the brain atrophy af-

fects many and different regions in different stages of

the disease. Therefore, researchers are focusing their

techniques in analyzing the pattern of the entire brain.

However, this leads to the ”curse of dimensionality”

because a brain image, like the ﬂuorodeoxyglucose

positron emission tomography (FDG-PET), contains

thousands of voxels (or features). Dimensionality re-

duction and feature selection techniques are therefore

fundamental for achieving high accuracy predictors

for the diagnosis of Alzheimer’s disease.

Some techniques are based in the segmentation

of the brain into Regions of Interest (ROIs), which

are associated with atrophy caused by the disease.

Then, voxel intensities from each ROI are used as

features (Zhang et al., 2011; Mikhno et al., 2012).

Some other dimensionality reduction techniques from

Machine Learning ﬁeld (Lopez et al., 2009; Segovia

et al., 2012), and feature selection techniques (Bi-

cacro et al., 2012; Chaves et al., 2009) have been ap-

plied to the diagnosis of AD.

In this paper, we propose a methodology to au-

Aidos H., Duarte J. and Fred A..

Finding Coherent Regions in PET Images for the Diagnosis of Alzheimer’s Disease.

DOI: 10.5220/0004802200120018

In Proceedings of the International Conference on Bioimaging (BIOIMAGING-2014), pages 12-18

ISBN: 978-989-758-014-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

tomatically extract features that represent interesting

regions of the brain and, consequently, reducing the

dimensionality of the space. One of the advantages of

this methodology is that brain images, like FDG-PET,

do not need to be pre-processed in order to remove the

background and the scalp. This is due to the choice of

the clustering algorithm, which is a variant of the DB-

SCAN (density-based spatial clustering of applica-

tions with noise) called XMT-DBSCAN (Tran et al.,

2012). Another advantage is that the space we ob-

tain is approximately 100× smaller when compared

to the original one, consisting of voxel intensities.

This happens because each region (cluster) obtained

by the clustering algorithm is represented by a feature,

which is a weighted mean of the voxel intensities of

that region.

This paper is organized as follows: section 2 ex-

plains each step of the proposed methodology and

section 3 presents the dataset used in this paper as

well the results obtained for the proposed method-

ology and for the classiﬁcation task using the voxel

intensity. Conclusions are drawn in Section 4.

2 THE PROPOSED

METHODOLOGY

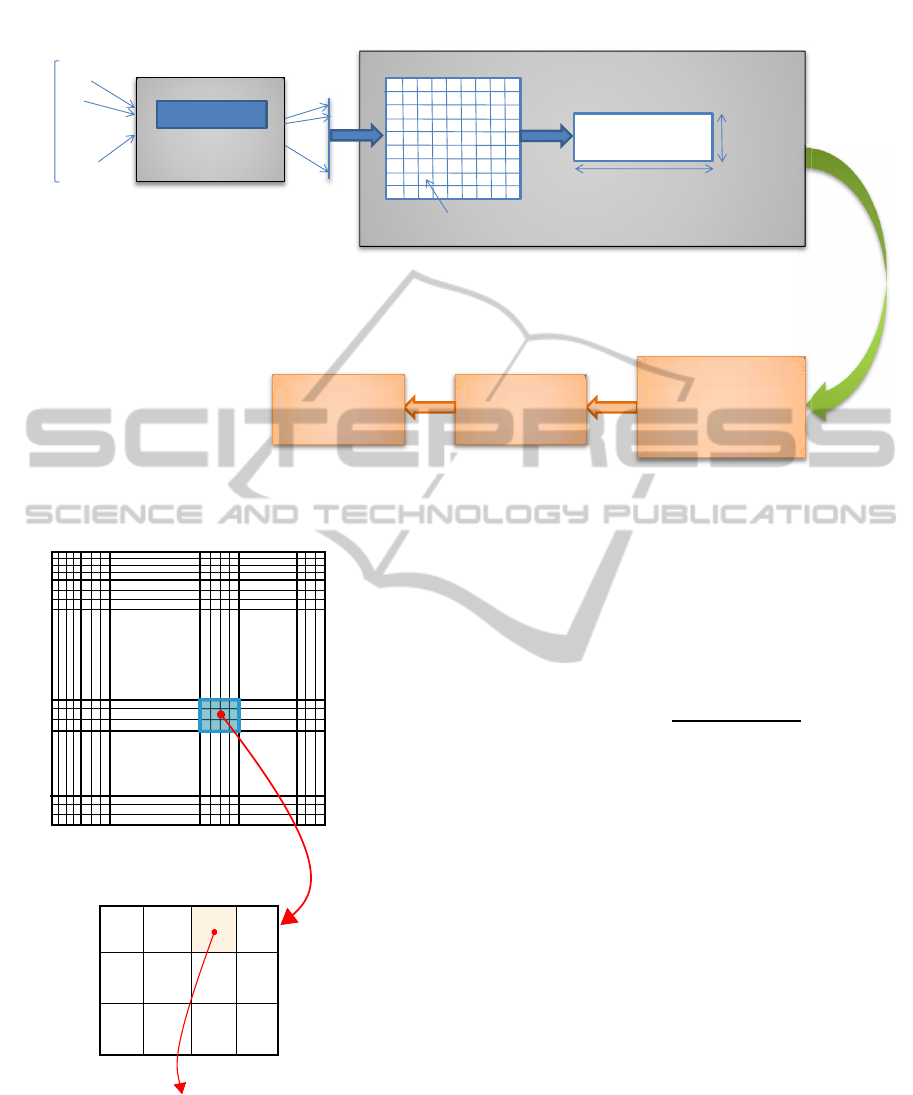
In order to analyze the FDG-PET scans for each task:

AD versus CN (Cognitive Normal), MCI versus CN

and AD versus MCI, we propose the methodology

shown in Figure 1. We start by segmenting each 3-D

image (a FDG-PET scan from a subject), followed by

a construction of a probability matrix indicating the

degree of belonging of each voxel to a region found

by the clustering/segmentation algorithm. Then, we

perform a feature extraction step using the voxel in-

tensities and the probability matrix, obtaining a fea-

ture space representation for each problem. Finally,

feature selection is applied and the subjects are clas-

siﬁed, using support vector machines.

2.1 Step 1: Image Segmentation

Over the years, several 3-D segmentation methods

have been developed such as region growing, wa-

tershed, among others (Arbel´aez et al., 2011; Tri-

pathi et al., 2012); watershed algorithm (Beucher and

Lantuejoul, 1979) is the most widely used. How-

ever, watershed tends to over-segment the 3-D images

when the data is dense and non-homogeneous,or gen-

erate under-segmentation results in the case of dense

regions with irregular shapes of objects. Since our

FDG-PET scans are noisy images that have regions

with different sizes, densities and irregular shapes,

we propose to use a version of the DBSCAN algo-

rithm, namely the XMT-DBSCAN (Tran et al., 2012),

to segment the 3-D images.

XMT-DBSCAN is an extension of the original

DBSCAN but has a few differences. Firstly, the local

density of a voxel (a pixel in DBSCAN) is computed

in the sub-window with size ws = (2w + 1) × (2w +

1)×(2w+1) centered in the voxel, instead of the ball

with radius eps. In our methodology, the local density

is computed as

density(v

ijk

) =

∑

all−elements

ijk

⊙ K

, (1)

where ⊙ is the element-wise product of two equally

sized data cubes, K

is a cubic Gaussian kernel with

standard deviation equal to ws/(4

2log(2)), I

ijk

the sub-window from the intensity image, and a

the number of non-zero values in K

The identiﬁcation of the voxels as core points,

border points and noise is similar to the original

DBSCAN. Another modiﬁcation to the original DB-

SCAN is in the deﬁnition of density-reachable chain

(Ester et al., 1996), which is modiﬁed to contain only

core voxels. This means that labeling the border

points is made in a post-processing step, at the end

of the algorithm, when all core points are identiﬁed.

2.2 Step 2: Coherence Matrix

After segmenting each 3-D image, we obtain a parti-

tion into regions (clusters) and we need to ﬁnd some

consensual information for each population (AD, CN

or MCI). In that sense, we construct a block coherence

matrix C, with as many blocks as the squared number

of subjects of a population. The idea is to perform a

pairwise comparison between the partitions obtained

by XMT-DBSCAN for each subject of a population.

Therefore,

C(µ(l, i),µ(p, j)) =

∩C

| · |C

, (2)

where µ(l, i) is the indexation function for the coher-

ence matrix C, |C

∩C

| is the number of voxels be-

longing to both C

and C

, with C

the region/cluster

i from subject l and C

the region/cluster j from sub-

ject p. The indexation function is given by

µ(l, i) = i+

l−1

∑

j=1

with m

the number of clusters in the partition of sub-

ject j, i.e., µ(l, i) gives the index corresponding to

cluster i of subject l, where each partition of a sub-

ject has m

clusters. Figure 2 shows an example of a

FindingCoherentRegionsinPETImagesfortheDiagnosisof

Alzheimer'sDisease

STEP 1:

Image segmentation

DBSCAN

A(B)

Parameters:

w, j, kernel

FDG-PET from

Population A (B)

Coherence matrix

Coherence matrix between subjects i and j

(values under 50% are discarded)

Degree of belonging

Number of Voxels

A(B)

most

coherent

clusters

),(

)(

ijk

STEP 4:

Feature Selection

Higher mutual

information

STEP 5:

Classification

Support vector

machines

STEP 3:

Feature Extraction

Feature space of size

)x(K

)

obtained from

equation (4)

STEP 2:

Coherence matrix

Figure 1: The proposed methodology.

...

......

...

C( (l,1), (p,3))

clusters

{

clusters

{

Figure 2: Coherence matrix.

coherence matrix.

The matrix C shows the degree of overlapping of

each pair of clusters. Since we want a region that is

common in most of the subjects, we consider that val-

ues under 50% of overlapping are discarded.

We start by searching the most coherent cluster in

matrix C and obtain a region R corresponding to the

union of all clusters with an overlapping over 50% to

the most coherent cluster found. Inside the region R ,

we compute the probability (for a certain population)

of each voxel belong to R as

ijk

,R ) =

∑

∈R

ijk

∈C

}

∑

∈R

∈R }

, (3)

where C

is the k-th cluster of region R , 1

ijk

∈C

}

is 1

if v

ijk

∈ C

, and 0 otherwise; v

ijk

is a voxel in the 3-D

image and A ∈ {AD,CN,MCI}. The numerator of the

previous equation is a count of the number of clusters

in R where the voxel belongs, and the denominator is

just the number of clusters in R . This process is re-

peated until no coherent clusters are left in matrix C.

Therefore, P

is K × N matrix, with K the number of

regions and N the number of voxels in the 3-D image.

2.3 Step 3: Feature Extraction

So far we have found regions containing relevant in-

formation for each population. Now we want to dis-

criminate AD vs CN, CN vs MCI and AD vs MCI.

This means that we will construct a feature space for

each of these problems using the voxels intensities

from two populations and the regions found in step

2 corresponding to the same two populations.

Consider that M

is the number of subjects from

population A and M

the number of subjects from

population B. Also, K

and K

are the number of

BIOIMAGING2014-InternationalConferenceonBioimaging

Population B Population A

K +K

K +1

K +2

A A

... ...

Population A Population B

M +M

M +1

M +2

A A

...

......

...

F(α(1, population A),β(2, population B))

Figure 3: New feature space representation obtained by fea-

ture extraction.

regions found in step 2 for population A and B, re-

spectively. We want to construct a feature space F

with M

+ M

samples and dimension K

+ K

, in

the following way

F(α(p,r),β(q,s)) =

∑

ijk

I(v

ijk

∈ S

) · P

ijk

)

∑

ijk

)

(4)

with r,s ∈ {population A,population B}. I(v

ijk

∈ S

)

is the intensity of voxel v

ijk

from subject p in popu-

lation r and P

ijk

) is the probability that voxel

ijk

belongs to region R

in population s. α(p,r) and

β(q,s) are indexation functions given by

α(p,r) =



p if r = population A

+ p if r = population B

and

β(q,s) =



q if s = population A

+ q if s = population B

respectively. α(p,r) is the indexation for subjects and

β(q,s) the indexation for regions, as illustrated in ﬁg-

ure 3.

Equation (4) is equivalent to compute a weighted

mean of the intensity of a subject, where some voxels

contribute more than others, obtaining a feature space

for each classiﬁcation task.

2.4 Step 4: Feature Selection

Typically, the number of voxels in a FDG-PET image

is very high and some of those voxels are unimportant

for the task in hand. So, it is very important to re-

duce the dimensionality of the space through feature

selection. We use mutual information (MI) to rank the

features and choose the ones with higher value.

Table 1: Clinical and demographic characteristics of each

group. Age and MMSE (Mini Mental State Exam) values

are means (± standard deviations).

Attributes AD MCI CN

Number of subjects 59 59 59

Age 78.26 77.71 77.38

(±6.62) (±6.88) (±4.87)

Sex (% of males) 57.63 67.80 64.41

MMSE 19.60 25.68 29.20

(±5.06) (±2.97) (±0.92)

Consider that x

is the i-th element of a vector rep-

resenting a feature x, and y a target value or label. The

MI between the random variable x

and y is given by

MI(i) =

∑

P(x

,y)log

P(x

,y)

P(x

)P(y)

. (5)

The probability density functions for MI were esti-

mated through the use of histograms.

2.5 Step 5: Classiﬁcation

After selecting the most relevant features for each of

the three diagnostic problems, we classify subjects

through the support vector machine (SVM) algorithm

with a linear kernel (Cortes and Vapnik, 1995). The

SVM algorithm is a popular classiﬁer in several ar-

eas, including diagnosis of neurological diseases like

Alzheimer.

3 EXPERIMENTS

3.1 Dataset

In this study, we used FDG-PET images for AD, MCI

and CN subjects, retrieved from the ADNI database.

The subjects were chosen to obey a certain criteria:

the Clinical Dementia Rating (CDR) should be 0.5 or

higher for AD patients, 0.5 for MCI patients and 0

for normal controls. This selection results in a dataset

composed by 59, 142 and 84 subjects for AD, MCI

and CN, respectively. Since our task is classiﬁcation

using the SVM algorithm, we decided to balanced the

classes by using a random sub-sampling technique.

Thus, 59 subjects from each MCI and CN groups

were selected randomly. Table 1 summarizes some

clinical and demographic information in each group.

The FDG-PET images have been pre-processed

to minimize differences between images: each image

was co-registered, averaged, reoriented (the anterior-

posterior axis of each subject was parallel to the AC-

PC line), normalized in its intensity, and smoothed

FindingCoherentRegionsinPETImagesfortheDiagnosisof

Alzheimer'sDisease

to uniform standardized resolution. A more detailed

description of the pre-processing is available in the

ADNI project webpage

The complete 64 × 64 × 30 FDG-PET images

were used, which means that no background or extra-

cranial voxels were excluded. We left those voxels

because the image segmentation step will automati-

cally discard them and only the relevant voxels will

be labeled.

3.2 Experimental Setup

The FDG-PET image of the brain of each individual

needs to be segmented with XMT-DBSCAN, the seg-

mentation algorithm proposed in the methodology. In

section 2, we state that XMT-DBSCAN has two pa-

rameters: window size w and ϕ which is a threshold

to identify core and border voxels (see (Ester et al.,

1996) for more details). We set w to 2 and 3, and ϕ

takes values from {0.3,0.5, 0.7}. The ﬁrst part of our

experiments consists in the analysis of the inﬂuence

of these parameters in the results.

In the feature selection step we discretized the

probability density functions through histograms with

8 bins and, after ranking the features according to the

MI, we choose the ones with higher value. We con-

sider several number of features selected by the MI,

according to table 2.

The ﬁnal step of the proposed methodology

consists in classifying subjects using a linear SVM.

We set the cost of misclassiﬁcation in SVM as

−16

−14

−12

−10

−8

−6

−4

−2

}

and performed a 20 × 10 nested cross-validation

procedure (Varma and Simon, 2006).

We compare the proposed methodology with the

one consisting of the voxel intensities, called MI-

SVM. In that strategy, we ﬁrst need to pre-process

the FDG-PET images to remove the background and

the scalp. Afterwards, steps 4 and 5 of the proposed

methodologyare applied. The number of selected fea-

tures used to classify the subjects are shown in table 2.

3.3 Results

Firstly, we want to study the inﬂuence of the two pa-

rameters (w and ϕ) of the image segmentation step

in the classiﬁer. Figure 4 shows the accuracy of the

classiﬁer for the considered parameters values.

In AD vs CN problem we see that the best result

is higher than 89% and it is given when we consider

a ϕ = 0.7 and w = 3 in the XMT-DBSCAN algo-

rithm. Also, this best value is obtained with a lower

http://adni.loni.usc.edu/methods/pet-analysis/

pre-processing/

90%

88%

86%

84%

82%

0 200 400 600 800 1000 1200 1400 1600

Number of features

Accuracy

w=2

0.3 0.5 0.7

0.3 0.5

w=3

(a) AD vs CN

w=2

0.3 0.5 0.7

0.3 0.5

w=3

0 200 400 600 800 1000 1200 1400 1600

Number of features

78%

Accuracy

76%

74%

72%

70%

68%

66%

64%

(b) MCI vs CN

72%

70%

68%

66%

64%

Accuracy

0 200 400 600 800 1000 1200 1400 1600

Number of features

w=2

0.3 0.5 0.7

0.3 0.5

w=3

Figure 4: Average accuracy of 20 × 10 nested cross-

validation of the proposed methodology for several different

parameters consider in the image segmentation step.

number of features, around 250 features, which cor-

responds to the all space for those parameters. More-

over, with w = 2 and ϕ = 0.3 we have the lowest ac-

curacy for different number of features and the maxi-

mum is when we have a space with 1000 features with

an accuracy of approximately 87%.

In MCI vs CN problem the worst result is for

w = 3 and ϕ = 0.7, opposite of what we see in AD

vs CN. Now the best result is higher than 76% and

it is given by w = 2 and ϕ = 0.5, which means that

we need a small sub-window to distinguish between

MCI subjects and CN subjects. Again, we only need

around 250 features for the better accuracy.

In the case of AD vs MCI, the worst results are for

w = 3 and ϕ = 0.3 and it is approximately 64%, but

the best result is obtained using only 50 features and

a small window and density in the XMT-DBSCAN

algorithm (w = 2 and ϕ = 0.3). For those parameters,

we notice that if we increase the number of features,

the accuracy decreases.

The two parameters we are discussing affects not

only the number of features of the space, but also the

BIOIMAGING2014-InternationalConferenceonBioimaging

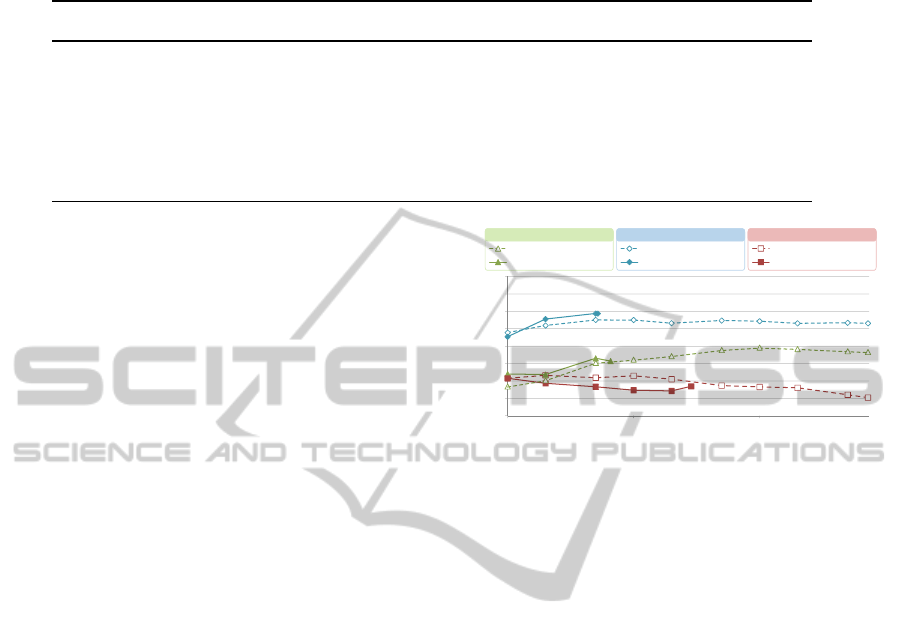
Table 2: Number of features used to tested the feature selection step. The maximum number of features used corresponds to

the complete feature space, as stated by columns 2-4, depending on the problem.

Parameter Max. features

Space AD vs CN MCI vs CN AD vs MCI Number of selected features

w = 2,ϕ = 0.3 1436 1413 1433 50, 100, 250, 500, 1000, Max. features

w = 2,ϕ = 0.5 1037 1057 1050 50, 100, 250, 500, 1000, Max. features

w = 3,ϕ = 0.3 476 476 502 50, 100, 250, Max. features

w = 3,ϕ = 0.5 332 328 342 50, 100, 250, Max. features

w = 3,ϕ = 0.7 260 284 268 50, 100, 250, Max. features

voxel intensity 36209 50, 100, 250, 500, 1000, 2500,

5000, 10000, 25000, Max. features

accuracy of the classiﬁer. From ﬁgure 4, we notice

that for distinguish between AD and CN subjects we

need to create large regions with high density (in-

tensity). This makes sense, since FDG-PET scans

of the brain measures the glucose used, and patients

with Alzheimer’s disease had a big decrease in brain

metabolism of glucose compared to a normal patient.

Moreover, if we want to distinguish between MCI pa-

tients and CN or AD patients, we need to decrease the

size of clusters, which leads to an increase of number

of regions/features and look for differences in more

speciﬁc locations of the brain. This happens because

MCI is a transition stage: some MCI patients may

convert to Alzheimer others just remain stable over

time or even remit.

Figure 5 compares the best result obtained with

the proposed methodology for each problem with the

methodology using the voxel intensity. For AD vs

CN our methodologyoutperformsMI-SVM with only

a few features. Even if we use the all space, MI-

SVM is always worst than our methodology. Some-

thing similar happens for MCI vs CN, using few fea-

tures (around 250 features) our methodology outper-

forms MI-SVM. However, if we increase the num-

ber of features until 5000, MI-SVM can predict better

than our methodology. In AD vs MCI, our best per-

formance is for the lowest number of features (50 fea-

tures) and it is comparable to MI-SVM; after that we

perform worst than MI-SVM. Notice that, MI-SVM

remains almost constant until 1000 features and then

the performance decreases. Moreover, our method-

ology starts to increase after the 1000 features. This

may indicate that we need more features to discrimi-

nate MCI subjects from AD subjects, which means we

need to decrease the size of the regions corresponding

to a decreasing in the parameters w and/or ϕ.

4 CONCLUSIONS

This paper proposes a methodology to ﬁnd interesting

regions in the brain to efﬁciently discriminate subjects

AD vs CN

MCI vs CN

AD vs MCI

MCI vs CN

Voxels selected by MI

Proposed (w=3, =0.5)

AD vs CN

Voxels selected by MI

Proposed (w=3, =0.7)

AD vs MCI

Voxels selected by MI

Proposed (w=2, =0.3)

Number of features

(log scale)

500 5000

100%

Accuracy

95%

90%

85%

80%

75%

70%

65%

60%

Figure 5: Average accuracy of 20 × 10 nested cross-

validation of the best curve from each problem in ﬁgure 4

compared to voxels intensities chosen through mutual infor-

mation and classiﬁed using SVM.

with Alzheimer’s disease from the ones with mild

cognitive impairment and from normal ones. The pro-

posed methodology has several stages: starts with a

segmentation of the FDG-PET image, followed by a

grouping of clusters to form regions with relevant in-

formation. Those regions form a feature space and

the most important ones are selected by ranking their

mutual information with the target output. Finally a

classiﬁer is used to identify the subjects.

For number of features under 100, the proposed

methodology outperforms another strategy consisting

in ranking the mutual information of features with the

target output, where the features are only the vox-

els intensities. Moreover, by comparing using all

the space in both strategies, our methodology out-

performs the other strategy, using a small number of

features. Another advantage of this methodology is

that the complete FDG-PET image was used, since

the segmentation algorithm can identify background

and extracranial voxels, which means we do not need

to pre-process the images to remove those voxels.

ACKNOWLEDGEMENTS

This work was supported by the Portuguese Founda-

tion for Science and Technology grants PTDC/SAU-

FindingCoherentRegionsinPETImagesfortheDiagnosisof

Alzheimer'sDisease

ENB/114606/2009 and PTDC/EEI-SII/2312/2012.

Data used in the preparation of this article were ob-

tained from the Alzheimer’s Disease Neuroimaging

Initiative (ADNI) database.

REFERENCES

Arbel´aez, P., Maire, M., Fowlkes, C., and Malik, J. (2011).

Contour detection and hierarchical image segmenta-

tion. IEEE Trans. on Pattern Analysis and Machine

Intelligence, 33(5):898–916.

Association, A. (2013). 2013 Alzheimer’s disease facts and

ﬁgures. Alzheimer’s & Dementia: The Journal of the

Alzheimer’s Association, 9(2):208–245.

Beucher, S. and Lantuejoul, C. (1979). Use of watersheds in

contour detection. In Int. Work. on Image Processing:

Real-time Edge and Motion Detection/Estimation.

Bicacro, E., Silveira, M., Marques, J. S., and Costa, D. C.

(2012). 3D image-based diagnosis of Alzheimer’s dis-

ease: bringing medical vision into feature selection. In

Int. Symp. on Biomedical Imaging, pages 134–137.

Chaves, R., Ramirez, J., Gorriz, J. M., Lopez, M., Alvarez,

I., Salas-Gonzalez, D., Segovia, F., and Padilla, P.

(2009). SPECT image classiﬁcation based on NMSE

feature correlation weighting and SVM. In IEEE Nu-

clear Science Symp. Conf. Record, pages 2715–2710.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Machine Learning, 20:273–297.

Ester, M., Kriegel, H.-P., Sander, J., and Xu, X. (1996).

A density-based algorithm for discovering clusters in

large spatial databases with noise. In Int. Conf. on

Knowledge Discovery and Data Mining, pages 226–

231.

Fan, Y., Batmanghelich, N., Clark, C., and Davatzikos, C.

(2008). Spatial patterns of brain atrophy in MCI pa-

tients, identiﬁed via high-dimensional pattern classi-

ﬁcation, predict subsequent cognitive decline. Neu-

roImage, 39:1731–1743.

Gerardin, E., Ch´etelat, G., Chupin, M., Cuingnet, R., Des-

granges, B., Kim, H.-S., Niethammer, M., Dubois, B.,

Leh´ericy, S., Garnero, L., Eustache, F., and Colliot, O.

(2009). Multidimensional classiﬁcation of hippocam-

pal shape features discriminates Alzheimer’s disease

and mild cognitive impairment from normal aging.

NeuroImage, 47(4):1476–1486.

Lopez, M., Ramirez, J., Gorriz, J. M., Salas-Gonzalez, D.,

Alvarez, I., Segovia, F., and Chaves, R. (2009). Multi-

variate approaches for Alzheimer’s disease diagnosis

using bayesian classiﬁers. In IEEE Nuclear Science

Symp. Conf. Record, pages 3190–3193.

Mikhno, A., Nuevo, P. M., Devanand, D. P., Parsey, R. V.,

and Laine, A. F. (2012). Multimodal classiﬁcation

of dementia using functional data, anatomical features

and 3D invariant shape descriptors. In Int. Symp. on

Biomedical Imaging, pages 606–609.

Morgado, P., Silveira, M., and Marques, J. S. (2013). Efﬁ-

cient selection of non-redundant features for the diag-

nosis of Alzheimer’s disease. In Int. Symp. on Biomed-

ical Imaging, pages 640–643.

Ram´ırez, J., G´orriz, J. M., Salas-Gonzalez, D., Romero,

A., L´opez, M.,

Alvarez, I., and G´omez-R´ıo, M.

(2013). Computer-aided diagnosis of Alzheimer’s

type dementia combining support vector machines

and discriminant set of features. Information Sciences,

237:59–72.

Segovia, F., G´orriz, J. M., Ram´ırez, J., Salas-Gonzalez, D.,

Alvarez, I., L´opez, M., and Chaves, R. (2012). A

comparative study of feature extraction methods for

the diagnosis of Alzheimer’s disease using the ADNI

database. Neurocomputing, 75:64–71.

Silveira, M. and Marques, J. S. (2010). Boosting Alzheimer

disease diagnosis using PET images. In Int. Conf. on

Pattern Recognition, pages 2556–2559.

Tran, T. N., Nguyen, T. T., Willemsz, T. A., van Kessel,

G., Frijlink, H. W., and van der Voort Maarschalk, K.

(2012). A density-based segmentation for 3D images,

an application for X-ray micro-tomography. Analytica

Chimica Acta, 725:14–21.

Tripathi, S., Kumar, K., Singh, B. K., and Singh, R. P.

(2012). Image segmentation: a review. Int. Jour-

nal of Computer Science and Management Research,

1(4):838–843.

Varma, S. and Simon, R. (2006). Bias in error estimation

when using cross-validation for model selection. BMC

Bioinformatics, 7(91).

Ye, J., Farnum, M., Yang, E., Verbeeck, R., Lobanov,

V., Raghavan, N., Novak, G., DiBernardo, A., and

Narayan, V. (2012). Sparse learning and stability se-

lection for predicting MCI to AD conversion using

baseline ADNI data. BMC Neurology, 12(46).

Zhang, D., Wang, Y., Zhou, L., Yuan, H., and Shen, D.

(2011). Multimodal classiﬁcation of Alzheimer’s dis-

ease and mild cognitive impairment. NeuroImage,

55(3):856–867.

BIOIMAGING2014-InternationalConferenceonBioimaging