Development of a Haptic Interface for Safe Human Robot Collaboration

Ioannis Iossiﬁdis

IComputer Science Insitute, Ruhr West University of Applied Sciences, 45470 M

ulheim an der Ruhr, Germany

Keywords:

Haptic Interface, Artiﬁcial Skin, Direct Physical Interaction, Safe Collaboration.

Abstract:

In the context of the increasing number of collaborative workplaces in industrial environments, where humans

and robots sharing the same workplace, safety and intuitive interaction is a prerequisite. This means, that the

robot can (1) have contact with his own body and the surrounding objects, (2) the motion of the robot can be

corrected online by the human user just by touching his artiﬁcial skin or (3) interrupt the action in dangerous

situations. In the current work we introduce a haptic interface (artiﬁcial skin) which is utilized to cover the

arms of an anthropomorphic robotic assistant. The touched induced input of the artiﬁcial skin is interpreted

and fed into the motor control algorithm to generate the desired motion and to avoid harm for human and

machine.

1 INTRODUCTION

Modern production processes require a ﬂexible use of

the available resources and can not be covered efﬁ-

ciently by conventional rigid automation strategies.

Work places in which man and machine collaborate

sharing the same workspace in order to accomplish

all of the required production steps contribute to a

ﬂexible design of production situation or a fast re-

arrangement at low costs. This implies that prepro-

grammed rigid machines should be replaced by au-

tonomous robotic assistant, which can be instructed

intuitively and used in a wide variety of production

scenarios.

Precondition for the use of such systems is the

warranty of the safety of the involved employees. The

security-related situation are characterized by the oc-

currence of intentional or unintentional contacts be-

tween man and machine. Both need to be allowed

but without the danger of harming humans or destroy-

ing the machines. We deﬁne this kind of interaction

as direct physical interaction by means of haptic and

other force/torque related sensors. In consequence

the two strongly linked aspects of physical interaction

and safety have to be tackled together by the design of

appropriate haptic sensors, the context sensitive inter-

operation of contact forces and the control of acceler-

ations and velocities of the manipulators.

In this work we introduce a haptic sensor provid-

ing the functionality of an artiﬁcial skin, detecting and

measuring contact forces and it’s position. The con-

tact forces are interpreted and the sensorial output is

fed into the motion planning of the robotic arm. In

order to handle motion constraints during the manip-

ulation task the geometric structure, described by the

closed form solution of the invers kinematics, of the

redundant robot arm is exploited.

In the following we describe the haptic sensor in

detail and sketch the closed form solution of the invers

kinematics of the robot arm in order to clarify how

contact forces are mapped to the arm motion. Finally

we describe the implementation and the experimen-

tal results in simulation and on the anthropomorphic

robot Cora (Iossiﬁdis et al., 2002).

2 TARGET SYSTEM

2.1 The Artiﬁcial Skin

The artiﬁcial skin, invented by the SIEMENS

robotics group, is based on a conductive foam, with

the main characteristic of changing conductivity prop-

erty when pressure is applied. The changing resistant

of the foam is utilized to measure the extend of the ap-

plied pressure and to design a sensor which can cover

arbitrary bodies in order to provide a touch sensitive

skin.

The sensor consists of two layers (two pads) of the

foam, each of equipped with two parallel electrodes.

The pads are arranged such that the electrodes are or-

Iossiﬁdis I..

Development of a Haptic Interface for Safe Human Roobt Collaboration.

DOI: 10.5220/0004803400610066

In Proceedings of the 4th International Conference on Pervasive and Embedded Computing and Communication Systems (PECCS-2014), pages 61-66

ISBN: 978-989-758-000-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Anthropomorphic robot CORA.

thogonal in order to calculate the position of the pres-

sure point of the associated pressure measure.

The electrodes are connected to a sensor board

equipped with A/D converters and a micro controller.

The electrodes of the upper pad are connected to 5 V

(one electrode to ground the other to 5 V) – if pres-

sure is applied the voltage drops according to the pres-

sure point. Both electrodes of the lower layer are con-

nected to the micro controller, who generates a peri-

odically varying voltage between 0 V and 5 V.

As soon a force is applied to the upper layer, the

voltage of the lower layer tuned to the voltage of the

upper layer according to the position of the pressure

point. The read out of the complete unit provides us

with a measure of the applied force and the position

of the pressure point.

We have covered two of CORA’s arm-modules

with the artiﬁcial skin mounted on a cylindric silicon

cuff (see ﬁgure 2). The advantage of the cylindric

cuff is that the vector valued contact force is obtain

directly from the scalar valued pressure measure. The

direction of the contact force deﬁnes the motion di-

rection of the related limb.

2.2 Robot CORA

CORA’s body consists of a redundant seven DoF ma-

nipulator connected to a one DoF trunk which is ﬁxed

on the edge of a table (see ﬁgure 1). CORA can ex-

ploit the redundant eight DoF of the arm-trunk con-

ﬁguration that guarantees a high degree of ﬂexibil-

ity with respect to manipulation tasks under exter-

Figure 2: The ﬁgure depicts the cylindric cuffs with the ar-

tiﬁcial skin which cover the squared module on the upper

arm (left) and the fore arm (right).

nal constraints. Grasping, for instance, is possible

in the whole workspace choosing different arm pos-

tures without the necessity of changing the position

or orientation of the end-effector. By turning the trunk

joint, the robot can also change its conﬁguration from

right- to left-handed. The sensor equipment and the

conﬁguration of the joints in CORA’s body and ma-

nipulator arm are anthropomorphic, which means that

they are structurally similar to the human body.

Two of CORA’s arm-modules are covered with the

artiﬁcial skin mounted on a cylindric silicon cuff (see

ﬁgure 2). The advantage of the cylindric cuff is that

a scalar pressure value can be interpreted directly as

a force vector perpendicular to the cylinder’s surface

deﬁning the direction in which the limb should be

moved (for more details see (Iossiﬁdis et al., 2002)).

2.3 Kinematics

2.3.1 Initial Conﬁguration

The sketched structure models (in correspondence to

humans) a one degree of freedom trunk, a one degree

of freedom shoulder elevation/depression with an at-

tached seven degree of freedom arm. The arm consist-

ing of a rotating trunk, spherical shoulder and wrist

joints, and an elbow joint, for a total of nine degrees

of freedom. The reference conﬁguration is show in

Figure 3.

Base Shoulder Elbow Hand

EEF

Figure 3: A total of eight revolute joints are ordered along

the effector to simulate a human arm with trunk, shoulder,

elbow and wrist.

The manipulator is composed of a series of roll

and pitch joints. The combination of a roll-pitch-roll-

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

joint is functionally equivalent to a spherical three

DoF joint like the human shoulder or wrist. Similar

to the example above, the twists are determined as

= ω









, ω

= ω









Support points can be chosen as





∑

i−1

k=1





for i = 1,3,5,7,

and





∑

i−1

k=1





for i = 2,4,6,8.

This yields the twist coordinates













, ξ







+ l







, ξ







+ l













+ l







, ξ

2,4,6,8













The transformation between the base and end-effector

coordinate frames in reference conﬁguration is

(0) =











∑

i=1





0 1







2.3.2 Forward Kinematics

The forward kinematics is calculated as the product of

exponential. On the basis of the simple ways of repre-

senting and calculating rigid transformations (for de-

tailed description see (Murray et al., 1994)), we can

move on to describe the transformation to the end ef-

fector of an open chain manipulator, that is, a chain

of n joints. For each joint, we deﬁne a joint twist ξ

that models the motion of the subsequent part of the

robot.

Let g

(0) be the transformation between the base

frame S of the manipulator and the end effector, or

tool frame T in the reference conﬁguration, that is,

when all joint angles

,...,θ

are set to zero.

By abusive convention, we refer to the amount of trans-

lation θ

of a prismatic joint k as angle, too, in order to

prevent cluttering up our language.

rsh

α Elbow Redundancy Angle

ee f

β Trunk Redundancy Angle

Figure 4: The ﬁgure depicts the kinematical structure and

the associated coordinate systems of an multi redundant

nine degree of freedom arm. α denotes the elbow angle,

β denotes the trunk angle and γ the shoulder angle.

Now we want to know what happens to the end ef-

fector after we apply a rigid transformation by moving

a joint. Starting at the base, we get to the end effector

via g

(0), which we then move by applying the rigid

transformation e

. Combining these two transfor-

mation in the right order, we get

(θ) = e

(0).

Here g

(θ) maps the center of the base frame to the

position of the end effector in the new conﬁguration

with θ

6= 0. Thinking the other way round, it re-

turns the S-coordinates of a point that we specify in

T -coordinates. So if we specify “0”, we refer to the

position of the end effector in the frame T centered at

that point. Applying g

(θ) returns the coordinates of

that point in frame S, centered at the base. Thus, we

can think of g

(θ) as enabling us to specify a point

in a moving frame T , and get back its position in the

motionless frame S.

To do the same for a conﬁguration in which sev-

eral joints have moved, i.e. θ

6= 0 for more than one i,

we just have to apply the appropriate transformation

in the right order. Conceptually speaking, we start at

the end effector and go up the joints along the manip-

ulator till we reach the base, moving each joint by the

appropriate angle θ

on the way. This yields

(θ) = e

·· ·e

(0) (1)

as the coordinate transformation from T to S in con-

ﬁguration θ = (θ

,. ..,θ

Equation (1) is called the product of exponentials

formula for the manipulator forward kinematics.

2.3.3 Closed Form Solution

For the solution of the overall system we assume that

the shoulder is positioned due to the boundary con-

dition determined by the object to be manipulated,

like turning shoulder towards the object to extend it’s

workspace (distances to objects greater the the length

of the arm) or to position the shoulder to an orienta-

tion that is orthogonal to the target direction (optimal

DevelopmentofaHapticInterfaceforSafeHumanRoobtCollaboration

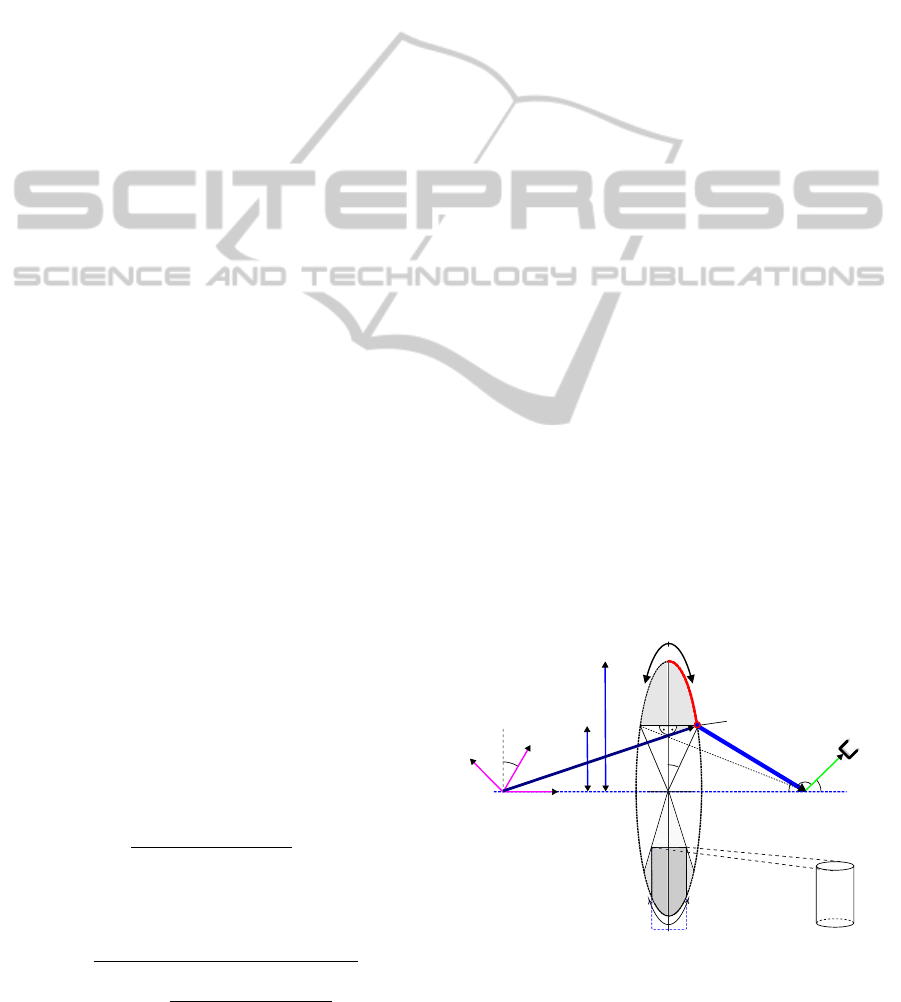
grasping position). The shoulder elevation/depression

is utilized to satisfy additional constraints, like the

avoidance of undesired conﬁgurations.

Given the shoulder position, which is determined

by the trunk angle and the shoulder angle, the inverse

kinematic mapping of the seven degree of freedom

has to be derived with respect to shoulder coordinate

system.

In the following we derive ﬁrst the inverse kine-

matics of the seven degree of freedom, exploiting it’s

geometric properties, and describe how the null space

motion can be utilized to satisfy constraints like ob-

stacle avoidance and joint limits.

Inverse Kinematics. Based on the work of (Kreutz-

Delgado et al., 1990) and (Hollerbach, 1984) the in-

verse kinematics problem for the eight degrees of

freedom manipulator is solved in closed form. In the

following derivation we denote the trunk angle with β

(correspond to θ

in the initial conﬁguration in ﬁgure

3).

We assume that the end effector position and hand

orientation is determined by the object to be grasped

and that the trunk angle β

will be choosen due to the boundary conditions

and costraints of the given task. First we transform the

given end effector position to the shoulder coordinate

system by:

ee f

= T

ee f

with







1 0 0 0

0 1 0 −(l

+ l

)

0 0 1 −l

0 0 0 1













cos(−θ

) − sin(−θ

) 0 0

sin(−θ

) cos(−θ

) 0 0

0 0 1 0

0 0 0 1







beeing the homogeneous transformation.

Given the hand orientation θ

(elevation) and φ

(azimuth) and the tool point q

ee f

, the vector q

from

the wrist to the hand reference tool-point (Fig. 4) is

determined as

= R

(φ

(θ

)

(2)

where R

, R

denote rotation matrices around the z-

and y-axes and l

denotes the segment length.

The redundant degree of freedom is deﬁned by the

redundancy circle, the center

−



(3)

of which lies on a ray pointing from the shoulder to

the wrist joint. The spatial position of the elbow lies

on this circle of radius r, with

r =

−



(4)

Expressing the wrist vector, q

, through two angles,

and θ

, the elbow position can be written as

= (R

(φ

(θ

(α) ˆe

)r + q

(5)

where R

and R

are rotation matrices around the x-

and the z-axis and the redundancy angle α character-

izes the position of the elbow on the redundancy circle

(Fig. 4). If α is speciﬁed, all limb vectors are known.

A straightforward solution of the inverse kinematics

determines the joint angles. ,θ

,θ

(for details see (Iossiﬁdis, 2013)).

Constraints for the Redundancy Circle. The re-

dundancy angle α spans all redundant arm conﬁgura-

tions consistent with the same tool position and ori-

entation. The rate of change of the redundancy an-

gle generates self-motion, which can be used to ac-

commodate the two additional constraints of obsta-

cle avoidance for the upper arm and joint limits at the

wrist. To do that, we must compute which sectors on

the redundancy circle is prohibited forbidden by these

constraints.

Any obstacle o

, that reaches up to the elbow, de-

ﬁnes a to-be-avoided segment on the redundancy cir-

cle centered on κ

and with an angular range of σ

(see

Fig. 5) Transforming limitations of joint angle range

into constraints on the redundancy circle is more com-

plicated. The most important joint angle limitation

concerns the wrist, where the lower arm and the hand

are spatially aligned. The angle µ between the hand

and the forearm q

must be larger than π/2, which

is true as long as

−(π − µ) ≤ θ

≤ π − µ. (6)

Fig. 5 illustrates that this can be used to compute the

corresponding allowed sector on the redundancy cir-

cle.

obs

forearm

obstacle

upper arm

elbow position

Figure 5: Geometrical construction to avoid joint conﬁgu-

rations at the wrist and an obstacle reaching into the redun-

dancy circle deﬁnes a to-be-avoided angular segment of that

circle.

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems

Figure 6: Null space motion of the elbow while the end effector is moving towards the target.

To do that, deﬁne a coordinate system the z

-axis

of which is aligned with the shoulder-wrist-axis of the

robot arm. If φ

and θ

describe the azimuth and ele-

vation of the wrist, then the transformed hand vector,

is:

= R

−θ

−φ

(7)

After the transformation, the redundancy circle lies

in a plane parallel to the x

-plane, so that we may

project q

onto that plane to obtain:

κ = arctan(q

) (8)

as the center of the prohibited sector of the redun-

dancy circle. The angular extent of the prohibited re-

gion κ ± δ follows from equation 6:

δ = arccos(h

/r) (9)

where h

, ψ, c and φ are auxiliary quantities, which

can be derived from ﬁgure 5:

= c · tan(ψ) (10)

c = |q

| − |q

| (11)

ψ = π −(µ + φ) (12)

φ = arccos







. (13)

The obstacle induced prohibited region on the re-

dundancy cycle is calculated analogous, with κ

the center of the prohibited region and δ

as it’s ex-

tend (ﬁgure 5).

3 IMPLEMENTATION AND

RESULTS

In the previous section we described the design of the

target system and the closed form solution for the in-

verse kinematics which is the mathematical basis for

the incorporation of the contact forces measured by

the artiﬁcial skin. Whereby forces detected by the

artiﬁcial skin around the upper arm is interpreted as

forces on the elbow and those detected by the artiﬁ-

cial skin around the fore arm as forces on the wrist.

The input of the artiﬁcial skin around the upper

arm generate a null space motion of the 7-degree-of-

freedom arm (motion of the elbow along redundancy

cycle (see 4) ). This motion does not affect the end

effector position and it’s orientation and is used to sat-

isfy motion constrained. Forces detected by the arti-

ﬁcial skin associated with the wrist is used to move

the end effector by the human operator to the desired

direction during a collaborative task (ﬁgure 8).

Goal directed trajectories for the end effector in

the following experiments are generated by means

of the attractor dynamics approach described in (Ios-

siﬁdis and Sch

oner, 2004; Iossiﬁdis and Sch

oner,

2006).

For the demonstration of performance of the sys-

tem, we conducted two experiments. In the ﬁrst ex-

periment (ﬁgure 6) we demonstrate how null space

motion of the robot arm is initiated while the end ef-

fector is moving towards a target without aborting it’s

motion, end effector position or orientation. In ﬁg-

ure 7 the contact force measured by the artiﬁcial skin

around the wrist initiates an arm motion in the direc-

tion of the applied force. The human intuitively make

use of the haptic interface in order to move the robot

arm to the desired position.

In the second experiment a human user intervene

in order to support the robot to avoid a collision with

the obstacle that has not been detected by the vision

sensor. In Fig. 8 A the robot arm starts its trajectory

towards the small object. To avoid a collision between

the elbow and an obstacle that has not been detected

by the vision sensor, the human operator touches the

skin on the upper cuff of the robot’s arm ( B - C ), in

order to force the robot to lift its elbow. The system

detects the force, determines its magnitude and cal-

Figure 7: Human operator pushes the wrist of the robot to

free the workspace.

DevelopmentofaHapticInterfaceforSafeHumanRoobtCollaboration

A B

C D

Figure 8: The human operator initiate a motion of the elbow

upward by touching the skin and helps the robot to avoid a

collision with the obstacle.

culates the force-direction with respect to the current

arm posture. On the basis of this estimate the robot

starts ( B ) its elbow-movement in the direction of the

detected force. In A - D the robot moves its elbow

without changing the intended trajectory of the end-

effector. In D the robot completes its trajectory and

grasps the object.

4 CONCLUSIONS

The presented work addressed and clarify the rela-

tion between safety aspects and intuitive direct physi-

cal interaction in collaborative working situations in-

volving man and robotic assistant systems. An hap-

tic interface was introduction able to cover arbitrary

robotic structures and providing the functionality of

an artiﬁcial skin. The cylindric cuffs covered by the

artiﬁcial skin transformed the scalar valued measure-

ments into a vector valued force which was fed into

the motion generation scheme. For the robotic sys-

tem we proposed an anthropomorphic design with an

redundant manipulator allowing us to satisfy simulta-

neously motion constraints and occurring requests by

the human operator.

This led to an system with a bidirectional physical

interaction channel providing intuitiv and ﬂexible in-

terrelationship between man and machine and safety

for both. The approach is implemented on the an-

thropomorphic robot CORA and evaluated in multiple

experiments.

REFERENCES

Hollerbach, J. (1984). Optimum kinematic design for a

seven degree of freedom manipulator. In 2nd Int.

Symp. Robotics Research, pages 215 –222.

Iossiﬁdis, I. (2013). Motion constraint satisfaction by

means of closed form solution for redundant robot

arms. In Proc. IEEE/RSJ International Conference on

Robotics and Biomimetics (Ro-Bio2013).

Iossiﬁdis, I., Bruckhoff, C., Theis, C., Grote, C., Faubel,

C., and Sch

oner, G. (2002). CORA: An anthropo-

morphic robot assistant for human environment. In

Proceedings. 11th IEEE International Workshop on

Robot and Human Interactive Communication, pages

392–398. IEEE.

Iossiﬁdis, I. and Sch

oner, G. (2004). Autonomous reach-

ing and obstacle avoidance with the anthropomorphic

arm of a robotic assistant using the attractor dynamics

approach. In Proc. IEEE International Conference on

Robotics and Automation ICRA ’04, volume 5, pages

4295—- 4300 Vol.5.

Iossiﬁdis, I. and Sch

oner, G. (2006). Dynamical Systems

Approach for the Autonomous Avoidance of Obsta-

cles and Joint-limits for an Redundant Robot Arm. In

2006 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems, pages 580–585. IEEE.

Kreutz-Delgado, K., Long, M., and Seraji, H. (1990). Kine-

matic analysis of 7 DOF anthropomorphic arms. In

Robotics and Automation, 1990. Proceedings., 1990

IEEE International Conference on, pages 824 – 830.

Murray, R., Li, Z., and Sastry, S. (1994). A mathematical

introduction to robotic manipulation. CRC Press.

PECCS2014-InternationalConferenceonPervasiveandEmbeddedComputingandCommunicationSystems