On the Robustness of the Biological Correlation Network Model

Kathryn M. Dempsey and Hesham H. Ali

College of Information Science & Technology, University of Nebraska at Omaha, Omaha, NE, 68182, U.S.A.

Keywords: Correlation Networks, Network Stability.

Abstract: Recent progress in high-throughput technology has resulted in a significant data overload. Determining how

to obtain valuable knowledge from such massive raw data has become one of the most challenging issues in

biomedical research. As a result, bioinformatics researchers continue to look for advanced data analysis

tools to analysis and mine the available data. Correlation network models obtained from various biological

assays, such as those measuring gene expression levels, are a powerful method for representing correlated

expression. Although correlation does not always imply causation, the correlation network has been shown

to be effective in identifying elements of interest in various bioinformatics applications. While these models

have found success, little to no investigation has been made into the robustness of relationships in the

correlation network with regard to vulnerability of the model according to manipulation of sample values.

Particularly, reservations about the correlation network model stem from a lack of testing on the reliability

of the model. In this work, we probe the robustness of the model by manipulating samples to create six

different expression networks and find a slight inverse relationship between sample count and network

size/density. When samples are iteratively removed during model creation, the results suggest that network

edges may or may not remain within the statistical parameters of the model, suggesting that there is room

for improvement in the filtering of these networks. A cursory investigation into a secondary robustness

threshold using these measures confirms the existence of a positive relationship between sample size and

edge robustness. This work represents an important step toward better understanding of the critical noise

versus signal issue in the correlation network model.

1 INTRODUCTION

The correlation network model has been used for

data modelling in multiple research studies

(Halappanavar et al., 2012); (Dempsey et al., 2011);

(Song et al., 2012); (Opgen-Rhein and Strimmer,

2007); (Horvath and Dong, 2008); (Verbitsky et al.,

2004); (Bender et al., 2008) that harness the power

of a network model to identify biological function.

While these studies have found great success in

identifying biological function (high degree nodes

can reflect essentiality (Halappanavar et al., 2012);

(Dempsey et al., 2011), clusters of nodes can

regulate or execute common cellular mechanisms

1,2

graph theoretic filters can remove noise from the

model while enhancing signal (Halappanavar et al.,

2012); (Dempsey et al., 2011); (Song et al., 2012);

(Opgen-Rhein and Strimmer, 2007)), the robustness

of the correlations used in the network model have

not been thoroughly examined.

Briefly, the correlation network model is

described as thus: a node represents a gene product

or probe from a high-throughput assay, such as a

DNA microarray or RNA-seq experiment. Each

experiment has some number of samples, n. For

each pair of genes or probes in the dataset, some

measure of correlation is applied. This correlation

assumes that there are at least three samples for each

gene/probe, and that none of the sample expression

values are missing, otherwise the correlation cannot

be performed for that pair. In cases where sample

size is small or experimental results are poor, a

majority of correlations may be rendered invalid, but

with improvement in current technologies this

becomes a much smaller issue.

For each pairwise comparison, a correlation

measure is used. Typically, this is the Pearson

correlation coefficient (which measure linear

relationships), but it can also include partial

correlation (where statistically calculated random

samples are not used in the correlation), Spearman

correlation (measuring relationships that are non-

linear using some function f), or other statistical

measures such as mutual information (measures the

186

M. Dempsey K. and H. Ali H..

On the Robustness of the Biological Correlation Network Model.

DOI: 10.5220/0004805801860195

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 186-195

ISBN: 978-989-758-012-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

dependence of behaviour of one variable based on

another’s behaviour). After the correlation is

computed, some hypothesis testing is done to filter

out only significant correlations. In addition to

significance filtering, filtering via correlation

threshold is typically performed to reduce network

size and remove non-meaningful correlations (such

as those around 0.00).

There are two main ways to filter a network:

hard thresholding or soft thresholding. Hard

thresholding removes edges based on a firm cut-off

value; typically this value falls between the ranges

of -1.00 ≤ ρ ≤ -0.70 and 0.70 ≤ ρ ≤ 1.00. This

threshold is typically chosen as it captures only

relationships that are descriptive of the behaviour of

two genes. For example, a correlation of 0.70 has a

coefficient of determination (R

which is equivalent

to ρ

) of 49%, meaning that if the correlation reflects

a true relationship, 49% of a given gene’s behaviour

can be attributed to the other gene, and vice versa.

Soft thresholding, popularized by Horvath and

Dong (2008) (called WGCNA), involves identifying

the threshold at which the network exhibits scale-

free properties which some particular networks are

expected to have, and extracting the subnetwork of

the original network such that the filtered network is

scale-free. Thus, comparing two sets of expression

data from the same model and cell line but under

different environmental conditions might involve

using different correlation values based on the soft

thresholding approach.

While many studies have used iterations of the

correlation network model with success, few studies

in network systems in biology have delved into the

robustness of correlations, and how that might affect

network structure. For example, if a sample is

removed from the network, does the correlation that

results remain the same value or does it change

significantly? The correlation, if originally had

fallen within the proposed threshold and after

sample removal failed to fall within the threshold,

might not be representative of a true relationship in

the data. This begs the question: How many samples

are sufficient to assume a robust network? These and

other questions, if answered, can lead to insights

about how to remove noise from a correlation

network, and which relationships can be trusted,

without having to integrate extraneous biological

information. The novelty of this work lies in the lack

of understanding of the stability or by contrast,

vulnerability of the correlation network model.

While correlation does not imply causative

relationship, the measure is still able to capture those

relationships that are causative; in capturing

everything the measure is prone to noise. This

research investigates the possibility of using the

strength of correlation to remove some of that noise

and also can be used as evidence to suggest the

beginning of data-driven experimental studies.

Bioinformatics deals largely with publicly available

data; however, the results of the research here

suggest that we can improve the requirements of

those studies (i.e. increasing sample number) for use

in systems biology.

2 METHODS

Briefly, this work describes a cursory review of the

effect that single sample removal has on Pearson

correlation coefficient in a hard-thresholded setting.

To investigate, networks were created, thresholded,

and then samples were iteratively removed to

determine effect on correlation value.

2.1 Network Creation

Three datasets were chosen to highlight the

difference in sample number; all datasets had 9 or

less samples, reflecting the current state of high-

throughput technology where most expression

experiments contain samples, at minimum, in

triplicate. The datasets chosen were:

 GSE5078 (Verbitsky et al., 2004) – Mus

musculus hippocampus mRNA, compared at 2

months and 15 months (Young and Middle-

Aged, respectively). Young dataset contains 9

samples and Middle-Aged dataset contains 9

samples.

 GSE5140 (Bender et al., 2008) – Mus musculus

whole brain mRNA, compared at untreated and

creatine-treatment (Untreated and Creatine,

respectively). The Untreated dataset contains 6

samples, and the Creatine dataset contains 6

samples.

 GSE46384 (Ikushima and Misaizu) –

Saccharomyces cerevisiae untreated or exposed

to 40g/l of isopropanol, (0IPA and 40IPA,

respectively). The 0IPA dataset contains 4

samples, and the 40IPA dataset contains 4

samples.

A threshold of 0.70 ≤ ρ ≤ 1.00 using Pearson

correlation coefficients was used to find correlated

expression relationships, and p-values were

computing using the Student’s T-test with a

threshold of p-value <0.0005 significance. Network

sizes for each are contained below in Table 1. The

GSE5140 networks were the largest by node count.

OntheRobustnessoftheBiologicalCorrelationNetworkModel

187

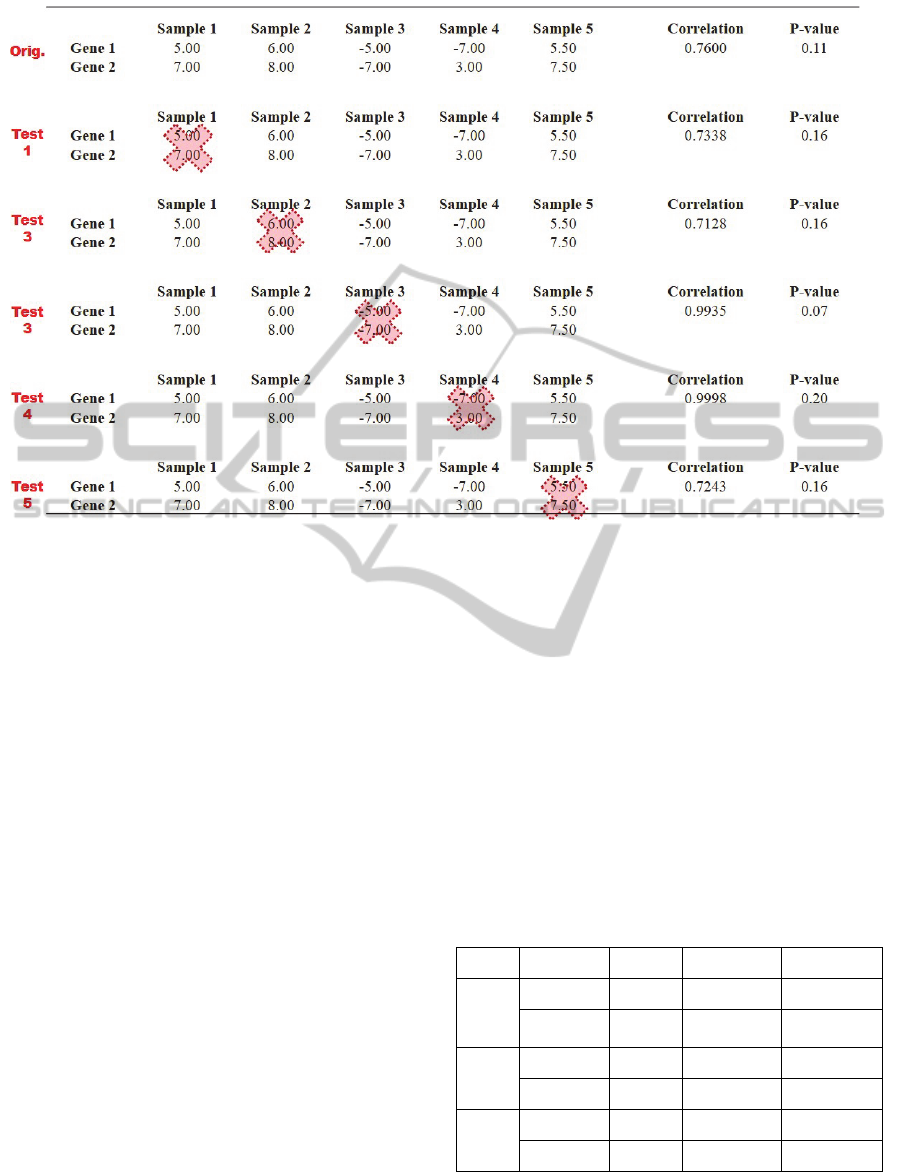
Figure 1: The process of removing samples to test robustness. The top rows (Orig) are the original correlation calculation

between five samples between Gene 1 and Gene 2. Samples 1-5 represent the expression values for each sample (can be

tissue, cell, etc.) In test 1, correlation is calculated between Samples 2-5, with Sample 1 removed for both Gene 1 and Gene

2. This results in a very slightly decreased correlation from the original (0.76 to 0.73) and a slightly increased p-value (0.11

to 0.16) meaning the correlation has less confidence. This occurs iteratively for each sample. If the correlation threshold

was 0.75 ≤ ρ ≤ 1.00 and a p-value <0.15, only the correlation for test 3 would pass the significance test, and its correlation

would pass the threshold test as well at 0.99. For this example, the PSC would be equal to 1/5 = 20%, the PTC would be 1/1

= 100%, and the PST would be 1/5, or 20%.

Despite being the smallest networks by node count,

the yeast GSE46384 networks were the densest at 8-

10% density. The GSE5078 networks were the

middle of the road in terms of node counts but had

the lowest density, meaning that these networks

were very sparse compared to total possible edges.

So, by density, there appears to be an inverse

relationship between sample size and resulting

network density. This is to be expected – using such

low sample counts to identify correlations means

that as more information becomes available, more

evidence is there to confirm or deny an actual

correlation. For example, it is easier to find a 100%

correlation of two probes with 3 samples than it is to

find a 100% correlation of two probes with 10

samples. (This does not, however, examine

significance). The GSE46384 networks had the

smallest amount of samples but the highest number

of edges per node on average. The GSE5140

network contained 6 samples and the middle of the

road density results; it should be noted that these

datasets contained the entire genome-wide set of

probes then available for mouse models. Finally, the

network with the most samples, GSE5078 at 9

samples results in the sparsest networks.

Table 1: Network edge counts. Column 1: GEO Series

number, Column 2: network name, Column 3: # nodes in

the thresholded/filtered network, Column 4: # edges in the

thresholded/filtered network, and Column 5: density of the

network, which is equal to Edge Count / (Node Count *

(Node Count -1)/2). We find that the lower the sample

count, the higher the density.

Dataset

Name Nodes Edges Density

GSE

5078

Young 12,390 923,794 1.2036%

Middle-

Aged

12,378 1,013,130 1.3226%

GSE

5140

Untreated 45,000 32,075,094 3.1679%

Creatine 45,004 33,349,407 3.2932%

GSE

46384

IPA0 6,301 1,616,710 8.1453%

IPA40 6,304 2,000,931 10.0716%

These types of results are typical of what is the

current standard in correlation networks. The more

samples there are, the more confident and strong the

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

188

correlation. Therefore, more noise can be removed

as sample number increases. We expect that the

GSE46384 network would be naturally filtered by

the addition of more samples, which would

strengthen relationships that actually exist via

strengthening correlations and their significance.

2.2 Robustness Testing

In datasets where sample size is small, there needs to

be some measure that limits the impact of errors or

outliers in the data. To accommodate potential error

and noise, we define robustness to determine the

reliability of the network model itself. Robustness of

a correlation is defined, in this particular study, as

the likelihood of a correlation to remain at or above

some threshold t after random sample removal. If a

correlation between two probes originally is 100%,

and falls to 90% after iterative sample removal, we

can say it is robust because it still falls within our

threshold of 0.70 ≤ ρ ≤ 1.00 (assuming both

correlations are also significant). If a correlation

between two probes originally is 100% and falls to

50% after individual sample removal, it would not

be considered a robust relationship. To test the

robustness of correlations according to sample

removal, a simple method was deduced. As per

normal network creation standards, networks were

made by pairwise computation of Pearson

Correlation between two probes and if the threshold

was met (0.70 ≤ ρ ≤ 1.00), hypothesis testing was

performed. If p-value was less than 0.0005, the edge

was considered for robustness testing.

To test robustness, samples were iteratively

removed from the gene pair vectors as shown in

Figure 1. For example, for two genes, each with five

samples, values of expression for sample 1 in both

probes were removed and correlation and

significance were calculated. If the correlation

between the manipulated probes was significant, the

correlation was kept. Next, sample 2 was removed,

and the correlation was again kept if it was

significant.

After all correlations and sample removal

correlations were reported, it was also necessary to

determine if the correlations found after sample

removal were also above or within the threshold

(within the bounds of the threshold = robust or

outside the bounds of the threshold = not robust).

To measure this, the following metrics were devised:

 Percentage of Significant Correlations (PSC): the

number of significant correlations versus the

total possible significant correlations (sample

number). This measures the percentage of

significant correlations that result when a

sample is removed – the higher the better. 100%

is optimal.

 Percentage of Threshold Correlations (PTC): the

number of correlations above some threshold t

versus the number of significant correlations.

This measures the percentage of significant

correlations that are above the threshold

required by the user. 100% again is optimal.

 Percentage of Significant Threshold Correlations

(PST): the number of correlations that are

significant and above some threshold t versus the

total possible significant correlations. This

measures the percentage of significant

correlations that are above the threshold when

some sample is removed. 100% is optimal.

Also computed was the standard deviation for each

set of significant correlations. The following

equations (Equations 1-3, below) define how PSC,

PTC, and PST were computed, where n is equal to

sample number, t is the threshold given, s

corr

is equal

to the count of significant correlations, and t

corr

equal to the count of significant correlations above

the threshold t.

1:  







2:   









3:   







Informally, PSC tells us the percentage of

correlations that remain statistically significant per

sample count, PTC tells us the percentage of

significant correlations that fall within the threshold,

and PST tells us the percentage of significant

correlations that fall within the threshold per sample

count.

2.3 Clustering and Enrichment

To test the biological function of normal versus

robustness tested networks, the top 5 clusters (based

on MCODE (Bader and Hogue, 2003) ranking) were

tested for biological function using the Gene Set

Enrichment Analysis tool via the Gene Trail (Backes

et al., 2007) tool (http://genetrail.bioinf.uni-sb.de/).

Clustering was performed using MCODE v.1.2

using the parameters: Degree cut-off of 10, Node

Score Cut-off of 0.2, Haircut set to True, K-core set

to 10, and Max Depth set to 10. The top 5 clusters

according to MCODE’s proprietary scoring method

(score = density * node count) and GSEA was

OntheRobustnessoftheBiologicalCorrelationNetworkModel

189

performed on node lists from each. GeneTrail

parameters used were: Only manually curated GO

annotations and a significance value of 0.05.

3 RESULTS

Comparing the scores of each network in terms of

PSC, PTC, and PST allows for characterization of

correlation robustness in a general way. In an ideal

network, all correlations are robust and sample size

is optimal for robustness. The goal of this research is

to address the robustness issue to determine the

ability of the correlation network model to represent

accurate biological information.

3.1 Non-optimal Correlations

To give a first insight into robustness, the original

network sizes were compared to network size when

correlations with no significant above-threshold

correlations are observed (Table 2). Here we

highlight the % Non-Robust Edges, which is the

percentage of edges in the original network that are

not robust, or those edges that do not fall within the

threshold t when a sample is removed. As sample

count increases, the level of non-robust edges

decreases.

Table 2: Insignificant, non-threshold robustness. Column

1: GEO Series #, Column 2: network name, Column 3:

edge # in the thresholded network, Column 4: edge # in

the thresholded network when non-robust, insignificant

edges are removed, Column 5: percentage of the original

network representing non-robust edges, 100% - (Robust

Edge Count/Original Edges). The number of removed

non-robust edges for any network is minimal, meaning

that significance of correlation at any sample size is trivial.

Dataset

Name

Original

Edges

Robust

Edge

Count

% Non-

Robust

Edges

GSE5078

Young 923,794 922,394 0.1515%

Middle-

Aged

1,013,130 1,011,586 0.1524%

GSE5140

Untreated 32,075,094 31,902,640 0.5377%

Creatine 33,349,407 33,121,663 0.6829%

GSE46384

IPA0 1,616,710 1,573,416 2.6779%

IPA40 2,000,931 1,930,502 3.5198%

However, the overall number of absolutely non-

robust edges overall is low, representing 0.1-3.5% of

the entire network edges. This means that the large

portion of edges in correlation networks are robust

to sample removal.

3.2 Variance in Robustness via PSC

To examine the distribution of robustness of

correlations, the PSC, PTC, and PST were calculated

for each correlation and mapped. These results for

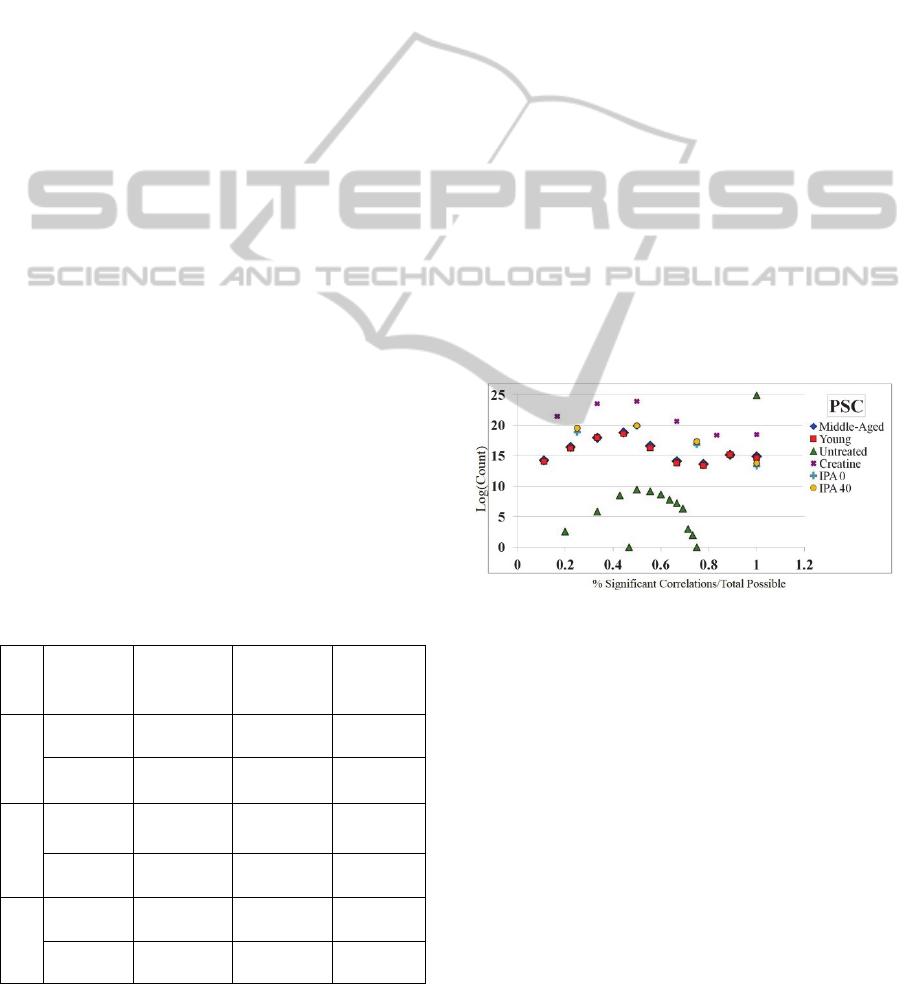
PSC are contained in Figure 2. This figure highlights

the number of significant correlations versus the

sample number (x-axis) and the log of the count of

PSC scores at that point (y-axis). For example, the

green triangle in the topmost right corner of Figure 2

represents a PSC score of 100% with a very high log

(count), meaning that a large majority of the

correlations in the Untreated network are significant

when a sample is removed. All networks except for

the Untreated network find an increase in PSC from

0-50% and then a decrease or stabilization in PSC

from 50-100%. This indicates that there are many

relationships that become insignificant when

samples are removed; these correlations where

significance is lost become good candidates for

removal.

Figure 2: The PSC score distribution for all 6 networks. X-

axis: PSC score - The number of significant correlations

versus the sample number. Y-axis: The log of the count of

PSC scores. This measure shows per probe pairing how

many of the sample-removed correlations are significant.

I.e., if a probe pair has 10 samples and 5 of them are

significant correlations when a sample is removed, it will

have a 50% PSC score. The scores above suggest that

there is a large majority of correlations that lose their

significance when a sample is removed.

The results for PTC are contained in Figure 3.

This figure highlights the number of significant,

above threshold correlations when samples are

removed versus total sample size (X-axis) versus the

log of the count of PTC scores at that point.

Interestingly, in all but the Untreated and Creatine

networks, all networks find that if a correlation

remains significant after a sample is removed, it is

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

190

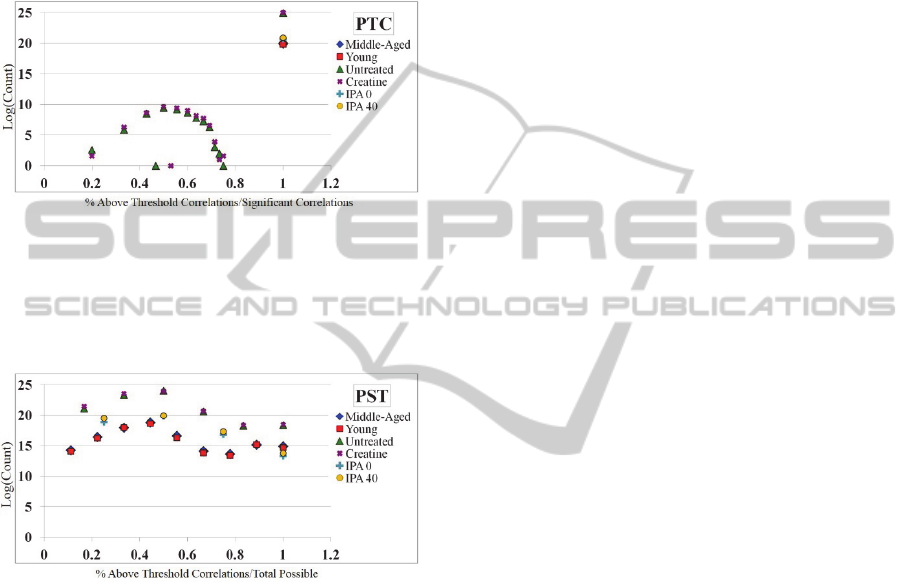
also within our given threshold t (100%). The

exception is in the Untreated and Creatine networks,

where there is again a distribution of scores from 20-

80% indicating that, for example, there is a portion

of relationships where sample removal results in a

correlation that is not within the given threshold t, or

not all sample-removed correlations that are

significant meet threshold requirements.

Figure 3: The PTC score distribution for all 6 networks.

X-axis: PTC score. Y-axis: The log of the count of PTC

scores. The results here indicate that for the majority of

networks, the number of significant correlations after

sample removal are also within threshold.

Figure 4: The PST score distribution for all 6 networks. X-

axis: PST score. Y-axis: The log of the count of PST

scores. The results here indicate that there is a distribution

of edges that do not meet the threshold and significance

requirements to be robust.

The results for PST are contained in Figure 4.

This figure highlights the number of significant,

above threshold correlations when samples are

removed versus significant sample-removed

correlations (X-axis) versus the log of the count of

PST scores at that point. The PST scores, perhaps

the most telling, reveal that there indeed exists a

distribution of correlations from approximately 10-

100%, where a large amount of edges relative to

network size find few significant above-threshold

correlations compared to significant correlations.

Interestingly, this number seems to drop off slightly

around 50%, and appears to stabilize or grow again.

Generally, this means that the large majority of

correlations within the network tend to be robust.

3.3 A Secondary Threshold?

How does this information impact the creation,

thresholding, and usage of the correlation network

model? Notoriously noisy (Reverter and Chan,

2008); (Song et al., 2012); (Opgen-Rhein amd

Strimmer, 20007), the correlation network model

tends to be underused due to the common reasoning

that “correlation does not imply causation;”

however, this does not mean that the measure does

not capture any information. Quite frankly, the

correlation measure captures all possible linear

relationship, but it is up to the user to determine if

those relationships are meaningful (Song et al.,

2012); (Opgen-Rhein and Strimmer, 2007). As such,

this research suggests that the correlation network

model may also benefit from having a secondary

threshold that is based on the robustness of the

correlation itself. While network size, density, and

absolutely non-robust edges seemed to be impacted

by sample size, the distribution of robust edges does

not appear to be significantly impacted by sample

size in our results above. Thus, it would appear that

correlations that are strong will become stronger by

the addition of samples, but will not become weaker

with single sample removal if the correlation is truly

representative of a biological co-regulated

relationship.

To begin to foray into the impact of a secondary

threshold, the natural dip in PSC, PTC, and PST

score distributions were used. This dip appears at or

around 50%, indicating that those correlations are at

least 50% likely to have a significant, within

threshold correlation after a sample is removed.

This 50% “secondary threshold” was used to

examine the effect of removing correlations where

robustness of PST is greater than or equal to 50%.

To clarify, consider two probes with 10 samples. If

each sample is individually removed and correlation

is calculated, the resulting correlation must be

significant and within the threshold t for at least

50% of the iterations (5 of the 10 correlations must

be significant and within t) for the edge to be

considered, otherwise it was thrown out. Removing

edges in this way reduces edge count; resulting

network sizes using this threshold are shown in

Table 3.

Using the secondary 50% PST threshold, we are

able to remove 40-80% of edges from the already

significance and thresholded original network.

Interestingly, the networks with the most samples

(Young and Middle-aged) found the highest edge

OntheRobustnessoftheBiologicalCorrelationNetworkModel

191

removal at 81.65% (Young) and 80.46% (Middle-

aged). This makes sense when you consider how

correlation is calculated – one would expect with 2

or 3 sample removal at a time, this edge reduction

percentage would decrease – but the magnitude of

edges that stand to be removed is very telling. This

means that, should the biological “signal” of the 2

thresholded network be equal to or greater than the

biological signal of the original network, that we are

able to reduce the network size (and thus

computational time and load of analysis of the

model) drastically.

3.4 Preliminary Functional Analysis

To examine how the model may also benefit from

having a secondary threshold to reduce noise,

preliminary functional analysis was performed on

original and robustness thresholded networks to see

if it is able to remove noise that confounds

biological signal. Clustering using MCODE was

performed on both the Young original network and

the Young 2

thresholded network, and the top 5

clusters were extracted (see Methods). After cluster

extraction, the nodes in each cluster were tested for

biological function using Gene Set Enrichment

Analysis. Only annotations with 4 or more observed

genes per cluster were considered. The results of this

enrichment on the Young network clusters are

shown in Figure 5. What was found is that for three

out of five of the original Young network clusters,

there were too many biological process annotations

to be relevant or helpful for decision support or to

determine the actual function (if any) of the cluster.

By comparison, each of the robustness network

filtered clusters contained 10 annotations or less.

The functions of these clusters need to be further

probed, but if the functions found in the robustness

thresholded clusters are found to be accurate, this

can be considered a major way to further remove

noise from the network and understand the functions

of the structures therein.

Top 10 Gene Ontology enrichment of clusters in

the middle-aged network clusters is shown in Figure

6. As in the young network, there were many

biological process tree annotations for original

clusters and fewer annotations in the robustness

filtered clusters. Future work will investigate the real

biological function of these clusters, and

additionally, the function of clusters in which

robustness is used as a filter. The results of this

approach might bring the speculation that robustness

filtered networks will return clusters with a more

refined biological function due to the fact that noise

(or correlations in which we are not confident) are

removed.

Table 3: Network edge reduction based on second

robustness threshold. Column 1: GEO Series number,

Column 2: network name, Column 3: # edges in the

thresholded/filtered network, Column 4: # edges in the

thresholded/filtered network after second thresholding,

and Column 5: percentage of edges that were removed

from the original network by this second threshold,

calculated as 100% - (2

Threshold edges/Original

Edges). These results indicate that the more samples

present, the more edges can be removed, possibly because

sample size improves correlation confidence.

Dataset

Name Edges

2nd

Threshold

Edges

Edge

Reduction

GSE5078

Young 923,794 169,524 81.65%

Middle-

Aged

1,013,130 197,977 80.46%

GSE5140

Untreated 32,075,094 18,925,611 41.00%

Creatine 33,349,407 17,935,181 46.22%

GSE46384

IPA0 1,616,710 1,092,630 32.42%

IPA40 2,000,931 1,189,808 40.54%

4 DISCUSSION

Network theory in systems biology remains in

relative infancy, and the correlation network is no

exception to benchmarking necessity. While high

performance computing techniques have typically

been found to be needed for fast and thorough

analysis of network models, laboratories do not

always have access to these types of resources. The

results of these studies allow for the following

potential conclusions to be inferred from studies on

robustness the correlation network model; additional

testing will be necessary to confirm or deny their

existence:

1. Sample size and network density are inversely

linked – the smaller the sample count, the higher

the density.

2. Sample size and non-robustness are inversely

linked – the smaller the sample size, the more

absolutely non-robust edges a network will have.

3. Based on the distribution of robust correlations

compared to sample number, correlation

networks can be thresholded to further remove

noise due to coincidental expression patterns.

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

192

Figure 5: Top 10 Gene Ontology enrichment terms of GSE5078 Young network clusters, original (left) and robustness

thresholded (right). Column headings include GO Term/Annotation, GO ID, Obs., or Observed number of genes with that

term, P-value, and Up or Down enrichment (whether or not the cluster is over or under enriched for that term based upon

the yeast genome).

GOTERM GOID Obs. P‐Val

↑or↓

Term# GOTERM GOID Obs. P‐Val

↑or↓

macro.metabolicproc. GO:0043170 15 0.04 up 1 systemproc. GO:0003008 60.05 up

cellularmacro.metabolic

proc.

GO:0044260 14 0.02 up 2 reg.ofmolecularfunction GO:0065009 5 0.01 up

reg.ofmetabolicproc. GO:0019222 13 0.05 up 3 celladhesion GO:0007155 5 0.03 down

reg.ofprimarymetabolic

proc.

GO:0080090 13 0.05 up 4

positivereg.ofmetabolic

proc.

GO:0009893 5 0.03 up

negativereg.ofcellularproc. GO:0048523 12 0.03 up 5 biologicaladhesion GO:0022610 5 0.03 down

reg.ofmacro.metabolicproc. GO:0060255 10 0.02 up 6

positivereg.ofcatalytic

activity

GO:0043085 4 0.03 up

nucleicacidmetabolicproc. GO:0090304 10 0.02 up 7

positivereg.ofmolecular

function

GO:0044093 4 0.03 up

transcription GO:0006350 9 0.04 up 8 reg.ofcatalyticactivity GO:0050790 4 0.03 up

macro.biosyntheticproc. GO:0009059 9 0.04 up 9

reg.ofgeneexpression GO:0010468 9 0.04 up 10

plasmamembrane GO:0005886 13 0.04 up 1 molecular_function GO:0003674 450.03 up

membrane GO:0016020 13 0.04 up 2 proteinbinding GO:0005515 15 0.03 up

catalyticactivity GO:0003824 10 0.05 up 3 primarymetabolicproc. GO:0044238 12 0.03 down

signaling GO:0023052 8 0.02 up 4 macro.metabolicproc. GO:0043170 9 0.05down

signalingpway GO:0023033 7 0.03 up 5 reg.ofcatalyticactivity GO:0050790 5 0.01 down

cellsurfacerec.linkedsignal

pway

GO:0007166 6 0.05 up 6 reg.ofmolecularfunction GO:0065009 5 0.01 down

positivereg.ofcatalytic

activity

GO:0043085 4 0.02 down

positivereg.ofmolecular

function

GO:0044093 4 0.02 down

9 organellepart GO:0044422 4 0.04 down

10 intracellularorganellepart GO:0044446 4 0.04 down

developmentalproc. GO:0032502 56 0.02 up 1 multicellularorganism.proc. GO:0032501 15 0.04 down

multicellularorganism.dev. GO:0007275 50 0.03 up 2 developmentalproc. GO:0032502 13 0.02 down

systemdev. GO:0048731 46 0.04 up 3 anatom.struct.dev. GO:0048856 13 0.02 down

nucleus GO:0005634 39 0.03 up 4 multicellularorganism.dev. GO:000727512 0.04down

cellulardevelopmentalproc. GO:0048869 37 0.00 up 5 celldifferentiation GO:0030154 9 0.03 down

celldifferentiation GO:0030154 34 0.00 up 6 reg.ofbiologicalproc. GO:0050789 8 0.04 down

Metabolicpways 1100 23 0.05 down 7 reg.ofcellularproc. GO:0050794 8 0.04 down

celldev. GO:0048468 22 0.05 up 8 membrane GO:0016020 4 0.04 up

signalingproc. GO:0023046 22 0.05 up 9

signaltransmission GO:0023060 22 0.05 up 10

biologicalreg. GO:0065007 17 0.03 down 1 biological_proc. GO:0008150 290.02 up

reg.ofbiologicalproc. GO:0050789 15 0.03 down 2 metabolicproc. GO:0008152 16 0.03 up

reg.ofcellularproc. GO:0050794 13 0.05 down 3 macro.metabolicproc. GO:0043170 7 0.04 up

catalyticactivity GO:0003824 11 0.03 up 4 proteinbinding GO:0005515 6 0.03 up

cytoplasm GO:0005737 7 0.02 up 5 signaltransduction GO:0007165 6 0.03 up

hydrolaseactivity GO:0016787 7 0.02 up 6 hydrolaseactivity GO:0016787 5 0.03 up

cytoplasmicpart GO:0044444 6 0.04 up 7

negativereg.ofmetabolic

proc.

GO:0009892 4 0.03 up

negativereg.ofmacro.

metabolicproc.

GO:0010605 4 0.03 up

9 proteinmetabolicproc. GO:0019538 4 0.05 up

signaling GO:0023052 30 0.04 up 1

anatom.struct.

morphogenesis

GO:0009653 5 0.04 up

signalingpway GO:0023033 26 0.02 up 2

anatom.struct.formation‐

morphogenesis

GO:0048646 5 0.04 up

signalingproc. GO:0023046 19 0.01 up 3

signaltransmission GO:0023060 19 0.01 up 4

proteinmetabolicproc. GO:0019538 17 0.05 up 5

smallmoleculemetabolic

proc.

GO:0044281 16 0.04 up 6

cellproliferation GO:0008283 14 0.05 down 7

signaltransduction GO:0007165 13 0.01 up 8

reg.ofmolecularfunction GO:0065009 13 0.03 up 9

cellularproteinmetabolic

proc.

GO:0044267 13 0.04 up 10

ROBUST

Cluster1Cluster2Cluster3Cluster5 Cluster4

ORIGINAL

OntheRobustnessoftheBiologicalCorrelationNetworkModel

193

Figure 6: Top 10 Gene Ontology enrichment terms of GSE5078 Mid network clusters, original (left) and robustness

thresholded (right). Colum-n headings include GO Term/Annotation, GO ID, Obs., or Observed number of genes with that

term, P-value, and Up or Down enrichment (whether or not the cluster is over or under enriched for that term based upon

the yeast genome).

GOTERM GOID Obs. P‐Val ↑or↓ Term# GOTERM GOID Obs. P‐Val ↑or↓

homeostatic

roc. GO:0042592 12 0.05 u

1multicell.or

anism.

roc. GO:0032501 23 0.01 u

cell‐cellsi

nalin

GO:0007267 10 0.01 u

roteinbindin

GO:0005515 21 0.03 u

transferaseactivity GO:0016740 8 0.01 down 3

multicell.organism.

develo

ment

GO:0007275 16 0.05 up

inflammator

res

onse GO:0006954 7 0.04 down 4 s

stemdevelo

ment GO:0048731 16 0.05 u

tictransmission GO:0007268 6 0.01 u

5si

nalin

GO:0023052 11 0.04 u

transferaseactivit

GO:0016772 5 0.01 down 6 si

nalin



GO:0023033 9 0.00 u

neuronalcellbod

GO:0043025 5 0.03 u

7or

anmor

h. GO:0009887 9 0.02 u

cellbod

GO:0044297 5 0.03 u

8si

naltransduction GO:0007165 9 0.03 u

solublefraction GO:0005625 5 0.04 down 9

cellsurfacereceptorlinked

nalin



GO:0007166 8 0.01 up

MAPKsignalingpway 4010 4 0.03 down 10

positiveregulationofcell

roliferation

GO:0008284 5 0.02 up

cell GO:0005623 32 0.03 down 1 cellular_com

onent GO:0005575 51 0.05 u

cellpart GO:0044464 32 0.03 down 2

intracellularmem.‐bounded

anelle

GO:0043231 20 0.04 down

intracellularorganelle GO:0043229 20 0.04 down 3

macromoleculebiosynthetic

roc.

GO:0009059 15 0.03 down

anatomicalstructuremorph. GO:0009653 15 0.04 up 4

cellularnitrogencompound

metab.

roc.

GO:0034641 13 0.02 up

catal

ticactivit

GO:0003824 5 0.01 down 5 nucleus GO:0005634 13 0.04 down

positiveregulationofimmune

stem

roc.

GO:0002684 4 0.02 up 6 extracellularregionpart GO:0044421 12 0.05 down

ulationofimmuneres

onse GO:0050776 4 0.02 u

7nucleicacidmetab.

roc. GO:0006139 12 0.05 u

8 localization GO:0051179 11 0.02 down

9extracellulars

ace GO:0005615 10 0.04 down

10 si

nalin



GO:0023033 10 0.02 down

cellular_com

onent GO:0005575 62 0.01 down 1 or

anmor

h. GO:0009887 9 0.01 down

biolo

ical_

roc. GO:0008150 59 0.02 down 2 celldifferentiation GO:0030154 9 0.01 down

roteinbindin

GO:0005515 30 0.02 down 3 cellulardevelo

mental

roc. GO:0048869 9 0.01 down

biologicalregulation GO:0065007 27 0.05 down 4

cellsurfacereceptorlinked

nalin



GO:0007166 9 0.04 down

ulationofcellular

roc. GO:0050794 23 0.03 down 5 nervouss

stemdevelo

ment GO:0007399 8 0.01 down

multicell.or

anism.

roc. GO:0032501 23 0.05 down 6 tissuedevelo

ment GO:0009888 7 0.02 down

multicell.organism.

develo

ment

GO:0007275 17 0.04 down 7 locomotion GO:0040011 6 0.01 down

systemdevelopment GO:0048731 17 0.04 down 8

positiveregulationofmetab.

roc.

GO:0009893 6 0.02 down

macromoleculemetab.proc. GO:0043170 15 0.02 down 9

positiveregulationof

macromoleculemetab.

roc.

GO:0010604 6 0.02 down

positiveregulationofbiological

roc.

GO:0048518 15 0.02 down 10

positiveregulationofgene

ression

GO:0010628 6 0.02 down

ulationofbiolo

ical

roc. GO:0050789 54 0.04 down 1 cellfraction GO:0000267 7 0.02 down

ulationofcellular

roc. GO:0050794 49 0.02 down 2 macromolecularcom

lex GO:0032991 7 0.04 u

nitro

enmetab.

roc. GO:0006807 24 0.01 down 3 cellulardevelo

mental

roc. GO:0048869 7 0.04 u

cellularnitro

enmetab.

roc. GO:0034641 24 0.01 down 4 catal

ticactivit

GO:0003824 5 0.01 down

bios

nthetic

roc. GO:0009058 23 0.03 down 5 solublefraction GO:0005625 5 0.02 down

nucleicacidmetab.

roc. GO:0006139 21 0.02 down 6 nervouss

stemdevelo

ment GO:0007399 4 0.03 u

eneex

ression GO:0010467 20 0.04 down 7 neuro

enesis GO:0022008 4 0.03 u

nucleicacidmetab.

roc. GO:0090304 20 0.04 down 8

enerationofneurons GO:0048699 4 0.03 u

ulationof

eneex

ression GO:0010468 19 0.04 down 9

regulationofmulticell.

anism.

roc.

GO:0051239 18 0.00 down 10

multicell.or

anism.

roc. GO:0032501 31 0.01 u

1bindin

GO:0005488 5 0.02 down

develo

mental

roc. GO:0032502 30 0.01 u

lasm GO:0005737 4 0.03 down

multicell.organism.

develo

ment

GO:0007275 28 0.01 up 3 regulationofbiologicalproc. GO:0050789 4 0.04up

anatomicalstructure

develo

ment

GO:0048856 28 0.03 up 4 regulationofcellularproc. GO:0050794 4 0.04 up

andevelo

ment GO:0048513 26 0.02 u

stemdevelo

ment GO:0048731 26 0.02 u

mem. GO:0016020 24 0.00 u

mem.

art GO:0044425 20 0.02 u

lasmamem. GO:0005886 19 0.00 u

ulationoftrans

ort GO:0051049 4 0.01 u

Cluster4Cluster5

ORIGINAL ROBUST

Cluster1Cluster2Cluster3

BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms

194

These studies allow us to speculate that there may be

room for improvement in network creation studies,

and further, that high-throughput experiments

intended for use in network models can benefit from

understanding the link between sample size and

relationship confidence. We expect that expansion of

these studies to more model organisms, sample

sizes, and conditions will reveal similar patterns.

4.1 Future Directions

Future work involving network robustness involves

examining the effects of random sample removal

(remove Sample 1 from Gene 1 and Sample 2 from

Gene 2) instead of coordinated sample removal

(remove Sample 1 from Genes 1 and 2). Further, this

direction begs the question of effects of N-sample

removal, where N represents the number of samples

to be removed at a time. Finally, to examine the

change in biological signal of the network, we intend

to pursue in depth the functional and pathway

enrichments of networks in their original states and

in secondary threshold states to see if the

information lost is noise or causative. This might

include enrichment with Gene Ontology in network

building, or usage of the rich wealth of information

available in NCBI’s Gene database to determine

whether or not a relationship is likely based on

known expression levels of a gene in given

organisms and tissues.

ACKNOWLEDGEMENTS

This publication was made possible by Grant

Number P20 RR16469 from the National Center for

Research Resources (NCRR), a component of the

National Institutes of Health (NIH) and it's contents

are the sole responsibility of the authors and do not

necessarily represent the official views of NCRR or

NIH.

REFERENCES

Halappanavar M., Feo J., Dempsey K., Ali H., Bhowmick

S. A Novel Multithreaded Algorithm for Extracting

Maximal Chordal Subgraphs. ICPP 2012:58-67.

Dempsey K., Bonasera S., Bastola D., Ali H. H. A novel

correlation networks approach for the identification of

gene targets. HICSS 2011:1-8.

Song L., Langfelder P., Horvath S. Comparison of co-

expression measures: Mutual information, correlation,

and model based indices. BMC Bioinformatics.

2012;13(1):328.

Opgen-Rhein R., Strimmer K. From correlation to

causation networks: A simple approximate learning

algorithm and its application to high-dimensional plant

gene expression data. BMC Syst Biol. 2007;1:37.

Horvath S., Dong J. Geometric interpretation of gene

coexpression network analysis. PLoS Comput Biol.

2008;4(8):e1000117.

Verbitsky M., Pavlidis P., Kandel E., Gilliam C., Yonan

A., Malleret G. Altered Hippocampal transcript profile

accompanies an age-related spatial memory deficit in

mice. Learn Mem 2004 May-Jun;11(3):253-60.

Bender A, Beckers J, Schneider I, Hölter SM et al.

Creatine improves health and survival of mice.

Neurobiol Aging 2008 Sep;29(9):1404-11.

Ikushima M., Misaizu A. GEO Accession GSE46384.

http://www.ncbi.nlm.nih.gov/geo/query/acc.cgi?acc=G

SE46384

Bader G. D., Hogue C. W. An automated method for

finding molecular complexes in large protein

interaction networks. BMC Bioinformatics 2003 Jan

13; 4:2.

Backes C., Keller A., Kuentzer J., Kneissl B., Comtesse

N., Elnakady Y. A., Müller R., Meese E., Lenhof H. P.

Genetrail – advanced gene set enrichment analysis.

Nucleic Acids Res 2007 Jul; 35(Web Server

Issue):W186-92.

Reverter A., Chan E. K. Combining partial correlation and

an information theory approach to the reversed

engineering of gene co-expression networks.

Bioinformatics. 2008;24(21):2491-2497.

Song L., Langfelder P., Horvath S. Comparison of co-

expression measures: Mutual information, correlation,

and model based indices. BMC Bioinformatics.

2012;13(1):328.

Opgen-Rhein R., Strimmer K. From correlation to

causation networks: A simple approximate learning

algorithm and its application to high-dimensional plant

gene expression data. BMC Syst Biol. 2007;1:37.

Song L., Langfelder P., Horvath S. Comparison of co-

expression measures: Mutual information, correlation,

and model based indices. BMC Bioinformatics.

2012;13(1):328.

Opgen-Rhein R., Strimmer K.. From correlation to

causation networks: A simple approximate learning

algorithm and its application to high-dimensional plant

gene expression data. BMC Syst Biol. 2007;1:37.

OntheRobustnessoftheBiologicalCorrelationNetworkModel

195