
Generating Features using Burrows Wheeler Transformation for
Biological Sequence Classification
Karthik Tangirala and Doina Caragea
Department of Computing and Information Sciences, Kansas State University, Manhattan, Kansas, U.S.A.
Keywords:
Burrows Wheeler Transformation, Machine Learning, Supervised Learning, Feature Selection, Dimensional-
ity Reduction, Biological Sequence Classification.
Abstract:
Recent advancements in biological sciences have resulted in the availability of large amounts of sequence data
(both DNA and protein sequences). The annotation of biological sequence data can be approached using ma-
chine learning techniques. Such techniques require that the input data is represented as a vector of features. In
the absence of biologically known features, a common approach is to generate k-mers using a sliding window.
A larger k value usually results in better features; however, the number of k-mer features is exponential in k,
and many of the k-mers are not informative. Feature selection techniques can be used to identify the most
informative features, but are computationally expensive when used over the set of all k-mers, especially over
the space of variable length k-mers (which presumably capture better the information in the data). Instead
of working with all k-mers, we propose to generate features using an approach based on Burrows Wheeler
Transformation (BWT). Our approach generates variable length k-mers that represent a small subset of k-
mers. Experimental results on both DNA (alternative splicing prediction) and protein (protein localization)
sequences show that the BWT features combined with feature selection, result in models which are better than
models learned directly from k-mers. This shows that the BWT-based approach to feature generation can be
used to obtain informative variable length features for DNA and protein prediction problems.
1 INTRODUCTION
Machine learning has been extensively used to ad-
dress prediction and classification problems in the
field of bioinformatics. Advancements in sequenc-
ing technologies have led to the availability of large
amounts of labeled data, especially in the form of bio-
logical sequences. This data can be used to learn clas-
sifiers for various sequence classification problems.
Most learning algorithms require a vectorial represen-
tation of the data in terms of features. Generally, the
more informative the features chosen to represent the
data, the better the resulting classifier. When avail-
able, biologically relevant features (e.g., known mo-
tifs or domains) have been successfully used. For ex-
ample, biologically informative motifs corresponding
to intronic and exonic regions of a gene are avail-
able for the organism, C. elegans (R ¨atsch et al., 2005;
Xia et al., 2008). The Intronic Regulatory Sequences
(IRS) and Exonic Splicing Enhancers (ESE) motifs
are used to learn models for predicting alternative
splicing events in genes.
However, for many problems such features are
not readily available. Alternatively, we can gener-
ate all possible motifs of a fixed length k (a.k.a., k-
mers) using a sliding window approach (Shah et al.,
2004; Chor et al., 2009; Melsted and Pritchard, 2011;
Caragea et al., 2011). If we want to work with
variable-lengths k-mers, we can use the sliding win-
dow approach repeatedly with different k values. One
drawback of the sliding window approach is that the
number of k-mers that it produces is exponential in
the length of the k-mer. Furthermore, among the re-
sulting features (k-mers), many are not informative,
sometimes acting as noise and misleading the classi-
fier. To address this problem, feature selection tech-
niques are used to reduce the number of features pro-
vided as input to the classifier.
It is computationally expensive to run feature se-
lection algorithms with all k-mers. Filtering k-mers
based on the frequency of occurrence is commonly
used to reduce the initial dimension of the feature
space. To gain understanding on what filtering criteria
may be used for the problem of predicting alternative
splicing events, we used existing data from C.elegans
for which informative features (in the form of IRS and
196
Tangirala K. and Caragea D..
Generating Features using Burrows Wheeler Transformation for Biological Sequence Classification.
DOI: 10.5220/0004806201960203
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2014), pages 196-203
ISBN: 978-989-758-012-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ESE) are known, and noticed that out of 210 features,
205 occurred at least twice in at least one sequence.
This means, we can filter the set of all k-mers by re-
moving the k-mers that don’t satisfy this constraint.
The reduced set should presumably include most in-
formative k-mers, while excluding many uninforma-
tive k-mers.
To capture this idea, in this paper, instead of us-
ing the sliding window approach to generate k-mers,
we present an approach that makes use of the Burrows
Wheeler Transformation (BWT) of a sequence to gen-
erate a more informative, reduced set of variable-
length k-mers (denoted by b-mers), which excludes
most of the uninformative k-mers. The b-mers in the
BWT reduced set have the property that occur mul-
tiple times (at least twice) in each sequence. Exper-
iments are conducted to evaluate the performance of
the b-mers as compared to the standard k-mers, when
feature selection is applied on top of either the b-mers
or the k-mers. For a more fair comparison, we also
generate features by filtering k-mers based on the fre-
quency of occurrence. We select the k-mers that oc-
cur at least twice in a sequence, and we refer to this
set of features as frequency-based filtered k-mers, de-
noted by f -mers. We should note that the set of f -
mers is different from the set of b-mers, as more filter-
ing is performed by BWT, as will be explained later.
The results on two biological sequence classification
problems (alternative splicing and protein localization
prediction) show better performance for the set of b-
mers (especially in the case of protein sequence clas-
sification). Furthermore, the size of the b-mers set
is significantly smaller than that of the sets of k-mers
and f -mers. This suggests that the BWT-based feature
generation approach can be successfully used as a di-
mensionality reduction technique, as it can reduce the
initial feature space to a large extent without losing
informative features.
The rest of the paper is organized as follows:
Section 2 discusses related work in applying Bur-
rows Wheeler Transformation and dimensionality re-
duction techniques to bioinformatics problems. Sec-
tion 3.1 explains the process of transforming a se-
quence using BWT. Further, Section 3.2 focuses on
the process of generating variable length motifs us-
ing BWT. Section 3.3 provides an overview of the
complete approach. In Section 4, we list the research
questions and the set of experiments conducted to ad-
dress the questions. The results for the experiments
conducted are presented in Section 5. Finally in Sec-
tion 6, we present conclusions and ideas for future
work.
2 RELATED WORK
2.1 BWT in Bioinformatics
Burrows Wheeler Transformation was first introduced
by Burrows and Wheeler (1994), to address the prob-
lem of data compression. The ability of BWT to ef-
ficiently identify multiple occurrences of a particular
fragment of a sequence generated significant interest
in this approach, especially in the field of bioinfor-
matics. Several applications on BWT have been de-
veloped for various biological problems.
Ferragina et al. (2000) proposed an approach
(FM-index) that uses Burrows Wheeler Transforma-
tion along with the suffix array data structure to ef-
ficiently find the number of occurrences of a pattern
within a compressed text. Besides finding the count,
the FM-index also identifies the location of all the pat-
terns in the original sequence. The authors proposed
an algorithm whose running time and storage space
are sub-linear with respect to the size of the data. Li
et al. (2009) developed SOAP2, a tool which is an
extension of SOAP (Li et al., 2008), which in turn
is an approach for gapped and ungapped alignment
of short oligonucleotides. SOAP2 replaced the origi-
nal seed strategy of SOAP with the Burrows Wheeler
Transformation indexing, and thus reduced the mem-
ory usage and increased the alignment speed. Lang-
mead et al. (2009) introduced a fast and memory ef-
ficient technique (Bowtie) for aligning short DNA se-
quences to a human genome. Bowtie uses Burrows-
Wheeler indexing in the process of aligning the short
sequences. Li et al. (2009) also aligned short reads to
a larger sequence (specifically genome) using BWT.
The proposed approach used the backward search
with BWT and performed top-down traversal on the
prefix trie of the genome. The approach improves the
efficiency of repeat finding for a large sequence when
compared to the state-of-the-art suffix array-based im-
plementation (Becher et al., 2009). Repeat finding is
one common application of the BWT-based approach
in the field of bioinformatics.
2.2 Feature Selection
In sequence-based classification problems and more
importantly when we are working with k-mers (or
b-mers), there is a fair chance of dealing with fea-
tures that are not informative. In such cases, using all
the features can mislead the classifier, thereby affect-
ing the performance. Feature selection addresses the
problem of removing features that are not informative
enough, for example by computing the mutual infor-
mation between each feature and the class variable.
GeneratingFeaturesusingBurrowsWheelerTransformationfor
BiologicalSequenceClassification
197

Feature selection can be essential in improving the
performance of the classifier, in addition to reducing
the dimensionality of the input feature space (which
affects the efficiency). Various feature selection tech-
niques have been proposed in the past (Ng et al., 1997;
Wiener et al., 1995; Battiti, 1994). Most of these tra-
ditional feature selection techniques need features to
be represented using a set of numerical values. Alter-
natively, feature selection techniques that are specific
to the problem of sequence classification have also
been proposed in the past. Due to the dependency
between the adjacent positions of a sequence, many
Markov models have been developed to address the
problem of feature selection. Salzberg et al. (1998)
used interpolation between different orders of Markov
models, known as interpolated Markov model (IMM)
along with a filter (χ
2
test) to select a subset of fea-
tures. Sayes et al. (2007) used the Markov blanket
multivariate approach (MBF) on top of a combination
of different measures of coding potential prediction to
retain informative features. Chuzhanova et al. (1998)
combined a genetic algorithm with a Gamma test to
obtain scores for feature subsets. The optimal subset
is then selected based on the scores. Zavaljevsky et al.
(2002) used selective kernel scaling for support vec-
tor machines (SVM) to compute the weights of the
features. Features with low weights are ignored sub-
sequently. Degroeve et al. (2002) addressed the prob-
lem of splice site prediction through feature selection,
by using a sequential backward method along with an
embedded evaluation criterion based on SVM.
In this paper, we present an approach based on
BWT that reduces the dimensionality of the input fea-
ture space to a large extent by retaining most of the
informative features. To the best of our knowledge,
such an approach has not been studied before in the
context of biological sequence classification.
3 METHODS
3.1 Burrows Wheeler Transformation
Burrows Wheeler Transformation produces a con-
text dependent permutation of an input sequence (set
of characters), such that characters adjoining similar
contexts are grouped together.
Given an input sequence S, we generate all possi-
ble rotations of the sequence (obtained by removing
the last character of the sequence and appending it as
a prefix). For a sequence of length n, the rotations
can be represented as a square matrix of dimension-
ality n×n. We then sort the matrix alpha-numerically
(the resulting matrix is referred to as R) and select the
last column of the sorted rotations. This last column
will give us the Burrows Wheeler Transformation of
S, denoted by “bwt[]” (an n dimensional array of char-
acters).
3.2 Feature Generation using BWT
BWT internally groups all the characters having the
same prefixes and lexicographically similar suffixes.
In what follows, we describe how we exploit this
property of BWT to generate features of variable
length (called b-mers). We start with an array of
sorted rotations R as input to the procedure for gen-
erating b-mers. In the BWT transformed sequence
(bwt[] = last column of R), we search for contiguous
occurrences of a character, x. Such a contiguous oc-
currence is referred to as a repetition. If we find a
repetition, we select the starting and ending positions
(indices: start,end) of the repetition in the bwt[]. We
then select the rotations in R from start to end indices
and search for a common prefix among the selected
rotations. If we find a match (prefix), we select the
prefix, “γ”, and append the repeated symbol x in front
of γ, producing the feature x + γ. Thus, a repetition of
length l in the bwt[], results in a feature that is repeated
at least l times in the original sequence. Furthermore,
the resulting features have variable length.
As noted in the introduction, in principle we can
filter variable length k-mers, based on the frequency
of occurrence in individual sequences (by selecting
only those that appear at least twice in a sequence,
denoted by f -mers). However, the BWT features have
additional properties that cannot be obtained by filter-
ing the set of all variable length k-mers. The prop-
erties are described in what follows. We should note
that these properties are verified implicitly when us-
ing the procedure described above, and we need not
check them explicitly. To make the presentation pre-
cise, we use the following notations.
As before, we denote the original sequence by S.
Let α be a sub-sequence of S. For a sequence, we refer
to the sub-sequence on the left side of the sequence
as a left segment, denoted by leftSeg, and the sub-
sequence on the right side of the sequence as a right
segment, denoted by rightSeg. For example, for the
sequence “tgct”, each of “t”, “tg”, “tgc” etc. can be
seen as leftSeg, while each of“t”, “ct”, “gct” etc. can
be seen as rightSeg. Let |α| be the length of the sub-
sequence α. Features generated with the BWT-based
approach have the following properties:
• Each feature occurs at least two times in the se-
quence.
• If a sub-sequence α of S has a leftSeg whose fre-
quency of occurrence in S is greater than the fre-
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
198

quency of α in S, then BWT returns that leftSeg as
a feature, if either start or end indices associated
with leftSeg are adjacent or between the start and
end indices associated with α. Besides that, the
leftSeg should also satisfy the next two properties.
Otherwise, BWT returns α as a feature, assuming
that the next two properties are satisfied by α.
• If α occurs multiple times in S, BWT returns α as
a feature, if there is no other sub-sequence of S,
β, such that α and β, have an identical leftSeg. In
case α and β have an identical leftSeg, BWT re-
turns the leftSeg, that is common to both α and β
as a feature if the remaining properties are satis-
fied by the common leftSeg.
• If α and β are two sub-sequences of S having
an identical rightSeg, which is preceded by two
different characters in the two sub-sequences α
and β, then BWT returns α if and only if at
least two of the rotations corresponding to α are
grouped together in the sorted rotations (i.e., they
are not inter-spread with rotations corresponding
to β) and if no other sub-sequence(s) of S, δ,
having length greater than α is associated with
the same set of grouped rotations (if rightSeg of
δ, having length |δ|-1 is a common prefix of all
the grouped rotations). If there is any such sub-
sequence, BWT returns the sub-sequence of max-
imum length (longest of all δs) associated with the
grouped rotations as feature, ignoring α. In either
case, the feature that is returned should satisfy all
the remaining properties.
Given these properties, if N
k−mers
represents the
number of variable length k-mers generated using the
sliding window approach, N
f−mers
represents the num-
ber of features generated by filtering the k-mers that
occur at least twice, and N
b−mers
represents the num-
ber of features generated using BWT, then N
k−mers
≥
N
f−mers
≥ N
b−mers
.
Example. Figure 1 shows the process of generat-
ing the features for a given input nucleotide sequence
“acgtcgacgtttacg”. The first step is to generate the
BWT sequence associated with the given input se-
quence. We add a delimiter “$” to mark the end
of the sequence. We generate all possible rotations
of the sequence. The rotations are sorted alpha-
numerically and the last column of the sorted rota-
tions is bwt[]. We then look for contiguous occur-
rences of nucleotides, “x” in the BWT sequence and
we observe two repetitions that have length at least
2, “aa” and “cccc”. For “aa”, indices start=7 and
end=8. We then select the rotations at indices 7 and
8 and search for a common prefix between these two
rotations. As can be seen, “cgt” is a common prefix
(γ) for both sequences. We select “cgt” (γ) and add
Figure 1: The process of generating features for a given in-
put sequence “acgtcgacgtttacg”. We generate all possible
rotations of the input sequence and sort the rotations alpha
numerically. The last column of the sorted rotations is the
BWT of the input sequence. Based on the contiguous oc-
currences of characters (repetitions) in BWT sequence, we
extract the features (b-mers).
“a” (x) as a prefix to it, resulting in the feature “acgt”
(x+γ). We repeat this process also for the second con-
tiguous sequence, and extract the feature “cg”. As
a result, the b-mers of “acgtcgacgtttacg” are “acgt”
(blocked) and “cg” (italicized).
Comparison with k-mers. If we attempt to identify
variable length k-mers that occur at least twice in a
sequence using the sliding window approach, we will
obtain the features “acgt”, “cg”, “cgt”, “acg”, “ac”,
“gt” and “tt”. Thus, we have 7 features in the set of f -
mers, whereas only 2 features in the set of b-mers. We
should note that the b-mers avoid most of the overlaps
as opposed to f -mers.
3.3 Overview of the Proposed Approach
In this section, we will summarize the details of the
complete process of generating the BWT-based fea-
tures and predicting the unseen test data. The in-
put to the complete process is a set of training se-
quences (S[1..n]) along with their associated class la-
bels (C[1..n]) (where each class label can take one
of the c possible values), and also number of fea-
tures to select. For each sequence S[i] (i∈{1...n}),
we construct an array of sorted rotations R, which is
used to generate BWT features as described in Sec-
tion 3.2. The features corresponding to each sequence
are appended to the total list of features, “F”, which
aggregates features for the whole dataset. Next, we
represent all the sequences using the set F of fea-
tures, thereby generating instances in vectorial form.
Specifically, an instance corresponding to a sequence
is a vector of frequency counts for the features F in
that sequence. We then apply a feature selection tech-
nique to select the most informative features (based
GeneratingFeaturesusingBurrowsWheelerTransformationfor
BiologicalSequenceClassification
199

on the number of features provided as an input) from
the total available pool of features. For feature selec-
tion, we used Entropy based Category Coverage Dif-
ference (ECCD) (Largeron et al., 2011). Finally, both
training and test sequences are represented using only
the selected features. A classifier is learned from the
training instances, and it is then used to predict the
test instances.
4 EXPERIMENTAL SETUP
In Section 4.1, we present the research questions ad-
dressed through our work. The set of experiments
conducted are presented in Section 4.2 and the de-
scription of the datasets used in Section 4.3.
4.1 Research Questions
Our experiments were motivated by the following re-
search questions:
• How does the number of b-mers compare to the
number of k-mers and f -mers?
• For a fixed number of features (selected using
ECCD), which feature set performs the best?
• For which type of the base classifier, naive Bayes
multinomial (NBM) or support vector machines
(SVM), are b-mers more effective?
• When used for DNA and protein sequences, in
which case are the b-mers more effective?
4.2 Experiments
To answer the first question, we simply count the
number of variable length k-mers, f -mers and b-mers
derived from the datasets used in our study. Specifi-
cally, we consider features of length 1 to 8 in the case
of DNA sequences, and of length 1 to 4 in the case of
protein sequences.
To answer the second question, for each feature
set, we vary the number of features to select from
25 to 3000 (specifically, 25, 50, 75, 100, 150, 250,
500, 1000, 1500, 2000, 2500, 3000) using the fea-
ture selection technique. For each number of fea-
tures selected, we learn classifiers based on the three
types of feature sets, respectively, and compare their
performance on test data. We perform 5-fold cross
validation. At each iteration of the cross-validation
procedure, features are derived and selected based on
the four training folds corresponding to that iteration.
Next, classifiers are learned from the same four folds
using the three types of representations, respectively.
The performance is evaluated on the fifth fold. We
use the area under the ROC curve (AUC) to measure
the performance. Results over the five folds are then
averaged. We trained both NBM and SVM classifiers
using the available training data. For SVM, we used
default Weka (Hall et al., 2009) parameters. Specif-
ically, a linear kernel is used along with parameters
C = 1 and ε=1.0e
−12
(no tuning is performed).
By performing experiments with both NBM and
SVM classifiers, we can compare their results and
thus answer the third question. Furthermore, by
performing experiments with both DNA and protein
datasets, we can analyze the results to understand for
which type of data, the b-mers representation is more
suitable, and thus answer the fourth question.
4.3 Datasets
We conducted experiments on both DNA and protein
datasets. For DNA, we used the alternative splicing
datasets of C. elegans (referred as CEdata) (R ¨atsch
et al., 2005), and a similar dataset constructed in
our lab based on mRNA to DNA alignments avail-
able through ALEXA (Griffith et al., 2008) for D.
melanogaster (referred to as DMdata). The C. el-
egans dataset consists of 3018 sequences belonging
to one of two classes: alternatively spliced (487)
and constitutive (2531) exons. The D. melanogaster
dataset consists of 1410 sequences labeled as either
alternatively spliced (164) or constitutive (1246) ex-
ons. For protein sequences, we used PSORTdbv.2.0
Gram-negative and Gram-positive protein sequences
(Gardy et al., 2005), for which the location informa-
tion is experimentally verified. The gram-negative
dataset consists of 1444 sequences belonging to one
of five classes: cytoplasm (278), cytoplasmic mem-
brane (309), periplasm (276), outer membrane (391)
and extracellular (190). The gram-positive dataset
consists of 541 sequences belonging to one of four
classes: Cytoplasmic (194), CytoplasmicMembrane
(103), Cellwall (61) and Extracellular (183). In the
case of multi-class classification using SVM classi-
fier, we use the one vs one strategy available in Weka.
Specifically, a classifier is learned for each pair of
classes. For a test instance, the class is predicted using
all pairwise classifiers. The class that is most often as-
signed to the instance will be assigned as final class to
that instance (max-wins strategy).
5 RESULTS
We perform the experiments described in Section 4.2
and report results in this section.
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
200

Table 1: Comparison of the number of features generated
using k-mers, f -mers and b-mers for the four datasets used,
averaged over 5 folds.
Dataset k-mers f -mers b-mers
CEdata 82229 64541 5049
DMdata 80740 11941 1954
Gram-negative 113657 7195 928
Gram-positive 75896 7623 1034
5.1 Feature Space Size
Table 1 presents the number of features generated
using all three techniques (k-mers, f -mers, b-mers),
averaged over five folds. We notice that the num-
ber of features in the set of k-mers is greater than
the number of features in the set of f -mers, which is
much greater than the number of features in the set
of b-mers. Therefore, using k-mers and f -mers will
increase the running time of feature selection tech-
niques by a large extent.
5.2 Variation of Performance with the
Number of Features
Figure 2 plots the AUC values of the SVM (labeled
(a) in the graph) and NBM (labeled (b)) classifiers
learned using different sets and numbers of features.
Each column of the graphs in Figure 2 corresponds to
one of the four datasets. Each curve in a graph corre-
sponds to one of the three feature sets (b-mers, k-mers
and f -mers), respectively. Given the large number of
features, we represent them on the log scale.
As can be seen in Figure 2, b-mers outperform k-
mers and f -mers in about 85% of the cases when used
with the SVM classifier and in about 63% of the cases
when used with NBM, suggesting that b-mers give
better results consistently, regardless of the classifier
used. For a relatively small number of features (25 to
500), b-mers result in better performance for most of
the cases considered. However, for a larger number
of features, k-mers and f -mers are slightly dominant
in the case of NBM, while b-mers still give better per-
formance with the SVM classifier. To understand why
this is the case, we should first note that for small fea-
ture sets, the set of k-mers includes features that are
the most informative for the class according to the fea-
ture selection criterion, many of these features being
variants of each other (i.e., features with overlaps). As
a consequence, for a small feature set, while the most
informative features will be included, not many of the
informative features will be included (in the sense that
the variations of an informative feature cover much of
the set and other informative features don’t make it
into that list). As opposed to that, the set of b-mers
consists of more informative features (as some vari-
ants may be excluded). This is probably why the set
of b-mers result in better performance for smaller size
feature sets. When the size of the feature set is large,
many (possibly most) informative features will be in-
cluded in the k-mers set, together with their variants.
However, some informative features or their variants
may not be included in the b-mers set, and thus the
performance of b-mers is not always better than that
of k-mers.
5.3 SVM versus NBM Classifier
As discussed earlier in Section 5.2, the SVM classifier
with b-mers outperforms the SVM with k-mers and f -
mers in about 85% of the cases, while that is the case
in only 63% cases for the NBM classifier. This sug-
gests that the SVM algorithm is able to make better
use of b-mers as compared to NBM.
5.4 DNA versus Protein Sequences
We performed t-tests to evaluate the significance of
the differences observed when comparing b-mers, k-
mers and f -mers (results not shown due to space con-
straints). Given that SVM gave better results, we per-
formed t-tests for the SVM results only.
According to the t-tests, differences are statisti-
cally significant (p-value≤0.05) mostly in the case
of protein sequences, but not so much in the case of
DNA sequences. For example, when comparing b-
mers and f -mers using the SVM classifier, b-mers are
significantly better in 20 out of 24 cases, while for
DNA sequences, they are better in 3 out of 24 cases
(corresponding to the 12 feature set sizes for two
DNA/protein datasets). We speculate that the main
reason for this behavior stems from the fact that the
size of the protein alphabet is larger than the size of
the DNA alphabet, and consequently the features have
smaller length for protein sequences as compared to
DNA sequences. Given the longer DNA features, it
is very possible that variations of a feature (obtained
by considering mismatches), which are equally im-
portant with respect to class, are not all captured by
the BWT-based approach. In other words, it is not
very probable that a sequence of length say 8 is re-
peated at least twice in a sequence, while it might be
repeated several times when a small number of mis-
matches is allowed. As opposed to that, in the case of
shorter protein features, say length 3, there is a bet-
ter chance that a feature is repeated several times in a
sequence, without any mismatches, which is captured
better by BWT-based approach.
Using the t-tests results, we have also observed
GeneratingFeaturesusingBurrowsWheelerTransformationfor
BiologicalSequenceClassification
201
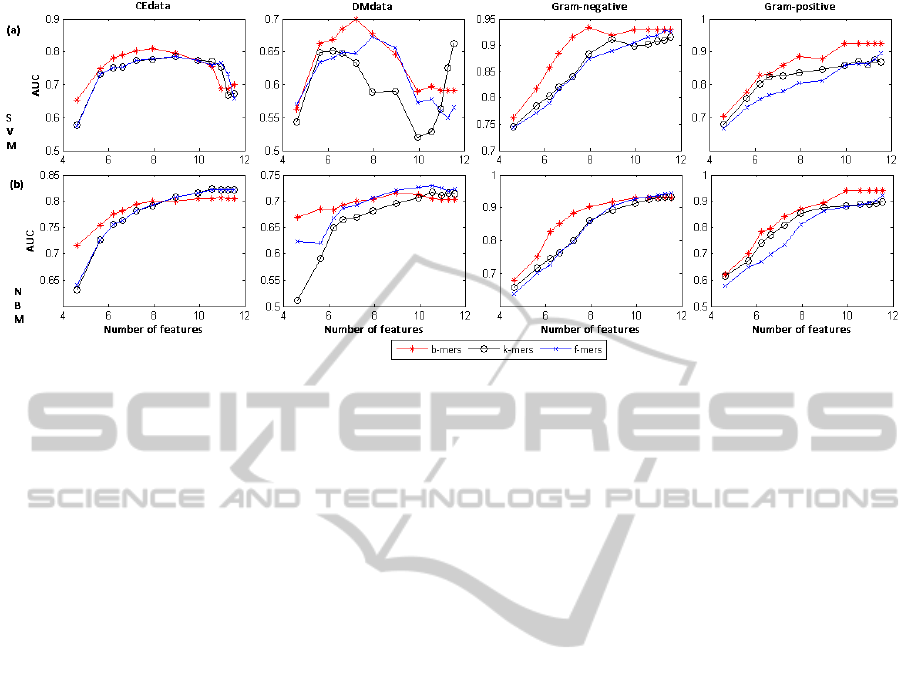
Figure 2: Variation of the performance (AUC values) with the number of features (shown on a log scale) for SVM (a) and
NBM (b) classifiers.
that the differences between b-mers and f -mers are
more significant than those between b-mers and k-
mers. In other words, b-mers result in better per-
formance as compared to f -mers in more cases than
when we compare them with k-mers. A possible ex-
planation for this is that the filtering criterion that we
use removes some of the informative features (from
b-mers and f -mers sets), while they are present in the
k-mers set. But given that overall the BWT approach
manages to retain more informative features that don’t
overlap much, as opposed to the filtering approach
where more overlapping features are present, for the
same number of features, the b-mers set is generally
better than the f -mers set. However, it is not always
better than the k-mers set, especially for larger fea-
tures sets, as the k-mers set might include informative
features that are not retained in the set of b-mers.
6 CONCLUSIONS AND FUTURE
WORK
6.1 Conclusions
We presented an approach for generating features
for sequence classification problems using Burrows
Wheeler Transformation (BWT). This approach can
be seen as a dimensionality reduction technique, as
the features obtained through BWT represent a sub-
set of the set of k-mers, generated using a sliding
window-based approach. To the best of our knowl-
edge, Burrows Wheeler Transformation has never
been used to generate features that are further used
to classify biological sequences. The results of our
experiments on both DNA and protein datasets show
that this attempt of using BWT to generate features
reduces the size of the input feature space, while re-
taining many of the informative features (especially in
the case of protein sequences, where informative fea-
tures are short and appear more frequently throughout
the sequence). Feature selection techniques, applied
on b-mers are faster and give better results as com-
pared to feature selection techniques applied directly
on k-mers. Given all the advantages of the BWT-
based features, we conclude that the BWT approach
can be seen as a powerful tool for generating an initial
pool of features for sequence classification problems.
6.2 Future Work
First, given the unsupervised nature of the BWT ap-
proach for generating a reduced set of features, it
would be interesting to investigate the performance
of the features generated using BWT in domain adap-
tation, semi-supervised and transductive settings.
Second, as BWT approach generates mostly non-
overlapping features and could miss informative fea-
ture variations, we would like to investigate the use
of a variant of the BWT approach, where we include
features with mismatches. By allowing certain mis-
matches, we expect an increase in the performance of
the classifiers (learned using BWT-based features) es-
pecially for DNA sequence classification problems.
Furthermore, a comparison of the BWT-based fea-
tures with k-mers that are grouped together into “mo-
tifs” based on overlaps, as well as with other dimen-
sionality reduction techniques would be another inter-
esting direction for future work.
Given that the best results were obtained with the
SVM algorithm, with default parameters, it would be
BIOINFORMATICS2014-InternationalConferenceonBioinformaticsModels,MethodsandAlgorithms
202

interesting to explore different kernels for SVM, and
perform tuning for different sets of parameters, in or-
der to further improve the performance.
Another interesting direction could be to analyze
the performance of features generated using BWT for
big data, with various feature selection techniques, in
addition to the ECCD technique used in this paper.
ACKNOWLEDGEMENTS
We would like to thank Ana Stanescu in the De-
partment of Computing and Information Sciences
at Kansas State University for making the D.
melanogaster data available for this study. We would
also like to acknowledge Dr. Adrian Silvescu for
insightful discussions regarding the BWT transform,
and Dr. Torben Amtoft for useful discussions regard-
ing time and space complexity of the algorithms stud-
ied in this paper.
REFERENCES
Battiti, R. (1994). Using mutual information for select-
ing features in supervised neural net learning. IEEE
Transactions on Neural Networks, 5:537–550.
Becher, V., Deymonnaz, A., and Heiber, P. (2009). Effi-
cient computation of all perfect repeats in genomic
sequences of up to half a gb, with a case study on the
human genome. Bioinformatics, 25(14):1746–1753.
Burrows, M. and Wheeler, D. J. (1994). A block-sorting
lossless data compression algorithm. Technical Re-
port 124, Digital Equipment Corp., Palo Alto, CA.
Caragea, C., Silvescu, A., and Mitra, P. (2011). Protein
sequence classification using feature hashing. In Proc.
of IEEE BIBM 2011, pages 538–543.
Chor, B., Horn, D., Levy, Y., Goldman, N., and Massing-
ham, T. (2009). Genomic DNA k-mer spectra: models
and modalities. GENOME BIOLOGY, 10.
Chuzhanova, N. A., Jones, A. J., and Margetts, S. (1998).
Feature selection for genetic sequence classification.
Bioinformatics, 14(2):139–143.
Degroeve, S., De Baets, B., Van de Peer, Y., and Rouz ´e, P.
(2002). Feature subset selection for splice site predic-
tion. Bioinformatics, 18(suppl 2):S75–S83.
Ferragina, P. and Manzini, G. (2000). Opportunistic data
structures with applications. In Proc. of the 41st Symp.
on Foundations of Computer Science, pages 390–398.
Gardy, J. L., Laird, M. R., Chen, F., Rey, S., Walsh, C. J.,
Ester, M., and Brinkman, F. S. L. (2005). Psortb
v.2.0: Expanded prediction of bacterial protein sub-
cellular localization and insights gained from compar.
proteome analysis. Bioinformatics, 21(5):617–623.
Griffith, M., Tang, M. J., Griffith, O. L., Morin, R. D.,
Chan, S. Y., Asano, J. K., Zeng, T., Flibotte, S., Ally,
A., Baross, A., Hirst, M., Jones, S. J. M., Morin,
G. B., Tai, I. T., and Marra, M. A. (2008). ALEXA: a
microarray design platform for alternative expression
analysis. Nature Methods, 5(2):118.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data min-
ing software: An update. SIGKDD Explor. Newsl.,
11(1):10–18.
Langmead, B., Trapnell, C., Pop, M., and Salzberg, S.
(2009). Ultrafast and memory-efficient alignment of
short DNA sequences to the human genome. Genome
Biology, 10(3):1–10.
Largeron, C., Moulin, C., and G `ery, M. (2011). Entropy
based feature selection for text categorization. In
Proc. of the 2011 ACM Symp. on Applied Computing,
SAC ’11, pages 924–928, New York, NY, USA. ACM.
Li, H. and Durbin, R. (2009). Fast and accurate short read
alignment with Burrows-Wheeler transform. Bioin-
formatics, 25(14):1754–1760.
Li, R., Li, Y., Kristiansen, K., and Wang, J. (2008). Soap:
short oligonucleotide alignment program. Bioinfor-
matics, 24(5):713–714.
Li, R., Yu, C., Li, Y., Lam, T.-W., Yiu, S.-M., Kristiansen,
K., and Wang, J. (2009). Soap2: an improved ul-
trafast tool for short read alignment. Bioinformatics,
25(15):1966–1967.
Melsted, P. and Pritchard, J. (2011). Efficient counting of
k-mers in dna sequences using a bloom filter. BMC
Bioinformatics, 12(1):1–7.
Ng, H. T., Goh, W. B., and Low, K. L. (1997). Feature se-
lection, perceptron learning, and a usability case study
for text categorization. SIGIR Forum, 31(SI):67–73.
R ¨atsch, G., Sonnenburg, S., and Sch ¨olkopf, B. (2005).
Rase: recognition of alternatively spliced exons in
c.elegans. Bioinformatics, 21(suppl 1):i369–i377.
Saeys, Y., Rouz `e, P., and Van De Peer, Y. (2007). In search
of the small ones: improved prediction of short exons
in vertebrates, plants, fungi and protists. Bioinformat-
ics, 23(4):414–420.
Salzberg, S. L., Delcher, A. L., Kasif, S., and White,
O. (1998). Microbial gene identification using in-
terpolated markov models. Nucleic Acids Research,
26(2):544–548.
Shah, M., Lee, H., Rogers, S., and Touchman, J. (2004). An
exhaustive genome assembly algorithm using k-mers
to indirectly perform n-squared comparisons in o(n).
In Proc. of IEEE CSB 2004, pages 740–741.
Wiener, E. D., Pedersen, J. O., and Weigend, A. S. (1995).
A neural network approach to topic spotting. In Proc.
of SDAIR-95, pages 317–332, Las Vegas, US.
Xia, J., Caragea, D., and Brown, S. (2008). Exploring al-
ternative splicing features using support vector ma-
chines. In Proc. of IEEE BIBM 2008, pages 231–238,
Washington, DC, USA. IEEE Computer Society.
Zavaljevski, N., Stevens, F. J., and Reifman, J. (2002). Sup-
port vector machines with selective kernel scaling for
protein classification and identification of key amino
acid positions. Bioinformatics, 18(5):689–696.
GeneratingFeaturesusingBurrowsWheelerTransformationfor
BiologicalSequenceClassification
203
