A Fuzzy Approach based on Dynamic Programming and Metaheuristics
for Selecting Safeguards for Risk Management for Information Systems
E. Vicente, A. Mateos and A. Jim
´
enez-Mart
´
ın
Decision Analysis and Statistics Group, Departamento de Inteligencia Artificial, Universidad Polit
´
ecnica de Madrid,
Campus de Montegancedo s/n, Boadilla del Monte, 28660 Madrid, Spain
Keywords:
Risk Analysis, Fuzzy Logic, Dynamic Programming, Simulated Annealing.
Abstract:
In this paper we focus on the selection of safeguards in a fuzzy risk analysis and management methodology
for information systems (IS). Assets are connected by dependency relationships, and a failure of one asset may
affect other assets. After computing impact and risk indicators associated with previously identified threats,
we identify and apply safeguards to reduce risks in the IS by minimizing the transmission probabilities of
failures throughout the asset network. However, as safeguards have associated costs, the aim is to select the
safeguards that minimize costs while keeping the risk within acceptable levels. To do this, we propose a
dynamic programming-based method that incorporates simulated annealing to tackle optimizations problems.
1 INTRODUCTION
There are several risk analysis and management
methodologies for information systems (IS) that con-
form to International Organization for Standardiza-
tion (ISO) standars, specifically the ISO 27000 fam-
ily of standars. Some examples of these method-
ologies are MAGERIT, by the Spanish Ministry of
Public Administrations (L
´
opez Crespo et al., 2006);
CRAMM (CCTA, 2003), by the Central Computing
and Telecommunications Agency (UK); or NIST SP
800-30 (Stoneburner and Gougen, 2002), by the Na-
tional Institute of Standard and Technology (USA).
These methodologies do not, however, consider
uncertain valuations, but use precise values on differ-
ent, usually percentage, scales. Boolean values are
sometimes even used to indicate whether or not assets
are dependent on each other regardless of the degree
of such dependency. In no case is vague or impre-
cise information about the input parameters allowed.
In our opinion, this is an important drawback of these
methodologies.
In (Vicente et al 2013a) we proposed an exten-
sion of the MAGERIT methodology based on clas-
sical fuzzy computational models. This methodology
includes the following milestones:
1. Identification and Valuation of Assets
An asset is anything that is of value to the or-
ganization and therefore requires protection. A
few data, information or business process assets
often account for the total value of an organiza-
tion’s assets. These assets are called terminal as-
sets. Other assets (support assets such as hard-
ware, software, personnel, facilities, ...) are valu-
able insofar as they are beneficial to the terminal
assets, and they inherit the terminal asset value,
according to the resulting benefit. Thus, support
assets have no intrinsic value; they take their value
from terminal assets.
The identified assets of the organization are then
valued. Some assets may have a monetary value
(how much money the organization would lose if
this asset stopped working), whereas others re-
quire a qualitative assessment (if an asset stops
working the losses would be very high, low,
medium...).
As mentioned above, the support assets inherit
their values from terminal assets depending on
how they influence each other. So, we have to de-
termine the dependency relationships of the termi-
nal assets with respect to support assets, and also
dependency relationships between support assets.
2. Threat Identification
A threat is an event that can trigger an incident
in the organization, causing damage or intangible
material loss to assets. Threats may be of natural
or human, accidental or deliberate origin. Some
threats can affect more than one asset. In such
35
Vicente E., Mateos A. and Jiménez-Martín A..
A Fuzzy Approach based on Dynamic Programming and Metaheuristics for Selecting Safeguards for Risk Management for Information Systems.
DOI: 10.5220/0004807800350045
In Proceedings of the 3rd International Conference on Operations Research and Enterprise Systems (ICORES-2014), pages 35-45
ISBN: 978-989-758-017-8
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

cases, threats can cause different impacts depend-
ing on what assets are affected. A detailed list of
threats is available in Annex C of ISO IEC 27005.
MAGERIT suggests two threat assessment mea-
sures: degradation, the damage that the threat can
cause to the asset, and frequency, how often the
threat materializes.
3. Identification and Valuation of impact and Risk
Indicators
It is then necessary to qualitatively identify the
consequences and establish impact and risk indi-
cators for the valued assets and threats. The im-
pact of a threat on an asset is the product of the
asset value multiplied by the respective degrada-
tion. Risk is the product of the impact of the threat
multiplied by the respective frequency.
4. Selection of Safeguards
Safeguards are measures for addressing threats.
They can be procedures, personnel policies, tech-
nical solutions or physical security measures at
the facilities. These safeguards can be preven-
tive, if they reduce the frequency of threats; or
palliative, if they reduce the degradation of assets
caused by threats (L
´
opez-Crespo et al., 2006).
As described below, experts use a linguistic term
scale (see Figure 1 and Table 1) to represent asset
values, their dependencies and the frequency and as-
set degradation associated with possible threats. Risk
analysis computations are then based on the trape-
zoidal fuzzy numbers associated with linguistic terms.
However, direct assignment based on a rigid lin-
guistic term scale is not always advisable since the
expert has no say in the number of linguistic terms
that the scale is to include and about the appearance of
their associate trapezoidal fuzzy numbers. In that case
we propose the use of the betting and lottery-based
method for fuzzy probability elicitation described in
(Vicente et al 2013c). Betting and lottery-based meth-
ods commonly used to assign probabilities can also
be used to assign fuzzy probabilities (Savage, 1954;
Finetti, 1964). In this section we briefly describe
these methods and show how a fuzzy number rep-
resenting the probability judgment can be extracted
from experts.
Betting Method. For two selected monetary values
x > y, the expert is given the option between either of
the two following gambles:
• b1: If event A happens, then you win x$. Other-
wise, you lose y$.
• b2: If event A does not happen, then you win y$.
Otherwise, you lose x$.
If the expert has no preference for either bet, the
respective expected utilities of both bets are equal,
and it follows that p(A) = x/(x + y). If the expert
chooses one of the two gambles, then the expected
utility of the selected gamble should be higher than
for the rejected gamble. Then, the analyst has to up-
date monetary values and offer the expert two new
gambles. Thus, an interactive process is enacted un-
til two alternative gambles are reached to which the
expert is indifferent.
Lottery-based methods. For a given probability
and monetary values x$ and y$, the expert is given
the choice between the following lotteries:
• l1: If event A happens, then you win x$. Other-
wise, you lose y$.
• l2: You win x$ with probability p, or y$ with
probability 1 − p.
If the expert has no preference for either of the lot-
teries, then the respective expected utilities are equal,
and it follows that p(A) = p. Otherwise, the expert
must readjust the value p, keeping the same mone-
tary values. This again generates an interactive pro-
cess, enacted until a couple of lotteries are reached to
which the expert is indifferent.
The betting and lottery-based methods assume
that the expert is able to provide a specific value for
the probability of an event. However, a more realis-
tic scenario is where experts have an imprecise and
vague idea of that value. Consequently, experts will
have an interval rather than a precise value in mind at
the point when they are indifferent to either bet or lot-
tery, that is, for the lottery-based method there will be
an interval [a,c] such that if p = [a,c], then the expert
has no preference for either lottery l1 or l2. Similarly,
the betting method can result in an interval of indif-
ference [b,d].
Current protocols for probability elicitation like
the above recommend the use of several methods to
test the consistency of the expert and the existence
of bias. In this regard, the development of betting
and lottery-based methods meets this recommenda-
tion and establishes the following:
• If [a,c]∩[b,d] = ∅, then the expert’s probabilistic
judgment was inconsistent.
• If any of the intervals is contained in the other
[a,c] ⊆ [b, d] (or [b, d] ⊆ [a, c]), then we as-
sume that the trapezoidal fuzzy number (b, a, c,d)
(or (a,b,d,c)) designates the expert probabilistic
judgment.
• If [a, c] ∩ [b,d] 6= ∅, is uncountable, and none of
the intervals is contained in the other, then, as-
suming that a ≤ b ≤ c ≤ d,(a,b,c,d) designates
the expert probabilistic judgment.
Thus, we consider the set of trapezoidal fuzzy
numbers with support in [0,1], TF[0,1], i.e.,
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
36

Table 1: Linguistic term scale.
Term Trapezoidal fuzzy number
Very Low (VL) (0, 0, 0, 0.05)
Low (L) (0, 0.075, 0.125, 0.275)
Medium-Low (ML) (0.125,0.275, 0.325, 0.475)
Medium (M) (0.325, 0.475, 0.525, 0.675)
Medium-High (MH) (0.525, 0.675, 0.725, 0.875)
High (H) (0.725, 0.875, 0.925, 1)
Very High (VH) (0.925, 1, 1, 1)
Figure 1: Linguistic term scale.
e
A = (a,b,c, d) with 0 ≤ a ≤ b ≤ c ≤ d ≤ 1
and with a trapezoidal function in the vertices
(a,0),(b,1),(c,1),(d,0) (Chen, 1996; Chen and
Chen, 2003; Chen and Chen, 2009; Vicente et al.,
2013b). Note that R is a subset of TF[0,1] if we
consider the injection (Vicente et al 2013a) φ : R →
T F [0, 1] ; a ≈ φ(a) = (a, a, a,a) =
e
a.
Consequently, the following operators proposed in
(Xu et al 2010) accounting for trapezoidal fuzzy num-
bers will be used to make computations:
Given
e
A
1
= (a
1
,b
1
,c
1
,d
1
),
e
A
2
= (a
2
,b
2
,c
2
,d
2
) ∈
T F[0,1], then:
•
e
A
1
⊕
e
A
2
= (a
1
+ a
2
− a
1
a
2
,b
1
+ b
2
− b
1
b
2
,c
1
+
c
2
− c
1
c
2
,d
1
+ d
2
− d
1
d
2
) and
•
e
A
1
⊗
e
A
2
= (a
1
a
2
,b
1
b
2
,c
1
c
2
,d
1
d
2
).
⊕ and ⊗ are two internal composition laws in
TF[0,1] that verify the commutative and associative
properties and both have a neutral element.
The assets of an IS are elements of value to the
organization and therefore require protection (servers,
files, personnel, facilities, hardware, software,...).
As cited before, these assets are interrelated
(L
´
opez Crespo et al, 2006), forming an acyclic graph,
where just a few data, information items or business
process assets often account for the total value of an
organization’s assets. These assets are called termi-
nal assets. Other assets (support assets, such as hard-
ware, software, personnel, facilities,...) are valuable
insofar as they are beneficial to the terminal assets.
In other words, the support assets inherit their values
from terminal assets depending on how they influence
each other, i.e., depending on the probability of that
any failure in an asset being transferred to the termi-
nal assets.
In general, we say asset A
j
directly depends on
asset A
i
, denoted by A
i
→ A
j
, if a failure in asset A
i
causes a failure in the asset A
j
with any given prob-
ability. This probability is usually referred to as the
degree of direct dependency of A
j
with respect to A
i
.
Note that in this fuzzy adaptation the degrees of di-
rect dependency between assets will be represented
by linguistic terms, which have associated trapezoidal
fuzzy numbers. We denote these degrees of direct de-
pendency by
^
d(A
i
,A
j
).
These dependencies form a directed acyclic graph
(to terminal assets), so that there may be intermediate
assets between any asset A
i
and a terminal asset A
k
which can propagate a fault generated in A
i
through to
the terminal A
k
. Our aim then is to compute the trans-
mission probability between A
i
and A
k
. This proba-
bility is called degree of indirect dependency between
A
i
and A
k
, which is denoted by
^
D(A
i
,A
k
) and can be
computed as follows (Vicente et al 2013a).
We denote by P={P
1
,...,P
s
} the set of paths in the
network connecting A
i
with A
k
. These paths are a se-
quence of arcs connecting a sequence of vertices, such
that the start vertex and the last vertex are A
i
and A
k
,
respectively. Then,
A) If all assets, excluding A
i
and A
k
, in the paths in P
are influenced by only one asset, then
^
D(A
i
,A
k
) =
s
⊕
j=1
^
D(A
i
,A
k
|P
j
) (1)
where
^
D(A
i
,A
k
|P
j
) =
^
d(A
i
,A
j
1
) ⊗
^
d(A
j
1
,A
j
2
) ⊗ ... ⊗
^
d(A
j
n
,A
k
) and
P
j
: (A
i
→ A
j
1
→ A
j
2
→ ... → A
j
n
→ A
k
).
B) Otherwise, we assume that the first r paths in P
are formed by assets (excluding A
i
and A
k
) influ-
enced by only one asset, and the remaining s − r
paths include at least one asset simultaneously in-
fluenced by two or more assets. Then, for the r
first paths, we proceed as in A), and we denote by
S the set including the s − r remaining paths. We
proceed with S as follows:
(i) Consider the set of non-terminal assets in S in-
fluenced by two or more assets, denoted by I,
and the subset of I including assets uninflu-
enced by any other asset in I, denoted by NI.
(ii) We consider an asset A
r
in NI. Then, we sim-
plify the paths in S that include asset A
r
making
A
i
→ A
r
→ ... → A
k
, with
^
d(A
i
,A
r
) =
^
D(A
i
,A
r
)
(computed as in A).
AFuzzyApproachbasedonDynamicProgrammingandMetaheuristicsforSelectingSafeguardsforRiskManagementfor
InformationSystems
37

(iii) Remove repeated paths from S and keep only
one instance.
(iv) Build I and NI again from S.
(v) If NI is not empty, go to (ii). Otherwise, the
algorithm finishes.
Let us denote the resulting set of paths by S=
{P
0
1
,...,P
0
m
} with m ≤ s − r. Then, the degree of
dependency of A
k
regarding A
i
is
^
D(A
i
,A
k
) =
r
⊕
j=1
^
D(A
i
,A
k
|P
j
)
m
⊕
l=1
^
D(A
i
,A
k
|P
0
l
). (2)
Once we have computed the degree of indirect
dependency between all assets regarding the termi-
nal assets, we can compute the accumulated values
for non-terminal assets
e
v
l
. These values usually have
three components (ISO/IEC serie 27000):
1. Availability. How much damage would it cause if
the asset is not available or cannot be used? This
is a typical services inspection.
2. Confidentiality. How much damage would it
cause if the asset is disclosed to someone it should
not be? This is a typical data inspection.
3. Integrity How much damage would it cause if the
asset is damaged or corrupt? This a typical data
inspection. Data can be manipulated, be wholly
or partially false, or even missing.
Therefore,
e
v
i
(l)
=
n
∑
k=1
((
^
D(A
i,
A
k
) ⊗
e
v
k
(l)
) (3)
where l denotes the lth component.
Once assets have been valueted, the next step in
the risk analysis methodology is to identify possible
threats and compute the corresponding impact and
risk indicators for the IS.
Threats are characterized by how often the threat
materializes (frequency)
e
f and by the degradation

D = (
e
d
1
,
e
d
2
,
e
d
3
) that the threat can cause to the three
asset components. Note again that the frequency and
degradation levels will be selected by the expert from
the linguistic term scale and, consequently, a trape-
zoidal fuzzy number will be associated with each of
them.
Then, the impact of a threat on an asset A
j
is
e
I
i
(l)
=
e
d
l
⊗
e
v
i
(l)
, (4)
and the risk to the asset is
e
R
i
(l)
=
e
I
i
(l)
⊗
e
f . (5)
The results of these operations will be fuzzy num-
bers belonging to TF[0,1], which, generally, do not
match up with the fuzzy numbers associated with the
linguistic terms of the scale. Thus, a similarity func-
tion must be used to identify the most similar trape-
zoidal fuzzy number in the linguistic term scale to the
fuzzy number output from computations.
Different similarity functions have been proposed
by several authors (Chen and Chen 2003, Chen and
Chen 2009, Gomathi and Sivaraman 2012, Xu et al
2010, Zhu and Xu 2012). In (Vicente et al 2013b) a
new similarity function was proposed on the basis of
the geometric distance between both fuzzy numbers,
the distance between their centroids and/or the ratio
between the common area and the joint area under the
membership functions.
Following the risk analysis and management
methodologies for IS, Section 2 deals with the selec-
tion of safeguards that can be enforced to reduce the
transmission probability of a failure throughout the
IS. The aim is to minimize costs while keeping the
risk at acceptable levels. To do this, we propose a
mixed technique based on dynamic programming and
metaheuristics, specifically, simulated annealing.
2 SELECTION OF PREVENTIVE
SAFEGUARDS
From equations (3), (4) and (5) and the algorithm for
computing degrees of indirect dependency, we can de-
rive the risk for the IS in each component l given a
threat with frequency
e
f and degradation
e
D =
n
e
d
l
o
3
l=1
in the support asset
e
A
i
as
e
R
i
(l)
=
n
∑
k=1
^
DD(A
i,
A
k
) ⊗
e
v
k
(l)
⊗
e
f ⊗
e
d
l
,
e
v
k
(l)
being the value (constant) assigned to the termi-
nal asset
e
A
k
in the component l.
Safeguards are measures for addressing threats.
They can be procedures, such as incident manage-
ment and documentation; personnel policies, such as
training and awareness of employees operating on
the IS; technical solutions, such as identification and
authentication mechanisms based on biometrics; or
physical security measures of the facilities, such as
temperature control systems.
These safeguards can be preventive, if they reduce
the frequency of threats; or palliative, if they reduce
the degradation caused by threats on assets (L
´
opez
Crespo 2006). As the degree of dependence between
two assets is the transmission probability of failures,
a special type of preventive safeguard is that which
reduces dependencies between support and terminal
assets.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
38

In this section we propose a method for reducing
the degrees of dependency from all support assets to
terminal assets minimizing the costs for the company.
As mentioned above, the probability of transmis-
sion of failure
^
D(A
i
,A
k
) is the result of fuzzy opera-
tions with the probabilities of transmission of failure
through intermediate assets linking the attacked sup-
port asset with other asset.
In each of these intermediate assets, safeguards
can be enforced to reduce the probability of transmis-
sion of a failure. The effect induced for a safeguard
in the probability of transmission of failures between
two assets A
u
and A
v
can also be defined as a lin-
guistic term, which is represented by a fuzzy number
e
e
u,v
∈ T F[0,1], so that if the degree of direct depen-
dency between the assets A
u
and A
v
is
^
d(A
u
,A
v
), then,
when we implement a safeguard with effect
e
e
u,v
, the
degree of direct dependency is reduced to
^
d(A
u
,A
v
) ⊗ (
e
1 
e
e
u,v
),
where  denotes the usual subtraction op-
eration between trapezoidal fuzzy num-
bers, i.e., (a
1
,a
2
,a
3
,a
4
)  (b
1
,b
2
,b
3
,b
4
) =
(a
1
− b
4
,a
2
− b
3
,a
3
− b
2
,a
4
− b
1
).
Note that  is not an internal composition law in
TF[0,1], however,
•
e
A,
e
B ∈ T F[0,1] ⇒
e
A ⊗ (
e
1 
e
B) ∈ T F[0,1],
•
e
A⊗(
e
1
e
B) ≤
e
A with the partial order of the trape-
zoidal fuzzy numbers (i.e.,
e
A ≤
e
B ⇔ a
1
≤ b
1
,a
2
≤
b
2
,a
3
≤ b
3
,a
4
≤ b
4
) and
•
e
A ⊗ (
e
1 
e
B) decreases with
e
B.
We consider the set of safeguards that hinder the
direct transmission of failure between A
u
and A
v
, S
u,v
.
Each safeguard S
u,v
p
∈ S
u,v
has a monetary cost c
u,v
p
and an effect
e
e
u,v
p
over
^
d(A
u
,A
v
), which is reduced to
^
d(A
u
,A
v
) ⊗ (
e
1 
e
e
u,v
p
).
The problem of keeping an acceptable level (low
or very low) for the failure transmission probabilities
among support and terminal assets with minimal costs
can be represented as follows:
min
∑
u,v
∑
p
c
u,v
p
x
u,v
p
s.t.
^
D(A
i
,A
k
) ≤
e
U
ik
∀i,k
x
u,v
p
∈
{
0,1
}
∀u,v, p
,
where i and k in the first set of constraints refer to
non-terminal and terminal assets, respectively,
e
U
ik
is a
residual value accepted by the experts, x
u,v
p
are the de-
cision variables (x
u,v
p
= 1 means that safeguard S
u,v
p
is
selected), and
^
D(A
i
,A
k
) is reassessed replacing values
^
d(A
u
,A
v
) by the affected values regarding the selected
safeguards:
^
d(A
u
,A
v
) ⊗

⊗
p
(
e
1 
e
e
u,v
p
)

,
where A
u
and A
v
are two consecutive assets connected
by an arc in some path between A
i
and A
k
.
Note that the fact that the usual order in T F[0,1] is
a partial order constitutes a very restrictive constraint
in our optimization problem, so we will use the con-
cept of similarity function to relax this constraint.
If we define a threshold α ∈ [0, 1] and a similar-
ity function S, the constraint
^
D(A
i
,A
k
) ≤
e
U
ik
∀i,k can
be replaced by S(
^
D(A
i
,A
k
),
e
U
ik
) ≥ α. Thus, the re-
strictiveness of the constraint increases proportionally
to the threshold value and the feasible solution set
will be composed of solutions that verify these soft-
ened/relaxed constraints.
Remember that indirect dependencies are recur-
sively computed following the algorithm described in
Section 1. Thus, the degree of dependency of the
support assets further away from the terminals can
be computed from the degree of dependency of the
closest assets. Therefore, the problem can be solved
in stages, and the principle of optimality in dynamic
programming is verified: Given an optimal sequence
of decisions, every subsequence is, in turn, optimal.
Then we proceed as follows:
• Let L
0
be the set of terminal assets.
• Consider L
1
including support assets whose chil-
dren belong to L
0
only (L
1
is not empty because
the graph is acyclic). Identify safeguards that min-
imize costs keeping the degrees of dependency
over their children at an acceptable level.
• Consider L
2
including support assets whose chil-
dren belong to L
0
∪ L
1
only. Identify safeguards
that minimize costs keeping the degrees of depen-
dency over L
0
under an acceptable level. Note that
the degrees of indirect dependency from the chil-
dren of L
2
to terminal assets have already been
computed in the previous stage, so we just need
to identify the direct degree of dependency over
assets in L
0
∪ L
1
.
• ...
• Consider L
i
including support assets whose chil-
dren belong to L
0
∪ L
1
∪ ... ∪ L
i−1
only. Iden-
tify safeguards that minimize costs keeping the
degrees of dependency over L
0
under an accept-
able level. Note that again we just need to iden-
tify the direct degree of dependency on assets of
L
0
∪ L
1
∪ ... ∪ L
i−1
.
• ...
AFuzzyApproachbasedonDynamicProgrammingandMetaheuristicsforSelectingSafeguardsforRiskManagementfor
InformationSystems
39

Simulated annealing (Kirkpartick et al 1983, Cerny
1985) is applied in each step of the algorithm to de-
rive the optimal selection of safeguards. It is a trajec-
torial metaheuristic which is named for and inspired
by annealing in metallurgy.
An initial feasible solution is randomly generated.
In each iteration a new solution y is randomly gen-
erated from the neighborhood of the current solution,
y ∈ N(x
i
). If the new solution is better than the cur-
rent one, then the algorithm moves to that solution
(x
i+1
= y), otherwise the movement to the worst solu-
tion is performed with certain probability.
Note that accepting worse solutions allows for a
more extensive search for the optimal solution and
avoids trapping in local optima in early iterations.
The probability of accepting a worse movement
is a function of both the temperature factor and the
change in the cost function.
The initial value of temperature (T ) is high, which
leads to a diversified search, since practically all
movements are allowed. As the temperature de-
creases, the probability of accepting a worse move-
ment falls. If the temperature is zero, then only better
movements will be accepted, which makes simulated
annealing work like hill climbing.
The pseudocode of simulated annealing for a min-
imization problem is as follows:
• Generate an initial feasible solution x
0
. Do x
∗
=
x
0
, f
∗
= f (x
0
), i = 0.
Select the initial temperature t
0
= T (t
i
tempera-
ture in the step i)
• Repeat until stopping criterion is satisfied:
– Randomly generate y ∈ N(x
i
)
∗ If f (y) − f (x
i
) ≤ 0, then
· x
i+1
= y
· If f (x
∗
) > f (y), then x
∗
= y, f
∗
= f (y)
∗ Else
· p ∼ U (0,1)
· If p ≤ e
−( f (y)− f (x
i
))/t
i
, then x
i+1
= y
· Else x
i+1
= x
i
– i = i + 1
– Update temperature
3 AN ILLUSTRATIVE EXAMPLE
Let us consider the IS shown in Figure 2 with the di-
rect degrees of dependency assessed by the experts
considering the linguistic terms of Table 1, which has
only one terminal asset, A
6
.
Figure 2: Direct dependencies in the IS.
The set of paths in the analysis of the influence of
A
1
over A
6
is P = {
• P
1
: (A
1
→ A
2
→ A
6
),
• P
2
: (A
1
→ A
2
→ A
3
→ A
6
),
• P
3
: (A
1
→ A
2
→ A
3
→ A
4
→ A
6
),
• P
4
: (A
1
→ A
3
→ A
6
),
• P
5
: (A
1
→ A
3
→ A
4
→ A
6
),
• P
6
: (A
1
→ A
4
→ A
6
),
• P
7
: (A
1
→ A
5
→ A
6
)}.
Asset A
3
is influenced by A
1
and A
2
, and A
4
is
influenced by A
1
and A
3
. Therefore, we proceed as in
B) of the algorithm described in Section 2, with r = 2
and S= {P
2
,P
3
,P
4
,P
5
,P
6
}, as follows:
(i) I = {A
3
,A
4
} and NI = {A
3
}.
(ii) Select A
3
, then simplify paths P
2
, P
3
, P
4
and P
5
to
– P
0
2
: (A
1
→ A
3
→ A
6
),
– P
0
3
: (A
1
→ A
3
→ A
4
→ A
6
),
– P
0
4
: (A
1
→ A
3
→ A
6
) and
– P
0
5
: (A
1
→ A
3
→ A
4
→ A
6
),
respectively, with
^
d(A
1
,A
3
) =
^
D(A
1
,A
3
) =

^
d(A
1
,A
2
)⊗
^
d(A
2
,A
3
)

⊕
^
d(A
1
,A
3
).
(iii) S=

P
0
2
,P
0
3
,P
6

since P
0
2
= P
0
4
and P
0
3
= P
0
5
.
(iv) I = {A
4
} and NI = {A
4
}.
(v) Go to (ii).
(ii) Select A
4
, then simplify paths P
0
3
and P
6
to
– P
00
3
: (A
1
→ A
4
→ A
6
), and
– P
0
6
: (A
1
→ A
4
→ A
6
),
respectively, with
^
d(A
1
,A
4
) =
^
D(A
1
,A
4
) =

^
d(A
1
,A
3
)⊗
^
d(A
3
,A
4
)

⊕
^
d(A
1
,A
4
).
(iii) S=

P
0
2
,P
00
3

since P
00
3
≡ P
0
6
.
(iv) I = ∅ y NI = ∅.
(v) The algorithm finishes since NI = ∅.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
40

Finally, S=

P
0
2
,P
00
3

and the degree of dependency
of A
6
regarding A
1
is
^
D(A
1
,A
6
) =
^
D(A
1
,A
6
|P
1
) ⊕
^
D(A
1
,A
6
|P
7
) ⊕
^
D(A
1
,A
6
|P
0
2
) ⊕
^
D(A
1
,A
6
|P
00
3
) =
(
^
d(A
1
,A
2
) ⊗
^
d(A
2
,A
6
)) ⊕ (
^
d(A
1
,A
5
) ⊗
^
d(A
5
,A
6
)) ⊕
(
^
d(A
1
,A
3
) ⊗
^
d(A
3
,A
6
)) ⊕ (
^
d(A
1
,A
4
) ⊗
^
d(A
4
,A
6
))
The degree of dependency of A
6
regarding A
1
is
D(A
1
,A
6
) = (0.980,0.999,0.999,1) if we consider
the linguistic terms of Table 1 show in Figure 3.
Let us consider a threat on asset A
1
with frequency
e
f = M and degradation
e
d = (H,H, H), then the risk
to asset A
1
is
e
R
1
(l)
= (0.23,0.415,0.485,0.675), l =
1,2,3.
We consider the asset network and the fuzzy direct
dependencies shown in Figure 2 corresponding to an
IS. Besides, the set of available safeguards of failure
transmission between support assets are shown in Ta-
bles 2-5.
We also consider the fuzzy threshold
e
U =
(0,0,0.1,0.2) below which the degree of dependency
between all assets and terminal assets will be accept-
able, and let α = 0.95. In other words, the similar-
ity of the degree of dependency after applying the se-
lected safeguards for the given
e
U must be at least 0.95.
The set of solutions in each stage is represented
by binary matrices, in which each row represents the
safeguards of S
uv
p
, which prevents the failure transmis-
sion from asset u to v considered in that stage.
We use the similarity function proposed by (Chen
1996): Given two trapezoidal fuzzy numbers
e
A =
(a
1
,a
2
,a
3
,a
4
) and
e
B = (b
1
,b
2
,b
3
,b
4
),
S(
e
A,
e
B) = 1 −
4
∑
i=1
| a
i
− b
i
|
4
.
Although other similarity functions have been pro-
posed in the literature (Chen and Chen 2003, 2009,
Sridevi and Nadarajan 2009, Xu et al 2010, Hejazi et
al 2011, Gomathi and Sivaraman 2012, Zhu and Xu
2012, Vicente et al 2013b), we have decided to use
the geometric distance between both fuzzy numbers
due to its low computational cost.
Dynamic programming is then executed as fol-
lows:
First, note that L
0
= {A
6
}, since the only terminal
asset in the IS in Figure 2 is A
6
.
• Stage 1: L
1
= {A
4
,A
5
}. We adjust the degrees of
dependency
^
D(A
4
,A
6
) =
^
d(A
4
,A
6
) ⊗

10
⊗
p
(
e
1 
e
e
4,6
p
x
4,6
p
)

=
V H ⊗

10
⊗
p
(
e
1 
e
e
4,6
p
x
4,6
p
)

and
^
D(A
5
,A
6
) =
^
d(A
5
,A
6
) ⊗

15
⊗
p
(
e
1 
e
e
5,6
p
x
5,6
p
)

=
Table 2: Safeguards for A
1
.
Tag Effect Cost Tag Effect Cost
S
1,2
1
L 100 S
1,3
1
MH 356
S
1,2
2
M 300 S
1,3
2
H 324
S
1,2
3
MH 550 S
1,3
3
L 110
S
1,2
4
M 430 S
1,3
4
ML 345
S
1,2
5
ML 125 S
1,3
5
VL 87
S
1,2
6
L 240 S
1,3
6
MH 345
S
1,2
7
VL 100 S
1,3
7
M 200
S
1,2
8
MH 324
S
1,2
9
VH 570
S
1,4
1
M 209 S
1,5
1
M 230
S
1,4
2
M 267 S
1,5
2
M 345
S
1,4
3
MH 342 S
1,5
3
L 187
S
1,4
4
VH 789 S
1,5
4
M 321
S
1,4
5
M 234 S
1,5
5
MH 345
S
1,4
6
M 356 S
1,5
6
H 543
S
1,4
7
M 276 S
1,5
7
MH 356
S
1,4
8
M 200 S
1,5
8
M 206
S
1,4
9
H 467 S
1,5
9
M 342
S
1,4
10
H 342
S
1,4
11
L 127
S
1,4
12
M 207
Table 3: Safeguards for A
2
.
Tag Effect Cost Tag Effect Cost
S
2,3
1
M 356 S
2,6
1
M 348
S
2,3
2
L 87 S
2,6
2
L 187
S
2,3
3
ML 267 S
2,6
3
ML 254
S
2,3
4
M 320 S
2,6
4
ML 367
SS
2,3
5
ML 156 S
2,6
5
ML 567
S
2,3
6
M 320 S
2,6
6
M 390
S
2,3
7
M 256 S
2,6
7
ML 256
S
2,3
8
M 300 S
2,6
8
M 307
S
2,3
9
L 200 S
2,6
9
L 235
S
2,6
10
ML 124
S
2,6
11
M 400
S
2,6
12
L 278
S
2,6
13
ML 260
H ⊗

15
⊗
p
(
e
1 
e
e
5,6
p
x
5,6
p
)

,
such that S

^
D(A
4
,A
6
),
e
U

≥ 0.95 and S

^
D(A
5
,A
6
),
e
U

≥
0.95,
e
e
4,6
p
being the effect induced for the safeguard
S
4,6
p
, p = 1, ...,10,
e
e
5,6
p
the effect induced for the
safeguard S
5,6
p
, p = 1,...,15, x
4,6
p
= 1 or x
4,6
p
= 0 if
the safeguard S
4,6
p
, p = 1,...,10, is selected or not,
AFuzzyApproachbasedonDynamicProgrammingandMetaheuristicsforSelectingSafeguardsforRiskManagementfor
InformationSystems
41

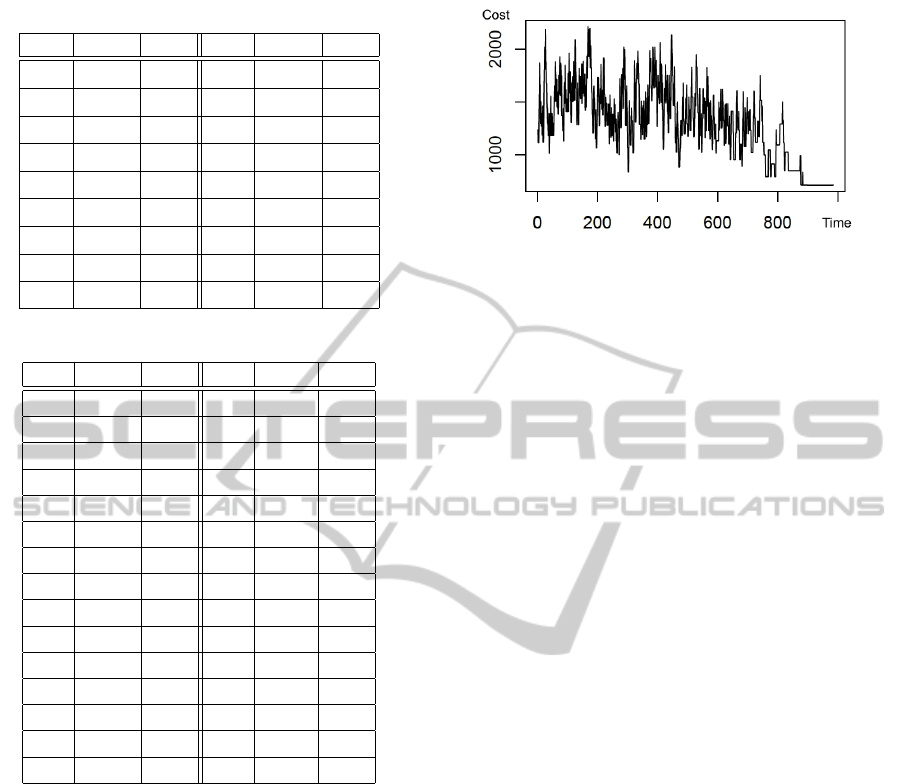
Table 4: Safeguards for A
3
.
Tag Effect Cost Tag Effect Cost
S
3,4
1
M 345 S
3,6
1
M 267
S
3,4
2
H 650 S
3,6
2
M 356
S
3,4
3
M 200 S
3,6
3
M 378
S
3,4
4
M 367 S
3,6
4
M 324
S
3,4
5
M 388 S
3,6
5
M 345
S
3,4
6
H 453 S
3,6
6
M 231
S
3,4
7
L 189 S
3,6
7
MH 453
S
3,4
8
L 256
S
3,4
9
M 345
Table 5: Safeguards for A
4
and A
5
.
Tag Effect Cost Tag effect Cost
S
4,6
1
M 260 S
5,6
1
M 200
S
4,6
2
M 245 S
5,6
2
M 210
S
4,6
3
ML 170 S
5,6
3
L 120
S
4,6
4
M 256 S
5,6
4
ML 234
S
4,6
5
M 367 S
5,6
5
M 267
S
4,6
6
M 289 S
5,6
6
MH 367
S
4,6
7
M 278 S
5,6
7
MH 366
S
4,6
8
M 345 S
5,6
8
M 254
S
4,6
9
M 240 S
5,6
9
ML 145
S
4,6
10
MH 435 S
5,6
10
L 206
S
5,6
11
M 306
S
5,6
12
M 345
S
5,6
13
M 280
S
5,6
14
L 178
S
5,6
15
MH 377
respectively, and x
5,6
p
= 1 or x
5,6
p
= 0 depending
on whether or not the safeguard S
5,6
p
, p = 1,...,15,
minimizing the cost.
As L
1
contains two elements, two optimization
problems must be solved in this stage, associated
with A
4
and A
5
, respectively.
Regarding asset A
4
, solutions are represented by
the vector x
4,6
= (x
4,6
1
,x
4,6
2
,...,x
4,6
10
), see Table 5,
where x
4,6
p
= 1 if the safeguard S
4,6
p
is selected.
The respective optimization problem to be solved
using simulated annealing is:
min c
4,6
1
x
4,6
1
+ ... + c
4,6
10
x
4,6
10
s.t.
S

^
D(A
4
,A
6
),
e
U

≥ 0.95
x
4,6
p
∈
{
0,1
}
, p = 1, ..., 10
. (6)
The optimal solution and the associated costs are
Figure 3: Objective function evolution in the optimum set-
ting of
^
D(A
5
,A
6
).
shown in the second row of Table 6, correspond-
ing to vector x
4,6
∗
= (0,1,1,1,0,0, 0, 0, 1,0).
Regarding asset A
5
, solutions are now represented
by the vector x
5,6
= (x
5,6
1
,x
5,6
2
,...,x
5,6
15
), see Table
5. The optimization problem to be solved is:
min c
5,6
1
x
5,6
1
+ ... + c
5,6
15
x
5,6
15
s.t.
S

^
D(A
5
,A
6
),
e
U

≥ 0.95
x
5,6
p
∈
{
0,1
}
, p = 1, ..., 15
. (7)
The evolution of the objective function over time
for the best solution found is shown in Figure 3.
The optimal solution and the associated costs are
shown in the first row of Table 6, corresponding to
vector x
5,6
∗
= (1,0,0,0,0,0, 1, 0, 1,0,0,0,0,0,0).
The new degrees of dependency after the applica-
tion of the selected safeguards and the respective
similarity to the fixed threshold,
e
U, are shown in
the first two rows of Table 7.
The purpose of this paper is to describe how a
mixture of dynamic programming techniques and
metaheuristics can efficiently solve the problem
and not to detail or compare the applied meta-
heuristic (simulated annealing) with others. How-
ever, we do think it is worthwhile to describe some
parameters used in the implementation and to re-
port a sensitivity analysis analyzing the effects
caused by the changes to these parameters.
– We randomly generate a sequence with binary
values and check if the similarity constraint is
verified to derive the initial solution. The length
of the binary sequence depends on the problem
(15 when dealing with x
5,6
, 10 when dealing
with x
4,6
...).
– The neighborhood of a solution is composed of
any solutions that can be derived by changing
the value of one of the binary elements of the
solution, selected at random. If the resulting
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
42

solution is not feasible (does not verify the sim-
ilarity constraint), then it is discarded and an-
other solution is generated in the neighborhood
until a feasible solution is found.
– The initial temperature assures acceptance
probabilities of worse solutions close to 0.9 in
the initial iterations of the algorithm. The ini-
tial temperature is computed to obtain a high
probability of acceptance (≥ 0.9) of any neigh-
bor of the initial solution, i.e., given the initial
solution x
0
, the minimum value T is computed
such that
e
−( f (y)− f (x
0
))/T
≥ 0.9, ∀y ∈ N(x
0
) and feasible,
with:
f (y) − f (x
0
) > 0.
In other words,
T = max
y∈N(x
0
)
f easible

−( f (y) − f (x
0
))
ln(0.9)

because if we have T ≥
−( f (y)− f (x
0
))
ln(0.9)
∀y ∈
N(x
0
) and feasible, with f (y) − f (x
0
) > 0,
then ln(0.9) ≤
−( f (y)− f (x
0
))
T
∀y ∈
N(x
0
) and feasible, with f (y) − f (x
0
) >
0, and since e
x
is an increasing
function, 0.9 ≤ e
−
(
f (y)−f (x
0
)
)
T
∀y ∈
N(x
0
) and feasible, with f (y) − f (x
0
) > 0.
The pseudocode, starting from x
0
=
(x
0
[1],...,x
0
[n]), as follows:
∗ y = x
0
, T = 0, i = 1.
∗ While i ≤ n. Do y[i] = 1 − y[i].
· If y is a feasible solution then, if
−( f (y)− f (x
0
))
ln(0.9)
> T , we have
T =
−( f (y) − f (x
0
))
ln(0.9)
.
· y = x
0
, i = i + 1.
The solution x
0
has at most n feasible neigh-
boring solutions. We have evaluated all neigh-
boring solutions that are worse than the initial
solution in those n steps.
In the unfortunate event that the initial solu-
tion is the worst of its neighborhood, the initial
value of the resulting T is null. Therefore we
must start from another initial solution. This
does not degrade the algorithm, because it can
return to the neighborhood of the discarded so-
lution at any time.
Thus the initial temperature that leads to the op-
timal solution over A
5
(for optimization prob-
lem (7)) is 3578.191.
Table 6: Optimal solutions and costs for each asset.
Asset Solution Cost
A
5
S
5,6
1
, S
5,6
7
, S
5,6
9
711
A
4
S
4,6
2
, S
4,6
3
, S
4,6
4
,S
4,6
9
911
A
3
S
3,6
1
, S
3,6
4
, S
3,6
6
, S
3,6
7
1275
A
2
S
2,3
7
, S
2,6
1
, S
2,6
5
, S
2,6
7
,S
3,6
10
1551
A
1
S
1,2
1
, S
1,3
2
, S
1,4
10
1236
Total cost 5684
The temperature is maintained constant for L =
20 iterations and then it decreases after multi-
plying by 0.95, so that, after h∗L iterations, the
temperature is t
h∗L
= 0.95
h
t
0
.
– The algorithm stops if f has not improved in
the last 100 iterations.
Table 7 shows the best solutions reached after run-
ning the algorithm with different values for α to
minimize
^
D(A
5
,A
6
). Note that if the constraint is
more restrictive, allowing only minor differences
with the threshold
e
U, the set of safeguards for im-
plementation will be larger. The same effect oc-
curs when we use a more accurate (with a smaller
support) threshold
e
U. Therefore, experts must
choose lower or higher levels of acceptable ac-
curacy regarding the dependency between assets,
i.e., the accepted risk considering this fact.
• Stage 2: L
2
= {A
3
}. The degrees of dependency
^
d(A
3,
A
6
) and
^
d(A
3,
A
4
) are adjusted by minimiz-
ing costs and incorporating the soft constraint
S

^
D(A
3
,A
6
),
e
U

≥ 0.95, where
^
D(A
3
,A
6
) =

^
d(A
3
,A
6
) ⊗

7
⊗
p=1
(
e
1 
e
e
3,6
p
x
3,6
p
)

⊕

^
d(A
3,
A
4
) ⊗

9
⊗
p=1
(
e
1 
e
e
3,4
p
x
3,4
p
)

⊗
^
D(A
4
,A
6
)

.
Note that
^
D(A
4
,A
6
) was computed
in Stage 1,
^
D(A
4
,A
6
) = V H ⊗
h
(
e
1 
e
e
4,6
2
) ⊗ (
e
1 
e
e
4,6
3
) ⊗ (
e
1 
e
e
4,6
4
) ⊗ (
e
1 
e
e
4,6
9
)
i
=
(0.016,0.072,0.104,0.269). The optimization
problem to be solved in this stage is
min c
3,6
1
x
3,6
1
+ ... + c
3,6
7
x
3,6
7
+
c
3,4
1
x
3,4
1
+ ... + c
3,4
9
x
3,4
9
s.t.
S

^
D(A
3
,A
6
),
e
U

≥ 0.95
x
3,6
p
∈
{
0,1
}
, p = 1, ..., 7
x
3,4
q
∈
{
0,1
}
,q = 1,...,9
.
The optimal solution and the associated cost is
AFuzzyApproachbasedonDynamicProgrammingandMetaheuristicsforSelectingSafeguardsforRiskManagementfor
InformationSystems
43

Table 7:
^
D(A
5
,A
6
) and associated costs for different α levels.
α
^
D(A
5
,A
6
) Similarity Cost
0.8 (0.05,0.23,0.27,0.46) 0.81 554
0.9 (0.02,0.09,0.12,0.30) 0.93 653
0.95 (0.01,0.07,0.11,0.28) 0.95 711
0.98 (0.00,0.03,0.06, 0.20) 0.98 1021
shown in the third row of Table 6, correspond-
ing to vectors x
3,6
∗
= (1,0,0,1,0, 1, 1) and x
3,4
∗
=
(0,0,0,0,0,0, 0, 0, 0). The new degree of depen-
dency after the application of the selected safe-
guards and the corresponding similarity to the
fixed threshold,
e
U, are shown in the third row of
Table 7.
• Stage 3: L
3
= {A
2
}. The degrees of depen-
dency
^
d(A
2
,A
3
) and
^
d(A
2
,A
6
) are adjusted mini-
mizing costs and incorporating the soft constraint
S

^
D(A
2
,A
6
),
e
U

≥ 0.95, where
^
D(A
2
,A
6
) =

^
d(A
2
,A
6
) ⊗

13
⊗
p=1
(
e
1 
e
e
2,6
p
x
2,6
p
)

⊕

^
d(A
2,
A
3
) ⊗

7
⊗
p=1
(
e
1 
e
e
2,3
p
x
2,3
p
)

⊗
^
D(A
3
,A
6
)

.
Note that
^
D(A
3
,A
6
) was computed in Stage
2,
^
D(A
3
,A
6
) = [
^
d(A
3
,A
6
) ⊗ (
e
1 
e
e
3,6
1
) ⊗ (
e
1 
e
e
3,6
4
) ⊗ (
e
1 
e
e
3,6
6
) ⊗ (
e
1 
e
e
3,6
7
)] ⊕ [
^
d(A
3,
A
4
)) ⊗
^
D(A
4
,A
6
)] = (0.008,0.059,0.096,0.301).
The optimal solution and the associated cost are
shown in the fourth row of Table 6, correspond-
ing to vectors x
2,3
∗
= (0,0,0,0,0, 0, 1, 0,0) and
x
2,6
∗
= (1, 0, 0,0,1,0,1,0,0, 1, 0, 0,0). The new
degree of dependency and similarity to
e
U, are
shown in the fourth row of Table 8.
• Finally, L
4
= {A
1
}. The degrees of dependency
^
d(A
1
,A
2
),
^
d(A
1
,A
3
),
^
d(A
1
,A
4
) and
^
d(A
1
,A
5
) are
adjusted minimizing the cost and considering the
soft constraint S

^
D(A
1
,A
6
),
e
U

≥ 0.95, where
^
D(A
1
,A
6
) =

^
d(A
1
,A
2
) ⊗

9
⊗
p=1
(
e
1 
e
e
1,2
p
x
1,2
p
)

⊗
^
D(A
2
,A
6
)

⊕

^
d(A
1,
A
3
) ⊗

7
⊗
p=1
(
e
1 
e
e
1,3
p
x
1,3
p
)

⊗
^
D(A
3
,A
6
)

⊕

^
d(A
1
,A
4
) ⊗

12
⊗
p=1
(
e
1 
e
e
1,4
p
x
1,4
p
)

⊗
^
D(A
4
,A
6
)

⊕

^
d(A
1
,A
5
) ⊗

9
⊗
p=1
(
e
1 
e
e
1,5
p
x
1,5
p
)

⊗
^
D(A
5
,A
6
)

.
Note that
^
D(A
2
,A
6
),
^
D(A
3
,A
6
),
^
D(A
4
,A
6
) and
Table 8: New degrees of dependency after applying safe-
guards.
Asset
^
D(A
j
,A
6
) Similarity
e
U
A
5
(0.015,0.077,0.114,0.280) 0.953
A
4
(0.016,0.072,0.104,0.269) 0.959
A
3
(0.008,0.059,0.096,0.301) 0.956
A
2
(0.008,0.057,0.094,0.316) 0.953
A
1
(0.005,0.045,0.082,0.327) 0.951
Figure 4: Risk in each component of A
1
before and after
implementation of optimal safeguards
^
D(A
5
,A
6
) were computed in previous stages,
^
D(A
2
,A
6
) = [
^
d(A
2
,A
6
) ⊗ ((
e
1 
e
e
2,6
1
) ⊗
(
e
1 
e
e
2,6
5
) ⊗ (
e
1 
e
e
2,6
7
) ⊗ (
e
1 
e
e
2,6
10
))] ⊕
[
^
d(A
2,
A
3
) ⊗

(
e
1 
e
e
2,3
7
)

⊗
^
D(A
3
,A
6
)] =
(0.008,0.057,0.094,0.316),
^
D(A
3
,A
6
) = (0.008,0.059,0.096,0.301),
^
D(A
4
,A
6
) = (0.016,0.072,0.104,0.269) and
^
D(A
5
,A
6
) = (0.01,0.07,0.11,0.28).
The optimal solution in this stage is shown in the
last row of Tables 6 and 7.
After implementing the best safeguards, the
risk caused by the previously considered
threat over asset A
1
in each component is
e
R
1
(l)
= (0.001,0.018,0.039,0.22), l = 1,2,3.
The risks associated with this threat before and af-
ter implementation of safeguards are illustrated along
with the risk threshold in Figure 4.
4 CONCLUSIONS
We propose a model for selecting safeguards to re-
duce risks in information systems based on the reduc-
tion of the degree of dependency between support as-
sets and terminal assets. As safeguards have associ-
ated costs, our aim is to select safeguards that mini-
mize costs while keeping the risk with acceptable lev-
els.
ICORES2014-InternationalConferenceonOperationsResearchandEnterpriseSystems
44

Although a metaheuristic could be used to solve
this optimization problem, dynamic programming
combined with simulated annealing was used because
of the special structure of the constraint set. This leads
to a more computationally efficient solution to the
safeguard selection problem. Also the fuzzy environ-
ment allows experts to provide imprecise and vague
failure propagation probabilities.
Another way to reduce system risk is to act on the
probability of threats to each asset materializing or re-
ducing the degradation of assets caused by threat ma-
terialization. This is a multiobjective problem (degra-
dation has three components), which will be consid-
ered in future research.
ACKNOWLEDGEMENTS
The paper was supported by Madrid Regional Gov-
ernment project S-2009/ESP-1685 and Spanish Min-
istry of Science and Innovation project MYTM2011-
28983-C03-03.
REFERENCES
Cerny, V. (1985). Thermodynamical Approach to the Trav-
eling Salesman Problem: An Efficient Simulation Al-
gorithm, Journal of Optimization Theory and Appli-
cations, 45, 41-51.
Chen, S.-M. (1996). New Methods for Subjective Mental
Workload Assessment and Fuzzy Risk Analysis, Cy-
bernetics Systems, 27, 449-472.
Chen, S.-J. and Chen, S.-M. (2003). Fuzzy Risk Analysis
Based on Similarity Measures of Generalized Fuzzy
Numbers. IEEE Transactions on Fuzzy Systems, 11,
45-56.
Chen, S.-J. and Chen, S.-M. (2009). Fuzzy Risk Analy-
sis Based on the Ranking of Generalized Trapezoidal
Fuzzy Numbers. Applied Intelligence, 26, 1-11.
CCTA Risk Analysis and Management Method (CRAMM),
Version 5.0. London: Central Computing and
Telecommunications Agency (CCTA), 2003.
Finetti, B. (1964). Foresight: its Logical Laws, its Sub-
jective Sources. In: H.E. Kyburg and H.E. Smokler
(eds.), Studies in Subjective Probability. New York:
Wiley.
Gomathi, V.L. and Sivaraman, G. (2012). A Novel Simi-
larity Measure between Generalized Fuzzy Numbers.
International Journal of Computer Theory and Engi-
neering, 4, 448-450.
ISO/IEC Serie 27000 International Organization for Stan-
dardization.
Hejazi, S. R., Doostparast, A. and Hosseini, S.M. (2011).
An Improved Fuzzy Risk Analysis based on a New
Similarity Measures of Generalized Fuzzy Numbers.
Expert Systems with Applications, 38, 9179-9185.
Kirkpatrick, S., Gelatt., C.D. and Vecchi, M. P. (1983).
Optimization by Simulated Annealing. Science, 220
(4598), 671-680.
L
´
opez Crespo, F., Amutio-G
´
omez, M.A., Candau, J. and
Ma
˜
nas, J.A. (2006). Methodology for Information Sys-
tems Risk. Analysis and Management (MAGERIT ver-
sion 2). Book I, Book II and Book III. Madrid: Minis-
terio de Administraciones P
´
ublicas.
Savage, L. J. (1954). The Foundations of Statistics. New
York: Wiley.
Sridevi, B. and Nadarajan, R. (2009). Fuzzy Similarity
Measure for Generalized Fuzzy Numbers. Interna-
tional Journal of Open Problems in Computer Science
and Mathematics, 2, 111-116.
Stoneburner, G. and Gougen, A. (2002). NIST 800-30 Risk
Management. Guide for Information Technology Sys-
tems. Gaithersburg: National Institute of Standard and
Technology.
Vicente, E., Jim
´
enez, A. and Mateos, A. (2013a). A Fuzzy
Approach to Risk Analysis in Information Systems.
Proceedings of the 2nd International Conference on
Operations Research and Enterprise Systems, 130-
133.
Vicente, E., Mateos, A. and Jim
´
enez, A. (2013b). A
New Similarity Function for Generalized Trapezoidal
Fuzzy Numbers. Lecture Notes on Computer Science,
7894, 400-411.
Vicente, E., Jim
´
enez, A. and A. Mateos, A. (2013c). An in-
teractive method of fuzzy probability elicitation in risk
analysis, Intelligent Systems and Decision Making for
Risk Analysis and Crisis Response, New York: CRC
Press, 223-228.
Xu, Z., Shang, S., Qian, W. and Shu, W. (2010). A Method
for Fuzzy Risk Analysis based on the New Similarity
of Trapezoidal Fuzzy Numbers. Expert Systems with
Applications, 37, 1920-1927.
Zu, L. and R. Xu (2012). Fuzzy risk analysis based
on similarity measure of generalized fuzzy num-
bers. Fuzzy Engineering and Operations Research.
Berlin/Heidleberg: Springer, 569-587.
AFuzzyApproachbasedonDynamicProgrammingandMetaheuristicsforSelectingSafeguardsforRiskManagementfor
InformationSystems
45