Feature Extraction in Pet Images for the Diagnosis of Alzheimer’s Disease

ao Duarte, Helena Aidos and Ana Fred

Instituto de Telecomunicac¸

oes, Instituto Superior T

ecnico, Lisbon, Portugal

Keywords:

Computer-Aided Diagnosis, Image Classiﬁcation, Image segmentation, Alzheimer’s Disease.

Abstract:

Alzheimer’s disease accounts for an estimated 60% to 80% of cases of dementia and its victims are mainly

elderly people. Recently, several computer-aided diagnosis systems have been developed, based on extracting

information from FDG-PET scans. 3-dimensional FDG-PET images, under a voxel-as-feature approach, lead

to high-dimensional feature spaces, which results in system performance problems. In order to reduce the

dimensionality of these images, multi-scale methods may be used as feature extraction. We propose a multi-

scale approach for feature extraction of 3-dimensional images to improve the performance of a diagnosis

system using clustering techniques. To evaluate the performance of our approach we applied it to a database

obtained from Alzheimer’s Disease Neuroimaging Initiative (ADNI) and compare it with Gaussian pyramid

technique. Experimental results have shown that the proposed approach is a good option for image feature

reduction, outperforming the Gaussian pyramid technique.

1 INTRODUCTION

Alzheimer’s disease (AD) is the most common type of

dementia and is characterized by gradual increasing

difﬁculty in remembering new information, caused by

disruption of brain cell function, which usually starts

in brain regions responsible for forming new memo-

ries (Alzheimer’s Association, 2013). Mild cognitive

impairment (MCI) is a condition in which a patient

has noticeable decreased thinking abilities, but does

not restrain the individual to perform everyday ac-

tivities (Alzheimer’s Association, 2013). People with

MCI have higher probabilities of developing AD than

cognitive normal (CN) people.

The early diagnosis of AD is very important to al-

low the patients, and their families, to take the neces-

sary arrangements that empowers patients to live in-

dependently as long as possible, and ﬁnd alternatives

when this is not possible. Despite AD has no cure,

early diagnosis may improve life quality and extend

life expectancy by enabling treatments to delay the

progression of AD symptoms. In order to facilitate

early diagnosis of the AD/MCI conditions, several

computer-aided diagnosis (CAD) systems have been

proposed, usually relying in processing of neuroim-

ages, such as, ﬂuorodeoxyglucose positron emission

tomography (FDG-PET) (Gray et al., 2012; Mart

ınez-

Murcia et al., 2012; Ill

an et al., 2011), magnetic res-

onance imaging (MRI) (Natarajan et al., 2012; Mald-

jian et al., 2003), and single photon emission com-

puted tomography (SPECT) images (Ramirez et al.,

2013). Also, some CAD systems combine several of

the previous imaging modalities (Gray et al., 2013;

Dukart et al., 2011; Zhang et al., 2011)

Analysis of neuroimages typically translates in

high-dimensional feature spaces, leading to system

performance problems (i.e. high computational and

memory costs), and also tends to lower the accu-

racy of the diagnosis. Hence, different techniques

should be used to reduce the dimensionality of the

neuroimages. Various feature extraction techniques

have been applied for the diagnosis of Alzheimer’s

disease (Segovia et al., 2012; Morgado et al., 2013b),

which are very important as the resulting features are

used to differentiate between AD, MCI and CN con-

ditions. Also, several feature selection techniques

(Savio and Gra

na, 2013; Morgado, 2012) have been

used to identify which (and how many) of these fea-

tures should be used by the classiﬁcation algorithms,

since many of the features are redundant or may not

have discriminative power. The selected features may

be thought as a partial view of the brain contain-

ing the most relevant regions of it, and some studies

have shown that using them improves accuracy (Mor-

gado et al., 2013a). Other studies suggest that using

volumes-of-interest may be worse that using whole-

brain information when a single imaging modality is

used, although when using several imaging modalities

561

Duarte J., Aidos H. and Fred A..

Feature Extraction in Pet Images for the Diagnosis of Alzheimer’s Disease.

DOI: 10.5220/0004808705610568

In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 561-568

ISBN: 978-989-758-018-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

the converse may be preferable (Dukart et al., 2011;

Dukart et al., 2013).

We present a dimensionality reduction approach

based on data clustering to reduce the high-

dimensional feature space of neuroimages. This ap-

proach may be used with several imaging modalities

and/or combined with other feature extraction tech-

niques. In this paper, our approach is applied to the

voxel intensities of FDG-PET images and compared

with a scale-space representation using the Gaussian

pyramid technique in three classiﬁcation problems:

AD vs CN, MCI vs CN, and AD vs MCI.

The remaining of this paper is organized as fol-

lows. Section 2 describes the feature extraction, selec-

tion, and classiﬁcation steps included in the method-

ology presented in this paper. Section 3 exhibits the

data set, the experimental design and the correspond-

ing results. Finally, section 4 concludes this paper.

2 METHODOLOGY

Our goal is to diagnose the condition of a given pa-

tient using its FDG-PET scan by learning from a set

of labeled images whose conditions are known. We

use voxel intensities, V (x, y, z), obtained directly from

the FDG-PET scan, to identify the condition of a pa-

tient. V (x, y, z) denotes the value of the FDG uptake

detected at the voxel located at the space position

(x, y, z), where x, y and z are integer numbers.

Our methodology to build a computer-aided diag-

nosis system capable of distinguishing different pa-

tient conditions has three steps: reduce the number

of features to improve system performance; select the

most important features; and, ﬁnally, train a classiﬁ-

cation algorithm. Note that, in this work we focus in

comparing feature extraction methods, namely, one

using the Gaussian pyramid and another using data

clustering. We also compare the previous techniques

that reduce the number of features with one strategy

that uses the whole-brain information. Also, we are

using the voxel intensities of FDG-PET images but

other imaging modalities, such as MRI or SPECT,

could be used instead.

2.1 Feature Extraction using the

Gaussian Pyramid

A problem when dealing with a 3-dimensional FDG-

PET image is the huge amount of features it contains,

which may degrade the performance of pattern recog-

nition algorithms. However, the intensities of voxels

that are close in space tend to be similar and, conse-

quently, some redundant information may be elimi-

nated.

The Gaussian pyramid (Burt, 1981) is a tech-

nique that creates a sequence of images which are

smoothed using a Gaussian average, and then scaled

down. These images are successively smaller due to

subsampling, and each voxel at a given level contains

the average neighborhood’s voxel intensity of the cor-

responding voxel on the previous level of the pyramid.

The technique works as follows. In the ﬁrst step,

the image is smoothed as

(x, y, z) =

∑

m=−2

∑

n=−2

∑

o=−2

w(m, n, o)V

l−1

(2x + m, 2y + n, 2z + o),

(1)

for l = 1, 2, ···, with V

(x, y, z) = V (x, y, z) where

represents the l

level of the pyramid, and

w(m, n, o) = w(m) · w(n) · w(o) is a weighting func-

tion or generating kernel. The level 0 corresponds

to the original image. The generating kernel used

in this work has width 5 and is deﬁned as w(m) =

w(n) = w(o) = w

m+3

, m ∈ {−2, −1, · ·· , 2}, where

w =

[1 4 6 4 1], which resembles a Gaussian func-

tion. In the second step, the image is subsampled by

a factor of two in each of the dimensions.

Figure 1 shows an example of applying the Gaus-

sian pyramid to a 128 × 128 × 60 FDG-PET image (a

slice for each image is shown).

2.2 Feature Extraction using Data

Clustering

We propose to perform feature extraction using a data

clustering algorithm. The objective of data cluster-

ing consists of dividing a data set, X , composed of n

data objects {x

, ·· · , x

}, into K clusters {C

, ·· · ,C

}

such that similar objects, x

, x

, are placed in the same

cluster, i.e {x

, x

} ∈ C

, and dissimilar objects are

grouped in different clusters, i.e. x

∈ C

, x

∈ C

, k 6=

l. The resulting labels of a partition P = {P

, ·· · , P

}

indicate the cluster to which each object belongs. We

intend to group voxels in a FDG-PET image into

clusters to reduce redundant information and, conse-

quently, decrease the number of features for the clas-

siﬁcation task. The clusters should represent regions

in the 3-dimensional space with similar voxel inten-

sities. The methodology to ﬁnd these regions is ex-

plained in the following.

Let V

(x, y, z) represent the voxel (x, y, z) of the

FDG-PET image in a database containing q im-

ages. First, a mean brain image V

∗

is computed by

averaging the corresponding voxel (x, y, z) over the

entire population:

∗

(x, y, z) =

∑

i=1

(x, y, z). (2)

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

562

(a) Original (b) Level 1 (c) Level 2 (d) Level 3 (e) Level 4

Figure 1: Gaussian pyramid example from a slice of a 3-dimensional FDG-PET image (all images are zoomed to the same

size).

Then, the voxels corresponding to background are

discarded, and the remaining n voxel intensities,

∗

(x, y, z), are stacked into a vector f = [ f

, ·· · , f

]

A vectorial representation of the data set X ∈ R

n×4

is built considering both the voxel intensities and the

corresponding position in space. This representation

is deﬁned as

X =







posX(1) posY (1) posZ(1)

posX(2) posY (2) posZ(2)

posX(n) posY (n) posZ(n)







, (3)

where posX(i), posY (i), posZ(i) are functions that

indicate the space position of the i

voxel in each axis

of the 3-dimensional space. In order to bring all of the

dimensions into proportion with one another, a nor-

malization step is performed such that: a) all dimen-

sions have mean 0; b) the 3 dimensions corresponding

to space location have standard deviation 1; c) and the

dimension corresponding to the voxel intensity have

standard deviation α > 0. α is a parameter that inﬂu-

ences the importance of voxel intensity in clustering.

Next, a partition of X into K clusters is obtained

by applying a clustering algorithm to it, and the labels

, ∀i ∈ {1, ·· · , n}, are used to identify the regions in

space.

Finally, a new representation for each image V

is build containing K features (one for each cluster).

The value for each feature k for a patient i is com-

puted as the average intensity of the voxels belonging

to the corresponding cluster C

. Figure 2 shows an

example of this approach. Images obtained using a

high number of clusters are very similar to the origi-

nal one, while images obtained using few clusters are

smother.

The proposed approach has two main advantages

over the Gaussian pyramid approach: it is very easy

to specify the number of features by simply speci-

fying the number of clusters to the clustering algo-

rithm; and each resulting feature may represent space

regions with distinct shapes and size, thus the features

are more meaningful.

The well-known K-means algorithm (MacQueen,

1967) was chosen to perform the brain segmenta-

tion, due to its low-computational cost, using random

initialization of the centroids, however any cluster-

ing algorithm could be used instead. K-means (lo-

cally) minimizes the within-cluster sum of squares:

∑

k=1

∑

∈C

||x

− x

, where ||x

− x

is the Eu-

clidean distance between x

and its closest cluster cen-

troid x

2.3 Feature Selection using Mutual

Information

Feature selection is the process of choosing a subset

of features in a data set. The resulting data represen-

tation should improve the performance of classiﬁers,

reduce computational and memory costs, and facili-

tate data visualization and data understanding (Guyon

and Elisseeff, 2003). To reduce the number of fea-

tures for our task, we use mutual information (MI)

between features and class labels to rank the features

and choose the ones with higher value. Let F ∈ R

be a vector representing a feature in a data set, f

i ∈ {1, · ·· , n} its value for the i

individual in a pop-

ulation of size n, and F a random variable represent-

ing the distribution of F obtained by building a his-

togram with m bins. Also, let Y be a random variable

representing the labels of the population containing c

classes. The mutual information between the feature

F and the labels Y is computed as

MI =

∑

j=1

∑

i=1

P(F = j, Y = i)log

P(F = j, Y = i)

P(F = j)P(Y = i)

, (4)

where P(F = j) is the probability of the j

bin, and

P(Y = i) the probability if the i

class.

2.4 Image Classiﬁcation

Once the feature extraction and the feature selection

steps are conducted, a supervised classiﬁcation algo-

rithm is applied as the ﬁnal step of the diagnostic

problem. In the learning phase, a classiﬁcation algo-

rithm produces a function, using labeled data, capable

of assigning appropriate labels to unlabeled examples.

In this case, given non-redundant and labeled repre-

sentations of FDG-PET scans, the algorithm learns to

identify the condition of a new FDG-PET image. In

FeatureExtractioninPetImagesfortheDiagnosisofAlzheimer'sDisease

563

(a) Original (b) K=36209 (c) K=4723 (d) K=656 (e) K=111

Figure 2: Example of applying the clustering methodology to a 128 × 128 × 60 FDG-PET image (only a slice for each image

is shown).

Table 1: Clinical and demographic characteristics of each

class. Age and MMSE (Mini Mental State Exam) are repre-

sented by the corresponding mean values and standard de-

viations.

Attributes AD MCI CN

Number of subjects 59 59 59

Age 78.26 77.71 77.38

(±6.62) (±6.88) (±4.87)

Sex (% of males) 57.63 67.80 64.41

MMSE 19.60 25.68 29.20

(±5.06) (±2.97) (±0.92)

this paper, we consider three classiﬁcation tasks: AD

vs CN, MCI vs CN, and AD vs MCI.

3 EXPERIMENTS

3.1 Data Set

In this study, we used FDG-PET images for AD, MCI

and CN subjects, retrieved from the ADNI database.

The subjects were chosen to obey a certain criteria:

the Clinical Dementia Rating (CDR) should be 0.5 or

higher for AD patients, 0.5 for MCI patients and 0 for

CN. This selection results in a dataset composed by

59, 142 and 84 subjects for AD, MCI and CN, respec-

tively. Since our task is classiﬁcation using the SVM

algorithm, we decided to balanced the classes. In that

sense, 59 subjects from each MCI and CN groups

were selected randomly. Table 1 summarizes some

clinical and demographic information.

The FDG-PET images have been pre-processed

to minimize differences between images: each image

was co-registered, averaged, reoriented (the anterior-

posterior axis of each subject was parallel to the AC-

PC line), normalized in its intensity, and smoothed to

uniform standardized resolution. Details of the pre-

processing are available in the ADNI project web-

page

http://adni.loni.usc.edu/methods/pet-analysis/pre-processing/

3.2 Experimental Design

To assess the performance of the two feature ex-

traction approaches, we applied the methodology de-

scribed in section 2. We chose the Support Vector

Machine (SVM) (Cortes and Vapnik, 1995) using a

linear kernel as the classiﬁer. The reason for this pref-

erence lies in the SVM being a common choice for the

purpose.

We applied the Gaussian pyramid technique to the

original voxel intensities to obtain 4 levels of feature

extraction. The clustering approach was performed,

also using the original voxel intensities, by applying

the K-means algorithm, setting the number of clus-

ters to the number of features obtained by the Gaus-

sian pyramid technique, so that we can fairly compare

both approaches. The values 2, 4 and 8 were tested

for the α parameter. Also, after the feature extrac-

tion step, the feature selection step was tested using

several number of features, as shown in table 2. Af-

ter some empirical testing, the number of bins to build

the features histograms for MI computation was set to

8, so that each bin could have a meaningful number of

points.

The parameter which controls the cost of mis-

classiﬁcation in the SVM was tuned from the set

C ∈ {2

−16

, 2

−14

, 2

−12

, 2

−10

, 2

−8

, 2

−6

, 2

−4

, 2

−2

, 2

} using a 10 × 10 nested cross-validation proce-

dure (Varma and Simon, 2006). The nested cross-

validation procedure was repeated 20 times for better

performance assessment.

3.3 Results

Figure 3 shows the mean accuracies obtained for the

AD vs CN problem using the Gaussian pyramid with

4 levels, and the clustering approach with the cor-

responding number of clusters. Figure 3a depicts

the results obtained for the level 1 of the Gaussian

pyramid and for applying K-means with 36209 clus-

ters. The clustering approach with α = 8 obtained

the best accuracy of 87.56% using 2500 features, fol-

lowed by the Gaussian pyramid using 250 features

with 87.55%. The differences are not signiﬁcant in

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

564

Table 2: Number of features for each level of the Gaussian pyramid (background removed) and corresponding number of

features tested for the feature selection step.

Level Total number of features Number of selected features

1 36209 50, 100, 250, 500, 1000, 2500, 5000, 10000, 25000, 36209

2 4723 50, 100, 250, 500, 1000, 2500, 4723

3 656 50, 100, 250, 500, 656

4 111 50, 100, 111

this case. Figure 3b shows the results for the second

level of the Gaussian pyramid technique and for K-

means with 4723 clusters. The clustering approach

with α = 2 achieved the best mean accuracy (88.14%)

using 1000 features. In general, the clustering ap-

proach was better than the Gaussian pyramid, for all

values of α. The results for the level 3 of Gaussian

pyramid and the clustering approach with 656 clus-

ters are presented in ﬁgure 3c. Usually, the clustering

approach was better than the Gaussian pyramid for all

values of α, being the best result of 88.21% obtained

using K-means with α set to 4. Figure 3c presents

the results for the fourth level of the Gaussian pyra-

mid and the corresponding clustering approach with

111 clusters. Again, the clustering approach almost

always outperforms the Gaussian pyramid for all val-

ues of α. The best result in this case was 84.94%

using α = 2. The overall best result for the AD vs CN

problem was obtained by reducing the original num-

ber of features to 656 using the clustering approach

with α = 4, and then selecting the best 500 features to

train the classiﬁer.

Figure 4 presents the results for the MCI vs CN

problem. The best results obtained for the level 1

of the Gaussian pyramid was 79.45%, and 79.5% for

the corresponding number of clusters for K-means, as

shown in ﬁgure 4a. Figure 4b presents the results for

the second level of the pyramid and for the cluster-

ing approach with 4723 clusters. Generally, K-means

with α = 2 obtains good results, but the highest accu-

racy (78.88%) was achieved by setting α = 8 and se-

lecting the top 2500 features. For the level 3 and 4 of

the Gaussian pyramid and the corresponding number

of clusters for the clustering approach, it can be seen

in ﬁgures 4c and 4d that the clustering approaches

with α = 2 and α = 4 are clearly better than the Gaus-

sian pyramid technique. Overall, the K-means with

656 clusters obtained, again, the highest mean accu-

racy (80.22%), selecting the top 250 features.

Figure 5 shows the results for the AD vs MCI

problem. For the case of the level 1 of the Gaus-

sian pyramid and the corresponding clustering results

(ﬁgure 5a), it can be seen that all feature extraction

methods perform better using a small number of fea-

tures. The best result was achieved by K-means with

72.36% using the top 100 features and α = 2. Figure

(a) Gaussian pyramid level 1, K-means 36209 clusters.

(b) Gaussian pyramid level 2, K-means 4723 clusters.

(d) Gaussian pyramid level 4, K-means 111 clusters.

Figure 3: Mean accuracies obtained for the AD vs CN prob-

lem using both the Gaussian pyramid and the data clustering

approach.

5b shows the mean accuracies for the second level of

the pyramid and for the clustering approach with 4723

clusters. As above, the best results were obtained us-

ing few features. K-means achieved again the best ac-

curacy with 70.31% using only 50 features and with

α = 8. Figures 5c and 5d presents the results for the

last two levels of the Gaussian pyramid and the cor-

FeatureExtractioninPetImagesfortheDiagnosisofAlzheimer'sDisease

565

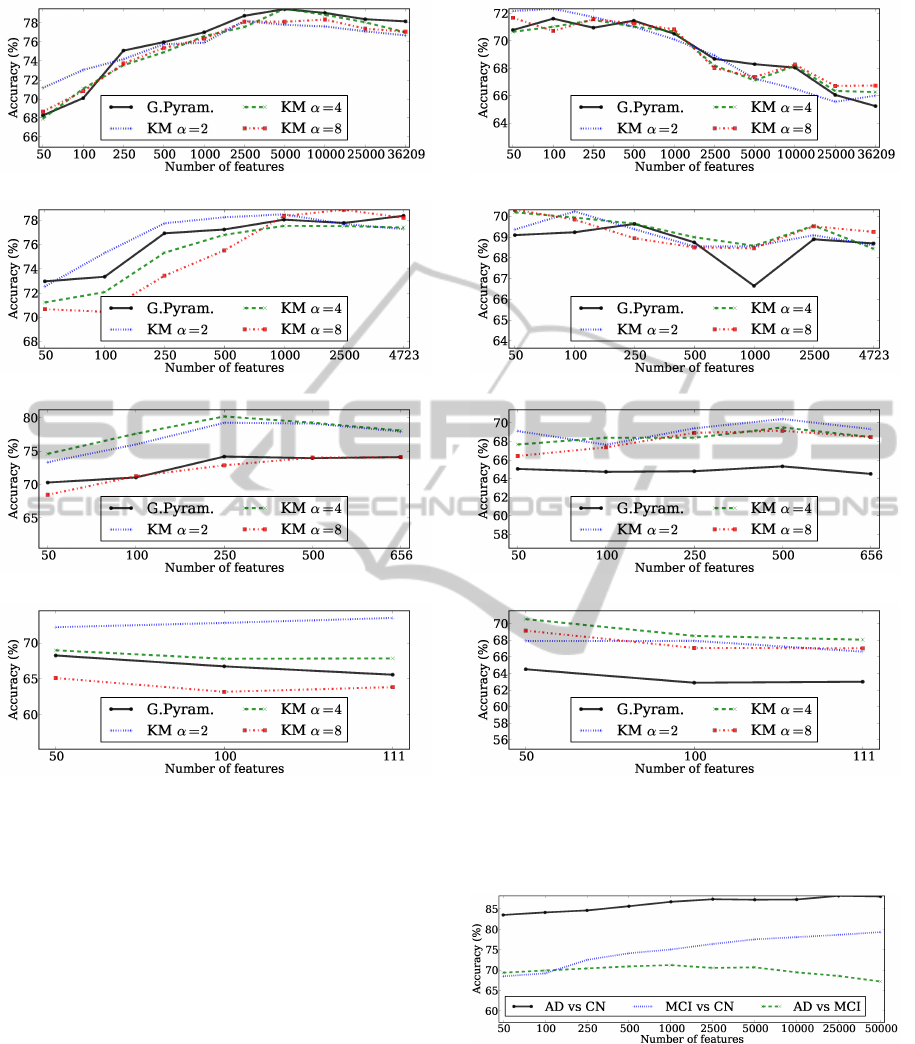
(a) Gaussian pyramid level 1, K-means 36209 clusters.

(b) Gaussian pyramid level 2, K-means 4723 clusters.

(d) Gaussian pyramid level 4, K-means 111 clusters.

Figure 4: Mean accuracies obtained for the MCI vs CN

problem using both the Gaussian pyramid and the data clus-

tering approach.

responding clustering results. It can be clearly seen

that the clustering approach outperforms the Gaus-

sian pyramid technique for all values of α. In the

ﬁrst case, the best result is obtained by K-means using

500 features and α = 2 with 70.42%, which is signif-

icantly higher than the 65.33% achieved by the Gaus-

sian pyramid. For the second case, the best result of

70.55% was achieved by setting α = 4 and selecting

the top 50 features, which is much superior that the

64.50% obtained by the Gaussian pyramid technique.

Overall, the best accuracy for the AD vs MCI prob-

lem (72.34%) was obtained by clustering the original

features with 36209 clusters with α = 2 and selecting

the top 100 features.

Next, we will compare the previous results with

the methodology without feature extraction, i.e., ap-

(a) Gaussian pyramid level 1, K-means 36209 clusters.

(b) Gaussian pyramid level 2, K-means 4723 clusters.

(d) Gaussian pyramid level 4, K-means 111 clusters.

Figure 5: Mean accuracies obtained for the AD vs MCI

problem using both the Gaussian pyramid and the data clus-

tering approach.

Figure 6: Mean accuracies obtained for the AD vs CN, MCI

vs CN, and AD vs MCI using the original voxel intensities

(i.e. without feature extraction).

plying feature selection directly over the original

voxel intensities. Figure 6 presents the correspond-

ing mean accuracies. This representation contains

297735 features, corresponding to the voxel intensi-

ties of the original images after removing the back-

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

566

Table 3: Best mean accuracy values and standard deviations obtained by not using any feature extraction technique and the

corresponding results for the best approach using feature extraction.

AD vs CN MCI vs CN AD vs MCI

Without Accuracy 88.22% 79.34% 71.25%

Feature Standard Deviation 1.19% 2.45% 1.70%

Extraction #Selected Features 25000 50000 1000

Accuracy 88.21% 80.22% 72.34%

With Standard Deviation 1.67% 2.27% 1.66%

Feature Feat. Sel. Approach K-means α = 4 K-means α = 4 K-means α = 2

Extraction #Reduced Features 656 656 36209

#Selected Features 500 250 100

ground. For the AD vs CN and MCI vs CN problems,

the accuracy increases as the number of selected fea-

tures grows. The best results were 88.22% for the

AD vs CN classiﬁcation task and 79.34% for the MCI

vs CN problem. For the AD vs MCI classiﬁcation

task, high number of features leads to lower accu-

racies. The best result in this case was 71.25%. A

summary showing the best results achieved with and

without performing feature extraction is presented in

table 3. The main conclusion is that using the pro-

posed clustering approach have similar results in the

AD vs CN, and better results in the MCI vs CN and

AD vs MCI using far fewer features.

4 CONCLUSIONS AND FUTURE

WORK

A new approach to reduce features in neuroimages

was proposed based on clustering similar brain re-

gions with respect to both voxel intensity values and

voxel space positions. We integrated it in a method-

ology for performing computer-aided diagnosis of

Alzheimer’s disease and mild cognitive impairment

conditions, and compared it with the Gaussian pyra-

mid technique.

Results have shown that the proposed approach

outperforms the Gaussian pyramid technique for fea-

ture reduction. This is more evident when the brain is

represented by a lower number of features, suggesting

that the clustering approach is more robust. Also, the

proposed feature extraction technique leads to simi-

lar or better classiﬁcation accuracies than using the

original voxel intensities but using a small fraction of

the number of features, which allows the development

of computer-aided diagnosis systems with fewer pro-

cessing and memory requirements.

In future work we intend to use constrained clus-

tering algorithms, capable of using a priori informa-

tion about speciﬁc domains. Our idea is to map infor-

mation about the neighborhood of the voxels as con-

straints in order to improve the brain segmentation.

We will also compare these approaches with recent

multi-scale techniques.

ACKNOWLEDGEMENTS

This work was supported by the Portuguese Founda-

tion for Science and Technology grants PTDC/SAU-

ENB/114606/2009 and PTDC/EEI-SII/2312/2012.

REFERENCES

Alzheimer’s Association (2013). Alzheimer’s disease facts

and ﬁgures Alzheimer’s association. ALZHEIMERS

& DEMENTIA, 9(2):208–245.

Burt, P. J. (1981). Fast ﬁlter transform for image processing.

Comp. graphics and image proc.

Cortes, C. and Vapnik, V. (1995). Support-vector networks.

Mach. Learn., 20(3):273–297.

Dukart, J., Mueller, K., Barthel, H., Villringer, A., Sabri,

O., and Schroeter, M. L. (2013). Meta-analysis

based SVM classiﬁcation enables accurate detection

of Alzheimer’s disease across different clinical centers

using FDG-PET and MRI. Psych. Res.: Neuroimag-

ing, 212(3):230 – 236.

Dukart, J., Mueller, K., Horstmann, A., Barthel, H., M

oller,

H. E., Villringer, A., Sabri, O., and Schroeter, M. L.

(2011). Combined evaluation of FDG-PET and MRI

improves detection and differentiation of dementia.

PLoS ONE, 6(3).

Gray, K., Wolz, R., Heckemann, R., Aljabar, P., Hammers,

A., and Rueckert, D. (2012). Multi-region analy-

sis of longitudinal FDG-PET for the classiﬁcation of

Alzheimer’s disease. NeuroImage, 60(1):221–229.

Gray, K. R., Aljabar, P., Heckemann, R. A., Hammers,

A., and Rueckert, D. (2013). Random forest-based

similarity measures for multi-modal classiﬁcation of

Alzheimer’s disease. NeuroImage, 65(0):167 – 175.

Guyon, I. and Elisseeff, A. (2003). An introduction to

variable and feature selection. J. Mach. Learn. Res.,

3:1157–1182.

FeatureExtractioninPetImagesfortheDiagnosisofAlzheimer'sDisease

567

Ill

an, I. A., G

orriz, J. M., Ram

ırez, J., Salas-Gonzalez, D.,

opez, M. M., Segovia, F., Chaves, R., G

omez-Rio,

M., and Puntonet, C. G. (2011).

F-FDG PET imag-

ing analysis for computer aided Alzheimer’s diagno-

sis. Inf. Sci., 181(4):903–916.

MacQueen, J. B. (1967). Some methods for classiﬁcation

and analysis of multivariate observations. In Cam, L.

M. L. and Neyman, J., editors, Proc. of the ﬁfth Berke-

ley Symposium on Mathematical Statistics and Prob-

ability, volume 1, pages 281–297. University of Cali-

fornia Press.

Maldjian, J. A., Laurienti, P. J., Kraft, R. A., and Bur-

dette, J. H. (2003). An automated method for neu-

roanatomic and cytoarchitectonic atlas-based interro-

gation of fMRI data sets. NeuroImage, 19(3):1233 –

1239.

Mart

ınez-Murcia, F. J., G

orriz, J. M., Ram

ırez, J., Puntonet,

C. G., and Salas-Gonzalez, D. (2012). Computer

aided diagnosis tool for Alzheimer’s disease based on

Mann-Whitney-Wilcoxon u-test. Expert Syst. Appl.,

39(10):9676–9685.

Morgado, P., Silveira, M., and Marques, J. (2013a). Efﬁ-

cient selection of non-redundant features for the diag-

nosis of Alzheimer’s disease. In Biomedical Imaging

(ISBI), 2013 IEEE 10th International Symposium on,

pages 640–643.

Morgado, P., Silveira, M., and Marques, J. S. (2013b). Di-

agnosis of Alzheimer’s disease using 3D local binary

patterns. Computer Methods in Biomechanics and

Biomedical Engineering: Imaging & Visualization,

1(1):2–12.

Morgado, P. M. M. (2012). Automated diagnosis of

Alzheimer’s disease using PET images. Master’s the-

sis, Instituto Superior T

ecnico - Universidade T

ecnica

de Lisboa.

Natarajan, S., Joshi, S., Saha, B. N., Edwards, A., Khot, T.,

Moody, E., Kersting, K., Whitlow, C. T., and Mald-

jian, J. A. (2012). A machine learning pipeline for

three-way classiﬁcation of Alzheimer patients from

structural magnetic resonance images of the brain. In

ICMLA, pages 203–208.

Ramirez, J., Gorriz, J., Salas-Gonzalez, D., Romero, A.,

Lopez, M., Alvarez, I., and Gomez-Rio, M. (2013).

Computer-aided diagnosis of Alzheimer’s type de-

mentia combining support vector machines and dis-

criminant set of features. Information Sciences - Pre-

diction, Control and Diagnosis using Advanced Neu-

ral Computations, 237(0):59 – 72.

Savio, A. and Gra

na, M. (2013). Deformation based feature

selection for computer aided diagnosis of Alzheimer’s

disease. Expert Systems with Applications, 40(5):1619

– 1628.

Segovia, F., G

orriz, J., Ram

ırez, J., Salas-Gonzalez, D.,

Alvarez, I., L

opez, M., and Chaves, R. (2012). A

comparative study of feature extraction methods for

the diagnosis of Alzheimer’s disease using the ADNI

database. Neurocomputing, 75(1):64 – 71.

Varma, S. and Simon, R. (2006). Bias in error estimation

when using cross-validation for model selection. BMC

Bioinformatics, 7(91).

Zhang, D., Wang, Y., Zhou, L., Yuan, H., and Shen, D.

(2011). Multimodal classiﬁcation of Alzheimer’s dis-

ease and mild cognitive impairment. NeuroImage,

55(3):856–867.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

568