
Bio-inspired Metaheuristic based Visual
Tracking and Ego-motion Estimation
J. R. Siddiqui and S. Khatibi
Department of Computing, Blekinge Institute of Technology, Karlskrona, Sweden
Keywords: Camera Tracking, Visual Odometry, Planar Template based Tracking, Particle Swarm Optimization.
Abstract: The problem of robust extraction of ego-motion from a sequence of images for an eye-in-hand camera
configuration is addressed. A novel approach toward solving planar template based tracking is proposed
which performs a non-linear image alignment and a planar similarity optimization to recover camera
transformations from planar regions of a scene. The planar region tracking problem as a motion
optimization problem is solved by maximizing the similarity among the planar regions of a scene. The
optimization process employs an evolutionary metaheuristic approach in order to address the problem
within a large non-linear search space. The proposed method is validated on image sequences with real as
well as synthetic image datasets and found to be successful in recovering the ego-motion. A comparative
analysis of the proposed method with various other state-of-art methods reveals that the algorithm succeeds
in tracking the planar regions robustly and is comparable to the state-of-the art methods. Such an application
of evolutionary metaheuristic in solving complex visual navigation problems can provide different
perspective and could help in improving already available methods.
1 INTRODUCTION
Accurate relative position estimation by keeping
track of salient regions of a scene can be
considered to be the core functionality of a
navigating body such as a mobile robot. These
salient regions are often referred to as “Landmarks”
and the process of position estimation and
registration of landmarks on a local representation
space (i.e. a Map) is called SLAM (Simultaneous
Localization and Mapping). The choice of
landmarks and their representation depends on the
environment as well as the configuration of a robot.
In the case of vision based navigation, feature
oriented land-marking is often employed, where
features can be represented in many ways (e.g. by
points, lines, ellipses and moments) (Torr and
Zisserman, 2000). Such techniques either do not
exploit rigidity of the scene (Eade and Drummond
2006; Davison, 2003; Scaramuzza et al., 2009) or
geometrical constraints are loosely coupled by
keeping them out of the optimization process (Klein
and Murray, 2009; Pirchheim and Reitmayr, 2011;
Wagner et al., 2009). These techniques can therefore
have inaccurate motion estimation due to small
residual errors incurred in each iteration which make
motion estimations inaccurate as these errors get
accumulated. In order to mitigate this, an additional
correction step is often added which either exploits a
robot’s motion model to predict the future state
using an array of extended Kalman-Filters
(Montemerlo et al., 2002) or minimizes the
integrated error calculated over a sequence of
motion (More, 1978).
Generally, feature-oriented ego-motion
estimation approaches (Zhou, Green et al., 2009;
Zhou, Wallace et al., 2009) follow three main steps;
feature extraction, correspondence calculation and
motion estimation. The extracted features are mostly
sparse and the process of extraction is decoupled
from motion estimation. Sparsification and
decoupling makes a technique less computationally
expensive and also allows it to handle large
displacements in subsequent images, however
accuracy suffers when the job is to localize a robot
and map the environment for a longer period of
time. Since finding correspondences is itself an
error-prone task, a large portion of the error is
introduced in a very early phase of motion
estimation.
There is another range of methods that utilize all
pixels of an image region when calculating camera
569
R. Siddiqui J. and Khatibi S..
Bio-inspired Metaheuristic based Visual Tracking and Ego-motion Estimation.
DOI: 10.5220/0004811105690579
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 569-579
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

displacement by aligning image regions and hence
enjoy higher accuracy due to exploitation of all
possible visual information present in the segments
of a scene (Irani and Anandan, 2000). These
methods are termed “direct image alignment” based
approaches for motion estimation because they do
not have feature extraction and correspondence
calculation steps and work directly on image
patches. Direct methods are often avoided due to
their computational expense which overpowers the
benefits of accuracy they might provide, however an
intelligent selection of the important parts of the
scene that are rich in visual information can provide
a useful way of dealing with the issue (Silveira et al.,
2008). In addition to being direct in their approach,
such methods can also better exploit the geometrical
structure of the environment by including rigidity
constraints early in the optimization process. The
use of all visual information in a region of an image
and keeping track of gain or loss in subsequent
snapshots of a scene is also relevant, since it is the
way some biological species navigate. For example,
there are evidences that desert ants use the amount
of visual information which is common between a
current image and a snapshot of the ant pit to
determine their way to the pit (Philippides et al.,
2012).
An important step in a direct image alignment
based motion estimation approach is the
optimization of similarity among image patches. The
major optimization technique that is extensively
used for image alignment is gradient descent
although a range of algorithms (e.g. Gauss-Newton,
Newton-Raphson and Levenberg-Marquardt
(Bjorck, 1996; More, 1978)) are used for calculation
of a gradient descent step. Newton’s method
provides a high convergence rate because it is based
on second order Taylor series approximation,
however, Hessian calculation is a computationally
expensive task. Moreover, a Hessian can also be
indefinite, resulting in convergence failure. These
methods perform a linearization of the non-linear
problem which can then be solved by linear-least
square methods. Since these methods are based on
gradient descent, and use local descent to determine
the direction of an optimum in the search space, they
have a tendency to get stuck in the local optimum if
the objective function has multiple optima. There
are, however, some bio-inspired metaheuristics that
mimic the behavior of natural organisms (e.g.
Genetic Algorithms (GAs) and Particle Swarm
Optimization (PSO) (Goldberg, 1989; Kennedy and
Eberhart, 1995; Baik et al., 2013) ) or the physical
laws of nature to cater this problem (Aarts and
Korst, 1988). These methods have two common
functionalities: exploration and exploitation. During
an exploration phase, like any organism explores its
environment, the search space is visited extensively
and is gradually reduced over a period of iterations.
The exploitation phase comes in the later part of a
search process, when the algorithm converges
quickly to a local optimum and the local optimum is
accepted as the global best solution. This two-fold
strategy provides a solid framework for finding the
global optimum and avoiding the local best solution
at the same time. In this case, PSO is interesting as it
mimics the navigation behavior of swarms,
especially colony movement of honeybees if an
individual bee is represented as a particle which has
an orientation and is moving with a constant
velocity. Arbitrary motion in the initial stage of the
optimization process ensures better exploration of
the search space and a consensus among the
particles reflects better convergence.
In this paper, the aim is to solve the problem of
camera motion estimation by directly tracking planar
regions in images. In order to learn an accurate
estimate of motion and to embed the rigidity
constraint of the scene in the optimization process, a
PSO based camera tracking is performed which uses
a non-linear image alignment based approach for
finding the displacement of camera within
subsequent images. The major contributions of the
paper are: a) a novel approach to planar template
based camera tracking technique which employs a
bio-metaheuristic for solving optimization problem
b) Evaluation of the proposed method using multiple
similarity measures and a comparative performance
analysis of the proposed method.
The rest of the paper is organized as follows: In
section 2 the most relevant studies are listed, in
section 3 the details of the method are described,
section 4 explains the experimental setup and
discussion of the results, and section 5 presents the
conclusion and potential future work.
2 RELEVANT WORK
There are many studies that focus on feature
oriented camera motion estimation by tracking a
template in the images. However, here we focus on
the direct methods that track a planar template by
optimizing the similarity between a reference and a
current image. A classic example of such a direct
approach toward camera motion estimation is the
use of a brightness constancy assumption during
motion and is linked to optical flow measurement
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
570

(Irani and Anandan, 2000). Direct methods based on
optical flow were later divided into two major
pathways: Inverse Compositional (IC) and Forward
Compositional (FC) approaches (Lucas and Kanade
1981; Baker and Matthews, 2004; Jurie and Dhome,
2002). The FC approaches solve the problem by
estimating the iterative displacement of warp
parameters and then updating the parameters by
incrementing the displacement. IC approaches, on
the other hand, solve the problem by updating the
warp with an inverted incremental warp. These
methods linearize the optimization problem by
Taylor-series approximation and then solve it by
least-square methods. In (Cobzas and Sturm, 2005) a
multi-plane estimation method along with tracking is
proposed in which region-based planes are firstly
detected and then the camera is tracked by
minimizing the SSD (Sum of Squared Differences)
between respective planar regions in 2D images.
Another example of direct template tracking is
(Cobzas and Sturm, 2005) which improves the
tracking method by replacing the Jacobian
approximation in (Baker and Matthews, 2004) with
a Hyper-plane Approximation. The method in
(Cobzas and Sturm, 2005) is similar to our method
because it embeds constraints in a non-linear
optimization process (i.e. Levenberg-Marquardt
(More, 1978)) although it differs from the method
proposed here since the latter employs a bio-inspired
metaheuristic based optimization process which
maximizes the mutual information in-between
images and also the proposed method does not use
constraints among the planes.
3 METHODOLOGY
The problem that is being addressed deals with
estimation of a robot’s state at a given time step that
satisfies the planarity constraint. Let
,
∈
be the state of the robot with
∈
,
∈
being
the position and orientation of the robot in Euclidean
space. Let’s also consider ,
to be the current and
reference image, respectively. If the current image
rotates ∈3 and translates ∈
from the
reference image in a given time step then the motion
in terms of homogeneous representation ∈3
can be given as:
̂
1
(1)
where ̂ is the skew symmetric matrix. It is
indeed this transformation that we ought to recover
given the current state of the robot and reference
template image.
3.1 Plane Induced Motion
It is often the case that the robot’s surrounding is
composed of planar components, especially in the
case of indoor navigation where most salient
landmarks are likely to be planar in nature. In such
cases the pixels in an image can be related to the
pixels in the reference image by a projective
homography H that represents the transformation
between the two images (Hartley and Zisserman,
2000). If
,,1
be the homogeneous
coordinates of the pixel in an image and
,
,1
be the homogenous coordinates of the
reference image then the relationship between the
two set of pixels can be written as given in equation
2.
∝
(2)
Let’s now consider that the plane that is to be
tracked or the plane which holds a given landmark
has a normal
∈
, which has its projection in
the reference image
. In case of a calibrated
camera, the intrinsic parameters, which are known,
can be represented in terms of a matrix ∈
.
If the 3D transformation between the frames is ,
then the Euclidean homography with a non-zeros
scale factor can be calculated as:
,
∝
(3)
3.2 Model-based Image Alignment
The next step after modeling the planarity of the
scene is to relate plane transformations in the 3D
scene to their projected transformations in the
images. For that reason a general mapping function
that transforms a 2D image given a projective
homography can be represented by a warping
operator w and is defined as follows:
,
,
(4)
If the normal of the tracked plane is known then the
problem to be addressed is that of metric model
based alignment or simply model based non-linear
image alignment. It is the transformation ∈3
that is to be learned by warping the reference image
and measuring the similarity between the warped
and the current image. Since the intensity of a pixel
is a non-linear function, we need a non-linear
optimization procedure. More formally, the task is to
learn an optimum transformation
that
maximizes the following:
Bio-inspiredMetaheuristicbasedVisualTrackingandEgo-motionEstimation
571

max
,
,
,
(5)
where is a similarity function and
is updated as
⇠
for every new image in the sequence.
3.3 Similarity Measure
In order for any optimization method to work
effectively and efficiently, the search space needs to
be modeled in such a way that it captures the
multiple optima of a function but at the same time
suppresses local optima by enhancing the global
optimum. It is also important that such modeling of
similarity must provide enough convergence space
so that the probability of missing the global
optimum is minimized. This job is performed by a
selection of similarity measure that is best suited for
a given problem context. An often used measure is
SSD (Sum of Squared Differences) that can be given
as:
,
(6)
where ‘N’ is the total number of pixels in a
tracked region of the image.
Similarly, another relevant similarity measure is the
cross correlation coefficient of the given two data
streams. Often a normalized version is used to
restrict the comparison space to the range [0, 1]. The
normalized cross correlation between a current
image patch and a reference image patch
, with
,
being their respective means, can be written as:
,
,
,
,
,
(7)
The similarity measures presented in equation 6 and
7 have the ability to represent the amount of
information that is shared by the two data streams;
however, as can be seen in figure 1, the convergence
space and the emphasis on the global optimum need
improvement. A more intuitive approach for
measuring similarity among the data is Mutual
Information (MI), taken from information theory,
that measures the amount of data that is shared
between the two input data streams (Shannon, 2001).
The application of MI in image alignment tasks
and its ability to capture the shared information have
also proven to be successful (Dowson and Bowden,
2006; Dowson and Bowden, 2008). The reason for
avoidance of MI in robotics tasks has been its
relatively higher computational expense, since it
involves histogram computation. However, the gains
are more than the losses, so we choose to use MI as
our main similarity measure. Formally, the MI
Figure 1: Convergence surface of various similarity
functions along with motion of a PSO particle on its way
towards convergence depicted by green path. First Row:
Sum of squared difference , Second Row: Normalized
Cross Correlation, Third Row: Mutual Information.
between two input images can be computed as:
,
,
,
,
(8)
where
,
,
,
are the entropy, joint
entropy and maximum allowable intensity value
respectively. Entropy according to Shannon
(Shannon, 2001) is the measure of variability in a
random variable I, whereas ‘i’ is the possible value
of I and
Pr is the probability
distribution function.
3.4 Optimization Procedure
The problem of robust retrieval of Visual Odometry
(VO) in subsequent images is challenging due to the
non-linear and continuous nature of the huge search
space. The non-linearity is commonly tackled using
linearization of the problem function; however, this
approximation is not entirely general due to
challenges in exact modeling of image intensity.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
572

Figure 2: A depiction of PSO particles (i.e. robot states)
taking part in an optimization process. Blue arrows show
the velocity of a particle and the local best solution is
highlighted by an enclosing circle.
Another route to solve the problem is to use non-
linear optimization such as Newton Optimization
which gives fairly good convergence due to the fact
that it is based on Taylor series approximation of the
similarity function. However, it requires
computation of the Hessian which is
computationally expensive and also it must be
positive definitive for a convergence to take place.
The proposed method seeks the solution to the
optimization problem presented in equation 5. In
order to find absolute global extrema and not get
stuck in local extrema we choose a bio-inspired
metaheuristic optimization approach (i.e. PSO).
Particle Swarm Optimization (PSO) is an
evolutionary algorithm which is directly inspired by
the grouping behavior of social animals, notably in
the shape of bird flocking, fish schooling and bee
swarming The primary reason for interest in learning
and modeling the science behind such activities has
been the remarkable ability possessed by natural
organisms to solve complex problems (e.g
scattering, regrouping, maintaining course, etc.) in a
seamlessly and robust fashion. The generalized
encapsulation of such behaviors opens up horizons
for potential applications in nearly any field. The
range of problems that can be solved range from
resource management tasks (e.g intelligent planning
and scheduling) to real mimicked behaviors by
robots. The particles in a swarm move collectively
by keeping a safe distance from other members in
order to avoid obstacles while moving in a
consensus direction to avoid predators and maintain
a constant velocity. This results in behavior in which
a flock/swarm moves towards a common goal (e.g. a
Hive, food source) while intra-group motion seems
random. This makes it difficult for predators to focus
on one prey while it also helps swarms to maintain
their course, especially in case of long journeys that
are common, e.g., for migratory birds. The exact
location of the goal is usually unknown as it is in the
case of any optimization problem where the
optimum solution is unknown. A pictorial depiction
of the robot’s states represented as particles in an
optimization process can be seen in figure 2.
PSO is implemented in many ways with varying
levels of bioinspiration reflected in terms of the
neighborhood topology that is used for convergence
(Günther and Nissen, 2009). Each particle maintains
it current best position
and global best
position. The current best position is available to
every particle in the swarm. A particle updates its
position based on its velocity, which is periodically
updated with a random weight. The particle that has
the best position in the swarm at a given iteration
attracts all other particles towards itself. The
selection of attracted neighborhood as well as the
force to which the particles are attracted depends on
the topology being used. Generally a PSO consists
of two broad functions: one for exploration and one
for exploitation. The degree and extend of time that
each function is performed depends again on the
topology being used. A common model of PSO
allows more exploration to be performed in the
initial iterations while it is gradually decreased and a
more localized search is performed in the later
iterations of the optimization process.
The process of PSO optimization starts with
initialization of the particles. Each particle is
initialized with a random initial velocity
and
random current position
represented by a k
dimensional vector where ‘k’ is the number of
degrees of freedom of the solution. The search space
is discretized and limited with a boundary constraint
|
|
,
∈
,
where
,
are lower and
upper bounds of motion in each dimension. This
discretization and application of boundary
constraints helps reduce the search space assuming
that the motion in between subsequent frames is not
too large. After initialization, particles are moved
arbitrarily in the search space to find the solution
that maximizes the similarity value as given in
equation 8. Each particle updates its position based
on its own velocity and the position of the best
particle in the neighborhood. The position and
velocity update is given in equation 9:
Bio-inspiredMetaheuristicbasedVisualTrackingandEgo-motionEstimation
573
1
1
1
(9)
where ω is the inertial weight and is used to
control the momentum of the particles. When a large
value of inertial weight is used, particles are
influenced more by their last velocity and collisions
might happen with very large values. The cognitive
(or self- awareness) component of the velocity
update is represented by
where
is the personal best solution of the particle.
Similarly, the social component is represented as
where
is the best solution in the
particle’s neighborhood. Randomness is achieved by
,
∈ 0,1 for cognitive and social components
respectively. The constant weights
,
control the
influence of each component in the update process.
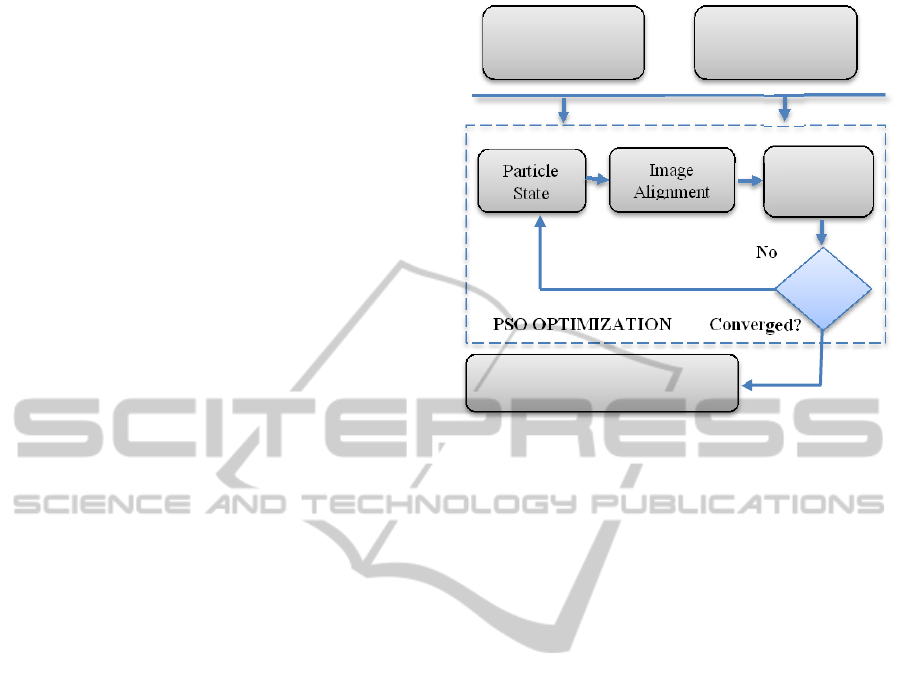
3.5 Tracking Method
The proposed plane tracking method consists of
three main steps: initialization, tracking and
updating. A pictorial depiction of the whole process
is given in figure 3. These steps are given as follows:
1) The planar area in the image that is to be
tracked is initialized in the first frame and an initial
normal of the plane is provided. If the plane
normal is not already known then a rough estimate
of the plane in the camera coordinate frame is
given. The search space of the problem is
discretized and constrained within an interval. PSO
is initialized with a random solution and a suitable
similarity function is provided.
2) The marked region in the template image is
aligned with a region in the current image and an
optimum solution of the 6-dof transformation is
obtained. The optimization process continues until
it meets one of the following conditions: (i) max
number of iterations is reached, (ii) the solution
has not improved in a number of consecutive
iterations, or (iii) a threshold for solution
improvement is reached.
3) The global camera transformation is updated
and process repeats.
4 EXPERIMENTAL RESULTS
In order to evaluate the proposed method, an
experiment setup must conform to the basic
assumptions of the planarity of the scene and small
subsequent motion. The planarity of the scene means
that there should be a dominant plane in front of the
camera whose normal is either estimated by using
Figure 3: System architecture of the proposed method.
another technique or using an approximated unit
normal without scale, however the rate of
convergence and efficiency is affected in the latter
case. The second important assumption of the
system is that the amount of motion in subsequent
frames is small, since large motions increase the
search space significantly. In addition to this, if the
planar region that is to be tracked is textured, the
results can be improved due to the presence of
greater variance of similarity between the reference
and the current image region. Keeping these
assumptions in mind, the algorithm was evaluated
for both simulated and real robotic motion.
4.1 Synthetic Sequence
The proposed method was evaluated on a benchmark
tracking sequence (Benhimane and Malis, 2007).
The sequence consisted of a real image with a
textured plane facing the camera and its 100
transformed variations, while the motion within the
subsequent transformation was kept small. The
tracking region was marked in the template image in
order to select the plane and the optimization
algorithm was initialized. The tracking method
succeeded in capturing the motion, as shown on
figure 4. In order to test behavior of the similarity
measures, the method was repeated with all three
similarity functions, and the error surface was
analyzed as seen in the figure 1, which also show the
path of a particle in the swarm on its way toward
convergence. It was found that MI provides a better
convergence surface than the other two participating
Yes
No
Converged? PSO OPTIMIZATION
Reference
Planner Region
Particle
State
Image
Ali
g
nment
Planner Region
in Current Image
Measure
Similarity
Update state
Plane Tracking & Ego-motion
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
574

similarity measures and hence it was used for later
stages of the evaluation process.
Figure 4: The result of the tracking when applied on a
benchmarking image sequence with synthetic
transformations.
Figure 5: The example images of experimental setup(s).
In order to determine whether the algorithm could
accommodate variations in the degrees of freedom,
the sequence was run multiple times with different
dimensions of the solution that was to be learned.
The increase in the number of parameters to be
learned affects the convergence rate, however the
algorithm successfully converged for all the
variations, as seen in figure 6. With an increase in
degrees of freedom, the search space expands
exponentially, making it harder to converge in the
same number of iterations as needed for lower
degrees of freedom. This can be catered for in
multiple ways: a) increasing the overall number of
iterations needed by the algorithm to converge, b)
increasing the number of iterations dedicated for
exploration, and c) putting more emphasis on
exploration by setting the appropriate inertial and
social weights in equation 9.
4.2 Real Sequence
The proposed tracking method was also tested on
two real image benchmarking datasets. The result of
evaluations for each dataset is given in forthcoming
sections.
4.2.1 MAV Dataset
A sequence of images that was recorded by a
downward looking camera mounted on a
quadrocopter (Lee et al., 2010). The sequence
consisted of 533 images with the resolution 752x480
recorded by flying the quadrocopter at ~15Hz while
it hovers at one meters above the ground. The
dataset provides VICON
TM
measurements which are
used as ground truth. The important variable that
was unavailable in this case of real images was the
absolute normal of the tracked plane. There could
have been two ways to solve this problem: using an
external plane detection method to estimate the
normal or using a rough estimate of the plane
(virtual-plane) and leaving the rest to optimization
processes. The former approach was preferable and
could lead to a better convergence rate. However, to
show the insensitivity of the proposed method to
absolute plane normal and depth estimates, we used
the latter approach for evaluation. The rest of the
parameterization and initialization process was
similar to the simulated sequence based evaluation
process described earlier.
As shown in figure 7, even though initial
transformation of the marked region was not correct
and the absolute normal was unknown; the tracking
method learned the correct transformation over a
period of time and successfully tracked the planar
region. A thorough error analysis was provided, as
shown in figure 8, which shows that the proposed
tracking method has robust tracking ability with very
low error rates when the motion is kept within the
bounds of the search space. A good way to keep the
motion small was attained by using high frame-rate
cameras.
4.2.2 Road Dataset
The second dataset consists of an image sequence
recorded by a car mounted camera (see figure 5) that
is driven in an urban environment (Warren et al.
2010). A total of 2800 images of resolution
1024x768 at 30Hz were used in the evaluation
process. The images contained multiple turns
performed by vehicle as well as with lighting
variation due to cloudy as well as bright sunny
weather. The GPS measurements are taken as the
ground truth for evaluation. The planar patches of
the road segment were used in the optimization
process. In order to reduce the effect of scale
ambiguity while estimating the motion of the
camera, the images were rectified so that ground
Bio-inspiredMetaheuristicbasedVisualTrackingandEgo-motionEstimation
575

plane normal becomes parallel to the image plane.
The motion of the vehicle on the road can be
approximated by a camera moving on a plane. This
approximation reduces the desired motion
parameters to three parameters
,
,Ω
whereas
former two represent the lateral and forward
translation while latter parameter represents the
angular motion along optical axis. The results of the
error analysis are presented in the figure 8.
Figure 6: Convergence with variation in DOF and
similarity measures. X,Y, Z, ,, represent motion
along various degrees of freedom. The rows represent
similarity measures SSD, NCC and MI respectively and
columns represent DOF (2 and 4).
4.3 Comparative Analysis
The proposed method performs camera tracking
using non-linear image alignment for optimization.
Comparative analyses with various modifications of
PSO and also with other state of the art methods
helped us to determine the method’s significance in
real applications. Figure 9 presents a comparison of
the multiple variations of PSO. The Trelea-PSO
(Trelea 2003) is good at converging to optimum
similarity values in all cases, although its
convergence rate is not the fastest due to being
explorative in nature. PSO common (Kennedy &
Eberhart 1995) on the other hand, finds its way
quickly towards solutions, although it may not find
global optima due to being more exploitative in
nature. A group of three state of the art plane
tracking methods (IC (Baker & Matthews 2004), FC
(Lucas and Kanade, 1981) and HA (Jurie and
Dhome, 2002)) are applied on the same image
sequence and a normalized root mean squared error
is measured for the image sequence and the number
of iterations. As it can be visualized from the figure
10, that the performance of the algorithm is
comparable to IC and FC while it performs better
than HA over mean squared error. In order to
address the randomness the experiment is repeated
multiple times and mean performance is measured.
Figure 7: The result of the tracking when applied on a
benchmarking image sequence with real transformations.
It can be noted that IC and HA miss the track of
the plane after the 40th iteration, most probably due
to intensity variation that is introduced in the
sequence for which Taylor series approximation
failed to capture the intensity function. As a
comparison, if we check the performance of the
methods with different degrees of freedom (see
figure 11), we can see that the proposed PSO-Track
method performs better on average. A relatively
larger error in one dimension of the translation, as
well as the rotation for the synthetic transformation
sequence, is observable which could be attributed to
the greater amount of motion in that direction. The
error computation for the real images contains only
the part of the sequence for which the marked region
is valid and remains in the field of view of the
camera.
5 CONCLUSIONS
In this paper, we presented a novel approach toward
solving a camera tracking problem by non-linear
alignment and tracking of the planar regions in the
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
576

Figure 8: Translation and rotation error of the proposed
tracking method plotted for each image in the dataset
(index). First row: error on the synthetic transformation
sequence, second row: error when MAV dataset is used.
Third row: translation and rotation error incurred by all the
participating methods on road dataset.
Figure 9: Comparison of the convergence rate for 2 and 4-
DOF over number of iterations (epochs).
images. A non-linear image alignment is performed
and correct parameters of the transformation are
recovered by optimizing the similarity between the
planar regions in the images. A thorough
comparative analysis of the method over simulated
and real sequence of images reveal that the proposed
method has ability to track planar surfaces when the
motion within the frames is not too large. Large
Figure 10: Performance comparison of proposed method
with other state-of-the-art plane tracking methods. From
top Left: performance of the methods using synthetic
transformations, result of MAV dataset. and performance
of road respectively.
Figure 11: Performance comparison of the proposed
method with other plane tracking methods over different
dimensions of the motion estimation. First chart is the
result of synthetic sequence, second chart shows the result
of first dataset and third chart shows the result of second
dataset.
motions could also be handled by increasing the
number of iterations for an exploration phase of the
method. The insensitivity of the method toward
brightness variations as well as to unavailability of
Bio-inspiredMetaheuristicbasedVisualTrackingandEgo-motionEstimation
577

true plane normal is also tested and algorithm has
been found resilient to such environmental changes.
A possible improvement could be a joint method
with other state-of-the-art methods such as Inverse
Compositional alignment. One way could be to
initialize the IC with the proposed technique which
is run for short number of iterations to obtain a
rough estimate of solution in global search space and
then IC is used for refinement of the solution.
Robust handling of occlusions could also be an
interesting future direction.
REFERENCES
Aarts, E. & Korst, J., 1988. Simulated annealing and
Boltzmann machines. Available at: http://
www.osti.gov/energycitations/product.biblio.jsp?osti_i
d=5311236 [Accessed February 16, 2013].
Baik, Y.K. et al., 2013. Geometric Particle Swarm
Optimization for Robust Visual Ego-Motion
Estimation via Particle Filtering. Image and Vision
Computing. Available at:
http://www.sciencedirect.com/science/article/pii/S026
2885613000760 [Accessed November 29, 2013].
Baker, S. & Matthews, I., 2004. Lucas-kanade 20 years
on: A unifying framework. International Journal of
Computer Vision, 56(3), pp.221–255.
Benhimane, S. & Malis, E., 2007. Homography-based 2d
visual tracking and servoing. The International
Journal of Robotics Research, 26(7), pp.661–676.
Bjorck, A., 1996. Numerical methods for least squares
problems, Society for Industrial Mathematics.
Available at: http://www.google.com/
books?hl=sv&lr=&id=ZecsDBMz5-IC&oi=fnd&pg=
PA1&dq=+Numerical+methods+for+least+squares+pr
oblems&ots=pv2cIqQLF_&sig=kWPokcP6qIVXpuuy
LRApvkBUrY4 [Accessed March 6, 2013].
Cobzas, D. & Sturm, P., 2005. 3d ssd tracking with
estimated 3d planes. In Computer and Robot Vision,
2005. Proceedings. The 2nd Canadian Conference on.
pp. 129–134. Available at: http://ieeexplore.ieee.org/
xpls/abs_all.jsp?arnumber=1443121 [Accessed
February 15, 2013].
Davison, A. J., 2003. Real-time simultaneous localisation
and mapping with a single camera. In Computer
Vision, 2003. Proceedings. Ninth IEEE International
Conference on. pp. 1403–1410. Available at:
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=1
238654 [Accessed February 16, 2013].
Dowson, N. & Bowden, R., 2006. A unifying framework
for mutual information methods for use in non-linear
optimisation. Computer Vision–ECCV 2006, pp.365–
378.
Dowson, N. & Bowden, R., 2008. Mutual information for
lucas-kanade tracking (milk): An inverse
compositional formulation. Pattern Analysis and
Machine Intelligence, IEEE Transactions on, 30(1),
pp.180–185.
Eade, E. & Drummond, T., 2006. Scalable monocular
SLAM. In Computer Vision and Pattern Recognition,
2006 IEEE Computer Society Conference on. pp. 469–
476. Available at: http://ieeexplore.ieee.org/
xpls/abs_all.jsp?arnumber=1640794 [Accessed
February 16, 2013].
Goldberg, D. E., 1989. Genetic algorithms in search,
optimization, and machine learning. Available at:
http://www.citeulike.org/group/712/article/125978
[Accessed February 16, 2013].
Günther, M. & Nissen, V., 2009. A comparison of
neighbourhood topologies for staff scheduling with
particle swarm optimisation. KI 2009: Advances in
Artificial Intelligence, pp.185–192.
Hartley, R. & Zisserman, A., 2000. Multiple view
geometry in computer vision, Cambridge Univ Press.
Available at: http://journals.cambridge.org/
production/action/cjoGetFulltext?fulltextid=289189
[Accessed February 17, 2013].
Irani, M. & Anandan, P., 2000. About direct methods.
Vision Algorithms: Theory and Practice, pp.267–277.
Jurie, F. & Dhome, M., 2002. Hyperplane approximation
for template matching. Pattern Analysis and Machine
Intelligence, IEEE Transactions on, 24(7), pp.996–
1000.
Kennedy, J. & Eberhart, R., 1995. Particle swarm
optimization. In Neural Networks, 1995. Proceedings.,
IEEE International Conference on. pp. 1942–1948.
Available at: http://ieeexplore.ieee.org/
xpls/abs_all.jsp?arnumber=488968 [Accessed
February 15, 2013].
Klein, G. & Murray, D., 2009. Parallel tracking and
mapping on a camera phone. In Mixed and Augmented
Reality, 2009. ISMAR 2009. 8th IEEE International
Symposium on. pp. 83–86. Available at:
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5
336495 [Accessed February 15, 2013].
Lee, G. H. et al., 2010. A benchmarking tool for MAV
visual pose estimation. In Control Automation
Robotics & Vision (ICARCV), 2010 11th International
Conference on. pp. 1541–1546. Available at:
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5
707339 [Accessed September 1, 2012].
Lucas, B. D. & Kanade, T., 1981. An iterative image
registration technique with an application to stereo
vision. In Proceedings of the 7th international joint
conference on Artificial intelligence. Available at:
http://www.ri.cmu.edu/pub_files/pub3/lucas_bruce_d_
1981_1/lucas_bruce_d_1981_1.ps.gz [Accessed
August 30, 2012].
Montemerlo, M. et al., 2002. FastSLAM: A factored
solution to the simultaneous localization and mapping
problem. In Proceedings of the National conference
on Artificial Intelligence. pp. 593–598.
More, J., 1978. The Levenberg-Marquardt algorithm:
implementation and theory. Numerical analysis,
pp.105–116.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
578

Philippides, A. et al., 2012. How Can Embodiment
Simplify the Problem of View-Based Navigation?
Biomimetic and Biohybrid Systems, pp.216–227.
Pirchheim, C. & Reitmayr, G., 2011. Homography-based
planar mapping and tracking for mobile phones. In pp.
27–36. Available at: http://www.scopus.com/
inward/record.url?eid=2-s2.0-
84055193420&partnerID=40&md5=e5215d84ef1b5a8
ad70c09c10c12de6c.
Scaramuzza, D., Fraundorfer, F. & Siegwart, R., 2009.
Real-time monocular visual odometry for on-road
vehicles with 1-point ransac. In Robotics and
Automation, 2009. ICRA’09. IEEE International
Conference on. pp. 4293–4299. Available at:
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5
152255 [Accessed September 2, 2012].
Shannon, C. E., 2001. A mathematical theory of
communication. ACM SIGMOBILE Mobile
Computing and Communications Review, 5(1), pp.3–
55.
Silveira, G., Malis, E. & Rives, P., 2008. An efficient
direct approach to visual SLAM. Robotics, IEEE
Transactions on, 24(5), pp.969–979.
Torr, P. & Zisserman, A., 2000. Feature based methods for
structure and motion estimation. Vision Algorithms:
Theory and Practice, pp.278–294.
Trelea, I. C., 2003. The particle swarm optimization
algorithm: convergence analysis and parameter
selection. Information processing letters, 85(6),
pp.317–325.
Wagner, D., Schmalstieg, D. & Bischof, H., 2009.
Multiple target detection and tracking with guaranteed
framerates on mobile phones. In Mixed and
Augmented Reality, 2009. ISMAR 2009. 8th IEEE
International Symposium on. pp. 57–64. Available at:
http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=5
336497 [Accessed February 16, 2013].
Warren, M. et al., 2010. Unaided stereo vision based pose
estimation. Available at: http://eprints.qut.edu.au/
39881/ [Accessed June 22, 2013].
Zhou, H., Green, P. R. & Wallace, A. M., 2009.
Estimation of epipolar geometry by linear mixed-
effect modelling. Neurocomputing, 72(16–18),
pp.3881–3890.
Zhou, H., Wallace, A. M. & Green, P. R., 2009. Efficient
tracking and ego-motion recovery using gait analysis.
Signal Processing, 89(12), pp.2367–2384.
Bio-inspiredMetaheuristicbasedVisualTrackingandEgo-motionEstimation
579
