
Decentralized Computation of Pareto Optimal Pure Nash Equilibria
of Boolean Games with Privacy Concerns
∗
Sofie De Clercq
1
, Kim Bauters
2
, Steven Schockaert
3
, Mihail Mihaylov
4
, Martine De Cock
1
and Ann Now´e
4
1
Dept. of Applied Mathematics, Computer Science and Statistics, Ghent University, Ghent, Belgium
2
School of Electronics, Electrical Engineering and Computer Science, Queen’s University, Belfast, U.K.
3
School of Computer Science and Informatics, Cardiff University, Cardiff, U.K.
4
Computational Modeling Lab, Vrije Universiteit Brussel, Brussels, Belgium
Keywords:
Boolean Games, Pure Nash Equilibria, Decentralized Learning.
Abstract:
In Boolean games, agents try to reach a goal formulated as a Boolean formula. These games are attractive
because of their compact representations. However, few methods are available to compute the solutions and
they are either limited or do not take privacy or communication concerns into account. In this paper we propose
the use of an algorithm related to reinforcement learning to address this problem. Our method is decentralized
in the sense that agents try to achieve their goals without knowledge of the other agents’ goals. We prove that
this is a sound method to compute a Pareto optimal pure Nash equilibrium for an interesting class of Boolean
games. Experimental results are used to investigate the performance of the algorithm.
1 INTRODUCTION
The notion of Boolean games or BGs has gained a lot
of attention in recent studies (Harrenstein et al., 2001;
Bonzon et al., 2006; Bonzon et al., 2007; Dunne et al.,
2008; Bonzon et al., 2012;
˚
Agotnes et al., 2013). We
explain the concept of a BG with the following exam-
ple (Bonzon et al., 2006).
Example 1
Consider the BG G
1
with N = {1, 2, 3} the set of
agents and V = {a, b, c} the set of Boolean action
variables. Agent 1 controls a, 2 controls b and 3 con-
trols c. Each Boolean variable can be set to true or
false by the agent controlling it. The goal of agent
1 is ϕ
1
= ¬a ∨ (a ∧ b ∧ ¬c). For agent 2 and 3 we
have ϕ
2
= a ↔ (b ↔ c) and ϕ
3
= (a ∧ ¬b ∧ ¬c) ∨
(¬a ∧ b ∧ c), respectively. We see that each goal is
a Boolean proposition and each agent aims to satisfy
its own goal, without knowledge of the other agents’
goals.
This game could, for instance, be understood as
three persons all being able to individually decide to
∗
This research was funded by a Research Foundation-
Flanders project.
go to a bar (set their variable to true) or to stay home
(set their variable to false), without knowing the in-
tentions of others. Given this intuition, the first per-
son either wants to meet the second person without
the third or wants to stay home. The second person
either wants to meet both the first and third person or
wants just one person to go to the bar. The third per-
son’s goal is either to only meet the second person or
to let the first person be alone in the bar. So generally
in BGs, agents try to satisfy an individual goal, which
is formulated as a propositional combination of the
possible action variables of the agents. A neighbour
of an agent i is an agent whose goal depends on an
action controlled by agent i. In Example 1 all agents
are each other’s neighbours.
The strength of BGs lies in their compact repre-
sentation, since BGs do not require utility functions
to be explicitly mentioned for every strategy profile.
Indeed, utility can be derived from the agents’ goals.
This advantage also has a downside: computing so-
lutions such as pure Nash equilibria (PNEs) is harder
than for most other game representations. Deciding
whether a PNE exists in a normal-form game is NP-
complete when the game is represented by the fol-
lowing items: (i) a set of players, (ii) a finite set of
actions per player, (iii) a function defining for each
50
De Clercq S., Bauters K., Schockaert S., Mihaylov M., De Cock M. and Nowe A..
Decentralized Computation of Pareto Optimal Pure Nash Equilibria of Boolean Games with Privacy Concerns .
DOI: 10.5220/0004811700500059
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 50-59
ISBN: 978-989-758-016-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

player which other players may influence their utility,
and (iv) the utility of each player, explicitly given for
all joint strageties of the player himself and the play-
ers influencing him (Gottlob et al., 2003). Deciding
whether a BG has a PNE, on the other hand, is Σ
P
2
-
complete
2
, even for 2-player zero-sum
3
games (Bon-
zon et al., 2006). This high complexity is undoubt-
edly part of the reason why, to the best of our knowl-
edge, there is no tailor-made method to compute the
PNEs of general BGs. However, some techniques are
described in the literature related to obtaining solu-
tions of BGs, e.g. finding PNEs for a certain class of
BGs or the use of bargaining protocols. These tech-
niques, and the differences from our approach, are
discussed in Section 5. Important to note is that, al-
though some of the existing approaches are also de-
centralized, none of them considers the issues of pri-
vacy and limited communication.
In this paper, we approach the problem of com-
puting a PNE of a BG, where we maintain privacy
of goals and reduce the amount of communication
among the agents. Agents could for instance be un-
willing or unable to share their goals, making a cen-
tralized approach unsuitable. Moreover, a central-
ized approach implies higher communication costs,
as agents exchange information with a central au-
thority. To cope with these concerns, we investigate
a decentralized algorithm, namely Win-Stay Lose-
probabilistic-Shift or WSLpS (Mihaylov, 2012). Our
solver is private in the sense that agents do not need to
communicate their goals, neither to a central author-
ity, nor to each other. To evaluate a goal, it is only
required to know what actions were chosen by all rel-
evant agents. Indeed, every agent communicates to
every relevant agent its own actions and whether its
goal is achieved, without specifying the goal.
The solution we obtain with WSLpS is Pareto op-
timal, a well-known and desirable property in game
theory. An outcome of a game is Pareto optimal if
no other outcome makes every player at least as well
off and at least one player strictly better off. Depend-
ing on the application, an additional advantage is that
WSLpS requires only the memory required to repre-
sent the current state. An agent does not remember
previous actions or outcomes, but only uses the last
outcome to choose new actions. As a comparison,
e.g. the Highest Cumulative Reward (HCR) (Shoham
and Tennenholtz, 1993) update rule in reinforcement
learning requires agents to remember the last l cho-
sen actions and outcomes. This advantage of WSLpS
2
This is also known as NP
NP
-complete, a complexity
class at the 2
nd
level of the Polynomial Hierarchy.
3
In zero-sum games, the utility of all players sums up to
0 for every outcome.
could play a crucial role in applications in which
agents have a limited memory, e.g. in wireless sensor
networks (Mihaylov et al., 2011).
The paper is structured as follows. First, some
backgroundon BGs and WSLpS is given in Section 2.
In Section 3 we describe how WSLpS can be used
to coordinate agents to a Pareto optimal PNE, i.e. to
teach agents how to set their action variables in or-
der to satisfy their goal. We prove that this algorithm
will converge to a Pareto optimal PNE iff there ex-
ists a global strategy for which all agents reach their
goal and the parameter choice satisfies an inequality.
In Section 4 we present the results of our experiments
and in Section 5 we discuss related work. Finally we
conclude the paper in Section 6.
2 PRELIMINAIRIES
In this section, we recall BGs and WSLpS, the algo-
rithm we will use to find solution of BGs.
2.1 Boolean Games
The logical language associated with a set of atomic
propositional variables (atoms) V is denoted as L
V
and contains:
• every propositional variable of V,
• the logical constants ⊥ and ⊤, and
• the formulas ¬ϕ, ϕ → ψ, ϕ ↔ ψ, ϕ∧ψ and ϕ∨ ψ
for every ϕ, ψ ∈ L
V
.
An interpretation of V is defined as a subset ξ of V,
with the convention that all atoms in ξ are set to true
(⊤) and all atoms in V \ξ are set to false (⊥). Such an
interpretation can be extended to L
V
in the usual way.
If a formula ϕ ∈ L
V
is true in an interpretation ξ, we
denote this as ξ |= ϕ. A formula ϕ ∈ L
V
is indepen-
dent from p ∈ V if there exists a logically equivalent
formula ψ in which p does not occur. The set of de-
pendent variables of ϕ, denoted as DV(ϕ), collects all
variables on which ϕ depends.
Definition 2.1 (Boolean Game (Bonzon et al., 2006)).
A Boolean game (BG) is a 4-tuple G = (N,V, π, Φ)
with N = {1,. . . , n} a set of agents, V a set of propo-
sitional variables, π : N → 2
V
a control assignment
function such that {π(1), . . ., π(n)} is a partition of
V, and Φ a collection {ϕ
1
, . .. , ϕ
n
} of formulas in L
V
.
The set V contains all action variables controlled by
agents. An agent can set the variables under its con-
trol to true or false. We adopt the notation π
i
for π(i),
i.e. the set of variables under agent i’s control (Bon-
zon et al., 2006). Every variable is controlled by ex-
actly one agent. The formula ϕ
i
is the goal of agent i.
DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns
51

For every p ∈ V we define π
−1
(p) = i iff p ∈ π
i
, so
π
−1
maps every variable to the agent controlling it.
Definition 2.2 (Relevant Agents, Neighbourhood and
Neighbours).
Let G = (N,V,π, Φ) be a BG. The set of relevant
variables for agent i is defined as DV(ϕ
i
). The set
of relevant agents RA(i) for agent i is defined as
∪
p∈DV(ϕ
i
)
π
−1
(p). The neighbourhood of agent i is
defined as Neigh(i) = { j ∈ N : i ∈ RA( j)}. We say
that j is a neighbour of i iff j ∈ Neigh(i) \ {i}.
Example 2
Let G
2
be a 2-player BG with π
i
= {a
i
}, ϕ
1
= a
2
and
ϕ
2
= a
1
∨ ¬a
2
. Then 1 is a relevant agent for 2, but
not for himself. The neighbourhoods in the game are
Neigh(1) = {2} and Neigh(2) = {1,2}.
Note that the relevant agents for agent i are all agents
controlling a variable on which agent i’s goal de-
pends (Bonzon et al., 2007). The neighbours of i are
all agents — excluding i — whose goal depends on a
variable under agent i’s control.
Definition 2.3 (Strategy Profile).
Let G = (N,V, π, Φ) be a BG. For each agent i ∈ N
a strategy s
i
is an interpretation of π
i
. Every n-tuple
S = (s
1
, . .. , s
n
), with each s
i
a strategy of agent i, is a
strategy profile of G.
Because π partitions V and s
i
⊆ π
i
, ∀i ∈ N, we
also use the set notation ∪
n
i=1
s
i
⊆ V for a strategy
profile S = (s
1
, . .. , s
n
). With s
−i
we denote the
projection of the strategy profile S = (s
1
, . .. , s
n
) on
N \ {i}, i.e. s
−i
= (s
1
, . .. , s
i−1
, s
i+1
, . .. , s
n
). If s
′
i
is
a strategy of agent i, then (s
−i
, s
′
i
) is a shorthand for
(s
1
, . .. , s
i−1
, s
′
i
, s
i+1
, . .. , s
n
).
The utility function for every agent i follows di-
rectly from the satisfaction of its goal.
Definition 2.4 (Utility Function).
Let G = (N,V, π, Φ) be a BG and let S be a strategy
profile of G. For every agent i ∈ N the utility function
u
i
is defined as u
i
(S) = 1 iff S |= ϕ
i
and u
i
(S) = 0
otherwise.
A frequentlyused solution conceptin game theory
is the notion of pure Nash equilibrium.
Definition 2.5 (Pure Nash Equilibrium).
A strategy profile S = (s
1
, . .. , s
n
) for a BG G is a pure
Nash equilibrium (PNE) iff for every agent i ∈ N, s
i
is
a best response to s
−i
, i.e. u
i
(S) ≥ u
i
(s
−i
, s
′
i
), ∀s
′
i
⊆ π
i
.
In Table 1, the PNEs of the BGs of Example 1 and 2
are listed, using set notation.
The strategy profile S = (
/
0,
/
0, { c}) = {c} is thus the
unique PNE of G
1
. This means that if the third per-
son goes to the bar, no individual person can change
Table 1: The PNEs of the BGs G
1
and G
2
.
BG G
1
G
2
PNEs {c}
/
0, { a
1
}, { a
1
, a
2
}
his action to improve the outcome for himself. So
the third person cannot improve his own situation by
leaving. Similarly the first and second person could
decide (individually) to come to the bar, but this indi-
vidual decision will not lead to a strictly better out-
come for them, since they already reach their goal
in S. Note that in Example 1 and 2, {c} respectively
{a
1
, a
2
} are the unique Pareto optimal PNEs.
2.2 Win-Stay Lose-probabilistic-Shift
We now recall Win-Stay Lose-probabilistic-Shift
(WSLpS) (Mihaylov,2012),thealgorithmwe will use
to compute solutions in BGs. WSLpS resembles a
reinforcement learning algorithm, because it teaches
agents which actions are most beneficial by reinforc-
ing the incentive to undertake a certain action which
has been successful in the past. The framework to
which it is applied consists of agents, which under-
take certain actions in pursuit of a goal. The agents
are connected with each other through neighbour re-
lations. Note that this concept of neighbours does not
necessarily correspond to Definition 2.2.
Using WSLpS, agents try to maximize a function
called success. There are multiple ways to choose this
function and the idea behind it is that, when every
agent has maximized its success function, all agents
must have reached their goal. In this paper we assume
that the function success, defined for each agent and
each strategy profile, only takes the values 0 and 1.
Given a certain strategy profile S, each agent eval-
uates its success function. If its value is 0 (i.e. the
agent gets negative feedback), it shifts actions with
probability β. In case of positive feedback, it sticks to
its strategy choice. WSLpS was originally introduced
to solve normal-form coordination games. In those
games, all agents control similar actions and they all
try to select a comparable action. For example, if mul-
tiple people want to meet each other in a bar, but for-
get to mention which bar, they should all choose the
same bar in order to meet. One could then define an
agent i to be successful in iteration it iff every neigh-
bour of agent i has picked a similar action as i in the
current strategy profile S
it
. Another option could be
that agent i is successful iff it picked a similar action
as a randomly selected neighbour. So in case of the
bar meeting example, an agent randomly thinks of a
friend and checks whether that friend is in the same
bar. If he is, the agent stays in that bar, if not, it goes
to a random bar with probability β.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
52

Initially the agents randomly choose how to act.
The strategy profile corresponding with this initial
choice is denoted as S
0
, with 0 the iteration num-
ber. WSLpS contains a parameter α ∈ ]0, 1], which
is used to compute the shift probability β in every it-
eration (see Section 3). The probability β depends on
the agent i and the strategy profile S
it
that was chosen
in the current iteration it. The stochasitc algorithm
WSLpS has converged if, with probability 1, no agent
changes its actions anymore.
3 APPLYING WSLpS TO BGs
We can use WSLpS to create an iterative solver for
BGs as follows. In the first iteration every agent ran-
domly sets each of the variables under its control to
true or false, without knowledge of the actions or
goals of the other agents. This can happen simultane-
ously for all agents. Subsequently every agent i eval-
uates the outcome. We assume that agents can check
whether their own goal is achieved. In some appli-
cations it is possible to evaluate a goal without com-
munication between agents, e.g. by observation of the
environment. If not, we allow agents to communicate
their actions to their neighbours. Further communica-
tion between agents is restricted to agents asking their
neighbours whether their goal is satisfied.
We use an additional parameter k, which deter-
mines the maximum number of neighbours we take
into account to evaluate the success function. With
this parameter we can control the amount of com-
munication between the agents. The range of k is
{1, 2, . . . , n}, and if |Neigh(i)| < k, we take i’s en-
tire neighbourhood into account. Therefore, we de-
fine k
′
(i) as min(k, |Neigh(i)|). We denote the set of
all possible subsets of Neigh(i) with k
′
(i) elements
as SS(i, k). For every i ∈ N we define the discretely
uniformly distributed random variable RS(i, k), which
can take all values in SS(i, k). The binomial coeffi-
cient
|Neigh(i)|
k
′
(i)
is the cardinality of SS(i, k). So for
any set rs ∈ SS(i, k), the probability P(RS(i, k) = rs)
is
|Neigh(i)|
k
′
(i)
−1
.
For a BG G = (N,V, π, Φ) the function
success : 2
V
× 2
N
→ {0, 1} is defined as
success(S, rs) = 1 iff u
j
(S) = 1, ∀ j ∈ rs and
success(S, rs) = 0 iff ∃ j ∈ rs : u
j
(S) = 0. For
every agent i ∈ N we define the random variable
success(S, RS(i, k)) which takes values in {0, 1}.
Specifically, success(S, RS(i,k)) = 1 with probability
∑
rs∈SS(i,k)
P(RS(i, k) = rs|success(S, rs) = 1). So the
random variable success(S, RS(i,k)) is 1 with prob-
ability 1 iff for any k
′
(i)-sized randomly selected
subset rs of Neigh(i) the goal of every agent in rs is
satisfied. If we observe the value rs ∈ SS(i, k) for
RS(i, k) in iteration it and success(S
it
, rs) = 1, this
positive feedback leads agent i to keep its current
strategy s
it
i
for the next iteration. If not, the negative
feedback drives the agent to independently flip each
of the variables under its control with a probability of
β(S, i, rs) = max(α −
|{ j∈rs|u
j
(S)=1}|
k
′
(i)
, 0). Flipping a
variable means setting the corresponding variable to
true if it was false and vice versa. Note that RS(i, k)
takes a different value in every iteration, but the same
value is used by i within one iteration. So to compute
the shift probability, the agent uses the same random
subset as it did to evaluate its success function.
WSLpS has converged if, with probability 1, no
agent changes its actions anymore. To prove the con-
vergence of WSLpS, we use Markov chains. A finite
Markov chain (MC) is a random process that transi-
tions from one state to another, between a finite num-
ber of possible states, in which the next state depends
only on the current state and not on the sequence of
states that preceded it (Grinstead and Snell, 1997).
If the transition probabilities between states do not
alter over time, the MC is homogeneous. WSLpS,
applied to a BG, induces a homogeneous finite MC.
Lemma 3.1.
Let G = (N,V,π, Φ) be a BG. Suppose WSLpS is ap-
plied to G and the strategy profile S was chosen in the
current iteration. For any strategy profile S
′
, the prob-
ability of S
′
being chosen in the next iteration only
depends on S.
Proof. For all strategy profiles S and S
′
, define
v(S, S
′
, i) = ((S \ S
′
) ∪ (S
′
\ S)) ∩ π
i
. Intuitively
v(S, S
′
, i) is the set of variables under agent i’s con-
trol which are either true in S and false in S
′
or the
other way around. Let the function w : 2
V
× 2
V
× N
be defined as w(S, S
′
, i) = 1 if v(S, S
′
, i) 6=
/
0 and 0 oth-
erwise. We will abbreviate the notations RS(i, k) and
SS(i, k) to resp. RS and SS. State S transitions to S
′
iff
every agent i ∈ N changes its strategy s
i
to s
′
i
. There-
fore it suffices to prove that, for every i, the probabil-
ity of i changing s
i
to s
′
i
only depends on S. Take an
arbitrary i ∈ N. Then either v(S, S
′
, i) 6=
/
0, i.e. agent i
controls at least one variable that is flipped during a
tranistion from S to S
′
, or v(S,S
′
, i) =
/
0, i.e. no vari-
ables controlled by i are flipped during a transition
from S to S
′
. In the first case, i can only change its
strategy from s
i
to s
′
i
if we observe a value rs ∈ SS
for RS such that success(S, rs) = 0. Moreover, i can
only change its strategy to s
′
i
if it flips every variable
in v(S, S
′
, i), which happens independently with prob-
ability β(S,i, rs). For the other variables controlled
DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns
53

by i, i.e. π
i
\ v(S, S
′
, i), i can only change its strategy
to s
′
i
if it does not flip any of those variables, which
happensindependently with probability 1−β(S, i, rs).
Since RS is a discrete random variable, the probability
of agent i transitioning from s
i
to s
′
i
is
∑
rs∈SS
(P(RS = rs)· (1− success(S, rs))
· β(S, i, rs)
|v(S,S
′
,i)|
· (1 − β(S,i, rs))
|π
i
\v(S,S
′
,i)|
).
In case v(S, S
′
, i) =
/
0, i can only change its strat-
egy from s
i
to s
′
i
if it does not flips variables. This
can happen in two ways: either success(S, rs) = 0 but
all variables keep their current truth assignment, or
success(S, rs) = 1. So in this case the probability of
agent i transitioning from s
i
to s
′
i
is
∑
rs∈SS
(P(RS = rs) · ((1− success(S, rs))
· (1 − β(S,i, rs))
|π
i
|
+ success(S, rs))).
We can compute the probability of S transitioning to
S
′
as
∏
i∈N
((1− w(S, S
′
, i)) ·
∑
rs∈SS
(P(RS = rs) · β(S, i, rs)
|v(S,S
′
,i)|
· (1 − success(S, rs)) · (1− β(S,i, rs))
|π
i
\v(S,S
′
,i)|
)
+ w(S, S
′
, i) ·
∑
rs∈SS
(P(RS = rs) · ((1− success(S, rs))
· (1 − β(S,i, rs))
|π
i
|
+ success(S, rs)))). (1)
It holds that P(RS = rs) = |SS(i, k)|
−1
with
|SS(i, k)| =
|Neigh(i)|
k
′
(i)
. It is now clear that the transi-
tion probability only depends on S.
Definition 3.1.
Let G = (N,V, π, Φ) be a BG. Then the random pro-
cess with all strategy profiles of G as possible states
and with the probability of state S transitioning to
state S
′
given by (1) is called the random process in-
duced by WSLpS applied to G and denoted as M
G
.
The following property follows immediately from
Lemma 3.1 and Definition 3.1.
Proposition 3.2.
Let G = (N,V,π, Φ) be a BG. Then M
G
is a homoge-
nous MC and every iteration of WSLpS applied to G
corresponds to a transition of states in M
G
.
An absorbing state of a MC is a state which tran-
sitions in itself with probability 1. An absorbing MC
(AMC) satisfies two conditions: (i) the chain has
at least one absorbing state and (ii) for each non-
absorbing state there exists an accessible absorbing
state, where a state u is called accessible from a state v
if there exists a positive m ∈ N such that the proba-
bility of state v transitioning in state u in m steps is
strictly larger than 0. AMCs have an interesting prop-
erty (Grinstead and Snell, 1997): regardless of the in-
titial state, the MC will eventually end up in an ab-
sorbing state with probability 1. As such the theory
and terminology of MCs offer an alternative formu-
lation for convergence of WSLpS: WSLpS applied to
a BG G converges iff M
G
is an AMC.
Proposition 3.3.
Let G = (N,V, π, Φ) be a BG with non-trivial goals,
i.e. RA(i) 6=
/
0, ∀i ∈ N. With α >
k−1
k
, WSLpS applied
to G converges iff G has a strategy profile S for which
every agent reaches its goal. Moreover, if WSLpS ap-
plied to G converges, it ends in a Pareto optimal PNE.
Proof. First note that S is an absorbing state of M
G
iff all agents get positive feedback for S with proba-
bility 1, i.e. success(S, rs) = 1, ∀rs ∈ ∪
i∈N
SS(i, k). We
claim this condition is equivalent with u
i
(S) = 1 for
all i. Since every agent must have at least one rele-
vant agent, success(S, rs) = 1 for all rs ∈ ∪
i∈N
SS(i, k)
directly implies u
i
(S) = 1 for every i. Conversely,
if u
i
(S) = 1 for all i, then all agents reach their
goal so in particular every neighbour of every agent
reaches its goal, implying success(S,rs) = 1 for all
rs ∈ ∪
i∈N
SS(i, k). So S is an absorbing state of M
G
iff
every agent reaches its goal in S. Consequently every
absorbing state S of M
G
is a Pareto optimal PNE.
WSLpS converges ⇒ ∃S, ∀i ∈ N : u
i
(S) = 1
This follows from the previous observation and the
fact that convergence of WSLpS applied to G corre-
sponds to M
G
ending up in an absorbing state.
WSLpS converges ⇐ ∃S, ∀i ∈ N : u
i
(S) = 1
Assume that there exists a strategy profile S
g
=
(s
g
1
, . . . , s
g
n
) of G with u
i
(S
g
) = 1 for every agent i. We
already reasoned in the beginning of the proof that S
g
is an absorbing state of M
G
, so it is sufficient to prove
that for each non-absorbingstate there exists an acces-
sible absorbing state. In that case M
G
is an AMC. Let
S
1
= (s
1
1
, . . . , s
1
n
) be an arbitrary non-absorbing state,
then ∃i
1
∈ N: u
i
1
(S
1
) = 0. Consequently there exists
at least one agent which influences i
1
(i.e. RA(i
1
) 6=
/
0)
and for every j ∈ RA(i
1
) there exists a rs ∈ SS( j, k)
with i
1
∈ rs. This implies that for every j ∈ RA(i
1
):
P(success(S
1
, j, RS(j,k)) = 0|S
1
, j) > 0.
There exists a strategy profile S
2
such that s
2
j
=
s
g
j
, ∀ j ∈ RA(i
1
), and for all j ∈ N \ RA(i
1
) either
s
2
j
= s
1
j
or s
2
j
= s
g
j
. Moreover, the probability of
S
1
transitioning to S
2
is non-zero, due to the fol-
lowing reasons. First, we already reasoned that the
probability of all j ∈ RA(i
1
) getting negative feed-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
54
back from S
1
is non-zero. Second, all agents with
positive feedback from S
1
stick with their current
strategy. Third, all agents with negative feedback
can change to any strategy with a non-zero proba-
bility; in particular, the probability that all agents
j, with negative feedback from S
1
, switch to s
g
j
is
non-zero. To see this, note that, given we observe
the value rs ∈ SS( j,k) for RS(j,k), the probabil-
ity of agent j flipping a variable is β(S
1
, j, rs) =
max(α −
|{ j
′
∈rs|u
j
′
(S
1
)=1}|
k
′
( j)
, 0). If agent j got nega-
tive feedback from S
1
, then success(S
1
, rs) = 0 and
there must be at least one neighbour j
′
of j with
u
j
′
(S
1
) 6= 1. Considering the fact that α >
k−1
k
and
k
′
( j) = min(k, |Neigh( j)|), it follows that α >
k
′
( j)−1
k
′
( j)
.
Therefore it holds that β(S
1
, j, rs) is in ]0,1[ if agent
j got negative feedback from S
1
. So irrespective of
whether the transition from s
1
j
to s
2
j
requires flipping
variables or not, the transition probability is non-zero.
Since u
i
1
(S
g
) = 1 and s
2
j
= s
g
j
, ∀ j ∈ RA(i
1
), it follows
that u
i
1
(S
2
) = 1. Either ∀i ∈ N: u
i
(S
2
) = 1, so S
2
is an
accessible absorbing state, or ∃i
2
∈ N: u
i
2
(S
2
) = 0.
As long as there exists an i
l
∈ N such that u
i
l
(S
l
) = 0
we can find a state S
l+1
= (s
l+1
1
, . . . , s
l+1
n
) such that
state S
l
can transition to S
l+1
with non-zero proba-
bility and such that s
l+1
j
= s
g
j
, ∀ j ∈ RA(i
l
), and for all
j ∈ N \RA(i
l
) either s
l+1
j
= s
l
j
or s
l+1
j
= s
g
j
. Moreover,
for every i
m
with 1 ≤ m ≤ l it holds that u
i
m
(S
l+1
) = 1
because ∀ j ∈ RA(i
m
) : s
l+1
j
= s
g
j
. To see this, note that
we assumed that every j ∈ RA(i
m
) switched to s
g
j
in
the transition from S
m
to S
m+1
. In all the next transi-
tions, either j kept the previous strategy or switched
to s
g
j
, so in any case we have s
l+1
j
= s
g
j
. Clearly l = n
is the maximum value for which S
l+1
will be an ab-
sorbing state accessible from S
1
.
In the basic WSLpS algorithm, agents are altru-
istic: they take the satisfaction of their neighbours’
goals into account to reach a solution. Indeed, if the
success function of all relevant agents of i is maxi-
mized, then automatically agent i’s goal is satisfied.
We can also consider an alternative function
success(S, i) = u
i
(S), where agents are self-centered
and only check whether their own goal is satisfied.
However, using this success function, convergence
to a Pareto optimal PNE is no longer guaranteed.
Consider e.g the BG in Example 2. There is one
global solution {a
1
, a
2
}, but for initial states {a
1
} or
/
0 agent 2 has reached its goal and will never alter his
action. We can also combine self-centered and altru-
istic behaviour in the function success(S, i, rs) = 1 iff
u
i
(S) = 1 and u
j
(S) = 1 for every j in a random k
′
(i)-
sized subset rs of neighbours of i. It is easy to see
that Proposition 3.3 remains valid with this success
function.
4 EXPERIMENTS
In this section, we investigate the convergence of
WSLpS in a number of simulations
4
All measure-
ments have been performed on a 2.5 GHz Intel Core
i5 processor and 4GB of RAM. A BG generator was
implemented with 3 parameters: (i) the number of
agents, (ii) the number of variables controlled by one
agent, and (iii) the maximum number of operators ap-
pearing in a goal. We randomly generate goals with
∧, ∨ and ¬ and make sure there is a solution in which
every agent reaches its goal. To this end, we first ran-
domly choose a strategy, and then repeatedly generate
clauses. If the clause is satisfied by the strategy it is
added as a goal to the problem instance; otherwise we
add its negation.
Experiment 1
In our first experiment we generate one BG G with 30
agents, 10 action variables per agent and a maximum
of 15 operators in every goal. We fix the parameter k
of WSLpS to 2 and run 1000 tests on G for various
values for α. Note that Proposition 3.3 only guaran-
tees convergence for α > 0.5. Figure 1 shows the av-
erage number of iterations to convergence in function
of α, within a 95% confidence interval of the mean.
Note that the X-axis does not have a linear scale.
0.505 0.51 0.52 0.53 0.54 0.55 0.56 0.6 0.7
2750
3000
3250
3500
3750
4000
4250
Parameter alpha
Average number of iterations
Figure 1: Iterations to convergence in function of α.
The best value for α lies close to the boundary for
convergence, namely 0.5. This observation has moti-
vated Experiment 3, where we will investigate more
closely how the optimal value for α relates to the the-
oretical boundary of
k−1
k
.
We see that α = 0.54 is the best tested value with
only 2851 (95% CI [2682, 3047]) iterations to conver-
gence on average, with an average computation time
of 62ms (95% CI [58, 66]). When we used the success
4
Implementations and data are available at http://
www.cwi.ugent.be/BooleanGamesSolver.html.
DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns
55

function mentioned at the end of Section 3 instead, i.e.
success(S, i) = 1 iff u
i
(S) = 1 and u
j
(S) = 1 for ev-
ery j in a random k
′
(i)-sized subset of i’s neighbours,
we observed that the convergence was much slower.
For α = 0.54, the average number of iterations to con-
vergence increased substantially to 22× 10
4
(95% CI
[21× 10
4
, 23× 10
4
]); note that this value is not shown
in Figure 1. This increase makes sense: agents start
changing their variables when their own goal is not
satisfied, even in case they do not influence their own
goal. Therefore these changes could drive the agents
away from a strategy that contributes to a global so-
lution. So our decentralized approach favors altruistic
agents. Hence, if agents cared about others, the whole
system will converge much faster, than if agents are
self-centered.
Experiment 2
For this experiment we look at the influence of the
ratio of the number of conjunctions to the number of
disjunctions per goal. To this end, we use a slightly
modified version of our generator, in which we first
guess a strategy and then randomly generate clauses
with the requirednumberof conjunctionsand disjunc-
tions, keeping only those which are satisfied by the
strategy. For each tested ratio, we generate one BG
with 26 agents and 4 variables per agent. We fix the
parameters to k = 2 and α = 0.54 and run 1000 tests
for all ratios. For the ratio 6/0 we do no reach conver-
gence within 10
8
iterations. Figure 2 shows the aver-
age number of iterations to convergence, in a 95% CI
of the mean, scaled logarithmically.
0/6 1/5 2/4 3/3 4/2 5/1
10
0
10
1
10
2
10
3
10
4
10
5
10
6
10
7
Number of conjunctions/disjunctions per goal
Average number of iterations
Figure 2: Iterations to convergence for ratios of conjunc-
tions/disjunctions.
If the goals only contain disjunctions, the average
number of iterations to convergence is 3 (95% CI
[2, 4]), with an average computation time of 2.1ms
(95% CI [2.0, 2.2]). As the number of conjunctions
increases compared to the number of disjunctions, the
average number of iterations to convergence also in-
creases. These results are intuitive: the more conjunc-
tions in the goals, the fewer absorbing states, so the
slower the convergence of WSLpS. Disjunctions have
the exact opposite effect. Note, however, that the po-
sitions of the operators in the goals and the (number
of different) action variables occuring in the goals can
also influence the number of absorbing states.
Experiment 3
In this experimentwe investigate the effect of parame-
ter k on the choice of parameter α. We have generated
one random BG G with 45 agents, 6 action variables
per agent and at most 14 operators occuring in every
goal. The maximum size of a neighbourhood in G
is 12. For each k we determine the best value for α by
empirical analysis, up to 2 digits accuracy, the result
of which is shown in Figure 3.
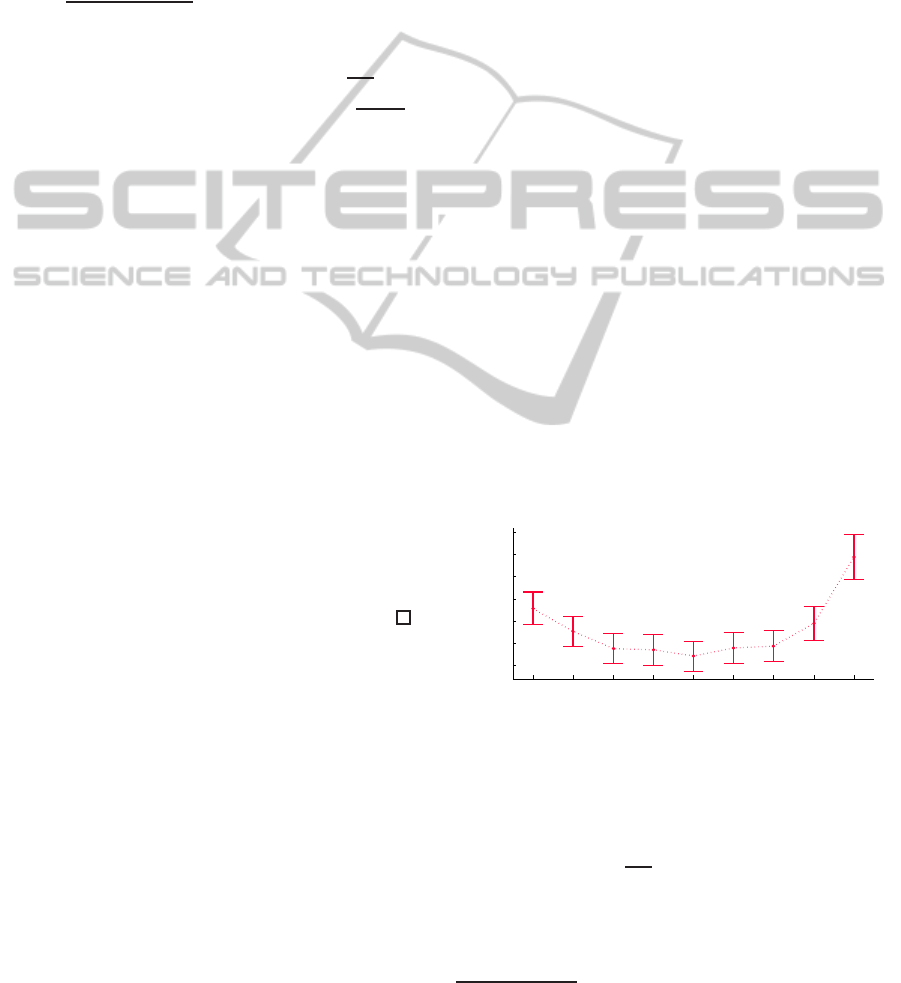
2 3 4 5 6 7 8 9 10 11 12
0.5
0.6
0.7
0.8
0.9
Parameter k
Parameter alpha
theoretical boundary
best alpha
Figure 3: Best α in function of k.
We see that the best value for α always lies surpris-
ingly close to the boundary value for convergence we
derived in Proposition 3.3. In Figure 4 we plot the
average number of iterations to convergence, within
a 95% CI based on 1000 tests, for different values
of k. For each k we fix α with the values of Figure 3.
The average number of iterations to convergence are
scaled logarithmically.
2 3 4 5 6 7 8 9 10 11 12
10
4
10
5
Parameter k
Average number of iterations
fixed alpha
computed alpha
Figure 4: Iterations to convergence in function of k.
In Figure 4 we notice something peculiar when the
value of α is fixed in this way: as we increase the
value of k, the average number of iterations to con-
vergence explodes. This is counterintuitive because
the higher k is, the more information the agents use
to evaluate their success function and choose new ac-
tions. However, some agents may have fewer than k
neighbours, i.e. k
′
(i) 6= k. For those agents another α
would be more suitable, but the basic WSLpS algo-
rithm uses the same α for all agents. To analyze
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
56

this effect, we use an alternative implementation of
WSLpS, in which every individual agent i computes
its own α as
1
100
floor(100·
k
′
(i)−1
k
′
(i)
) + 0.01. Using this
new implementation, we repeat our experiments for
different values of k. The results are also plotted in
Figure 4. This time we get more intuitive results:
WSLpS converges faster when more neighbours are
asked whether their goal is satisfied. Note however
that a higher k implies higher communication costs.
One can thus trade off communication costs for con-
vergence speed.
5 RELATED WORK
In this section we discuss related work and explain
how it differs from ours. One aspect in which it can
differ is the studied solution concept. Indeed, there
exist many solution concepts of BGs besides PNEs,
e.g. the (weak and strong) core (Dunne et al., 2008;
Bonzon et al., 2012), verifiable equilibria (
˚
Agotnes
et al., 2013) and stable sets (Dunne et al., 2008), al-
though this latter term is also used to describe certain
coalitions (Bonzonet al., 2007). In this paper we have
restricted the discussion to PNEs, since it is one of
the most common, intuitive and straightforward solu-
tion concepts in gametheory (Daskalakiset al., 2006).
Note that not all BGs necessarily have a PNE, but
our method is restricted to BGs with a strategy profile
such that every agent reaches its goal, which automat-
ically implies the existence of a PNE. Indeed, a strat-
egy profile satisfying all agents’ goals is by definition
a PNE.
In (Dunne et al., 2008), a bargaining protocol for
BGs is introduced. Agents negotiate in rounds by
successively proposing an outcome which the oth-
ers can accept or reject. Under the quite severe re-
striction that the goals of the agents are positive (i.e.
only ∧ and ∨ may be used), the negotiations end dur-
ing the first round and any strategy profile resulting
from the negotiations is Pareto optimal if the agents
follow specific negotiation strategies. If the restric-
tion is not met, the negotiations can last n rounds —
with n the number of agents — and obtaining a so-
lution is not guaranteed. Like WSLpS, this bargain-
ing protocol is decentralized. It has, however, some
privacy concerns: in contrast to WSLpS, it assumes
that agents know each other’s goals because they try
to make a proposal which is at least as good as the
previous one for all agents which still need to make
a proposal. With an example we illustrate that, even
when the assumption of positive goals and knowledge
of each other’s goals is met, the bargaining protocol
might not be a feasible method. Consider for instance
the situation where agents have to decide which road
to pick to go from point A to point B. Assuming that
all roads are equally suitable, it might be a realistic
assumption that all agents know each other’s goals,
since all agents will probably want to balance the load
on the roads. But clearly it is not realistic that hun-
dreds or thousands of agents will negotiate to decide
who will take which road. In this kind of situations,
involving a large number of agents, WSLpS can nar-
row the communication down to a feasible level, by
choosing a small k. Interestingly, the class of BGs
for which the bargaining protocol is guaranteed to ob-
tain a solution is a subclass of the class of BGs for
which WSLpS is guaranteed to converge to a solu-
tion. Indeed, if the goals of the agents are positive,
then clearly every agent reaches its goal in the strat-
egy profile S = V. Therefore, the restriction on BGs
formulated in Proposition 3.3 is met. Moreover, the
class of BGs in which agents’ goals are positive is
a strict subset of the class of BGs for which a strategy
profile exists such that every agent reaches its goal,
since e.g. the BG in Example 2 does not belong to the
first class, but does belong to the second class.
In (Bonzon et al., 2007), a centralized algorithm
is provided to compute PNEs of BGs for which the ir-
reflexive part of the dependency graph is acyclic. The
dependency graph of a BG connects every agent with
its relevant agents. A BG for which the irreflexive
part of the dependency graph is acyclic has at least
one PNE (Bonzon et al., 2007). Moreover, the au-
thors show that PNEs of BGs can also be found by
computing the PNEs of subgames of the BG. More
specifically, a BG is decomposed using a collection
of stable sets which covers the total set of agents.
It is shown that if there exists a collection of PNEs
of the subgames — with exactly one PNE for ev-
ery subgame — such that the strategies of agents be-
longing to multiple stable sets of the covering agree,
then the strategy profile obtained by combining these
strategies is a PNE of the original BG. It is, how-
ever, important to note that a decomposition based on
stable sets cannot remove or break cycles in the de-
pendency graph. Indeed, the decomposition is only
used to speed up the computation of the PNEs by di-
viding the problem in smaller problems (divide-and-
conquer). Therefore, the usage of the centralized al-
gorithm combined with the decomposition is still re-
stricted to BGs for which the irreflexive part of the
dependency graph is acyclic. It is easy to verify that
there are BGs which meet the restriction of this algo-
rithm but do notmeet the condition of Proposition 3.3.
An example of such a BG is the 2-player BG with
π
i
= {a
i
}, ϕ
1
= a
1
and ϕ
2
= ¬a
1
∧ ¬a
2
. Similarly,
there exist BGs which do have a strategy profile such
DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns
57

that every agent reachesits goal, but cannot be tackled
by the algorithm in (Bonzon et al., 2007). To see this,
consider e.g. the 2-player BG defined by π
i
= {a
i
},
ϕ
1
= a
1
↔ a
2
and ϕ
2
= a
1
↔ ¬a
2
. Note however that
is makes less sense to combine both approaches into
a hybrid algorithm to tackle a wider space of BGs. In-
deed, centralized and decentralized approaches both
have their specific application areas. In some appli-
cations, agents are unable to communicate with each
other, e.g. due to high communication costs or the
lack of common communication channels, and there
might not be a central entity either, making a cen-
tralized approach unsuitable. Consider for instance
the earlier mentioned load balancing problem. Even
though it would be in their advantage, it is question-
able whether e.g. human car drivers would let a cen-
tral authority dictate which road to take to drive to
work. Moreover, some agents’ goals might be to
take a specific road, for some private reason. It is
unlikely that humans would be willing to share this
information with a central authority. Therefore, the
private goal assumption, made by WSLpS, could be
very valuable in some application areas. Due to the
decentralized nature of WSLpS, agents do not need
to share any private information and therefore, un-
like most centralized algorithms, our approach is said
to respect the privacy of agents. In other contexts,
e.g. where the agents are truck drivers on a private
domain, owned and instructed by a company, a cen-
tralized approach might be suitable. Note however
that the BG corresponding to the load balancing prob-
lem does not satisfy the condition that its dependency
graph is acyclic, since every agent depends on every
other agent.
In (Wooldridge et al., 2013), taxation schemes
are investigated for BGs with cost functions. These
BGs impose costs on the agents, depending on which
actions they undertake (Dunne et al., 2008). Via
the agents’ utility, these costs allow for a more fine-
graned distinction between strategy profiles. A tax-
ation scheme in (Wooldridge et al., 2013) consists
of an external agent, called the principal, which im-
poses additional costs to incentivise the agents to ra-
tionally choose an outcome that satisfies some propo-
sitional formula Γ. For example, one can define a
taxation scheme such that the resulting BG has at
least one PNE and all PNEs satisfy Γ. In contrast
to WSLpS, this approach is centralized: a central en-
tity uses global information to find a taxation scheme.
Moreover, these taxation schemes are not developed
with the aim of computing solutions of the original
BG, but they are used to send the agents in certain
desirable directions. The scheme alters the original
solutions such that the agents are coordinated to new,
more desirable solutions.
In (
˚
Agotnes et al., 2013) the privacy of agents is
implicitely adressed by extending the BG framework
with an individual set of observable actions for ev-
ery agent. With these sets, a new solution concept of
verifiable equilibria is defined. These equilibria differ
from others because, when playing the correspond-
ing strategies from the standard notion of Nash equi-
librium, agents are actually able to know they have
reached an equilibrium. However, the authors assume
that the agents can see the complete game: the ac-
tions, the goals, who controls which action variables
and who can observe which action variables. So, in
contrast to WSLpS, the agents are unable to keep their
goal private and the privacy is restricted to the obser-
vation of certain actions. Moreover, the new concept
is introduced more from an uncertainty point of view
than from a privacy point of view.
6 CONCLUSIONS
We proposed a decentralized approach to find so-
lutions of BGs, based on the WSLpS algorithm.
Our method addresses privacy concerns, in the sense
that agents are not required to share their goal with
each other. We have empirically observed that agents
can converge to a global solution with little commu-
nication. Moreover, we discovered and analyzed a
trade-off between the convergence speed of WSLpS
and the communication costs. We have also proved
that, whenever an outcome exists for which every
agent reaches its goal and the parameter choice sat-
isfies the restriction α >
k−1
k
, WSLpS converges
to a Pareto optimal PNE. Furthermore, simulations
have shown that this theoretical boundary for α in-
dicates the most efficient parameter choice, namely
by choosing α marginally larger than
k−1
k
. More-
over, it was emperically found that the performance
of WSLpS can further be improved by letting α de-
pend on the agent, choosing agent i’s α marginally
larger than
k
′
(i)−1
k
′
(i)
.
REFERENCES
˚
Agotnes, T., Harrenstein, P., van der Hoek, W., and
Wooldridge, M. (2013). Verifiable equilibria in
Boolean games. In Proc. IJCAI ’13.
Bonzon, E., Lagasquie-Schiex, M.-C., and Lang, J. (2007).
Dependencies between players in Boolean games. In
Proc. ECSQARU ’07, volume 4724 of LNCS, pages
743–754. Springer.
Bonzon, E., Lagasquie-Schiex, M.-C., and Lang, J.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
58

(2012). Effectivity functions and efficient coalitions
in Boolean games. Synthese, 187:73–103.
Bonzon, E., Lagasquie-Schiex, M.-C., Lang, J., and Zanut-
tini, B. (2006). Boolean games revisited. In Proc.
ECAI ’06, pages 265–269. ACM.
Daskalakis, C., Goldberg, P., and Papadimitriou, C. (2006).
The complexity of computing a Nash equilibrium. In
Proc. STOC ’06, pages 71–78. ACM.
Dunne, P., van der Hoek, W., Kraus, S., and Wooldridge, M.
(2008). Cooperative Boolean games. In Proc. AAMAS
’08, volume 2, pages 1015–1022. IFAAMAS.
Gottlob, G., Greco, G., and Scarcello, F. (2003). Pure Nash
equilibria: hard and easy games. In Proc. TARK ’03,
pages 215–230. ACM.
Grinstead, C. and Snell, J. (1997). Introduction to Proba-
bility. American Mathematical Society.
Harrenstein, P., van der Hoek, W., Meyer, J.-J., and Wit-
teveen, C. (2001). Boolean games. In Proc. TARK
’01, pages 287–298. MKP Inc.
Mihaylov, M. (2012). Decentralized Coordination in Multi-
Agent Systems. PhD thesis, Vrije Universiteit Brussel,
Brussels.
Mihaylov, M., Le Borgne, Y.-A., Tuyls, K., and Now´e, A.
(2011). Distributedcooperation in wireless sensor net-
works. In Proc. AAMAS ’11.
Shoham, Y. and Tennenholtz, M. (1993). Co-learning and
the evolution of social activity. Technical report, Stan-
ford University.
Wooldridge, M., Endriss, U., Kraus, S., and Lang, J. (2013).
Incentive engineering for Boolean games. Artificial
Intelligence, 195:418–439.
DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns
59
