
Finding Outliers in Satellite Patterns by Learning Pattern Identities
Fabien Bouleau
1
and Christoph Schommer
2
1
SES Engineering, Chateau de Betzdorf, L-6815 Betzdorf, Luxembourg
2
University of Luxembourg, Dept. of Computer Science and Communication, Kirchberg, Luxembourg
Keywords:
Data Mining, Time Series, Machine Learning, Pattern Identification.
Abstract:
Spacecrafts provide a large set of on-board components information such as their temperature, power and
pressure. This information is constantly monitored by engineers, who capture the outliers and determine
whether the situation is abnormal or not. However, due to the large quantity of information, only a small
part of the data is being processed or used to perform anomaly early detection. A common accepted research
concept for anomaly prediction as described in literature yields on using projections, based on probabilities,
estimated on learned patterns from the past (Fujimaki et al., 2005) and data mining methods to enhance the
conventional diagnosis approach (Li et al., 2010). Most of them conclude on the need to build a pattern identity
chart. We propose an algorithm for efficient outlier detection that builds an identity chart of the patterns using
the past data based on their curve fitting information. It detects the functional units of the patterns without
apriori knowledge with the intent to learn its structure and to reconstruct the sequence of events described by
the signal. On top of statistical elements, each pattern is allotted a characteristics chart. This pattern identity
enables fast pattern matching across the data. The extracted features allow classification with regular clustering
methods like support vector machines (SVM). The algorithm has been tested and evaluated using real satellite
telemetry data. The outcome and performance show promising results for faster anomaly prediction.
1 INTRODUCTION
The major concerns for satellite operations are the
safety, reliability and durability of the spacecraft fleet.
The spacecrafts are being constantly exposed to the
space weather: radiations, solar flares, peaks of tem-
perature, etc. Besides, due to the distance, there is no
direct visibility on the spacecraft and no way to ex-
amine or fix it. The only health information available
is the sensors information it sends to earth. It is an in-
stant reading of all the on-board sensors (like a snap-
shot) sent at regular intervals of one or two seconds.
Once rebuilt, each sequence of data associated to its
sensor is a continuous time series expanding over sev-
eral years.
Anomaly detection and prediction techniques are
being constantly developed, in order to perform early
detection and avoid the failures, since they have a
cost. They may impact the spacecraft lifetime, its ca-
pacity, or in the worst case end up with a total loss of
control of the satellite. For the most part, expert sys-
tems have been built using satellite engineers’ knowl-
edge. These systems will trigger an alarm before the
anomaly happens. They are thus limited by the satel-
lite engineers knowledge and experience, since they
know only a limited part of the model and spacecraft
history. A study run by ESOC
1
(Mart
´
ınez-Heras et al.,
2012) shows that only 10% of the on-board sensors
data is actually being watched. On top of that, the
amount of data to process reaches terabytes. Process-
ing the whole set of data to perform detection and
classification is nowadays too much time consuming.
There is consequently no systematic classification and
analysis.
The most common way to tackle anomalies con-
sists in looking at data from the past for similar be-
havior in order to identify the root cause and to search
for indicators to help early detection. Currently, sus-
picious satellite data is classified manually by the data
experts themselves. In this paper, we propose an algo-
rithm for efficient outlier detection that builds a char-
acteristics chart for each patterns using the data from
the past using its curve fitting information, in order to
enable anomaly detection and eventually prediction.
Each detected pattern is thus allotted a characteris-
1
European Space Operations Centre, responsible for
controlling the European Space Agency (ESA) satellites
and space probes.
113
Bouleau F. and Schommer C..
Finding Outliers in Satellite Patterns by Learning Pattern Identities.
DOI: 10.5220/0004814301130120
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 113-120
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Conceptual Design. The data flows from the telemetry down to the anomaly detection/prediction. Our algorithm
is represented by the two boxes in-between: the analysis part processes the patterns in order to extract their characteristics
charts, composed of the percentiles explained in section 3.3 and other elements listed in section 3.4. The learning part aims
to compare the newly incoming patterns with the pool of already classified ones, as described in the sections 3.1 and 3.2. The
resulting status vector is then built from the comparisons. The algorithm also integrates the detected anomalies as an updated
characteristics chart, which is then reprocessed.
tics chart with the most relevant statistical elements.
This pattern identity chart allows fast pattern match-
ing across the data and pattern classification. In the
following section, we will present the state of the art
approaches in the space industry. We will then intro-
duce our algorithm for fast pattern matching and the
subsequent techniques that can be used for detecting
the pattern, fuzzy comparison, to measure the quality
of the match and window sliding. The results are pre-
sented and discussed in the next part. We will even-
tually conclude by summarizing the contributions of
this paper in the last part.
2 CONVENTIONAL
APPROACHES TO OUTLIER
DETECTION BY SATELLITE
OPERATOR ENGINEERS
Expert systems are built on the knowledge of the
satellite engineer, sometimes based on the manufac-
turer’s inputs. They apply to one part of the system
only and usually focus on a specific anomaly. Though
very accurate, the number of these systems grows
fast and each of them requires weeks or sometimes
months to be created.
Currently, the model-based approach is handled
the following ways. The first consists in identifying
the signature of the device instead of the anomaly.
The model is then implemented to reproduce its be-
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
114
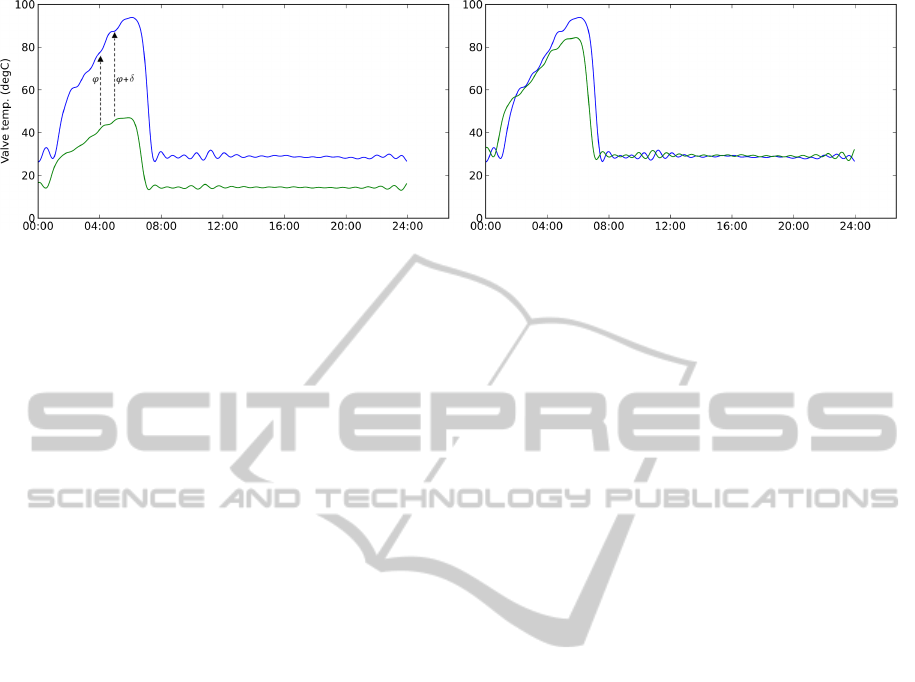
Figure 2: Fourier series representation of two thermal signatures f
1
(lower curve) and f
2
(upper curve). We apply the affine
transforms on the f
1
curve to obtain f
0
1
, which appears on the plot on right hand side. The algorithm evaluated the best fit with
a = 0.502 and k = 0.21, using the points at 180
◦
and 190
◦
.
havior. Anomalies can tentatively be reproduced and
analyzed by satellite engineers depending on the in-
puts. The second model-based approach is to build
a fully fledged model of the spacecraft, commonly
designated as simulator, to either test the maneuvers
against it or use its data output as predicted behavior.
The model-based approach nevertheless suffers
from its lack of flexibility with regards to internal and
environmental reconfigurations. The model needs to
be updated as soon as the satellite hardware is altered
(broken gyro for instance). On top of that, environ-
mental elements such as space weather may alter the
measures. The effort to develop and maintain such a
model is merely prohibitive and only some parts are
considered due to the overall complexity of the satel-
lite.
Systematic analysis methods emerge, relying clas-
sification techniques such as support vector machines
for pattern recognition. These techniques are never-
theless subject to performance issues as the cloud of
point grows. Besides, most of them require complete
reprocessing if only a subset needs to be taken into
account.
All these traditional approaches rely on apriori
knowledge based on a narrow set of data and the data
mining methods suffer from performance issues in-
duced by scalability limitation. The synthesized data
based outlier detection approach is been increasingly
considered. The concept is to use the curve fitting data
to perform pattern matching using specific techniques
and properties. Each pattern is described by an iden-
tity chart in which appear the curve fitting data and
other relevant statistical elements. This identity chart
is then used to perform fast pattern matching across
the entire database. As for the curve fitting, Fourier
series propose an interesting set of properties that al-
low efficient pattern comparison and match quality
measurement. Furthermore, using the sliding window
technique as described by (Beringer and H
¨
ullermeier,
2006) would enable efficient reclassification of the
patterns while saving reprocessing time and therefore
keeping the fast pattern matching performance at its
best.
The existing outlier detection techniques of the
three categories supervised (like support vector ma-
chines), semi-supervised (like transductive support
vector machines or heuristics) and unsupervised (like
k-Means) all rely on cloud of points rather than a re-
duced dataset. The order of magnitude for a single
parameter over the entire lifetime of one spacecraft
(roughly 15 years) is around 500 million points to
process. Besides, this data is globally non-stationary:
some elements are bound to seasonal effects, some to
external factors like solar flares, moon attraction, etc.,
or simply the orbital position of the satellite. Most
algorithms scale with the dimensionality of the in-
put data, inducing a problem of computational cost.
To address this issue, approaches like Symbolic Ag-
gregate approXimation (Lin et al., 2003) as well as
the ones described in Data mining in time series
databases (Last et al., 2004) target the reduction of
dimensionality. It nevertheless performs a systematic
reduction, regardless the semantics of the data. It ob-
viously does not make sense to compare Volts with
Ampers, as does trying to make the intensity signa-
ture of battery charge and discharge match. Detecting
the different phases of a signal, be it power or thermal
signature for instance, is henceforth paramount and
will be addressed by our algorithm.
Although we are following up the thermal signa-
tures of satellite thrusters dataset only along this paper
for the sake of clarity of the explanations, our algo-
rithm has been applied alike over different types of
geostationary satellites and different types of sensor
measures (battery voltage, tank pressure, etc.).
FindingOutliersinSatellitePatternsbyLearningPatternIdentities
115

3 PROPOSED OUTLIER
IDENTIFICATION SYSTEM
Our approach to perform outlier identification is to
extract the features of the time series and enable tra-
ditional classification algorithms. Depending on the
context, the data analysis may nevertheless differ and
require re-classification. Our method provides fast
data processing algorithms by using synthesized in-
formation.
The first question is which curve fitting technique
shall be used in our case in order to preserve ef-
ficiency. From our analysis of the different meth-
ods, we came to the conclusion that discrete Fourier
transform is the most suitable in the case of satellite
telemetry. First of all, because of the interesting prop-
erties of Fourier with regards to the convolution of
two series and how they can be easily factorized that
we elaborate below. Besides, due to the oscillating
nature of the signals and the background induced by
spectrum analysis, most analysis algorithms use this
technique. The curve fitting step is therefore already
available and normalized in the database.
In this section, we introduce how in our method-
ology we proceed to compare two patterns using the
curve fitting information, along with the interesting
properties. We will also show how we measure the
quality of our match, the tools we use for horizontal
identification and eventually how we define the pat-
tern’s characteristics chart.
3.1 Pattern Comparison
Given two Fourier series f
1
and f
2
of the same fre-
quency:
f
1
(t) = k
1
+
N
∑
i=1
a
i,1
cos(iωt + ϕ) + b
i,1
sin(iωt + ϕ)
(1)
f
2
(t) = k
2
+
N
∑
i=1
a
i,2
cos(iωt + ϕ) + b
i,2
sin(iωt + ϕ)
(2)
Once factorized, the convolution R( f
1
, f
2
,t) can
then be written the following way:
R( f
1
, f
2
,t) = k
1
− k
2
+
N
∑
i=1
(a
i,1
−a
i,2
)cos(iωt+ϕ)
+(b
i,2
−b
i,2
)sin(iωt+ϕ)
(3)
The resulting Fourier series represents the dis-
tance between the two original Fourier series f
1
and
f
2
. Let
b
R be the representation of R( f
1
, f
2
,t) in the
frequency domain. We define the quality of the com-
parison ρ(
b
R) by the following equation:
ρ(
b
R) =
N
∑
i=1
b
R(i)
i
2
(4)
Vertical scaling and translation are the only two
purely mathematical transforms we need for the com-
parison. The horizontal transforms require deeper un-
derstanding of the signal itself and will be covered in
the next section. Since the nature of the pattern is
affected, and henceforth the quality of the compari-
son, the measures of the transforms will be kept in the
characteristics chart of the pattern. The transforms are
modeled the following way:
a =
f
2
(ϕ + δ) − f
2
(ϕ)
f
1
(ϕ + δ) − f
1
(ϕ)
k = f
2
(ϕ) − a × f
1
(ϕ)
f
0
1
(θ) = a × f
1
(θ) + k
(5)
3.2 Pattern Reconsolidation
The second diagram on figure 2 shows that even
though we have a good performance match after the
vertical transforms, the algorithm is still missing it.
We are hence introducing the concept of sliding pat-
tern which consists in circularly drifting one of the
two series to the right or to the left.
As for the modeling, let θ be the circular drift
component defined as 0 ≤ θ < 2π. The f
2
series equa-
tion would then be written as follows:
f
2
(t) = k
2
+
N
∑
i=1
a
i,2
cos(iωt + ϕ + θ)+b
i,2
sin(iωt + ϕ + θ)
(6)
The best value of θ is then determined by look-
ing for the minimal ρ(
b
R) as per equation 4. From
there, different approaches are applicable. The most
straightforward (and less optimized) is to cycle θ by
even steps. Other more accurate techniques can also
be applied, such as dichotomy or stochastic research.
Stochastic research remains better since it tackles the
extrema problem.
3.3 Pattern Functional Units
As previously stated, each parameter of the satellite
telemetry comes as a long time series. The individual
patterns that will be required for the training set for
the classification can be either provided or must be al-
gorithmically determined. The telemetry stream and
its curve fit are extracted on a daily basis, regardless
the semantics. This is an arbitrary decision based on
the satellite engineers as there is one station-keeping
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
116
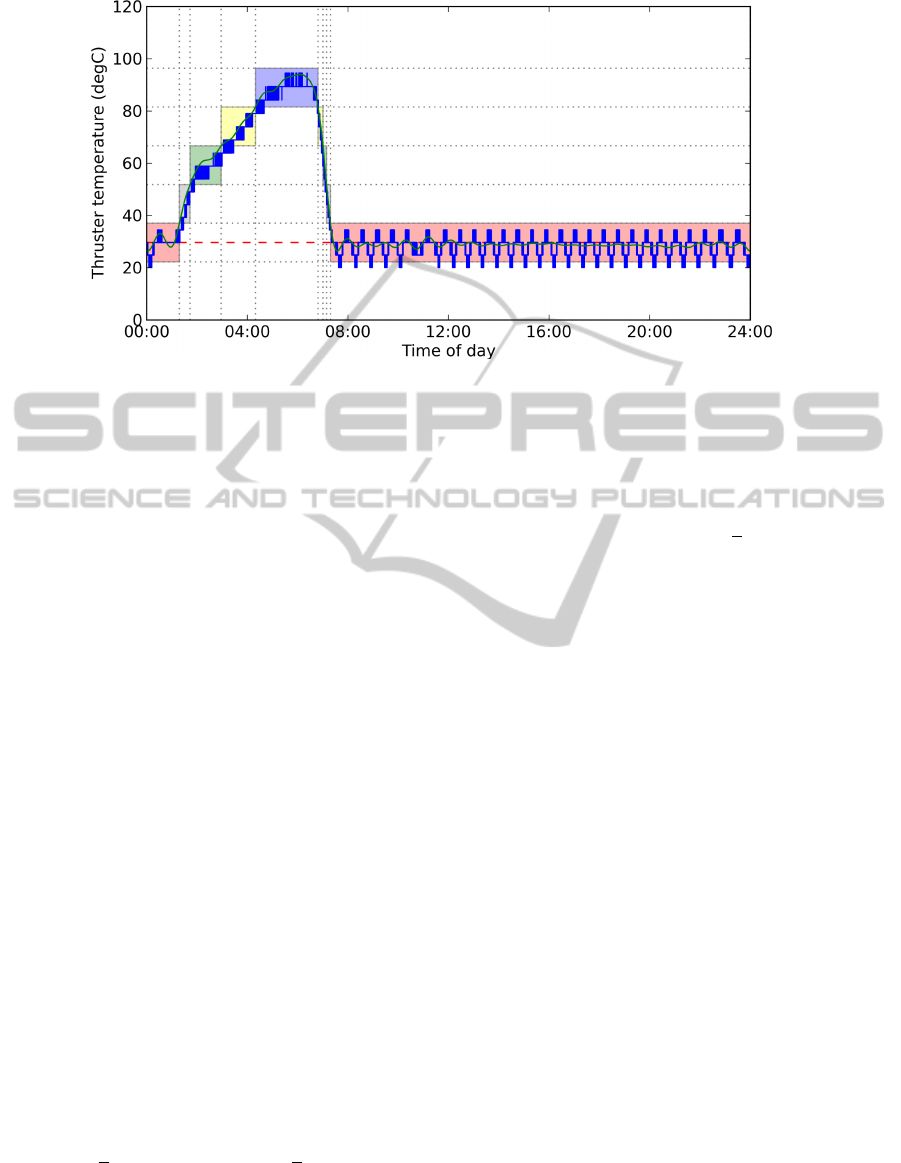
Figure 3: Original data plot divided by the percentiles method. The green curve represents the Fourier series and the dashed
red line the median, used as basepoint to calculate the percentiles. In this example, without apriori knowledge, the blocks
captured the idle phase (red block around the median) and the ”thruster fired” phase. Further analysis show that the fired
phase can be split in 3 steps, that the algorithm still needs to learn.
maneuver per day. The temperature constantly in-
creases between 12am and 8am that day represents
the maneuvers itself, the thruster being idle for the
rest of the day.
With regards to classification, the different events
need to be isolated in an unsupervised way. The al-
gorithm must hence be capable to learn the pattern
structure without apriori knowledge. One intermedi-
ate alternative is to use the information databases in
which the burn times are scheduled by the engineers.
It would nevertheless then relies on user’s input and
can therefore not adapt to new or unexpected situa-
tions. Another approach is to extract the information
from the ground control system itself, where the com-
mand are actually sent to the spacecraft. If this is
more deterministic and accurate, it is still driven by
human actions and enters in the semi-supervised cat-
egory. Some of the actions may furthermore be ini-
tiated by the satellite itself and will thus not be cap-
tured.
For the reasons aforementioned, if these solutions
can be considered as helpers, a proper unsupervised
method is still needed. Our approach is to divide the
signal horizontally by using the percentiles method.
The first element of the percentiles method is the me-
dian
e
m. Let n ∈ N and p the percentile step (p = 0.5
for intervals of 50%). The horizontal areas are defined
by the following thresholds:
n −
1
2
p
e
m ≤ y
n
(x) <
n +
1
2
p
e
m (7)
Let A = ((a
0
, b
0
), . . . , (a
n
, b
n
)) be the DFT coeffi-
cients. The blocks intervals are delimited the follow-
ing way:
X
n
= DT F(A)∩
n −
1
2
p
e
m (8)
Curve fitting with Fourier in the context has the
drawback of smoothing the data. In order not to
miss any outlier, the characteristics chart must there-
fore enumerate the peaks. In this method, we keep
the residuals information per block. With X
i
=
{(x
i,1
, x
0
i,1
), . . . , (x
i,n
, x
0
i,n
)} the list of block intervals
and f (i) the Fourier series, we define S
n
as:
S
n
=
|X
n
|
∑
j=1
x
0
n, j
∑
i=x
n, j
(y − f (i))
2
(9)
As represented on figure 3, the pattern can thus
be subdivided into functional blocks, that will figure
in the characteristics chart. In our original example,
we know by experience that the upper blocks repre-
sent the different phases of the thruster burn while
the lowest one the idle period. As for the characteris-
tics chart, we will not only keep the quantitative block
representation, but the sequence itself. This will help
on one hand to split the active from the idle phases
and, on the other hand to characterize the remain-
ing steps of the thruster burn, which are ”fired”, ”on-
time” and ”cooldown”.
3.4 Definition of the Characteristics
Chart
The characteristics chart is the element to gather all
the features of the studied pattern. The signals how-
FindingOutliersinSatellitePatternsbyLearningPatternIdentities
117

Table 1: Performance of the daily data collection phase for the 16 thermal signatures for a single day. This shows that the data
is made available within 2 minutes.
Collected element Quantity of processed data Processing time
Fourier transform ∼43200 points 8s
Residuals calculation ∼43200 points 75.6s
Percentile blocks calculation 30 FFT coefficients 1.38s
Blocks processing 56 blocks 0.39s
Cumulated results 85.37s
Table 2: Performance of our pattern comparison algorithm for the 16 thermal signatures. The analysis time of the two months
of data decreases to 6 minutes, whereas processing the original cloud of points requires approximately 60 minutes.
Thruster identifier Patterns Vertical scalings Horizontal drifts Processing time
E1inj 42 41 54 15.37s
E2inj 41 24 47 13.92s
W1inj 45 30 63 22.26s
W2inj 42 39 54 14.87s
E1val1 58 59 85 22.87s
E2val1 58 5 58 18.78s
N1val1 57 32 67 20.64s
N2val1 58 46 87 24.03s
N3val1 56 62 101 25.51s
N4val1 59 91 123 29.96s
W1val1 57 41 70 20.81s
W2val1 58 53 67 20.08s
E1val2 57 55 88 25.26s
E2val2 59 17 59 20.16s
W1val2 59 58 91 25.51s
W2val2 58 50 73 24.23s
Cumulated results 864 703 1187 344.26s
ever must be put in their original context. As we de-
fine it, the chart shall comprise the immutable (or ref-
erence) elements:
• Fourier series, as per equation (1)
• Percentiles blocks, as per equation (8)
• Per-block residuals, as per equation (9)
• Timestamp
• Spacecraft context
The timestamp information is usually represented
as day of year plus the year. The day of year allows
the classification of seasonal patterns, while the year
information indicates the elderness of the data. The
spacecraft context elements can be subdivided in two
categories: the spacecraft configuration and its sta-
tus. The configuration part represents the setup of
the spacecraft (switch, valves, etc.) while the status
describes its condition such as a defective sensor or
a broken CPU. This chart remains flexible and addi-
tional features can be experimentally added, such as
ephemeris data and space weather.
The characteristics charts are then classified and
linked with each other in order to preserve the analyt-
ical elements:
• Pattern matching quality, as per equation (4)
• Transform elements, as per equations (5) and (6)
This set of information defines our knowledge
database. It will most likely be stored in a relational
database, for taking advantage of the indexing engine.
4 EXPERIMENTAL VALIDATION
The validation of our approach is quite difficult for
three reasons. First of all, in order to be accurate, the
telemetry of the entire lifetime of the satellite should
be processed. In this paper we will run it on the most
recent subset, that consists in two months of data. Be-
sides, only the propulsion subsystem is analyzed be-
low, the outliers and anomalies of the power subsys-
tem for instance being very difficult for the satellite
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
118

engineers to detect and explain. The propulsion sub-
system henceforth provide a better second sight for
validation. Eventually, despite several anomaly de-
tection and curve fitting techniques exist such as (Li
et al., 2010) and (Fujimaki et al., 2005) none of them
actually plainly address the problematic.
Our experiments dataset is the thrusters tempera-
ture telemetry, since related to our original example.
We are focusing here on the propulsion subsystem of
a single spacecraft. It is composed of 18 parameters,
16 of which representing the thrusters thermal signa-
ture, 1 of which is the timestamp (day-of-year) and
the last being the thruster identifier. The propulsion
subsystem is known to be subject to seasonality, due
to the exposition to the sun. The timestamp parame-
ter is therefore relevant in the analysis. The thruster
identifier provides its cardinality (north, south, west
or east) and correlates with the type of maneuver per-
formed (south-north translation, west-east drift, etc.).
The performance measures depend on how the im-
plementation is performed (programming language,
optimizations, etc.) and the hardware it is run on. To
obtain our results, we have developed the algorithm
using IPython and Matplotlib, since they are accessi-
ble for free to everyone. The benchmarks have been
performed on a HP Proliant DL580 Intel Xeon E7420
dual CPU quad-core 2GHz running Debian 7 amd64.
Table 1 shows the data collection performance for
one day of telemetry on 16 thrusters. It includes
the Fourier fit for the pattern comparison optimiza-
tion, the percentiles blocks calculation for learning
the functional blocks, the Fourier fit residuals per
block for compensating the smoothing effect of the
Fourier series, and the extraction of statistical ele-
ments (median, mode, minmum and maximum) to
search for the optimal thresholds for the percentiles.
Table 2 presents the outlier detection performance
by only using the data presented above. The origi-
nal cloud of data at this stage is completely ignored.
The performance is the best with minimal transforms
and processing time. A higher number of transforms
means additional iterations and wasted processing
time. The ideal case would be to identify the match-
ing points of f
1
into f
2
and calculate the necessary
transforms to achieve it in one iteration only.
As a conclusion, we can observe that the char-
acteristics charts as proposed in our algorithm have
been extracted for the last two months of thruster ther-
mal data in less than six minutes and is ready for be-
ing processed with regular classification technique.
The match rankings are also made available in our
database along the charts in order to mitigate the clas-
sification and re-classify the case being.
5 CONCLUSIONS
In this paper, we have addressed the problem of out-
lier detection in large data warehouse. For this, we
have developed an algorithm using curve fitting infor-
mation to speed up the patterns comparison and effi-
ciently extracting the patterns features for classifica-
tion. Processing years of cumulated time series for
outlier detection is thus made possible.
We have also addressed the problem of data
smoothing induced by Fourier fitting with the per-
centiles method. The nature of the pattern is then re-
fined using the statistical information of the generated
blocks.
In order to keep some flexibility in the analysis,
the pattern matching algorithm introduces the concept
of match quality (equation (4)) on top of pattern trans-
forms. The resulting relevance vector mitigates the
results, allows fuzzy classification and provides met-
rics for re-classification.
The performance of our method is given by ex-
perimenting on a relevant subset of data. Measurable
efficiency elements are provided in terms of quan-
tity and speed. The results show an acceptable ra-
tio in terms of exploitability and availability of the
data: both the data collection and data mining parts
are achieved within minutes and the number of itera-
tions is kept minimal.
The horizontal best fit method by sliding the pat-
tern as presented in our algorithm is a topic of on-
going and future work. In this respect, the technique
can be extended using the sliding window technique
described by (Beringer and H
¨
ullermeier, 2006) or by
determining the functional units of the blocks defini-
tions as per the percentiles method.
The percentiles method on the other hand is
mainly applicable to horizontally shaped time series
such as battery charge cycle in the power subsys-
tem. Improving the semantics detection in differently
shaped signals is a topic of on-going and future work.
Clustering techniques on external information such as
the maneuvers schedule and the spacecraft change of
state can be used to enhance the resulting definitions.
As a conclusion to this paper, we will note that our
approach provides accurate characteristics chart for
the propulsion subsystem of the spacecraft. It extracts
the essential patterns information to enable systematic
processing in the satellite engineers analysis. Beyond,
it preprocesses the pattern matching for classification.
This approach provides directions for further fast out-
lier identification techniques in time-series data.
FindingOutliersinSatellitePatternsbyLearningPatternIdentities
119

ACKNOWLEDGEMENTS
This work has been made within the research project
SPACE, which is an interdisciplinary research project
between the University Luxembourg, Department of
Computer Science and SES Engineering. We thank
all the SPACE members as well as all the SES en-
gineers for their kind support. The views expressed
herein represent the authors’ views only and do not in
any way bind or commit SES Engineering itself.
REFERENCES
Azevedo, D. N. R. and Ambr
´
osio, A. M. Dependability in
satellite systems: An architecture for satellite teleme-
try analysis.
Beringer, J. and H
¨
ullermeier, E. (2006). Online clustering
of parallel data streams. Data & Knowledge Engineer-
ing, 58(2):180–204.
Bouleau, F. and Schommer, C. (2013). Outlier identifica-
tion in spacecraft monitoring data using curve fitting
information. In European Conference on Data Analy-
sis 2013, page 158.
Das, K., Bhaduri, K., and Votava, P. (2011). Distributed
anomaly detection using 1-class svm for vertically
partitioned data. Statistical Analysis and Data Min-
ing, 4(4):393–406.
Deng, K., Moore, A., and Nechyba, M. (1997). Learning to
recognize time series: Combining arma models with
memory-based learning. In IEEE Int. Symp. on Com-
putational Intelligence in Robotics and Automation,
volume 1, pages 246 – 250.
Fujimaki, R., Yairi, T., and Machida, K. (2005). An
anomaly detection method for spacecraft using rele-
vance vector learning. In Ho, T., Cheung, D., and
Liu, H., editors, Advances in Knowledge Discovery
and Data Mining, volume 3518 of Lecture Notes in
Computer Science, pages 785–790.
Fukushima, Y. Telemetry data mining with svm for satellite
monitoring.
Isaksson, C. and Dunham, M. H. (2009). A comparative
study of outlier detection algorithms. In Machine
Learning and Data Mining in Pattern Recognition,
pages 440–453. Springer.
Keogh, E. (2004). T5: Data mining and machine learning
in time series databases.
Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.
(2001). Locally adaptive dimensionality reduction for
indexing large time series databases. In Proceedings
of the 2001 ACM SIGMOD international conference
on Management of data, SIGMOD ’01, pages 151–
162, New York, NY, USA. ACM.
Keogh, E., Lonardi, S., and chi’ Chiu, B. Y. (2002). Finding
surprising patterns in a time series database in linear
time and space. In In In proc. of the 8th ACM SIGKDD
International Conference on Knowledge Discovery
and Data Mining, pages 550–556. ACM Press.
Last, M., Kandel, A., and Bunke, H. (2004). Data mining
in time series databases. World scientific Singapore.
L
´
etourneau, S., Famili, F., and Matwin, S. (1999). Data
mining for prediction of aircraft component replace-
ment. Special Issue on Data Mining.
Li, Q., Zhou, X., Lin, P., and Li, S. (2010). Anomaly de-
tection and fault diagnosis technology of spacecraft
based on telemetry-mining. In Systems and Control
in Aeronautics and Astronautics (ISSCAA), 2010 3rd
International Symposium on, pages 233–236.
Lin, J., Keogh, E., Lonardi, S., and Chiu, B. (2003). A sym-
bolic representation of time series, with implications
for streaming algorithms. In Proceedings of the 8th
ACM SIGMOD workshop on Research issues in data
mining and knowledge discovery, DMKD ’03, pages
2–11, New York, NY, USA. ACM.
Mart
´
ınez-Heras, J.-A., Donati, A., Sousa, B., and Fischer, J.
(2012). Drmust–a data mining approach for anomaly
investigation.
Rebbapragada, U., Protopapas, P., Brodley, C. E., and Al-
cock, C. (2009). Finding anomalous periodic time se-
ries. Machine learning, 74(3):281–313.
Saleh, J. and Castet, J. (2011). Spacecraft Reliability and
Multi-State Failures: A Statistical Approach. John
Wiley & Sons.
Yairi, T., Kawahara, Y., Fujimaki, R., Sato, Y., and
Machida, K. (2006). Telemetry-mining: A machine
learning approach to anomaly detection and fault di-
agnosis for space systems. In Proceedings of the
2nd IEEE International Conference on Space Mission
Challenges for Information Technology, SMC-IT ’06,
pages 466–476, Washington, DC, USA. IEEE Com-
puter Society.
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
120
