Modeling and Algorithm for Dynamic Multi-objective Weighted

Constraint Satisfaction Problem

Tenda Okimoto

1,2

, Tony Ribeiro

, Maxime Clement

and Katsumi Inoue

Transdisciplinary Research Integration Center, Tokyo, Japan

National Institute of Informatics, Tokyo, Japan

The Graduate University for Advanced Studies, Tokyo, Japan

Pierre and Marie Curie University, Paris, France

Keywords:

Dynamic Multi-objective Weighted CSP, (l, s)-Pareto Solution.

Abstract:

A Constraint Satisfaction Problem (CSP) is a fundamental problem that can formalize various applications

related to Artiﬁcial Intelligence problems. A Weighted Constraint Satisfaction Problem (WCSP) is a CSP

where constraints can be violated, and the aim of this problem is to ﬁnd an assignment that minimizes the

sum of weights of the violated constraints. Most researches have focused on developing algorithms for solv-

ing static mono-objective problems. However, many real world satisfaction/optimization problems involve

multiple criteria that should be considered separately and satisﬁed/optimized simultaneously. Additionally,

they are often dynamic, i.e., the problem changes at runtime. In this paper, we introduce a Multi-Objective

WCSP (MO-WCSP) and develop a novel MO-WCSP algorithm called Multi-Objective Branch and Bound

(MO-BnB), which is based on a new solution criterion called (l, s)-Pareto solution. Furthermore, we ﬁrst for-

malize a Dynamic MO-WCSP (DMO-WCSP). As an initial step towards developing an algorithm for solving a

DMO-WCSP, we focus on the change of weights of constraints and develop the ﬁrst algorithm called Dynamic

Multi-Objective Branch and Bound (DMO-BnB) for solving a DMO-WCSPs, which is based on MO-BnB.

Finally, we provide the complexity of our algorithms and evaluate DMO-BnB with different problem settings.

1 INTRODUCTION

A Constraint Satisfaction Problem (CSP) (Mack-

worth, 1992) is a problem that ﬁnds a consistent

assignment of values to variables. A surprisingly

wide variety of Artiﬁcial Intelligence problems can

be formalized as CSPs, e.g., resource allocation

problem (Cabon et al., 1999), scheduling (Verfail-

lie et al., 1996), combinatorial auctions (Sandholm,

1999), and bioinformatics (Backofen and Gilbert,

2001). A Weighted Constraint Satisfaction Problem

(WCSP) (Schiex et al., 1995; Larrosa and Schiex,

2004) is a CSP where constraints can be violated. The

aim of this problem is to ﬁnd an assignment that min-

imizes the sum of weights of the violated constraints.

Most researches on CSPs and WCSPs have fo-

cused on developing algorithms for solving static

mono-objective problems. However, many real world

satisfaction/optimization problems involve multiple

criteria that should be considered separately and satis-

ﬁed/optimized simultaneously. Additionally, they are

often dynamic, i.e., the problem changes at runtime.

In this paper, we formalize a Multi-Objective

Weighted Constraint Satisfaction Problem (MO-

WCSP) which is a WCSP that involves multiple

criteria. We also develop a novel MO-WCSP al-

gorithm called Multi-Objective Branch and Bound

(MO-BnB), which is based on a new solution cri-

terion called (l, s)-Pareto solution. This algorithm

utilizes branch and bound technique and depth-ﬁrst

search strategy, and ﬁnds a subset of Pareto front us-

ing adjustable parameters l and s. In MO-WCSPs,

generally, since trade-offs exist among criteria, there

does not exist an ideal assignment, which minimizes

all criteria simultaneously. Thus, we characterize the

solution of MO-WCSPs using the concept of Pareto

optimality. Solving a MO-WCSP is to ﬁnd the Pareto

front. The Pareto Front is a set of (weighted) cost vec-

tors obtained by Pareto optimal solutions. An assign-

ment is a Pareto optimal solution, so there does not

exist another assignment that improves all of the cri-

teria. A MO-WCSP can be represented using a graph

called constraint graph, in which a node represents a

variable and an edge represents a constraint. In MO-

420

Okimoto T., Ribeiro T., Clement M. and Inoue K..

Modeling and Algorithm for Dynamic Multi-objective Weighted Constraint Satisfaction Problem.

DOI: 10.5220/0004816704200427

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 420-427

ISBN: 978-989-758-015-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

WCSPs, even if a constraint graph has the simplest

tree structure, the size of the Pareto front, i.e., the

number of Pareto optimal solutions, is often exponen-

tial in the number of cost vectors. In such problems,

ﬁnding all Pareto optimal solutions is not realistic.

Furthermore, we ﬁrst introduce a Dynamic Multi-

Objective Weighted Constraint Satisfaction Problem

(DMO-WCSP) which is deﬁned by a sequence of

static MO-WCSPs. As an initial step towards devel-

oping an algorithm for DMO-WCSPs, we focus on

the change of weights of constraints, i.e., we assume

that only the weight of each constraint changes at run-

time. However, the change is unpredictable, i.e., it is

not known in advance how the weights will change

in the next problem in a sequence. This assumption

requires a reactive approach, i.e., we need to solve

each MO-WCSP in a sequence one by one. We also

develop the ﬁrst algorithm called Dynamic Multi-

Objective Branch and Bound (DMO-BnB) for DMO-

WCSPs, which is based on MO-BnB. Finally, we pro-

vide the complexities of these two algorithms, respec-

tively. In section evaluation, we evaluate the perfor-

mance of DMO-BnB with different problem settings.

A Multi-Objective Constraint Optimization Prob-

lem (MO-COP) (Rollon and Larrosa, 2006; Perny and

Spanjaard, 2008; Marinescu, 2010) is the extension

of a mono-objective Constraint Optimization Prob-

lem (COP) (Dechter, 2003; Schiex et al., 1995). A

COP is a problem where the goal is to ﬁnd an as-

signment of values to variables so that the sum of the

resulting costs is optimized. This problem is quite

similar to a WCSP. An MO-COP is a COP that in-

volves multiple criteria. For MO-COPs, various com-

plete algorithms have been developed (Rollon and

Larrosa, 2006; Rollon and Larrosa, 2007; Marinescu,

2009). In an MO-COP, the size of the Pareto front

is exponential in the number of variables, i.e, all as-

signments are Pareto optimal solutions in the worst

case. Since ﬁnding all Pareto optimal solutions be-

comes easily intractable, it is important to consider

fast but incomplete algorithms for large-scale appli-

cations. Also, various incomplete algorithms have

been developed (Rollon and Larrosa, 2006; Perny and

Spanjaard, 2008; Marinescu, 2010). Compared to

these MO-COP algorithms, our proposed algorithm

DMO-BnB is for solving a Dynamic MO-WCSP.

Furthermore, there exists several works on Dy-

namic CSPs (DynCSP) (Dechter and Dechter, 1988;

Faltings and Macho-Gonzalez, 2002). Compared to

these previous works, there exists no work on con-

sidering multiple criteria in a dynamic environment,

as far as the authors are aware. Also, compared to

evolutionary algorithms (Deb et al., 2002; Bringmann

et al., 2011) for Multi-Objective Optimization Prob-

lems (MOOPs), the advantage of our algorithm is that

it can guarantee to ﬁnd all Pareto optimal solutions

and DMO-BnB is an algorithm for DMO-WCSPs.

About application domains of DMO-WCSPs, we

believe that sensor networks would be a promising

area. This problem is a kind of resource allocation

problems which can be formalized as a COP and a

WCSP. For example, consider a sensor network in a

territory, where each sensor can sense a certain area

in this territory. When we consider this problem with

multiple criteria, e.g., data management, quality and

quantity of observation data, and electrical consump-

tion, it can be formalized as a MO-WCSP. Also, when

we consider this problem in a dynamic environment,

e.g., when we need to sense some objectives that in-

vade this territory and move to different areas at run

time, we can apply DMO-WCSP technique.

2 PRELIMINARIES

A Weighted Constraint Satisfaction Problem

(WCSP) (Larrosa and Schiex, 2004) is deﬁned by a

tuple < V, D,C

>, where V is a set of variables, D is

a set of domains, C

is a set of weighted constraints.

A variable x

takes its value from a ﬁnite, discrete

domain D

. A constraint relation (i, j) means there

exists a constraint relation between x

and x

. Each

constraint relation (i, j) has a weight w

, where

∑

(i, j)∈C

= 1. For x

and x

, which have a con-

straint relation, the cost for an assignment {(x

, d

)} is deﬁned by a weighted cost function

, d

) =

(

0 (i, j) is satisfied.

(i, j) is unsatisfied.

(1)

For a value assignment to all variables A, let us denote

R(A) =

∑

(i, j)∈C

,{(x

),(x

)}⊆A

, d

), (2)

where d

∈ D

and d

∈ D

. Solving a WCSP is to ﬁnd

an assignment that minimizes the sum of the value

of all weighted cost functions. When all (weighted)

constraints are satisﬁed, the resulting weighted cost is

zero, and in case all constraints are unsatisﬁed, the to-

tal cost is one. A WCSP can be represented using a

graph called constraint graph, in which a node repre-

sents a variable and an edge represents a constraint.

In thi paper, we assume that all constraints are bi-

nary for simplicity. However, relaxing this assump-

tion to general cases is relatively straight forward.

Example 1 (WCSP). Figure 1 shows a graph col-

oring problem with three variables x

, x

and x

Each variable has to choose a different color with

ModelingandAlgorithmforDynamicMulti-objectiveWeightedConstraintSatisfactionProblem

421

weight

0.1

0.3

0.6

Figure 1: Example of WCSP.

its neighbors and takes its value from a discrete do-

main {black, white}. The right table represents the

weights of all constraints, e.g., when all variables

choose black, all constraints are not satisﬁed, and the

total weighted cost is w

+ w

= 1. The solu-

tions of this problem, i.e, an assignments which mini-

mizes the sum of the weighted costs, are {(x

, black),

, black), (x

, white)} and {(x

, white), (x

, white),

, black)}, and the resulting weighted cost is 0.1.

3 MULTI-OBJECTIVE WCSP

In this section, we formalize a Multi-Objective

Weighted Constraint Satisfaction Problem (MO-

WCSP). Furthermore, we introduce a new solution

criterion called (l, s)-Pareto solution and develop an

algorithm for obtaining all (l, s)-Pareto solutions.

3.1 Model

A Multi-Objective Weighted Constraint Satisfaction

Problem (MO-WCSP) is deﬁned by a tuple <

V, D, C

>, where V is a set of variables, D is a set of

domains, C

= {C

, ...,C

} is a set of multi-

objectiveweighted constraints, where m is thenumber

of objectives. For an objective h (1 ≤ h ≤ m) and a

value assignment to all variables A, let us denote

(A) =

∑

(i, j)∈C

,{(x

),(x

)}⊆A

, d

), (3)

where d

∈ D

and d

∈ D

. Then, the sum of the val-

ues of all weighted cost functions for m objectives

is deﬁned by a cost vector, denoted R(A) = (R

(A),

. . ., R

(A)). When all constraints are satisﬁed, the

resulting cost vector is (0, 0, ..., 0), and in case all

constraints are unsatisﬁed, the resulting cost vector is

(1, 1, ..., 1). Finding an assignment that minimizes all

objective simultaneously is ideal. However, in gen-

eral, since trade-offs exist among objectives, we can-

not obtain such an ideal assignment. Thus, the (op-

timal) solution of a MO-WCSP is characterized by

using the concept of Pareto optimality. A MO-WCSP

can be also represented using a constraint graph.

Deﬁnition 1 (Dominance). For a MO-WCSP and two

cost vectors R(A) and R(A

′

) obtained by assignments

weight

0.1

0.3

0.6

weight

0.6

0.3

0.1

, x

) cost vector

(b, b,b) (1,0)

(b, b,w) (0.1,0,4)

(b, w, b) (0.3,0.7)

(w,b, b) (0.6,0.9)

(w,w,b) (0.1,0.4)

(w,b, w) (0.3,0.7)

(b, w, w) (0.6,0.9)

(w,w,w) (1,0)

Figure 2: Example of bi-objective-WCSP.

A and A

′

, we say that R(A) dominates R(A

′

), denoted

by R(A) ≺ R(A

′

), iff R(A) is partially less than R(A

′

i.e., (i) it holds R

(A) ≤ R

′

) for all objectives h,

and (ii) there exists at least one objective h

′

, such that

′

(A) < R

′

Deﬁnition 2 (Pareto Optimal Solution). For a MO-

WCSP and an assignment A, we say A is the Pareto

optimal solution, iff there does not exist another as-

signment A

′

, such that R(A

′

) ≺ R(A).

Deﬁnition 3 (Pareto Front). For a MO-WCSP, a set

of cost vectors obtained by Pareto optimal solutions is

called a Pareto front. Solving a MO-WCSP is to ﬁnd

the Pareto front.

Example 2 (MO-WCSP). We use the same problem

as in Example 1. Figure 2 shows the tables forweights

and cost vectors for a bi-objective WCSP, where w

represents a weight for objective one and w

for ob-

jective two. For objective one, constraints are same

as in Example 1, i.e., each variable must choose a dif-

ferent color with its neighbors. For the constraints

of objective two, we require that each variable has

to choose the same color with its neighbors. The

right table shows the weighted cost table obtained by

all combination of assignments. When all variables

choose black, the total weighted cost for objective

one is 1, i.e., all constraints are unsatisﬁed, and 0 for

objective two, i.e., all constraints are satisﬁed. The

Pareto optimal solutions of this problemare { {(x

, b),

, b), (x

, b)}, {(x

, b), (x

, w)}, {(x

, w),

, w), (x

, b)}, {(x

, w), (x

, w)} } and the

obtained Pareto front is {(1, 0),(0.1, 0.4)}.

For a MO-WCSP with m objectives, a vector

R(A) = (r

, ..., r

) obtained by an assignment A, a

constant vector l = (l

, ...l

), and a non-negative in-

teger s, where r

and l

are costs for objective h

(1 ≤ h ≤ m), we deﬁne the following novel solution

criteria, l-weak, s-sum, and (l, s)-Pareto solutions.

Deﬁnition 4 (l-weak Pareto Solution). For a MO-

WCSP, we call that A is an l-weak Pareto solution,

iff A is a Pareto optimal solution and it holds r

≤ l

for all objectives h (1 ≤ h ≤ m).

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

422

Deﬁnition 5 (s-sum Pareto Solution). For a MO-

WCSP, we call that A is an s-sum Pareto solution, iff

A is a Pareto solution and it holds r

+ ... + r

≤ s.

Deﬁnition 6 ((l, s)-Pareto Solution). For a MO-

WCSP, we call that A is a (l, s)-Pareto solution, iff

A is an l-weak and an s-sum Pareto solution.

Intuitively, we try to avoid violated constraints

with hight weighted costs adjusting a constant vec-

tor l and want to restrict the sum of weighted costs

of all objectives with a parameter s. In our Ex-

ample 2, when we set l to (0.6, 0.6), and s to 0.7,

we can ignore the Pareto optimal solutions {{(x

, b),

, b), (x

, b)}, {(x

, w), (x

, w)}}. The

(l, s)-Pareto solutions of this problem are {{(x

, b),

, b), (x

, w)}, {(x

, w), (x

, b)}}. For the

cost vector (0.1, 0.4) obtained by these two assign-

ments, they are l-Pareto solutions, since the weighted

costs, i.e., 0.1 for objective one and 0.4 for objective

two, are less than 0.6 (= l

= l

). They are also s-

sum Pareto solutions, since the total weighted costs

of two objectives, i.e., 0.1 + 0.4 = 0.5, are less than

0.7 (= s). Thus, they are the (l, s)-Pareto solutions.

When we set l = (1, 1) and s = 2, i.e., no restriction,

the set of (l,s)-Pareto solutions is the same as the set

of all Pareto optimal solutions.

3.2 Algorithm

We introduce a novel algorithm called Multi-

Objective Branch and Bound (MO-BnB) which can

ﬁnd all (l, s)-Pareto solutions for MO-WCSPs. This

algorithm utilizes a branch and bound technique and

depth-ﬁrst search strategy that are well-known tech-

niques for solving constraint optimization problems.

Algorithm 1 and 2 show the pseudo-code of MO-

BnB. We assume that a variableordering is given. The

input is a MO-WCSP, a constant vector l, and a non-

negative integer s, and the output is the entire set of

(l, s)-pareto solutions (line 1 and 2 in Algorithm 1).

MO-BnB starts with an empty pareto front and a null

cost vector and solves the ﬁrst variable according to

the variable ordering (line 7-10 in Algorithm 1). It

chooses a value for the variable and updates the cost

vector according to the cost tables (step 1 in Algo-

rithm 2). At this moment the obtained cost vector c

has to ensure three properties:

• c is not dominated by the constant vector l

• the sum of the elements of c is not larger than s

• c is not dominated by the current Pareto front PS

If one of the three properties is violated, MO-BnB

branches on the next value of the variable. When its

domain is completely explored, the search branches to

the previous variable and continues the solving (step

Algorithm 1: MO-BnB.

1: INPUT : a MO-WCSP P, a constant vector l and a non-negative integer

2: OUTPUT : the set of all (l, s)-pareto solutions PS

3: Root: the root of P

4: AS: an assignment of variables

5: Cost: the cost vector of AS

6: PS: a set of pairs <cost vector, set of assignments>

7: AS ←

8: PS ←

9: Cost ← null vector

// Launch solving from the root

10: PS ← first.solve(AS,Cost, PS,l, s)

11: return PS

Algorithm 2: Solve(AS,Cost,PS).

1: INPUT : <AS,Cost,PS, l, s>

2: OUTPUT : PS the set of all (l, s)-pareto solutions

3: for each value v

of the variable domain do

4: AS ← v

5: local

cost ← null vector

// step 1: Compute local cost of the choice

6: for each constraint with an ancestor a do

7: v

← value of a in AS

8: local

cost ← local cost + cost(v

, v

)

// cost(v

, v

) is a vector given by the constraint

9: end for

10: new

cost ← Cost + local cost

// step 2: Bound checking

11: if r

> l

, r

∈ new cost, l

∈ l then

12: AS ← (AS \ v

)

13: continue

14: end if

15: if

∑

∈new

cost

> s then

16: AS ← (AS \ v

)

17: continue

18: end if

19: if new cost is dominated by PS then

20: AS ← (AS \ v

)

21: continue

22: end if

// step 3.1: New pareto solution

23: if AS is complete then

24: E ← all elements of PS dominated by new

cost

25: PS ← PS\ E

26: PS ← PS ∪ {(new cost, AS)}

27: continue

28: end if

// step 3.2: Continue solving

29: PS ← next.solve(AS,Cost, PS)

30: AS ← (AS \ v

)

31: end for

32: return PS

2 in Algorithm 2). When a complete assignment is

formed, i.e. no variable left to be assigned, a new

solution is added to the Pareto front PS. All previ-

ous dominated solutions are removed from the Pareto

front and the search continues with the next values

of the variable (step 3.1 in Algorithm 2). If c ful-

ﬁlls the three properties, it continues the solving with

the next variable according to the ordering (step 3.2

in Algorithm 2). The search stops when the whole

search space has been covered by the Branch and

Bound search. MO-BnB ﬁnally outputs the entire set

of (l, s)-Pareto solutions of the MO-WCSP.

Theorem 1. For a MO-WCSP, the memory required

by MO-BnB is O(md

) and the required computa-

ModelingandAlgorithmforDynamicMulti-objectiveWeightedConstraintSatisfactionProblem

423

tion time is O(nmd

+ md

). (which belongs to

O(md

)), where m is the number of objectives, d is

the maximal domain size of variables, and n is the

number of variables.

Proof. Let P be a MO-WCSP and PF be the pareto

front of P. In the worst case, all possible combina-

tions of assignments of variables are Pareto optimal

solutions, i.e., there exists d

Pareto optimal solu-

tions. Thus, with each assignment being associated

with a weighted cost vector of size m, the number of

Pareto optimal solutions is bounded by O(d

). Since

MO-BnB only requires to store the Pareto front dur-

ing solving, its memory use is bound by O(md

Let ST be the number of partial assignment of P

and k be a non-negative integer (1 ≤ k ≤ n). Consider

that only one variable can change its value at a given

time. When no pruning occurs, and since there are

possible assignments for the ﬁrst k variables in a

variable ordering, the number of partial assignments

is given by

∑

k=1

|D|

n+1

− 1

|D| − 1

− 1. Each time a

new value is assigned to a variable, MO-BnB :

• updates the current cost vector c, this operation is

linear in the size of the vector, i.e., (n− 1) × m,

• checks if c is dominated by a constant vector l,

this operation is linear in the size of the vector: m,

• checks if the sum of the element of c is superior to

the parameter s, this operation is linear in the size

of the vector: m.

• checks if c is dominated by the current pareto

front, this operation is linear in the size of the

pareto front: |PF|.

If no pruning occurs, ST represents the maximal oc-

currence of the four above operations. Solving a MO-

WCSP by MO-BnB is then bound by O(|ST| × ((n−

1)m+m+m+|PF|)) = O((

n+1

−1

d−1

−1)+((n+1)m+

)), which belongs to O(nmd

+ md

). Thus, the

runtime complexity belongs to O(md

4 DYNAMIC MO-WCSP

In this section, we formalize a Dynamic Multi-

Objective Weighted Constraint Satisfaction Problem

(DMO-WCSP) which is the extension of a MO-

WCSP. Furthermore, we develop the ﬁrst com-

plete DMO-WCSP algorithm called Dynamic Multi-

Objective Branch and Bound (DMO-BnB) which is

based on MO-BnB. We also provide its complexity.

4.1 Model

A Dynamic Multi-Objective Weighted Constraint Sat-

isfaction Problem, we denote DMO-WCSP, is deﬁned

by a sequence of static MO-WCSPs

< MO-WCSP

, MO-WCSP

, ..., MO-WCSP

> .

(4)

Solving a DMO-WCSP is to ﬁnd a sequence of Pareto

fronts

< PF

, PF

, ..., PF

>, (5)

where PF

(0 ≤ i ≤ k) is the Pareto front of MO-

WCSP

. In our model, it allows to change the number

of variables, constraints, objectives, domain size, and

weights of constraints. In this paper, as an initial step

towards developing an algorithm for solving a DMO-

WCSP, we focus on the change of the weights of con-

straints. Since the change is unpredictable, i.e., it is

not known in advance how the weights will change in

the next problem in a sequence, it requires a reactive

approach. For dynamic problems, there exist two ap-

proaches, i.e., proactive and reactive. For a proactive

approach, all MO-WCSPs in a sequence are known

in advance. Since we know the changes among MO-

WCSPs in a sequence, one possible goal of this ap-

proach is to ﬁnd a common solution in a sequence.

On the other hand, for a reactive approach, since the

next problem MO-WCSP

i+1

becomes known only af-

ter current problem MO-WCSP

was solved, it re-

quires to solve each MO-WCSP in a sequence one by

one. The goal is to ﬁnd a sequence of Pareto fronts.

4.2 Algorithm

We develop the ﬁrst DMO-WCSP algorithm called

Dynamic Multi-Objective Branch and Bound (DMO-

BnB) which is based on MO-BnB. In DMO-BnB, we

reuse the (l, s)-Pareto solutions of the previous prob-

lem, and compute the weighted cost vector which is

utilized as an upper bound for the current problem.

More speciﬁcally, we modiﬁed our algorithm MO-

BnB as follows. The input contains PS

i−1

which

is the Pareto front of the previous problem. DMO-

BnB initializes the Pareto front of the new problem

with PS

i−1

by replacing line 8 in Algorithm 1 by:

PS ← compute(P, PS

i−1

). For each assignment of

i−1

, it computes the new cost vector. The rest of its

pseudo-code is almost the same as that of MO-BnB.

Theorem 2. Let k be the size of the sequence of a

DMO-WCSP. The memory required by DMO-BnB is

given by O(md

) and the required computation time

is given by O(kmd

), where m is the number of ob-

jectives, d is the maximal domain size of variables, n

is the number of variables.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

424

Proof. Solving a DMO-WCSP has the same memory

complexity as solving one MO-WCSP with MO-BnB.

To solve the initial MO-WCSP of a sequence, DMO-

BnB needs to store its Pareto front in the memory,

where the complexity belongs to O(md

). For the

next MO-WCSP, DMO-BnB reuses the Pareto front

of the previous MO-WCSP. It updates the previous

Pareto front by computing the new cost vectors of

each (l,s)-Pareto solution and checks the dominance.

The memory use of this operation is bounded by the

size of the Pareto front, i.e., O(md

). Since DMO-

BnB solves the problems one by one, the memory use

of this algorithm is bounded by O(md

For the computation time, it solves the initial MO-

WCSP of a sequence from scratch. Its complex-

ity belongs to O(md

). To solve the next MO-

WCSP, DMO-BnB starts by revising the previous

Pareto front. For each assignment, it computes a

new cost vector. For each variable, it checks at most

n− 1 constraints. Since there are n variables in an as-

signment, the complexity of this operation belongs to

O(mn

). Since there is d

possible assignments, this

operation belongs to O(d

× mn

). We also check the

dominance among l, s, and previous |PF|, i.e., m +

m+ |PF|. The complexity of the whole preprocessing

is O(d

× (mn

+ m + m + |PF|)) = O(d

× (mn

2m + md

)) = O(mn

+ 2md

+ md

) which be-

longs to O(md

) This preprocessing is done be-

fore solving each MO-WCSP from a sequence, ex-

cept the initial problem. The complexity of solv-

ing a DMO-WCSP with k MO-WCSPs belongs to

O((k−1)(md

)+k(md

) = O(2kmd

−md

) that

belongs to O(kmd

5 EVALUATION

In this section, we evaluate the performanceof DMO-

BnB. In our experiments, we use the following prob-

lem instances. We generate DMO-WCSPs, where the

sequence contains ten MO-WCSPs. All the tests are

made with density one, i.e., complete graph which is

the most difﬁcult problem. For each objective of a

MO-WCSP in a sequence, we generate the same com-

plete graph and choose the weight of a constraint uni-

formly at random so that the sum of the weights of all

constraints is one. Each data point in a graph repre-

sents the average of 50 problem instances. We imple-

mented DMO-BnB in C++ and carried out all exper-

iments on one core running at 2.6GHz with 12GB of

RAM. For a constant vector l, we mostly use setting

l = (l

, ..., l

) with l

= l

, 1 ≤ i, j ≤ m and set ten

hours time limit for the experimentation.

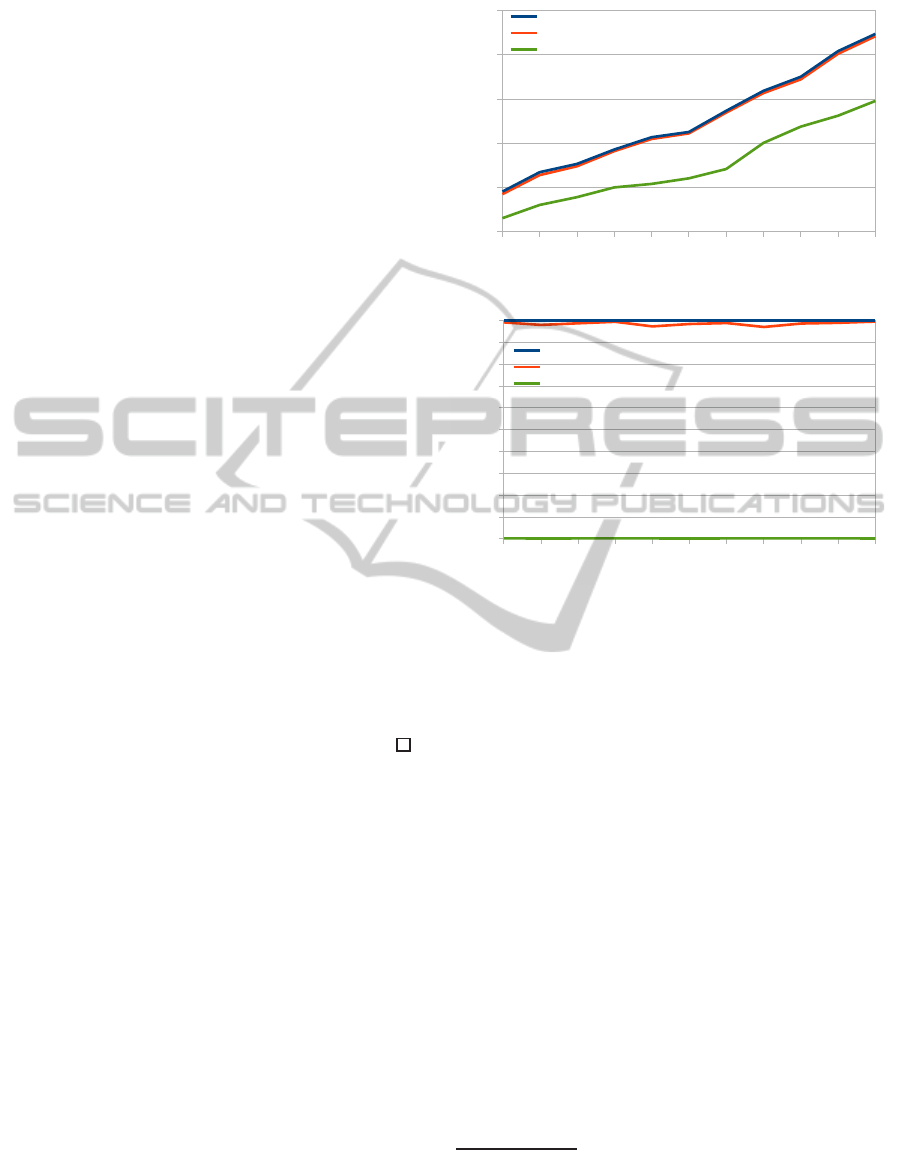
Figure 3 represents the run time of DMO-BnB

          





































Figure 3: Results of run time for s = 1, 2, and 3.

          

























































Figure 4: Results of ratio for s = 1, 2, and 3.

with different s, varying the number of variables, do-

main size is two, the number of objectives is three,

and each value of l is one, i.e., no restriction with l.

The x axis represents the number of variables and y

axis shows the run time. Note that three is the max-

imal value for s, since the number of objectives is

three. We can see that the results for s = 2 and s = 3

are almost same, but the run time improves when

we set s is equal to one. This is because when we

set small s, the solution space becomes smaller, i.e.,

the number of (l, s)-Pareto solutions that DMO-BnB

ﬁnds, in general, becomes smaller

. Figure 4 shows

the ratio of the number of (l, s)-Pareto solutions ob-

tained by DMO-BnB in all Pareto optimal solutions.

When we set that s is three, i.e., no restriction, DMO-

BnB ﬁnds all Pareto optimal solutions which means

100%. In case s is two, the (l, s)-Pareto solutions are

more than 95% of all Pareto optimal solutions. How-

ever, when we decrease s to 1, i.e., strong restriction,

the obtained (l, s)-Pareto solutions are less than 1% of

all. This is because, in our experiments, most Pareto

There is no guarantee that the run time always becomes

smaller, when we set small s. It depends on the Pareto sur-

face which we don’t know in advance. In a special case,

it may happen that Pareto solutions exist only in a speciﬁc

solution area so that the run times for all s are almost same.

ModelingandAlgorithmforDynamicMulti-objectiveWeightedConstraintSatisfactionProblem

425

Table 1: Results of run time and ratio of obtained (l, s)-Pareto solutions. Naive represents the results where MO-BnB is

iteratively applied without any re-used of previous results.

# Var Run time/Precision (and Run time improvement)

Naive s=4 (l=1.0) s=3 (l=1.0) s=2 (l=1.0) s=1 (l=1.0)

10 2.28s 2.11s/100% (7.45%) 2.1s/100% (0.47%) 2.03s/99.21% (3.79%) 0.13s/0.09% (93.83%)

11 7.15s 6.54s/100% (8.53%) 6.51s/100% (0.45%) 6.31s/98.03% (3.51%) 0.46s/0.12% (92.96%)

12 14.97s 14.01s/100% (6.41%) 13.95s/100% (0.42%) 13.45s/98.78% (3.99%) 1.05s/0.07% (92.5%)

13 60.72s 56.18s/100% (7.47%) 55.95s/100% (0.46%) 54.04s/99.46% (3.81%) 2.94s/0.06% (94.76%)

14 207.14s 192.68s/100% (6.54%) 192.51s/100% (0.55%) 186.67s/97.36% (3.57%) 5.88s/0.08% (96.96%)

15 826.72s 762.39s/100% (7.78%) 758.35s/100% (0.52%) 737.54s/98.488% (3.26%) 22.36s/0.03% (97.06%)

optimal solutions exist in the solution space

, where

≤ 1, o

≤ 1, and o

+ o

> 1. We

can see that there is a trade-off between the run time

and the ratio of obtained (l,s)-Pareto solutions, i.e.,

when we set a strong restriction like s = 1, we can

ﬁnd (l,s)-Pareto solutions quickly, but the ratio of ob-

tained (l, s)-Pareto solutions becomes low.

Figure 5 represents the run time of DMO-BnB

with different l, varying the number of variables, do-

main size is two, the number of objectives is three,

and the parameter s is three, i.e., no restriction with

s. Note that one is the maximal value for each el-

ement of a constant vector l. We can see that all

results are almost same

, i.e., adjusting l does not

help to decrease the run time. However, the ratio of

obtained (l, s)-Pareto solutions increases signiﬁcantly

compared to that of in Figure 4. Figure 6 shows the

ratio of obtained (l,s)-Pareto solutions in all Pareto

optimal solutions. We can see that the ratio of ob-

tained (l, s)-Pareto solutions is more than 75% for all

tests. Speciﬁcally, when the number of variables is

20, DMO-BnB can ﬁnd more than 90% of all Pareto

optimal solutions. We consider that adjusting l is suit-

able for obtaining more (l, s)-Pareto solutions, but not

for the run time. We will examine in greater detail

why the ratio becomes higher, when the number of

variables increases.

Table 1 represents the results of run time and ra-

tio of (l, s)-Pareto solutions obtained by DMO-BnB,

where the domain size increases from two to three,

and from three to four for the number of objectives.

Because of the page limitation, we only show the re-

sults for different values of s. We obtained the similar

results as in Figure 3 and 4. The run time of DMO-

BnB for s = 2, 3, and 4 are almost same, but it can

ﬁnd (l, s)-Pareto solutions very quickly in case s = 1.

When the number of variables is 15, the run times for

s = 2, 3, and 4 are more than 730s, but in case s = 1, it

Even when we chose the weight of each constraint uni-

formly at random, we observed these results. We will ex-

amine it for different graph structures, e.g., scale-free, small

world, and tree instead of complete graph.

In case l is less than 0.5, we could not obtain any (l, s)-

Pareto solutions in these problem instances.

          

































Figure 5: Results of run time for l = 0.6, 0.8, and 1.0.

          

















































Figure 6: Results of ratio for l = 0.6, 0.8, and 1.0.

is 22.3s, i.e., 97% improvement. The ratio of obtained

(l, s)-Pareto solutions is more than 97% for s = 2, 3,

and 4, while it is less than 0.03% for s = 1. For a con-

stant vector l, we also obtained the similar results as

in Figure 5 and 6.

In summary, these experimental results reveal that

adjusting parameter s is suitable when we want to ﬁnd

(l, s)-Pareto solutions quickly. On the other hand, in

case we want to have a number of (l, s)-Pareto solu-

tions, adjusting a constant vector l is a good strategy.

As we shown in Figure 4, we obtained the extreme

results for the ratio of (l, s)-Pareto solutions, i.e., al-

most everything for s= 2 and 3, or almost nothing for

s = 1. One might imagine that is it possible to obtain

the results between them. We additionally examine

with a real number of s using the same problem in-

stances of Figure 3 and 4. We show the run time and

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

426

          







































Figure 7: Results of run time for s = 1, 1.2, 2, and 3.

          























 

 





























Figure 8: Results of ratio for s = 1, 1.2, 2, and 3.

the ratio of (l, s)-Pareto solutions for s = 1.2 in Fig-

ure 7 and 8. We can see that it is possible to obtain the

results between extreme results for s = 1 and 2, e.g.,

we can obtain the ratio from 40% to 65% for s = 1.2.

6 CONCLUSIONS

In this paper, we introduced a MO-WCSP and de-

veloped a novel algorithm MO-BnB, which is based

on a new solution criterion called (l,s)-Pareto solu-

tion. Furthermore, we ﬁrst introduced a DMO-WCSP

which is deﬁned by a sequence of static MO-WCSPs.

As an initial step towards developing an algorithm for

solving a DMO-WCSP, we focused on the change of

weights of constraints and developed the ﬁrst algo-

rithm DMO-BnB which is based on MO-BnB. We

also providedthe complexity of our algorithms. In the

experiments, we evaluated our algorithm DMO-BnB

with different problem settings. Our experimental

results showed that adjusting parameter s is suitable

when we want to ﬁnd (l, s)-Pareto solutions quickly.

In case we want to have a number of (l, s)-Pareto so-

lutions, adjusting a constant vector l is good strategy.

For future work, we want to abandon the as-

sumption of this paper that considers only changes of

weights of constraints, and develop a novel algorithm

for DMO-WCSPs. We also consider to develop an

incomplete algorithm for DMO-WCSPs. Since ﬁnd-

ing all Pareto optimal solutions becomes easily in-

tractable, it is important to consider to develop a fast

but incomplete algorithm for large-scale applications.

Finally, we will develop algorithms based on scalar-

ization methods (Ehrgott, 2005; Marler and Arora,

2004; Miettinen, 1999). Also, we intend to apply our

algorithm on challenging real world problems, e.g.,

sensor network and scheduling problems.

REFERENCES

Backofen, R. and Gilbert, D. (2001). Bioinformatics and con-

straints. Constraints, 6(2/3):141–156.

Bringmann, K., Friedrich, T., Neumann, F., and Wagner,

M. (2011). Approximation-guided evolutionary multi-

objective optimization. In IJCAI, pages 1198–1203.

Cabon, B., de Givry, S., Lobjois, L., Schiex, T., and Warners,

J. P. (1999). Radio link frequency assignment. Con-

straints, 4(1):79–89.

Deb, K., Agrawal, S., Pratap, A., and Meyarivan, T. (2002). A

fast and elitist multiobjective genetic algorithm: NSGA-

II. IEEE Trans. Evolutionary Computation, 6(2):182–

197.

Dechter, R. (2003). ConstraintProcessing. MorganKaufmann

Publishers.

Dechter, R. and Dechter, A. (1988). Belief maintenance in

dynamic constraint networks. In AAAI, pages 37–42.

Ehrgott, M. (2005). Multicriteria Optimization. Springer.

Faltings, B. and Macho-Gonzalez, S. (2002). Open constraint

satisfaction. In CP, pages 356–370.

Larrosa, J. and Schiex, T. (2004). Solving weighted csp

by maintaining arc consistency. Artiﬁcial Intelligence,

159(1-2):1–26.

Mackworth, A. (1992). Constraint Satisfaction. In Encyclope-

dia of Artiﬁcial Intelligence, pages 285–293.

Marinescu, R. (2009). Exploiting problem decomposition in

multi-objective constraint optimization. In CP, pages

592–607.

Marinescu, R. (2010). Best-ﬁrst vs. depth-ﬁrst and/or search

for multi-objective constraint optimization. In ICTAI,

pages 439–446.

Marler, R. and Arora, J. (2004). Survey of multi-objective

optimization methods for engineering. Structural and

Multidisciplinary Optimization, 26(6):369–395.

Miettinen, K. (1999). Nonlinear Multiobjective Optimization.

Kluwer Academic Publishers, Boston.

Perny, P. and Spanjaard, O. (2008). Near admissible algo-

rithms for multiobjective search. In ECAI, pages 490–

494.

Rollon, E. and Larrosa, J. (2006). Bucket elimination for mul-

tiobjectiveoptimization problems. Journal of Heuristics,

12(4-5):307–328.

Rollon, E. and Larrosa, J. (2007). Multi-objectiveRussian doll

search. In AAAI, pages 249–254.

Sandholm, T. (1999). An algorithm for optimal winner de-

termination in combinatorial auctions. In IJCAI, pages

542–547.

Schiex, T., Fargier, H., and Verfaillie, G. (1995). Valued con-

straint satisfaction problems: Hard and easy problems.

In IJCAI, pages 631–639.

Verfaillie, G., Lemaˆıtre, M., and Schiex, T. (1996). Russian

doll search for solving constraint optimization problems.

In AAAI/IAAI, Vol. 1, pages 181–187.

ModelingandAlgorithmforDynamicMulti-objectiveWeightedConstraintSatisfactionProblem

427