Time-segmentation- and Position-free Recognition from Video of

Air-drawn Gestures and Characters

Yuki Nitsuma, Syunpei Torii, Yuichi Yaguchi and Ryuichi Oka

Image Processing Laboratory, University of Aizu, Ikki-machi Turuga, Fukushima, Japan

Keywords:

Gesture Recognition, Segmentation-free Recognition, Position-free Recognition, Moving Camera, Dynamic

Programming.

Abstract:

We report on the recognition from video streams of isolated alphabetic characters and connected cursive textual

characters, such as alphabetic, hiragana a kanji characters, drawn in the air. This topic involves a number of

difﬁcult problems in computer vision, such as the segmentation and recognition of complex motion from video.

We utilize an algorithm called time-space continuous dynamic programming (TSCDP) that can realize both

time- and location-free (spotting) recognition. Spotting means that prior segmentation of input video is not

required. Each of the reference (model) characters used is represented by a single stroke composed of pixels.

We conducted two experiments involving the recognition of 26 isolated alphabetic characters and 23 Japanese

hiragana and kanji air-drawn characters. Moreover we conducted gesture recognition experiments based on

TSCDP and showed that TSCDP was free from many restrictions imposed upon conventional methods.

1 INTRODUCTION

Recognition from a video stream of air-drawn ges-

tures and characters will be an important technology

for realizing verbal and nonverbal communication in

human-computer interaction. However, it is still a

challenging research topic involving a number of dif-

ﬁcult problems in computer vision, such as segmenta-

tion in both time and spatial position, and the recog-

nition of complex motion from a video. According to

a survey (Ong and Ranganath, 2005) on gesture and

sign language recognition, the following restrictions

are necessary for realizing a gesture or sign language

recognition system:

• long-sleeved clothing

• colored gloves

• uniform background

• complex but stationary background

• head or face stationary or with less movement

than hands

• constant movement of hands

• ﬁxed body location and pose-speciﬁc initial hand

location

• face and/or left hand excluded from ﬁeld-of-view

• vocabulary restricted or unnatural signing to avoid

overlapping hands or hands occluding face

• ﬁeld-of-view restricted to the hand, which is kept

at ﬁxed orientation and distance to camera

We utilized an algorithm called time-space continu-

ous dynamic programming (TSCDP) (Oka and Mat-

suzaki, 2012) to be free from these restrictions.

TSCDP can realize both position- and segmentation-

free (spotting) recognition of a reference point (pixel)

trajectory from a time-space pattern such as a video.

Spotting means that prior segmentation along the time

and spatial axes of the input video is not required. To

apply TSCDP, we made a reference model of each

character, represented by a single stroke composed

of pixels and their location parameters. TSCDP can

be applied to two kinds of characters in the air, both

isolated and connected characters. Spotting recog-

nition via TSCDP is better suited than conventional

methods for recognizing connected air-drawn charac-

ters. This is because time segmentation is required to

separate connected characters into individual charac-

ters, and because position variation can be large when

connected characters are drawn in the air. We used

a video of air-drawn isolated characters, unadorned

with tagging data such as start or end times or location

of the characters. To obtain video data for connected

characters, we used a famous work from Japanese lit-

erature (the “Waka of Hyakunin Isshu”), drawn in the

air. We made a set of reference point trajectories, each

of which represented a single stroke corresponding to

588

Nitsuma Y., Torii S., Yaguchi Y. and Oka R..

Time-segmentation- and Position-free Recognition from Video of Air-drawn Gestures and Characters.

DOI: 10.5220/0004816805880599

In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 588-599

ISBN: 978-989-758-018-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

an alphabetic, hiragana or kanji character.

2 RELATED WORK

There has been much research into recognizing air-

drawn characters. The projects described below

aimed to recognize isolated air-drawn characters, but

recognition from a video stream of connected air-

drawn characters has not yet been investigated. Okada

and Muraoka et al. (Okada and Muraoka, 2003;

Kolsch and Turk, 2004; Yang et al., 2002) proposed a

method for extracting hand area with brightness val-

ues, together with the position of the center of the

hand, and evaluated that technique. Horo and Inaba

(Horo and Inaba, 2006) proposed a method for con-

structing a human model from images captured by

multiple cameras and obtaining the barycentric po-

sition for this model. By assuming that the ﬁnger-

tip voxels would be those furthest from this posi-

tion, they could extract the trajectory of the ﬁngertips

and were then able to recognize characters via con-

tinuous dynamic programming (CDP) (Oka, 1998).

Sato et al. (Sato et al., 2010) proposed a method that

used a time-of-ﬂight camera to obtain distances, ex-

tract hand areas, and calculate some characteristic

features. They then achieved recognition by compar-

ing reference features and input features via a hidden

Markov model. Nakai and Yonezawa et al. (Nakai and

Yonezawa, 2009; Gao et al., 2000) proposed a method

that used an acceleration sensor (e.g., Wii Remote

Controller) to obtain a trajectory which was described

in terms of eight stroke directions. They then recog-

nized characters via a character dictionary. Scaroff

et al. (Sclaroff et al., 2005; Alon, 2006; Chen et al.,

2003; Gao et al., 2000) proposed a matching method

for time-space patterns using dynamic programming

(DP). Their method used a sequence of feature vectors

to construct a model of each character. Each feature

vector was composed of four elements, namely the lo-

cation (x,y) and the motion parameters (v

) (more

precisely, their mean and variance). Their method

therefore requires users to draw characters within a

restricted spatial area of a scene. Moreover, move-

ment in the background or video captured by a mov-

ing camera is not accommodated, because the motion

parameters for the feature vector of the model would

be strongly affected by any movement in the input

video.

These conventional methods (except for the

method of Ezaki et al. (Ezaki et al., 2010), which

used an acceleration sensor) use local features com-

prising depth, color, location parameters, and motion

parameters, etc., to construct each character model.

They then applied algorithms such as DP or a hidden

Markov model to match models to the input patterns.

Such methods remain problematic because such lo-

cal features are not robust when confronted with the

demandingly severe characteristics of the real world.

For recognizing air-drawn characters, conventional

methods perform poorly if there are occlusions, spa-

tial shifting of the characters drawn in the scene, mov-

ing backgrounds, or moving images captured by a

moving camera.

3 CDP

CDP (Oka, 1998) recognizes a temporal sequence

pattern from an unbounded, non-segmented, tempo-

ral sequence pattern. TSCDP is a version of CDP that

is extended by embedding the space parameter (x, y)

into CDP. To show how TSCDP differs from CDP,

we ﬁrst explain CDP. The algorithm in eqn. (3) calcu-

lates the optimal value of the evaluation function in

eqn. (1). Deﬁne a reference sequence g(τ), 1 ≤ τ ≤ T

and an input sequence f (t),t ∈ (−∞,∞). Deﬁne no-

tations P = (−∞,t],Q = [1,T ], i = 1,2,...,T,t(i) ∈

P,τ(i) ∈ Q, a function r(i) mapping from τ(i) to t(i)

and a vector of functions r = (r(1),r(2),...,r(T )).

There is a constraint between r(i) and r(i + 1) as de-

termined by the local constraint of CDP, as shown in

Figure 1(a). Then the minimum value of the evalua-

tion function is given by

D(t,T ) = min

∑

i=1

{d(r(i),t(i))} (1)

where t(1) ≤ t(2) ≤ · · · ≤ t(T ) = t.

The recursive equation in eqn. (3) gives the minimum

for the evaluation function in equation (1) by accumu-

lating local distances deﬁned by

d(t,τ) = || f (t) − g(τ)||. (2)

The recursive equation for determining D(t, T ) is then

described by

D(t,τ) = min







D(t − 2,τ − 1) + 2d(t − 1,τ) + d(t, τ);

D(t − 1,τ − 1) + 3d(t, τ);

D(t − 1,τ − 2) + 3d(t, τ − 1) + 3d(t, τ).

(3)

The boundary condition is D(t,τ) = ∞, t ≤ 0, τ 6∈

[1,T ]. When accumulating local distances optimally,

CDP performs time warping to allow for variation

from half to twice the reference pattern. The selec-

tion of the best local paths is performed by the recur-

sive equation in eqn. (3). Figure 1 shows two types of

local constraints used in CDP for time normalization.

In this paper, we use type (a). Other normalization

such as from one quarter to four times can be realized

in the similar way.

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

589

(a) Time normalization from half to twice (b) Time normalization from one third to thrice

Figure 1: Two types of local constraints used in CDP. The number attached to each edge (arrow) indicates weight of the path.

4 TSCDP

We adopted a new concept for devising an algorithm

called TSCDP (Oka and Matsuzaki, 2012), which has

two advantages. First, the algorithm can perform

position-free and robust matching between a refer-

ence pattern and an input video captured by a cam-

era in real situations, which might include position

shifting, complex or moving backgrounds, and oc-

clusions. Second, the algorithm can also perform

both recognition and temporal segmentation in a sin-

gle process. Therefore, no segmentation is required

before applying TSCDP. The original paper of (Oka

and Matsuzaki, 2012) proposed this algorithm, but the

TSCDP algorithm based on the concept was neither

well implemented nor evaluated by applying real mo-

tion data. Therefore we conducted both rigorous im-

plementation of the algorithm and experimental eval-

uation with real data. In addition to isolated air-drawn

characters, TSCDP can recognize connected cursive

characters, without start and end times having to be

speciﬁed.

4.1 Evaluation Function for TSCDP

Deﬁne a reference time-space pattern, i.e., a pixel-

based time-space series over a time interval, by

Z(ξ(τ), η(τ)),τ = 1,2,...,T, (4)

where (ξ(τ),η(τ)) is the location in a two-

dimensional plane and Z is the pixel with a gray scale

or color value at that location. Deﬁne an unbounded

input time-space pattern with pixels of gray scale or

color values as

f (x,y,t),(1 ≤ x ≤ M, 1 ≤ y ≤ N, 1 ≤ t < ∞), (5)

where M,N indicate space sizes. Let

(τ) = ξ(τ) − ξ(τ − 1), v

(τ) = η(τ) − η(τ − 1) (6)

be the respective differences in ξ, η along a refer-

ence trajectory. TSCDP does not use parameters ξ, η

explicitly in either the solution algorithm or the lo-

cal distance shown later. In the recursive expres-

sion of eqn. (10), difference parameters v

are used

instead of ξ, η. This enables TSCDP to become

position-free when recognizing moving objects from

a video. The local distance is deﬁned by

d(x, y, τ,t) = kZ(ξ(τ),η(τ)) − f (x,y,t)k. (7)

Next, we deﬁne the minimum value for the evaluation

function. Deﬁne the following notations:

x(i) ∈ X, y(i) ∈ Y, ξ(i) ∈ X , η(i) ∈ Y,

x = x(T ), y = y(T ),

τ(T ) = T, t(T ) = t, (8)

a mapping function u

:(ξ(i),η(i)) → (x(i),y(i)),

Let w = (r,u

,...,u

) be a vector of functions,

where a vector of functions r is deﬁned as for CDP.

The optimized function is deﬁned by

S(x,y,T,t) = min

{

∑

i=1

d(x(i), y(i), τ(i),t(i))}. (9)

4.2 Algorithm for TSCDP

When recognizing isolated or connected air-drawn

characters, temporal shrinking and expansion can oc-

cur together with spatial shifting. The following for-

mula is the algorithm to determine S(x,y,T,t) by per-

forming time-space warping. The allowable ranges

for shrinking and expansion in time and space are

each from half to twice the reference point trajectory.

Temporal shrinking and expansion from half to twice

is realized by the CDP part embedded in TSCDP. Spa-

tial shrinking and expansion from half to double is re-

alized by the second minimum calculation of TSCDP

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

590

using a parameter set A. Here, we use a parameter set

{

,1,2}, which allows spatial shrinking and expan-

sion from half to twice the reference pattern.

A = {

,1,2},

S(x,y,1,t) = 3d(x,y,1,t);

2 ≤ τ ≤ T :

S(x,y,τ,t) = min

α∈A

min











S(x − α · v

(τ),y − α ·v

(τ),τ − 1,t − 2)

+2d(x, y, τ,t − 1) + d(x, y, τ,t);

S(x − α · v

(τ),y − α ·v

(τ),τ − 1,t − 1)

+3d(x, y, τ,t);

S(x − α · (v

(τ) + v

(τ − 1)),

y −α ·(v

(τ) + v

(τ − 1)),τ −2,t −1)

+3d(x − α· v

(τ),

y −α ·v

(τ),τ − 1,t) + 3d(x,y,τ,t).

(10)

The boundary condition is deﬁned by

S(x,y,τ,t) = ∞, d(x,y,τ,t) = ∞,

if (x,y) 6∈ [M,N], t ≤ 0, τ 6∈ [1,T ].

We explain the basic mechanism of the local com-

putation of TSCDP. Eqn. (10) below works for

time-space optimization of the evaluation shown by

eqn. (9) as illustrated in Figure 2. The function of the

time normalization part of eqn. (10) is the same as that

for CDP. The function for space normalization is sim-

ply added to CDP by introducing (x, y)-space to (t,τ)

space. That is, we consider an algorithm working in

a four-dimensional space, (x,y,t, τ). There are three

candidate paths in the scheme of CDP. Space normal-

ization is realized by through each of three paths of

CDP. The simplest case is the third path shown in Fig-

ure 2. The third path of TSCDP includes the third

path of CDP in the four-dimensional space. The two

times t and t − 1 appearing in the third path of CDP

have three points of τ, namely τ,τ − 1,τ − 2. There-

fore we can consider three points in 4D space. Then

the locations of (x,y)-coordinates each from the three

points have τ parameters, respectively. We consider

that each difference between them of the τ parameter

corresponds to each difference of (x,y) of images in

the input video. The difference of (x,y) is represented

by using (v

), as shown in Figure 2. Then we em-

bed the suitable parameters of (v

) into S(x, y, τ,t)

and d(x,y,τ,t) of eqn. (10). In this situation, only

space parameter (x, y) is embedded. No space nor-

malization is realized. If the size of (v

) is modi-

ﬁed, space normalization of the reference pattern can

be realized. Now we consider three types of space

size modiﬁcation at each local optimization, namely

{

,1,2}. This means that any combination of local

spatial size modiﬁcations from half to twice the ref-

erence pattern can be realized. This function is real-

ized by introducing parameters, α, A = {

,1,2}, and

min

α∈A

into the recursive TSCDP equation. The ﬁrst

and second candidate paths of eqn. (10) are handled

in a similar way to the third.

Figure 2: Eqn. (10) realizes an optimal pixel matching using

three candidate paths for time normalization by accumula-

tion of local distance between pixel values of a reference

and an input video. The ﬁgure shows how the third path

works during optimal path selection in 4D space. The other

two paths work in a similar way.

Eventually, the allowable time-space search ar-

rives at the time-space point (x,y,T,t), where the op-

timal matching trajectory is determined by TSCDP,

as shown in Figure 4 for the reference pattern shown

in Figure 3. The allowable search area is dependent

on the reference model for the pixel sequence. That

is, each reference model has its own allowable search

area. This differs from conventional DP matching al-

gorithms, which have the same search areas for all

reference sequences.

Figure 3: A reference pattern (pixel sequence) made by

drawing one stroke sequence (a sequence of location pa-

rameters, ((ξ(τ),η(τ)),τ = 1,2,..., T ) on a two-dimensional

plane, where the length of stroke correspond to T ) of the

reference pattern. Each pixel value Z(ξ(τ),η(τ)) of the ref-

erence pattern is assigned a constant skin color.

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

591

Figure 4: Search space for TSCDP in arriving at the time-

space point (x,y,T,t). Each reference model has its own

search space.

4.3 Time-segmentation-free and

Position-free Recognition

Time-space spotting recognition of a reference pat-

tern from an input video is determined frame by frame

by formula (11), using [local area], which refers to an

area composed of locations satisfying S(x,y,T,t) ≤ h

(where h is a given threshold value). The optimal ac-

cumulated value S(x, y, T,t) at each time t indicates

a two-dimensional scalar ﬁeld with respect to (x,y).

Location (x,y) is called a recognition location if it

satisﬁes the condition S(x,y,T,t) ≤ h. A recognition

location indicates that a category represented by a ref-

erence pattern is recognized at time t ∈ [0,T ] and lo-

cation (x,y). Usually, locations neighboring a recog-

nition location are also recognition locations, because

these locations have similar matching trajectories in

the 4D ((x,y,τ,t)) space. We call such locations the

local area of recognition locations.

At each time t, we can ﬁnd an arbitrary number of

local areas of recognition locations, depending upon

the number of existing time-space patterns, which are

optimally matched with a reference pattern. Then we

can determine a location, denoted by (x

∗

), giving

the minimum value of S(x, y,T,t) for each local area

of recognition locations. The number of these loca-

tions is the number of recognition locations at time

t. A local area of recognition locations can be cre-

ated at an arbitrary position on the (x,y)-plane de-

pending on the query video. This procedure based

on S(x,y,T,t) is the realization of the position-free

(spotting) recognition of TSCDP. On the other hand,

a local minimum location (x

∗

) has time parame-

ter t. If we consider a time series of a local min-

imum location, we can detect a time duration, de-

noted by [t

], satisfying S(x

∗

,T,t) ≤ h,t ∈ [t

The minimum value, denoted by S(x

∗

,T,t

reco

among S(x

∗

,T,t), t ∈ [t

], corresponds to the

recognition considering time-space axes. The time

reco

indicates the end time of a recognized pattern in

an input query video determined without any seg-

mentation in advance. The starting time of the rec-

ognized pattern is determined by back-tracing the

matching paths of TSCDP, starting from t

reco

. This

procedure is the realization of time-segmentation-free

(spotting) recognition based on TSCDP. The follow-

ing are the algorithms for the above procedures. The

term [local area] in the following formulae is the local

area of recognition locations in the above discussion.

∗

,T,t) = arg min

(x,y)∈[local area]

{S(x,y,T,t)} (11)

Spotting recognition for multiple categories is deter-

mined by using multiple reference patterns. Deﬁne

the i-th reference pattern of a pixel series that corre-

sponds to the i-th category by

(ξ(τ),η(τ)),τ = 1, 2, . ..,T

. (12)

TSCDP then detects one or more S

∗

,t) val-

ues as frame-by-frame minimum accumulation values

for which

∗

,t)

≤ h is satisﬁed. The following

equations determine the spotting result for multiple

categories:

∗

(t) = argmin

∗

,T,t)

(13)

∗

,t) = min

(x,y)∈[local area]

(x,y,T,t). (14)

Figure 5 shows the time-segmentation-free (spotting)

recognition of connected cursive air-drawn charac-

ters.

5 RECOGNIZING ISOLATED

AND CONNECTED

AIR-DRAWN CHARACTERS

The ﬁrst step in recognizing air-drawn characters via

TSCDP is to make a model of each character cat-

egory as a reference pattern for TSCDP. Such a

TSCDP reference pattern (model) is determined by

a stream of pixels forming a trajectory on a two-

dimensional plane. This procedure corresponds to a

learning procedure for making a model used in con-

ventional on- or off-line character recognition. But

our method is different from conventional learning

methods. We do not use sample videos for making

reference patterns for TSCDP. A reference pattern of

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

592

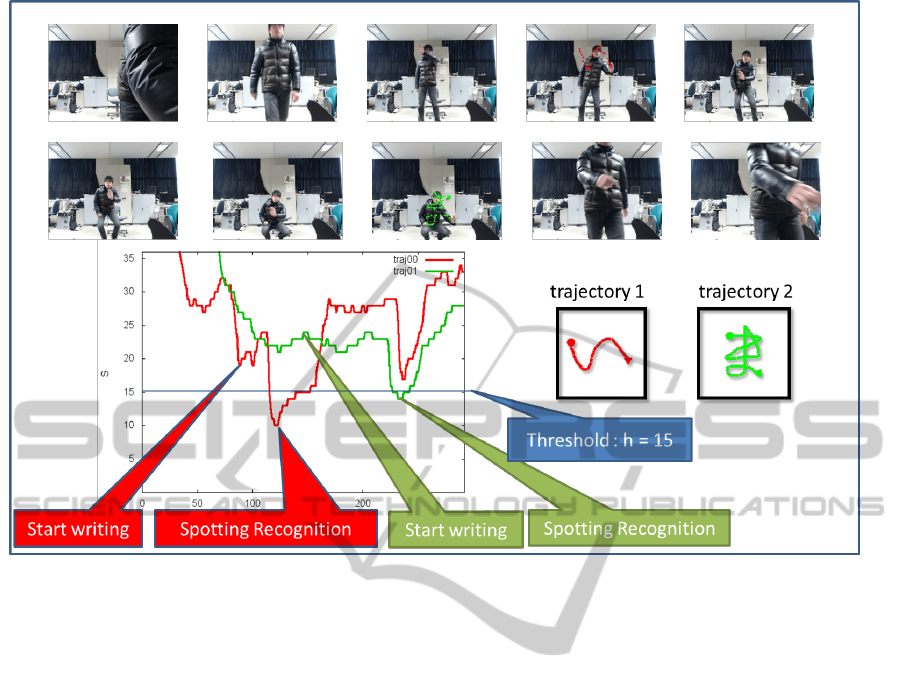
Figure 5: Time-segmentation-free recognition for connected characters. Two connected characters are separately recognized

at different time points without any advance segmentation.

TSCDP is made by air-drawing one stroke projected

on a two-dimensional plane. A stroke is a sequence

of pixel location parameters ξ(τ),η(τ), τ = 1,2,...,T .

The length of stroke corresponds to T . Each lo-

cation of the stroke is assigned a pixel value, de-

noted by Z(ξ(τ),η(τ)), expressing a constant skin

color. Finally, a reference pattern is represented by

Z(ξ(τ), η(τ)),τ = 1, 2, ...,T . The second step is treat-

ment of single-stroke representation of a model. The

stream is composed of connected straight or curved

lines. Categories for characters such as ‘C,’ ‘O,’ and

‘Q’ are easy to represent representing a one-stroke

model. However, most other characters, including

those from the alphabet or Japanese hiragana or kanji

characters, cannot be drawn as a single stroke. For

these characters, we make a one-stroke model for

each character by connecting its separate strokes with

additional strokes in the air. These additional strokes

are not part of the actual strokes belonging to the char-

acter itself. Using this kind of modeling for each char-

acter allows TSCDP to be adopted for their recogni-

tion.

We prepared single-stroke models for each cate-

gory of alphabetic and Japanese hiragana and kanji

characters. The input pattern is obtained from a video

capturing isolated characters or a sequence of con-

nected cursive characters drawn by human hand in the

air. We do not specify start and end times for each

drawing, even for isolated characters. Furthermore,

neither a color ﬁnger cap, nor gloves, nor any special

device is required. Applying TSCDP to a character

model with category number i, we obtain i

∗

(t), where

the time t is called the spotting time. If multiple i

∗

(t)

values are detected, the output for the time is deter-

mined by selecting the category with the maximum

stroke length.

6 EXPERIMENTS

6.1 Database and Performance for a

Comparison Study

We use videos obtained by capturing air-drawn ges-

tures and characters made with one stroke in a

position-free style. Some of these gesture videos in-

clude large occlusion, multiple gestures in a single

scene, or connected characters. Some were captured

by a moving camera with moving backgrounds. There

had been no experiment in the past applying conven-

tional methods to such real data. Therefore, it seems

impossible to compare our method with the conven-

tional methods described in such papers (Okada and

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

593

Muraoka, 2003; Horo and Inaba, 2006; Sato et al.,

2010; Nakai and Yonezawa, 2009). Moreover our

database is rather small. Therefore the experiments

in this paper are regarded as preliminary trials to in-

vestigate whether or not TSCDP can loosen the many

constraints mentioned in the introduction, before ap-

plying a large amount of real world data. For recog-

nizing air-drawn characters, we apply two kinds of

spotting recognitions using the same TSCDP. Final

decision algorithms are different from each other, as

mentioned in section 4.

6.2 Experimental Conditions

Figure 6(a) shows a set of reference patterns for an al-

phabet of 26 categories, each of which is a one-stroke

model. In addition, we manually constructed a set of

(a) Alphabet

(b) Hiragana & kanji

Figure 6: List of reference patterns. Each reference pattern

is made with a single stroke.

one-stroke characters, as seen in Figure 6(b). These

one-stroke characters are used in the Waka poem and

are to be regarded as the reference patterns when ap-

plying TSCDP in parallel. Figure 7 shows a sheet of

paper upon which the famous Japanese “Waka Imako-

muto” from the “Hyakunin Isshu” is written. We

showed this example to the participants, who were in-

structed to write the Waka in the air using connected

characters. The experimental conditions were as fol-

Figure 7: Waka shown to participants drawing a sequence

of connected cursive characters in the air.

lows.

• Video:

– Frames per second: 20 fps

– Resolution: 200 × 150 pixels

– RGB color was used (8 bits per color)

• Reference patterns for characters:

– A single stroke reference pattern was con-

structed manually for each character.

– A spatial distance of 3 pixels along a stroke in

the plane (ξ,η) corresponding to 50 ms in pa-

rameter τ of Z. These parameters were ﬁxed for

all reference patterns. The total length L pixels

of each stroke determined T = (L/3)×50 ms in

• Scene:

– Each participant wrote isolated characters in

the air without start or end time being speciﬁed.

They also wrote connected characters in the air,

column by column, without a speciﬁed start or

end time.

• There were three participants.

• The list of hiragana and kanji models (26 alpha-

betic characters) for recognizing isolated charac-

ters is shown in Figure 6(a).

• The list of models (23 references) for recogniz-

ing connected characters is shown in Figure 6(b).

A writing style for connected cursive characters

(Figure 7) was shown to each person in advance.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

594

• Parameters:

– The spotting recognition threshold was h = 15

(ﬁxed).

– Z = (R, G, B) = (190, 145, 145) (ﬁxed).

– The Euclidian norm was used for calculating

local distance.

6.3 Constraint-free Characteristics of

TSCDP

As mentioned in the introduction, most conventional

methods for realizing recognition systems are subject

to many restrictions. A system based on TSCDP can

dispense with many of them, as our experimental re-

sults indicate. We did not use long-sleeved clothing or

colored gloves. Using a reference pattern composed

of pixels with a constant skin color, TSCDP optimally

matches only an existing pixel sequence in an input

video without identifying any areas of hand or ﬁnger.

The inferred skin tone is roughly determined, with-

out deep investigation, but TSCDP works well using

the heuristically derived skin color. TSCDP seems ro-

bust to variation of skin color, and is also robust when

faced with complex and moving backgrounds because

TSCDP matches only with a sequence of pixels (a

macroscopic and speciﬁed motion with time length

T ), so that moving backgrounds, including head or

face movement, do not interfere with the total accu-

mulation value of local distances if moving T back-

grounds do not have a similar motion to a reference

pattern with a period of around length T . Figure 8 il-

lustrates the recognition of a gesture in a complex and

moving background.

TSCDP allows non-linear variations from half to

twice the velocity of movement by the CDP part

of TSCDP. Figure 5 illustrates time-segmentation

recognition without any segmentation of start and end

time after adapting non-linear time variations. Con-

straints of ﬁxed body location and pose-speciﬁc ini-

tial hand location are required by conventional meth-

ods because they are position-dependent when they

match a model sequence and a video. The model

of conventional methods is made by features includ-

ing location parameters, so that whole target match-

ing procedures are still location-dependent. A refer-

ence pattern of TSCDP also has location parameters.

However the dependency of location is relaxed by di-

rectly embedding the location difference u

(τ),v

(τ)

into time-warping candidate paths. The position-free

characteristic property is then realized in TSCDP, as

mentioned in §4.3. The allowance for spatial shrink-

ing and expansion is also realized by embedding path

selection for contracting and dilating spatial size us-

ing both u

(τ),v

(τ) and a set of parameters A in the

recursive equation of TSCDP. Figure 9 shows a ref-

erence pattern that is recognized at different positions

when multiple and similar time-space patterns exist in

a video.

TSCDP also is robust when presented with over-

lapping hands or occlusion, because these cases in-

crease only a relatively small part of accumulated

value S(x,y,T,t), depending on the spatial and tem-

poral size of overlapping hands or hands over face or

occlusion by objects between the camera and subject.

Figure 10 shows how a gesture is correctly recognized

even in the presence of occlusion. A reference pattern

Figure 10: The upper the ﬁgure shows the case in which the

occlusion occurs at the beginning period in drawing the ‘S’

character. The lower the ﬁgure shows the case in which the

occlusion occurs during the middle period. TSCDP recog-

nizes character gestures correctly for both cases.

can be made by any kind of single-stroke sequence

projected on a two-dimensional plane. Therefore, a

reference pattern with complex shape and long dura-

tion is acceptable. Chinese kanji characters belong

to this category. It becomes even easier to recognize

complex and long reference patterns by TSCDP be-

cause they are more distinguishable from one another.

Complex reference patterns allow a large vocabu-

lary. Figure 11 shows recognition of complex Chi-

nese characters including a character “kuru” (“come”

in English), which is the last one in Figure 6(b). A set

of gesture patterns caused by various ﬁelds-of-view

of a hand is generated by non-linear time and space

deformations of the reference pattern.

Let {F(x, y)|(x,y) ∈ R} be an image of object at

a ﬁxed time t

, where R is a raster (two-dimension

pixel area) and deﬁne t ≥ t

as a time. Deﬁne a dis-

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

595

Figure 8: Recognition of an air-drawn gesture under situation the condition of a complex scene with moving objects in the

background. The scene includes people walking in the background, and the static background is a normal ofﬁce environment.

Figure 9: A reference pattern is recognized at different positions (right and down, left and up positions), each of which

corresponds to an existing similar trajectory in a video.

Figure 11: Complex Chinese characters are recognized by TSCDP.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

596

tance p(t)[cm] between a camera and an object, and

a parameter c whose value is determined by calibra-

tion. If the camera moves p(t) forward or backward

relative to the object, then the two-dimensional im-

age of an object shrinks or expands, which simple

geometric property is described by {F(x × c

p(t

)

p(t)

,y ×

p(t

)

p(t)

)|(x,y) ∈ R}, where c is regarded as a parameter

to transform a value of distance ratio to pixel size.

If the conditions of range

≤ x × c

p(t

)

p(t)

≤ 2x and

≤ y × c

p(t

)

p(t)

≤ 2y are satisﬁed, the space normal-

ization of TSCDP works well.

On the other hand, let deﬁne x(t) a pixel size of

rightward or leftward motion of the camera at time t

from x(t

) = 0, where x(t) > 0 for rightward motion

and x(t) < 0 for leftward motion, assuming no verti-

cal movement. Then the two-dimensional image of

an object expands to right or left direction and is de-

scribed by {F(x +x(t), y)|(x, y) ∈ R}. If the condition

of range

≤ x(t) ≤ 2x is satisﬁed, then the space nor-

malization of TSCDP works well.

Let F(t) be an image of the object at t with simul-

taneous combination of two kinds of a camera motion.

Then F(t) is determined by:

F(t) = {F((x+x(t)})×c

p(t

)

p(t)

,y×c

p(t

)

p(t)

)|(x,y) ∈ R}.

If the conditions of the range,

≤ (x + x(t)}) ×

p(t)

≤ 2x and

≤ y × c

p(t

)

p(t)

≤ 2y, are satisﬁed, the

space normalization of TSCDP well works.

If time shrinking or expansion occurs as a side ef-

fect of camera motion, time normalization of TSCDP

works well, scaling from half to twice. This reason-

ing is equivalent to saying that if a pixel trajectory

is included in F(t), (t ∈ [t

,t]) and also belongs to

the time-space area of Figure 5 of a reference pat-

tern, then the pixel trajectory is well recognized by

TSCDP. Otherwise the accumulated local distance S

increases depending on the size of the part of trajec-

tory out of the time-space area of Figure 5. If the in-

creased accumulated distance S is smaller than thresh-

old h, then the trajectory is well recognized. If we set

a higher threshold value h, the recognition system be-

comes more robust to largely deformed input patterns

at the cost of increasing error rate. Robustness and

error rate are traded-off in determining the threshold

value h.

Figure 12 shows that a continuously deforming

image of a gesture is well recognized in a video which

captures the gesture under changing distance from

and orientation to the camera.

6.4 Experimental Results for Isolated

Character Recognition

For recognition of isolated characters by TSCDP,

there were two types of errors, confused recognition

and missing recognition. Missing recognition can oc-

cur because, even for isolated characters, a thresh-

old value is used to determine whether or not a spot-

ting output is obtained. If all TSCDP output values

∗

,t)/(3T

) are above the threshold value h

for i = 1,2,...,N, and t ∈ (−∞,+∞), there will be no

output recognition from the input video. The recogni-

tion rates are shown in Table 1.

Table 1: Results of the ﬁrst experiment.

Result Total Subject A Subject B Subject C

Correct 62.6% 46.2% 61.5% 80.1%

Missing 5.1% 0.0% 3.8% 11.5%

Confusion 32.3% 33.8% 34.7% 18.4%

Figure 13: Confusion matrix of recognition results for iso-

lated characters.

Figure 13 shows the confusion matrix for the

recognition of isolated characters.

6.5 Experimental Results for Connected

Character Recognition

Researching recognition of connected characters by

TSCDP, there were three types of errors. The ﬁrst,

“missing (M),” means that no category was detected at

the correct time. The second, “ghost (G),” means that

an output appeared at an incorrect time. The third,

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

597

(a) starting image of the moving camera. (b) ending image of the moving camera.

Figure 12: A moving camera captures a deforming gesture caused by different distance and orientation to the camera. TSCDP

can recognize the deforming gesture.

“confusion (F),” means that a category was detected at

the correct time but the category was incorrect. Cor-

rect output, “correct (C),” means that correct output

was obtained at the correct time. We can then deter-

mine each recognition rate as follows.

• Correct rate =

(M + G + F +C)

× 100%

• Missing rate =

(M + G + F +C)

× 100%

• Ghost rate =

(M + G + F +C)

× 100%

• Confusion rate =

(M + G + F +C)

× 100%

The recognition rates are shown in Table 2, where

Ghost rate = 0%, and the confusion matrix is shown

in Figure 14.

Table 2: Results of the second experiment.

Result Total Subject A Subject B Subject C

Correct 64.4% 82.8% 62.1% 48.3%

Missing 11.1% 3.4% 17.2% 13.8%

Confusion 24.5% 13.8% 20.7% 37.9%

7 CONCLUSIONS

This study conﬁrmed that TSCDP can work well for

recognizing both isolated and connected cursive air-

drawn characters from a video. In particular, con-

nected air-drawn characters can be recognized with-

out time-segmentation in advance. Moreover, we pre-

sented several experimental results of gesture recog-

nition that demonstrate how TSCDP is free from

many constraints, including position restrictions, that

are imposed by conventional methods for realizing a

recognition system of gesture or sign language.

Figure 14: Confusion matrix of recognition results for con-

nected alphabetic hiragana and kanji characters.

REFERENCES

Alon, J. (2006). Spatiotemporal Gesture Segmentation. Dis-

sertation for Doctor of Philosophy, Boston University.

Chen, F., Fu, C., and Huang., C. (2003). Hand gesture

recognition using a real-time tracking method and hid-

den markov models. Image and Video Computing,

21(8):745–758.

Ezaki, N., Sugimoto, M., Kiyota, K., and Yamamoto, S.

(2010). Character recognition by using acceleration

sensor: Proposing a character input method using wi-

imote [in Japanese]. Meeting on Image Recognition

and Understanding, IS2–48:1094–1098.

Gao, W., Ma, J., J.Wu, and Wang, C. (2000). Sign lan-

guage recognition based on hmm/ann/dp. Interna-

tional Journal of Pattern Recognition and Artiﬁcial

Intelligence, 14(5):587–602.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

598

Horo, T. and Inaba, M. (2006). A handwriting recog-

nition system using multiple cameras [in Japanese].

Workshop on Interactive Systems and Software

(WISS2006).

Kolsch, M. and Turk, M. (2004). Robust hand detection. In

Proc. Sixth IEEE International Conference on Auto-

matic Face and Gesture Recognition, pages 614–619.

Nakai, M. and Yonezawa, H. (2009). Aerial handwrit-

ten character recognition using an acceleration sensor

[in Japanese]. Forum on Information Technology, H–

19:133–134.

Oka, R. (1998). Spotting method for classiﬁcation of real

world data. The Computer Journal, 41(8):559–565.

Oka, R. and Matsuzaki, T. (2012). Robustness for

time-spatial deformation of an occlusion realized

in time-space continuous dynamic programming [in

Japanese]. Joint Technical Meeting on Informa-

tion Processing and Innovative Industrial Systems,

27(6):873–891.

Okada, T. and Muraoka, Y. (2003). Letter input system for

handwriting gestures [in Japanese]. Transactions of

the Institute of Electronics, Information and Commu-

nication Engineers, D-II J86-D-II(7):1015–1025.

Ong, S. C. W. and Ranganath, S. (2005). Automatic sign

language analysis: A survey and the future beyond

lexical meaning. Pattern Analysis and Machine In-

telligence, 27(6):873–891.

Sato, A., Shinoda, K., and Furui, S. (2010). Sign language

recognition using time-of-ﬂight camera [in Japanese].

Meeting on Image Recognition and Understanding,

IS3–44:1861–1868.

Sclaroff, S., Betke, M., Kollios, G., Alon, J., Athitsos, V.,

Li, R., Magee, J., and Tian, T.-P. (2005). Tracking

analysis and recognition of human gestures in video.

ICDAR: Int. Conf. on Document Analysis and Recog-

nition.

Yang, M., Ahuja, N., and Tabb, M. (2002). Extraction of

2d motion trajectories and its application to hand ges-

ture recognition. Pattern Analysis and Machine Intel-

ligence, 24(8):1061–1074.

Time-segmentation-andPosition-freeRecognitionfromVideoof

Air-drawnGesturesandCharacters

599