
Self-Optimizing Algorithms for Mobile Ad Hoc Networks
based on Multiple Mobile Agents
Yasushi Kambayashi
1
, Tatsuya Shinohara
2
and Munehiro Takimoto
2
1
Department of Computer and Information Engineering, Nippon Institute of Technology, 4-1 Gakuendai, Miyashiro-machi,
Minamisaitama-gun, 345-8501 Japan
2
Department of Information Sciences, Tokyo University of Science 2641 Yamazaki, Noda 278-8510 Japan
Keywords: Mobile Ad Hoc Network, Mobile Software Agent, Multi-agent System, Multi-robot System, Self-organizing
System, Swarm Intelligence, Optimization.
Abstract: This paper presents algorithms that form optimal connecting configurations for Mobile Ad Hoc Networks
(MANETs). MANET is a computer network that is dynamically formed by autonomous mobile nodes.
Today, the communication network is one of the most important infrastructures. When it is lost by either
natural or accidental disaster, the recovery of the communication network should be one of the first
priorities. We are proposing a way of constructing an extemporized communication network on the spot by
a herd of mobile robots that communicate by wireless link. The networks we are considering are formed by
multiple relay robots; therefore the algorithms are naturally distributed ones and executed by the herd of
relay robots. The relay robots move cooperatively but without any central control. In order to collect and to
distribute enough information to coordinate the behaviours of participating relay robots, we employ mobile
software agents that we have developed and succeeded in using many applications. There are a number of
multi-robot systems that take advantage of MANET, and look for efficient use of relay robot while
maintaining connectivity. Our study contributes this line of investigation. The numerical experiments show
that our algorithms provide optimal configurations in certain cases.
1 INTRODUCTION
In the modern society, the communication network
is one of the most important infrastructures. When it
is lost by either natural or accidental disaster, the
recovery of the communication network should be
one of the first priorities. Under such an assumption
we have conducted a project that constructs an
extemporized communication network on the spot
by a herd of mobile robots that communicate by
wireless link. They are expected to form a Mobile
Ad Hoc Network.
Mobile Ad Hoc Network (MANET) is a
computer network that is dynamically formed by
autonomous mobile nodes. Such mobile nodes are
connected through wireless links without relying on
any central controller or established infrastructure.
The participating mobile nodes can freely and
dynamically self-organize into arbitrary and
temporary network topologies.
The application we have in our mind is
constructing a temporary communication network in
a contaminated area polluted by radioactive
substances or dangerous gas because of natural or
accidental disaster that prevent human activities.
Under such conditions, constructing MANET by
using a multi-robot system should be a natural
choice. It may be desirable for us to connect
arbitrary two points. For example, we may want to
connect the control centre of a nuclear power station
and a reactor with problems by using scattered
mobile robots with minimum costs so that robots can
work as long as possible without human intervention.
A multi-robot system consists of a large number
of homogeneous robots that have limited capacity,
but when combined into a group, they can generate
more complex behaviours (Parker, 2008). In multi-
robot systems, robots communicate with each other
to achieve cooperative behaviours. There are three
major advantages of multi-robot systems over single
robot systems (Stone and Veloso, 2000) (Yasuda
and Ohkura, 2005). The first is parallelism; a task
can be achieved by autonomous and asynchronous
robots in a system. The second is robustness; this is
156
Kambayashi Y., Shinohara T. and Takimoto M..
Self-Optimizing Algorithms for Mobile Ad Hoc Networks based on Multiple Mobile Agents.
DOI: 10.5220/0004818901560163
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 156-163
ISBN: 978-989-758-016-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

realized through redundancy. The system can have
more robots than required for a certain task. The
third is scalability; a robot can be added to or
removed from the system easily. We have taken
advantage of these properties.
We have implemented several multi-robot
systems such as cooperatively assemble themselves
at energy-wise optimal locations (Kambayashi et al.,
2012), and serialize themselves (Shintani et al.,
2011). For all the multi-robot systems, we have
designed and implemented multi-agent systems that
control the robot systems. A control system based
on multiple software agents can control robots
efficiently. Multi-agent systems introduced
modularity, reconfigurability and extensibility to
control systems which had been traditionally
monolithic. It has made easier the development of
control systems on distributed environments such as
multi-robot systems.
On the other hand, excessive interactions among
agents in the multi-agent system may cause
problems in multi-robot environments. In order to
mitigate the problems of excessive communication,
we have developed mobile agent methodologies for
distributed environments (Kambayashi and
Takimoto, 2005). In a mobile agent system, each
agent can actively migrate from one site to another
site. Since a mobile agent can bring the necessary
functionalities with it and perform its tasks
autonomously, it can reduce the necessity for
interaction with other sites. In the minimal case, a
mobile agent requires that the connection is
established only when it performs migration (Binder
et al., 2001).
We have achieved energy saving multi-robot
systems through multiple mobile software agents
that migrate in a herd of mobile robots to collect
information about them, as well as drive the
minimum number of them based on the collected
information. Moving software agents instead of
physical robots greatly save energy consumption.
In this paper, we propose a multi-robot system
that employs MANET through which software
agents migrate. By using the software agents, the
relay robots in MANET can cooperatively
coordinate themselves into optimal locations to
make the shortest communication route with a
minimum number of relay robots. We propose two
algorithms to form a optimal route via relay robots,
and discuss the pros and cons of the two.
The structure of the balance of this paper is as
follows. In the second section, we describe the
background of our research. In the third section, we
present the two algorithms to form optimal
configurations. In the fourth section, we present the
numerical experiments through simulations to
demonstrate the effectiveness of our algorithms and
discuss our observations. In the fifth section, we
conclude our discussions and suggest future work.
2 BACKGROUNDS
There are a number of multi-robot systems that take
advantage of MANET. Heo and Varshney
considered the sensor coverage problem for the
deployment of wireless sensor networks (Heo and
Varshney, 2003). They have proposed a distributed
algorithm for the deployment of mobile nodes, not
necessary autonomous robots, to cover a certain
region by limited number of nodes and limited
communication range. They focus on the sensor
coverage problem and did not discuss the multi-hop
relay problem of ours.
Voyles et al. introduced a new multi-hop
protocol (Voyles et al., 2009). As we have done,
they used Bluetooth ad hoc wireless communication
for use in sparse, highly volatile networks by multi-
robot system. They developed a hybrid routing
protocol, i.e. proactive and reactive routing protocol,
demonstrated a high data transfer rate and showed
low recovery time in various cases. Their protocol
could cope with frequent network failures in not-so-
good network topologies. The authors claimed that
their protocol provided the best compromise
between latency and throughput for sparse highly
volatile networks. They, however, acknowledged
that routing protocols solve only part of problems in
multi-robot systems. They were aware of the need
for methodologies for maintaining efficient
connectivity of nodes while simultaneously
achieving task goals. We believe our humble study
can contribute this line of investigation. We are not
aware of any study of creating optimal route with
minimum number of relay robots.
As Voyles et al. have done, we have employed
Bluetooth ad hoc wireless communication called
scatternet (Cuomo et al., 2004). A scatternet is a
number of interconnected piconets that supports
communication between Bluetooth-equipped devices.
Figure 1 shows a scatternet that consists of three
piconets. A piconet is the type of connection that is
formed between two or more Bluetooth-equipped
devices. Since a piconet consists of one master node
and at most seven slave nodes, it can only handle at
most eight devices. Therefore a considerably large
scale ad hoc net must be formed by using scatternet.
Scatternets can be formed when a member of one
Self-OptimizingAlgorithmsforMobileAdHocNetworksbasedonMultipleMobileAgents
157

piconet (either the master or one of the slaves) elects
to participate as a slave in a second, separate piconet.
The device participating in both piconets can relay
data between members of both ad hoc networks.
Figure 1: Three piconets construct a scatternet.
One of the most closely related previous researches
is the “chain based path formation” of swarms of
robots conducted by Nouyan and Dorigo (Nouyan
and Dorigo, 2006). The concept of robot chains
stems from Goss and Deneubourg (Goss and
Deneubourg, 1992). A similar system was
implemented by Drogoul and Ferber (Drogoul and
Ferber, 1992). As these previous approaches, in the
system of Nouyan and Dorigo, every robot in a
chain emitted a signal indicating its position in the
chain, and they utilized the “cyclic directional
patterns” in order to give the chains directionality.
Unlike our proposing system, their purpose of
the research was investigating the capabilities of the
swarm robots that were self-organizing into chains
from random positions. They have found the impact
of the two parameters which determine the rate at
which a robot aggregates into, and disaggregates
from, a chain. They have also shown that their
system scales quite well with respect to the number
of robots. They, however, did not claim any
particular application for that chain forming, and
they stated that they were interested in studying
control algorithms that allow swarm of robots to
form arbitrary shapes instead of serializing.
Our purpose, on the other hand, is improving an
already established MANET connection with
arbitrary two points with scattered mobile robots
with minimum costs.
3 ALGORITHMS
The basic concept of optimizing the arrangement of
mobile robots that relay ad hoc communication is to
serialize the relay robots, and then to make
redundant robots leave from the relay line as shown
in Figure 2.
In order to make the relay robots move to form a
line, it is necessary to obtain the vector value of each
pair of adjacent robots. In order to accomplish this
we employ a mobile software agent to travel from
the source robot (robot A) to the destination robot
(robot E) as shown in Figure 3.
Figure 2: Optimal configuration.
Figure 3: The mobile agent is created at the source robot
and travels toward the destination while obtaining the
vector values.
Assume robot A is communicating with robot E by
using ad hoc wireless communication with several
relay robots. We also assume that both of them are
engaging some tasks at their current locations and
cannot move. Each time the mobile software agent
migrates one robot to another robot (one hop); it
checks the source robot through the camera on the
destination robot and obtains the vector value from
the destination to the source robot. Therefore, when
the mobile agent arrives at the final destination robot
(robot E), it has a sequence of vector values of all
the pairs of adjacent relay robots.
Upon arriving at the destination robot, the
software agent goes back the same route from the
destination robot to the source robot, and gives the
corresponding vector values to all the relay robots as
shown in Figure 4. When the mobile agent
distributes the vector value to each corresponding
relay robot, it adjusts the vector value so that it
points to the destination node robot. When the
mobile agent arrives at the source robot where that
agent was created, and the agent completes
distributing all the vector values it has collected
during the forward travel, its task is over and
vanishes.
Figure 5 shows the vector values given by the
mobile agent. Each letter represents the end robots
end robot
relay robot
connection
A A E E
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
158
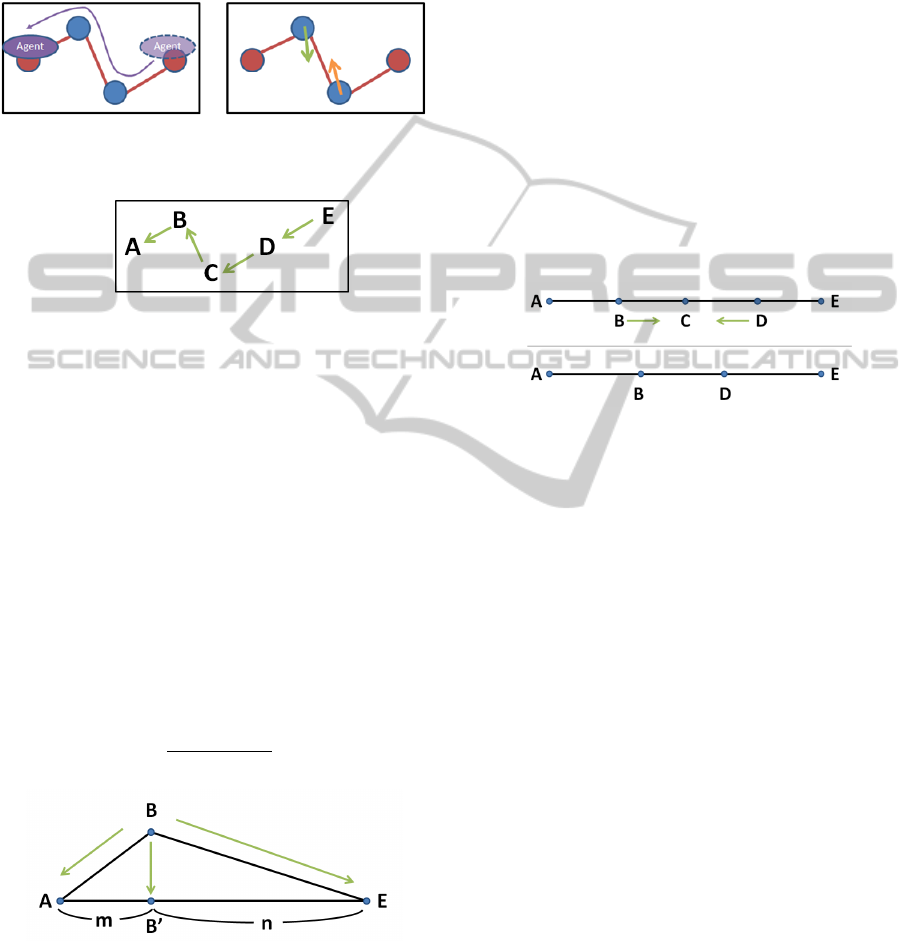
and relay robots. Robot A is the source robot where
the mobile agent was created and E is the destination
robot. Since robot A and E cannot move, we want to
make other robots B, C, and D move to form a
straight line (optimal formation) to relay the ad hoc
connection.
Figure 4: The mobile agent distributes the vector values to
all the relay robots.
Figure 5: Each robot has its vector value.
3.1 Algorithm 1: Move All the
Participants
The moving algorithm makes all the participating
robot that are relaying the communication from the
source robot, i.e. robot A, to the destination, robot E,
move to form a straight line from A to E. The
algorithm consists of two phases. The first one is to
form a straight line, and then the second phase finds
redundant relay robots.
The idea is as follows. As shown in Figure 6, the
desired straight line is AE; therefore we want to
move the relay robot at point B to point B’. In order
to achieve this requirement, we need to obtain the
vector value ′
as follows:
′
(1)
Figure 6: The first phase; a relay robot moves to an
internal dividing point.
Since
and
are known values, and m is the
number of hops from the source point of robot A and
n is the number of hops from the destination point of
robot E, it is straightforward to calculate the vector
value ′
.
When applying this algorithm to the relay robots,
all the relay robots move to the internal dividing
points on the line AE, and distances between
adjacent robots are shorten. Then some redundant
robot must be produced. Redundant robots means
two or more relay robots exist in a range of ad hoc
connection. When a relay robot recognizes it is
redundant itself, it tries to leave from the connection.
We describe the leaving algorithm in Section 3.3 in
detail. After successfully forming a straight line in
the first phase, the robots on the connection
sequence start to eliminate further redundancy in the
second phase as follows.
The second phase begins by dividing the relay
robots into roughly two groups, the left half and the
right half as shown in Figure 7.
Figure 7: The second phase; a robot in the left group
moves toward right-hand side and a robot in the right half
group moves toward left-hand side to find a redundant
robots.
The relay robots in the left half group move toward
the right hand side as far as they can maintain their
connection to the adjacent relay robots, and the relay
robots in the right half group move toward the left
hand side also as far as they can maintain their
connection, so that some relay robots can have new
and redundant connection.
When new connection is produced and a relay
robot becomes redundant, it tries to leaves from the
connection. We describe how a redundant relay
robot departs from the connection in section 3.3.
3.2 Algorithm 2: Move Minimum
Number of the Participants
Since moving all the participating relay robots are
rather inefficient, it is desirable if we can move
minimum number of robots to form the same
straight line. For this purpose, we extend the
algorithm 1 as follows. First, we number all the
relaying robots and if we have more than twice as
many robots as we need to construct a straight line
connection, we only move the even numbered robots.
If we do not have such enough robots, we choose the
least necessary number of robots from the source
A
E E
A
Self-OptimizingAlgorithmsforMobileAdHocNetworksbasedonMultipleMobileAgents
159

robot side, and move them.
Since we know the straight line distance from the
source robot to the destination robot, it is
straightforward to calculate the least number of
robots to maintain the connection.
3.3 Relay Robot’s Leaving from the
Connection
As described in the previous sections, when we have
succeeded in forming a straight line connection of
the relaying robot, we have some redundant robots.
In this section we describe how to find the redundant
relay robots, and how to make them leave from the
connection.
When the relay robots move based on the
syntheses of vector values described in the previous
section, some of them find new connections. Figure
8 shows the situation that moving relay robots (blue
ones) find a new connection, and one of them
becomes redundant.
Figure 8: A redundant robot leaves from the connection.
When a relay robot finds a new connection, it
notifies its finding to the neighbouring robots. If a
relay robot receives such notifications from both of
the adjacent robots, it recognizes it is the redundant
node of the connection (Figure 8-3). Then that relay
robot requests both of the adjacent robots the
permissions of leave (Figure 8-4), and if it receives
the acknowledgements from both of them (Figure 8-
5), it disconnects and leaves from the connection
(Figure 8-6).
When two adjacent relay robots find them
redundant and request for leave simultaneously, the
request-for-leave messages make collision each
other as shown in Figure 9. In such situation, the
two relay robots cancel their request for leave and
try again after randomly selected waiting time.
Figure 9: The collision of the request-for-leave.
Figure 10 shows another case of disconnection of relay.
In this case, the relay robot C wants to move upward to
straighten the connection A to D. But to do so, it must
leave the connection range with robot E. If it finds
connection to robot E is not active at that time, it cuts the
connection to E and moves outside of the connection
range of E, and otherwise it stays in the connection range
of E. In that case, it cannot move and stay at the current
position.
Figure 10: A relay robot disconnects to move to the
optimal location.
4 NUMERICAL EXPERIMENTS
In order to demonstrate the effectiveness of our
algorithms in a realistic environment, we have
implemented a simulator for ad hoc networks based
on multiple mobile robots, and conducted numerical
experiments. On the simulator, communication
scope, moving and rotating speed of robots, and time
lags required in agent migration and object
recognition are based on the data obtained from the
preliminary study using a herd of i-Robots Create
and Bluetooth scatternet. In the experiments, we set
the following conditions:
1. Robots are scattered in a 440×380 rectangular
field in the simulator.
2. The number of the robots is one hundred.
3. Each robot is represented as a circle that radius is
five.
4. The communication range of each robot is
seventy-five.
5. The distance that each robot can move in one
step is two.
6. The coordinates of the source and destination
robots are (10, 10) and (430, 370), respectively.
request for leave
re
q
uest for leave
find new connection
re
q
uest for leave
permission for leave
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
160
7. Their initial locations of other ninety-eight robots
are randomly decided without overlapping.
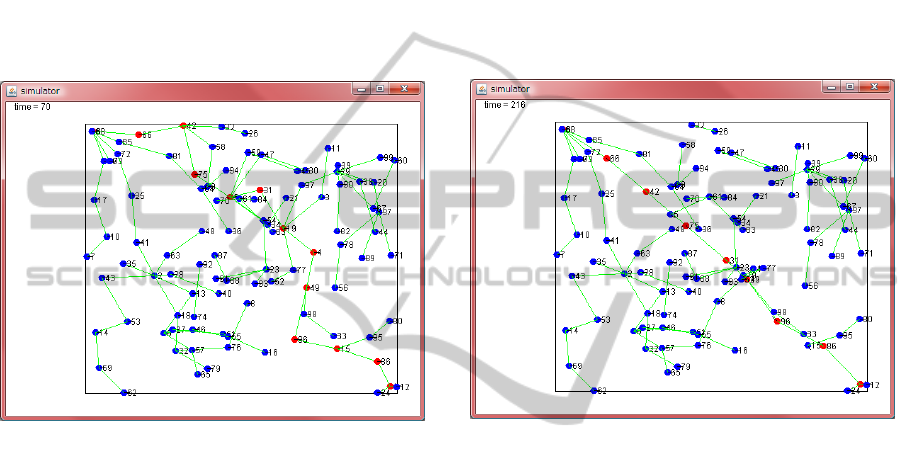
The Figure 11 shows the initial configuration.
The green lines indicate the established links of
robots via wireless ad hoc network. The red nodes
indicate the robots that are contributing to the
communication from the source node robot at the
upper left corner to the destination node robot at the
bottom right corner. Eleven robots are participating
in forming a connection from the source robot to the
destination robot. The blue nodes indicate robots
that are not participating in that particular
communication.
Figure 11: The initial configuration.
The Figure 12 shows the stable configuration after
216 steps in the simulation that employs the first
algorithm that moves all the participating robots.
We have observed that four robots out of eleven left
the connection. The report says the total distance
and total angles all the participating robot move and
rotate are 814 and 3990, respectively.
The Figure 13 shows the stable configuration
after 150 steps in the simulation that employs the
second algorithm that moves minimum number of
robots. The algorithm also produces connection
with seven robots, that is the optimal configuration
from the source robot to the destination robot, but it
moves only seven robots out of eleven. The total
distance and total angles that seven robots move and
rotate are 452 and 580, respectively.
From the observation above, it may appear that
the algorithm that moves minimum number of robots
is superior to the algorithm that moves all the
participating robots. But we have found that the
algorithm that moves minimum number of robots
has not always succeeded in reducing the number of
the relay robots minimal. The above example is the
ideal case. The Figure 14 shows the success rates of
the two algorithms. The two graphs show how
much percent could actually depart from the
connection successfully. The Figure 14a shows the
case of moving all the participating robots and
Figure 14b shows the case of moving the minimum
number of robots. The algorithm that moves all the
participants successfully remove all the redundant
robots (100%) sixty-three out of hundred patterns.
On the other hand, Figure 14b shows that the
algorithm that moves minimum number of robots
cannot achieve such successes. The algorithm failed
to remove entire redundant robots in most cases.
Figure 12: The stable configuration after moving all the
participating relay robots.
The reason why the second algorithm that moves the
minimum number of relay robots shows such low
success rate is frequent occurrences of deadlocks.
As we mentioned in the previous section, a relay
robot that have plural active connection often cannot
move. Even in one sequence of connections, we
have found frequent deadlocks. In contrast, the first
algorithm makes all the participating robots move
toward the same straight line, the robot rarely stack
in deadlocks.
The Figure 15 and 16 show the moving distances
and rotation degrees, respectively. The algorithm
that moves all the participants takes twice as long as
the algorithm that moves only minimal participants.
Also the former algorithm takes three times as much
degree as the latter algorithm. This phenomenon can
be easily understood, because the algorithm that
moves all the participants consists of two phases as
well as moves more number of robots.
In addition to the inefficiency, the algorithm that
moves all the participants has one big disadvantage.
That is the number of disconnections of network
links. We have found the algorithm that moves all
Self-OptimizingAlgorithmsforMobileAdHocNetworksbasedonMultipleMobileAgents
161
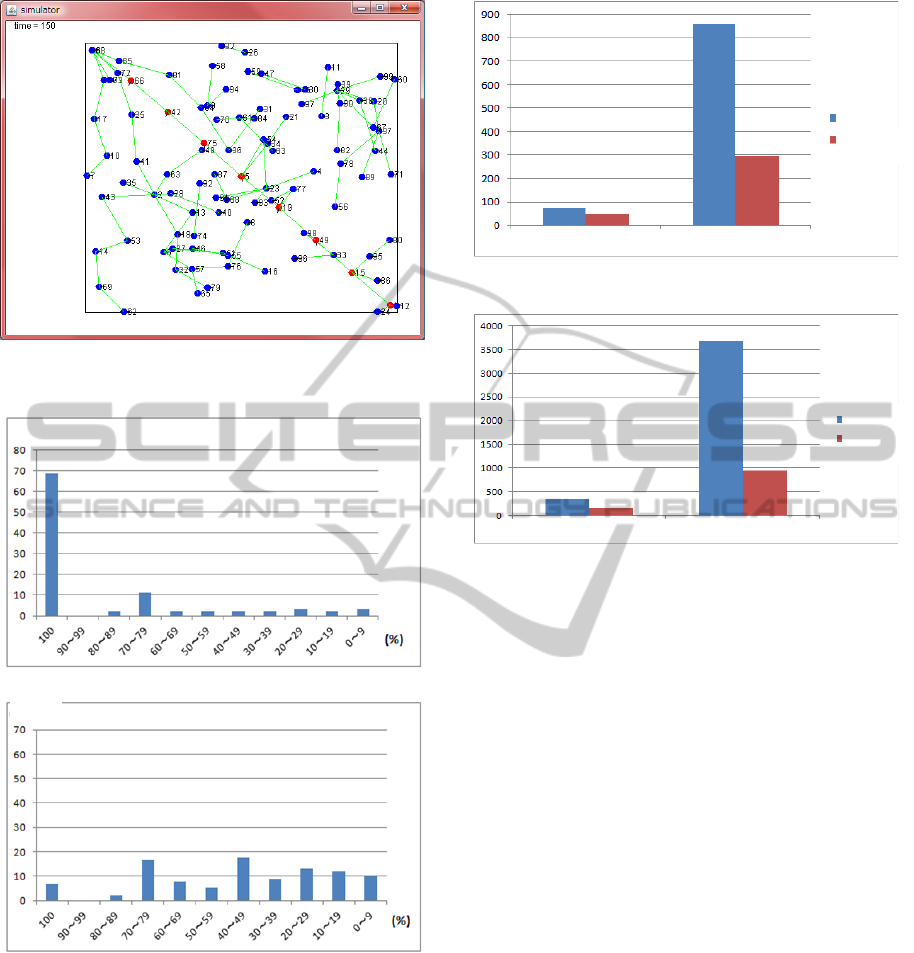
Figure 13: The stable configuration after moving the
minimum numbers of participating relay robots.
(a): The success rate of moving all the participants.
(b): The success rate of moving the minimum participants.
Figure 14: The success rates of the two algorithms.
the participants disconnect links about three times as
many as the algorithm that moves minimal
participants. Moreover, the algorithm that moves all
the participants tends to change the network
topologies and thus produces many disconnected
robots.
Therefore if we focus to provide optimal
connection only between certain two nodes, the first
algorithm that moves all the participants excels at
Figure 15: The moving distances.
Figure 16: The rotating degrees.
forming the optimal configuration. If we observe
wider scope, however, and find several ad hoc
connections request their own optimal formations
simultaneously, we may have another story. In such
cases, the side effects produced by moving relay
robots for one sequence of connections affect other
sequences of connections. The situation where
multiple ad hoc connections are active in parallel is
so complex that measuring the side effects are hard
to accomplish.
In our present study, we consider only one
sequence of connections, and have to conclude that
moving all the relay robots almost always provides
the optimal configuration, but that algorithm may
produces side effects that we yet to know how
harmful they are. We only know that the fewer the
moved relay robots, the less side effects occur.
As the future work we need to investigate the
situation where multiple connections of ad hoc
wireless network exist simultaneously. The situation
should not be difficult to handle; simply we need to
add one mobile agent for each connection. Then the
autonomous mobile software agent should all the
jobs. We believe our model is quite scalable. We
only need to polish the first algorithm so that the
entire moving cost is minimal, or to polish the
second algorithm so that the success rate is high.
all move
all move
minimum
move
minimum
move
distance per robot total distance
degrees per robot total degrees
times
times
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
162

5 CONCLUSIONS AND FUTURE
WORK
We have presented two algorithms that form optimal
configuration of ad hoc networks with multiple
mobile robots. One algorithm moves all the
participants and succeeds in configuring the optimal
connection (minimal number of relay robots) more
than sixty percent. But this algorithm naturally takes
more time to reach stable configuration and moves
more robots, and thus consumes more energy. The
other algorithm moves only minimum participants
and often fails to produce optimal connection. It
often fails to eliminate redundant robots too. But
this algorithm is naturally more efficient. For
connecting certain two nodes, the algorithm that
moves all the participants provides better result.
However, this algorithm changes the network
topologies and thus produces more disconnected
robots. When we consider the network topologies
changes a lot in multiple robot environments, and
such environments need to connect arbitrary pairs of
nodes, this side effect may cause serious problem.
Therefore we need to investigate the algorithm that
moves minimum participants and improve the
success rate of that algorithm.
An additional problem may occur in the cases of
applications of both algorithms, due to the constraint
of piconet. Since Bluetooth allows a master can
have only seven slaves, if a master already has the
maximum number of slaves, it cannot connect to a
new node even though it finds a new node as shown
in Figure 17. In order to establish a new connection,
it must cut one of the existing connections.
Selecting the most promising relay robots is a big
problem worth to investigate. We plan to pursue
this direction too.
Figure 17: Too many slaves.
REFERENCES
Binder, W., Hulaas, J. G., and Villaz, A., 2001. Portable
resource control in the j-seal2 mobile agent system. In
Proc. of the fifth international conference on
Autonomous agents, AGENTS ’01, 222–223.
Correll, N., Bachrach, J., Vickery, D., Rus, D., 2009. Ad-
hoc Wireless Network Coverage with Networked
Robots that Cannot Localize, In IEEE International
Conference on Robotics and Automation.
Cuomo, F., Melodia, T., Akyildiz, I. F., 2004. Distributed
self-healing and variable topology optimization
algorithms for QoS provisioning in scatternets, IEEE
Journal on Selected Areas in Communications, 22(7),
1220-1236.
Drogoul, A., Ferber, J., 1992. From Tom Thumb to the
dockers: Some experiments with foraging robots. In
From Animals to Animats 2. Proc. of the 2nd Int. Conf.
on Simulation of Adaptive Behavior (SAB92), MIT
Press, Cambridge, MA, 451–459.
Goss, S., Deneubourg, J.L., 1992. Harvesting by a group
of robots. In: Proc. of the 1
st
European Conf. on
Artificial Life, MIT Press, Cambridge, MA, 195–204.
Heo, N., Varshney, P. K., 2003. A Distributed Self
Spreading Algorithm for Mobile Wireless Sensor
Networks, In IEEE Wireless Communications and
Networking Conference.
Kambayashi, Y. and Takimoto, M., 2005. Higher-Order
Mobile Agents for Controlling Intelligent Robots.
International Journal of Intelligent Information
Technologies, 1(2), 28–42.
Kambayashi, Y., Yamachi, H., Takimoto, M., 2012.
Feasibility Studies of the Intelligent Cart System.
Communications in Information Science and
Management Engineering, 2(6), 1-8.
Nguyen, C. Q., Leong, B., Matson, E. T., Smith, A., .
Wachs, J. P., 2010. AWARE: Autonomous Wireless
Agent Robotic Exchange, In ICIRA 2010, 3
rd
International Conference on Intelligent Robotics and
Application, LNAI 6276, 198-208.
Poduri, S., Sukhatme, G. S., 2004. Constrained Coverage
for Mobile Sensor Networks, In IEEE International
Conference on Robotics and Automation, 165-172.
Parker, L. E., 2008. Distributed intelligence: overview of
the field and its application in multi-robot systems,
Journal of Physical Agents, 2(1), 5-14.
Nouyan, S., Dorigo, M., 2006. Chain Based Path
Formation in Swarms of Robots, In Ant Colony
Optimization and Swarm Intelligence, LNCS 4150,
120-131.
Shintani, M., Lee, S., Takimoto, M., Kambayashi, Y.,
2011. A Serialization Algorithm for Mobile Robots
Using Mobile Agents with Distributed Ant Colony
Clustering. In Knowledge-based and Intelligent
Information and Engineering Systems, (KES 2011).
LNAI 6881, 260-270.
Voyles, R. M., Bae, J., Larson, A. C., Ayad, M. A., 2009.
Wireless video sensor networks for sparse, resource
constrained, multi-robot teams, Intelligent Service
Robotics, 2(4), 235-246.
Self-OptimizingAlgorithmsforMobileAdHocNetworksbasedonMultipleMobileAgents
163
